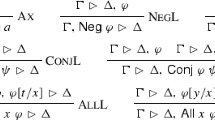Intuitionistic Podelski-Rybalchenko Theorem and Equivalence Between Inductive Definitions and Cyclic Proofs

Abstract

A cyclic proof system gives us another way of representing inductive and coinductive definitions and efficient proof search. Podelski-Rybalchenko termination theorem is important for program termination analysis. This paper first shows that Heyting arithmetic HA proves Kleene-Brouwer theorem for induction and Podelski-Rybalchenko theorem for induction. Then by using this theorem this paper proves the equivalence between the provability of the intuitionistic cyclic proof system and that of the intuitionistic system of Martin-Lof’s inductive definitions when both systems contain HA.

1 Introduction

This paper studies two subjects: intuitionistic Podelski-Rybalchenko theorem for induction, and equivalence between intuitionistic system of Martin-Löf’s inductive definitions and an intuitionistic cyclic proof system.

Podelski-Rybalchenko theorem [18] states that if a transition invariant is a finite union of well-founded relations then the transition invariant is also well-founded. This gives us good sufficient conditions for analysis of program termination [18]. Intuitionistic provability of this theorem is also interesting; if we can show this theorem is provable in some intuitionistic logical system, the theorem also gives us not only termination but also an upper bound of computation steps of a given program. For this purpose, we have to replace well-foundedness in the theorem by induction principle, since well-foundedness is a property of negation of existence and induction principle can show a property of existence. We say Podelski-Rybalchenko theorem for induction when we replace well-foundedness by induction principle in Podelski-Rybalchenko theorem. [3] shows Podelski-Rybalchenko theorem for induction is provable in intuitionistic second-order logic. [5] shows that this theorem for induction is provable in Peano arithmetic, by using the fact that Peano arithmetic can formalize Ramsey theorem. However until now it was not known whether Podelski-Rybalchenko theorem for induction is provable in some intuitionistic first-order logic. This paper will show this theorem for induction is provable in Heyting arithmetic and answer this question.

An inductive/coinductive definition is a way to define a predicate by an expression which may contain the predicate itself. The predicate is interpreted by the least/greatest fixed point of the defining equation. Inductive/coinductive definitions are important in computer science, since they can define useful recursive data structures such as lists, trees, and streams, and useful notions such as bisimulations. Inductive definitions are important also in mathematical logic, since they increase the proof theoretic strength. Martin-Löf’s system of inductive definitions given in [16] is one of the most popular systems of inductive definitions. This system has production rules for an inductive predicate, and the production rule determines the introduction rules and the elimination rules for the predicate.

[8, 11] proposed an alternative formalization of inductive definitions, called a cyclic proof system. A proof, called a cyclic proof, is defined by proof search, going upwardly in a proof figure. If we encounter the same sequent (called a bud) as some sequent we already passed (called a companion) we can stop. The induction rule is replaced by a case rule, for this purpose. The soundness is guaranteed by some additional condition, called a global trace condition, which can show the case rule decreases some measure of a bud from that of the companion. In general, for proof search, a cyclic proof system can find an induction formula in a more efficient way than Martin-Löf’s system, since a cyclic proof system does not have to choose fixed induction formulas in advance. A cyclic proof system enables us to get efficient implementation of theorem provers with inductive definitions [7, 9, 10, 12]. A cyclic proof system can also give us another logical system for coinductive predicates, since a coinductive predicate is a dual of an inductive predicate, and sequent calculus is symmetric for this dual.

[8, 11] investigated Martin-Löf’s system $\mathbf{LKID}$ of inductive definitions in classical logic for the first-order language, and the cyclic proof system ${\mathbf{CLKID}^\omega }$ for the same language, showed the provability of ${\mathbf{CLKID}^\omega }$ includes that of $\mathbf{LKID}$, and conjectured the equivalence.

As the second subject, this paper studies the equivalence for intuitionistic logic, namely, the provability of the intuitionistic cyclic proof system, called ${\mathbf{CLJID}^\omega }$, is the same as that of the intuitionistic system of Martin-Lof’s inductive definitions, called $\mathbf{LJID}$. This question is theoretically interesting, and answers will potentially give new techniques of theorem proving by cyclic proofs to type theories with inductive/coinductive types and program extraction by constructive proofs.

This paper first points out that the countermodel of [4] also shows the equivalence is false in general. Then this paper shows the equivalence is true under arithmetic, namely, the provability of ${\mathbf{CLJID}^\omega }$ is the same as that of $\mathbf{LJID}$, when both systems contain Heyting arithmetic $\mathbf{HA}$.

There are not papers that study the equivalence for intuitionistic logic or Kleene-Brouwer theorem for induction in intuitionistic first-order logic. For Podelski-Rybalchenko theorem for induction, [3] intuitionistically showed it but the paper used second-order logic.

Section 2 proves Kleene-Brouwer theorem for induction and Podelski-Rybalchenko theorem for induction. Section 3 defines $\mathbf{LJID}$ and ${\mathbf{CLJID}^\omega }$ and discuss a cyclic proof system for streams. Section 4 discusses the countermodel, defines ${\mathbf{CLJID}^\omega +\mathbf{HA}}$ and ${\mathbf{LJID}+\mathbf{HA}}$, states the equivalence theorem, and explains ideas of the equivalence proof. Section 5 discusses proof transformation and proves the equivalence theorem. Section 6 discusses related work. We conclude in Sect. 7.

2 $\mathbf{HA}$-Provable Podelski-Rybalchenko Theorem for Induction

This section will prove Podelski-Rybalchenko theorem for induction, inside Heyting arithmetic $\mathbf{HA}$. First we will prove Kleene-Brouwer theorem for induction, inside $\mathbf{HA}$. This is done by carefully using some double induction. This theorem is new. Next we will show induction for the set $\mathrm{MS}$ of monotonically-colored subsequences. Monotonically-colored subsequences are used in ordinary proof of Ramsey theorem and we will show some intuitionistic property of them. Then by applying Kleene-Brouwer theorem to a part of $\mathrm{MS}$ and some orders $>_{u,\mathrm{Left}}$ and $>_{u,\mathrm{Right}}$, we will obtain two Kleene-Brouwer relations $>_{\mathrm{KB}1,r}$ and $>_{\mathrm{KB}2,r}$ and show their induction principle. These two relations are simple but necessary preparation for the next relation. Then by applying Kleene-Brouwer theorem to some lifted tree determined by $>_{\mathrm{KB}2,r}$ and the relation $>_{\mathrm{KB}1,r}$, we will obtain a Kleene-Brouwer relation $>_{\mathrm{KB},r}$ and show its induction principle. This relation is a key of the proof. Then we will show that induction for decreasing transitive sequences is reduced to induction for Erdös trees with the relation $>_{\mathrm{KB},r}$. An Erdös tree is some set of monotonically-colored sequences and implicitly used in ordinary proof of Ramsey theorem. Since Erdös trees are in the lifted tree, by combining them, finally we will prove Podelski-Rybalchenko theorem for induction.

2.1 Kleene-Brouwer Theorem

We will show Kleene-Brouwer theorem for induction, which states that if we have both induction principle for a lifted tree (namely $\langle u\rangle *T$ for some tree T) with respect to the one-step extension relation and induction principle for relations on children, then we have induction principle for the Kleene-Brouwer relation. We can prove it by refining an ordinary proof of Kleene-Brouwer theorem for orders.

We assume Heyting arithmetic $\mathbf{HA}$ is defined in an ordinary way with constants and function symbols $0, s, +, \times$. We define $x < y$ by $\exists z.x+s z=y$ and $x \le y$ by $x=y \vee x<y$. We can assume some coding of a sequence of numbers by a number in Heyting arithmetic, because the definitions on pages 115–117 of [19] work also in $\mathbf{HA}$. We write $\langle t_0,\ldots ,t_n \rangle$ for the sequence of $t_0,\ldots ,t_n$. We also write |t|, and $(t)_u$ for the length of the sequence t, and the u-th element of the sequence t respectively. We write $*$ for the concatenation operation of sequences.

We write $>_R$ or > for a binary relation. We write $<_R$ for the binary relation of the inverse of $>_R$. For notational simplicity, we say X is a set in order to say there is some first-order formula Fx such that $x \in X \mathrel \leftrightarrow Fx$. Then we also say $t \in X$ in order to say Ft. We write $y <_R x \in X$ for $y <_R x \wedge y \in X$. We write $x \in \sigma$ when x is an element of the sequence $\sigma$. We write $U^{<\omega }$ for the set of finite sequences of elements in U. For a set S of sequences, we write $\langle u\rangle *S$ for $\{ \langle u\rangle *\sigma \ |\ \sigma \in S\}$. For a set U and a binary relation $>_R$ for U, the induction principle for $(U,>_R)$ is defined as

$$\begin{aligned}&\mathrm{Ind}(U,>_R,F) \equiv \forall x \in U((\forall y<_R x \in U.Fy) \mathbin \rightarrow Fx) \mathbin \rightarrow \forall x \in U.Fx, \\&\mathrm{Ind}(U,>_R) \equiv \mathrm{Ind}(U,>_R,F) \ \hbox {(for every formula }Fx\hbox {)}. \end{aligned}$$

For a set U a set T is called a tree of U if $T \subseteq U^{<\omega }$ and T is nonempty and closed under prefix operations. Note that the empty sequence is a prefix of any sequence. As a graph, the set of nodes is T and the set of edges is $\{ (x,y) \in T^2 \ |\ y = x *\langle u\rangle \}$. We call a set $T \subseteq U^{<\omega }$ a lifted tree of U when there are a tree $T' \subseteq U^{<\omega }$ and $r \in U$ such that $T=\langle r\rangle *T'$. We define $\mathrm{LiftedTree}(T,U)$ as a first-order formula that means T is a lifted tree of U.

For $x,y \in U^{<\omega }$ we define the one-step extension relation $x >_\mathrm{ext}y$ if $y = x * \langle u \rangle$ for some u. For a set $T \subseteq U^{<\omega }$ and $\sigma \in U^{<\omega }$, we define $T_\sigma$ as $\{ \rho \in T \ |\ \rho = \sigma * \rho ' \}$. Note that $T_\sigma$ is a subset of T. For a nonempty sequence $\sigma$, we define $\mathrm{first}(\sigma )$ and $\mathrm{last}(\sigma )$ as the first and the last element of $\sigma$ respectively.

The next lemma shows induction implies $x\not >x$. The proof is in [6].

Lemma 2.1

If $\mathbf{HA}\mathrel \vdash \mathrm{Ind}(U,>)$, then $\mathbf{HA}\mathrel \vdash \forall x,y \in U(y < x \mathbin \rightarrow y \ne x)$.

Definition 2.2

(Kleene-Brouwer Relation). For a set U, a lifted tree T of U, and a set of binary relations $>_u$ on U for every $u \in U$, we define the Kleene-Brouwer relation $>_\mathrm{KB}$ for T and $\{ (>_u) \ |\ u \in U\}$ as follows: for $x,y \in T$, $x >_\mathrm{KB}y$ if (1) $x = z * \langle u, u_1 \rangle * w_1$, $y = z * \langle u, u_2 \rangle * w_2$, and $u_1 >_u u_2$ for some $z,u,u_1,w_1,u_2,w_2$, or (2) $y = x * z$ for some $z \ne \langle \ \rangle$.

When $(>_u)$ is some fixed $(>)$ for all u, for simplicity we call the relation $(>_\mathrm{KB})$ the Kleene-Brouwer relation for T and >.

Note that $(>_\mathrm{KB})$ is a relation on T. This Kleene-Brouwer relation is slightly different from ordinary Kleene-Brouwer order for the following points: it creates a relation instead of an order, it uses a set of relations indexed by an element, and it is defined for a lifted tree instead of a tree (in order to use indexed relations).

The next theorem shows induction principle for the Kleene-Brouwer relation.

Theorem 2.3

(Kleene-Brouwer Theorem for Induction). If $\mathbf{HA}\mathrel \vdash \mathrm{LiftedTree}(T,U)$, $\mathbf{HA}\mathrel \vdash \mathrm{Ind}(T,>_\mathrm{ext})$ and $\mathbf{HA}\mathrel \vdash \forall u\in U.\mathrm{Ind}(U,>_u)$, then $\mathbf{HA}\mathrel \vdash \mathrm{Ind}(T,>_\mathrm{KB})$.

Proof

By induction on $(T,>_\mathrm{ext})$ with the induction principle $\mathrm{Ind}(T,>_\mathrm{ext})$, we will show $\forall \sigma \in T.\mathrm{Ind}(T_\sigma ,>_\mathrm{KB}).$ After we prove it, we can take $\sigma$ to be $\langle \ \rangle$ to show the theorem, since $T_{\langle \ \rangle }=T$.

Fix $\sigma \in T$ in order to show $\mathrm{Ind}(T_\sigma ,>_\mathrm{KB})$. Note that we can use induction hypothesis for every $\sigma *\langle u\rangle \in T$:

$$\begin{aligned} \mathrm{Ind}(T_{\sigma *\langle u\rangle },>_\mathrm{KB}). \end{aligned}$$

(1)

Assume

$$\begin{aligned} \forall x \in T_\sigma ((\forall y <_\mathrm{KB}x \in T_\sigma . Fy) \mathbin \rightarrow Fx) \end{aligned}$$

(2)

in order to show $\forall x \in T_\sigma .Fx$. For simplicity we write F(X) for $\forall x\in X.Fx$. Let $Gu \equiv F(T_{\sigma * \langle u \rangle })$. By $\mathrm{Ind}(U,>_{\mathrm{last}(\sigma )})$ we will show the following claim.

Claim: $\forall u \in U.Gu$.

Fix $u \in U$ in order to show Gu.

By IH for v with $>_{\mathrm{last}(\sigma )}$ we have

$$\begin{aligned} v <_{\mathrm{last}(\sigma )} u \mathbin \rightarrow F(T_{\sigma * \langle v \rangle }). \end{aligned}$$

(3)

We can show

$$\begin{aligned} \forall x\in T_{\sigma *\langle u\rangle }((\forall y<_\mathrm{KB}x \in T_{\sigma *\langle u\rangle }.Fy) \mathbin \rightarrow (\forall y <_\mathrm{KB}x \in T_\sigma . Fy)) \end{aligned}$$

(4)

as follows. Fix $x\in T_{\sigma *\langle u\rangle }$, assume

$$\begin{aligned} \forall y <_\mathrm{KB}x \in T_{\sigma *\langle u\rangle }.Fy \end{aligned}$$

(5)

and assume $y <_\mathrm{KB}x \in T_\sigma$ in order to show Fy. By definition of $>_\mathrm{KB}$, we have $y \in T_{\sigma * \langle v \rangle }$ for some $v <_{\mathrm{last}(\sigma )} u$, or $y \in T_{\sigma * \langle u \rangle }$. In the first case, Fy by (3). In the second case, Fy by (5). Hence we have shown (4).

Combining (4) with (2), we have

$$\begin{aligned} \forall x \in T_{\sigma *\langle u\rangle }((\forall y <_\mathrm{KB}x \in T_{\sigma * \langle u\rangle }.Fy) \mathbin \rightarrow F(x)). \end{aligned}$$

(6)

By IH (1) for $\sigma * \langle u \rangle$, we have $\mathrm{Ind}(T_{\sigma * \langle u \rangle }, >_\mathrm{KB})$, namely,

$$\begin{aligned} \forall x \in T_{\sigma *\langle u\rangle }((\forall y <_\mathrm{KB}x \in T_{\sigma * \langle u\rangle }.Fy) \mathbin \rightarrow Fx) \mathbin \rightarrow \forall x \in T_{\sigma *\langle u\rangle }.Fx. \end{aligned}$$

(7)

By (6), (7), $F(T_{\sigma * \langle u\rangle })$. Hence we have shown the claim.

If $y <_\mathrm{KB}\sigma \in T_\sigma$, we have $y \in T_{\sigma * \langle u\rangle }$ for some u, since $y <_\mathrm{KB}\sigma$ implies $y \ne \sigma$ by definition of $\mathrm{KB}$ and Lemma 2.1 for $>_u$. By the claim, Fy. Hence

$$\begin{aligned} \forall y<_\mathrm{KB}\sigma \in T_\sigma .Fy. \end{aligned}$$

(8)

By letting $x:=\sigma$ in (2), we have $(\forall y<_\mathrm{KB}\sigma \in T_\sigma .Fy) \mathbin \rightarrow F\sigma$. By (8), $F\sigma$. Combining it with the claim, $\forall x\in T_\sigma .Fx$. $\square$

2.2 Proof Ideas for Podelski-Rybalchenko Theorem for Induction

In this subsection we will explain proof ideas of Theorem 2.15.

A sequence $u_1>_R u_2>_R u_3 >_R \ldots$ is called transitive when $u_i >_R u_j$ for any $i<j$. We say the edge from u to v is of color R when $u >_{R} v$. A sequence is called monotonically-colored when for any element there is a color such that the edge from the element to any element after it in the sequence has the same color.

Definition 2.4

For a set U and a relation > for U, we define the set $\mathrm{DS}(U,>)$ of decreasing sequences as $\{ \langle x_0, \ldots , x_{n-1}\rangle \ |\ n \ge 0, x_i \in U, \forall i<n-1.(x_i > x_{i+1}) \}$.

We define the set $\mathrm{DT}(U,>)$ of decreasing transitive sequences by $\{ \langle x_0, \ldots , x_{n-1}\rangle \ |\ n\ge 0, x_i \in U, \forall i(\forall j \le n-1.(i < j \mathbin \rightarrow x_i > x_j)) \}$.

We define $>_{R_1\cup \ldots \cup R_k}$ as the union of $>_{R_i}$ for all $1 \le i \le k$. We define $>_{R_1+\ldots +R_k}$ as the disjoint union of $>_{R_i}$ for all $1 \le i \le k$. (Whenever we use it, we implicitly assume the disjointness is provable in $\mathbf{HA}$.)

We define $\mathrm{Monoseq}_{R_1,\ldots ,R_k}(x)$ to hold when $x = \langle x_0,\ldots ,x_{n-1}\rangle \in \mathrm{DT}(U,>_{R_1+ \ldots + R_k})$ and $\forall i<n-1.(\forall j \le n-1.(i < j \mathbin \rightarrow \displaystyle \mathop \bigwedge _{1 \le l \le k}( x_i>_{R_l} x_{i+1} \mathbin \rightarrow x_i >_{R_l} x_j)))$. Note that n may be 0.

We define $\mathrm{MS}$ as $\{ x \in \mathrm{DT}(U,>_{R_1+ \ldots + R_k}) \ |\ \mathrm{Monoseq}_{R_1,\ldots ,R_k}(x) \}$.

$\mathrm{MS}$ is the set of monotonically-colored finite sequences. Note that $\mathrm{MS}_{\langle r\rangle }$ is a subset of $\mathrm{MS}$ (by taking T and $\sigma$ to be $\mathrm{MS}$ and $\langle r\rangle$ in our notation $T_\sigma$) and a lifted tree of U for any $r \in U$.

We will show Podelski-Rybalchenko theorem for induction stating that if a transition invariant $>_{\varPi }$ is a finite union of relations $>_\pi$ such that each $\mathrm{Ind}(>_\pi ^n)$ is provable for some n, and each $(>_\pi )$ is decidable, then $\mathrm{Ind}(>_{\varPi })$ is provable.

First each $\mathrm{Ind}(>_\pi )$ is obtained by $\mathrm{Ind}(>_\pi ^n)$. Next by the decidability of each $(>_\pi )$, we can assume all of $(>_\pi )$ are disjoint to each other. For simplicity, we explain the idea of our proof for well-foundedness instead of induction principle.

Assume the relation $>_{\varPi }$ has some infinite decreasing transitive sequence

$$\begin{aligned} u_1>_{\varPi }u_2>_{\varPi }u_3 >_{\varPi }\ldots \end{aligned}$$

in order to show contradiction.

The set $\mathrm{MS}$ will be shown to be well-founded with the one-step extension relation. For a decreasing transitive sequence x of U, a lifted tree $T \in U^{<\omega }$ is called an Erdös tree of x when the elements of x are the same as elements of elements of T, every element of T is monotonically-colored, and the edges from a parent to its children have different colors. Let $\mathrm{ET}$ be a function that returns an Erdös tree of a given decreasing transitive sequence. Then we consider

$$\begin{aligned} \mathrm{ET}(\langle u_1\rangle ), \mathrm{ET}(\langle u_1,u_2\rangle ), \mathrm{ET}(\langle u_1,u_2,u_3\rangle ), \ldots . \end{aligned}$$

Define $\mathrm{MS}_{\langle r\rangle }$ as the set of sequences beginning with r in $\mathrm{MS}$. Define $>_{\mathrm{KB}1,r}$ as the Kleene-Brouwer relation for the lifted tree $\mathrm{MS}_{\langle r\rangle }$ and some left-to-right-decreasing relation on children of the lifted tree. Define $>_{\mathrm{KB}2,r}$ as the Kleene-Brouwer relation for the lifted tree $\mathrm{MS}_{\langle r\rangle }$ and some right-to-left-decreasing relation on children of the lifted tree. By Kleene-Brouwer theorem, $(>_{\mathrm{KB}1,r})$ and $(>_{\mathrm{KB}2,r})$ are well-founded. Define $\mathrm{ET}2(\langle u_1,\ldots ,u_n\rangle )$ as the $(>_{\mathrm{KB}2,u_1})$-sorted sequence of elements in $\mathrm{ET}(\langle u_1,\ldots ,u_n\rangle )$. Then consider

$$\begin{aligned} \mathrm{ET}2(\langle u_1\rangle ), \mathrm{ET}2(\langle u_1,u_2\rangle ), \mathrm{ET}2(\langle u_1,u_2,u_3\rangle ), \ldots . \end{aligned}$$

Define $>_{\mathrm{KB},r}$ as the Kleene-Brouwer relation for $>_{\mathrm{KB}1,r}$ and the set of $(>_{\mathrm{KB}2,r})$-sorted finite sequences of elements in $\mathrm{MS}_{\langle r\rangle }$. This definition is a key idea. By this definition, we can show the most difficult step in this proof:

$$\begin{aligned} \mathrm{ET}2(\langle u_1\rangle )>_{\mathrm{KB},u_1} \mathrm{ET}2(\langle u_1,u_2\rangle )>_{\mathrm{KB},u_1} \mathrm{ET}2(\langle u_1,u_2,u_3\rangle ) >_{\mathrm{KB},u_1} \ldots . \end{aligned}$$

Since $(>_{\mathrm{KB},u_1})$ is well-founded by Kleene-Brouwer theorem, we have contradiction. Hence we have shown $u_1>_{\varPi }u_2>_{\varPi }u_3 >_{\varPi }\ldots$ terminates.

In general we need classical logic to derive induction principle from well-foundedness, but the idea we have explained will work well for showing induction principle in intuitionistic logic.

2.3 Proof of Podelski-Rybalchenko Theorem for Induction

This subsection gives a proof of Podelski-Rybalchenko Theorem for Induction.

The next lemma shows that induction principle for each relation implies induction principle for monotonically-colored sequences. This lemma can be proved by refining Lemma 6.4 (1) of [3] from second-order logic to first-order logic. The proof is given in [6].

Lemma 2.5

If $\mathbf{HA}\mathrel \vdash \mathrm{Ind}(\mathrm{DT}(U,>_{R_{i}}), >_\mathrm{ext})$ for all $1 \le i \le k$, then $\mathbf{HA}\mathrel \vdash \forall r\in U.\mathrm{Ind}(\mathrm{MS}_{\langle r\rangle },>_\mathrm{ext})$.

Next we create Kleene-Brouwer relations $>_{\mathrm{KB}1,r}$ and $>_{\mathrm{KB}2,r}$ for monotonically-colored sequences beginning with r. Then we consider the set of $(>_{\mathrm{KB}2,r})$-sorted finite sequences of monotonically-colored finite sequences beginning with r. It is a lifted tree. Then, by induction principle for $\mathrm{MS}$, the lifted tree is well-founded with the one-step extension relation. The Kleene-Brouwer relation for the lifted tree and $>_{\mathrm{KB}1,r}$ gives us $>_{\mathrm{KB},r}$ for the lifted tree. Since an Erdös tree is in the lifted tree, this will later show induction principle for Erdös trees.

Definition 2.6

For $u \in U$, we define $>_{u,\mathrm{Left}}$ for U by: $u_1 >_{u,\mathrm{Left}} u_2$ if $u >_{R_j} u_1$, $u >_{R_l} u_2$, and $j<l$ for some j, l.

We define $>_{\mathrm{KB}1,r}$ for $\mathrm{MS}_{\langle r\rangle }$ as the KB relation for $\mathrm{MS}_{\langle r\rangle } \subseteq U^{<\omega }$ and $(>_{u,\mathrm{Left}}) \subseteq U^2$ for all $u \in U$.

For $u \in U$, we define $>_{u,\mathrm{Right}}$ for U by: $u_1 >_{u,\mathrm{Right}} u_2$ if $u_1 <_{u,\mathrm{Left}} u_2$.

We define $>_{\mathrm{KB}2,r}$ for $\mathrm{MS}_{\langle r\rangle }$ as the KB relation for $\mathrm{MS}_{\langle r\rangle } \subseteq U^{<\omega }$ and $(>_{u,\mathrm{Right}}) \subseteq U^2$ for all $u \in U$.

We define $>_{\mathrm{KB},r}$ for $\mathrm{DS}(\mathrm{MS}_{\langle r\rangle },>_{\mathrm{KB}2,r})_{\langle \langle r\rangle \rangle }$ as the KB relation for $\mathrm{DS}(\mathrm{MS}_{\langle r\rangle },>_{\mathrm{KB}2,r})_{\langle \langle r\rangle \rangle } \subseteq \mathrm{MS}_{\langle r\rangle }^{<\omega }$ and $>_{\mathrm{KB}1,r}$.

$>_{u,\mathrm{Left}}$ is the left-to-right-decreasing order of children of u in some ordered tree of U in which the edge label $R_i$ is put to an edge (x, y) such that $x >_{R_i} y$, each parent has at most one child of the same edge label, and children are ordered by their edge labels with $R_1< \ldots < R_k$. Similarly $>_{u,\mathrm{Right}}$ is the right-to-left-decreasing order of children of u in the ordered tree.

Definition 2.7

For $u \in U \subseteq N$, finite $T \subseteq \mathrm{MS}$ such that $\forall \rho \in T.\forall v \in \rho .(v>_{R_1+\ldots +R_k} u)$, and for $\sigma \in T$, we define the function $\mathrm{insert}$ by:

$$\begin{aligned}&\mathrm{insert}(u,T,\sigma ) = \\&\qquad \mathrm{insert}(u,T,\sigma *\langle v\rangle ) \mathrm{\ if\ } \mathrm{last}(\sigma )>_{R_i} u, v = \mu v.(\sigma *\langle v\rangle \in T \wedge \mathrm{last}(\sigma ) >_{R_i} v), \\&\qquad T \cup \{ \sigma *\langle u\rangle \} \mathrm{\ otherwise}, \end{aligned}$$

where $\mu v.F(v)$ denotes the least element v with the natural number order such that F(v). Formally $\mathrm{insert}(u,T,\sigma )=T'$ is an abbreviation of some $\mathbf{HA}$-formula $G(u,T,\sigma ,T')$. It is the same for $\mathrm{ET}$ below.

For $x \in \mathrm{DT}(U,>_{R_1+ \ldots + R_k}) - \{\langle \ \rangle \}$, we define $\mathrm{ET}(x) \subseteq \mathrm{MS}$ by

$$\begin{aligned}&\mathrm{ET}(\langle u\rangle ) = \{ \langle u\rangle \}, \\&\mathrm{ET}(x * \langle u\rangle ) = \mathrm{insert}(u,\mathrm{ET}(x),\langle \mathrm{first}(x)\rangle ) {\ \mathrm if\ } x \ne \langle \ \rangle . \end{aligned}$$

Note that $\mathrm{insert}(u,T,\sigma )$ adds a new element u to the set T at some position below $\sigma$ to obtain a new set. $\mathrm{ET}(x)$ is an Erdös tree obtained from the decreasing transitive sequence x.

The next lemma (1) states a new element is inserted at a leaf. It is proved by induction on the number of elements in T. The claim (2) states that edges from a parent to its children have different colors. It is proved by induction on the length of x.

Lemma 2.8

(1) For $u \in U$, $T \subseteq \mathrm{MS}$, and $\sigma \in T$, if $u \notin \rho$ for all $\rho \in T$, $\sigma = \langle x_0,\ldots ,x_{n-1}\rangle$, $x_i >_{R_j} x_{i+1}$ implies $x_i >_{R_j} u$ for all $i<n-1$, and $\mathrm{insert}(u,T,\sigma )=T'$, then there is some $\rho \in T_\sigma$ such that $\rho *\langle u\rangle \in \mathrm{MS}$, $T'=T + \{\rho *\langle u\rangle \}$, and $\rho *\langle u\rangle$ is a maximal sequence in $T'$.

(2) If $\sigma *\langle u,u_1\rangle *\rho _1, \sigma *\langle u,u_2\rangle *\rho _2 \in \mathrm{ET}(x)$, $u >_{R_i} u_1$, and $u >_{R_i} u_2$, then $u_1=u_2$.

Definition 2.9

For $x \in \mathrm{DT}(U,>_{R_1+ \ldots + R_k}) - \{\langle \ \rangle \}$, we define

$$\begin{aligned} \mathrm{ET}2(x) \equiv \langle x_0,\ldots ,x_{n-1}\rangle \end{aligned}$$

where $\{x_0,\ldots ,x_{n-1}\} = \mathrm{ET}(x)$ and $\forall i<n-1.(x_i >_{\mathrm{KB}2,\mathrm{first}(x)} x_{i+1})$.

Note that $>_{\mathrm{KB}2,\mathrm{first}(x)}$ is a total order on $\mathrm{ET}(x)$ by Lemma 2.8 (2). $\mathrm{ET}2(x)$ is the decreasing sequence of all nodes in the Erdös tree $\mathrm{ET}(x)$ ordered by $>_{\mathrm{KB}2,\mathrm{first}(x)}$.

The next lemma shows $\mathrm{ET}2$ is monotone. It is the key property of reduction in Lemma 2.11.

Lemma 2.10

$\mathbf{HA}\mathrel \vdash \forall r \in U.\forall x,y \in \mathrm{DT}(U,>_{R_1+ \ldots + R_k})_{\langle r\rangle }. (x>_\mathrm{ext}y \mathbin \rightarrow \mathrm{ET}2(x) >_{\mathrm{KB},r} \mathrm{ET}2(y))$.

Proof

Fix $r \in U$ and $x,y \in \mathrm{DT}(U,>_{R_1+ \ldots + R_k})_{\langle r\rangle }$ and assume $x >_\mathrm{ext}y$. Let $y = x * \langle u\rangle$. Then $\mathrm{ET}(y)=\mathrm{insert}(u,\mathrm{ET}(x),\langle r\rangle )$. By Lemma 2.8 (1), we have $\sigma$ such that $\mathrm{ET}(y) = \mathrm{ET}(x) + \{ \sigma *\langle u\rangle \}$. Then we have two cases:

Case 1. $\mathrm{last}(\mathrm{ET}2(x)) >_{\mathrm{KB}2,r} \sigma *\langle u\rangle$.

Then $\mathrm{ET}2(y) = \mathrm{ET}2(x) *\langle \sigma *\langle u\rangle \rangle$. By definition, $\mathrm{ET}2(x) >_{\mathrm{KB},r} \mathrm{ET}2(y)$.

Case 2. $\sigma *\langle u\rangle >_{\mathrm{KB}2,r} \tau$ for some $\tau \in \mathrm{ET}2(x)$.

Let $\rho$ be the next element of $\sigma *\langle u\rangle$ in $\mathrm{ET}2(y)$. Then $\mathrm{ET}2(x) = \alpha * \langle \rho \rangle * \beta$ and $\mathrm{ET}2(y) = \alpha * \langle \sigma *\langle u\rangle ,\rho \rangle * \beta$. By definition of $\mathrm{ET}2$, $\sigma *\langle u\rangle >_{\mathrm{KB}2,r} \rho$. Since $\sigma *\langle u\rangle$ is maximal in $\mathrm{ET}(y)$ by Lemma 2.8 (1), there is no $\alpha \ne \langle \ \rangle$ such that $\sigma *\langle u\rangle *\alpha = \rho$. Hence $\sigma *\langle u\rangle <_{\mathrm{KB}1,r} \rho$. Hence $\mathrm{ET}2(x) >_{\mathrm{KB},r} \mathrm{ET}2(y)$. $\square$

The next lemma shows that induction for decreasing transitive sequences is reduced to induction for Erdös trees with $>_{\mathrm{KB},r}$.

Lemma 2.11

$\mathbf{HA}\mathrel \vdash \forall r \in U.\mathrm{Ind}(\mathrm{ET}2(\mathrm{DT}(U,>_{R_1+ \ldots + R_k})_{\langle r\rangle }), >_{\mathrm{KB},r})$ implies $\mathbf{HA}\mathrel \vdash \mathrm{Ind}(\mathrm{DT}(U,>_{R_1+ \ldots + R_k}), >_\mathrm{ext})$.

Proof sketch

In order to show $\mathrm{Ind}(\mathrm{DT}(U,>_{R_1+ \ldots + R_k}), >_\mathrm{ext})$ for F, define $Gy \equiv \forall z \in \mathrm{DT}(z \ne \langle \ \rangle \mathbin \rightarrow \mathrm{ET}2(z)=y \mathbin \rightarrow Fz)$ and use $\mathrm{Ind}(\mathrm{ET}2(\mathrm{DT}(U,>_{R_1+ \ldots + R_k})_{\langle r\rangle }), >_{\mathrm{KB},r})$ for G and Lemma 2.10. The proof is in [6]. $\square$

The next lemma shows induction holds when we restrict the universe. The proof is in [6].

Lemma 2.12

$\mathbf{HA}\mathrel \vdash \mathrm{Ind}(U,>)$ and $\mathbf{HA}\mathrel \vdash V \subseteq U$ imply $\mathbf{HA}\mathrel \vdash \mathrm{Ind}(V,>)$.

The next lemma shows induction is implied from induction for decreasing sequences. The proof is in [6].

Lemma 2.13

$\mathbf{HA}\mathrel \vdash \mathrm{Ind}(\mathrm{DS}(U,>), >_\mathrm{ext})$ implies $\mathbf{HA}\mathrel \vdash \mathrm{Ind}(U, >)$.

The next lemma shows induction for a power of a relation implies induction for the relation. The proof is in [6].

Lemma 2.14

$\mathbf{HA}\mathrel \vdash \mathrm{Ind}(U,>^n)$ implies $\mathbf{HA}\mathrel \vdash \mathrm{Ind}(U,>)$.

Define

$$\begin{aligned}&\mathrm{Trans}(U,>_R) \equiv \forall xyz \in U(x>_R y \wedge y>_R z \mathbin \rightarrow x>_R z), \\&\mathrm{Decide}(U,>_R) \equiv \forall xy \in U(x>_R y \vee \lnot (x>_R y)). \end{aligned}$$

The next theorem states that if some powers of relations $>_{R_i}$ have induction principle, $>_{R_i}$ are decidable and their union is transitive, then the union has induction principle. This theorem is the same as Theorem 6.1 in [5] except $\mathbf{HA}$ and the decidability condition $\mathrm{Decide}(U,>_{R_i})$.

Theorem 2.15

(Podelski-Rybalchenko Theorem for Induction). If $\mathbf{HA}\mathrel \vdash \mathrm{Ind}(U,>_{R_1}^{n_1})$, $\mathbf{HA}\mathrel \vdash \mathrm{Decide}(U,>_{R_1})$, ..., $\mathbf{HA}\mathrel \vdash \mathrm{Ind}(U,>_{R_k}^{n_k})$, $\mathbf{HA}\mathrel \vdash \mathrm{Decide}(U,>_{R_k})$, and $\mathbf{HA}\mathrel \vdash \mathrm{Trans}(U, >_{R_1 + \ldots + R_k})$, then $\mathrm{Ind}(U, >_{R_1 + \ldots + R_k})$.

Proof

We will discuss in $\mathbf{HA}$.

By Lemma 2.14, we can replace $n_i$ by 1 and obtain $\mathrm{Ind}(U,>_{R_i})$. In order to obtain disjoint relations, we define $>_{R_1'}$ as $>_{R_1}$ and $>_{R_{i+1}'}$ as $(>_{R_{i+1}})-(>_{R_1'}) - \ldots - (>_{R_i'})$. Then $(>_{R_1'})$, ..., $(>_{R_k'})$ are disjoint and $\forall xy \in U(x>_{R_1\cup \ldots \cup R_k} y \mathbin \rightarrow x >_{R_1'+\ldots +R_k'} y)$ by $\mathrm{Decide}(U,>_{R_i})$ for $1 \le i \le k$. Since $(>_{R_i'}) \subseteq (>_{R_i})$, $\mathrm{Ind}(U, >_{R_i'})$. For simplicity, from now on we write $>_{R_i}$ for $>_{R_i'}$ in this proof. We will show $\mathrm{Ind}(U, >_{R_1+\ldots +R_k})$.

From $\mathrm{Ind}(U,>_{R_i})$, by replacing induction on elements by induction on sequences, we have $\mathrm{Ind}(\mathrm{DT}(U,>_{R_i}),>_\mathrm{ext})$ for $1 \le i \le k$. By Lemma 2.5, we have $\forall r\in U.\mathrm{Ind}(\mathrm{MS}_{\langle r\rangle }, >_\mathrm{ext})$. Apparently $\forall u\in U.\mathrm{Ind}(U,>_{u,\mathrm{Left}})$. By taking U to be U, T to be $\mathrm{MS}_{\langle r\rangle }$, and $>_u$ to be $>_{u,\mathrm{Left}}$ in Theorem 2.3 for $>_{\mathrm{KB}1,r}$, we have $\forall r\in U.\mathrm{Ind}(\mathrm{MS}_{\langle r\rangle }, >_{\mathrm{KB}1,r})$. By Theorem 2.3 for $>_{\mathrm{KB}2,r}$, we have $\forall r\in U.\mathrm{Ind}(\mathrm{MS}_{\langle r\rangle }, >_{\mathrm{KB}2,r})$ similarly. By replacing induction on elements by induction on sequences, we have $\forall r\in U.\mathrm{Ind}(\mathrm{DS}(\mathrm{MS}_{\langle r\rangle },>_{\mathrm{KB}2,r}),>_\mathrm{ext})$. Since $\mathrm{DS}(\mathrm{MS}_{\langle r\rangle },>_{\mathrm{KB}2,r})_{\langle \langle r\rangle \rangle }$ is a subset of $\mathrm{DS}(\mathrm{MS}_{\langle r\rangle }, >_{\mathrm{KB}2,r})$, from Lemma 2.12, we have $\forall r\in U.\mathrm{Ind}(\mathrm{DS}(\mathrm{MS}_{\langle r\rangle },>_{\mathrm{KB}2,r})_{\langle \langle r\rangle \rangle },>_\mathrm{ext})$. By taking T to be $\mathrm{DS}(\mathrm{MS}_{\langle r\rangle },>_{\mathrm{KB}2,r})_{\langle \langle r\rangle \rangle }$, U to be $\mathrm{MS}_{\langle r\rangle }$, and $(>_u)$ to be $(>_{\mathrm{KB}1,r})$ in Theorem 2.3 for $>_{\mathrm{KB},r}$, we have $\forall r\in U.\mathrm{Ind}(\mathrm{DS}(\mathrm{MS}_{\langle r\rangle },>_{\mathrm{KB}2,r})_{\langle \langle r\rangle \rangle }, >_{\mathrm{KB},r})$. This is a key step of this proof. Since $\mathrm{ET}2(\mathrm{DT}(U,>_{R_1+ \ldots + R_k})_{\langle r\rangle }) \subseteq \mathrm{DS}(\mathrm{MS}_{\langle r\rangle },>_{\mathrm{KB}2,r})_{\langle \langle r\rangle \rangle }$, by Lemma 2.12, we have $\forall r\in U.\mathrm{Ind}(\mathrm{ET}2(\mathrm{DT}(U,>_{R_1+ \ldots + R_k})_{\langle r\rangle }), >_{\mathrm{KB},r})$. By Lemma 2.11, $\mathrm{Ind}(\mathrm{DT}(U,>_{R_1+ \ldots + R_k}), >_\mathrm{ext})$. By $\mathrm{Trans}(U, >_{R_1 + \ldots + R_k})$, $\mathrm{DT}(U,>_{R_1+ \ldots + R_k})$ is $\mathrm{DS}(U,>_{R_1+ \ldots + R_k})$. Hence we have $\mathrm{Ind}(\mathrm{DS}(U,>_{R_1+ \ldots + R_k}), >_\mathrm{ext})$. From Lemma 2.13, by replacing induction on sequences by induction on elements, we have $\mathrm{Ind}(U, >_{R_1+ \ldots + R_k})$. $\square$

3 Cyclic Proofs

3.1 Intuitionistic Martin-Löf’s Inductive Definition System $\mathbf{LJID}$

We define an intuitionistic Martin-Löf’s inductive definition system, called $\mathbf{LJID}$.

The language of $\mathbf{LJID}$ is determined by a first-order language with inductive predicate symbols. The logical system $\mathbf{LJID}$ is determined by production rules for inductive predicate symbols. These production rules mean that the inductive predicate denotes the least fixed point defined by these production rules.

We assume the first order terms $t,u, \ldots$. We assume $\forall x$ and $\exists y$ are less tightly connected than other logical connectives. To save space, we sometimes write Pxy and Fxy for P(x, y) and F(x, y).

For example, the production rules of the inductive predicate symbol N are

These production rules mean that N denotes the smallest set closed under 0 and s, namely the set of natural numbers.

The inference rules of $\mathbf{LJID}$ contains the introduction rules and the elimination rules for inductive predicates, determined by the production rules. These rules describe that the predicate actually denotes the least fixed point. In particular, the elimination rule describes the induction principle.

For example, the above production rules give the introduction rules

and the elimination rule

This elimination rule describes mathematical induction principle.

Fig. 1.

Inference rules

The inference rules are given in Fig. 1 where for $(P_i\ R)$ we assume the production rule

and for $(\mathrm{Ind}\ P_j)$ we assume a predicate $F_i$ for each $P_i$ and the minor premises are defined as

$$\begin{aligned} {\varGamma }, Q_{i1}\overrightarrow{u}_{i1}, \ldots , Q_{in_i}\overrightarrow{u}_{in_i}, F_1\overrightarrow{t}_{i1}, \ldots , F_{im_i}\overrightarrow{t}_{im_i} \mathrel \vdash F_i\overrightarrow{t}_i \end{aligned}$$

for each production rule

Note that the antecedents and the succedents are sets and the succedent is empty or a formula.

The system $\mathbf{LJID}$ is the same as the system obtained from classical Martin-Löf’s inductive definition system $\mathbf{LKID}$ defined in [11] by restricting every sequent to intuitionistic sequents and replacing $(\mathbin \rightarrow L)$, $(\vee R)$, and $(\mathrm{Ind}\ P_j)$ accordingly. The provability of the system $\mathbf{LJID}$ is the same as that of the natural deduction system given in [16].

3.2 Cyclic Proof System ${\mathbf{CLJID}^\omega }$

An intuitionistic cyclic proof system, called ${\mathbf{CLJID}^\omega }$, is defined as the system obtained from classical cyclic proof system ${\mathbf{CLKID}^\omega }$ defined in [11] by restricting every sequent to intuitionistic sequents and replacing $(\mathbin \rightarrow L)$ and $(\vee R)$ in the same way as $\mathbf{LJID}$. Note that the global trace condition in ${\mathbf{CLJID}^\omega }$ is the same as that in ${\mathbf{CLKID}^\omega }$ (Definition 5.5 of [11]).

Namely, the inference rules of ${\mathbf{CLJID}^\omega }$ are obtained from $\mathbf{LJID}$ by replacing $(\mathrm{Ind}P_j)$ by

where the case distinctions are

$$\begin{aligned} {\varGamma },\overrightarrow{u}=\overrightarrow{t}, Q_1\overrightarrow{u}_1, \ldots , Q_n\overrightarrow{u}_n, P_1\overrightarrow{t}_1, \ldots , P_m\overrightarrow{t}_m \mathrel \vdash {\varDelta }\end{aligned}$$

for each production rule

A cyclic proof in ${\mathbf{CLJID}^\omega }$ is defined by (1) allowing a bud as an open assumption and requiring a companion for each bud, (2) requiring the global trace condition.

The global trace condition [8, 10] is the condition that for every infinite path in the infinite unfolding of a given cyclic proof, there is a trace that passes main formulas of case rules infinitely many times. The global trace condition ensures that when we think some measure by counting case rules, the measure of a bud is smaller than that of the companion. For example, in the next example the companion (a) uses Px0y, but the bud (a) uses Px0y where x is $x'$ and $x' < x$, so their actual meanings are different even though they are of the same form. The global trace condition guarantees the soundness of a cyclic proof system.

An example of a cyclic proof (trivial steps are omitted) is as follows:

where the mark (a) denotes the bud-companion relation, and the production rules are

Note that the predicate P is addition on natural numbers and the proof is, essentially, deriving the arithmetic identity $x + 0 = x$.

We call an atomic formula an inductive atomic formula when its predicate symbol is an inductive predicate symbol.

3.3 Cyclic Proofs for Coinductive Predicates

This subsection shows how we can use a cyclic proof system to formalize coinductive predicates. Since a coinductive predicate is a dual of an inductive predicate, and sequent calculus is symmetric for this dual, we can construct a cyclic proof system for coinductive predicates. For example, for stream predicates we can define a cyclic proof system $\mu \nu \mathrm{LK}$ from ${\mathbf{CLKID}^\omega }$ as follows:

• (1) Add function symbols $\mathrm{head}$, $\mathrm{tail}$, and the pair $\langle \ , \ \rangle$ with the axioms $\langle x,y\rangle =\langle x',y'\rangle \mathbin \rightarrow x=x' \wedge y=y'$ and $x=\langle \mathrm{head}\ x,\mathrm{tail}\ x\rangle$, and a coinductive predicate symbol P with its coproduction rule

  

  which means P is defined coinductively by this rule. Note that P represents the set of streams $\langle x_0, \langle x_1, \langle x_2, \langle \ldots \rangle \rangle \rangle$ such that $Q(x_i,\langle x_{i+1}, \langle x_{i+2}, \langle \ldots \rangle \rangle )$ for all i.

• (2) Add the inference rules $(P\ R)$ and $(\mathrm{Case}\ P)$ in the same way as ${\mathbf{CLKID}^\omega }$, namely,

  

• (3) We call an atomic formula a coinductive atomic formula when its predicate symbol is a coinductive predicate symbol. We define a cotrace as a sequence of coinductive atomic formulas in the succedents of a path such that two atomic formulas are related by an inference rule in a similar way to a trace defined in [11]. The global trace and cotrace condition is the condition that for every infinite path in the infinite unfolding of a given cyclic proof, the path contains either a trace that passes main formulas of case rules infinitely many times, or a cotrace that passes main formulas of rules $(P\ R)$ infinitely many times.

• (4) A cyclic proof is a preproof that satisfies the global trace and cotrace condition.

Example. We define the bit stream predicate $\mathrm{BS}$ by the following coproduction rules:

where $\mathrm{Bit}$ is an ordinary predicate symbol with the axiom $\mathrm{Bit}\ x \mathrel \leftrightarrow x=0 \vee x=1$. The inference rules from this production rule are:

Then we can show $x=\langle 0,x\rangle \mathrel \vdash \mathrm{BS}\ x$, namely, the zero stream is a bit stream, as follows (trivial steps are omitted):

where (a) denotes the bud-companion relation.

The cyclic proof system $\mu \nu \mathrm{LK}$ is sound for the standard model.

Theorem 3.1

If a sequent is provable in $\mu \nu \mathrm{LK}$, then it is true in the standard model where a coinductive predicate is interpreted as the greatest fixed point that satisfies the coproduction rules.

Proof sketch

We add an ordinary predicate symbol ${\tilde{Q}}$ with the axiom ${\tilde{Q}}yx \mathrel \leftrightarrow \lnot Qyx$ and add an inductive predicate symbols ${\tilde{P}}$ with the production rules

In the standard model, P is the greatest solution of the equation

$$\begin{aligned} Px \mathrel \leftrightarrow \exists yx'(x=\langle y,x'\rangle \wedge Qyx' \wedge Px') \end{aligned}$$

and ${\tilde{P}}$ is the least solution of the equation

$$\begin{aligned} {\tilde{P}}x \mathrel \leftrightarrow {\tilde{Q}}(\mathrm{head}\ x)(\mathrm{tail}\ x) \vee {\tilde{P}}(\mathrm{tail}\ x). \end{aligned}$$

By putting $\lnot$ on both sides of the equation for P and taking y and $x'$ to be $\mathrm{head}\ x$ and $\mathrm{tail}\ x$, we can show $\lnot P$ is a solution of the equation for ${\tilde{P}}$. Hence ${\tilde{P}}x \mathbin \rightarrow \lnot Px$ is true. In the same say by putting $\lnot$ on both sides of the equation for ${\tilde{P}}$, and using $x=\langle \mathrm{head}x, \mathrm{tail}x\rangle$, we can show $\lnot {\tilde{P}}$ is a solution of the equation for P. Hence $\lnot {\tilde{P}}x \mathbin \rightarrow Px$ is true. Therefore ${\tilde{P}}x \mathrel \leftrightarrow \lnot Px$ is true.

We define a transformation $(\ )^-$ for a sequent and a proof, in order to replace P by ${\tilde{P}}$. For a sequent J, we define $J^-$ by replacing P by $\lnot {\tilde{P}}$ and then moving an atomic formula $\lnot {\tilde{P}}t$ of the antecedent to ${\tilde{P}}t$ of the succedent and moving an atomic formula $\lnot {\tilde{P}}t$ of the succedent to ${\tilde{P}}t$ of the antecedent.

Given a cyclic proof $\pi$, we define $\pi ^-$ by replacing each sequent J by $J^-$ and then replacing $(P\ R)$ by

and replacing $(\mathrm{Case}P)$ by

Then a cotrace in $\pi$ corresponds to a trace in $\pi ^-$. Hence $\pi ^-$ is a cyclic proof of $J^-$ in ${\mathbf{CLKID}^\omega }$ when $\pi$ is a cyclic proof of J in $\mu \nu \mathrm{LK}$. By the soundness of ${\mathbf{CLKID}^\omega }$, $J^-$ is true in the standard model. Since ${\tilde{P}}x \mathrel \leftrightarrow \lnot Px$ is true, J is true in the standard model where P is interpreted as the greatest fixed point. $\square$

4 Equivalence Between $\mathbf{LJID}$ and ${\mathbf{CLJID}^\omega }$

This section studies the equivalence between ${\mathbf{CLJID}^\omega }$ and $\mathbf{LJID}$.

4.1 Countermodel and Addition of Heyting Arithmetic

This subsection gives a countermodel and adds arithmetic to the logical systems.

The counterexample given in [4] also shows that the equivalence between ${\mathbf{CLJID}^\omega }$ and $\mathbf{LJID}$ does not hold in general, because the proof of the statement H in [4] is actually in ${\mathbf{CLJID}^\omega }$, and $\mathbf{LJID}$ does not prove H since $\mathbf{LKID}$ does not prove H. This gives us the following theorem (it is not new in the sense [4] immediately implies it).

Theorem 4.1

There are some signature and some set of production rules for which the provability of ${\mathbf{CLJID}^\omega }$ is not the same as that of $\mathbf{LJID}$.

There is a possibility of the equivalence under some conditions. We will show the equivalence holds by adding arithmetic to both systems.

We add arithmetic to both $\mathbf{LJID}$ and ${\mathbf{CLJID}^\omega }$.

Definition 4.2

${\mathbf{CLJID}^\omega +\mathbf{HA}}$ and ${\mathbf{LJID}+\mathbf{HA}}$ are defined to be obtained from ${\mathbf{CLJID}^\omega }$ and $\mathbf{LJID}$ by adding Heyting arithmetic. Namely, we add constants and function symbols $0, s, +, \times$, the inductive predicate symbol $N$, the productions for $N$, and Heyting axioms:

4.2 Equivalence Theorem

In this subsection we state the equivalence theorem and explains proof ideas.

First we assume a new inductive predicate symbol $P'$ for each inductive predicate symbol P and define the production rules of $P'$ in the same way as [5].

Definition 4.3

We define the production rule of $P'$

for each production rule of P

where $v,v_1,\ldots ,v_m$ are fresh variables.

We write ${\mathbf{LJID}+\mathbf{HA}}+({\varSigma },{\varPhi })$ for the system ${\mathbf{LJID}+\mathbf{HA}}$ with the signature ${\varSigma }$ and the set ${\varPhi }$ of production rules. Similarly we write ${\mathbf{CLJID}^\omega +\mathbf{HA}}+({\varSigma },{\varPhi })$. For simplicity, in ${\varPhi }$ we write only P for the set of production rules for P. We define ${\varSigma }_N = \{0,s,+,\times ,<,N\}$ and ${\varPhi }_N = \{N\}.$ We write $P''$ for $(P')'$.

The next theorem shows the equivalence of ${\mathbf{LJID}+\mathbf{HA}}$ and ${\mathbf{CLJID}^\omega +\mathbf{HA}}$ with signatures.

Theorem 4.4

(Equivalence of ${\mathbf{LJID}+\mathbf{HA}}$ and ${\mathbf{CLJID}^\omega +\mathbf{HA}}$). Let ${\varSigma }= {\varSigma }_N \cup \{\overrightarrow{Q},\overrightarrow{P}, \overrightarrow{P}'\}$ and ${\varPhi }= {\varPhi }_N \cup \{ \overrightarrow{P}, \overrightarrow{P}'\}$. Then the provability of ${\mathbf{CLJID}^\omega +\mathbf{HA}}+({\varSigma },{\varPhi })$ is the same as that of ${\mathbf{LJID}+\mathbf{HA}}+({\varSigma },{\varPhi })$.

We explain our ideas of proofs of this theorem. [5] shows the equivalence between classical systems by using classical Podelski-Rybalchenko theorem for induction. This proof goes well even if we replace classical systems by intuitionistic systems except that we have to replace classical Podelski-Rybalchenko theorem for induction by intuitionistic Podelski-Rybalchenko theorem for induction. Since we proved intuitionistic Podelski-Rybalchenko theorem for induction in Theorem 2.15, by combining them, we can show the equivalence between $\mathbf{LJID}$ and ${\mathbf{CLJID}^\omega }$.

5 Proof Transformation

This section gives the proof of the equivalence. More detailed discussions are given in [6]. We define proof transformation from ${\mathbf{CLJID}^\omega +\mathbf{HA}}$ to ${\mathbf{LJID}+\mathbf{HA}}$. First we will define stage numbers and path relations, and then define proof transformation using them.

For notational convenience, we assume a cyclic proof ${\varPi }$ in this section. Let the buds in ${\varPi }$ be $J_{1i} \ (i \in I)$ and the companions be $J_{2j} \ (j \in K)$. Assume $f:I \rightarrow K$ such that the companion of a bud $J_{1i}$ is $J_{2,f(i)}$.

5.1 Stage Numbers for Inductive Definitions

In this subsection, we define and discuss stage transformation.

We introduce a stage number to each inductive atomic formula so that the argument of the formula comes into the inductive predicate at the stage of the stage number. This stage number will decrease by a progressing trace. A proof in ${\mathbf{LJID}+\mathbf{HA}}$ will be constructed by using the induction on stage numbers.

First we give stage transformation of an inductive atomic formula. We assume a fresh inductive predicate symbol $P'$ for each inductive predicate symbol P and we call it a stage-number inductive predicate symbol. $P'(\overrightarrow{t},v)$ means that the element $\overrightarrow{t}$ comes into P at the stage v. We transform $P(\overrightarrow{t})$ into $\exists vP'(\overrightarrow{t},v)$. We call a variable v a stage number of $\overrightarrow{t}$ when $P'(\overrightarrow{t},v)$. $P(\overrightarrow{t})$ and $\exists vP'(\overrightarrow{t},v)$ will become equivalent by inference rules introduced by the transformation of production rules. We call $P'(\overrightarrow{t},v)$ a stage-number inductive atomic formula.

Secondly we give stage transformation of a production rule. We transform the production of P into the production of $P'$ given in Definition 4.3.

Next we give the stage transformation of a sequent. For given fresh variables $\overrightarrow{v}$, we transform a sequent J into $J^\circ _{\overrightarrow{v}}$ defined as follows. We define ${\varGamma }^\bullet$ as the set obtained from ${\varGamma }$ by replacing $P(\overrightarrow{t})$ by $\exists vP'(\overrightarrow{t},v)$. For fresh variables $\overrightarrow{v}$, we define $({\varGamma })^\circ _{\overrightarrow{v}}$ as the sequent obtained from ${\varGamma }^\bullet$ by replacing the i-th element of the form $\exists vP'(\overrightarrow{t},v)$ in the sequent ${\varGamma }^\bullet$ by $P'(\overrightarrow{t},v_i)$. We define $({\varGamma }\mathrel \vdash {\varDelta })^\bullet$ by ${\varGamma }^\bullet \mathrel \vdash {\varDelta }^\bullet$, and define $({\varGamma }\mathrel \vdash {\varDelta })^\circ _{\overrightarrow{v}}$ by $({\varGamma })^\circ _{\overrightarrow{v}} \mathrel \vdash {\varDelta }^\bullet$.

We write $(a_i)_{i \in I}$ for the sequence of elements $a_i$ where i varies in I. We extend the notion of proofs by allowing open assumptions. We write ${\varGamma }\mathrel \vdash _{\mathbf{CLJID}^\omega +\mathbf{HA}}{\varDelta }$ with assumptions $(J_i)_{i \in I}$ when there is a proof with assumptions $(J_i)_{i \in I}$ and the conclusion ${\varGamma }\mathrel \vdash {\varDelta }$ in ${\mathbf{CLJID}^\omega +\mathbf{HA}}$.

Definition 5.1

In a path $\pi$ in a proof, we define $\mathrm{Ineq}(\pi )$ as the set of the forms $v > v'$ and $v = v'$ for any stage numbers $v,v'$ eliminated by every case distinction in $\pi$.

The proof of the next proposition gives stage transformation of a proof into a proof of the stage transformation of the conclusion of the original proof. We write ${\varPi }^\circ$ for the stage transformation of ${\varPi }$.

Proposition 5.2

(Stage Transformation). For any fresh variables $\overrightarrow{v}$, if ${\varGamma }\mathrel \vdash _{\mathbf{CLJID}^\omega +\mathbf{HA}}{\varDelta }$ with assumptions $({\varGamma }_i \mathrel \vdash {\varDelta }_i)_{i \in I}$ without any buds, then for some fresh variables $(\overrightarrow{v}_i)_{i \in I}$ we have $({\varGamma })^\circ _{\overrightarrow{v}} \mathrel \vdash _{\mathbf{CLJID}^\omega +\mathbf{HA}}{\varDelta }^\bullet$ with assumptions $(\mathrm{Ineq}(\pi _i),({\varGamma }_i)^\circ _{\overrightarrow{v}_i} \mathrel \vdash {\varDelta }_i^\bullet )_{i \in I}$ without any buds, where $\pi _i$ is the path from the conclusion to the assumption $({\varGamma }_i)^\circ _{\overrightarrow{v}_i} \mathrel \vdash {\varDelta }_i^\bullet$.

5.2 Path Relation

In this section, we will introduce path relations and discuss them.

We assume a subproof ${\varPi }_j$ of ${\varPi }$ such that it does not have buds, its conclusion is $J_{2j}$ and its assumptions are $J_{1i} \ (i \in I_j)$.

For J in ${\varPi }^\circ _j$, we define $\widetilde{J}$ as $\langle v_1,\ldots ,v_k \rangle$ where J is ${\varGamma }^\circ _{v_1\ldots v_k} \mathrel \vdash {\varDelta }^\bullet$.

For a path $\pi$ from the conclusion to an assumption in ${\varPi }_j^\circ$, we write ${\check{\pi }}$ for the corresponding path in ${\varPi }$. We extend this notation to a finite composition of $\pi$’s. By the correspondence $(\check{\ })$, a stage-number inductive atomic formula in ${\varPi }^\circ _j$ corresponds to an inductive atomic formula in ${\varPi }$, and a path, a trace, and a progressing trace in ${\varPi }^\circ _j$ correspond to the same kind of objects in ${\varPi }$.

Definition 5.3

For a finite composition $\pi$ of paths in $\{ {\varPi }_j^\circ \ |\ j \in K\}$ such that ${\check{\pi }}$ is a path in the infinite unfolding of ${\varPi }$, we define the path relation $\tilde{>}_{\pi }$ by

$$\begin{aligned} x \tilde{>}_{\pi } y \equiv |x|=|\widetilde{J}_2| \wedge |y|=|\widetilde{J}_1| \wedge \displaystyle \mathop \bigwedge _{F(q_1,q_2)} (x)_{q_2} > (y)_{q_1} \wedge \displaystyle \mathop \bigwedge _{G(q_1,q_2)} (x)_{q_2} = (y)_{q_1} \end{aligned}$$

where $J_1$ and $J_2$ are the top and bottom sequents of $\pi$ respectively, ${\check{J}}_1$ and ${\check{J}}_2$ are those of the path ${\check{\pi }}$, $F(q_1,q_2)$ is that there is some progressing trace from the $q_2$-th atomic formula in ${\check{J}}_2$ to the $q_1$-th atomic formula in ${\check{J}}_1$, $G(q_1,q_2)$ is that there is some non-progressing trace from the $q_2$-th atomic formula in ${\check{J}}_2$ to the $q_1$-th atomic formula in ${\check{J}}_1$.

We define $B_1$ as the set of paths from conclusions to assumptions in ${\varPi }^\circ _j \ (j \in K)$. We define B as the set of finite compositions of elements in $B_1$ such that if $\pi \in B$ then ${\check{\pi }}$ is a path in the infinite unfolding of ${\varPi }$.

Definition 5.4

For $\pi \in B$, define $x >_{\pi } y$ by

$$\begin{aligned} x>_{\pi } y \equiv (x)_0=j \wedge (y)_0=f(i) \wedge (x)_1 \tilde{>}_{\pi } (y)_1, \end{aligned}$$

where $J_{1i}$ is the top sequent of ${\check{\pi }}$, and $J_{2j}$ is the bottom sequent of ${\check{\pi }}$.

Note that $(\, )_0$ and $(\, )_1$ are operations for a number that represents a sequence of numbers defined in Sect. 3. The first element is a companion number.

Lemma 5.5

$\{ >_{\pi } \ |\ \pi \in B \}$ is finite.

Proof

Define $C_n$ as $\{ >_{\pi _1\ldots \pi _m} \ |\ m \le n, \pi _i \in B_1 \}$. Since $>_{\pi }$ is a relation on $N \times N^{\le p}$ where p is the maximum number of inductive atomic formulas in the antecedents of ${\varPi }$, there is L such that $|C_n| \le L$ for all n. Then we have the least n such that $C_{n+1}=C_n$. Then $|\{ >_{\pi } \ |\ \pi \in B \}|=|C_n|$. $\square$

The next lemma is the only lemma that uses the global trace condition.

Lemma 5.6

For all $\pi \in B$, there is $n>0$ such that $\mathrel \vdash _\mathbf{HA}\mathrm{Ind}(U,>_\pi ^n)$.

We define $>_{\varPi }$ as $\bigcup \{ >_{\pi } \ |\ \pi \in B \}$. Note that $>_{\varPi }$ is transitive, since the top sequent of $\pi _1$ is the bottom sequent of $\pi _2$ by the first element, and $((>_{\pi _1}) \circ (>_{\pi _2})) \subseteq (>_{\pi _1\pi _2})$.

5.3 Proof Transformation

This section gives proof transformation.

The next lemma shows we can replace (Case) rules of ${\mathbf{CLJID}^\omega +\mathbf{HA}}$ by (Ind) rules of ${\mathbf{LJID}+\mathbf{HA}}$.

Lemma 5.7

If there is a proof with some assumptions and without any buds in ${\mathbf{CLJID}^\omega +\mathbf{HA}}$, then there is a proof of the same conclusions with the same assumptions in ${\mathbf{LJID}+\mathbf{HA}}$.

The next is a key lemma and shows each bud in a cyclic proof is provable in ${\mathbf{LJID}+\mathbf{HA}}$, which is proved by using Theorem 2.15.

Lemma 5.8

For every bud J of a proof in ${\mathbf{CLJID}^\omega +\mathbf{HA}}$ and fresh variables $\overrightarrow{v}$, $(J)^\circ _{\overrightarrow{v}}$ is provable in ${\mathbf{LJID}+\mathbf{HA}}$.

The next is the main proposition stating that a cyclic proof is transformed into an $({\mathbf{LJID}+\mathbf{HA}})$-proof with stage-number inductive predicates.

Proposition 5.9

If a sequent J is provable in ${\mathbf{CLJID}^\omega +\mathbf{HA}}+({\varSigma }_N \cup \{ \overrightarrow{P} \}, {\varPhi }_N \cup \{ \overrightarrow{P} \})$, then J is provable in ${\mathbf{LJID}+\mathbf{HA}}+({\varSigma }_N \cup \{N', \overrightarrow{P}, \overrightarrow{P}' \}, {\varPhi }_N \cup \{ \overrightarrow{P}, \overrightarrow{P}' \})$ where $N', \overrightarrow{P}'$ are the stage-number inductive predicates of $N, \overrightarrow{P}$.

The next shows conservativity for stage-number inductive predicates.

Proposition 5.10

(Conservativity of $\varvec{N'}$ and $\varvec{P''}$). Let ${\varSigma }= {\varSigma }_N \cup \{\overrightarrow{Q},\overrightarrow{P}, \overrightarrow{P}'\}$, ${\varPhi }= {\varPhi }_N \cup \{ \overrightarrow{P}, \overrightarrow{P}'\}$, ${\varSigma }' = {\varSigma }\cup \{N',\overrightarrow{P}''\}$, and ${\varPhi }' = {\varPhi }\cup \{N', \overrightarrow{P}''\}$. Then ${\mathbf{LJID}+\mathbf{HA}}+({\varSigma }',{\varPhi }')$ is conservative over ${\mathbf{LJID}+\mathbf{HA}}+({\varSigma },{\varPhi })$.

Proof of Theorem 4.4. (1) ${\mathbf{LJID}+\mathbf{HA}}+({\varSigma },{\varPhi })$ to ${\mathbf{CLJID}^\omega +\mathbf{HA}}+({\varSigma },{\varPhi })$.

For this claim, we can obtain a proof from the proof of Lemma 7.5 in [11] by restricting every sequent into intuitionistic sequents and replacing $\mathbf{LKID}+({\varSigma },{\varPhi })$ and ${\mathbf{CLKID}^\omega }+({\varSigma },{\varPhi })$ by $\mathbf{LJID}+({\varSigma },{\varPhi })$ and ${\mathbf{CLJID}^\omega }+({\varSigma },{\varPhi })$ respectively.

(2) ${\mathbf{CLJID}^\omega +\mathbf{HA}}+({\varSigma },{\varPhi })$ to ${\mathbf{LJID}+\mathbf{HA}}+({\varSigma },{\varPhi })$.

Let ${\varSigma }' = {\varSigma }\cup \{N',\overrightarrow{P}''\}$ and ${\varPhi }' = {\varPhi }\cup \{N', \overrightarrow{P}''\}$. Assume J is provable in ${\mathbf{CLJID}^\omega +\mathbf{HA}}+({\varSigma },{\varPhi })$. By Proposition 5.9, J is provable in ${\mathbf{LJID}+\mathbf{HA}}+({\varSigma }',{\varPhi }')$. By Proposition 5.10, J is provable in ${\mathbf{LJID}+\mathbf{HA}}+({\varSigma },{\varPhi })$. $\square$

6 Related Work

The conjecture 7.7 in [11] (also in [8]) is that the provability of $\mathbf{LKID}$ is the same as that of ${\mathbf{CLKID}^\omega }$. In general, the equivalence was proved to be false in [4], by showing a counterexample. However, if we restrict both systems to only the natural number inductive predicate and add Peano arithmetic to both systems, the equivalence was proved to be true in [20], by internalizing a cyclic proof in $\mathrm ACA_0$ and using some results in reverse mathematics. [5] proved that if we add Peano arithmetic to both systems, ${\mathbf{CLKID}^\omega }$ and $\mathbf{LKID}$ are equivalent, namely the equivalence is true under arithmetic, by showing arithmetical Ramsey theorem and Podelski-Rybalchenko theorem for induction.

This paper shows that similar results as shown in [5] hold for intuitionistic logic, namely, the provability of $\mathbf{LJID}$ is the same as that of ${\mathbf{CLJID}^\omega }$ if we add Heyting arithmetic to both systems.

The results of this paper immediately give another proof to the equivalence under arithmetic for classical logic shown in [5] by using the fact ${\varGamma }\mathrel \vdash _{{\mathbf{CLKID}^\omega +\mathbf{PA}}} {\varDelta }$ implies $E,{\varGamma },\lnot {\varDelta }\mathrel \vdash _{{\mathbf{CLJID}^\omega +\mathbf{HA}}}$ for some finite set E of excluded middles.

By taking $\overrightarrow{Q}$ and $\overrightarrow{P}$ to be empty in Theorem 4.4, we have conservativity of ${\mathbf{CLJID}^\omega +\mathbf{HA}}$ over ${\mathbf{LJID}+\mathbf{HA}}$ with only the inductive predicate N, which answers the question (iv) in Sect. 7 of [20].

[15] presented the first logical system for inductive/coinductive predicates. [17] also gave a similar system. They are both based on a finite system with unfold and fold, and limited to propositional logic. [21] showed the completeness of the system by using a cyclic proof system but it is also limited to propositional logic. [2, 14] investigated cyclic proof systems for inductive/coinductive predicates. [1, 13] also used cyclic proof systems for inductive/coinductive predicates to show some completeness results. But these systems are all limited to propositional logic.

7 Conclusion

We have first shown intuitionistic Podelski-Rybalchenko theorem for induction in HA, and we have secondly shown the provability of the intuitionistic cyclic proof system is the same as that of the intuitionistic system of Martin-Lof’s inductive definitions when both systems contain HA. We have also constructed a cyclic proof system $\mu \nu \mathrm{LK}$ for stream predicates.

One future work would be to construct a cyclic proof system for coinductive predicates in a general way and show the equivalence between the cyclic proof system and other logical systems for coinductive predicates.