Abstract
Bisimulation and bisimilarity are fundamental notions in comparing state-based systems. Their extensions to a variety of systems have been actively pursued in recent years, a notable direction being quantitative extensions. In this paper we present an abstract categorical framework for such extended (bi)simulation notions. We use coalgebras as system models and fibrations for organizing predicates—following the seminal work by Hermida and Jacobs—but our focus is on the structural aspect of fibrational frameworks. Specifically we use morphisms of fibrations as well as canonical liftings of functors via Kan extensions. We apply this categorical framework by deriving some known properties of the Hausdorff pseudometric and approximate bisimulation in control theory.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
In the study of transition systems, bisimulation relations are a fundamental concept, and their categorical study revealed the importance of coalgebras. One approach to characterise bisimilarity is via liftings of the coalgebra functor along fibrations [12], which are a well-established framework to attach relational structures on categories for modelling transition systems and programming languages [14].
Recently, there is emerging interest in quantitative analysis of transition systems. Behavioural metrics were introduced in [5, 7] to refine bisimilarity for probabilistic transition systems. Metrics give a real number for each pair of states in a transition system, while a relation can only provide a bit for each pair (whether the pair is in the relation or not). Therefore a metric can indicate a degree to which the behaviour of two states differ, whereas a bisimilarity relation can only indicate whether or not those behaviours differ. From this observation, a common desideratum for behavioral metrics associated with coalgebras is that two states should have distance 0 if and only if they are bisimilar.
Bisimilarity and behavioural metrics are also analogous on a categorical level. Behavioural metrics were recently shown to be constructible from liftings of the coalgebra functor to categories of (pseudo)metrics [2, 3], similar to how Hermida-Jacobs bisimulations are constructed from liftings of a functor to the category of relations. This type of construction is known generally as a coalgebraic predicate and can be performed when a lifting of the coalgebra functor is known.
These developments present two natural issues. The first is an open-ended quest for liftings of functors in general fibrations. These liftings are the rare ingredient in forming coalgebraic predicates, so having a variety of liftings in a variety of fibrations allows us to express more coalgebraic predicates. The second issue is more recent and concerns the desired relationship between behavioural metrics and bisimilarity mentioned above. Given some liftings in different fibrations, is there a relationship between the liftings we can use to verify a relationship between the coalgebraic predicates they define on a given coalgebra?
The main contributions of this paper pertain to these two issues:
-
We propose two methods to lift functors along fibrations, both of which generalise existing constructions. The first is the codensity lifting of endofunctors, generalising Baldan et al.’s Kantorovich lifting [3] to arbitrary fibrations. This lifting also represents a further development of the codensity lifting of monads [15]. The second is the construction of an enriched left Kan extension using the canonical symmetric monoidal closed structure [17] on the total category in fibrations. This generalises Balan et al.’s construction [2] of enriched left Kan extension for quantale-enriched small categories.
Apart from these lifting methods, we derive several methods to combine existing liftings. Using these methods, we construct the Hausdorff metric as the pushforward of the lifting of the list functor along a particular transformation.
-
We propose the use of predicate morphisms to translate between these liftings. We use these translations to provide facilities for establishing relationships between the coalgebraic predicates provided by these liftings on coalgebras. We illustrate the utility of this approach with two examples. First, we demonstrate the translation of approximate functions to \(\epsilon \)-approximate relations, which is the key technical tool used in control theory. Second, we translate metrics to relations to show the kernels of many behavioural metrics are bisimilarity relations.
Outline. In Sect. 2, we recall the important technical background for this work, particularly focusing on a class of fibrations where each fibre category is a lattice. In Sect. 3, we recall the construction of Hermida-Jacobs bisimulations and general coalgebraic predicates. As mentioned above, these require a lifting of a functor. Existence of such liftings is not guaranteed, and in Sect. 4 we present a few generalizations of extant techniques for producing liftings in particular fibrations to our more general class of fibrations. Finally, in Sect. 5, we use so-called predicate morphisms to establish relationships between coalgebraic predicates, focusing on deriving approximate functions from \(\epsilon \)-approximate relations and deriving bisimilarity as the kernel of behavioural metrics.
2 Background
In this paper, we are interested in finding data about a wide variety of state-based transition systems. This data comes in a variety of types: relations, unary predicates, and pseudometrics are frequently found in the literature. Data of a particular type can also satisfy a variety of properties. For example, we are interested in both a relation consisting of the states with exactly the same behaviours, and a relation where the behaviours of the first member in the pair is a subset of the behaviours of the second member of the pair.
We capture these degrees of flexibility with three largely orthogonal categorical abstractions. First, we use coalgebras as a means of modeling many kinds of transition systems. Second, fibrations represent the types of data we are interested in deriving about the states of a coalgebra. Finally, functor liftings together with a property of fibrations allow us to model the different ways the same type of data may be created. We review each of these concepts separately here.
We assume familiarity with basic category theory, but not necessarily with the theory of fibrations.
2.1 Coalgebras
Coalgebras are our tool of choice for modeling state-based transition systems. Given a \(\mathbf{Set}\) endofunctor F, an F-coalgebra is a pair (I, f) consisting of a set I and a function \(f: I \rightarrow FI\). The set is often called the carrier of the coalgebra, while the function provides the transition structure of the coalgebra.
This pair is usually interpreted as a transition system under the following scheme. The (object part of the) functor F is thought of as an operation which sends a set of states to the set of all possible transition structures on that set. The set I is the set of states of a transition system. Under this interpretation, FI is then set of all the possible transition structures available using the set of states I, so the transition structure map \(f: I\rightarrow FI\) assigns one of these possible transition structures to every state in I.
A coalgebra morphism \(\phi : (I, f) \rightarrow (J, g)\) is a function on the underlying state sets \(\phi : I \rightarrow J\) which respects the transitions in the source coalgebra, meaning \(g\circ \phi = F\phi \circ f\). F-coalgebras together with their morphisms form a category we denote by \(\mathbf{Coalg}(F)\).
By varying the functor F, we can capture a wide variety of transition system types, including deterministic and nondeterministic finite automata, Mealy and Moore machines, probabilistic transition systems, Markov decision processes, Segala systems and many more. For more background on the theory of coalgebra, we recommend consulting [20].
2.2 Fibrations
A fibration over a category \(\mathbb {B}\) is a functor \(\pi : \mathbb {E}\rightarrow \mathbb {B}\) with a cartesian lifting property. We will describe this property later, but intuitively, it allows us to take the inverse image of objects in \(\mathbb {E}\) along morphisms in \(\mathbb {B}\). The source category of the fibration, \(\mathbb {E}\), is referred to as the “total category” and the target is the “base category”.
Often the total category of a fibration is depicted vertically above the base category and language referencing this physical configuration is common. An object or morphism \(\dot{a}\) in \(\mathbb {E}\) is above or over an object or morphism a in \(\mathbb {B}\) means \(\pi \dot{a} = a\). The collection of objects and morphisms above an object I and the \(\mathrm{id}_I\) morphism is called the fibre over I. Each of these fibres is itself a subcategory of \(\mathbb {E}\), denoted by \(\mathbb {E}_I\).
Now we discuss the cartesian lifting property. In a fibrationFootnote 1 over \(\mathbb {B}\), for every morphism \(f: I \rightarrow J\) in \(\mathbb {B}\) and every object Y in \(\mathbb {E}\) above J, there is a morphism \(\dot{f}: f^*Y \rightarrow Y\) such that \(\dot{f}\) is above f (hence \(f^*Y\) is above I). This morphism is called a cartesian lifting of f with Y and is further required to satisfy the following universal property: for all morphisms \(g: K \rightarrow I\) in \(\mathbb {B}\) and \(\dot{h}: Z \rightarrow Y\) in \(\mathbb {E}\) above \(f\circ g\), there is a unique morphism \(\dot{g}: Z \rightarrow f^*Y\) above g such that \(\dot{h} = \dot{f}\circ \dot{g}\).
The operation sending Y to \(f^*Y\) is often called pullback.Footnote 2
Pullback also sends morphisms in \(\mathbb {E}_J\) to morphisms in \(\mathbb {E}_I\) by the universal property. Straightforward checks show that the assignment \(Y\mapsto f^*Y\) extends to a functor \(f^*:\mathbb {E}_J\rightarrow \mathbb {E}_I\). When \(g^*f^*=(f\circ g)^*\) and \(\mathrm{id}_I^*=\mathrm{Id}_{\mathbb {E}_I}\) holds, we say that the fibration is split.
A functor \(\pi \) is a cofibration if \(\pi ^{op}:\mathbb {E}^{op}\rightarrow \mathbb {B}^{op}\) is a fibration, and bifibration if \(\pi \) and \(\pi ^{op}\) are fibrations. Pullback in \(\pi ^{op}\) is denoted by \(f_*\), and called pushforward. In a bifibration, the pullback \(f^*\) is a right adjoint to pushforward \(f_*\) [14, Lemma 9.1.2].
A common scenario encountered in the study of fibrations is that each fibre \(\mathbb {E}_I\) has a categorical structure, say X, and pullback functors preserve these fibrewise structures. When this is the case, we say that the fibration has fibred X. For instance, a fibration \(\pi :\mathbb {E}\rightarrow \mathbb {B}\) has fibred final objects if (1) each fibre \(\mathbb {E}_I\) has a final object, and (2) for any morphism \(f:I\rightarrow J\), the pullback functor \(f^*:\mathbb {E}_J\rightarrow \mathbb {E}_I\) preserves final objects. The fibrewise structure and the structure on the total category often have a close relationship. We state it next for the case X = “limit”.
Theorem 1
([14]). Let \(\pi :\mathbb {E}\rightarrow \mathbb {B}\) be a fibration and \(\mathbb {D}\) be a category. If \(\mathbb {B}\) has limits of shape \(\mathbb {D}\), and \(\pi \) has fibred limits of shape \(\mathbb {D}\), then \(\mathbb {E}\) also has limits of shape \(\mathbb {D}\).
The dual version of this theorem also holds, replacing fibration with cofibration, limit with colimit and pullback with pushforward.
We also mention the preservation of fibrations by functor-category construction:
Theorem 2
For any fibration \(\pi :\mathbb {E}\rightarrow \mathbb {B}\) and category \(\mathbb {C}\), \(\pi \circ -:[\mathbb {C},\mathbb {E}]\rightarrow [\mathbb {C},\mathbb {B}]\) is also a fibration.
In this work, we are interested in state-based transition systems. Hence, the fibrations we are most interested in have \(\mathbb {B}= \mathbf{Set}\). Indeed, most of the total categories we are interested in are sets equipped with some extra structure, such as sets with relations or sets with a metric. In these cases, the forgetful functor is usually a fibration.
Example 3
The forgetful functors from the following categories to \(\mathbf{Set}\) are fibrations:
-
\(\mathbf{Pre}\) is the category of preorders and monotone functions between them.
-
\(\mathbf{ERel}\) is the category of endorelations. An object is a pair (I, R) of a set I and a relation \(R \subseteq I\times I\). Morphisms are functions which preserve the relation, meaning \(f: (I, R) \rightarrow (J, S)\) is a function \(f: I \rightarrow J\) such that \(i~R~i'\) implies \(f(i)~S~f(i')\).
-
\(\mathbf{RERel}\) is the category of \(\mathbb {R}^+\)-indexed endorelations.Footnote 3 That is, an object is a pair (I, R) of \(I\in \mathbf{Set}\) and a \(\mathbb {R}^+\)-indexed family \(\{R_\epsilon \}_{\epsilon \in \mathbb {R}^+}\) of endorelations on I monotone in the index, so \(\delta \le \epsilon \) implies \(R_\delta \subseteq R_\epsilon \). Morphisms are required to preserve the relation at each value \(\epsilon \), meaning \(i~R_\epsilon ~i'\) implies \(f(i)~S_\epsilon ~f(i')\) for all \(\epsilon \).
-
\(\mathbf{BVal}\) is the category of all \(\mathbb {R}^+\)-valued binary endorelations. Objects in this category are pairs (I, r) of a set I together with a function \(r: I\times I \rightarrow \mathbb {R}^+\), with no constraints. Morphisms in this category are required to be non-expansive, so \(f: (I, r) \rightarrow (J, s)\) satisfies \(s(f(i), f(i')) \le r(i, i')\) for all \(i, i' \in I\).
-
\(\mathbf{PMet}_b\) is the full subcategory of \(\mathbf{BVal}\) consisting of b-bounded pseudometric spaces, for a fixed bound \(b\in (0,\infty ]\).Footnote 4 An extended pseudometric is an \(\infty \)-bounded pseudometric, and the category of extended pseudometrics is called \(\mathbf{EPMet}\).
-
\(\mathbf{Top},\mathbf{Meas}\) are the categories of all topological/measurable spaces and continuous/measurable functions between them, respectively.
-
\(\mathbb {V}\text {-}\mathbf{Cat}\), with a commutative quantale \(\mathbb {V}\), is the category of small \(\mathbb {V}\)-categories and \(\mathbb {V}\)-functors between them. The forgetful functor extracts the object part of small \(\mathbb {V}\)-categories. This category is used in [2] as a generalisation of metric spaces.
Technically, a fibration is a functor, particularly the forgetful functor in the examples above. In these examples, however, the functor is relatively unremarkable, so we will abuse terminology slightly and refer to the fibration by the name of the total category.
Cartesian morphisms in \(\mathbf{ERel}\) preserve and reflect their source relation, in \(\mathbf{RERel}\) they preserve and reflect the relation at each index, and in \(\mathbf{BVal}\) and \(\mathbf{PMet}_b\) they are isometries, replacing the inequality in the condition for non-expansiveness with equality.
2.3 \(\mathbf{CLat}_\wedge \)-Fibrations Over \(\mathbf{Set}\)
In this paper, we focus on the fibrations over \(\mathbf{Set}\) such that (1) each fibre category is a complete lattice and (2) pullbacks preserve all meets in fibres. Such fibrations bijectively correspond to functors of type \(\mathbf{Set}^{op}\rightarrow \mathbf{CLat}_\wedge \) via the Grothendieck construction, where the codomain is the category of complete lattices and meet-preserving functions between them. Following [1, Sect. 4.3], we call such fibrations \(\mathbf{CLat}_\wedge \)-fibrations over \(\mathbf{Set}\), or simply \(\mathbf{CLat}_\wedge \)-fibrations in this paper. This is a restricted class of topological functors to \(\mathbf{Set}\) [13], where each fibre category is a poset.
There are indeed many examples of \(\mathbf{CLat}_\wedge \)-fibrations over \(\mathbf{Set}\), covering a wide range of mathematical objects, including preorders, predicates, relations, pseudometrics, topologies, \(\sigma \)-fields and so on. In particular, every fibration listed in Example 3 is a \(\mathbf{CLat}_\wedge \)-fibration.
We introduce a notation: for objects \(X,Y\in \mathbb {E}\) in a \(\mathbf{CLat}_\wedge \)-fibration \(\pi : \mathbb {E}\rightarrow \mathbf{Set}\) and a function \(f:\pi X\rightarrow \pi Y\), by \(f:X\mathbin {\dot{\rightarrow }}Y\) we mean the sentence: “there exists a (necessarily unique) \(\dot{f}:X\rightarrow Y\) such that \(\pi \dot{f}=f\)”. For instance, in the \(\mathbf{CLat}_\wedge \)-fibration \(\pi :\mathbf{Top}\rightarrow \mathbf{Set}\), \(f:X\mathbin {\dot{\rightarrow }}Y\) is equivalent to the sentence “a function \(f:\pi X\rightarrow \pi Y\) is a continuous function from X to Y.
Despite their simple definition, \(\mathbf{CLat}_\wedge \)-fibrations have many useful properties. Let \(\pi :\mathbb {E}\rightarrow \mathbf{Set}\) be a \(\mathbf{CLat}_\wedge \)-fibration. The following properties are well-known:
-
\(\pi \) is a split bifibration. (Each fibre is a poset and each pullback functor \(f^*:\mathbb {E}_J\rightarrow \mathbb {E}_I\) has a left adjoint \(f_*:\mathbb {E}_I\rightarrow \mathbb {E}_J\) by the adjoint functor theorem.)
-
\(\pi \) is faithful and has left and right adjoints, mapping \(I\in \mathbf{Set}\) to the least and greatest elements in \(\mathbb {E}_I\), respectively. We name the left adjoint \(\varDelta :\mathbf{Set}\rightarrow \mathbb {E}\). Intuitively, it constructs discrete spaces of given sets.
-
\(\mathbb {E}\) has small limits and colimits by Theorem 1.
-
\(\pi \) uniquely lifts arbitrary limits and colimits that exist in \(\mathbf{Set}\), including large ones. We describe this for the case of colimits. For any diagram \(F:\mathbb {D}\rightarrow \mathbb {E}\) and a colimiting cocone \(\{\iota _D:\pi FD\rightarrow C\}_{D\in \mathbb {D}}\) of \(\pi F\) in \(\mathbf{Set}\), there exists a unique colimiting cocone \(\{\dot{\iota }_D: FD\rightarrow \dot{C}\}_{D\in \mathbb {D}}\) of F in \(\mathbb {E}\) such that \(\pi \dot{\iota }_D=\iota _D\). The colimit \(\dot{C}\) is given as \(\bigvee _{D\in |\mathbb {D}|}(\iota _D)_*(FD)\). The same statement holds for coends instead of colimits.
-
The change-of-base of a \(\mathbf{CLat}_\wedge \)-fibration \(\pi :\mathbb {E}\rightarrow \mathbf{Set}\) along any \(F:\mathbf{Set}\rightarrow \mathbf{Set}\) is again a \(\mathbf{CLat}_\wedge \)-fibration.
Another less known, but important fact is that the total category \(\mathbb {E}\) of any \(\mathbf{CLat}_\wedge \)-fibration over \(\mathbf{Set}\) carries a canonical (affine) symmetric monoidal closed (SMC for short) structure. The one on \(\mathbf{Top}\) is described in [4, 21]. The following construction of the SMC structure is a reformulation of the one given in [17] using fibred category theory.
- The tensor unit :
-
is a chosen terminal object 1.
- The tensor product :
-
of \(X,Y\in \mathbb {E}\) is constructed as follows. Let us define \(\pi X\cdot Y\) to be the coproduct of \(\pi X\)-many copies of Y. We explicitly construct it above \(\pi X\times \pi Y\) by
$$\begin{aligned} \pi X\cdot Y=\bigvee _{x\in \pi X}(x,-)_*Y, \end{aligned}$$where \((x,-):\pi Y\rightarrow \pi X\times \pi Y\) is the function that pairs an argument with a specified \(x\in \pi X\). We similarly define \(X\cdot \pi Y\) to be the coproduct of \(\pi Y\)-many copies of X, again constructed above \(\pi X\times \pi Y\). We then define the tensor product of X and Y to be the join of these two in the fibre over \(\pi X\times \pi Y\):
$$\begin{aligned} X\otimes Y=(\pi X\cdot Y)\vee (X\cdot \pi Y). \end{aligned}$$This tensor product classifies bi-\(\mathbb {E}\)-morphisms in the following sense: a function f satisfies \(f:X\otimes Y\mathbin {\dot{\rightarrow }}Z\) if and only if \(f(x,-):Y\mathbin {\dot{\rightarrow }}Z\) and \(f(-,y):X\mathbin {\dot{\rightarrow }}Z\) holds for any \(x\in \pi X\) and \(y\in \pi Y\).
- The closed structure :
-
of \(X,Y\in \mathbb {E}\) is constructed as follows. We first construct the product \(\pi X\pitchfork Y\) of \(\pi X\)-many copies of Y above \(\mathbf{Set}(\pi X,\pi Y)\) by
$$\begin{aligned} \pi X\pitchfork Y=\bigwedge _{x\in \pi X}(-(x))^* Y, \end{aligned}$$where \(-(x):\mathbf{Set}(\pi X,\pi Y)\rightarrow \pi Y\) is the function that evaluates an argument function with a specified \(x\in \pi X\). We then define the closed structure \(X\multimap Y\) to be the pullback of \(\pi X\pitchfork Y\) along the morphism part \(\pi _{X,Y}:\mathbb {E}(X, Y)\rightarrow \mathbf{Set}(\pi X, \pi Y)\) of \(\pi \):
$$\begin{aligned} X\multimap Y=\pi _{X,Y}^*(\pi X\pitchfork Y). \end{aligned}$$
We note that both \(\pi :\mathbb {E}\rightarrow \mathbf{Set}\) and its left adjoint \(\varDelta :\mathbf{Set}\rightarrow \mathbb {E}\) are strict symmetric monoidal (for \(\mathbf{Set}\) we take the cartesian monoidal structure).
Example 4
We illustrate the bifibrational structure of \(\mathbf{BVal}\). Let us recall the order relation in the fibre categories. The following are equivalent: (1) in the fibre \(\mathbf{BVal}_I\), \((I,r)\le (I,s)\) holds, (2) \(\mathrm{id}_I\) is a nonexpansive function from (I, r) to (I, s), and (3) \(s(x,y)\le r(x,y)\) holds for all \(x,y\in I\). Note the apparent disparity between (1) and (3): though \(r \le s\) in the fibre order, s has smaller values than r pointwise.
Next, let \((I,r)\in \mathbf{BVal}\) and  be functions. The pullback \((H,f^*r)\) and the pushforward \((J,g_*r)\) are given by
be functions. The pullback \((H,f^*r)\) and the pushforward \((J,g_*r)\) are given by
The fibrational construction of the canonical SMC structure on \(\mathbf{BVal}\) yields the following tensor product and closed structure:
2.4 Liftings
Another major object of study in this work are liftings of a functor. Given a \(\mathbf{Set}\) endofunctor F and two functors \(\pi : \mathbb {E}\rightarrow \mathbf{Set}\) and \(\rho : \mathbb {F}\rightarrow \mathbf{Set}\), a lifting of F is a functor \({\dot{F}}: \mathbb {E}\rightarrow \mathbb {F}\) such that \(\rho \circ {\dot{F}} = F \circ \pi \). In many of the cases we consider \(\pi =\rho \), so \({\dot{F}}\) is an endofunctor on the domain of \(\pi \). To emphasize this particular situation we will call such an \({\dot{F}}\) an endolifting. In [11], endoliftings were called modalities.
Obviously, we will also usually be considering a situation where \(\pi \) and \(\rho \) are \(\mathbf{CLat}_\wedge \)-fibrations. In such a case, restricting a lifting to a particular fibre yields a functor between fibre categories: \({\dot{F}}|_I: \mathbb {E}_I \rightarrow \mathbb {F}_{FI}\). Some liftings also specially respect the cartesian morphisms of the fibrations they operate between. A lifting is called a fibration morphism if it sends cartesian morphisms in \(\mathbb {E}\) to cartesian morphisms in \(\mathbb {F}\).
Notation. We pause here to set out some notational conventions, some of which have already been used. \(\mathbf{Set}\) is the category of sets and functions. Typical objects of \(\mathbf{Set}\) are denoted I, J, and K and typical morphisms are denoted f, g, and h. Generally, F is a \(\mathbf{Set}\) endofunctor, \(C_I\) is the constant-to-I \(\mathbf{Set}\) endofunctor, \(-^*\) is the list functor, and \(P_\mathrm{fin}\) is the finite (covariant) powerset functor.
Abstract categories are denoted \(\mathbb {D}\), \(\mathbb {E}\), and \(\mathbb {F}\) and are often the total category for a \(\mathbf{CLat}_\wedge \)-fibrations over \(\mathbf{Set}\) with functors \(\pi \) or \(\rho \). In such a case, applying a dot or two over a \(\mathbf{Set}\)-related entity denotes an entity in the total category above the named \(\mathbf{Set}\)-related entity. For example, \(\dot{I}\) is an object in the total category, \(\dot{f}\) is a morphism in the total category, \(\dot{\times }\) is the binary product in the total category, and \({\dot{F}}\) is a lifting of F to the total category. We will also generally use X, Y, and Z as objects in a total category.
Two fibrations—\(\mathbf{BVal}\) and \(\mathbf{ERel}\)—are important enough to merit their own notations. Generally, r and s will denote the function in a \(\mathbf{BVal}\) object, while R and S are the relation in an \(\mathbf{ERel}\) object. Generally, writing a \(\hat{\cdot }\) or \(\tilde{\cdot }\) over a \(\mathbf{Set}\)-related entity has the same meaning as a dot over that entity, but particularly for the total categories \(\mathbf{BVal}\) and \(\mathbf{ERel}\), respectively.
The length of a list is denoted \({{\mathrm{len}}}\) and subscripts shall be used to select an element from a list at the indicated (zero-indexed) list position.
3 Endoliftings and Invariants
In this section, we describe how \(\mathbf{CLat}_\wedge \)-fibrations and liftings of a functor F to that fibration can be used to define data about every F-coalgebra. Perhaps the best-known instance of this construction creates Hermida-Jacobs bisimulations from the canonical relation lifting of a functor along \(\mathbf{ERel}\rightarrow \mathbf{Set}\). We describe this example first, particularly for polynomial functors F.
3.1 Relation Liftings Define Coalgebraic Relations
Recall from the previous section the fibration \(\mathbf{ERel}\) has objects consisting of pairs (I, R) where I is a set and \(R \subseteq I\times I\) is a relation on that set. The fibre category \(\mathbf{ERel}_I\) is (isomorphic to) the lattice of relations on I with a vertical morphism from (I, R) to (I, S) if and only if \(R \subseteq S\).
A consequence of the equivalence between inclusion of relations in a fibre and the existence of a vertical morphism between them is that any functor between fibre categories in \(\mathbf{ERel}\) is necessarily a monotone function on relations with respect to the usual inclusion ordering.
Two important cases where we can apply this fact are (1) \(\mathbf{ERel}\) liftings of functors restricted to a fibre and (2) pullbacks along \(\mathbf{Set}\) functions, since these are both functors between fibre categories. If \(\widetilde{F}\) is an \(\mathbf{ERel}\) lifting of F, then \(\widetilde{F}|_{\mathbf{ERel}_I}\) is a monotone function \(\mathbf{ERel}_I\rightarrow \mathbf{ERel}_{FI}\). Similarly, if \(f: I \rightarrow FI\) is an F-coalgebra structure on I, pullback along f is a monotone function \(f^*: \mathbf{ERel}_{FI}\rightarrow \mathbf{ERel}_{I}\).
Composing the above functions yields a monotone function \(f^*\circ \widetilde{F}|_{\mathbf{ERel}_{FI}}\) on \(\mathbf{ERel}_{I}\). Since \(\mathbf{ERel}_{I}\) is a complete lattice, this composite monotone function has a greatest fixed point, which we denote by \((I, \nu {\widetilde{F}}_{(I, f)})\). The relation \(\nu {\widetilde{F}}_{(I, f)}\) picked out in this greatest fixed point has historically turned out examples of great interest.
Perhaps foremost among these examples is the so-called canonical relation lifting, which yields bisimilarity as its greatest fixed point. We recall the description of this lifting for polynomial endofunctors.Footnote 5 The polynomial \(\mathbf{Set}\) endofunctors are precisely those generated by the following grammar:
We can create an \(\mathbf{ERel}\) lifting for any polynomial P with constructions for each of the inductive cases.
Definition 5
(canonical relation lifting). Let  and \(\widetilde{\times }\) be the coproduct and binary product operations in \(\mathbf{ERel}\), respectively. (These exist by Theorem 1.) The canonical relation lifting of a polynomial \(\mathbf{Set}\) functor P is:
and \(\widetilde{\times }\) be the coproduct and binary product operations in \(\mathbf{ERel}\), respectively. (These exist by Theorem 1.) The canonical relation lifting of a polynomial \(\mathbf{Set}\) functor P is:

Given a polynomial \(\mathbf{Set}\) functor P and a P-coalgebra (I, f), we can use the canonical relation lifting \({{\mathrm{Rel}}}(P)\) to form the function \(f^* \circ {{\mathrm{Rel}}}(P)|_{\mathbf{ERel}_I}\). Postfixed points of this function in \(\mathbf{ERel}_I\) give a useful general definition of bisimulation on (I, f) [12]. The greatest postfixed point \(\nu {{{\mathrm{Rel}}}(P)}_{(I, f)}\) is bisimilarity on this coalgebra.
Example 6
As two examples of the canonical relation lifting, we present bisimulation on coalgebras of the list functor and on coalgebras of the finite powerset functor. These examples will be referenced later when we construct behavioural metrics on the same coalgebra types similarly to how we do it here.
The list functor is defined as \((-)^* = \coprod _{n \in \omega } \prod _{i \in n} \mathrm{Id}\). Following the inductive definition above, each summand in the coproduct, \(\prod _n \mathrm{Id}\), sends a relation R to the n-fold repetition of R: two lists \(k, \ell \) of length n are related by \({{\mathrm{Rel}}}(\prod _n \mathrm{Id})(R)\) if \(k_i R \ell _i\) holds for \(0 \le i < n\). The canonical relation lifting for \(\coprod _{n \in \omega } \prod _n \mathrm{Id}\) then relates two lists \(k, \ell \) of arbitrary length if and only if \({{\mathrm{len}}}(k) = {{\mathrm{len}}}(\ell )\) (they come from the same index in the coproduct), and \(k_i R \ell _i\) holds for \(0\le i < {{\mathrm{len}}}(k)\). In other words, \((k, \ell ) \in {{\mathrm{Rel}}}(\prod _n \mathrm{Id})(R)\).
The finite powerset functor is the quotient of the list functor by the transformation \(set_I: I^* \rightarrow P_\mathrm{fin}I\) given by \(set_I: (i_1, \ldots , i_n) \mapsto \{i_1, \ldots , i_n\}\). The pushforward of the lifting for the list functor along this natural transformation is the usual definition of bisimulation for the finite powerset functor. Explicitly,
3.2 Generalizing Hermida-Jacobs Bisimulation
The necessary components to define Hermida-Jacobs bisimulation conveniently can be found in any \(\mathbf{CLat}_\wedge \)-fibration with any endolifting of any functor. Thus, we can define the abstract counterpart of a bisimulation. This terminology is intended to echo [11].
Definition 7
Let \({\dot{F}}\) be a endolifting for F. An \({\dot{F}}\)-invariant [on an F-coalgebra (I, f)] is an \({\dot{F}}\)-coalgebra \((X, \alpha )\) [such that \(\pi X = I\) and \(\pi \alpha = f\)].
An \({\dot{F}}\)-invariant morphism is an \({\dot{F}}\)-coalgebra morphism.
\({\dot{F}}\)-invariants and \({\dot{F}}\)-invariant morphisms together form a category, in fact exactly the category \(\mathbf{Coalg}({\dot{F}})\). \({\dot{F}}\)-invariants also evidently sit over F-coalgebras according to \(\pi \), so we name the functor sending \(\mathbf{Coalg}({\dot{F}})\) to \(\mathbf{Coalg}(F)\).
Definition 8
Given a endolifting \({\dot{F}}\) on a functor F, the underlying coalgebra functor \(\mathbf{Coalg}(\pi ):\mathbf{Coalg}({\dot{F}})\rightarrow \mathbf{Coalg}(F)\) is defined as
Since \(\pi \) is faithful in a \(\mathbf{CLat}_\wedge \)-fibration, the coalgebra structure \(\alpha \) of an \({\dot{F}}\)-invariant \((X,\alpha )\) on (I, f) is unique. Therefore, an alternative definition of an \({\dot{F}}\)-invariant on (I, f) is an object X above I such that there exists a (necessarily unique) morphism \(\alpha :X\rightarrow \dot{F}X\) above f.
Yet another definition of an \({\dot{F}}\)-invariant can be derived from the lattice structure of \(\mathbb {E}_I\). For each coalgebra (I, f), there is a monotone function \(f^*\circ {\dot{F}}|_{\mathbb {E}_I}: \mathbb {E}_I \rightarrow \mathbb {E}_{FI} \rightarrow \mathbb {E}_I\) as described above. An \({\dot{F}}\)-invariant on (I, f) is then precisely a postfixed point for this function.
A useful consequence of this last characterization is the observation that since each fibre \(\mathbb {E}_I\) is a complete lattice, Knaster-Tarski ensures the \({\dot{F}}\)-invariants on (I, f) form a complete sublattice. In particular
Definition 9
The greatest \({\dot{F}}\)-invariant on an F-coalgebra (I, f) always exists and is called the \({\dot{F}}\)-coinductive invariant. We denote the \({\dot{F}}\)-coinductive invariant on (I, f) by \(\nu {{\dot{F}}}_{(I, f)}\).
We can alternatively reach \(\nu {{\dot{F}}}_{(I,f)}\) by the final sequence argument inside the fibre \(\mathbb {E}_I\); this is the approach taken in [3]. In [11], coinducive invariants were called coinductive predicates.
\({\dot{F}}\)-similarities give final objects within each fibre category, but there is no assurance of a final object in the total category, nor that final objects are preserved by coalgebra morphisms. The next result, which reorganizes results presented in [11, Sect. 4], sets out some conditions entailing these desiderata.
Theorem 10
Let \({\dot{F}}\) be a endolifting for F. If it preserves cartesian morphisms,
-
1.
[11, Proposition 4.1]. The underlying coalgebra functor \(\mathbf{Coalg}(\pi ):\mathbf{Coalg}({\dot{F}})\rightarrow \mathbf{Coalg}(F)\) is a fibration where pullbacks are the same as in the fibration \(\pi \).
-
2.
Each pullback functor of \(\mathbf{Coalg}(\pi )\) preserves final objects (hence \(\mathbf{Coalg}({\dot{F}})\) has fibered final objects).
-
3.
If additionally \(\mathbf{Coalg}(F)\) has a final object \(\nu F\), then \(\mathbf{Coalg}({\dot{F}})\) has a final object.
For the item 2 and 3 of the above theorem, see also [11, Corollary 4.3].
This theorem is a fibred counterpart of some results in Sect. 6 of [3]. To see this, we instantiate Theorem 10 with the following data: the \(\mathbf{CLat}_\wedge \)-fibration \(\pi :\mathbf{PMet}_b\rightarrow \mathbf{Set}\) (Sect. 2), a functor \(F:\mathbf{Set}\rightarrow \mathbf{Set}\) having a final F-coalgebra \(\nu F\) and a lifting \({\dot{F}}\) of F along \(\pi \) that preserves cartesian \(\mathbf{PMet}_b\) morphisms (isometries). Then
-
Theorem 6.1 in [3] is equivalent to the conclusion of (this instance of) item 3 of Theorem 10.
-
Let \(I=(I,f)\) be an F-coalgebra, and \(!_I:I\rightarrow \nu F\) be the unique F-coalgebra morphism. The behavioural distance of I in [3] corresponds to the pullback \(!_I^*(\nu {\dot{F}}_{\nu F})\) in our fibrational language.
-
Theorem 6.2 in [3] corresponds to \(\nu F_I=!_I^*(\nu {\dot{F}}_{\nu F})\), which follows from (this instance of) item 2 of Theorem 10.
4 Constructions of Liftings Along \(\mathbf{CLat}_\wedge \)-Fibrations
There are many examples of liftings of functors in well-known fibrations, such as the fibration of relations or pseudometrics. Some of these liftings even form classes which cover all functors, such as the canonical relation lifting or the generalized Kantorovich liftings of [3], which ensure every functor has a lifting in \(\mathbf{ERel}\) and \(\mathbf{PMet}_b\) respectively. In this work we are considering a variety of fibrations, so a natural concern is whether liftings of \(\mathbf{Set}\) functors exist in all of these \(\mathbf{CLat}_\wedge \)-fibrations.
In this section, we generalize a variety of constructions known in particular fibrations to arbitrary \(\mathbf{CLat}_\wedge \)-fibrations. In Sects. 4.1 and 4.2, we give two constructions, the first using enriched left Kan extensions and the second using codensity liftings. Then in Sect. 4.3 we mention how to use the categorical structure of the \(\mathbf{CLat}_\wedge \)-fibration to create new liftings from old.
Hence, in this section we find ourselves with the ingredients F and \(\pi \):

and seek to create an endolifting of F in a variety of ways.
4.1 Lifting by Enriched Left Kan Extensions
The canonical SMC structure on \(\mathbb {E}\) (Sect. 2) allows us to discuss enriched liftings of F to \(\mathbb {E}^e\), the self-enriched category of \(\mathbb {E}\) with its SMC structure. To discuss this, we introduce some \(\mathbb {E}\)-categories and \(\mathbb {E}\)-functors.
-
By \(\mathbb {E}^e\) we mean the self-enriched \(\mathbb {E}\)-category of \(\mathbb {E}\) (that is, \(\mathbb {E}^e(X,Y)\,{=}\,X\,{\multimap }\, Y\)).
-
Since the left adjoint \(\varDelta :\mathbf{Set}\rightarrow \mathbb {E}\) of \(\pi \) (see Sect. 2.3) is strict monoidal, it yields the change-of-base 2-functor \(\varDelta _*:\mathbf{CAT}\rightarrow \mathbb {E}\text {-}\mathbf{CAT}\). It takes a locally small category \(\mathbb {C}\) and returns the \(\mathbb {E}\)-category \(\varDelta _*\mathbb {C}\) defined by \(\mathbf{Obj}(\varDelta _*\mathbb {C})=\mathbf{Obj}(\mathbb {C})\) and \((\varDelta _*\mathbb {C})(I,J)=\varDelta (\mathbb {C}(I,J))\).
-
For any functor \(G:\mathbb {C}\rightarrow \mathbb {E}\), we define the \(\mathbb {E}\)-functor \(\underline{G}:\varDelta _*\mathbb {C}\rightarrow \mathbb {E}^e\) by: \(\underline{G}I=GI\), and \(\underline{G}_{I,J}:(\varDelta _*\mathbb {C})(I,J)\rightarrow \mathbb {E}^e(GI,GJ)\) is the mate of \(G_{I,J}:\mathbb {C}(I,J)\rightarrow \mathbb {E}(GI,GJ)\) with the adjunction \(\varDelta \dashv \pi \); recall that \(\pi (\mathbb {E}^e(X,Y))=\pi (X\multimap Y)=\mathbb {E}(X,Y)\) by construction.
The following is a generalisation of [2, Theorem 3.3].
Theorem 11
Consider the situation (1). Let \(C:\mathbf{Set}\rightarrow \mathbb {E}\) be a functor such that \(\pi C=F\). Then there is an enriched left Kan extension \({\dot{F}}\) of \(\underline{C}:\varDelta _*\mathbf{Set}\rightarrow \mathbb {E}^e\) along \(\underline{\varDelta }:\varDelta _*\mathbf{Set}\rightarrow \mathbb {E}^e\) such that its underlying functor \({\dot{F}}_0:\mathbb {E}\rightarrow \mathbb {E}\) (see [16]) is a lifting of F along \(\pi \).
Proof
Since the codomain \(\mathbb {E}^e\) of \(\underline{C}\) has \(\mathbb {E}\)-tensors, the enriched left Kan extension can be computed by the enriched coend:
see [16, (4.25)]. We define the body of this coend by \(B(I,J)=\mathbb {E}^e(\underline{\varDelta }I,X)\otimes \underline{C}J\). It is an \(\mathbb {E}\)-functor of type \((\varDelta _*\mathbf{Set})^{op}\otimes \varDelta _*\mathbf{Set}\rightarrow \mathbb {E}^e\). Similarly, we define an ordinary functor \(\overline{B}:\mathbf{Set}^{op}\times \mathbf{Set}\rightarrow \mathbb {E}\) by \( \overline{B}(I,J)=B(I,J)\) on objects and \( \overline{B}(f,g)=\pi B_{(I,J),(I',J')}(f,g)\) on morphisms. A calculation shows that \(\overline{B}\) is equal to the ordinary functor \(\lambda {(I,J)}~.~(LI\multimap X)\otimes CJ\).
Because the codomain of B is \(\mathbb {E}^e\), the enriched coend can be computed as an ordinary colimit of the following large diagram in \(\mathbb {E}\) [16, Sect. 2.1]:

where I, J ranges over all objects in \(\mathbf{Set}\), and \(l_{I,J}\) and \(r_{I,J}\) are the uncurrying of \(B(I,-)_{J,I}\) and \(B(-,J)_{I,J}\), respectively.
In \(\mathbb {E}\), \(\varDelta I\otimes X\) is a tensor of X with \(I\in \mathbf{Set}\) because
We name the passage from right to left \(\phi \). The bottom objects of diagram (2) are thus tensors of B(I, J) with \(\mathbf{Set}(J,I)\) for each \(I,J\in \mathbf{Set}\), and moreover, by easy calculation, we have \(l_{I,J}=\phi (\overline{B}(I,-))\) and \(r_{I,J}=\phi (\overline{B}(-,J))\). Therefore a colimit of the diagram (2) can be computed as an ordinary coend of \(\overline{B}:\mathbf{Set}^{op}\times \mathbf{Set}\rightarrow \mathbb {E}\).
To compute this (large) coend of \(\overline{B}\), it suffices to show that the coend of \(\pi \overline{B}\) exists in \(\mathbf{Set}\), because \(\pi \) uniquely lifts coends. We have a natural isomorphism \(\iota _{I,J}:\pi \overline{B}(I,J)\rightarrow \mathbf{Set}(I,\pi X)\times FJ\), and the right hand side has a coend \(\{i_I:\mathbf{Set}(I,\pi X)\times FI\rightarrow F\pi X\}_{I\in \mathbf{Set}}\) defined by \(i_I(f,x)=Ffx\). Therefore since \(\pi \) uniquely lifts colimits (Sect. 2.3), we obtain a coend of \(\overline{B}\). To summarise, the enriched left Kan extension is computed as
Example 12
Let \(\pi :\mathbf{Pre}\rightarrow \mathbf{Set}\) be the \(\mathbf{CLat}_\wedge \)-fibration from the category \(\mathbf{Pre}\) of preorders and \(F:\mathbf{Set}\rightarrow \mathbf{Set}\) be a functor. We compute the enriched left Kan extension \(\mathbf{Lan}_{\underline{\varDelta }}{\underline{\varDelta F}}\). For \((X,\le )\in \mathbf{Pre}\), the enriched left Kan extension \(\mathbf{Lan}_{\underline{\varDelta }}{\underline{\varDelta F}}(X,\le _X)\) is the preorder on FX generated from the following binary relation:
where \(p_i:(\le _X)\rightarrow X\) is the composite of the inclusion \((\le _X)\hookrightarrow X\times X\) of the preorder relation and the projection function \(\pi _i:X\times X\rightarrow X\).
When F is the powerset functor P, the enriched left Kan extension \(\mathbf{Lan}_{\underline{\varDelta }}{\underline{\varDelta P}}(X,\le _X)\) gives the Egli-Milner preorder \(\sqsubseteq _X\) on PX, as computed in [2, Example 3.8]:
4.2 Codensity Lifting of Endofunctors
As an analog to the codensity lifting of monads along \(\mathbf{CLat}_\wedge \)-fibrations [15, Proposition10], we give a method to lift \(\mathbf{Set}\)-endofunctors along \(\mathbf{CLat}_\wedge \)-fibrations. We retain the name and call it the codensity lifting (of \(\mathbf{Set}\)-endofunctors). We demonstrate in Example 15 that it subsumes the Kantorovich lifting in [3].
Consider the situation (1). We take the category \(\mathbf{Set}^F\) of F-algebras and the associated forgetful functor \(U:\mathbf{Set}^F\rightarrow \mathbf{Set}\). It comes with a natural transformation \(\alpha :FU\rightarrow U\), whose components are defined by the F-algebra structure: \(\alpha _{(A,a)}=a:FA\rightarrow A\).
The codensity lifting of F is defined with respect to a lifting parameter for F, which is a pair (R, S) of functors from a discrete category \(\mathbb {A}\) such that \(\pi S=UR\):

Then the codensity lifting \({F}^{[R,S]}\) of F with respect to the above lifting parameter (R, S) is defined by the following fibred meet:
The codensity lifting can be characterise as a vertex of a pullback when the codensity monad \(\mathbf{Ran}_{S}S\) exists. Suppose that \(\mathbf{Ran}_{S}S\) exists. Since the \(\mathbf{CLat}_\wedge \)-fibration \(\pi :\mathbb {E}\rightarrow \mathbf{Set}\) preserves all limits, \(\pi \mathbf{Ran}_{S}S\) is a right Kan extension of \(\pi S\) along S. We then take the mate of the natural transformation \(\alpha R:F\pi S\rightarrow \pi S\) with the right Kan extension of \(\pi S\) along S, and obtain \(\overline{\alpha R}:F\pi \rightarrow \pi \mathbf{Ran}_{S}S\).
Theorem 13
Suppose that \(\mathbf{Ran}_{S}S\) exists. Then \(F^{[R,S]}\) is the vertex of the following pullback in the fibration \([\mathbb {E},p]:[\mathbb {E},\mathbb {E}]\rightarrow [\mathbb {E},\mathbf{Set}]\):

The codensity lifting enjoys the following universal property. First, we introduce a partial order on the liftings of F by: \({\dot{F}}\le {\ddot{F}}\) if and only if \(\dot{F}X\le \ddot{F}X\) holds for all \(X\in \mathbb {E}\). Moreover, we say that a lifting \({\dot{F}}\) of F along \(\pi \) makes S an algebra above R if, \(\alpha _{RA}:\dot{F}SA\mathbin {\dot{\rightarrow }}SA\) holds for all \(A\in \mathbb {A}\).
Theorem 14
Consider the situation (1) and a lifting parameter given as (3). The codensity lifting \({F}^{[R,S]}\) of F is the largest lifting of F that makes S an algebra above R.
Example 15
Fix a bound \(b\in (0,\infty ]\) for metrics. We show that the Kantorovich lifting in [3] is a codensity lifting along the \(\mathbf{CLat}_\wedge \)-fibration \(\pi :\mathbf{PMet}_b\rightarrow \mathbf{Set}\). Let \(\alpha :F[0,b]\rightarrow [0,b]\) be an F-algebra; in [3] it is called an evaluation function. We then form the following lifting parameter: \(\mathbb {A}=1\), \(R=([0,b],\alpha )\), and \(S=([0,b],d_e)\), where \(d_e\) is the standard Euclidean distance \(d_e(x,y)=|x-y|\) on [0, b]. Then the codensity lifting with this parameter yields the following construction of pseudometric:
This is exactly the Kantorovich lifting in [3, Definition 3.1].
4.3 Combining Liftings
We have seen two methods to lift endofunctors. In this section, we discuss building new liftings from existing ones. Below we set up a suitable category in which these operations are characterised as categorical constructions.
Let \(\pi :\mathbb {E}\rightarrow \mathbf{Set}\) be a \(\mathbf{CLat}_\wedge \)-fibration. Then \(\pi \circ -:[\mathbb {E},\mathbb {E}]\rightarrow [\mathbb {E},\mathbf{Set}]\) is a partial order bifibration with fibred meets of arbitrary size. We take the following change-of-base of this fibration along \(-\circ \pi \):

The vertex of this change-of-base is the category \(\mathbf{Lift}(\pi )\) of liftings along \(\pi \). An object is a pair \((F,{\dot{F}})\) of an endofunctor \(F:\mathbf{Set}\rightarrow \mathbf{Set}\) and its lifting \({\dot{F}}:\mathbb {E}\rightarrow \mathbb {E}\) along \(\pi \). A morphism from \((F,{\dot{F}})\) to \((G,\dot{G})\) is a pair \((\alpha ,\dot{\alpha })\) of natural transformations \(\alpha :F\rightarrow G\) and \(\dot{\alpha }:{\dot{F}}\rightarrow \dot{G}\) such that \(\pi \dot{\alpha }=\alpha \pi \).
The derived vertical leg \(q:\mathbf{Lift}(\pi )\rightarrow [\mathbf{Set},\mathbf{Set}]\) is also a partial order bifibration with fibred meets (of arbitrary size). Since \([\mathbf{Set},\mathbf{Set}]\) has small limits and colimits, by Theorem 1, \(\mathbf{Lift}(\pi )\) has small limits and colimits, hence small products and coproducts.
The bifibredness of q, together with these products and coproducts give us a recipe to combine liftings.
-
Identity and Constant. The lifting of \(\mathrm{Id}_\mathbf{Set}\) is \(\mathrm{Id}_\mathbb {E}\), while the lifting of the constant functor \(C_I(J)\equiv I\) is \(\dot{C}_I(X)\equiv \varDelta I\).
-
Product and Coproduct. Let \((F_i,{\dot{F}}_i)\) be an I-indexed family of liftings along \(\pi \). Then their product and coproduct are computed pointwise.
-
Pullbacks and Pushforwards. For a lifting \((F,{\dot{F}})\) along \(\pi \) and natural transformations
 , the pullback lifting \(\alpha ^*F\) above H and pushforward lifting \(\beta _* F\) above G are computed pointwise in the fibration \(\pi :\mathbb {E}\rightarrow \mathbf{Set}\):
, the pullback lifting \(\alpha ^*F\) above H and pushforward lifting \(\beta _* F\) above G are computed pointwise in the fibration \(\pi :\mathbb {E}\rightarrow \mathbf{Set}\):
In particular, these constructions ensure all polynomial and finitary functors in \(\mathbf{Set}\) have at least one lifting in every \(\mathbf{CLat}_\wedge \)-fibration.
4.4 The Hausdorff Pseudometric
As an example of how liftings can be constructed with these basic operations, we demonstrate the construction of the Hausdorff pseudometric on finite sets in a \(\mathbf{BVal}\) lifting of the finite powerset functor. Our version of the Hausdorff distance will take a \(\mathbf{BVal}\) object (I, d) and create a \(\mathbf{BVal}\) object (\(P_\mathrm{fin}I\), \(\mathcal{H}d\)).
Recall that the finite powerset can be realized as a quotient of a polynomial functor with the following construction. First, recall the list functor: \((-)^* = \coprod _{n \in \omega } \prod _{i \in n} \mathrm{Id}\). This is patently a polynomial functor. Then the finite powerset functor is the quotient of the list functor by the natural transformation \(set_I: I^* \rightarrow P_\mathrm{fin}I\) from Example 6.
We can build up a \(\mathbf{BVal}\) lifting of the finite powerset functor in parallel with this construction. First, using the product and coproduct in \(\mathbf{BVal}\) we derive a \(\mathbf{BVal}\) lifting for the list functor. Given a \(\mathbf{BVal}\) object (I, d) the lifted distance on lists \(k, \ell \in I^*\) is:
Then a \(\mathbf{BVal}\) lifting for the finite powerset functor arises as the pushforward of the list lifting along the transformation set. In Example 4, we found pushforward in \(\mathbf{BVal}\) explicitly so, \(\displaystyle {}\mathcal{H}d(J, K) = \inf _{\begin{array}{c} k \in I^*:\ set(k) = J \\ \ell \in I^*:\ set(\ell ) = K \end{array}} d^*(k, \ell )\). We have denoted this distance \(\mathcal{H}d\) since it turns out to be equal to the usual Hausdorff distance. However, this is not the usual formulation for the Hausdorff distance, so we briefly discuss why this is equivalent.
The usual definition of Hausdorff distance for a metric space is
where \(J, K \subseteq I\). Typically the Hausdorff distance is also restricted to nonempty compact subsets of the metric space so that \(\mathcal{H}d\) is truly a metric. (Otherwise \(\mathcal{H}d(J, K) \,{=}\, 0\) does not imply \(J \,{=}\, K\), for example.) Since we are interested in pseudometrics anyway, we do not place any such restriction on the domain of \(\mathcal{H}d\).
In the finite case, the Hausdorff distance has a game theoretic interpretation as the result of a two-turn game played between a lazy walker (Gerry) and an antagonist (Tony). In the first round, Tony picks a starting point from either J or K for Gerry. In the second round, Gerry walks from Tony’s starting point in J(K) to any point in K(J). The result of the game is the distance Gerry walks. Gerry’s goal is to minimize this distance; Tony’s goal is to maximize it.
Gerry’s optimal strategy is straightforward. Given a starting point, Gerry finds the distances to the (finitely many) points in the other set and picks the least one. Since Gerry’s optimal strategy is clear, Tony can make a list consisting of all the points in \(J\,\cup \,K\) and the distance Gerry will have to walk if that point is used as the starting point. Then Tony’s optimal strategy is to pick the starting point corresponding to the greatest distance on this list.
This analysis indicates we can interchange the order of the players and obtain a game with the same result: Gerry can first announce where he will walk given every possible choice of starting point, then Tony picks one of the choices offered by Gerry. If Tony is given two lists k and \(\ell \) by Gerry, he will be to force the result of this modified game to be
where \(d^*\) is the list distance defined above. Gerry’s best strategy is to pick k and \(\ell \) with the closest corresponding distances possible, making the final result of this modified game
where the constraints \(set(k) = J\) and \(set(\ell ) = K\) express the fact that Gerry must make a choice for every single starting point. Since these games have the same result, we know
Therefore, our formulation of the Hausdorff distance is equal to the usual formulation of the Hausdorff distance, modulo the consideration that we are satisfied with a pseudometric and so do not confine our definition to nonempty compact sets.Footnote 6
5 The Category of Endoliftings
In Sect. 3, we defined endoliftings and their instantiations to \({\dot{F}}\)-invariants on particular coalgebras. We showed that with certain constraints on the ambient categories, the \({\dot{F}}\)-coinductive invariant exists and is preserved by coalgebra morphisms. In Sect. 4, we showed that endoliftings exist in many \(\mathbf{CLat}_\wedge \)-fibrations, and gave several constructions and combinators for producing endoliftings in these general conditions. In this section, we we observe that endoliftings can be collected into a category using the following definition.
Definition 16
A endolifting morphism from one endolifting \((\pi :\mathbb {E}\rightarrow \mathbf{Set}, {\dot{F}})\) to another \((\rho :\mathbb {F}\rightarrow \mathbf{Set}, {\ddot{F}})\) is a lifting \(H: \mathbb {E}\rightarrow \mathbb {F}\) of \(\mathrm{Id}_\mathbf{Set}\) (i.e. \(\pi = \rho \circ H\)) such that \(H\circ {\dot{F}} = {\ddot{F}} \circ H\).
Endolifting morphisms do not appear in the story of Hermida-Jacobs bisimulations or the coalgebraic predicates defined analogously, but we will observe this category is a useful abstraction for comparing coalgebraic invariants of various endoliftings.
A concrete goal in this section is to establish some general conditions under which a \(\mathbf{BVal}\) coinductive invariant has an \(\mathbf{ERel}\) coinductive invariant at its kernel. Results of this type are pursued, for example, in [6].
5.1 Quantitative and Qualitative Liftings
We begin by focusing on three \(\mathbf{CLat}_\wedge \)-fibrations introduced in Sect. 2.3, namely \(\mathbf{ERel}\), \(\mathbf{RERel}\), and \(\mathbf{BVal}\). These total categories consist of sets together with endorelations, real-indexed families of endorelations, and “distance” functions (which satisfy no metric axioms other than having codomain nonnegative reals), respectively.
These fibrations have many functors between them:

where (the object parts of) each of these functors are given by
Note that the two functors between \(\mathbf{ERel}\) and \(\mathbf{RERel}\) are actually a real-indexed family of functors, where \(\epsilon \in [0, \infty )\). It may help to think of S as Stratifying a distance function into a family of relations and L as finding the Least index where the relation holds. As usual, the empty infimum in the definition of L is the maximum element, namely \(\infty \).
These functors patently do not change the index set I associated with each of the objects in the total category. Each of these functors is also defined to be the identity on morphisms.Footnote 7 Therefore, these are liftings of the identity on \(\mathbf{Set}\).
We define the composite functor \(T\epsilon =(-\epsilon )\circ S\). This functor sends \((I,r)\in \mathbf{BVal}\) to \((I,\{(x,y)~|~r(x,y)\le \epsilon \})\in \mathbf{ERel}\), truncating the distance function r at \(\epsilon \). The fact that \(T\epsilon \) is a right adjoint, as depicted in the diagram above, will be an important fact later on.
The functor T0 gives the kernel of a distance function, namely the relation consisting of pairs which are at distance 0. A common desideratum of pseudometric liftings or more generally \(\mathbf{BVal}\) liftings is that the kernel of the \({\hat{F}}\)-coinductive invariant function in \(\mathbf{BVal}\) is bisimilarity in \(\mathbf{ERel}\) (i.e. the \({{\mathrm{Rel}}}(F)\)-coinductive invariant where \({{\mathrm{Rel}}}(F)\) is the canonical relation lifting of F, defined in Sect. 3.1). We show how to establish this result for the Hausdorff metric in a highly reusable manner.
5.2 \(T \epsilon \) Is a Endolifting Morphism Between Kripke Polynomial Functors
Next, we show that \(T \epsilon \) is a endolifting morphism from every polynomial functor in \(\mathbf{BVal}\) to the polynomial functor of parallel shape in \(\mathbf{ERel}\). This result is the backbone of our proof that \(T \epsilon \) is a endolifting morphism from the Hausdorff lifting of the finite powerset functor to the canonical relation lifting of the finite powerset functor.
Proposition 17
For all \(\epsilon \in [0, \infty )\), \(T \epsilon \) is a endolifting morphism:
-
1.
from \(\mathrm{Id}_\mathbf{BVal}\) to \(\mathrm{Id}_\mathbf{ERel}\),
-
2.
from \({\hat{C}}_A\) to \(\widetilde{C}_A\) where \(C_A\) is the constant-to-A functor, and
-
3.
from \({\hat{F}}_1\hat{\times }{\hat{F}}_2\) to \({{\mathrm{Rel}}}(F_1)\widetilde{\times }{{\mathrm{Rel}}}(F_2)\), given that it is a morphism from \({\hat{F}}_i\) to \({{\mathrm{Rel}}}(F_i)\), and
-
4.
from \({\hat{\coprod }}_i {\hat{F}}_i\) to
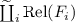 , given that it is a morphism from \({\hat{F}}_i\) to \({{\mathrm{Rel}}}(F_i)\)
, given that it is a morphism from \({\hat{F}}_i\) to \({{\mathrm{Rel}}}(F_i)\)
Therefore, \(T \epsilon \) is a endolifting morphism from any polynomial functor in \(\mathbf{ERel}\) to the polynomial functor of the same shape in \(\mathbf{BVal}\).
This establishes \(T\epsilon \) as a endolifting morphism between polynomial functors, but we also want it to be a endolifting morphism from the Hausdorff lifting of \(P_\mathrm{fin}\) to the canonical relation lifting in \(\mathbf{BVal}\). That is, we want to show \(T \epsilon : \mathcal{H}\rightarrow {{\mathrm{Rel}}}(P_\mathrm{fin})\) is a endolifting morphism. A reasonable strategy, given the proof we just completed, would be to hope that if \(T\epsilon \) is a endolifting morphism between two liftings of a functor, then it is a morphism between the pushforward of those functors along a natural transformation in the base category. In general this is not true, but liftings satisfying a simple side condition do have this property.
Proposition 18
Suppose \(\tau : P \rightarrow F\) is a natural transformation in \(\mathbf{Set}\), \(T\epsilon : \hat{P}\rightarrow \widetilde{P}\) (Sect. 5.1) is a endolifting morphism from a \(\mathbf{BVal}\) lift of P to an \(\mathbf{ERel}\) lift of P, and \({\hat{F}}\) and \(\widetilde{F}\) are the pushforwards of \(\hat{P}\) and \(\widetilde{P}\) along \(\tau \). Further suppose for every set I, every \(f, f' \in FI\) and \(r: I \times I \rightarrow \mathbb {R}^+\), the lower bound for \(\{\hat{P}r(p, p'): \tau p = f \text { and } \tau p' = f'\}\) is achieved in this set. Then \(T\epsilon \) is a endolifting morphism from \({\hat{F}}\) to \(\widetilde{F}\).
We can now apply this proposition to obtain the following corollary.
Corollary 19
\(T\epsilon \) is a endolifting morphism from \(\mathcal{H}\) to \({{\mathrm{Rel}}}(P_\mathrm{fin})\).
Proof
Proposition 17 shows \(T\epsilon \) is a endolifting morphism from the standard \(\mathbf{BVal}\) lifting for the list functor to the standard \(\mathbf{ERel}\) lifting for the list functor. We know \(\mathcal{H}\) and \({{\mathrm{Rel}}}(P_\mathrm{fin})\) are the pushforwards of these list functors along \(set_X\) in their respective total categories.Footnote 8 Hence to apply Proposition 18 we only need to show for all finite sets \(J, K \subseteq I\), and all distances \(r: I \times I \rightarrow \mathbb {R}^+\), there exist lists \(k^\dagger \) and \(\ell ^\dagger \) such that \(set(k^\dagger ) = J\), \(set(\ell ^\dagger ) = K\) and \(r^*(k^\dagger , \ell ^\dagger ) = \displaystyle {}\inf _{\begin{array}{c} set (k) = J \\ set (\ell ) = K \end{array}} r^*(k, \ell )\). We noted this in the Hausdorff distance section, where these dagger lists represent Gerry’s optimal strategy.
5.3 Approximate Bisimulations: An Example from Control Theory
Here we present an example from a rather different context: approximate bisimulation by Girard and Pappas [8]. Defined as a binary relation on a metric space that is subject to the “mimicking” condition, the notion is widely used in control theory as a quantitative relaxation of usual (Milner-Park) bisimulation that allows bounded errors. Its principal use is in bounding errors caused by some abstraction of dynamical systems: given the original dynamics \({\mathcal {S}}\), one derives its abstraction \({\mathcal {A}}\); by exhibiting an \(\epsilon \)-approximate bisimulation between \({\mathcal {S}}\) and \({\mathcal {A}}\), one then shows that the difference between the trajectory of \({\mathcal {A}}\) and that of \({\mathcal {S}}\) is bounded by \(\epsilon \). Such abstraction methods include: state space discretization (e.g. in [10]) and ignoring switching delays [18]. See [9] for an overview.
In the above scenario, an \(\epsilon \)-approximate bisimulation between \({\mathcal {S}}\) and \({\mathcal {A}}\) is synthesized through analysis of the continuous dynamics of \({\mathcal {S}}\): for example the incremental stability of \({\mathcal {S}}\) yields an approximate bisimulation via its Lyapunov-type witness. Another common strategy for finding an approximate bisimulation is via a bisimulation function. Our goal here is to describe the latter strategy in the current coalgebraic and fibrational framework.
We fix the set O of output values together with a distance function \(d:O\times O\rightarrow \mathbb {R}^+\), and a U-labelled finitely branching LTS \((Q,\delta :Q\rightarrow U\pitchfork P_{fin}Q)\) with an output function \(o:Q\rightarrow O\), where \(\pitchfork \) denotes the power operation [19, p. 70]. An \(\epsilon \)-approximate bisimulation relation is a binary relation \(R\subseteq Q\times Q\) such that
The difference from the usual Milner-Park bisimulation is that R is additionally required to witness the \(\epsilon \)-proximity of outputs of related states q and \(q'\).
A bisimulation function is a quantitative (real-valued) witness for an approximate bisimulation. In many settings in control theory where dynamics are smooth and described by ordinary differential equations, such real-valued functions are easier to come up with than an approximate bisimulation itself. For the above LTS, a function \(v:Q\times Q\rightarrow \mathbb {R}^+\) is a bisimulation function if it satisfies, for each \(q,q'\in Q\),
A crucial fact is that a bisimulation function v gives rise to an \(\epsilon \)-approximate bisimulation \(\{(q,q')~|~v(q,q')\le \epsilon \}\). See e.g. [9].
We move on to give a categorical account of this construction. We use the following functor as a coalgebra signature:
We can then package a U-labelled finitely branching LTS and an output function into a single F-coalgebra \(Q=(Q,\langle o,\delta \rangle :Q\rightarrow FQ)\).
Firstly, the endolifting that captures \(\epsilon \)-approximate bisimulations consists of
Secondly, the endolifting that captures bisimulation functions consists of
Indeed, by unfolding the definitions the following can be observed: \({\tilde{F}}_\epsilon \)-invariants on Q are nothing but \(\epsilon \)-approximate bisimulations; and \({\hat{F}}\)-invariants on Q are bisimulation functions. Thanks to Proposition 17 and Corollary 19, the functor \(T\epsilon \)—that sends a function \(v:Q\times Q\rightarrow \mathbb {R}^+\) to the relation \(\{(q,q')~|~v(q,q')\le \epsilon \}\)—is a endolifting morphism from \({\hat{F}}\) to \({\tilde{F}}\). Therefore \(T\epsilon \) transfers a \({\hat{F}}\)-invariant v on Q to a \({\tilde{F}}_\epsilon \)-invariant \(T\epsilon v\) on Q, that is, a bisimulation function to an \(\epsilon \)-approximate bisimulation.
5.4 Endolifting Morphisms Preserve Final Coalgebras
We next state a result which we can use to ensure that the coinductive invariant in the source of a endolifting morphism is sent to the coinductive invariant in the target of that morphism.
Lemma 20
Suppose H is a endolifting morphism from \((\pi :\mathbb {E}\rightarrow \mathbf{Set},{\dot{F}})\) to \((\rho :\mathbb {F}\rightarrow \mathbf{Set},{\ddot{F}})\) which is also a fibration map. Suppose additionally that H preserves fibred meets. Then \(H(I, \nu {{\dot{F}}}_{(I, f)}) = (I, \nu {{\ddot{F}}}_{(I, f)})\).
Proof
Preservation of top elements ensures \(H\top _{\mathbb {E}_I} = \top _{\mathbb {F}_I}\). Since H is a fibration map and a endolifting morphism, we get \(H(f^*{\dot{F}}(A_I)) = f^* {\ddot{F}}(H(A_I))\) for all \(A_I \in \mathbb {E}_I\). Combining this with the above observation ensures H sends the final sequence in the fiber \(\mathbb {E}_I\) to the final sequence in the fiber \(\mathbb {F}_I\). Finally, H preserving meets ensures H will send the \({\dot{F}}\)-coinductive invariant for (I, f) to the \({\ddot{F}}\)-coinductive invariant for (I, f).
Note \(T\epsilon \) satisfies most of the conditions in this lemma. Since we are interested in concluding something about the kernel of a behavioural metric, we specialize to the case where \(\epsilon = 0\) where these conditions are all satisfied.
Corollary 21
If T0 is a endolifting morphism from \(({\hat{F}}, \mathbf{BVal})\) to \(({\dot{F}}, \mathbf{ERel})\), then the behavioural metric induced by \({\hat{F}}\) has the coalgebraic predicate induced by \({\dot{F}}\) at its kernel.
Proof
\(T\epsilon \) is a fibration map and a right adjoint, and thus preserves all fibred meets.
All our work from the previous section establishing that \(T\epsilon \) is a endolifting morphism from \(\mathcal{H}\) to \({{\mathrm{Rel}}}(P_\mathrm{fin})\) now pays off.
Corollary 22
The Hausdorff behavioural metric on \(P_\mathrm{fin}X\) has \(P_\mathrm{fin}\)-bisimilarity at its kernel.
Above, we also showed T0 is a endolifting morphism between many other \(\mathbf{BVal}\) and \(\mathbf{ERel}\) liftings (Proposition 17). Therefore, we could also derive an analog of Corollary 21 for these pairs and conclude behavioural metrics of the \(\mathbf{BVal}\) lift have bisimilarity (the coalgebraic relation of the corresponding \(\mathbf{ERel}\) lift) at their kernels.
6 Conclusions and Future Work
We presented a fibrational framework for various extensions of (bi)simulation notions. On the categorical side our focus has been on structural aspects of fibrations such as fibration morphisms and lifting by Kan extensions; on the application side we took examples from quantitative reasoning about systems. This has allowed us to capture known constructions in more abstract and general terms, such as the Hausdorff pseudometric and approximate bisimulation in control theory.
As future work, we shall investigate conditions under which the two liftings in Sect. 4—one by left Kan extension and the other involving right Kan extension—coincide. We would then compare this coincidence and the Kantorovich-Wasserstein duality, which is the coincidence of the metric on probability distributions computed by sup and inf. We mentioned that \(\mathbf{Top}\) and \(\mathbf{Meas}\) are examples of \(\mathbf{CLat}_\wedge \)-fibrations; their use in reasoning about systems will also be explored.
Notes
- 1.
In this work we always assume that a cleavage is given to a fibration.
- 2.
In this paper we shall use the word pullback in this fibrational sense. This usage generalizes the word’s common meaning as a limit of a cospan in a category. Specifically, the latter gives a (fibrational) pullback in a codomain fibration. See [14].
- 3.
Throughout this paper, we write \(\mathbb {R}^+= [0, \infty ]\).
- 4.
A b-bounded pseudometric on a set I is a function \(r: I\times I \rightarrow [0, b]\) which satisfies the axioms of a pseudometric: (1) \(r(i, i) = 0\), (2) \(r(i, i') = r(i', i)\), and (3) \(r(i, i'') \le r(i, i') + r(i', i'')\) for all \(i, i', i'' \in I\). A pseudometric drops only the definiteness condition of a metric, so \(r(i, i') = 0\) does not imply \(i = i'\) when r is a pseudometric. This is crucial for our intended application to coalgebras where distinct states may have identical behaviours and we wish the distance between two states to reflect the difference in their behaviours only.
- 5.
The canonical relation lifting can in fact be defined for all functors using image factorization in \(\mathbf{Set}\). We use the less-general inductive version as we will need it in Sect. 5.
- 6.
A more technical proof of the same result proceeds by first showing the Hausdorff distance on the left is a lower bound for \(d^*(k, \ell )\) given the constraints on k and \(\ell \). The fact that J and K are finite is crucial so that the value of the left-hand side must be witnessed at a particular entry in one of the lists. Then it can be shown that this lower bound is sharp by a particular choice of k and \(\ell \) witnessing Gerry’s optimal strategy, so indeed the left-hand side is the greatest lower bound for the collection of values on the right-hand side.
- 7.
Morphisms in each of these categories are \(\mathbf{Set}\)-functions which satisfy conditions regarding the extra data in the total category. (That is, functions which preserve the source relation, shrink the source distance, etc.). It is straightforward to show \(f: X \rightarrow Y\) is a morphism in \(\mathbb {A}\) implies \(f: FX \rightarrow FY\) is a morphism in \(\mathbb {B}\) by writing down the extra conditions on f imposed by \(\mathbb {A}\) and \(\mathbb {B}\) where \(F: \mathbb {A}\rightarrow \mathbb {B}\) is any of the four functors defined above.
- 8.
Recall \(set_X\) from Example 6.
References
Azevedo de Amorim, A., Gaboardi, M., Hsu, J., Katsumata, S.Y., Cherigui, I.: A semantic account of metric preservation. In: Proceedings of the 44th ACM SIGPLAN Symposium on Principles of Programming Languages (POPL 2017), pp. 545–556 (2017). https://doi.org/10.1145/3009837.3009890
Balan, A., Kurz, A., Velebil, J.: Extensions of functors from set to V-cat. In: Proceedings of the 6th Conference on Algebra and Coalgebra in Computer Science (CALCO 2015), pp. 17–34 (2015). https://doi.org/10.4230/LIPIcs.CALCO.2015.17
Baldan, P., Bonchi, F., Kerstan, H., König, B.: Behavioral metrics via functor lifting. In: Proceedings of the 34th International Conference on Foundation of Software Technology and Theoretical Computer Science (FSTTCS 2014), pp. 403–415 (2014). https://doi.org/10.4230/LIPIcs.FSTTCS.2014.403
Borceux, F.: Handbook of Categorical Algebra 2. In: Encyclopedia of Mathematics and Its Applications, vol. 51. Cambridge University Press, Cambridge (1994)
van Breugel, F., Worrell, J.: A behavioural pseudometric for probabilistic transition systems. Theor. Comput. Sci. 331(1), 115–142 (2005)
Chatzikokolakis, K., Gebler, D., Palamidessi, C., Xu, L.: Generalized bisimulation metrics. In: Baldan, P., Gorla, D. (eds.) CONCUR 2014. LNCS, vol. 8704, pp. 32–46. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44584-6_4
Desharnais, J., Jagadeesan, R., Gupta, V., Panangaden, P.: The metric analogue of weak bisimulation for probabilistic processes. In: Proceedings of the 17th IEEE Symposium on Logic in Computer Science (LICS 2002), pp. 413–422 (2002)
Girard, A., Pappas, G.J.: Approximation metrics for discrete and continuous systems. IEEE Trans. Autom. Control 52(5), 782–798 (2007). https://doi.org/10.1109/TAC.2007.895849
Girard, A., Pappas, G.J.: Approximate bisimulation: a bridge between computer science and control theory. Eur. J. Control 17(5–6), 568–578 (2011). https://doi.org/10.3166/ejc.17.568-578
Girard, A., Pola, G., Tabuada, P.: Approximately bisimilar symbolic models for incrementally stable switched systems. IEEE Trans. Autom. Control 55(1), 116–126 (2010)
Hasuo, I., Cho, K., Kataoka, T., Jacobs, B.: Coinductive predicates and final sequences in a fibration. Electron. Notes Theor. Comput. Sci. 298, 197–214 (2013). https://doi.org/10.1016/j.entcs.2013.09.014
Hermida, C., Jacobs, B.: Structural induction and coinduction in a fibrational setting. Inf. Comput. 145(2), 107–152 (1998). https://doi.org/10.1006/inco.1998.2725
Herrlich, H.: Topological functors. Gen. Topol. Appl. 4(2), 125–142 (1974). https://doi.org/10.1016/0016-660X(74)90016-6. http://www.sciencedirect.com/science/article/pii/0016660X74900166
Jacobs, B.: Categorical Logic and Type Theory. Studies in Logic and the Foundations of Mathematics, vol. 141. Elsevier Science, Amsterdam (1999)
Katsumata, S., Sato, T.: Codensity liftings of monads. In: Proceedings of the 6th Conference on Algebra and Coalgebra in Computer Science (CALCO 2015), pp. 156–170 (2015). https://doi.org/10.4230/LIPIcs.CALCO.2015.156
Kelly, G.M.: Basic Concepts of Enriched Category Theory. Lecture Notes in Mathematics, vol. 64. Cambridge University Press, Cambridge (1982)
Kelly, G.M., Rossi, F.: Topological categories with many symmetric monoidal closed structures. Bull. Aust. Math. Soc. 31(1), 41–59 (1985). https://doi.org/10.1017/S0004972700002264
Kido, K., Sedwards, S., Hasuo, I.: Bounding Errors Due to Switching Delays in Incrementally Stable Switched Systems (Extended Version) (2017). arXiv:1712.06311
Lane, S.M.: Categories for the Working Mathematician. Graduate Texts in Mathematics, vol. 5. Springer, New York (1978). https://doi.org/10.1007/978-1-4757-4721-8
Rutten, J.: Universal coalgebra: a theory of systems. Theor. Comput. Sci. 249(1), 3–80 (2000). https://doi.org/10.1016/S0304-3975(00)00056-6
Činčura, J.: Tensor products in the category of topological spaces. Comment. Math. Univ. Carol. 20(3), 431–446 (1979)
Acknowledgement
This research was supported by ERATO HASUO Metamathematics for Systems Design Project (No. JPMJER1603), JST. The authors are grateful to anonymous reviewers, whose constructive comments helped to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 IFIP International Federation for Information Processing
About this paper
Cite this paper
Sprunger, D., Katsumata, Sy., Dubut, J., Hasuo, I. (2018). Fibrational Bisimulations and Quantitative Reasoning. In: Cîrstea, C. (eds) Coalgebraic Methods in Computer Science. CMCS 2018. Lecture Notes in Computer Science(), vol 11202. Springer, Cham. https://doi.org/10.1007/978-3-030-00389-0_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-00389-0_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-00388-3
Online ISBN: 978-3-030-00389-0
eBook Packages: Computer ScienceComputer Science (R0)


 , the pullback lifting
, the pullback lifting 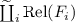 , given that it is a morphism from
, given that it is a morphism from 