Keywords

1 Introduction

There is increasing interest in Photoacoustic tomography (PAT) for both clinical and preclinical imaging [1], as it has the potential to provide molecular and functional information with high spatial resolution [2]. For preclinical imaging it is often possible to make measurements all around the object, but for clinical imaging, PAT scanners with access to just one side of the tissue are typically required. In addition, clinical imaging typically requires high frame rates [3]. The frame rate is determined both by the time taken for the data acquisition as well as by the image reconstruction time. Compressed sensing can dramatically reduce data acquisition time, but then suitable image reconstruction approaches are required, which are typically slow due to the large number of iterations required. This paper proposes to use an approximate and fast model within a deep learning framework for PAT image reconstruction from sparse data measured using a planar scanner.

2 Forward and Inverse Models

2.1 Photoacoustic Tomography

In PAT, a short pulse of near-infrared light is absorbed by chromophores in tissue. For a sufficiently short pulse, a spatially-varying pressure increase f will result, which will initiate an ultrasound (US) pulse (photoacoustic effect), which then propagates to the tissue surface. The measurement consists of the detected waves in space-time at the boundary of the tissue; this set of pressure time series constitutes the PA data g. This acoustic propagation is commonly modeled by the following initial value problem for the wave equation [4],

$$\begin{aligned} (\partial _{tt} - c^2 \varDelta ) p(\mathbf {x},t) = 0, \quad p(\mathbf {x},t = 0) = f(\mathbf {x}), \quad \partial _t p(\mathbf {x},t = 0) = 0. \end{aligned}$$
(1)

The measurement of the PA signal is then modeled as a linear operator \(\mathcal {M}\) acting on the pressure field \(p(\mathbf {x},t)\) restricted to the boundary of the computational domain \(\varOmega \) and a finite time window (see [2, 5] for details on measurement systems):

$$\begin{aligned} g = \mathcal {M} \, p_{|\partial \varOmega \times (0,T)}. \end{aligned}$$
(2)

Equations (1) and (2) define a linear mapping

$$\begin{aligned} Af=g, \end{aligned}$$
(3)

from initial pressure f to measured pressure time series g, which constitutes the acoustic forward problem in PAT. The corresponding image reconstruction step constitutes the acoustic inverse problem to (3).

2.2 Fast Approximate Forward and Inverse Models

When the measurement points lie on a plane (\(z=0\)) outside the support of f, the pressure there can be related to f by [4]:

$$\begin{aligned} p(x,y,t) = \frac{1}{c^2} \mathcal {F}_{k_x,k_y}\left\{ \left\{ \mathcal {C}_{\omega }\left\{ B(k_x,k_y,\omega ) \tilde{f}(k_x,k_y,\omega ) \right\} \right\} \right\} , \end{aligned}$$
(4)

where \(\tilde{f}(k_x,k_y,\omega )\) is obtained from \(\hat{f}(\mathbf {k})\) via the dispersion relation \((\omega /c)^2 = k_x^2+k_y^2+k_z^2\) and \(\hat{f}(\mathbf {k}) = \mathcal {F}_{\mathbf {x}}\{f(\mathbf {x})\}\) is the 3D Fourier transform of \(f(\mathbf {x})\). \(\mathcal {C}_{\omega }\) is a cosine transform from \(\omega \) to t, \(\mathcal {F}_{k_x,k_y}\) is the 2D inverse Fourier Transform on the detector plane. The weighting factor,

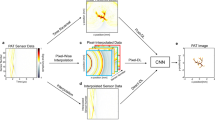
$$\begin{aligned} B(k_x,k_y,\omega ) = \omega /\left( \text {sgn}(\omega )\sqrt{(\omega /c)^2 - k_x^2 - k_y^2}\right) , \end{aligned}$$
(5)

contains an integrable singularity which means that if Eq. (4) is evaluated by discretisation on a rectangular grid, (thus enabling the application of FFT for efficient calculation), then aliasing in p(x, y, t) results. An accurate model employing Eq. (4) would require suitable measures to deal with the singularity, whereas evaluation using FFT leads to a fast but approximate forward model. To control the degree of aliasing, all components of B for which \(k_x^2+k_y^2 > (\omega /c)^2\sin ^2\theta _{\max }\) were set to zero. This is equivalent to assuming only waves arriving at angles up to \(\theta _{\max }\) from normal incidence are detected. There is a trade-off: the greater the range of angles included, the greater the aliasing, as illustrated in Fig. 1.

By inverting Eq. 4, it can also be used as a method for mapping from the measured data g to an estimate of f [6]. In this case, there is no singularity to contend with, but the estimate of f will suffer from limited-view artifacts [7]. We will denote these two k-space methods as \(A_{\mathcal {F}}\) and \(A_{\mathcal {F}}^\dagger \) for the forward and backward projections, respectively.

Fig. 1.
figure 1

Approximate forward model. Top left: 2D phantom with a line detector (red line). Bottom left: ideal data. The effect of two different levels of angle thresholding of the incident waves is shown in the middle column and the resulting backprojection of the approximate data in the right column. (Color figure online)

Full size image

3 Learned Reconstruction with Approximate Models

In order to use an approximate forward model, such as described above, in an iterative reconstruction method, a correction must be incorporated. Here Deep Learning, specifically convolutional neural networks, offer an ideal framework to learn a correction to an approximate model. This can be done in two ways, either by learning an explicit correction of the forward model and subsequently applying an iterative scheme, or learning the correction inside a learned iterative reconstruction scheme. This study will concentrate on the second approach.

3.1 Learned Iterative Reconstruction

Photoacoustic reconstructions from subsampled data measured over a limited detection aperture are typically computed by solving a variational problem as the minimisation of the sum of a data-fidelity term and a regularisation, \(\mathcal {R}\), term enforcing certain regularities of the solution \(f^*\) as

$$\begin{aligned} f^*=\mathop {\mathrm {arg}~\mathrm {min}}\limits _{f} \frac{1}{2}\Vert Af-g\Vert _2^2+ \alpha \mathcal {R}(f), \end{aligned}$$
(6)

where \(\alpha >0\) is a weighting parameter. It has been shown in several studies [8,9,10,11] that these techniques can efficiently deal with the limited view artefacts, but tend to require a larger number of iterations to converge and are additionally limited by the expressibility of the chosen regularisation term. Recently it has been shown that one can instead learn such an iterative scheme to speed up the reconstruction and additionally learn an effective regularisation for the data at hand [12,13,14]. This is achieved by formulating a simple CNN \(G_{\theta _k}\), with learned parameters \(\theta _k\), that computes an iterative update. Given a current iterate \(f_k\), then the CNN combines \(f_k\) with the gradient \(\nabla d(f_k,g)\) of the fidelity term in (6), such that

$$\begin{aligned} f_{k+1}=G_{\theta _k}(f_k,\nabla d(f_k,g)). \end{aligned}$$
(7)

In the following we learn each of the networks separately; i.e. starting with an initial \(f_0\), we train \(G_{\theta _0}\) and compute the update \(f_{1}\) by (7). Then we train the subsequent networks for a set amount of iterates. This separation is done due to computational restrictions in memory and evaluation of the forward and backward projections.

Fig. 2.
figure 2

Network architecture for an iterative gradient update with approximate models. Each network gets the iterate \(f_k\) and the approximate gradient information \(\nabla _\mathcal {F} d(f_k,g) := A_\mathcal {F}^\dagger (A_\mathcal {F}f_k-g)\) as input. The output \(f_{k+1}\) is a residual update to the previous iterate. The multiscale structure is introduced to remove artefacts from the gradient.

Full size image

3.2 An Iterative Gradient Network

We propose to use an approximate model \(A_\mathcal {F}\) as described in Sect. 2.2. This model will be used to compute the gradient information in (7), i.e. we have \(\nabla _\mathcal {F} d(f_k,g) := A_\mathcal {F}^\dagger (A_\mathcal {F}f_k-g)\approx \nabla d(f_k,g)\). By the application of the fast and approximate forward model we introduce artefacts to the gradient information, but these are highly structured, as illustrated in Fig. 1. Multiscale networks, such as a residual U-Net, have been proven to be efficient in detecting and removing artefacts in images [15]. Thus, we believe that a multiscale network can be efficiently used to remove these artefacts. On the other hand, smaller gradient informed networks are more robust to perturbations in the measurement geometry or the imaged target, as suggested in [14].

In this work we propose to balance both approaches, by combining a deep gradient descent network proposed in [14] with a small mutliscale network in order to deal successfully with artefacts in the gradient, while still possessing the ability to generalise well with respect to changes in the measurement geometry. The particular network structure chosen for this application is illustrated in Fig. 2. The two inputs, current iterate \(f_k\) and the approximate gradient \(\nabla _\mathcal {F} d(f_k,g)\), go through two separate convolutional pipelines with filter size \(3^3\). The results are then combined by concatenation and downsampled with a maxpool layer to a courser scale. The result of the courser scale is concatenated with the result of the two initial convolutional pipelines and the channel size successively reduced to one channel, which is added as a residual update to the input iterate \(f_k\) and projected onto the positive set to produce the new iterate \(f_{k+1}\).

4 Computational Results for In-Vivo Measurements

4.1 Data Acquisition and Preparation

In-vivo measurements of a human subject have been taken with the planar sensor described in [16]. For faster acquisition the scanner uses a 16 beam interrogation laser to measure the PA signal. In total we obtained 27 fully-sampled limited-view measurements used in this study. Since this is not sufficient for training an iterative reconstruction algorithm, we have additionally used a large dataset of 1024 volumes of blood vessels segmented from lung CT scans as described in [14] of size \(240\times 240\times 80\). We then simulated accurate sub-sampled limited-view photoacoustic measurement data of the segmented lung vessels with a sub-sampling factor of 4 and a randomly generated 16 beam sub-sampling pattern for each sample, (see Fig. 3 for example patterns). Additionally, we have varied the sound speed in the simulations to be uniformly distributed in \([1560\text {m/s},1600\text {m/s}]\) and added normally distributed noise to the data with varying intensity, such that the resulting signal’s SNR is roughly between 10 to 30. These variations have been done to increase robustness to variations in the measurements.

Fig. 3.
figure 3

Randomly generated sub-sampling pattern with the 16 beam scanner geometry and a sub-sampling factor of 4; black dots indicate interrogated points on the sensor. (Left) Pattern used for experimental sample I, (Right) pattern used for experimental sample II.

Full size image

4.2 Training of Proposed Network

We have pre-trained the networks \(G_{\theta _k}\) on the simulated data from segmented lung vessels. Given the simulated measurement g, the initial reconstruction is computed by the k-space backprojection, i.e. \(f_0=A^\dagger _\mathcal {F}g\), as described in Sect. 2.2. We have trained in total 5 iterative networks \(G_{\theta _k}\) for \(k=0,\dots ,4\). Each network is trained in TensorFlow with the Adam algorithm for 30 epochs with an initial learning rate of \(2\cdot 10^{-4}\) and a \(\ell ^2\)-loss. The training of each iterate takes about 14 hours; with initialisation and computations between iterates the whole pre-training takes a bit under 4 days on a single Titan Xp GPU.

After pre-training we have taken 25 of the in-vivo measurements and produced synthetically 4 times sub-sampled data with a 16 beam pattern. As reference reconstruction we have taken a total variation (TV) constrained reconstruction of the fully-sampled limited-view data. We have then performed an update training of the pre-trained networks with the 25 samples to adjust the algorithm to in-vivo artefacts not present in simulated data. The update training is performed for 8 epochs with a learning rate of \(10^{-4}\) and we minimised the \(\ell ^2\)-error to the reference TV reconstructions from fully-sampled limited-view data.

4.3 Reconstructions of In-Vivo Measurements

The reconstruction with the trained network is performed on 2 samples of in-vivo limited-view measurements with 4 times sub-sampling, the corresponding sub-sampling pattern is shown in Fig. 3. The resulting reconstructions for both samples are shown in Figs. 4 and 5. Evaluation of the projections take each 1.6 s and of the network 0.45 s, hence one iterate takes a bit less than 4 s. The total computation time for 5 iterates with initialisation is about 20 s on a single Titan Xp GPU. For comparison we have computed TV reconstructions of the same sub-sampled data for both test cases. The regularisation parameter was chosen, such that PSNR to the reference reconstruction is maximised. The resulting reconstructions are shown in Fig. 6 and take approximately 11 min.

Fig. 4.
figure 4

Sample I: reconstruction of in-vivo measurements from 4\(\times \) undersampled 16-beam pattern (maximum intensity projections). PSNR in comparison to the reference from fully-sampled limited-view data: backprojection 33.5672, FF-PAT 42.1749.

Full size image
Fig. 5.
figure 5

Sample II: reconstruction of in-vivo measurements from 4\(\times \) undersampled 16 beam pattern (maximum intensity projections). PSNR in comparison to the reference from fully-sampled limited-view data: backprojection 34.4372, FF-PAT 42.0388.

Full size image
Fig. 6.
figure 6

TV reconstructions (20 iterations, maximum intensity projections) of in-vivo measurements from 4\(\times \) undersampled 16-beam pattern. PSNR in comparison to the reference from fully-sampled limited-view data: Sample I 41.1576, Sample II 42.1391.

Full size image

4.4 Discussion

In both cases, the image quality of the Fast Forward PAT (FF-PAT) reconstructions is clearly improved with respect to the initial backprojection. Even though we have used approximate projection operators, the results suggest that the proposed network generalises well and incorporates the approximate gradient in a useful manner. In comparison to the TV reconstruction, FF-PAT is competitive with respect to PSNR computed in comparison to the reference reconstructions: higher for Sample I and similar for Sample II. In terms of visual quality, the FF-PAT reconstructions can be considered superior due to strong blocky artefacts present in the TV reconstructions, especially in the background where small details are present (compare in Sample II). Furthermore, reconstruction times are reduced by a factor of 32. In comparison to learned iterative reconstructions with the accurate model, see [14], image quality is competitive with a speed-up of FF-PAT by factor 8.

5 Conclusions

Iterative reconstructions are necessary in restricted measurement geometries to successively negate limited-view artefacts. This involves the repeated evaluation of forward and backward projections, which can be costly in high-resolution and 3D. We have successfully shown that one can use approximate models instead in a learned iterative reconstruction algorithm, where the network also learns to negate approximation artefacts in the gradient. We achieve a speed-up of up to 32 compared to established TV reconstructions and providing superior reconstructions. While this study applies for planar sensors in PAT, the framework can be extended to different measurement geometries and possibly other modalities.