Abstract
In this chapter we review conventional vector calculus from the standpoint of a generalized exposition in terms of exterior calculus and the theory of forms. This generalization allows us to distill the important elements necessary to operate the basic machinery of conventional vector calculus. This basic machinery is then redefined in a discrete setting to produce appropriate definitions of the domain, boundary, functions, integrals, metric and derivative. These definitions are then employed to demonstrate how the structure of the discrete calculus behaves analogously to the conventional vector calculus in many different ways.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The familiar integration by parts formula,
$$\int_{a}^{b}u\,\mathrm{d}{v}=uv\Bigm |_{a}^{b}-\int_a^bv\,\mathrm{d}{u}$$is simply a corollary to the Fundamental Theorem that uses the product rule of differentiation.
- 2.
In this section we will denote elements of general vector spaces with the common “overbar” notation, as in \(\bar {\boldsymbol {x}}\). This is to distinguish them from vectors in ℝ3 encountered in standard vector calculus, which will be denoted as \(\vec {F}\). We will adopt similar convention for forms, using the “tilde” notation, as in \(\tilde{\boldsymbol{\omega}}\).
- 3.
The distinction between a “differential form” and a “form” (a.k.a. an “algebraic” form or a “linear” form) stems from whether the vector space V is viewed as the tangent space to a manifold, i.e., if
 , in which case the elements of
, in which case the elements of 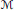 are the differential operators for curves along
are the differential operators for curves along  . Indeed the exterior algebra of forms and many of their geometrical interpretations hold even if V is not considered as a tangent space.
. Indeed the exterior algebra of forms and many of their geometrical interpretations hold even if V is not considered as a tangent space. - 4.
As a simple, illustrative example, consider a one-dimensional coordinate system defined in units of centimeters with a position vector at the origin extending to the location at 500 centimeters. If the unit of measurement were to change from centimeters to meters, the basis vectors will become longer and our position vector, if it physically represents the same position, will now extend only 5 meters. Therefore, the coordinate increments are larger in the new system, but the value of the coefficient describing the contravariant vector is smaller.
- 5.
A Riemannian metric on a manifold
 is a family of positive definite inner products defined at each
is a family of positive definite inner products defined at each  that is differentiable over all
that is differentiable over all 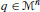 . A manifold equipped with a Riemannian metric is called a Riemannian manifold.
. A manifold equipped with a Riemannian metric is called a Riemannian manifold. - 6.
In the differential forms literature this same process is sometimes described by the so-called musical isomorphisms, ♯ and ♭, where \(\tilde{\boldsymbol{\alpha}}^{\sharp}\) is the contravariant version of the form \(\tilde{\boldsymbol{\alpha}}\), and \(\bar {\boldsymbol {v}}^{\flat}\) is the covariant version of the vector \(\bar {\boldsymbol {v}}\).
- 7.
Note that subsets of
 exist on which \(\tilde{\boldsymbol{\omega }}\) is exact. For example, within the unit disk with the point at the origin removed and a “cut” along the positive x axis θ is single-valued. Changing the topology of the region in this way is analogous to branch cuts that are defined in complex analysis and the theory of Riemann surfaces.
exist on which \(\tilde{\boldsymbol{\omega }}\) is exact. For example, within the unit disk with the point at the origin removed and a “cut” along the positive x axis θ is single-valued. Changing the topology of the region in this way is analogous to branch cuts that are defined in complex analysis and the theory of Riemann surfaces. - 8.
When dealing with complicated, non-orientable spaces, it is often noted that the Hodge star operator maps p-forms to pseudo-(n−p)-forms. Pseudoforms are forms who change sign whenever the orientation specified for the underlying manifold reverses [142]. We will not make the distinction between forms and pseudoforms here, although the concept of pseudoforms may help conceptualize the operation of the discrete Hodge star that maps between the primal and dual complexes (see Sect. 2.3.4). Note that the distinction between forms and pseudoforms is closely related to that of straight and twisted forms, polar and axial vectors, and across and through variables [48].
- 9.
Here the Hodge star is defined as operating only on p-forms, however the Hodge star operator has been recently extended to operate also on p-vectors [189], with several interesting implications.
- 10.
It is also possible to phrase the inner product between two arbitrary p-forms expressed as the exterior product of p individual 1-forms in terms of the inner product defined on 1-forms [99] with the expression
$$ \left\langle {\tilde u^1 \wedge \cdots \wedge \tilde u^p ,\tilde \upsilon ^1 \wedge \cdots \wedge \tilde \upsilon ^p } \right\rangle _p = \det \left( {\left[ {\begin{array}{*{20}c} {\left\langle {\tilde u^1 ,\tilde \upsilon ^1 } \right\rangle } & \cdots & {\left\langle {\tilde u^1 ,\tilde \upsilon ^p } \right\rangle } \\ \vdots & \ddots & \vdots \\ {\left\langle {\tilde u^p ,\tilde \upsilon ^1 } \right\rangle } & \cdots & {\left\langle {\tilde u^p ,\tilde \upsilon ^p } \right\rangle } \\ \end{array}} \right]} \right). $$ - 11.
Here the notation ⇔ is meant to convey that these forms and vectors correspond. Oftentimes the vectorfield corresponding to a form is termed a “proxy” field [48]. Of course it is possible to map a form to its corresponding vector using the metric tensor, but for this discussion we do not require this level of detail.
- 12.
The Laplace–Beltrami operator is a special case of the Laplace–de Rham operator restricted to p=0 and defined on Riemannian manifolds.
- 13.
Cliques play an important role in Markov Random Fields (due to the Hammersley–Clifford Theorem [31]) and the identification of cliques with simplices allows us to consider p-cliques as geometric objects with dimension p.
- 14.
These boundary cells are sometimes referred to as the faces of the p-cell, which can be confused with the usage of the term face to describe a 2-cell. We shall reserve the term “face” for a 2-cell only.
- 15.
We define the incidence matrix as the transpose of \(\boldsymbol {\mathsf {A}}\) and \(\boldsymbol {\mathsf {B}}\) since we will see in the next section that \(\boldsymbol {\mathsf {A}}\) and \(\boldsymbol {\mathsf {B}}\) play a more prominent role than the incidence matrices \(\boldsymbol {\mathsf {A}}^{\mathsf{T}}\) and \(\boldsymbol {\mathsf {B}}^{\mathsf{T}}\).
- 16.
In the remainder of the book, we will adopt Strang’s [360] notation and adopt \(\boldsymbol {\mathsf {x}}\) to represent 0-cochains while using \(\boldsymbol {\mathsf {y}}\) to represent 1-cochains. However, in this chapter we will continue to use \(\boldsymbol {\mathsf {c}}^{p}\) to represent a p-cochain.
- 17.
Recall that integration is a pairing of chains and cochains that does not require any metric information whatsoever.
- 18.
The (oriented) cycle double cover conjecture [340] postulates that every bridgeless graph has a cycle set which admits the type of duality discussed here. See Sect. 4.1.2.1 for more discussion.
- 19.
In the context of finite elements, the search for a definitive discrete Hodge star operator has been elusive [47, 178, 199, 248]. In other discrete calculus formulations—in which the goal is to provide a discretized version of calculus (e.g., [102])—several formulations of the Hodge star operator have been suggested, including the Galerkin–Hodge star operator that has many advantageous properties [248]. However a fundamental difficulty arises in defining an operator that converges in the limit of finer mesh sizes to the continuum operator. In the present framework (i.e., the discrete formulation of calculus) the definition of the Hodge star is straightforward and is provided by the well-defined inner product on any cochain basis, all of which are finite-dimensional.
- 20.
So as to not deviate completely from the literature, we forgo cumbersome but explicit notation, e.g., ⋆ p and \(\star_{n-p}^{-1}\), that could be employed to help limit the ambiguity of this overloaded operator.
- 21.
Throughout the applications sections of the book, multiple scalar (data) fields associated with a node will be referred to as a tuple and denoted as \(\tilde{x}\). In contrast, the word vector will be reserved for either conventional (continuous) vectors denoted as \(\vec{x}\) or column vectors denoted as \(\boldsymbol {\mathsf {x}}\).
- 22.
We employ the term flow field to represent a 1-cochain throughout the text. This term is used because flows are common 1-cochains (e.g., the maximum flow problem optimizes a 1-cochain) and the term instills a sense of direction for the flow through each edge.
References
Agarwal, S., Branson, K., Belongie, S.: Higher order learning with graphs. In: Proc. of the 23rd Int. Conf. on Mach. Learn., vol. 148, pp. 17–24 (2006)
Apostol, T.M.: Calculus, vol. 1, 2nd edn. Wiley, New York (1967)
Belkin, M., Niyogi, P.: Laplacian eigenmaps and spectral techniques for embedding and clustering. In: Advances in Neural Information Processing Systems, vol. 14, pp. 585–591. MIT Press, Cambridge (2001)
Bell, N., Hirani, A.N.: PyDEC: A Python library for Discrete Exterior Calculus. http://code.google.com/p/pydec/ (2008)
Bell, N., Hirani, A.N.: PyDEC: Algorithms and software for Discretization of Exterior Calculus (2010, in preparation)
Besag, J.: Spatial interaction and the statistical analysis of lattice systems. Journal of the Royal Statistical Society. Series B 36(2), 192–236 (1974)
Biggs, N.: Algebraic Graph Theory. Cambridge Tracts in Mathematics, vol. 67. Cambridge University Press, Cambridge (1974)
Biggs, N.: Algebraic potential theory on graphs. Bulletin of the London Mathematical Society 29, 641–682 (1997)
Bochev, P.B., Hyman, J.M.: Principles of mimetic discretizations of differential operators. In: Arnold, D.N., Bochev, P.B., Lehoucq, R.B., Nicolaides, R.A., Shashkov, M. (eds.) Compatible Spatial Discretizations. The IMA Volumes in Mathematics and Its Applications, vol. 142, pp. 89–119. Springer, New York (2006)
Bossavit, A.: Computational Electromagnetism. Academic Press, San Diego (1998)
Bossavit, A.: Applied differential geometry—a compendium. http://butler.cc.tut.fi/~bossavit/BackupICM/Compendium.html (2005)
Boykov, Y., Kolmogorov, V.: Computing geodesics and minimal surfaces via graph cuts. In: Proceedings of International Conference on Computer Vision, vol. 1 (2003)
Branin, F.H. Jr.: The algebraic-topological basis for network analogies and the vector calculus. In: Proc. of Conf. on Generalized Networks, pp. 453–491, Brooklyn, NY (1966)
Cheeger, J.: A lower bound for the smallest eigenvalue of the Laplacian. In: Gunning, R. (ed.) Problems in Analysis, pp. 195–199. Princeton University Press, Princeton (1970)
Chung, F.: Laplacians and the Cheeger inequality for directed graphs. Annals of Combinatorics 9(1), 1–19 (2005)
Chung, F.R.K.: The Laplacian of a hypergraph. In: Proc. of a DIMACS Workshop, Discrete Math. Theoret. Comput. Sci., vol. 10, pp. 21–36. Am. Math. Soc., Providence (1993)
Chung, F.R.K.: Spectral Graph Theory. Regional Conference Series in Mathematics, vol. 92. Am. Math. Soc., Providence (1997)
Darling, R.: Differential Forms and Connections. Cambridge University Press, Cambridge (1994)
Desbrun, M., Hirani, A.N., Leok, M., Marsden, J.E.: Discrete exterior calculus. arXiv:math.DG/0508341 (2005)
Desbrun, M., Kanso, E., Tong, Y.: Discrete differential forms for computational modeling. In: Proc. of SIGGRAPH (2005)
Desbrun, M., Polthier, K.: Discrete differential geometry. Computer Aided Geometric Design 24(8–9), 427 (2007)
Dodziuk, J.: Difference equations, isoperimetric inequality and the transience of certain random walks. Transactions of the American Mathematical Society 284, 787–794 (1984)
Dodziuk, J., Kendall, W.S.: Combinatorial Laplacians and isoperimetric inequality. In: Ellworthy, K.D. (ed.) From Local Times to Global Geometry, Control and Physics. Pitman Research Notes in Mathematics Series, vol. 150, pp. 68–74. Longman, Harlow (1986)
Doyle, P., Snell, L.: Random Walks and Electric Networks. Carus Mathematical Monographs, vol. 22. Math. Assoc. Am., Washington (1984)
Eckmann, B.: Harmonische Funktionen und Randwertaufgaben in einem Komplex. Commentarii Mathematici Helvetici 17, 240–245 (1945)
Evans, L.C.: Partial Differential Equations. Graduate Studies in Mathematics, vol. 19. Am. Math. Soc., Providence (2000)
Flanders, H.: Differential Forms. Academic Press, New York (1963)
Frankel, T.: The Geometry of Physics: An Introduction, 2nd edn. Cambridge University Press, Cambridge (2004)
Grady, L.: Random walks for image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence 28(11), 1768–1783 (2006)
Gross, P.W., Kotiuga, P.R.: Electromagnetic Theory and Computation: A Topological Approach. Cambridge University Press, Cambridge (2004)
Harrison, J.: Geometric Hodge star operator with applications to the theorems of Gauss and Green. Mathematical Proceedings of the Cambridge Philosophical Society 140(1), 135–155 (2006). doi:10.1017/S0305004105008716
Hassin, R.: Maximum flow in (s, t) planar networks. Information Processing Letters 13(3), 107 (1981)
Hestenes, D.: Space-Time Algebra. Gordon and Breach, New York (1966)
Hiptmair, R.: Discrete Hodge-operators: an algebraic perspective. In: Teixeira, F.L. (ed.) Geometric Methods for Computational Electromagnetics. Progress in Electromagnetics Research, vol. 32, pp. 247–269. EMW Publishing, Cambridge (2001). Chap. 10
Hirani, A.N.: Discrete exterior calculus. Ph.D. thesis, California Institute of Technology (2003)
Jancewicz, B.: The extended Grassmann algebra of ℝ3. In: Baylis, W.E. (ed.) Clifford (Geometric) Algebras with Applications to Physics, Mathematics, and Engineering, pp. 389–421. Birkhäuser, Boston (1996). Chap. 28.
Jiang, X., Lim, L.H., Yao, Y., Ye, Y.: Statistical ranking and combinatorial Hodge theory. Mathematical Programming (to appear)
Kirchhoff, G.: Über die Auflösung der Gleichungen, auf welche man bei der Untersuchung der linearen Verteilung galvanischer Ströme geführt wird. Annalen der Physik und Chemie 72, 497–508 (1847)
Kotiuga, P.: Theoretical limitations of discrete exterior calculus in the context of computational electromagnetics. IEEE Transactions on Magnetics 44(6), 1162–1165 (2008). doi:10.1109/TMAG.2007.915998
Lichnerowicz, A.: Théorie globale des connexions et des groupes d’holonomie. Edizioni Cremonese, Roma (1962)
Mattiusi, C.: The finite volume, finite difference, and finite elements methods as numerical methods for physical field problems. Advances in Imaging and Electron Physics 113, 1–146 (2000)
Matveev, S.V.: Lectures on Algebraic Topology. EMS Series of Lectures in Mathematics. European Mathematical Society, Zürich (2006)
Milnor, J.: On the relationship between differentiable manifolds and combinatorial manifolds. In: Collected Papers of John Milnor, vol. III: Differential Topology, pp. 19–28. Am. Math. Soc., Providence (1956)
Muhammad, A., Egerstedt, M.: Control using higher order Laplacians in network topologies. In: Proc. of the 17th Int. Symp. on Math. Theory of Networks and Systems, pp. 1024–1038 (2006)
Munkres, J.R.: Elements of Algebraic Topology. Perseus Books, Cambridge (1986)
Nemhauser, G.L., Wolsey, L.A.: Integer and Combinatorial Optimization. Wiley-Interscience, New York (1999)
Papadimitriou, C.H., Steiglitz, K.: Combinatorial Optimization. Dover, New York (1998)
Poincaré, H.: Analysis situs. Journal de l’École Polytechnique 2(1), 1–123 (1895)
Roth, J.P.: An application of algebraic topology to numerical analysis: On the existence of a solution to the network problem. Proceedings of the National Academy of Sciences of the United States of America 41(7), 518–521 (1955)
Schutz, B.F.: Geometrical Methods of Mathematical Physics. Cambridge University Press, Cambridge (1980)
Seymour, P.: Sums of circuits. In: Bondy, J.A., Murty, U.R.S. (eds.) Graph Theory and Related Topics, pp. 341–355. Academic Press, New York (1979)
Shi, J., Malik, J.: Normalized cuts and image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence 22(8), 888–905 (2000)
Spivak, M.: A Comprehensive Introduction to Differential Geometry, vol. 1, 3rd edn. Publish or Perish, Houston (2005)
Strang, G.: Introduction to Applied Mathematics. Wellesley-Cambridge Press, Wellesley (1986)
Strang, G.: Computational Science and Engineering. Wellesley-Cambridge Press, Wellesley (2007)
Sullivan, J.M.: A crystalline approximation theorem for hypersurfaces. Ph.D. thesis, Princeton University, Princeton, NJ (1990)
Tonti, E.: On the geometrical structure of the electromagnetism. In: Gravitation, Electromagnetism and Geometrical Structures, for the 80th Birthday of A. Lichnerowicz, pp. 281–308. Pitagora Editrice, Bologna (1995)
Tonti, E.: A direct discrete formulation of field laws: The cell method. Computer Modeling in Engineering and Sciences 2(2), 237–258 (2001)
Veblen, O., Whitehead, J.: The Foundations of Differential Geometry. Cambridge University Press, Cambridge (1932)
Warnick, K.F., Selfridge, R.H., Arnold, D.V.: Teaching electromagnetic field theory using differential forms. IEEE Transactions on Education 40(1), 53–68 (1997)
Weinreich, G.: Geometrical Vectors. University of Chicago Press, Chicago (1998)
Weyl, H.: Repartición de corriente en una red conductora. Revista Matemática Hispano-Americana 5(6), 153–164 (1923)
Whitney, H.: Non-separable and planar graphs. Transactions of the American Mathematical Society 34, 339–362 (1932)
Whitney, H.: Geometric Integration Theory. Princeton University Press, Princeton (1957)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2010 Springer-Verlag London Limited
About this chapter
Cite this chapter
Grady, L.J., Polimeni, J.R. (2010). Introduction to Discrete Calculus. In: Discrete Calculus. Springer, London. https://doi.org/10.1007/978-1-84996-290-2_2
Download citation
DOI: https://doi.org/10.1007/978-1-84996-290-2_2
Publisher Name: Springer, London
Print ISBN: 978-1-84996-289-6
Online ISBN: 978-1-84996-290-2
eBook Packages: Computer ScienceComputer Science (R0)


 , in which case the elements of
, in which case the elements of 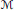 are the differential operators for curves along
are the differential operators for curves along  . Indeed the exterior algebra of forms and many of their geometrical interpretations hold even if V is not considered as a tangent space.
. Indeed the exterior algebra of forms and many of their geometrical interpretations hold even if V is not considered as a tangent space. is a family of positive definite inner products defined at each
is a family of positive definite inner products defined at each  that is differentiable over all
that is differentiable over all 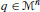 . A manifold equipped with a Riemannian metric is called a Riemannian manifold.
. A manifold equipped with a Riemannian metric is called a Riemannian manifold. exist on which
exist on which