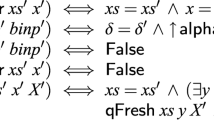CSP is Expressive Enough for π

Abstract

Recent results show that Hoare’s CSP, augmented by one additional operator, can express every operator whose operational semantics are expressible in a new notation and are therefore “CSP-like.” In this paper we show that π-calculus fits into this framework and therefore has CSP semantics. Rather than relying on the machinery of the earlier result we develop a much simpler version from scratch that avoids the extra operator and is sufficient for π-calculus: a much generalised relabelling operator that is expressed in terms of the others. We present a number of different options for the semantics of fresh names, showing how they give semantics that are largely congruent to each other. Finally, we begin the investigation of how these new semantics might be analysed and exploited.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

16.1 Introduction

When I contributed [15] to the volume celebrating Tony’s 60th birthday, CSP was just half as old as it is now. I wrote then how remarkable it was that it should have stood the test of so many challenges unimagined by Tony when he created it, and of how frustrating it was to work academically on something that was so “right first time,” since one was denied the usual joys of refining and changing it. I have continued to be surprised by its ability to capture new concepts in modelling concurrency and interaction. The present paper recalls recent work quantifying this expressive power and shows that CSP can both represent the π-calculus and provide the vehicle for a wide range of new semantics for that notation.

I can report, however, that my previous frustration has been reduced, since I have finally found an operator to be missing from Tony’s original CSP: this will be described below.

When I first described my new expressibility results to Tony, part of his response was “Which operators of CCS satisfy your definition? Which ones don’t? What about π-calculus?” This paper answers these questions.

While other languages for concurrent systems are often defined in terms of their operational semantics, the CSP approach [6, 16] has always been to regard behavioural models such as traces $\mathcal{T}$, stable failures $\mathcal{F}$, failures-divergences $\mathcal{N}$ and infinite traces-failures-divergences $\mathcal{U}$ as equally important means of expression. Thus any operator must make sense over these behavioural models in which details of individual linear runs of the processes are recorded by an observer who cannot, of course, see the internal action τ.

Nevertheless CSP has a well-established operational semantics, and congruence with that is perhaps the main criterion for the acceptability of any new model that is proposed.

Operational semantic definitions of languages have the advantage that they are direct, understandable, and of themselves carry no particular obligation to prove congruence results such as those alluded to above. On the other hand definitions in abstract models, intended to capture the extensional meaning of a program in some sense, have the advantage of “cleanliness” and allow us to reason about programs in the more abstract models. The most immediate benefit of CSP models in this respect is that they bring a theory of refinement, which in turn gives refinement checking (with low complexity at the implementation end, as in FDR) as a natural vehicle for specification and verification.

The author has recently [20] defined what it means for an operational semantics to be CSP-like, in the sense that it does not require any basic powers beyond what the semantics of the various CSP operators already have. In this paper we will show that the π-calculus (the version presented in [23]) is CSP-like.

The main result of [20] is that every CSP-like operator can be simulated up to strong bisimulation in CSP extended by one more operator. The proof there constructs a very general but complex “machine” for simulating any such operator. In the present paper we will give significantly more straightforward CSP representations (not needing the additional operator) of the constructs we need to give π-calculus a semantics.

In the next section we recall the definitions of a CSP-like operational semantics and the new operator Θ _A needed to complete the general simulation result, as well as summarising the techniques used in that proof. In the following section we will, since it is needed for π-calculus, show how the usual CSP renaming operator can be extended into a much generalised relabelling operator that can nevertheless be expressed in terms of standard CSP operators.

There are three significant issues that arise when attempting to give a CSP semantics to π-calculus. The first is the π-calculus containing choices such as τ.P+x(y) ⋅Q that are resolved by τ; while no CSP operator ever reacts to one of its arguments performing the invisible τ. The second is that the CCS parallel operator used in π-calculus is very different to that in CSP. The third is the requirement that names in π-calculus are generated freshly, without collisions. Since the first two of these arise in CCS, we examine the problem of translating CCS into CSP in Section 16.4. The third problem is handled using generalised relabelling in Section 16.5, where the translation into CSP of π-calculus is presented.

There seems to be quite a bit of choice in how one handles freshness in the CSP model, and we present a number of options that give (at least for the best-known CSP models) the same equivalence between π-calculus terms.

Throughout this paper, when talking primarily about CSP, Σ ₀ will denote the alphabet that our underlying language of processes uses to communicate with each other and with the external environment. We will frequently need to extend this alphabet to allow us to build CSP models of operators not directly contained in CSP. This extended alphabet will be termed Σ. We will later define a corresponding alphabet Σ _π for the embedding of π-calculus into CSP.

Our main references for CSP and π-calculus are respectively [16] and [23]. Our notation is drawn largely from these.

16.2 CSP is Very Expressive

Though originally given semantics in behavioural models such as traces $\mathcal{T}$ and failures-divergences $\mathcal{N}$, CSP has long had a congruent operational semantics [2, 4]. By congruent here, we mean that the sets of behaviours obtained by observing the LTS created by a process’s operational semantics are the same as those calculated in the corresponding behavioural model by a denotational semantics. The operational semantics of CSP and some congruence proofs can be found in [16].

There is a lengthy discussion of what makes an operationally defined operator CSP-like in [20]. The first part of the conclusion is that a CSP-like operator has a two-part arity (m,I), where m is the finite number of process arguments that are turned on at the start of execution, and I indexes a possibly infinite family of arguments that are initially off. (Infinite nondeterministic choice and ?x :A→P(x) for infinite A both have I infinite and m=0. The first action of either of these constructs selects a single one of these off operands to turn on, and the rest are discarded.)

When defining a family of operators {OP _λ∣λ∈Λ}, the actions of OP _λ(P ₁,…,P _m(λ),Q) are determined by λ and the initial actions of the on arguments P _i :they are all the actions deducible under a set of rules determined by λ. There are two sorts of rule:

• A rule promoting a τ action for each on argument: these take the form:

  $$\frac{{P}_{i}{ \tau \atop \rightarrow } {P}_{i}^{\prime}} {OP({P}_{1},\ldots,{P}_{i},\ldots,{P}_{m},\mathbf{Q}){ \tau \atop \rightarrow } OP({P}_{1},\ldots,{P^{\prime}}_{i},\ldots,{P}_{m},\mathbf{Q})}$$

  First suggested for CSP in [13], these are termed patience rules by van Glabbeek [25] when giving a set of operational rules that respect weak bisimulation.

• An arbitrary collection of rules based on the visible actions of the P _i . Each such rule of OP _λ is represented as a tuple (ϕ,x,β,f,ψ,χ) where

  • ϕ is a partial function from {1,…,m(λ)} to Σ ₀ (the alphabet of the underlying processes). Its meaning is that, in order for this transition to fire, each argument P _j such that j∈dom(ϕ) must be able to perform the action ϕ(j) and become some P′ _j . Note that this imposes no condition if dom(ϕ) is empty: this corresponds to an action that the operator can perform without reference to an on argument, like the initial a in a→P.

  • x is the action in Σ ₀ ∪{ τ} that OP _λ (P,Q) performs as a consequence of the condition expressed in ϕ being satisfied.

  • β is the index of the operator that forms the result state of this action.

  • f is a total function from {1,…,k} for some k=k(λ)≥0 to I(λ) that represents, in some chosen order, the indexes of the components of Q (the off arguments), that are started up when the rule fires (i.e. become on).

  • ψ :{ 1,…,m(β){→} 1,…,m(λ)+k(λ)} is the (total) function that selects each of the resulting state’s on arguments. It must include the whole of {m(λ)+1,…,m(λ)+k(λ)} in its range.

  • χ :I(β)→I(λ) is the total function that selects the off arguments of OP _β .

These rules give us all the information we need to form the state that results after the action it generates once we state the following. Whenever an on argument P _i is present in the result state, then it is in its original state if i∉dom(ϕ) and, if ϕ(i)=a then P _i is in state P _i ′ such that ${P}_{i}{ a \atop \rightarrow } {P}_{i}^{\prime}$ in the result.

To illustrate this way of representing operators, we will show how some CSP+ operators fit into this framework. None of them, in fact, need to be defined together with any other operator apart from the identity id whose arity is $(1,\emptyset )$ and which has the rules $\{(\{(1,a)\},a,\mathbf{id},\emptyset,\{(1,1)\},\emptyset )\mid a \in {\Sigma }_{0}\}$. Here and below we represent the same functions and partial functions as sets of pairs.

• a→ ⋅has arity (0,{−1}) and the single rule $(\emptyset,a,\mathbf{id},\{(1,-1)\},\{(1,1)\},\emptyset )$. We have used a negative number to index the off argument since it is a convenient way of making sure that they are disjoint from the on indices. id is (the index of) the identity operator. Thus here k=1 (the number of off arguments turned on) and the resulting operator id has no off arguments.

• □ has arity $(2,\emptyset )$ and, for each a∈Σ ₀, the rules$(\{(1,a)\},a,\mathbf{id},\emptyset,\{(1,1)\},\emptyset )$ and $(\{(2,a)\},a,\mathbf{id},\emptyset,\{(1,2)\},\emptyset )$.

• ∖X has arity $(1,\emptyset )$ and the rules $(\{(1,a)\},\tau, \backslash X,\emptyset,\{(1,1)\},\emptyset )$ for all a∈X and $(\{(1,a)\},a,\backslash X,\emptyset,\{(1,1)\},\emptyset )$ for all a∈Σ ₀∖X.

• ∥ _X has arity $(2,\emptyset )$ and rules $(\{(1,a),(2,a)\},a,\parallel_{X},\emptyset,\{(1,1),(2,2)\},\emptyset )$ for all a∈X and both $(\{(1,a)\},a,\parallel_{X},\emptyset,\{(1,1),(2,2)\},\emptyset )$ and {(2,a)},a,∥ _X ,$\emptyset,\{(1,1),(2,2)\},\emptyset )$ for all a∉X.

• △(interrupt) has arity $(2,\emptyset )$ and, for each a∈Σ ₀, the rules$(\{(1,a),a,\bigtriangleup,\emptyset,\{(1,1),(2,2)\},\emptyset )$ and $(\{(2,a),a,\mathbf{id},\emptyset,\{(1,2)\},\emptyset )$. This is the interrupt operator.

The reader might like to compare these with the conventional (Structured Operational Semantics, or SOS) descriptions of the operational semantics of CSP given in Chapter 7 of [16]. They express exactly the same semantics when combined with the principle of promoting τs from on arguments. In fact, the CSP-like operators are precisely those that can be presented in this way. It is, however, possible to describe many operators in the SOS style which cannot be translated into the above form: those that are not CSP-like.

Consider the CSP-like operator P Θ _A Q, which we will read P throw Q. It has arity (1,{−1}) and the rule $(\{(1,a)\},a,\mathbf{id},\{(1,-1)\},\{(1,1)\},\emptyset )$ for each a∈A as well as $(\{(1,b)\},b,{\Theta }_{A},\emptyset,\{(1,1)\},\{(-1,-1)\})$ for each b∈Σ ₀ - A.

PΘ _A Q runs the process P until it communicates an event in A – which you might think of as a set of exceptions – at which point it hands control over directly to Q. It has much in common with the interrupt operator△, except that here it is an event of P rather than one of Q that triggers the hand-over to Q: in PΘ _A Q you could say that P passes the baton over to A, whereas, in P△Q, Q can take it at any time by performing a visible event.

In [19], the author showed that Θ _A adds strictly to the expressive power of the CSP language and that△can be expressed in terms of Θ _A and the rest of CSP.

In [20], the author showed that CSP+(CSP augmented by Θ _A ) is capable of simulating any operator with CSP-like operational semantics: for any such operator OP(P ₁,…,P _m ,Q) we can define a CSP+context C _OP (P ₁,…,P _m ,Q) that is strongly bisimilar to it. This is done by building a complex “machine” that can interpret any rule of the form outlined above appropriately, and always have the right set of argument processes turned on so that the right τs are promoted by CSP.

One of the most important consequences of this result is the following: every language whose operators are all CSP-like has a denotational semantics in every denotational model of CSP. Thus, by showing that a language is CSP-like in this way one simultaneously equips it with many different new semantic models with an automatic representation in each.

The established denotational models of CSP take the form of recording one or more sorts of behaviour that an observer might see on a single run of the process: these are linear as opposed to branching behaviours. In [17, 18], the author defined what a behavioural model of CSP is in the cases of finite observation models and divergence-strict models. These are congruences that are relational images of two specific models. In the finite observation case this is the model $\mathcal{F}\mathcal{L}$ that observes sequences of the form

$$\begin{array}{rcl} \langle {A}_{0},{b}_{1},{A}_{1},{b}_{2},\ldots,{A}_{n-1},{b}_{n},{A}_{n}\rangle & & \\ \end{array}$$

where the b _i are the visible events performed by the process, and A _i is either the stable acceptance set offered by the process in the state from which b _i+1 occurs, or • meaning that stability was not observed. The final acceptance set can be $\emptyset$, meaning that the process is deadlocked.

In the strict divergence case, two further components are added to get a model ${\mathcal{F}\mathcal{L}}^{\Downarrow \omega }$: infinite sequences of the same sort, and finite sequences with the final A _n replaced by ⇑, meaning that the process divergences (performs an infinite sequence of τ actions). By strict divergence we mean that all extensions of any divergence are also considered to be behaviours of the process: no attempt is made to distinguish two processes on the basis of what they can or cannot do after their first possibility to diverge.

The infinite sequence case is necessary to get a congruence for CSP if unboundedly nondeterministic constructs are used. We will find that π-calculus is an exception to this rule.

In the original draft of [20], the π-calculus was used as an example to show how general the concept of a CSP-like operational semantics is. We there demonstrated the existence of a CSP semantics for it as a consequence of the above result. The complexity of our simulation machine means, however, that its translation into CSP+is scarcely clear, and the fact that Θ _A is not actually required becomes obscured.

The present paper therefore refines these techniques so that the translation into standard CSP, and hence the structure of the resulting semantics in CSP’s models, become significantly clearer.

16.3 Generalised Relabelling

The main challenge we will have to meet in giving a CSP semantics to π-calculus is dealing with the concept of fresh names. We will find ourselves needing to change names on-the-fly as a process progresses, in a way that is much more flexible than the usual CSP renaming operator P[[R]]. Therefore, in this section, we introduce a generalised relabelling operator P〈〈G〉〉 and show that it can be expressed using a combination of standard CSP operators.

CSP has two operators that work by changing the labels on a process’s actions: hiding and renaming. The first changes a selection of labels to τ and the second maps each action of a process P to a selection of one or more. In each case the mapping on labels does not change as the process progresses, and no action is blocked from occurring.

We can regard both these operators as instances of relabelling: replacing each visible action of P with an action (or perhaps a choice of actions). We call this “relabelling” rather than “renaming” because x may be τ and so invisible to the environment.¹ As hiding shows, there is no reason why a visible action should not be replaced by τ. It would, however, not be CSP-like even to let the operator notice τ’s performed by P: these must always be promoted as τs. In generalised relabelling, we will allow two features not seen in either renaming or hiding:

• We will allow the replacement mapping to vary as the process progresses.

• We will allow the replacement mapping to forbid certain visible actions by P: such actions will map to empty choices of options. So, for example, P∥ _A STOP equivalent to the generalised relabelling that maps every event not in A to itself, and has no image for events in A.

The second of these points is clear cut. The first leaves it open as to what can influence the variation of the mapping. It might be the sequence of visible events that P has performed; it might be the sequence of events that these have been mapped to; or it might be nondeterministic. Or, of course, it might be any combination of these. We will initially consider the first of these, which covers the case of the first generalised renaming HDT used in this paper.

Suppose G is a relation on Σ ₀, ${\Sigma }_{0}^{{_\ast}}$ and ${\Sigma }_{0}^{\tau }$, where (a,t,x)∈G says that whenever process P can perform the event a after trace t, the relabelled process P〈〈G〉〉 can perform x. We can give this operator a natural, CSP-like, operational semantics in SOS style as follows:

$$\frac{P{ \tau \atop \rightarrow } P^{\prime}} {P\langle \!\langle G\rangle \!\rangle { \tau \atop \rightarrow } P^{\prime}\langle \!\langle G\rangle \!\rangle }\qquad \frac{P{ a \atop \rightarrow } P^{\prime},(a,\langle \rangle,x) \in G} {P\langle \!\langle G\rangle \!\rangle { x \atop \rightarrow } P^{\prime}\langle \!\langle G/\langle a\rangle \rangle \!\rangle }$$

where $G/t =\{ (a,s,x) | (s,t\hat{ }s,x) \in G\}$.

In our new style of presenting operational semantics, this translates to 〈〈G〉〉 having the rule $(\{(1,a)\},x,\langle \!\langle G/\langle a\rangle \rangle \!\rangle,\emptyset,\{(1,1)\},\emptyset )$ for each (a,〈〉,x)∈G.

Adapting the techniques developed for the most straightforward case of the main theorem of [20], we can re-cast the above operator using two conventional renamings (one one-to-many and one many-to-one), parallel composition with a regulator process, and the hiding of a single event.

We extend the alphabet Σ to include all pairs of the form (a,x) for a∈Σ ₀ and $x \in {\Sigma }_{0} \cup \{ \tau \} = {\Sigma }_{0}^{\tau }$ as well as the alphabet Σ ₀ of the original processes and the special visible event tau, which takes the place of τ in building up the semantics, and will actually become τ via hiding at the outermost level, as we will see below.

We can define two renamings:

$$\begin{array}{rcl} E =\{ (a,(a,x))\mid a \in {\Sigma }_{0} \wedge x \in {\Sigma }_{0}^{\tau }\}\quad C =\{ ((a,x),\underline{x})\mid a \in {\Sigma }_{ 0} \wedge x \in {\Sigma }_{0}^{\tau }\}& & \\ \end{array}$$

where $\underline{a} = a$ for a∈Σ ₀, and $\underline{\tau } = tau$.

Clearly P[[E]][[C]] maps every event of P to all events in Σ ₀ ∪ {tau}, but we can be a lot more selective by running P[[E]] in parallel with a regulator process. Define

$$\begin{array}{rcl} Reg(G) = \square \{(a,x) \rightarrow Reg(G/\langle a\rangle )\mid (a,\langle \rangle,x) \in G\}& & \\ \end{array}$$

It should be clear that

$$\begin{array}{rcl} (P[[E]] \parallel_{\Sigma} Reg(G))[[C]] \backslash \{tau\}\qquad ({\ast})& & \\ \end{array}$$

has precisely the same actions as P〈〈G〉〉, and that these two processes are strongly bisimilar on the assumption that the guarded recursion defining Reg(G) does not introduce any τ actions (as discussed in [20], there are two alternative operational semantics for recursion in CSP, one of which introduces a τ for each unfolding and one of which does not).

It is obviously important for practical purposes whether G is, or is not, finitary (respectively finitary relative to P) in the sense that G∕s has only finitely many values as s varies (or varies over the traces of P). For we will be able to simulate Q〈〈G〉〉 for general Q (or P〈〈G〉〉 for specific P) using a finite-state regulator just when these apply.

This implementation illustrates how the concept of one-to-many renaming in CSP, as introduced by Hoare, is enormously powerful in allowing us to express a wide variety of constructs that seem at first sight to be beyond what CSP can express. Even more elaborate one-to-many renamings are used in creating the machine in [20].

As well as conventional renaming and hiding (both history independent in the sense that the relabelling does not depend on what actions have occurred before), the following operations on processes are instances of finitary relabellings:

• Hide every second visible event performed by P.

• Hide all visible events equal to the preceding one.

• Rename all odd-numbered tock events to tick.

• Prevent all a actions not immediately preceded by member of A.

Rather than deriving the regulator process from G, we can gain maximum freedom in allowing the mapping to vary by instead allowing Reg to be any divergence-free process whose alphabet is ${\Sigma }_{0} \times {\Sigma }_{0}^{\tau }$. The relabelling will be said to be deterministic just when Reg is.

We will use this format for presenting most of the relabellings in this paper, even when they could have been given in terms of relations.

16.4 CCS

Since π-calculus is built on top of CCS [9, 10], it is useful to consider that language before proceeding to our ultimate goal.

There is a CCS operator, namely+, that stands out as not being CSP-like, since this can be resolved by a τ action performed by either of its operands. This is impossible for CSP-like operators since they have to promote τs without changing their own state. Apart from that, the constant Nil is equivalent to the CSP STOP; the operational semantics of α.P for α≠τ are identical to those of CSP prefix or prefix-choice. The semantics of recursion in CCS is essentially² identical to the non-τ version in CSP, and the CCS relabelling operation is a case of CSP renaming. Let us consider the rest of the language: parallel composition|, and restriction∖α.

The structure of Σ ₀ (as we again call the set of visible action names used in creating processes) with an operator $\overline{\alpha }$ (with $\overline{\overline{\alpha }} = \alpha$ and $\overline{\alpha }\neq \alpha$) causes no difficulties to CSP, although naturally the usual CSP notation does not automatically handle the relationship between α and $\overline{\alpha }$: it has to be programmed explicitly as we do in the CSP model of|below.

The CCS restriction operator has semantics

$$\frac{P{ x \atop \rightarrow } P^{\prime}} {P \backslash \alpha { x \atop \rightarrow } P^{\prime} \backslash \alpha }(x\not\in \{\alpha,\overline{\alpha }\})$$

Since α is not τ, this is trivially CSP-like, and indeed is equivalent to the CSP construct $P \parallel_{\{\alpha,\overline{\alpha }\}}STOP$ as well as being a generalised relabelling of the sort seen in the last section.

The CCS parallel operator is much more interesting. It has semantics

$$\frac{P{ x \atop \rightarrow } P^{\prime}} {P\vert Q{ x \atop \rightarrow } P^{\prime}\vert Q}\qquad \frac{Q{ x \atop \rightarrow } Q^{\prime}} {P\vert Q{ x \atop \rightarrow } P\vert Q^{\prime}}\qquad \frac{P{ \alpha \atop \rightarrow } P^{\prime} \wedge Q{ \overline{\alpha } \atop \rightarrow } Q^{\prime}} {P\vert Q{ \tau \atop \rightarrow } P^{\prime}\vert Q^{\prime}}$$

This is CSP-like, with arity (2,∅) and one set of transition rules for each of these three clauses: the first two have $(\{(1,\alpha )\},\alpha,\vert,\emptyset,\{(1,1),(2,2)\},\emptyset )$ and $(\{(2,\alpha )\},\alpha,\vert,\emptyset,\{(1,1),(2,2)\},\emptyset )$ for all α∈Σ ₀, and the final clause is modelled by $(\{(1,\alpha ),(2,\overline{\alpha })\},\tau,\vert,\emptyset,\{(1,1),(2,2)\},\emptyset )$ for all α∈Σ ₀.

Note how similar these are to the rules for ∥ _X quoted earlier. The main structural difference is that both sorts of rules apply to all visible events, rather than being partitioned by X.

The following representation of | in CSP is much simpler than the simulation produced by the [20] machine. Extend Σ ₀ by a separate copy Σ ₁= { α′∣α∈Σ ₀}. Let IP (Identity plus Prime) be the renaming that maps α∈Σ ₀ to both α and α′, and let IDP (Identity plus Dual Prime) map each such α to α and $\overline{\alpha }^{\prime}$. Then P|Q is equivalent to the CSP construct defined

$$\begin{array}{rcl} P{\vert }_{ccs}Q = (IP(P) \parallel_{{\Sigma }_{1}}IDP(Q)) \backslash {\Sigma }_{1}& & \\ \end{array}$$

in the sense that the two processes are strongly bisimilar.

We can therefore conclude that, except for+, CCS is CSP-like.

It is possible to simulate the whole of CCS in CSP, but in a slightly more complex way that does not imply full compositionality over CSP models or a straightforward theory of refinement. An elementary way of doing this is to replace the event τ by a visible analogue (say tau as we have seen elsewhere in this paper), and produce models of CCS operators that model the syntax τ.P by tau→P. Finally, at the outermost level (in common with the implementation of generalised relabelling given in the previous section) we would hide tau. Thus the model of a closed piece P of CCS syntax would be the CSP term P′∖{tau}, where P′ is the syntax of P with all operators replaced by their CSP analogues. In this model the analogue of+would be □, since tau does resolve □, and the model of parallel would be as above (noting that tau is not synchronised) except that the outer hiding ∖Σ ₁ would be replaced by the renaming that sends all members of Σ ₁ to tau.

This provides a way of calculating the operational semantics of a CCS term using those of CSP, and also an easy method for using CSP tools such as FDR [15] on such terms.

It is not, in fact, necessary to leave all the tau actions visible as we build up a term, only those that might resolve a+operator for which our present process becomes (directly or indirectly) an argument. A little structural analysis shows that the only relevant taus are those that are the first action that our process performs. It follows that if we apply the following generalised relabelling (standing for “Hide Delayed Taus”), and presented in the relational form discussed earlier, to any term as we build up P′, the final result is not affected:

$$\begin{array}{rcl} \begin{array}{rcl} HDT & =&\{(a,s,f(s,a))\mid a \in {\Sigma }_{0} \wedge s \in {\Sigma }_{0}^{{_\ast}}\} \\ & &\mbox{ where $f(tau,s) = \tau $ for $s\neq \langle \rangle $, $f(a,s) = a$ otherwise.}\end{array} & & \\ \end{array}$$

This operator might well be useful if one wants to apply CSP model compressions such as those of FDR [22] in a hierarchical way to CCS constructs, as might the simpler observation that it is always safe to hide any tau at a level in the syntax above any+.

This translation will allow any finite-state CCS process to be checked on FDR against the types of specification that FDR supports.

An obvious question then arises: can one model CSP in CCS? The immediate answer to this is “no” since CCS cannot model the multi-way synchronisations permitted by CSP: as soon as two events are synchronised in CCS they are hidden. Another consequence of this is that it is seemingly impossible, in CCS, to implement the style of generalised relabelling discussed in the previous section for the same reason: synchronising P and Reg would hide the event. Of course there may be further interesting questions to ask here about subsets of CSP or extensions of CCS.

16.5 The π-Calculus

The π-calculus [11, 12, 23] builds on the notation of CCS by adding the concepts of name binding and name passing into the language. Like CCS, it does not need process alphabets to define parallel, and therefore the way it expresses mobility is more implicit than one in which passing a label along a channel explicitly changes the alphabets at the two ends, as seems natural for a direct mobile extension of CSP.

The following syntax for the π-calculus is taken from [23]:

• $\sc{prefixes}\pi ::= \overline{x}y\mid x(z)\mid \tau \mid [x = y]\pi$

• processes P ::=S∣P|P∣νz P∣ !P

• summations S ::=0∣π.P∣S+S′

Here, $\overline{x}y$ represents the sending of the name y via x (akin to the CSP action x!y) and x(z) is a construct binding z that represents the receipt of z over x (akin to x?z). Like CCS and unlike CSP it has a construct representing the explicit introduction of τ, and one can guard actions with the assertion that pairs of names are the same.

The process constructs are the same as in CCS except that the infinite replication !P (equivalent to P| !P) takes the place of recursion and νx P replaces P∖x. The effect of having summations in a separate syntactic class is to allow+only to appear in restricted contexts (similar to the “guarded choice” construct introduced as a precursor to □ in CSP in both of [6, 16]). Some presentations of the π-calculus omit+. Others generalise replication to full recursion μp.P, and we shall follow this latter school. We therefore add μp.P and p to the syntax of processes, where p represents a process identifier. (We will not, therefore, directly consider !P, regarding it as equivalent to μp.P|τ.p.)

The restriction on the use of+imposed by this syntax is crucial in allowing us to give π-calculus semantics in CSP. When giving semantics to summations we will still need to leave τ visible as tau; but for the main semantics (of processes) this is not necessary. We will therefore find that this version of π-calculus fits more smoothly and compositionally into the world of CSP than does CCS.

In our treatment of π-calculus we assume unless stated otherwise that the set Name is countably infinite with a fixed enumeration {n ₀,n ₁,…}. If N is a nonempty subset of names then μ(N) is the name with least index in N, and when Name∖N is nonempty γ(N) denotes μ(Name∖N). The visible events communicated by π-calculus processes, and making up Σ _π (which plays the role of Σ ₀ for our treatment of π-calculus) are of two forms: x.y represents the input of name y over the channel represented by name x, and $\overline{x}.y$ represents the corresponding output of y over x.

The theory of the π-calculus is complex. This is less because processes can pass names around and use them as channels as it is because of the way new names are “created” fresh and distinct from all others, and may be exported from their original scope.

Our goal is to find a way of dealing with this in CSP in a way that implements the above policy successfully and does not create any artificial distinctions between processes on the basis of exactly which fresh names they extrude.

Example To illustrate the power of the π-calculus, and provide an example for our later semantics, consider the following description of a variable-length buffer. This consists of a chain of processes, which initially consists of the single process C(in,out,split,export), which uses the channels in and $\overline{out}$ as the buffer input and output, respectively. Each process additionally has a channel along which it can be told to split in two and one from which the environment can choose to accept outputs in place of them proceeding down the chain. See Fig. 16.1 to see how it might evolve from top to bottom, with the single cell splitting to form two, and then the left-hand one splitting in turn.

$$\begin{array}{rcl} \begin{array}{rcl} C(i,o,s,e)& =&i(y).(\overline{o}x.C(i,o,s,e) + \overline{e}x.C(i,o,s,e)) \\ & & +\: s(z).\nu m\,\nu s^{\prime}\,\overline{z}s^{\prime}.(C(i,m,s^{\prime},z)\vert C(m,o,s,e))\end{array} & & \\ \end{array}$$

Each command to split (i.e. input on s) inputs a new name z from the environment, and that is used as the external output (e) channel of the new node. A new channel name also has to be extruded to the environment: the one to split the new node. That is the first output along z.

Fig. 16.1

One cell evolving into three

So in the transformation of the top line of the figure to the second, the environment sends z along split, and the process replies by sending s back along z. Sending z′ along s then causes the second split, with s′ being sent back along z′.

This is a somewhat contrived example, designed to use a lot of channel names (input, internal and extruded) to help our later understanding of the semantics of names. The semantics of the π-calculus rely on every name that the process creates being different from each other and from all that the environment has passed to it by that time. No such restriction applies to the environment, though obviously this particular example makes most sense when every name sent by the environment is also fresh.

We now identify two choices that have to be made when constructing our π-calculus semantics.

• 1. We can ensure that no artificial distinctions arise thanks to the precise choice of names in two ways.

  • The first is to create processes such that, whenever a name is extruded, it is picked nondeterministically from all permitted ones. We will call this the nondeterministic approach.

  • The second is to ensure that each fresh name that emerges from a process is completely predictable based on knowledge of the preceding trace. We will implement this by ensuring that the name is always the one with least index that might legitimately appear, and call this the standardised approach.

• 2. One of the trickiest problems in giving the semantics is to ensure that names input by a process from the environment do not get confused with a name that may already exist in the process’s scope without having been extruded. It is a basic assumption that these names are different, so how do we achieve this?

  • One approach is to allow the environment, at any time, to output any name to the process. The semantics then has to perform an operation related to α-conversion on any fresh and unextruded name it holds that clashes. We will call this the unified approach.

  • The opposite of this, which we will call the bipartite approach, is to split the fresh name space into two infinite parts and allocate one to the process and the other to the environment. In other words, the process will simply assume at all times that the environment will not output any name to it that is in that part of the process’s fresh name space unless that name has previously been extruded by the process.

In this paper we will first consider the unified name space approach, providing an initial translation into CSP followed by constructs that respectively map this into the nondeterministic and standardised approaches. We then summarise the differences in how these steps are taken in the bipartite approach.

We would expect any semantics for π-calculus to have complete symmetry in those names that the environment generates as fresh (though in the unified approach the symmetries will be more complex since they will need to factor in the fact that the names chosen by the environment affect the values of the names chosen subsequently by the process). We would expect any nondeterministic semantics to have complete symmetry in the names chosen by the process.

Think, for a moment, about how these decisions would affect our example. Note that, in it, the creation of names is a distributed activity: when we have split the original cell into N pieces, any one of them can input new names from the environment and generate fresh ones without interacting with the others. And yet all of our models except for the nondeterministic, bipartite approach seem to rely on there being some sort of instantaneous passing of information between the different cells. In the unified approach one cell has to “know” which names have input by another from the environment so it can avoid generating that name itself. In the standardised approach two cells that are simultaneously able to output channel names to the environment seem to need to know whether the other has done so yet. On the other hand, if (i) the available names for a cell are nondeterministically split into two infinite parts when it splits and (ii) the environment is prevented from creating any of these names, there is no such problem.

Arguably, what the other approaches are doing is placing each process in a framework that forces us to think of processes as sequential, or at least to look at parallel processes through a prism that makes them look sequential. In that sense they are doing no more than what happens when we use an LTS semantics or one based on any of the usual CSP models, for these are all inherently sequential. But this does suggest that an attempt to give a true concurrency semantics might follow the nondeterministic and bipartite approach to names.

16.5.1 Preserving Inequality

The π-calculus is fairly straightforward to translate into our CSP extended by| _ccs , with the exception of its handling of freshness. We first show how to translate summations. If S is a summation then csp[S]₊ will be a CSP term in which τ actions remain visible as tau. The corresponding semantics for a process P is written csp[P].

• csp[0]₊=STOP

• csp[[x=y]π.P]₊=csp[π.P]₊≮x=y≯STOP

• csp[τ.P]₊=tau→csp[P]

• csp[x(y).P]₊=x?z→csp[P[z∕y]]

• csp ${[\overline{x}y.P]}_{+} = \overline{x}.y \rightarrow$ csp[P]

• csp[S+S′]₊=csp[S]₊ □ csp[S′]₊

Here X≮b≯Y is Hoare’s infix representation conditional choice: it equals X if b it true and Y if b is false.

We can interpret a summation as a process via hiding, and both process identifiers and recursion translate directly into CSP:

• csp[S]=csp[S]₊∖{tau}

• csp[p]=p

• csp[μp.P]=μp.csp[P]

The remaining constructs are parallel P|Q and restriction ν z P. These are more difficult because of the way they handle fresh names. The effects we want to achieve are set out below.

• ν z P creates a fresh name z′ for the placeholder z that is used within P. This is different from all other names known to P at the point of creation and all names that P sees subsequently that cannot result from other processes reflecting z′ back to P.

• ν z P may extrude this z′ from this scope by means of output $\overline{x } z^{\prime}$ on some other channel (i.e. x≠z′).

• After this extrusion, ν z P may use the name z′ as a channel name, output it again, etc. However, before the extrusion any of P’s communications that use it as a channel name are blocked. This, by analogy with CCS restriction P∖α, explains why this operator is called “restriction.” In our example it means that no communication on our internal channels m,m′⋯are visible on the outside, because these channel names are never extruded.

• In the parallel composition P|Q, the processes P and Q never extrude the same fresh name.

• Because of the way in which interactions between P and Q are hidden, P may extrude a fresh name z to Q or vice-versa, without the external environment seeing z. This expansion of the scope of z is restricted as above: it may not use the name z in a visible way until z has been extruded from the parallel composition via output on a different channel.

• Each fresh name extruded from P|Q must be different from all names either P or Q knew originally or subsequently input.

The above must hold for any strategy for assigning and managing the fresh names created within a term P. We use the term “managing” here because there is no sensible way, within the unified approach to name choice, of ensuring that once a fresh value z has been created but not yet extruded, the external environment does not independently invent the same name (we will call this a name collision). If this happened it would cause confusion both in the environment and the process P.

This is why we need to use relabelling. In the instance above, one thing we could do would be to pick a further fresh name z′ not known to P, and apply the renaming [[z,z′∕z′,z]] (transposing the two names) to P from the point where the environment communicates z to it. Thus P will see z as z′ (correctly, a value that is fresh to it and distinct from the z it already knows about) and the environment will, if and when P ultimately extrudes z the outside world will see it as z′ (correctly, a value it has not seen before). Since neither z nor z′ has appeared in the trace before this point, each of these names only has a single role in the whole trace. We will use relabellings such as this to avoid collisions both for νz P and P|Q, the latter because of the scope expansion issues discussed above.

We will introduce a relabelling called OF(N,K,P) (“output first”). Here N is a set of names that the process P might extrude but are not known to the environment. K (disjoint from N) is the set of names initially known to both P and environment: we think of this as their common knowledge. OF(N,K,P) introduces a transposition of the above form each time the process inputs from the environment a name that clashes with a member of N. The set N may diminish as the process evolves since some of the names in it may be extruded; and K may increase as P learns more names.

In order to keep track of the transpositions that are introduced as the system evolves, we need to introduce a parameter ξ that is a bijection on Name. At any time, ξ will be the the function that maps names as seen on the inside of the relabelling to the corresponding names seen by the environment. While this function will evolve as the system progresses, as soon as a name has been seen in a trace of P its image remains fixed thereafter. It follows that, at the end of a trace, ξ is a permutation on Name that translates P’s view to the environment’s view of every member in the trace. Initially, ξ is the identity function, and remains so on the initial members of K.

The most straightforward way of presenting OF is by defining a Reg _OF process that creates the relabelling using the construction (∗).

In the following, as with OF, we assume that K and N (the set of potentially fresh names yet to emerge from the process) are disjoint. Reg _OF (K,N,ξ) takes the form

$$\begin{array}{rcl} \square \{(a,b) \rightarrow Re{g}_{OF}(K^{\prime},N^{\prime},\xi^{\prime})\mid (a,b,K^{\prime},N^{\prime},\xi^{\prime}) \in C\}& & \\ \end{array}$$

where a is the process P’s event, b is the environment’s view of the same event, and C is a set of clauses that we will describe below, each representing a different sort of event that the relabelling allows.

We consider the cases of output $\overline{x}.y$ and input x.y events separately, splitting these depending on which of K and Ny belongs to. In both cases we restrict x to be K: it is part of the role of OF to prevent P from using names in N before these have been extruded from scope; and if our semantics are sensible P could never use a channel name that is outside K ∪N.

We now enumerate the various clauses of Reg _OF (K,N,ξ):

• If both the channel and data are part of common knowledge, then an input does not change the parameters:

  $$\begin{array}{rcl} \{(x.y,\xi (x).\xi (y)) \rightarrow {\mathit{Reg}}_{OF}\ (K,N,\xi )\mid x,y \in K\}& & \\ \end{array}$$

• If both the channel and data are part of common knowledge, then an output does not change the parameters:

  $$\begin{array}{rcl} \{(\overline{x}.y,\overline{\xi (x)}.\xi (y)) \rightarrow {\mathit{Reg}}_{OF}\ (K,N,\xi )\mid x,y \in K\}& & \\ \end{array}$$

• If P outputs a name in N, then this is removed from N and added to K

  $$\begin{array}{rcl} \{(\overline{x}.y,\overline{\xi (x)}.\xi (y)) \rightarrow {\mathit{Reg}}_{OF}\ (K \cup \{ x\},N - \{ x\},\xi )\mid x \in K,y \in N\}& & \\ \end{array}$$

• If P inputs a name outside K ∪N, then this is equivalent to the environment extruding a name to P, so it is added to the common knowledge:

  $$\begin{array}{rcl} \{(x.y,\xi (x).\xi (y)) \rightarrow {\mathit{Reg}}_{OF}\ (K \cup \{ x\},N,\xi )\mid x \in K,y\not\in N \cup K\}& & \\ \end{array}$$

• Finally, if P was to input a name y in N, then this is a name collision, since the environment has yet to be told of N by P. However, in the unified approach, there is nothing to stop the environment inventing such a name independently. Therefore, the mapping ξ is changed so that the new name maps outside K ∪N under ξ⁻¹. The simplest way to do this is to transpose x and the name γ(K ∪N), which we recall is the one with least index not in this set. We write this transposition (which maps all other names to themselves) as xp(x,γ(K ∪N)). The clauses of this type are thus

  $$\begin{array}{rcl} \{(x.n,\xi (x).\xi (y)) \rightarrow {\mathit{Reg}}_{OF}(K \cup \{ n\},N,\xi \circ xp(x,n))\mid x \in K,y \in N\}& & \\ \end{array}$$

  where n=γ(K ∪N).

Notice that all of the above English descriptions are formulated from the point of view of P, with the already established permutation ξ assumed.

It is these transpositions in OF that represent the analogy of α-conversion that we discussed earlier. Both of these things have the role of avoiding clashes between external and bound identifiers. While traditional α-conversion does not change the semantics of a term, our transpositions do, but this is only because “bound” identifiers in π-calculus can, unusually, be seen from the outside.

This relabelling is deterministic since there is only one way Reg _OF (K,N,ξ) can perform any given action, and clearly it has no τ-generated nondeterminism. Indeed, since there is only one action that Reg _OF (K,N,ξ) can perform for any given action seen by the environment, OF(N,K, ⋅) could be presented as a relabelling generated by a relation between P’s visible actions, the environment’s visible actions and the environment’s traces. But since it does evolve naturally a step at a time, the above presentation is probably the best.

We are now very close to being able to give a semantics to νz P, but before we do that we need to establish what the right values are to use for K and N when we come to use OF. We will also need a semantic mechanism to keep the fresh names invented by two parallel processes distinct.

The best way to do these things is to add parameters κ and σ to the semantics so they become csp[S]₊κσ and csp[P]κσ. κ will represent the initial common knowledge of names by P and its environment or context: a finite set of names that includes all free names in P. σ will be an infinite set of names, disjoint from κ, that are available to be used as fresh. So, for example, we will now have csp[P+Q]₊κσ=csp[P]₊κσ □ csp[Q]₊κσ and (the only clause given to date with a significant change) csp[x(y).P]₊κσ=x?y→csp[P]₊(κ ∪ {y})(σ- { y}).

We can then write

$$\begin{array}{rcl} \mbox{ \sc{csp}}[\nu z\,P]\kappa \sigma = OF(\{\gamma (\sigma )\},\:\kappa,\:\mbox{ \sc{csp}}[P[\gamma (\sigma )/z]](\kappa \cup \{ \gamma (\sigma )\})(\sigma - \{ \gamma (\sigma )\}))& & \\ \end{array}$$

In other words, the name with least index not in κ is chosen to bind to z, and this name is then “protected” by the OF operator, which also prevents it from being used as a channel by P until it has been output.

The interactions between P and Q in P|Q are calculated in the same way as in CCS. It follows that the same CSP construction we used in the last section can be used here provided we sort out what happens to the sets of names that P and Q use and generate, and provided we ensure that P|Q obeys the rules discussed above for it being an expanded scope for some of these generated names.

The parameter σ gives us the ability to keep the names that P and Q generate distinct from each other. To do this we assume that we have functions Π _i for i=1,2,3 such that, for any infinite set σ of names, {Π ₁(σ),Π ₂(σ),Π ₃(σ)} partitions σ into three infinite sets. [One such triple of functions would allocate the names of increasing index in σ to the three sets in a round robin fashion.] In evaluating csp[P|Q]κσ these three sets will respectively represent the sets of fresh names that might be generated by P, by Q, and outside this system.

We can then define csp[P|Q]κσ to be

$$\begin{array}{rcl} OF({\Pi }_{1}(\sigma ) \cup {\Pi }_{2}(\sigma ),\:\kappa,\:\mbox{ \sc{csp}}[P]\kappa ({\Pi }_{1}(\sigma )){\vert }_{ccs}\mbox{ \sc{csp}}[Q]\kappa ({\Pi }_{2}(\sigma )))& & \\ \end{array}$$

The role of OF here is to protect any fresh names extruded from P or Q into P|Q but not yet to the environment. Since it does not know exactly which fresh names have been extruded in this way, it protects the whole of the set Π ₁(σ) ∪Π ₂(σ). Here, of course| _ccs is the CSP translation given earlier of the CCS operator|.

Note that as far as P’s and Q’s choices of names are concerned, we have used what amounts to the bipartite approach by ensuring that they choose from disjoint sets.

16.5.2 Nondeterministic Fresh Names

We might say that the above clauses give a provisional semantics, since they suffer from the lack of abstraction discussed above caused by specific choices of fresh names.

In many ways the most elegant approach to this problem is to apply a mapping that in effect maps each assignment of fresh names to a representation of its symmetry class: the processes that might have been obtained under a different strategy for assigning fresh names.

We can attempt to do this by identifying each semantic value csp[P]κσ with the nondeterministic composition of the set of its values under renamings that change the choices of fresh names it picks from σ. The following operator is perhaps the most natural way to do this.

$$\begin{array}{rcl} NFN(P,\sigma ) = \sqcap \{P[[\xi \cup i{d}_{(Name - \sigma )}]]\mid \xi : \sigma \rightarrow \sigma,\mbox{ $\xi $ bijection}\}\quad (\dag )& & \\ \end{array}$$

One can gain much insight into CSP models and the way to use them correctly for π-calculus by analysing whether this approach works or not.

We will now show that there are pairs of processes P and Q that we would like to regard as semantically equivalent for which there is no such ξ with csp[P]κσ[[ξ]]=csp[Q]κσ.

If we have a process that has two different behaviours on which it extrudes a free name, it should not matter whether these two names are the same or different. Consider, for example, $P = \tau.(\nu z\,\overline{x}z.0) + \tau.(\nu z\,\overline{y}z.0)$ (where the above semantics will always output the same fresh name via whichever of $\overline{x}$ and $\overline{y}$ the environment chooses) and $Q = \tau.(\nu z\,\overline{x}z.0) + \tau.(0\vert (\nu z\,\overline{y}z.0))$ (where, depending on Π ₂, it may not, and we will assume not). No renaming of the above form can map P to Q. For similar reasons the CSP operational semantics of P and Q with construct (†) applied to them are not bisimilar, since no bijection ξ can map the state P to the state Q.

Thus the initial choice of a single permutation does not characterise semantic equivalence in a model where processes are represented as tree structures.

One of the main differences in CSP-style models based on linear observations of processes is that they deliberately obscure when choices are made: hence the CSP distributivity law a→(R ⊓S)=(a→R) ⊓(a→S), for example. A CSP-style semantics of the processes P and Q above will only let you look at things that occur down a linear observation. However, the structure of P above means that it will not let you examine the consequences of outputting on channels $\overline{x}$ and $\overline{y}$ in the same observation; only in two separate ones. It should not therefore matter, in this style of model, if the choice of a permutation ξ is made initially or in stages as long as every name that actually appears is mapped to the same place as in ξ.

We would expect such a model of csp[P]κσ still to output the same name along these two channels and csp[Q]κσ probably to output different ones, so the provisional semantics of P and Q will still be different even if we only record process traces. However, when we look at the effect on their traces of the (†) construct, these two values are mapped to the same value. The point is that any trace of csp[P]κσ will be the result of some ξ being applied to a trace of csp[Q]κσ, and vice versa. The fact that different ξ may be needed for different traces is immaterial: every trace of csp[P]κσ will be a trace of NFN(csp[Q]κσ,σ) and vice versa.

We can conclude that, at least for the finite traces semantics of CSP, construction (†) gives the provisional CSP semantics the necessary abstraction. There are subtle problems, however, when we come to study types of behaviour that appear in other CSP models. These are, on the one hand, refusal and acceptance sets and, on the other, behaviours recording infinite traces. To avoid this second sort of difficulty, let us assume for the time being that we are interpreting CSP over a model that does not have infinite traces.

Most CSP models have refusal or acceptance sets to enable us to detect things like deadlock. These can lead to undesirable semantic differences between π-calculus terms in two related ways. For example, consider the processes

$$\begin{array}{rcl} \nu y\,\overline{x}y.\nu z.\overline{x}z.0\qquad (\nu y\,\overline{x}y.0)\vert (\nu z\,\overline{x}z.0)& & \\ \end{array}$$

Each of them simply extrudes two fresh names in succession along $\overline{x}$, and they ought to be regarded as equivalent.

With conventional failures-based models, in which refusal sets are sets of events, these two processes are not equivalent under the NFN mapping. For the left-hand process will have failures of the form $(\langle \rangle,\Sigma - \{\overline{x}.n\})$, while the largest refusal sets on ⟨⟩ of the right-hand process will omit $\overline{x}.n$ and $\overline{x}.m$ for two different names n and m: in effect the parallel structure gives the environment a “choice” of two different names.

A further difficulty arises in more elaborate CSP models such as refusal testing where it is possible to see the refusal or acceptance of an event that extrudes a name several steps before it actually appears in the trace. Such a name might or might not get relabelled between these two appearances, which can again lead to undesired inequivalences as well as some confusing-looking observed behaviours.

There is a simple solution to both these problems: in languages such as π-calculus where all communication between processes happens over point-to-point channels, and processes inputting on a channel always do so non-selectively – they cannot accept some communications on it but refuse others – we get a better model of refusal and acceptance sets by constructing them solely of channel names, not events. This was recognised for occam in [14].

It will therefore be impossible to tell, in any “channel-based” CSP-style model, between the sequential and parallel processes above that extrude fresh names, to see any fresh name in a recorded behaviour before it is extruded, or indeed to make the same sort of distinctions based on non-fresh names. Thus, for example, $\overline{x}y\,.\,P + \overline{x}z\,.\,Q$ and $\tau \,.\,\overline{x}y\,.\,P + \overline{x}z\,.\,Q$ will be identified as processes (though not as summations) in any such model.

Given any of these channel-based CSP models $\mathcal{M}$ we can therefore give a proper semantics to the π-calculus. The semantics for a summation and a process will be written³ ${\mathcal{M}}_{\sqcap }^{1}{[S]}_{+}\kappa \sigma$ and ${\mathcal{M}}_{\sqcap }^{1}[P]\kappa \sigma$, which are defined to be the respective CSP interpretations over $\mathcal{M}$ of the terms:

$$\begin{array}{rcl} NFN(\mbox{ \sc{csp}}{[S]}_{+}\kappa \sigma,\sigma )\quad \mathrm{and}\quad NFN(\mbox{ \sc{csp}}[P]\kappa \sigma,\sigma )& & \\ \end{array}$$

The superscript 1 here means that this is a semantics using a single (unified) name space, and ⊓means that this is the nondeterministic semantics. The alternatives for these are 2 (bipartite) and μ (standardised).

These can readily be turned into denotational semantics. The preliminary semantics csp[P]κσ can already be interpreted in this way if we add an extra parameter ρ: an environment that maps process identifiers to functions from common knowledge sets κ and fresh-name sets σ to $\mathcal{M}$.⁴ They will thus be written ${\mathcal{M}}_{\sqcap }^{1}[P]\rho \kappa \sigma$. Thus the semantics of a process identifier is given by ρ(p)κσ. The semantics of each non-recursive operator is then just the interpretation over $\mathcal{M}$ of the CSP syntax into which we have already translated it, applied to sub-terms as appropriate. The semantics of recursion is just the same fixed-point calculation that is appropriate for $\mathcal{M}$: sometimes a refinement-least fixed point, sometimes a subset-least fixed point, and sometimes something more complex as in [17].

The full denotational semantics is then obtained in the same way except that for some syntactic forms (parallel, restriction) it is necessary to apply the operator NFN( ⋅,σ) (interpreted as an operator over $\mathcal{M}$) to the result.

NFN( ⋅,σ) was presented above as the nondeterministic choice of a set of renamings. It is easy to reformulate it as a nondeterministic relabelling, if desired.

Since no name other than a member of fn(P) means anything special to a π-calculus term P, we must expect that, for any permutation η of Name -fn(P), the processes P and P[[η]] are equivalent. Since we give meaning to members of κ -fn(P) and σ, we cannot expect that ${\mathcal{M}}_{\sqcap }^{1}[P]\kappa \sigma = {\mathcal{M}}_{\sqcap }^{1}[P]\kappa \sigma [[\eta ]]$ in general, but we can expect that

$$\begin{array}{rcl}{ \mathcal{M}}_{\sqcap }^{1}[P]\rho \kappa \sigma = {\mathcal{M}}_{ \sqcap }^{1}[P]\rho ({\eta }^{-1}(\kappa ))({\eta }^{-1}(\sigma ))[[\eta ]]& & \\ \end{array}$$

The infinite nondeterministic choice used in NFN actually goes beyond the CSP syntax that some of the standard models can handle, specifically those which, like the failures-divergences model $\mathcal{N}$, have representations of divergence but not other infinite behaviours such as infinite traces. The reason for this limitation is that when a process has unbounded nondeterminism it is not possible to infer whether P∖X can diverge from its finite traces alone. Hiding appears in our CSP translation of π-calculus as part of the definition of| _ccs . Fortunately, however, the symmetry of π-calculus semantics under permutations on names means that whenever there are arbitrarily long finite traces of terms P and Q that combine under|to give prefixes of a fixed finite trace, then there is also a pair of infinite traces with the same property.⁵ It follows that whenever there are arbitrarily long finite traces created by the part of the CSP construction of| _csp other than hiding, that the hiding maps to prefixes of a given trace s, then (i) there is an infinite trace of the same process that hides to a prefix of s and (ii) s itself is recorded as a divergence by divergence strictness.

It is therefore not necessary to use CSP models involving infinite traces if one wishes to handle strict divergence accurately in π-calculus. If, however, we want to calculate the infinite traces for other reasons or to handle non-strict divergence using the techniques developed in [17], we need to use a model that represents them explicitly. As we said above, this brings with it the danger of distinguishing processes that we would naturally hope to be equivalent: consider the following pair of processes:

$$\begin{array}{rcl} \mu p\,.\,\mathbf{\nu} z\,\overline{x}z\,.\,p\quad \mathrm{and}\quad \mu p\,.\,\mathbf{\nu} y\,\mathbf{\nu} z\,\overline{x}z\,.\,p& & \\ \end{array}$$

These both output an infinite supply of fresh names over channel $\overline{x}$. There is every reason for wanting to identify them, and indeed the terms P and νy P when y is not free in P. A little thought, however, will reveal that our csp[ ⋅] semantics will have $\mu p\,.\,\mathbf{\nu} z\,\overline{x}z\,.\,p$ output all the enumerated fresh names one by one, whereas $\mu p\,.\,\mathbf{\nu} y\,\mathbf{\nu} z\,\overline{x}z\,.\,p$ will only output every other one.

For finite traces, this problem is easily remedied by an appropriate permutation η: any injective finite partial function from a set to itself can be extended to a permutation. This does not work for infinite traces: once we map the single infinite trace of the right-hand process to the single infinite trace of the left-hand one, there is nowhere left to map all the names that the right-hand process has missed out. We must therefore conclude that the semantics we have built to date, if interpreted over a model with infinite traces, makes undesirable distinctions between processes.

We can also conclude that the semantic values it creates are not always closed, in the sense that if every prefix of an infinite trace is present, then so is the infinite trace itself. This is not in itself worrying, but it means that the nondeterministic interpretation of π-calculus provides the only example known to the author of a semantics involving hiding in which models like $\mathcal{N}$ work accurately despite the processes not being closed!

An easy, if perhaps extreme, way of solving this problem is to move to having an uncountable set of Name; the point being that such a set can never be used up, even in an infinite trace. It is difficult to see how we can otherwise solve it in the nondeterministic spirit of NFN, at least in the unified case, when one considers how the environment is also allowed to pick an infinity of fresh names in some infinite traces.

To avoid these difficulties and more complex arguments later in this paper, in this paper’s initial treatment of π-calculus via CSP we will only consider CSP models where each recorded behaviour only involves a finite number of names in each trace: ones that are relational images of either $\mathcal{F}\mathcal{L}$ (as described earlier) or ${\mathcal{F}\mathcal{L}}^{\Downarrow }$ (with strict divergence but without infinite behaviours), in their channel-based versions where all the acceptance sets consist only of channel names.

The fact that a π-calculus term only “knows” a finite set of names immediately, coupled with the way in which we are using channel-based models, means that all these acceptance sets are themselves finite. It follows that only finitely many members of Name appear in any behaviour recorded in $\mathcal{F}\mathcal{L}$ or ${\mathcal{F}\mathcal{L}}^{\Downarrow }$. We will use this fact repeatedly. We will refer to these as finite behaviour models.

This restriction allows one immediate simplification. The nondeterministic choice in the definition of NFN is over an uncountable set of functions. Over a model in which only finitely many names appear in a trace it is equivalent to additionally restrict the set of bijections to those which, except for a finite set of names, are equivalent to the identity. This is now a countable choice.

16.5.3 Standardised Fresh Names

The CSP semantics that emerges from the nondeterministic approach given above has much to recommend it, not least the symmetry. It can, however, be viewed as unnecessarily infinitary, depending as it does on infinite nondeterministic choice.

We can solve this problem by removing from the process all opportunities to choose the fresh names it extrudes. We ensure that each name to appear in this way is always the least allowed: the member of σ with least index that has not already appeared in the trace. We can achieve this with a relabelling SFN(P,K,S) (standardised fresh names) presented in a similar style to OF, namely via its regulator process Reg _SFN (K,S,ξ). This is, like Reg _OF , formed by composing a sets of clauses with □. The parameters are similar to those used for Reg _OF , except that this time the parameters are based mainly on the external view of the system since it is that which we standardising.

• K (initially κ) is the external view of the current common knowledge.

• S (initially σ) is the external view of the set of free names that are available to be extruded by the system.

• ξ is a partial function, with domain K, that maps the external view of common knowledge to the internal one. Initially this is the identity function on κ.

The clauses forming Reg _SFN are:

• If both the channel and data are part of common knowledge, then an input does not change the parameters:

  $$\begin{array}{rcl} \{(\xi (x).\xi (y),x.y) \rightarrow {{\it { Reg}}}_{SFN}(K,N,\xi )\mid x,y \in K\}& & \\ \end{array}$$

• If both the channel and data are part of common knowledge, then an output does not change the parameters:

  $$\begin{array}{rcl} \{(\overline{\xi (x)}.\xi (y),\overline{x}.y) \rightarrow {{\it { Reg}}}_{SFN}(K,N,\xi )\mid x,y \in K\}& & \\ \end{array}$$

• If P outputs a fresh name x (one not in range(ξ)=ξ(K)), then this is seen on the outside as the least index member of S.

  $$\begin{array}{rcl} \begin{array}{r} \{(\overline{\xi (x)}.y,\overline{x}.m) \rightarrow {{\it { Reg}}}_{SFN}(K \cup \{ m\},S - \{ m\},\xi + [m\mapsto y]\mid \\ m = \mu (S),x \in K,y\not\in \xi (K)\}\end{array} & & \\ \end{array}$$

• If P inputs a fresh name, then we standardise this so that it is always the one with least index not in K.

  $$\begin{array}{rcl} \begin{array}{r} \{(\xi (x).\gamma (z),x.y) \rightarrow {\mathit{Reg}}_{SFN}(K \cup \{ y\},S - \{ y\},\xi + [y\mapsto \gamma (z)]) \\ \mid z = \xi (K),x \in K,y\not\in K\}\end{array} & & \\ \end{array}$$

The way we formulated this last clause means that we have not only standardised the way in which fresh names are extruded from P, but also the names that P inputs as fresh from the environment. The latter is not strictly necessary to achieve the standardised external view of our process, but (i) it has a pleasing symmetry and (ii) it might well make for more efficient automated verification.

As with NFN, we can add this new operator to the CSP translation

$$S[P] = (\mbox{ \sc{csp}}[P](fn(P))N)\langle \!\langle SFN(fn(P),N)\rangle \!\rangle$$

where fn(P) is the set of free names in P and N′=Name∖fn(P). We can also construct a denotational semantics based on any channel-based CSP model if we add an environment of the same form as used in the nondeterministic semantics.

We have the following interesting property of the relabellings used in our two semantics:

Lemma 1.

This result is about CSP processes defined over the alphabet Σ _π which respect the π-calculus discipline that no name not in the initial set K is used as a channel before it is input or output over another channel, and such that the names it thus “creates” through output are confined to the infinite set S disjoint from K.

For any such process:

• (a) For any permutation ξ of names that is the identity on Name ∖ S, P〈〈SFN(K,S)〉〉 = P[[ξ]]〈〈SFN(K,S)〉〉 holds up to strong bisimulation.

• (b) The equivalence P〈〈SFN(K,S〉〉)=NFN(P,S)〈〈SFN(K,S)〉〉 holds in every finite-behaviour CSP model.

The first part simply says that it does not matter how the fresh names generated by P are permuted if they are to be renamed into standard order. The second part then follows because in any such model the 〈〈SFN(K,S)〉〉 operator is distributive over nondeterministic choice.

This lemma implies that the equivalence induced by the nondeterministic semantics is at least as fine as that induced by the standardised one.

If we were to allow CSP models recording behaviours with an infinity of names in individual traces, part (b) of this lemma would not hold in reverse (i.e. with the roles of NFN and SFN transposed). This is because applying 〈〈SFN(K,S)〉〉 to a behaviour b that extrudes an infinity of Name from S always maps it to one in which the whole of S appears. This means that 〈〈SFN(K,S)〉〉 will identify pairs of behaviours that no permutation on S can. This is the same issue we saw when discovering undesirable inequivalences created by the nondeterministic semantics with infinite traces.

If, however, a behaviour b only involves a finite number of names, then the result of applying 〈〈SFN(K,S)〉〉 to it is certain to leave an infinite set of names unrecorded in b. As in the earlier example, it is then possible to extend the finite injective mapping from S to itself, created by Reg _SFN by the time it has communicated all the names used in b, to a bijection. This proves the following inverse of the lemma above.

Lemma 2.

Under the same conditions as Lemma 1,

$$\begin{array}{rcl} NFN(P,S) = NFN(P\langle \!\langle SFN(K,S)\rangle \!\rangle,S)& & \\ \end{array}$$

holds in any channel-based, finite-behaviour CSP model.

We can collect these two results into the following theorem:

Theorem 16.1.

In any such channel-based, finite-behaviour model of CSP the standardised and nondeterministic semantics for π-calculus represent the same equivalence over process terms.

The author believes that in cases, beyond the scope of this paper, of models including infinite-name behaviours, the standardised semantics will give the correct equivalences. In future discussions in this paper we will concentrate on the standardised form.

The parameters κ⊇fn(P) and infinite σ disjoint to κ are structurally important to the semantics, but however they are chosen within these constraints they do not change the equivalence induced by the semantics, as is demonstrated by Lemma 4 below. The crucial result needed to establish this is Lemma 3: the role it plays is that it allows us to disentangle the fresh names picked by process and environment.

If b is any finite-name behaviour from a channel-based CSP model, $\mathcal{M}$ let enames(b,K) be the (necessarily finite) set of names first input from the environment that are not in the common knowledge set K. We then have the following:

Lemma 3.

If P is a π-calculus process with fn(P) ⊆ κ, and σ (disjoint from κ) is infinite, then

$$\begin{array}{rcl} b \in {\mathcal{M}}_{\mu }^{1}[P]\kappa \sigma \Leftrightarrow b \in {\mathcal{M}}_{ \mu }^{1}[P]\kappa (\sigma - enames(b,K))& & \\ \end{array}$$

Lemma 4.

If P and Q are π-calculus processes with fn(P) ∪ fn(Q) ⊆ κ ∩ κ′, and σ (disjoint from κ) and σ′ (disjoint from κ′) are infinite, then over any finite-behaviour channel-based CSP model $\mathcal{M}$ we have

$$\begin{array}{rcl}{ \mathcal{M}}_{\mu }^{1}[P]\kappa \sigma = {\mathcal{M}}_{ \mu }^{1}[Q]\kappa \sigma \Leftrightarrow {\mathcal{M}}_{ \mu }^{1}[P]\kappa^{\prime}\sigma^{\prime} = {\mathcal{M}}_{ \mu }^{1}[Q]\kappa^{\prime}\sigma^{\prime}& & \\ \end{array}$$

It follows that we can talk about the congruence on π-calculus induced by a given CSP model of this type, rather than needing to calculate it relative to a particular κ and σ. In deciding the equivalence of two processes we can compare their semantics with κ=fn(P) ∪fn(Q) and σ=Name-κ. The above lemma demonstrates inter alia that this is an equivalence relation.

16.5.4 Bipartite Semantics

In the above semantics we ensured that a pair of parallel processes P|Q never create names that collide with each other. Our main reason for doing this was to ensure that two fresh names output directly to the environment respectively by P and Q do not collide. It has the side effect, however of meaning that when P inputs a fresh name created by Q or vice versa they never need to call upon the transpositions of OF to avoid collisions.

The only entity that we have not been able to control enough to prevent collisions is the external environment, because we have always allowed it to output any name to the process we are observing. It is this that characterises the unified approach.

In the bipartite approach, the set σ or S of names that the process can choose from is not only infinite, but its complement (the names either initially known or available to be created fresh by the environment) is also infinite. We replace the parameter κ, which we will not need with the bipartite treatment of freshness, with a different set, ζ. This represents the set of names which it is legitimate to receive as inputs over channels. Before the process has started to run ζ is always the complement of σ, but at some points in the semantics it is a proper subset of the complement, the difference being the fresh names that the process has created (and so are no longer in σ) but not yet extruded.

Rather than giving this alternative semantics in detail, we summarise the differences below. The translations of the input and output constructs are now as follows, noting we are defining a second translation csp2[ ⋅]:

$$\begin{array}{rcl} \begin{array}{rcl} \mbox{ \sc{csp}2}{[x(y).P]}_{+}\zeta \sigma & =&x?y : \zeta \rightarrow \mbox{ \sc{csp}2}{[P]}_{+}\zeta \sigma \\ \mbox{ \sc{csp}2}{[\overline{x}y]}_{+}\zeta \sigma & =&\overline{x}.y \rightarrow \mbox{ \sc{csp}2}{[P]}_{+}(\zeta \cup \{ y\})\sigma \end{array} & & \\ \end{array}$$

We get a considerable simplification by being able to drop the most complicated part of the OF relabelling. OF can in fact be replaced by parallel composition with a process BOF(ζ) (bipartite output first) that enforces the discipline that no name not in ζ can be used as a channel before being output by the process:

$$\begin{array}{rcl} \begin{array}{rcl} BOF(Z)& =&\square \{x?y : Z \rightarrow BOF(Z)\mid x \in Z\} \\ & &\square \\ & &\square \{\overline{x}?y : Name \rightarrow BOF(Z \cup \{ y\})\mid x \in Z\}\end{array} & & \\ \end{array}$$

The translation of νz P thus becomes

$$\begin{array}{rcl} \mbox{ \sc{csp}2}[\nu z\,P]\zeta \sigma = BOF(\zeta ) \parallel_{{\Sigma }_{\pi}}\mbox{ \sc{csp}2}[P[\mu (\sigma )/z]]\zeta (\sigma - \{ \mu (\sigma )\})& & \\ \end{array}$$

There is no need to have the function Π ₃ in the semantics of|: all we need are functions Π′ ₁ and Π′ ₂ that partition σ into two disjoint infinite sets, with each process having the other’s σ incorporated into its ζ, as are any names in Name -(ζ ∪σ) since these have already been declared at the point the parallel composition is started, and we could easily have given the output end of such a channel to P and the input end to Q. csp2[P|Q]ζσ is defined to be

$$\begin{array}{rcl} BOF(\zeta ) \parallel_{{\Sigma}_{\pi }}(\mbox{ \sc{csp}2}[P]{N}_{1}({\Pi }_{1}^{\prime}(\sigma )){\vert }_{ccs}\mbox{ \sc{csp}2}[Q]{N}_{2}({\Pi }_{2}^{\prime}(\sigma )))& & \\ \end{array}$$

where N _i =Name -Π′ _i (σ).

There is one important respect in which things get more involved. The reasons for needing to use channel-based CSP models are equally valid in this bipartite model, but the use of these models is not quite as easy to justify since processes no longer have the “no selective input” property. Just as with the argument earlier that demonstrated that the $\mathcal{N}$ semantics of divergence is correct despite the fact that processes are not closed, we need to move outside CSP’s established “comfort zone.” In order for the channel-based models to be valid, we need to ensure that whenever two processes are running in parallel, one inputting and one outputting a value v on a given channel c, if the inputting process is in a state where it can accept any input on c, then it can also accept v, even though there may be values that it does not accept.

This is always true of our CSP models of the π-calculus. This is because the only inputs that csp2[x(y) ⋅P]ζσ cannot make are names that have been reserved for P to generate freshly, or has already generated but not output yet. These are different from (i) the names created by the external environment by the bipartite structure, (ii) names created by other parallel processes, because of the way we use Π ₁ ′ and Π ₂ ′, and (iii) names previously output by P, by construction.

csp2[P] suffers from the same failures of abstraction due to exact choices of fresh names as the unified version csp[P]. We have the same two choices of how to fix these, using the same operators NFN(P,σ) and 〈〈SFN(κ,σ)〉〉. The first of these can be used without alteration, as can the second if it is only used at the outside of the semantics. We cannot incorporate this version into a denotational semantics ${\mathcal{M}}_{\mu }^{2}[P]\rho \zeta \sigma$ since it requires the parameter κ. There are two choices: either to incorporate this parameter into the semantics, or to use a modified SFN′(σ) that does not standardise how external names appear to the process P, something that is not necessary semantically.

It is interesting to note that one of our four CSP semantics, namely ${\mathcal{M}}_{\sqcap }^{2}[P]\zeta \sigma$, is defined without any use of generalised renaming, though it does use both elaborate renamings and parallel composition with processes that limit traces. This is related to our remark earlier that this semantics is the only where no instantaneous influence between seemingly independent parallel processes is required.

We have already seen that the two unified semantics give the same equivalence, and the equivalence they give is independent of reasonable choices for κ and σ. Simpler arguments of the same type work for the two bipartite semantics. Therefore, we will know that all four agree if we can prove that the two nondeterministic semantics agree.

Theorem 16.2.

For a finite-behaviour channel-based CSP model $\mathcal{M}$ and π-calculus process P, we have

• ${\mathcal{M}}_{\sqcap }^{2}[P](Name - \sigma )\sigma =\{ b \in {\mathcal{M}}_{\sqcap }^{1}[P](fn(P))\sigma \mid enames(b) \cap \sigma = \emptyset \}$ whenever $\sigma \cap fn(P) = \emptyset$ and both σ and Name ∖ σ are infinite.

• ${\mathcal{M}}_{\sqcap }^{1}[P]fn(P)\sigma = \sqcap \{{\mathcal{M}}_{\sqcap }^{2}[P](Name - \sigma^{\prime})\sigma^{\prime}\mid \sigma^{\prime} \subseteq \sigma$ , (Name ∖ σ′) infinite} for any infinite σ disjoint from fn(σ).

• Consequently, the congruences induced by ${\mathcal{M}}_{\sqcap }^{1}[\cdot ]$ and ${\mathcal{M}}_{\sqcap }^{2}[\cdot ]$ are the same.

Part (a) of this result says that behaviours b of P in a bipartite name space are just those that happen in the unified name space where the environment did not choose to inject any names that it would have been banned from doing so under bipartite rules. The fact that we are in a channel-based model is vital here.

Part (b) essentially observes that for any finite behaviour b of the unified semantics, there is an infinite subset σ′ of σ left when we remove enames(b), and b will belong to ${\mathcal{M}}_{\sqcap }^{2}[P](Name - \sigma^{\prime})\sigma^{\prime}$.

It follows that the choice of which semantics to adopt is largely down to personal taste. For the author, the unified nondeterministic semantics has much to recommend it because it removes the arbitrary choices implicit in the choice of an enumeration for Name – the semantic value generated by NFN is independent of which enumeration is used in constructing csp[ ⋅] – and a partition of that set into process and environment names. On the other hand it seems likely that the bipartite standardised approach is best suited to most automatic verification methods.

Recall our expandable buffer example, with its four initial names K in the common knowledge of process and environment, and where there are three families of names that get introduced as it proceeds: the z _i introduced by the environment, the s _i extruded by the process, and the m _i used internally by the process but never seen in traces. In the following we will assume that each z _i devised by the environment is fresh.

• In the ${\mathcal{M}}_{\sqcap }^{1}[\cdot ]$ semantics, any trace in which all the s _i and z _i are different (and different from K) is allowed.

• In the ${\mathcal{M}}_{\mu }^{1}[\cdot ]$ semantics, there are less traces, since each s _i is always the name with least index not seen up to that point.

• With ${\mathcal{M}}_{\sqcap }^{2}[\cdot ]$, the s _i and z _i are chosen from two predetermined separate pots.

• And in ${\mathcal{M}}_{\mu }^{2}[\cdot ]$, the sequence of s _i is fixed at the outset since they are chosen in order from a pot that is not used for any other purpose.

One of the most interesting things we might observe about this is that nothing in a trace reveals the values or even presence of the m _i to the outside world. In particular the standardised ${\mathcal{M}}_{\mu }^{1}[\cdot ]$ semantics seems to use up all the names for the visible names, leaving none for the m _i . Whether or not one regards this as paradoxical depends on one’s standpoint: certainly we would not want the abstract semantic value of a process to depend on whether it used a name internally or not.

16.6 Properties and Future Work

We have simultaneously introduced a large number of new semantics for π-calculus, simply because there is one⁶ for every channel-based CSP model that does not give a representation to infinite traces. We cannot hope to explore all their properties here. In this section, therefore, we restrict ourselves to establishing a few basic properties and setting out a research programme to explore further possibilities.

Throughout this section, the $\mathcal{M}$ semantics of a π-calculus process P will be understood to mean the standardised (SFN) semantics calculated over the channel-based CSP model $\mathcal{M}$ over a unified name space with parameters fn(P) and Name∖fn(P)

16.6.1 Refinement and Refinement Checking

The most obvious consequence of having a CSP semantics is that it gives a language a natural notion of refinement. We define refinement, relative to a given model $\mathcal{M}$, by

$$\begin{array}{rcl} P {\sqsubseteq }_{M}Q \equiv {\mathcal{M}}_{\mu }^{1}[P]\kappa \sigma \sqsubseteq {\mathcal{M}}_{ \mu }^{1}[Q]\kappa \sigma & & \\ \end{array}$$

for any κ containing fn(P) ∪fn(Q), which is the same as the $\mathcal{M}$-equivalence, as processes, of P and τ.P+τ.Q (simply a translation of the CSP construct P ⊓Q). This equational characterisation means that the definitions of refinement do not depend on which of the four options is chosen.

Our constructions, Lemma 4, and the properties of refinement in CSP imply that⊑ _M has the compositionality properties one would want, namely

$$\begin{array}{rcl} P {\sqsubseteq }_{M}Q \Rightarrow C[P] {\sqsubseteq }_{M}C[Q]& & \\ \end{array}$$

for any context C.

As in CSP, one process refines another if its behaviours are a subset of those of the second process. Thus one process trace refines another if all its traces are ones of the second, and so on.

In CSP models that record only finitely observable behaviours (a category that does not include divergence), there is a refinement-maximal process, always equivalent to the simply divergent term μ p.τ.p. There is a refinement-minimal member of the CSP model, but no π-calculus process represents it since the minimal member has the capability of using every name on the first step as an output channel. No π-calculus term can do that. It is possible to construct a minimal process in the traces model subject to knowing the set of names K initially: imagine a system constructed using the replication !C and !D of two sorts of cell. A C is initialised with one name x and can then endlessly either input x(y) or output a fresh name $\overline{x}z$ where z is introduced by ν z (and in either case it initialises a further C with name y or z) or initialise a D with value x.

$$\begin{array}{rcl} C = c(x).\mu\,\,p.\nu\,\,z.(x(y).\overline{c}y.p + \overline{x}z.\overline{c}z.p + \overline{d}x.p)& & \\ \end{array}$$

D is initialised with two names and then endlessly outputs one over the other.

$$\begin{array}{rcl} D = d(x).d(y).\mu p.\overline{x}y.p& & \\ \end{array}$$

The process is then defined νcνd!C|!D|C′[k ₁∕x]|⋯|C′[k _n ∕x] where C′ is an initialised copy of C.

The !C=μp.C|τ.p construction could not be used in the same way in building refinement-minimal elements of other finite-behaviour models such as stable failures $\mathcal{F}$ because it is never stable itself. It is, nevertheless, possible to adapt the above construction to build a refinement-minimal element for $\mathcal{F}$ for a given initial knowledge K. This is left as an exercise to the ingenious reader!

In FDR, the main mode of verifying processes is to show that they refine other CSP processes representing their specifications. Since our constructions have, in effect, embedded π-calculus within CSP, we have considerable freedom in how to formulate refinement checks using a mixture of the two languages.⁷ A reasonably general model is provided by checks of the form

$$\begin{array}{rcl} Spec {\sqsubseteq }_{M}C[Imp]& & \\ \end{array}$$

where Spec is either a CSP or π-calculus process and C is a possibly null CSP context.

So, for example, deadlock freedom is equivalent to the refinement check

$$\begin{array}{rcl} \mu p.\tau.p {\sqsubseteq }_{F}Imp \backslash Events& & \\ \end{array}$$

and we can use the lazy abstraction construction from CSP, as in the following fault tolerance check from Chapter 12 of [16] that goes a little beyond the model above:

$$\begin{array}{rcl} Imp \parallel_{E}STOP {\sqsubseteq }_{F}(Imp \parallel_{E} CHAOS(E))\backslash E& & \\ \end{array}$$

where E is a set of events that trigger erroneous behaviour within Imp. This specification says that whatever externally visible behaviour appears with these error events allowed also happens when they are banned.

16.6.2 Prospects for Using FDR

Having formulated specifications as refinement checks, it is interesting to ask whether they can be run on FDR, since this might provide a powerful additional tool to apply to systems designed in π-calculus.

FDR achieves its considerable speed by concentrating on finite-state systems, allowing most checks to be performed in time linear (or sublinear if compressions are used) in the number of states of the implementation. It concentrates on what is the central case of CSP, namely of a number of finite-state processes connected by a static harness built of parallel, hiding and renaming operators.

This is challenged by two aspects of π-calculus. Firstly, π-calculus assumes that every x(y) input communication offers an infinite range of inputs. Secondly, π-calculus networks are frequently dynamic and potentially unbounded in size, as seen both in our buffer example and in the construction above that built the trace-refinement-minimal process. This takes them outside FDR’s “comfort zone” and probably out of its range altogether.

It therefore seems sensible to start by looking at π-calculus networks that create static networks and which generate only finitely new names using ν z P constructs.

We therefore consider networks which take the form

$$\begin{array}{rcl} \mathbf{\nu} {x}_{1}\,\mathbf{\nu} {x}_{2}\ldots \mathbf{\nu} {x}_{n}\,({P}_{1}\vert {P}_{2}\vert \ldots \vert {P}_{m})& & \\ \end{array}$$

where the P _i make no use of the operators | and ν x and are therefore finite-state except for the precise names they contain.

The author conjectures that the majority of trace refinement checks involving such processes can be performed finitely in the following way, thanks to Lazić’s theory of data independence in CSP [8].

• Use the bipartite approach to semantics.

• Use a type of n+k+2 names, of which n are tied to the identifiers x ₁,…,x _n , k are the externally visible names in the system, and the final two are “extras.” The reason for there are just two extra names is that every π-calculus term, with the exception of the inequality constraints for fresh names, satisfies the condition PosConjEqT from [8], which states that no two members of the data-independent type (here Name) are ever compared for equality except in such a way that the consequences of equality are always trace refined by the consequences of inequality. In π-calculus, both (obviously) equality guards [x=y] and communication in P|Q represent equality tests of this sort. The first use of any extra name must be as an input along a preexisting channel. Lazić’s results show that in similar circumstances, it usually suffices to consider a check in which the data-independent type is of size one or two greater than the number of distinct constant values. This represents a threshold value for the refinement check. Thus initially, and until the process has extruded one or more of the names x _i , inputs are restricted to the other k+2 names L.

• Regarding the identifiers x _i as constants, replace the system with (P ₁|…|P _m )∥ Σ _π BOF(L).

• This process may well not be symmetric in the names x _i , but if it is refinement checked against a process that is symmetric in them (for example, by not referring to them at all, as will presumably be the case when the system does not extrude names) it should be equivalent to check that the unsymmetric version refines the specification.

Data independence will, in fact, be applicable to all π-calculus descriptions of systems: it is impossible to create π-calculus processes that are not data independent, at least using the syntax we have adopted for it.

Another class of system that uses an unbounded collection of fresh values has already been widely studied in CSP, namely cryptographic protocols where the values are keys, nonces, etc. (This connection has already been exploited in the Spi Calculus [1].) Several related methods for turning naturally infinite-state refinement checks involving these into finite-state ones have been developed for these protocols [21, 7]. These methods use a combination of recycling values that no longer have any meaning to the system and making room for this by identifying “out of date” values.

It would be interesting to see whether these same techniques can be employed usefully for π-calculus systems that generate an infinite number of fresh names in their lifetimes, but only have a finite number meaningful at any one time.

Using the present version of FDR it is not possible to analyse networks that grow unboundedly. It should, however, be possible to analyse ones that are dynamic but only have a bounded number of active (i.e. nonzero processes in π-calculus terms) at any one time and only have a finite number of patterns that these processes follow. We would need to create a CSP process definition Flex that could be initialised to behave like one of these patterns and returns to the state Flex once the first pattern has finished. When a process executes a parallel command P|Q it would implement one of these (say P) itself and initialise one of the available Flexes to behave like Q.

16.6.3 Full Abstraction

All the well-known CSP models are fully abstract with respect to one or more simple tests that can be made of processes in the sense that two processes P and Q are identified in the model if and only if, for all CSP contexts C[ ⋅], C[P] passes each of the tests if and only if C[Q] does. (See [16, 18, 19] for information on this.) Thus, for example, the finite traces model $\mathcal{T}$ is fully abstract with respect to the test “P has the trace ⟨a⟩” for an arbitrarily chosen visible event a, and the failures divergences model $\mathcal{N}$ is fully abstract with respect to the test “neither deadlocks nor diverges on ⟨⟩.”

It is clear that, when a given CSP model $\mathcal{M}$ has such a property, then two π-calculus terms P and Q are identified in it if and only if all CSP contexts applied to them give the same results for the tests. It is interesting to ask whether the same will hold for π-calculus contexts. The author believes that most of these results will indeed carry across in this way, but resolving these questions is beyond the scope of this paper.

16.6.4 Comparison

Equivalences for π-calculus terms have previously been given in terms of bisimulation relations of different sorts. Over other process calculi it is true that bisimulations relations generally give finer equivalences than CSP-style models, except that some bisimulations (e.g. weak) do not make the same distinctions based on the potential to diverge that some CSP models do. The author expects that the same will be true for π-calculus.

It seems to the author that the semantics of π-calculus in CSP models have the merit of simplicity, in the sense that each recorded behaviour only gives a single value to each name, whichever of our four options is picked. These models seem no less natural for π-calculus than they do for CSP. Indeed, given that in a unified name space it is inevitable that any branching-lime model for π-calculus there will be recorded behaviours on which the name declared in νz P will appear with two different values, the use of linear observations seems particularly appropriate here.

While our four different ways of treating the fresh names of π-calculus create different models of a process, they do not change the equivalence induced by the translation. This is in contrast to the usual bisimulation-based equivalences for the languages (early, late, barbed, etc.).

16.7 Conclusions

We have illustrated the enormous expressive power of Hoare’s CSP by giving a number of semantics to π-calculus. The author hopes that in addition to providing this demonstration of the power of CSP this paper will also be the key to new understandings and process analysis methods for π-calculus, and that for some audiences it might provide a relatively comprehensible way of explaining the semantics of that notation. In particular, it will be interesting to see if the existence of compositional theories of refinement for π-calculus will have any applications.

In addition to the topics for further work highlighted in the previous section, there is a further open end to be explored, namely the topic of models with infinite traces. Since an infinite trace can contain an infinite number of fresh names, several of the arguments we have used in this paper no longer apply, and it becomes possible for a single trace to contain every single name if there are only finitely many of these.

While this may or may not be apparent to the reader, the author discovered on numerous occasions that the semantic decisions made in the design of π-calculus were absolutely crucial to the creation of a reasonably elegant semantics for it in CSP. A prime example of this is the rule that no fresh name can be used as a channel until it has been passed along another channel is necessary for ensuring that the first time a name appears in a behaviour in a channel-based model is as the “data” field of an actually communicated event. This is key to a number of things working properly in the CSP semantics. Thus, at least to the author, this work demonstrated not only the power of CSP, but also the great elegance of the π-calculus.