Abstract
We present a new and relatively elementary method for studying the solution of the initial-value problem for dispersive linear and integrable equations in the large-t limit, based on a generalization of steepest descent techniques for Riemann-Hilbert problems to the setting of \({\overline {\partial }}\)-problems. Expanding upon prior work (Dieng and McLaughlin, Long-time asymptotics for the NLS equation via \({\overline {\partial }}\) methods, arXiv:0805.2807, 2008) of the first two authors, we develop the method in detail for the linear and defocusing nonlinear Schrödinger equations, and show how in the case of the latter it gives sharper asymptotics than previously known under essentially minimal regularity assumptions on initial data.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Since
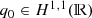 implies that (1 + |x|)q
0(x) is square-integrable, it follows by Cauchy-Schwarz that
implies that (1 + |x|)q
0(x) is square-integrable, it follows by Cauchy-Schwarz that 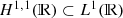 , which in turn implies that the reflection coefficient r(z) is well-defined for each
, which in turn implies that the reflection coefficient r(z) is well-defined for each 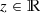 .
. - 2.
In many works on long-time asymptotics for the Cauchy problem (1)–(2) written before the Digital Library of Mathematical Functions was freely available (e.g., [8, 9]), the solution of Riemann-Hilbert Problem 3 was developed in terms of the related function \(D_\nu (y):=U(-\tfrac {1}{2}-\nu ,y)\). Since most formulæ in [18, §12] are phrased in terms of U(⋅, ⋅), we favor the latter.
- 3.
All L p norms of matrix-valued functions in this section depend on the choice of matrix norm, which we always take to be induced by a norm on
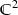 .
.
References
M. Borghese, R. Jenkins, and K. D. T.-R. McLaughlin, “Long time asymptotic behavior of the focusing nonlinear Schrödinger equation,” Ann. Inst. H. Poincaré Anal. Non Linéaire35, no. 4, 887–920, 2018.
S. Cuccagna and R. Jenkins, “On the asymptotic stability of N-soliton solutions of the defocusing nonlinear Schrödinger equation,” Commun. Math. Phys.343, 921–969, 2016.
P. Deift, A. Its, and X. Zhou, “Long-time asymptotic for integrable nonlinear wave equations,” in A. S. Fokas and V. E. Zakharov, editors, Important Developments in Soliton Theory 1980–1990, 181–204, Springer-Verlag, Berlin, 1993.
P. Deift and X. Zhou, “A steepest descent method for oscillatory Riemann–Hilbert problems. Asymptotics for the mKdV equation,” Ann. Math.137, 295–368, 1993.
P. Deift and X. Zhou, “Long-time asymptotics for integrable systems. Higher order theory,” Comm. Math. Phys.165, 175–191, 1994.
P. Deift and X. Zhou, Long-time behavior of the non-focusing nonlinear Schrödinger equation — A case study, volume 5 of New Series: Lectures in Math. Sci., University of Tokyo, 1994.
P. Deift and X. Zhou, “Perturbation theory for infinite-dimensional integrable systems on the line. A case study,” Acta Math.188, no. 2, 163–262, 2002.
P. Deift and X. Zhou, “Long-time asymptotics for solutions of the NLS equation with initial data in a weighted Sobolev space,” Comm. Pure Appl. Math.56, 1029–1077, 2003.
M. Dieng and K. D. T.-R. McLaughlin, “Long-time asymptotics for the NLS equation via \({\overline {\partial }}\) methods,” arXiv:0805.2807, 2008.
A. R. Its, “Asymptotic behavior of the solutions to the nonlinear Schrödinger equation, and isomonodromic deformations of systems of linear differential equations,” Dokl. Akad. Nauk SSSR261, 14–18, 1981. (In Russian.)
R. Jenkins, J. Liu, P. Perry, and C. Sulem, “Soliton resolution for the derivative nonlinear Schrödinger equation,” Commun. Math. Phys., doi.org/10.1007/s00220-018-3138-4, 2018.
J. Liu, P. A. Perry, and C. Sulem, “Long-time behavior of solutions to the derivative nonlinear Schrödinger equation for soliton-free initial data,” Ann. Inst. H. Poincaré Anal. Non Linéaire35, no. 1, 217–265, 2018.
K. D. T.-R. McLaughlin and P. D. Miller, “The \(\overline {\partial }\) steepest descent method and the asymptotic behavior of polynomials orthogonal on the unit circle with fixed and exponentially varying nonanalytic weights,” Intern. Math. Res. Papers2006, Article ID 48673, 1–77, 2006.
K. D. T.-R. McLaughlin and P. D. Miller, “The \(\overline {\partial }\) steepest descent method for orthogonal polynomials on the real line with varying weights,” Intern. Math. Res. Notices2008, Article ID rnn075, 1–66, 2008.
P. D. Miller and Z.-Y. Qin, “Initial-boundary value problems for the defocusing nonlinear Schrödinger equation in the semiclassical limit,” Stud. Appl. Math.134, no. 3, 276–362, 2015.
N. I. Muskhelishvili, Singular Integral Equations, Boundary Problems of Function Theory and Their Application to Mathematical Physics, Second edition, Dover Publications, New York, 1992.
P. A. Perry, “Inverse scattering and global well-posedness in one and two space dimensions,” in P. D. Miller, P. Perry, and J.-C. Saut, editors, Nonlinear Dispersive Partial Differential Equations and Inverse Scattering, Fields Institute Communications, volume 83, 161–252, Springer, New York, 2019. https://doi.org/10.1007/978-1-4939-9806-7_4.
F. W. J. Olver, A. B. Olde Daalhuis, D. W. Lozier, B. I. Schneider, R. F. Boisvert, C. W. Clark, B. R. Miller, and B. V. Saunders, eds., NIST Digital Library of Mathematical Functions, http://dlmf.nist.gov/, Release 1.0.17, 2017.
H. Segur and M. J. Ablowitz, “Asymptotic solutions and conservation laws for the nonlinear Schrödinger equation,” J. Math. Phys.17, 710–713 (part I) and 714–716 (part II), 1976.
V. E. Zakharov and S. V. Manakov, “Asymptotic behavior of nonlinear wave systems integrated by the inverse method,” Sov. Phys. JETP44, 106–112, 1976.
X. Zhou, “The L 2-Sobolev space bijectivity of the scattering and inverse-scattering transforms,” Comm. Pure Appl. Math.51, 697–731, 1989.
Acknowledgements
The first two authors were supported in part by NSF grants DMS-0451495, DMS-0800979, and the second author was supported by NSF Grant DMS-1733967. The third author was supported in part by NSF grant DMS-1812625.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Science+Business Media, LLC, part of Springer Nature
About this chapter
Cite this chapter
Dieng, M., McLaughlin, K.D.TR., Miller, P.D. (2019). Dispersive Asymptotics for Linear and Integrable Equations by the \(\overline {\partial }\) Steepest Descent Method. In: Miller, P., Perry, P., Saut, JC., Sulem, C. (eds) Nonlinear Dispersive Partial Differential Equations and Inverse Scattering. Fields Institute Communications, vol 83. Springer, New York, NY. https://doi.org/10.1007/978-1-4939-9806-7_5
Download citation
DOI: https://doi.org/10.1007/978-1-4939-9806-7_5
Published:
Publisher Name: Springer, New York, NY
Print ISBN: 978-1-4939-9805-0
Online ISBN: 978-1-4939-9806-7
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


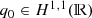 implies that (1 + |x|)q
0(x) is square-integrable, it follows by Cauchy-Schwarz that
implies that (1 + |x|)q
0(x) is square-integrable, it follows by Cauchy-Schwarz that 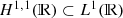 , which in turn implies that the reflection coefficient r(z) is well-defined for each
, which in turn implies that the reflection coefficient r(z) is well-defined for each 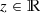 .
.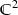 .
.