The Fracture of Brittle Solids

Abstract

Traditionally, mechanical engineering design has been based almost entirely on the use of ductile metals. They are tough, are relatively strong, and can readily be formed into complicated shapes. A great deal of research has been devoted to the processing and mechanical behavior of these materials, and design methods for their use are rather well established. By contrast, relatively little attention has been given, in the past, by mechanical engineers, to materials showing brittle behavior. Civil engineers have used such materials, but generally in situations where they are in compression and with generous safety factors being allowed. In recent years, however, there has been an increasing interest in the use of brittle solids in engineering design. Perhaps the principal reason for this is that the materials which have the greatest strength at very high temperatures are brittle at ambient temperature, for example, graphite, aluminum oxide, beryllium oxide, silicon carbide, and silicon nitride. If such materials could be fabricated and used, reliably, the economic advantages would be considerable in many high-temperature applications. The usefulness of brittle materials is, of course, not confined to elevated temperatures. In many other situations, the properties of specific brittle materials (e.g., wear and corrosion resistance, high compressive strength, low neutron absorption in the case of BeO, transparency in the case of quartz and glass, etc.) make them attractive to the designer.

Problems

• 1. A series of ten tensile tests on a brittle solid gave the following values:

  $$ \begin{array}{l}\kern0.55em 6,600,\kern1.45em 8,070,\kern1.5em 8,900,\kern1.5em 9,500,\kern1.5em 9,830\kern0.37em \mathrm{psi}\\ {}10,350,\kern1em 10,890,\kern1em 11,350,\kern1em 11,920,\kern1em 12,570\kern0.37em \mathrm{psi}\end{array} $$

  The mean strength is 10,000 psi and the standard deviation is 1,820 psi.

  Assuming that a 2-parameter Weibull distribution can be fitted to these values, estimate m in several different ways.

  Can you make an estimate of the lowest strength that would be observed if 100 such specimens were tested?

  If a new set of specimens is prepared with the specimen volume ten times that of the original specimens, what do you estimate as the mean strength of the larger specimens?

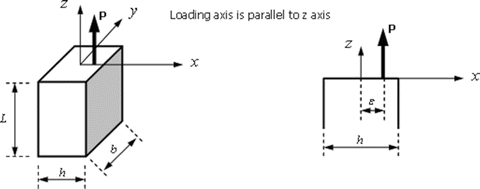
• 2. We consider tension tests on a specimen of rectangular cross-section. If the loading axis is parallel to the geometrical axis of the specimen, but eccentric by distance ε, then the specimen is subjected to a force P and a moment P ^ε. Thus, the maximum tensile stress in the specimen is

  $$ {\sigma}_{\max }=\frac{P}{bh}+\frac{6P\varepsilon }{b{h}^2} $$

  • (a) For a brittle solid containing flaws distributed through its volume in which the probability of failure of unit volume may be taken as

    $$ F\left(\sigma \right)=1-{e}^{-{\left(\sigma /{\sigma}_0\right)}^m}, $$

    you are asked to obtain an expression for the ratio:

    $$ \frac{\mathrm{Median}\ \mathrm{fracture}\ \mathrm{load}\ \left(\varepsilon =h/6\right)}{\mathrm{Median}\ \mathrm{fracture}\ \mathrm{load}\ \left(\varepsilon =0\right)} $$

  • (b) Compare this result with the ratio of fracture loads (for $\varepsilon =\mathrm{h}/6$ and $\varepsilon =\theta$) which would be predicted for a brittle material with no variability in strength. Explain physically why the ratios differ.

    

• 3. Consider the pure bending of a beam of rectangular cross section of a brittle solid. Assuming that fracture under tensile states of stress may be predicted using a two-parameter Weibull distribution, you are asked to obtain an expression for the median value of moment required to fracture the beam. That is, ${M}_{\mathrm{median}}=f\left(b,h,L,{\sigma}_0,m\right)$. Recall that the stress at a distance y from the neutral axis is given by $\sigma =\frac{My}{I}$.

  

• 4. A frequently used design rule specifies that the strength value used in structural calculations should be taken as Mean Strength − 3 Standard Deviations. This rule, apparently, is based on the assumption that the strength values follow a Normal Distribution. In any event, if we are dealing with brittle solids, whose strength values follow a two-parameter Weibull Distribution say with m = 10, would this design rule overestimate or underestimate the strength of the weakest specimen in a batch of size N?

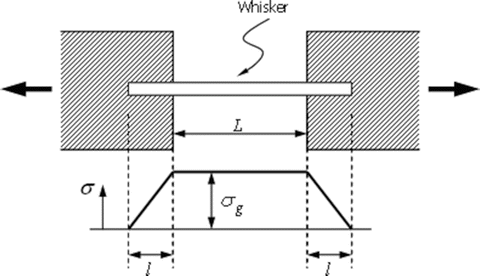
• 5. In testing short whiskers of a brittle material, the ends are embedded in a low strength matrix to which the loading is applied. As a result, the stress at each end of the whisker increases linearly over a length l from zero to the value σ _g . The stress σ _g is that in the “gauge length” L. If L is short, many whiskers will break in the grips and we do not want to discard these observations. For this reason, you are asked to derive an expression for the cumulative distribution function G(σ) (i.e., probability that a given whisker will break at or below a gauge section stress level σ _g ) which includes the probability of failure occurring in the grips. From this result can you suggest a simple expression for the effective gauge length in such a test.

  We assume that flaws are distributed along the length of these whiskers rather than volume or area and use a two-parameter Weibull distribution.

  

• 6. A bundle is made from a large number of filaments. The individual filaments show a great deal of variability and their breaking loads follow an exponential distribution. That is, the survival probability is given by $S(x)={e}^{-\lambda x}$ where λ is the one parameter of the exponential distribution.

  What fraction of the filaments will survive at the maximum load-carrying capacity of the bundle?

  What is the average fracture load which would be observed in testing single filaments (expressed in terms of λ)?

• 7. Tests on ten glass filaments gave the following values of fracture load in pounds 6.1, 6.5, 8.5, 9.2, 11.5, 14.0, 15.0, 25.0, 30.0, 32.0 (the average is 15.8 lb).

  What would have been the maximum load-carrying capacity if these ten filaments had been tested as a bundle.

  It has been suggested that very strong bundles could be obtained by proof testing all filaments such that we discard all but the strongest 20 %.

  You are asked to predict the ratio: Strength of a bundle made from the survivors of such a proof test ÷ Strength of a bundle made from filaments that have not been proof tested. Both bundles are assumed to have the same (large) number of filaments.

• 8. Assuming a volume distribution of flaws, a 2-parameter Weibull distribution has been obtained for a granitic rock. The values are m = 13 and ${\sigma}_0=1,200\kern0.37em \left(\mathrm{psi}\hbox{-} \mathrm{in}.\ \mathrm{units}\right)$.

  You are asked to consider a test in which a cylindrical hole of radius R _j in a very large diameter cylindrical block of length L is pressurized. Assuming that the pressure P cannot penetrate any cracks present at the bore, you are asked to obtain an expression for the median pressure to produce fracture. Ignore radial and axial stresses and take the hoop stress as ${\sigma}_{\theta }=p{\left({R}_j/r\right)}^2$. First, obtain a general result $\left(p\kern0.5em \mathrm{median}/{\sigma}_0\right)=f\left(\dot{m},{R}_j,L\right)$. Then specialize this for m = 13, ${\sigma}_0=1,200$, R = 0.5 in., L = 10 in.

• 9. Three sets of bending tests were made on specimens of a brittle solid of three different sizes. The results were:

  	Tests A (15 specimens)	Tests B (4 specimens)	Tests C (4 specimens)
  Strength (psi)	1,587, 1,801, 1,923	1,835, 2,163	2,028, 2,062
  	1,954, 1,623, 1,863	2,190, 2,274	2,428, 2,616
  	1,923, 2,015, 1,679
  	1,863, 1,953, 2,137
  	1,709, 1,893, 1,953
  Average strength (psi)	1,858	2,116	2,283

  You are asked to use all this information to make an estimate of the Weibull parameter m for this material. One general approach for estimating m is sufficient.