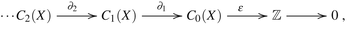Abstract
In the framework of the PDE’s algebraic topology, previously introduced by A. Prástaro, are considered exotic differential equations, i.e., differential equations admitting Cauchy manifolds N identifiable with exotic spheres, or such that their boundaries ∂ N are exotic spheres. For such equations are obtained local and global existence theorems and stability theorems. In particular the smooth (four-dimensional) Poincaré conjecture is proved. This allows to complete the previous Theorem 4.59 in Prástaro (Essays in Mathematics and Its Applications (Dedicated to Stephen Smale for his 80th birthday), Springer, Heidelberg/New York/Dordrecht/London, pp. 369–419, 2012) also for the case n = 4.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
- 2.
In this paper we denote by SX the suspension of a topological space X. (For details and general informations on algebraic topology see e.g. [61, 92, 98, 99, 101]. In this paper we will use the following notation: \(\thickapprox \) homeomorphism; \(\mathop{\cong}\) diffeomorphism; ≊ homotopy equivalence; ≃ homotopy.) Therefore SE n is the suspension of the CW-complex E n .
- 3.
E is finite iff there is an integer N such that E n = S n−N E N for n ≥ N and the complex E N is finite.
- 4.
If n > 1 then G must be abelian.
- 5.
If F is cofinal and \(K_{n} \subset E_{n}\) is a finite subcomplex, then there is an m such that \(S^{m}K_{n} \subset F_{n+m}\). Intersection of two cofinal subspectra is cofinal and if G ⊂ F ⊂ E are subspectra such that F is cofinal in E and G is cofinal in F, then G is cofinal in E. An arbitrary union of cofinal subspectra is cofinal.
- 6.
Let E and F be spectra and f: E → F a function. If F ′ ⊂ F is a cofinal subspectrum then there is a cofinal subspectrum E ′ ⊂ E with \(f(E^{{\prime}}) \subset F^{{\prime}}\). (Composition of maps is now possible!) In the category \(\mathcal{S}\) any spectrum is equivalent to any cofinal subspectrum of its.
- 7.
For any topological space X we set\(X^{+} \equiv X \sqcup \{{\ast}\}\). (If X is not compact X + is the Alexandrov compactification to a point.) In particular if \(X = I \equiv [0, 1] \subset \mathbb{R}\), then one takes {∗} as base point.
- 8.
- 9.
Here we have used the fact that E(SX) is a cofinal subspectrum of Σ E(X) and hence the inclusion i: E(SX) → Σ E(X) induces an isomorphism i ∗.
- 10.
Let \(\mathcal{U}\) be an abelian category. A differential object in \(\mathcal{U}\) is a pair (A,d) where \(A \in Ob(\mathcal{U})\) and \(d \in \mathrm{Hom}_{\mathcal{U}}(A; A)\) such that d 2 = 0. Let \(\mathcal{D}(\mathcal{U})\) be the category of differential objects in \(\mathcal{U}\) . We call homology the additive functor \(H: \mathcal{D}(\mathcal{U}) \rightarrow \mathcal{U}\) , given by \(H(A,d) =\ker (d)/\mbox{ im}\ \ (d) = Z(A)/B(A)\) , where Z(A) is the set of cycles of A and B is the set of boundaries of A. H(A) is the homology of (A,d). Then, a spectral sequence in the category \(\mathcal{U}\) is a sequence of differential objects of \(\mathcal{U}\) : {E n ,d n }, n = 1, 2,…, such that H(E n ,d n ) = E n+1 , n = 1, 2,…. (See, e.g., [43, 57].)
- 11.
For the homological definition of orientability see next Remark 3.
- 12.
In particular, for k = n, \(F_{k}\mathop{\cong}O(n)\), and for k = 1, \(F_{1}\mathop{\cong}S^{n-1}\).
- 13.
By the Stiefel–Whitney classes of an n-dimensional manifold M, one means the corresponding classes of TM.
- 14.
Universal classifying space for the group SO(n).
- 15.
If M is a closed and connected manifold of dimension k, admitting a finite triangulation, then \(H_{k}(M; \mathbb{Z}_{2})\mathop{\cong}\mathbb{Z}_{2}\). The fundamental class of M is \([M] =\sum _{i}v_{i}^{k}\), i.e., the sum of all k-simplexes.
- 16.
A partition (i1 ,…,i r ) of n is nondyadic if none of the i β are of the form 2 s − 1.
- 17.
Pontrjagin numbers are determined by means of homonymous characteristic classes belonging to \(H^{\bullet }(BG, \mathbb{Z})\) , where BG is the classifying space for G-bundles, with G = S p (n).
- 18.
\(\mathbb{R}\mathbb{P}^{k}\) are orientable manifolds iff \(k \in \mathbb{N}\) is odd. P(2 r − 1,s2 r ) are orientable manifolds. One has \(\dim P(m,n) = m + 2n\).
- 19.
In Table 4 are resumed relations between spectra, generalized (co)homologies, and some distinguished examples. Let us emphasize the relation with Brown’s representable theorem. A functor \(F: (\mathcal{W}^{\bullet {\prime}})^{op} \rightarrow \mathcal{S}_{et}\) is representable, i.e., F is equivalent to \(\mathrm{Hom}_{\mathcal{W}^{\bullet {\prime}}}(-; C)\) for some CW-complex C, iff the following conditions are satisfied. (i)(Wedge axiom). \(F(\vee _{\alpha }X_{\alpha })\mathop{\cong}\prod _{\alpha }F(X_{\alpha })\); (ii)(Mayer–Vietoris axiom). For any CW complex W covered by two subcomplexes U and V, and any elements u ∈ F(U), v ∈ F(V ), such that u and v restrict to the same element of \(F(U\bigcap V )\), there is an element w ∈ F(W) restricting to u and v, respectively. In the particular case of singular cohomology, one has \(H^{n}(X; A)\mathop{\cong}\mathrm{Hom}(X; K(A,n))\), i.e., the singular cohomology functor is representable. Thanks to extended versions of Brown’s representable theorem one can prove that all homology theories come from spectra, or by considering multiplicative operations, all homology theories come from ring spectra with multiplication μ: E ∧ E → E and the unity η: E(S 0) → E.
- 20.
These module structures \(\mathcal{A}^{\bullet }\times H^{\bullet }(X; \mathbb{Z}_{p}) \rightarrow H^{\bullet }(X; \mathbb{Z}_{p})\) , allow us to understand that there are strong constraints just on the space X in order to obtain cohomology spaces \(H^{\bullet }(X; \mathbb{Z}_{p})\) with a prefixed structure. For example, do not exist spaces X with \(H^{\bullet }(X; \mathbb{Z}_{p}) = \mathbb{Z}[\alpha ]\) , unless α has dimension 2 or 4, where there examples \(\mathbb{C}P^{\infty }\) and \(\mathbb{H}P^{\infty }\).
- 21.
A cohomology operations is a natural transformation between cohomology functors. One says that a cohomology operation is stable if it commutes with the suspension functor S. For example the cup product squaring operator H n (X; R) → H 2n (X; R), x↦x ∪ x, where R is a ring and X a topological space, is an instable cohomology operation. Instead, are stable the following Steenrod operations: \(Sq^{i}: H^{n}(X; \mathbb{Z}_{2}) \rightarrow H^{n+i}(X; \mathbb{Z}_{2})\) and \(P^{i}: H^{n}(X; \mathbb{Z}_{2}) \rightarrow H^{n+2i(p-1)}(X; \mathbb{Z}_{2})\) . (In Table 5 are resumed some fundamental properties of Sq i.)
- 22.
A Galois field (or finite field) is a field that contains only finitely many elements. These are classified by q = p k if they contains q elements. Each Galois field with q elements is the splitting field of the polynomial x q − x. Recall that the splitting field of a polynomial p(x) over a field K is a field extension L of K over which p(x) factorizes into linear factors x − a i , and such that a i generates L over K, i.e, L = K(a i ). (In Table 6 are reported some properties of field extensions useful in the paper.) The extension L of minimal degree over K in which p splits exists and is unique up to isomorphism, identified by the Galois group of p. (In Table 7 are reported some fundamental properties and examples of Galois groups.)
- 23.
\(\mathcal{A}^{\bullet }\) has a natural structure of Hopf algebra with commutative, associative comultiplication \(\psi: \mathcal{A}^{\bullet }\rightarrow \mathcal{A}^{\bullet }\otimes \mathcal{A}^{\bullet }\), given by \(\psi (\mathcal{A}^{k}) =\sum _{i+j=k}\mathcal{A}^{i} \otimes \mathcal{A}^{j}\). Let us denote by \(\mathcal{A}_{\bullet }\equiv \mathrm{Hom}_{\vert \vert }(\mathcal{A}^{\bullet }; \mathbb{F}_{q}) = \oplus _{n}\mathcal{A}_{n} = \oplus _{n}\mathrm{Hom}_{\mathbb{F}_{q}}(\mathcal{A}^{n}; \mathbb{F}_{q})\) the dual vector space to \(\mathcal{A}^{\bullet }\). One has the canonical evaluation pairing \(<,>: \mathcal{A}^{\bullet }\times \mathcal{A}_{\bullet }\rightarrow \mathbb{F}_{q}\), < f, α > = α(f). One has the following isomorphism of \(\mathbb{F}_{q}\)-Hopf algebras \(\mathcal{A}_{\bullet }\mathop{\cong}\mathbb{F}_{q}[\xi _{1},\xi _{2},\xi _{3},\cdots \,,\xi _{k},\cdots \,]\), where \(\deg (\xi _{k}) = q^{k-1}\), \(k \in \mathbb{N}\), and comultiplication \(\phi: \mathcal{A}_{\bullet }\rightarrow \mathcal{A}_{\bullet }\otimes \mathcal{A}_{\bullet }\), given by \(\phi (\xi _{k}) =\sum _{i+j=k}\xi _{i}^{q^{j} } \otimes \xi _{j}\).
- 24.
The (co)homological interpretation of the Bockstein operator is associated with a short exact sequence
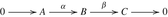 of chain complexes in an abelian category. In fact to such a sequence there corresponds a long exact sequence
of chain complexes in an abelian category. In fact to such a sequence there corresponds a long exact sequence 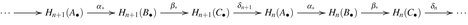 . The boundary maps \(\delta _{n+1}: H_{n+1}(C_{\bullet }) \rightarrow H_{n}(A_{\bullet })\) are just the Bockstein homomorphisms. In particular, if
. The boundary maps \(\delta _{n+1}: H_{n+1}(C_{\bullet }) \rightarrow H_{n}(A_{\bullet })\) are just the Bockstein homomorphisms. In particular, if 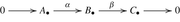 is a short exact sequence of abelian groups and \(A_{\bullet } = E_{\bullet } \otimes A\), \(B_{\bullet } = E_{\bullet } \otimes B\), \(C_{\bullet } = E_{\bullet } \otimes C\), with E
• a chain complex of free, or at least torsion free, abelian groups, then the Bockstein homomorphisms are induced by the corresponding short exact sequence
is a short exact sequence of abelian groups and \(A_{\bullet } = E_{\bullet } \otimes A\), \(B_{\bullet } = E_{\bullet } \otimes B\), \(C_{\bullet } = E_{\bullet } \otimes C\), with E
• a chain complex of free, or at least torsion free, abelian groups, then the Bockstein homomorphisms are induced by the corresponding short exact sequence 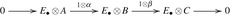 . Similar considerations hold for cochain complexes. in such cases the Bockstein homomorphism increases the degree, i.e., \(\beta: H^{n}(C^{\bullet }) \rightarrow H^{n+i}(A^{\bullet })\).
. Similar considerations hold for cochain complexes. in such cases the Bockstein homomorphism increases the degree, i.e., \(\beta: H^{n}(C^{\bullet }) \rightarrow H^{n+i}(A^{\bullet })\). - 25.
The third integral Stiefel–Whitney class is the obstruction to a spin c-structure on X. (In Table 8 are also summarized, for any convenience, fundamental properties of the Whitney-Stiefel classes.)
- 26.
Let us also emphasize that we can recognize webs on PDEs, by looking inside the geometric structure of PDEs. By means of such webs, we can solve (lower dimensional) Cauchy problems. This is important in order to decide about the “admissibility” of integral manifolds in integral bordism problems. However these aspects are not explicitly considered in this paper. They are studied in some details in other previous works about the PDE’s algebraic topology by A. Prástaro [3, 4]. For complementary informations on geometry of PDEs, see, e.g., Refs. [4, 8–10, 25, 26, 28, 40, 41, 56, 58, 59, 61–69, 80].
- 27.
In other words the quantum bordism group of E k is the integral bordism group of \(J_{n}^{k}(W)\) relative to E k . (This language reproduces one in algebraic topology for couples (X, Y ) of differentiable manifolds, where Y ⊂ X.)
- 28.
- 29.
- 30.
\(\mathfrak{C}ons(E_{k})\) can be identified with the spectral term \(E_{1}^{0,n-1}\) of the spectral sequence associated with the filtration induced in the graded algebra \(\varOmega ^{\bullet }(E_{\infty }) \equiv \oplus _{q\geq 0}\varOmega ^{q}(E_{\infty })\), by the subspaces \(C\varOmega ^{q}(E_{\infty }) \subset \varOmega ^{q}(E_{\infty })\). (For abuse of language we shall call “conservation laws of k-order”, characteristic integral (n − 1)-forms too. Note that \(C\varOmega ^{0}(E_{k}) = 0\). See also Refs. [57–60, 62].)
- 31.
It is important to note that can be \(\mathcal{I}(E_{k})^{p}\not =0\) even if E k is p-cohomologic trivial, i.e., \(H^{p}(E_{k}; \mathbb{R}) = 0\) . This, for example, can happen if E k is contractible to a point.
- 32.
For example for the d’Alembert equation one can see that for any conservation law ω one has < ω, N > = 0, where N is any admissible one-dimensional compact integral manifold of d ′ A), but \(\omega \not\in [0] \in E_{1}^{0,n-1}\).
- 33.
- 34.
For the definition of the groups Θn , see [74].
- 35.
It is well known that the Schönflies problem is related to extensions of the Jordan–Brouwer theorem. (See, e.g., [42].) Let us emphasize that the lemma does not necessitate to work in the category of topological spaces. In fact, it is well known that topological embeddings f: S2 → S 3 do not necessarily have simply connected the two separate components of S 3 ∖f(S 2 ). In fact this is just the case of the Alexander horned sphere Σ 2 ⊂ S 3 [5].
- 36.
The reduced homology groups \(\tilde{H}_{p}(X)\), of non-empty space X, are the homology groups of the augmented chain complex:
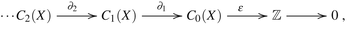
, where ε can be considered generated by the chain \([\varnothing ]\mapsto X\), sending the simplex with no-vertices (empty simplex) to X, i.e., \(\epsilon (\sum _{i}n_{i}\sigma ) =\sum _{i}n_{i}\). Since ε ∂ i = 0, ε induces a map \(H_{0}(X) \rightarrow \mathbb{Z}\) with kernel \(\tilde{H}_{0}(X)\), so one has \(H_{0}(X)\mathop{\cong}\tilde{H}_{0}(X)\bigoplus \mathbb{Z}\), and \(H_{p}(X)\mathop{\cong}\tilde{H}_{p}(X)\), \(\forall p > 0\). Therefore, we get \(\tilde{H}_{0}(pt)\mathop{\cong}0\). Furthermore, one has \(\tilde{H}_{p}(X,A)\mathop{\cong}H_{p}(X,A)\), for any couple (X, A), \(X \supset A\not =\varnothing \), and \(\tilde{H}_{p}(X) = H_{p}(X,x_{0})\).
- 37.
The Rokhlin invariant of a spin 3-manifold X is the signature of any spin 4-manifold V, such that ∂ V = X, is well defined mod 16. A spin structure exists on a manifold M, if its second Stiefel–Whitney class is trivial: w 2(M) = 0. These structures are classified by \(H^{1}(M; \mathbb{Z}_{2})\mathop{\cong}H_{1}(M; \mathbb{Z}_{2})\). Therefore, homology 3-spheres have an unique spin structure, hence for them the Rokhlin invariant is well defined. In particular the Poincaré homology sphere bounds a spin 4-manifold with intersection form E 8, so its Rokhlin invariant is 1.
- 38.
These are three-dimensional manifolds endowed with a S 1-bundle structure over a two-dimensional orbifold. (See, e.g., [84].)
- 39.
The existence of such a manifold X can be proved following a strategy similar to the one to prove Lemma 11.
References
Adams, J.F.: Stable Homotopy and Generalized Homology. University of Chicago Press, Chicago (1974)
Adem, J.: The relations on Steenrod powers of cohomology classes. In: Algebraic Geometry and Topology, A Symposium in Honor of S. Lefschetz, pp. 191–238. Princeton University Press, Princeton, NJ (1957)
Agarwal, R.P., Prástaro, A.: Geometry of PDE’s.III(I): webs on PDE’s and integral bordism groups. The general theory. Adv. Math. Sci. Appl. 17(1), 239–266 (2007); Geometry of PDE’s.III(II): webs on PDE’s and integral bordism groups. Applications to Riemannian geometry PDE’s. Adv. Math. Sci. Appl. 17(1), 267–281 (2007)
Agarwal, R.P., Prástaro, A.: Singular PDE’s geometry and boundary value problems. J. Nonlinear Conv. Anal. 9(3), 417–460 (2008); On singular PDE’s geometry and boundary value problems. Appl. Anal. 88(8), 1115–1131 (2009)
Alexander, J.W.: An example of simply connected surface bounding a region which is not simply connected. Proc. Nat. Acad. Sci. 10(1), 8–10 (1924)
Boileau, M., Paoluzzi, L., Zimmermann, B.: A characterization of S 3 among homology spheres. Geom. Topol. Monogr. 4, 83–103 (2008)
Bott, R., Milnor, J.W.: On the parallelizability of spheres. Bull. Am. Math. Soc. 64, 87–89 (1958)
Bryant, R.L., Chern, S.S., Gardner, R.B., Goldshmidt, H.L., Griffiths, P.A.: Exterior Differential Systems. Springer, New York (1991)
Cartan, E.: Les systéms differentiels extérieurs et leurs applications géométriques. Hermann, Paris (1945)
Cartan, H.: Sur l’itération des opérations de Steenrod. Comment. Math. Helv. 29, 40–58 (1955)
Casson, A.: Fibrations over spheres. Topology 6, 489–499 (1967)
Cerf, J.: Sur les difféomorphismes de la sphére de dimension trois (Γ 4 = 0). Lecture Notes in Mathematics, vol. 53. Springer, Berlin/New York (1968)
Cheeger, J.: Finiteness theorems for Riemannian manifolds. Am. J. Math. 92, 61–74 (1970)
Chow, B., Knopp, D.: Ricci Flow: An Introduction. Mathematical Surveys and Monographs, vol. 119. American Mathematical Society, Providence (2004)
Chow, B., Chu, S.C., Gliekenstein, D., Guenther, C., Isenberg, J., Ivey, T., Knopf, D., Lu, P., Luo, F., Ni, L.: The Ricci Flow: Techniques and Applications: Part I: Geometric Aspects. Mathematical Surveys Monographs, vol. 135. American Mathematical Society, Providence (2008)
Chow, B., Chu, S.C., Gliekenstein, D., Guenther, C., Isenberg, J., Ivey, T., Knopf, D., Lu, P., Luo, F., Ni, L.: The Ricci Flow: Techniques and Applications: Part II: Analytic Aspects. Mathematical Surveys Monographs, vol. 144. American Mathematical Society, Providence (2008)
Dold, A.: Erzewgende der Thomschen algebra \(\mathfrak{N}\). Math. Zeitschr. 65, 25–35 (1956)
Donaldson, S.K.: Self-dual connections and the topology of smooth 4-manifolds. Bull. Am. Math. Soc. 8, 81–83 (1983)
Donaldson, S.K.: An application of gauge theory to four dimensional topology. J. Differ. Geom. 18, 279–315 (1983)
Dubrovin, B.A., Fomenko, A.T., Novikov, S.P.: Modern Geometry-Methods and Applications. Part I; Part II; Part III. Springer, New York (1990). (Original Russian edition: Sovremennaja Geometrie: Metody i Priloženia. Moskva: Nauka, 1979)
Ferry, S., Ranicki, A.A., Rosenberg, J.: Novikov conjecture, rigidity and index theorems. In: Proceedings of 1993 Oberwolfach Conference. London Mathematical Society Lecture Notes, vols. 226, 227. Cambridge University Press, Cambridge (1995)
Freedman, M.H.: The topology of four-dimensional manifolds. J. Differ. Geom. 1(3), 357–453 (1982)
Freedman, M., Quinn, F.: Topology of 4-Manifolds. Princeton Mathematical Series, vol. 39. Princeton University Press, Princeton (1990)
Freedman, M.H., Taylor, L.R.: A universal smoothing of four-space. J. Differ. Geom. 24(1), 69–78 (1986)
Goldschmidt, H.: Integrability criteria for systems of non-linear partial differential equations. J. Differ. Geom. 1, 269–307 (1967)
Goldschmidt, H.: On the non-linear cohomology of Lie equations. V. J. Differ. Geom. 16, 595–674 (1981)
Gompf, R.E.: Three exotic \(\mathbb{R}^{4}\)’s and other anomalies. J. Differ. Geom. 18, 317–328 (1983); An infinite set of exotic \(\mathbb{R}^{4}\)’s. J. Differ. Geom. 21, 283–300 (1985)
Gromov, M.: Partial Differential Relations. Springer, Berlin (1986)
Hamilton, R.S.: Three-manifolds with positive Ricci curvature. J. Differ. Geom. 17, 255–306 (1982)
Hamilton, R.S.: Four-manifolds with positive Ricci curvature operator. J. Differ. Geom. 24, 153–179 (1986)
Hamilton, R.S.: Eternal solutions to the Ricci flow. J. Differ. Geom. 38, 1–11 (1993)
Hamilton, R.S.: The formation of singularities in the Ricci flow. Surv. Differ. Geom. 2, 7–136 (1995)
Hamilton, R.S.: A compactness property for solutions of the Ricci flow on three-manifolds. Commun. Anal. Geom. 7, 695–729 (1999)
Hirsch, M.: Obstruction theories for smoothing manifolds and mappings. Bull. Am. Math. Soc. 69, 352–356 (1963)
Hirsch, M.: Differential Topology. Springer, New York (1976)
Kawakami, T.: Algebraic and Nash realizations of vector bundles and triviality of equivariant algebraic and Nash vector bundles. Bull. Fac. Educ. Wakayama Univ. Nat. Sci. 57, 1–10 (2001)
Kervaire, M.A., Milnor, J.W.: Groups of homotopy spheres: I. Ann. Math. 77(3), 504–537 (1963)
Kirby, R.C., Siebenman, L.C.: On the triangulation of manifolds and the Hauptveruntumg. Bull. Am. Math. Soc. 75, 742–749 (1969)
Klingenberg, W.: Neue ergebnisse über konvexe flächen. Comment. Math. Helv. 34, 17–36 (1960)
Krasilshchik, I.S., Lychagin, V.V., Vinogradov, A.M.: Jet Spaces and Nonlinear Partial Differential Equations. Gordon & Breach, New York (1986)
Lychagin, V., Prástaro, A.: Singularities of Cauchy data, characteristics, cocharacteristics and integral cobordism. Differ. Geom. Appl. 4, 283–300 (1994)
Mazur, B.: On embeddings of spheres. Bull. Am. Math. Soc. 65, 59–65 (1959)
McCleary, J.: User’s Guide to Spectral Sequences. Publish or Perish, Delaware (1985)
Milnor, J.: On manifolds homeomorphic to the 7-sphere. Ann. Math. 64(2), 399–405 (1956)
Milnor, J.: The Steenrod algebra and its dual. Ann. Math. 67(2), 150–171 (1958)
Milnor, J.: An unique factorization theorem for 3-manifolds. Am. J. Math. 84, 1–7 (1965)
Milnor, J., Moore, J.: On the structure of Hopf algebras. Ann. Math. 81(2), 211–264 (1965)
Moise, E.: Affine structures in 3-manifolds. V. The triangulation theorem and Hauptvermuntung. Ann. Math. Sec. Ser. 56, 96–114 (1952)
Moise, E.: Geometric Topology in Dimension 2 and 3. Springer, Berlin (1977)
Munkres, J.R.: Obstructions to smoothing a piecewise differential homeomorphisms. Ann. Math. 72, 521–554 (1960); Obstructions to imposing differentiable structures. Ill. J. Math. 8, 361–376 (1964)
Nash, J.: Real algebraic manifolds. Ann. Math. 56(2), 405–421 (1952)
Ohkawa, T.: The injective hull of homotopy types with respect to generalized homology functors. Hiroshima Math. J. 19, 631–639 (1989)
Perelman, G.: The entropy formula for the Ricci flow and its geometry applications (2002). arXiv:math/0211159
Perelman, G.: Ricci flow with surgery on three-manifolds (2003). arXiv:math/0303109
Pontrjagin, L.S.: Smooth manifolds and their applications homotopy theory. Am. Math. Soc. Transl. 11, 1–114 (1959)
Prástaro, A.: Quantum geometry of PDE’s. Rep. Math. Phys. 30(3), 273–354 (1991). doi:10.1016/0034-4877(91)90063-S
Prástaro, A.: Geometry of PDE’s and Mechanics. World Scientific, Denvers, CO (1996)
Prástaro, A.: Quantum and integral (co)bordisms in partial differential equations. Acta Appl. Math. 51, 243–302 (1998). doi:10.1023/A:1005986024130
Prástaro, A.: (Co)bordism groups in PDE’s. Acta Appl. Math. 59(2), 111–202 (1999). doi:10.1023/A:1006346916360
Prástaro, A.: (Co)bordism groups in quantum PDE’s. Acta Appl. Math. 64(2/3), 111–217 (2000). doi:10.1023/A:1010685903329
Prástaro, A.: Quantized Partial Differential Equations. World Scientific, Singapore (2004)
Prástaro, A.: Geometry of PDE’s. I: integral bordism groups in PDE’s. J. Math. Anal. Appl. 319, 547–566 (2006). doi:10.1016/j.jmaa.2005.06.044
Prástaro, A.: Geometry of PDE’s. II: variational PDE’s and integral bordism groups. J. Math. Anal. Appl. 321, 930–948 (2006). doi:10.1016/j.jmaa.2005.08.037
Prástaro, A.: (Un)stability and bordism groups in PDE’s. Banach J. Math. Anal. 1(1), 139–147 (2007)
Prástaro, A.: Geometry of PDE’s. IV: Navier-Stokes equation and integral bordism groups. J. Math. Anal. Appl. 338(2), 1140–1151 (2008). doi:10.1016/j.jmaa.2007.06.009
Prástaro, A.: On the extended crystal PDE’s stability.I: the n-d’Alembert extended crystal PDE’s. Appl. Math. Comput. 204(1), 63–69 (2008). doi:10.1016/j.amc.2008.05.141. doi:10.1016/j.amc.2008.05.141
Prástaro, A.: On the extended crystal PDE’s stability.II: entropy-regular-solutions in MHD-PDE’s. Appl. Math. Comput. 204(1), 82–89 (2008). doi:10.1016/j.amc.2008.05.142
Prástaro, A.: Extended crystal PDE’s stability.I: the general theory. Math. Comput. Model. 49(9–10), 1759–1780 (2009). doi:10.1016/j.mcm.2008.07.020
Prástaro, A.: Extended crystal PDE’s stability.II: the extended crystal MHD-PDE’s. Math. Comput. Model. 49(9–10), 1781–1801 (2009). doi:10.1016/j.mcm.2008.07.021
Prástaro, A.: Surgery and bordism groups in quantum partial differential equations.I: The quantum Poincaré conjecture. Nonlinear Anal. Theory Methods Appl. 71(12), 502–525 (2009). doi:10.1016/j.na.2008.11.077
Prástaro, A.: Surgery and bordism groups in quantum partial differential equations.II: Variational quantum PDE’s. Nonlinear Anal. Theory Methods Appl. 71(12), 526–549 (2009). doi:10.1016/j.na.2008.10.063
Prástaro, A.: Exotic heat PDE’s. Commun. Math. Anal. 10(1), 64–81 (2011). arXiv: 1006.4483[math.GT]
Prástaro, A.: Quantum extended crystal PDE’s. Nonlinear Stud. 18(3), 447–485 (2011). arXiv:1105.0166[math.AT].
Prástaro, A.: Exotic heat PDE’s.II. In: Pardalos, P.M., Rassias, Th.M. (eds.) Essays in Mathematics and Its Applications (Dedicated to Stephen Smale for his 80th birthday.), pp. 369–419 Springer, Heidelberg/New York/Dordrecht/London (2012). doi:10.1007/978-3-642-28821-0. arXiv: 1009.1176[math.AT]
Prástaro, A.: Exotic n-D’Alembert PDE’s. In: Georgiev, G., Pardalos, P., Srivastava, H.M. (eds.) Stability, Approximation and Inequalities. (Dedicated to Themistocles M. Rassias for his 60th birthday.), pp. 571–586. Springer, New York (2012). arXiv:1011.0081[math.AT]
Prástaro, A.: Quantum extended crystal super PDE’s. Nonlinear Anal. Real World Appl. 13(6), 2491–2529 (2012). doi:10.1016/j.nonrwa.2012.02.014. arXiv: 0906.1363[math.AT]
Prástaro, A.: Quantum exotic PDE’s. Nonlinear Anal. Real World Appl. 14(2), 893–928 (2013). doi:10.1016/j.nonrwa.2012.04.001. arXiv:1106.0862[math.AT]
Prástaro, A.: Extended crystal PDE’s (2008–2011). arXiv: 0811.3693[math.AT]
Prástaro, A.: Strong reactions in quantum super PDE’s. I: quantum hypercomplex exotic super PDE’s (2012–2013). arXiv:1205.2984[math.AT]
Prástaro, A., Rassias, Th.M.: Ulam stability in geometry of PDE’s. Nonlinear Funct. Anal. Appl. 8(2), 259–278 (2003)
Quillen, D.: Elementary proofs of some results of cobordism theory using Steenrod operations. Adv. Math. 7, 29–56 (1971)
Radó, T.: Uber den Begriff von Riemannsche Fläche. Acta Sci. Math. (Szeged) 2, 101–120 (1924)
Schoen,R.S., Yau, S.T.: Conformally flat manifolds, Kleinian groups and scalar curvature. Invent. Math. 92(1), 47–71 (1988)
Scott, P.: The geometries of 3-manifolds. Bull. Lond. Math. Soc. 15(5), 401–407 (1983)
Serre, J.P.: Cohomologie module 2 des complexes d’Eilenberg MacLane. Comment. Math. Helv. 27, 198–232 (1953)
Smale, S.: Generalized Poincaré conjecture in dimension greater than four. Ann. Math. 74(2), 391–406 (1961)
Smale, S.: On the structure of manifolds. Am J. Math. 84, 387–399 (1962)
Smale, S.: Differentiable dynamical systems. Bull. Am. Math. Soc. 73, 747–817 (1967)
Smith, L.: An algebraic introduction to the Steenrod algebra. Geom. Topol. Monogr. 11, 327–348 (2007)
Stong, R.E.: Notes on Bordism Theories. Am. Math. Studies. Princeton University Press, Princeton (1968)
Sullivan, D.: On the Hauptvermuntung for manifolds. Bull. Am. Math. Soc. 73, 598–600 (1967)
Switzer, A.S.: Algebraic Topology-Homotopy and Homology. Springer, Berlin (1976)
Taubes, C.H.: Self-dual connections on non-self-dual 4-manifolds. J. Differ. Geom. 17, 139–170 (1982)
Taubes, C.H.: Gauge theory on asymptotically periodic 4-manifolds. J. Differ. Geom. 25, 363–430 (1987)
Thom, R.: Quelques propriétés globales des variétés differentiable. Comment. Math. Helv. 28, 17–88 (1954)
Tognoli, A.: Su una congettura di Nash. Ann. Scuola Norm. Sup. Pisa 27, 167–185 (1973)
Tuschmann, W.: Geometric diffeomorphism finiteness in low dimensions and homotopy group finiteness. Math. Ann. 322(2), 413–420 (2002)
Wall, C.T.C.: Determination of the cobordism ring. Ann. Math. 72, 292–311 (1960)
Wall, C.T.C.: Surgery on Compact Manifolds. London Mathematical Society Monographs, vol. 1. Academic Press, New York (1970); Ranicki, A.A. (ed.) American Mathematical Society Surveys and Monographs, vol. 69, 2nd edn. American Mathematical Society (1999)
Whitehead, J.H.C.: Manifolds with transverse fields in Euclidean spaces. Ann. Math. 73, 154–212 (1961)
Warner, F.W.: Foundations of Differentiable Manifolds and Lie Groups, Scott, Foresman, Glenview, IL (1971)
Weyl, H.: Zur Infinitesimalgeometrie: Einertnung der projectiven und der konformen Auffassung, Selecta Hermann Weyl, pp. 249–261. Birkhäuser-Verlag, Basel/Stuttgart (1956)
Wu, W.-T.: Sur les puissances de Steenrod. Colloque de Topologie de Strasbourg, 1951, no. IX, La Biblioteque Nationale et Universitaire de Strasbourg, 9 (1952)
Acknowledgements
I would like thank my colleague Themistocles Rassias for inviting me to write my contribution for this Springer book. A similar version of this work was early put on arXiv.1101.0283 [math.AT].
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer Science+Business Media New York
About this chapter
Cite this chapter
Prástaro, A. (2014). Exotic PDEs. In: Pardalos, P., Rassias, T. (eds) Mathematics Without Boundaries. Springer, New York, NY. https://doi.org/10.1007/978-1-4939-1124-0_16
Download citation
DOI: https://doi.org/10.1007/978-1-4939-1124-0_16
Published:
Publisher Name: Springer, New York, NY
Print ISBN: 978-1-4939-1123-3
Online ISBN: 978-1-4939-1124-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


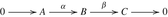 of chain complexes in an abelian category. In fact to such a sequence there corresponds a long exact sequence
of chain complexes in an abelian category. In fact to such a sequence there corresponds a long exact sequence 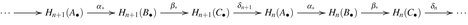 . The boundary maps
. The boundary maps 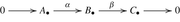 is a short exact sequence of abelian groups and
is a short exact sequence of abelian groups and 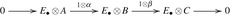 . Similar considerations hold for cochain complexes. in such cases the Bockstein homomorphism increases the degree, i.e.,
. Similar considerations hold for cochain complexes. in such cases the Bockstein homomorphism increases the degree, i.e.,