A Glimpse of Young Tableaux

Abstract

We defined in Chap. 6 Young’s lattice Y, the poset of all partitions of all nonnegative integers, ordered by containment of their Young diagrams.

8.1 Appendix 1: The RSK Algorithm

We will describe a bijection between permutations $\pi \in \mathfrak{S}_{n}$ and pairs (P, Q) of SYT of the same shape $\lambda \vdash n$. Define a near Young tableau (NYT) to be the same as an SYT, except that the entries can be any distinct integers, not necessarily the integers $1,2,\ldots,n$. Let P _ij denote the entry in row i and column j of P. The basic operation of the RSK algorithm consists of the row insertion $P \leftarrow k$ of a positive integer k into an NYT P = (P _ij ). The operation P ← k is defined as follows: let r be the least integer such that P _1r  > k. If no such r exists (i.e., all elements of the first row of P are less than k), then simply place k at the end of the first row. The insertion process stops, and the resulting NYT is P ← k. If, on the other hand, r does exist then replace P _1r by k. The element k then “bumps” P _1r : = k′ into the second row, i.e., insert k′ into the second row of P by the insertion rule just described. Either k′ is inserted at the end of the second row, or else it bumps an element k′ to the third row. Continue until an element is inserted at the end of a row (possibly as the first element of a new row). The resulting array is P ← k.

8.11. Example 

Let

$$\displaystyle{P = \begin{array}{cccl} 3 & \quad 7 & \quad 9 &\quad 14 \\ 6 &\quad 11 &\quad 12 \\ 10&\quad 16 \\ 13 \\ 15\end{array} }$$

Then P ← 8 is shown below, with the elements inserted into each row (either by bumping or by the final insertion in the fourth row) in boldface. Thus the 8 bumps the 9, the 9 bumps the 11, the 11 bumps the 16, and the 16 is inserted at the end of a row. Hence

$$\displaystyle{(P \leftarrow 8) = \begin{array}{cccc} 3 & \quad 7 & \quad \boldsymbol{8} &\quad 14 \\ 6 & \quad \boldsymbol{9} &\quad 12 \\ 10&\quad \boldsymbol{1}1 \\ 13 &\quad \boldsymbol{1}6 \\ 15\end{array} }$$

We omit the proof, which is fairly straightforward, that if P is an NYT not containing k, then P ← k is an NYT. We can now describe the RSK algorithm. Let $\pi = a_{1}a_{2}\cdots a_{n} \in \mathfrak{S}_{n}$. We will inductively construct a sequence $(P_{0},Q_{0})$, $(P_{1},Q_{1})$, $\ldots,(P_{n},Q_{n})$ of pairs $(P_{i},Q_{i})$ of NYT of the same shape, where P _i and Q _i each have i squares. First, define $(P_{0},Q_{0}) = (\emptyset,\emptyset )$. If $(P_{i-1},Q_{i-1})$ have been defined, then set $P_{i} = P_{i-1}\leftarrow a_{i}$. In other words, P _i is obtained from P _i − 1 by row inserting a _i . Now define Q _i to be the NYT obtained from Q _i − 1 by inserting i so that Q _i and P _i have the same shape. (The entries of Q _i − 1 don’t change; we are simply placing i into a certain new square and not row-inserting it into Q _i − 1.) Finally let $(P,Q) = (P_{n},Q_{n})$. We write $\pi { \mathrm{RSK} \atop \rightarrow } (P,Q)$.

8.12. Example 

Let $\pi = 4273615 \in \mathfrak{S}_{7}$. The pairs $(P_{1},Q_{1}),\ldots$, $(P_{7},Q_{7}) = (P,Q)$ are as follows:

$$\displaystyle{\begin{array}{lcl} \underline{P_{i}} &\ \ &\underline{Q_{i}} \\ 4 &\ \ &1\\ 2 &\ \ &1\\ \\ \\ 4 &\ \ &2\\ 2\:7 &\ \ &1\:3\\ \\ \\ 4 &\ \ &2\\ 2\:3 &\ \ &1\:3\\ \\ \\ 4\:7 &\ \ &2\:4\\ 2\:3\:6 &\ \ &1\:3\:5\\ \\ \\ 4\:7 &\ \ &2\:4\\ 1\:3\:6 &\ \ &1\:3\:5\\ \\ \\ 2\:7 &\ \ &2\:4\\ \\ \\ 4 &\ \ &6 \\ 1\:3\:5&\ \ &1\:3\:5\\ \\ \\ 2\:6 &\ \ &2\:4\\ \\ \\ 4\:7 &\ \ &6\:7 \end{array} }$$

8.13 Theorem 

The RSK algorithm defines a bijection between the symmetric group $\mathfrak{S}_{n}$ and the set of all pairs (P,Q) of SYT of the same shape, where the shape λ is a partition of n.

Proof (Proof (sketch)). 

The key step is to define the inverse of RSK. In other words, if π↦(P, Q), then how can we recover π uniquely from (P, Q)? Moreover, we need to find π for any (P, Q). Observe that the position occupied by n in Q is the last position to be occupied in the insertion process. Suppose that k occupies this position in P. It was bumped into this position by some element j in the row above k that is currently the largest element of its row less than k. Hence we can “inverse bump” k into the position occupied by j, and now inverse bump j into the row above it by the same procedure. Eventually an element will be placed in the first row, inverse bumping another element t out of the tableau altogether. Thus t was the last element of π to be inserted, i.e., if $\pi = a_{1}a_{2}\cdots a_{n}$ then a _n  = t. Now locate the position occupied by n − 1 in Q and repeat the procedure, obtaining a _n − 1. Continuing in this way, we uniquely construct π one element at a time from right to left, such that $\pi \mapsto (P,Q)$.

The RSK-algorithm provides a bijective proof of Corollary 8.5, that is,

$$\displaystyle{\sum _{\lambda \vdash n}{({f}^{\lambda })}^{2} = n!.}$$

8.2 Appendix 2: Plane Partitions

In this appendix we show how a generalization of the RSK algorithm leads to an elegant generating function for a two-dimensional generalization of integer partitions. A plane partition of an integer n ≥ 0 is a two-dimensional array $\pi = (\pi _{ij})_{i,j\geq 1}$ of integers $\pi _{ij} \geq 0$ that is weakly decreasing in rows and columns, i.e.,

$$\displaystyle{\pi _{ij} \geq \pi _{i+1,j},\quad \pi _{ij} \geq \pi _{i,j+1},}$$

such that $\sum _{i,j}\pi _{ij} = n$. It follows that all but finitely many π _ij are 0, and these 0’s are omitted in writing a particular plane partition π. Given a plane partition π, we write | π |  = n to denote that π is a plane partition of n. More generally, if L is any array of nonnegative integers we write | L | for the sum of the parts (entries) of L.

There is one plane partition of 0, namely, all π _ij  = 0, denoted ∅. The plane partitions of the integers 0 ≤ n ≤ 3 are given by

$$\displaystyle{\begin{array}{lllllllllll} \emptyset \ \ &1\ \ &2\ \ &11\ \ &1\ \ &3\ \ &21\ \ &111\ \ &11\ \ &2\ \ &1\\ \\ \\ & & & &1 & & & &1 &1 &1\\ \\ \\ & & & & & & & & & &1 \end{array} }$$

If $\mathrm{pp}(n)$ denotes the number of plane partitions of n, then $\mathrm{pp}(0) = 1$, $\mathrm{pp}(1) = 1$, $\mathrm{pp}(2) = 3$, and $\mathrm{pp}(3) = 6$.

Our object is to give a formula for the generating function

$$\displaystyle{F(x) =\sum _{n\geq 0}\mathrm{pp}(n){x}^{n} = 1 + x + 3{x}^{2} + 6{x}^{3} + 13{x}^{4} + 24{x}^{5} + \cdots \,.}$$

More generally, we will consider plane partitions with at most r rows and at most s columns, i.e., π _ij  = 0 for i > r or j > s. As a simple warmup, let us first consider the case of ordinary partitions $\lambda = (\lambda _{1},\lambda _{2},\ldots )$ of n.

8.14 Proposition 

Let p _s (n) denote the number of partitions of n with at most s parts. Equivalently, p _s (n) is the number of plane partitions of n with at most one row and at most s columns [why?]. Then

$$\displaystyle{\sum _{n\geq 0}p_{s}(n){x}^{n} =\prod _{ k=1}^{s}{(1 - {x}^{k})}^{-1}.}$$

Proof.

First note that the partition λ has at most s parts if and only if the conjugate partition λ′ defined in Chap. 6 has largest part at most s. Thus it suffices to find the generating function $\sum _{n\geq 0}p^{\prime}_{s}(n){x}^{n}$, where p′ _s (n) denotes the number of partitions of n whose largest part is at most s. Now expanding each factor ${(1 - {x}^{k})}^{-1}$ as a geometric series gives

$$\displaystyle{\prod _{k=1}^{s} \frac{1} {1 - {x}^{k}} =\prod _{ k=1}^{s}\left (\sum _{ m_{k}\geq 1}{x}^{m_{k}k}\right ).}$$

How do we get a coefficient of x ⁿ? We must choose a term ${x}^{m_{k}k}$ from each factor of the product, 1 ≤ k ≤ s, so that

$$\displaystyle{n =\sum _{ k=1}^{s}m_{ k}k.}$$

But such a choice is the same as choosing the partition λ of n such that the part k occurs m _k times. For instance, if s = 4 and we choose m ₁ = 5, m ₂ = 0, m ₃ = 1, m ₄ = 2, then we have chosen the partition λ = (4, 4, 3, 1, 1, 1, 1, 1) of 16. Hence the coefficient of x ⁿ is the number of partitions λ of n whose largest part is at most s, as was to be proved.

Note that Proposition 8.14 is “trivial” in the sense that it can be seen by inspection. There is an obvious correspondence between (a) the choice of terms contributing to the coefficient of x ⁿ and (b) partitions of n with largest part at most r. Although the generating function we will obtain for plane partitions is equally simple, it will be far less obvious why it is correct.

Plane partitions have a certain similarity with SYT, so perhaps it is not surprising that a variant of RSK will be applicable. Instead of NYT we will be dealing with column-strict plane partitions (CSPP). These are plane partitions for which the nonzero elements strictly decrease in each column. An example of a CSPP is given by

$$\displaystyle{ \begin{array}{ccccccc} 7&\quad 7&\quad 4&\quad 3&\quad 3&\quad 3&\quad 1\\ 4&\quad 3&\quad 3&\quad 1 \\ 3&\quad 2\\ 2&\quad 1 \\ 1 \end{array} }$$

(8.17)

We say that this CSPP has shapeλ = (7, 4, 2, 2, 1), the shape of the Young diagram which the numbers occupy, and that it has five rows, seven columns, and 16 parts (so $\lambda \vdash 16$).

If P = (P _ij ) is a CSPP and k ≥ 1, then we define the row insertionP ← k as follows: let r be the least integer such that P _1, r  < k. If no such r exists (i.e., all elements of the first row of P are greater than or equal to k), then simply place k at the end of the first row. The insertion process stops, and the resulting CSPP is P ← k. If, on the other hand, r does exist, then replace P _1r by k. The element k then “bumps” P _1r : = k′ into the second row, i.e., insert k′ into the second row of P by the insertion rule just described, possibly bumping a new element k′ into the third row. Continue until an element is inserted at the end of a row (possibly as the first element of a new row). The resulting array is P ← k. Note that this rule is completely analogous to row insertion for NYT: for NYT an element bumps the leftmost element greater than it, while for CSPP an element bumps the leftmost element smaller than it.

8.15. Example 

Let P be the CSPP of (8.17). Let us row insert 6 into P. The set of elements which get bumped are shown in bold:

$$\displaystyle{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 7\quad &7\quad &\boldsymbol{4}\quad &3\quad &3\quad &3\quad &1\\ 4\quad &\boldsymbol{3} \quad &3\quad &1\quad \\ 3\quad &\boldsymbol{2}\quad \\ 2\quad &\boldsymbol{1}\quad \\ 1\quad \end{array} }$$

The final 1 that was bumped is inserted at the end of the fifth row. Thus we obtain

$$\displaystyle{(P \leftarrow 6) = \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 7\quad &7\quad &6\quad &3\quad &3\quad &3\quad &1 \\ 4\quad &4\quad &3\quad &1\quad \\ 3\quad &3\quad \\ 2\quad &2\quad \\ 1\quad &1\quad \end{array} }$$

We are now ready to describe the analogue of RSK needed to count plane partitions. Instead of beginning with a permutation $\pi \in \mathfrak{S}_{n}$, we begin with an r ×s matrix A = (a _ij ) of nonnegative integers, called for short an r ×s $\mathbb{N}$ -matrix. We convert A into a two-line array

$$\displaystyle{w_{A} = \left (\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} u_{1}\quad &u_{2}\quad &\cdots \quad &u_{N} \\ v_{1}\quad &v_{2}\quad &\cdots \quad &v_{N} \end{array} \right ),}$$

where

• $u_{1} \geq u_{2} \geq \cdots \geq u_{N}$.

• If i < j and $u_{i} = u_{j}$, then $v_{i} \geq v_{j}$.

• The number of columns of w _A equal to ${ i\above 0.0pt j}$ is a _ij . (It follows that N = ∑a _ij .)

It is easy to see that w _A is uniquely determined by A, and conversely. As an example, suppose that

$$\displaystyle{ A = \left [\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0\quad &1\quad &0\quad &2\\ 1\quad &1\quad &1\quad &0 \\ 2\quad &1\quad &0\quad &0 \end{array} \right ]. }$$

(8.18)

Then

$$\displaystyle{w_{A} = \left (\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 3\quad &3\quad &3\quad &2\quad &2\quad &2\quad &1\quad &1\quad &1\\ 2\quad &1\quad &1\quad &3\quad &2\quad &1\quad &4\quad &4\quad &2 \end{array} \right ).}$$

We now insert the numbers $v_{1},v_{2},\ldots,v_{N}$ successively into a CSPP. That is, we start with P ₀ = ∅ and define inductively $P_{i} = P_{i-1} \leftarrow v_{i}$. We also start with Q ₀ = ∅ and at the ith step insert u _i into Q _i − 1 (without any bumping or other altering of the elements of Q _i − 1) so that P _i and Q _i have the same shape. Finally let $(P,Q) = (P_{N},Q_{N})$ and write $A{ \mathrm{RS{K}^{^{\prime}}} \atop \rightarrow } (P,Q)$.

8.16. Example 

Let A be given by (8.18). The pairs $(P_{1},Q_{1}),\ldots$, $(P_{9},Q_{9}) = (P,Q)$ are as follows:

$$\displaystyle{\begin{array}{lcl} \underline{P_{i}} &\ \ &\underline{Q_{i}} \\ 2 &\ \ &3\\ 2\:1 &\ \ &3\:3 \\ 2\:1\:1&\ \ &3\:3\:3\\ 3\:1\:1 &\ \ &3\:3\:3\\ \\ \\ 2 &\ \ &2\\ 3\:2\:1 &\ \ &3\:3\:3\\ \\ \\ 2\:1 &\ \ &2\:2 \end{array} }$$

$$\displaystyle{\begin{array}{lcl} 3\:2\:1\:1&\ \ &3\:3\:3\:2\\ \\ \\ 2\:1&\ \ &2\:2 \\ 4\:2\:1\:1&\ \ &3\:3\:3\:2\\ \\ \\ 3\:1&\ \ &2\:2\\ \\ \\ 2 &\ \ &1\\ 4\:4\:1\:1&\ \ &3\:3\:3\:2\\ \\ \\ 3\:2 &\ \ &2\:2\\ \\ \\ 2\:1&\ \ &1\:1 \\ 4\:4\:2\:1&\ \ &3\:3\:3\:2\\ \\ \\ 3\:2\:1&\ \ &2\:2\:1\\ \\ \\ 2\:1 &\ \ &1\:1\end{array} }$$

It is straightforward to show that if $A{ \mathrm{RS{K}^{^{\prime}}} \atop \rightarrow } (P,Q)$, then P and Q are CSPP of the same shape. We omit the proof of the following key lemma, which is analogous to the proof of Theorem 8.13. Let us just note a crucial property (which is easy to prove) of the correspondence $A{ \mathrm{RS{K}^{^{\prime}}} \atop \rightarrow } (P,Q)$ which allows us to recover A from (P, Q), namely, equal entries of Q are inserted from left to right. Thus the last number placed into Q is the rightmost occurrence of the least entry. Hence we can inverse bump the number in this position in P to back up one step in the algorithm, just as for the usual RSK correspondence $\pi { \mathrm{RSK} \atop \rightarrow } (P,Q)$.

8.17 Lemma 

The correspondence $A{ \mathrm{RS{K}^{^{\prime}}} \atop \rightarrow } (P,Q)$ is a bijection from the set of r × s matrices of nonnegative integers to the set of pairs (P,Q) of CSPP of the same shape, such that the largest part of P is at most s and the largest part of Q is at most r.

Define ρ(λ, μ) to be the partition for which this merged diagram is the Ferrers diagram. The above example shows that

$$\displaystyle{\rho (532,631) = 544211.}$$

The map $(\lambda,\mu )\mapsto \rho (\lambda,\mu )$ is clearly a bijection between pairs of partitions (λ, μ) with k distinct parts and partitions ρ whose main diagonal (of the Ferrers diagram) has k dots. Equivalently, k is the largest integer j for which ρ _j  ≥ j. Note that

$$\displaystyle{ \vert \rho \vert = \vert \lambda \vert + \vert \mu \vert -\ell (\lambda ). }$$

(8.19)

We now extend the above bijection to pairs (P, Q) of CSPP of the same shape. If ${\lambda }^{i}$ denotes the ith column of P and μ ⁱ the ith column of Q, then let π(P, Q) be the array whose ith column is $\rho {(\lambda }^{i}{,\mu }^{i})$. For instance, if

$$\displaystyle{P = \begin{array}{cccc} 4&\quad 4&\quad 2&\quad 1 \\ 3 &\quad 1 &\quad 1 \\ 2 \end{array} \ \ \mbox{ and}\ \ Q = \begin{array}{cccc} 5&\quad 3&\quad 2&\quad 2 \\ 4 &\quad 2 &\quad 1 \\ 1 \end{array} }$$

then

$$\displaystyle{\pi (P,Q) = \begin{array}{cccc} 4&\,\,4&\,\,2&\,\,1 \\ 4 &\,\,2 &\,2 &\,\,1 \\ 4&\,\,2 \\ 2 \\ 2 \end{array} }$$

It is easy to see that π(P, Q) is a plane partition. Replace each row of π(P, Q) by its conjugate to obtain another plane partition π′(P, Q). With π(P, Q) as above we obtain

$$\displaystyle{\pi ^{\prime}(P,Q) = \begin{array}{cccc} 4&\,\,3&\,\,2&\,\,2 \\ 4 &\,\,3 &\,\,1 &\,\,1 \\ 2&\,\,2&\,\,1&\,\,1 \\ 1 &\,\,1 \\ 1&\,\,1 \end{array} }$$

Write | P | for the sum of the elements of P and write max(P) for the largest element of P, and similarly for Q. When we merge P and Q into π(P, Q), max(P) becomes the largest part of π(P, Q). Thus when we conjugate each row, max(P) becomes the number $\mathrm{col}(\pi ^{\prime}(P,Q))$ of columns of π′(P, Q) [why?]. Similarly, max(Q) becomes the number $\mathrm{row}(\pi ^{\prime}(P,Q))$ of rows of π(P, Q) and of π′(P, Q). In symbols,

$$\displaystyle\begin{array}{rcl} \max P& =& \mathrm{col}(\pi ^{\prime}(P,Q)), \\ \max Q& =& \mathrm{row}(\pi ^{\prime}(P,Q)).{}\end{array}$$

(8.20)

Moreover, it follows from (8.19) that

$$\displaystyle{ \vert \pi ^{\prime}(P,Q)\vert = \vert \pi (P,Q)\vert = \vert P\vert + \vert Q\vert -\nu (P), }$$

(8.21)

where ν(P) denotes the number of parts of P (or of Q).

We now have all the ingredients necessary to prove the main result of this appendix.

8.18 Theorem 

Let $\mathrm{pp}_{rs}(n)$ denote the number of plane partitions of n with at most r rows and at most s columns. Then

$$\displaystyle{\sum _{n\geq 0}\mathrm{pp}_{rs}(n){x}^{n} =\prod _{ i=1}^{r}\prod _{ j=1}^{s}{(1 - {x}^{i+j-1})}^{-1}.}$$

Proof.

Let A = (a _ij ) be an r ×s $\mathbb{N}$-matrix. We can combine the bijections discussed above to obtain a plane partition π(A) associated with A. Namely, first apply RSK to obtain $A{ \mathrm{RS{K}^{^{\prime}}} \atop \rightarrow } (P,Q)$, and then apply the merging process and row conjugation to obtain $\pi (A) =\pi ^{\prime}(P,Q)$. Since a column ${ i\above 0.0pt j}$ of the two-line array w _A occurs a _ij times and results in an insertion of j into P and i into Q, it follows that

$$\displaystyle\begin{array}{rcl} \vert P\vert & =& \sum _{i,j}ja_{ij}, \\ \vert Q\vert & =& \sum _{i,j}ia_{ij}, \\ \max (P)& =& \max \{j : a_{ij}\neq 0\}, \\ \max (Q)& =& \max \{i: a_{ij}\neq 0\}.\end{array}$$

Hence from (8.20) and (8.21), we see that the map A↦π(A) is a bijection from r ×s $\mathbb{N}$-matrices A to plane partitions with at most r rows and at most s columns. Moreover,

$$\displaystyle\begin{array}{rcl} \vert \pi (A)\vert & =& \vert P\vert + \vert Q\vert -\nu (P) {}\\ & =& \sum _{i,j}(i + j - 1)a_{ij}. {}\\ \end{array}$$

Thus the enumeration of plane partitions is reduced to the much easier enumeration of $\mathbb{N}$-matrices. Specifically, we have

$$\displaystyle\begin{array}{rcl} \sum _{n\geq 0}\mathrm{pp}_{rs}(n){x}^{n}& =& \sum _{ \begin{array}{c}\pi \\ \mathrm{ row}(\pi )\leq r \\ \mathrm{col}(\pi )\leq s \end{array}}{x}^{\vert \pi \vert } {}\\ & =& \sum _{r\times s\ \mathbb{N}\text{-}\mathrm{matrices}\ A}{x}^{\sum (i+j-1)a_{ij} } {}\\ & =& \prod _{i=1}^{r}\prod _{ j=1}^{s}\left (\sum _{ a_{ij}\geq 0}{x}^{\sum (i+j-1)a_{ij} }\right ) {}\\ & =& \prod _{i=1}^{r}\prod _{ j=1}^{s}{(1 - {x}^{i+j-1})}^{-1}. {}\\ \end{array}$$

Write pp _r (n) for the number of plane partitions of n with at most r rows. Letting s → ∞ and then r → ∞ in Theorem 8.18 produces the elegant generating functions of the next corollary.

8.19 Corollary 

We have

$$\displaystyle\begin{array}{rcl} \sum _{n\geq 0}\mathrm{pp}_{r}(n){x}^{n}& =& \prod _{ i\geq 1}{(1 - {x}^{i})}^{-\min (i,r)},{}\end{array}$$

(8.22)

$$\displaystyle\begin{array}{rcl} \sum _{n\geq 0}\mathrm{pp}(n){x}^{n}& =& \prod _{ i\geq 1}{(1 - {x}^{i})}^{-i}.{}\end{array}$$

(8.23)

Note. Once one has seen the generating function

$$\displaystyle{ \frac{1} {(1 - x)(1 - {x}^{2})(1 - {x}^{3})\cdots }}$$

for one-dimensional (ordinary) partitions and the generating function

$$\displaystyle{ \frac{1} {(1 - x){(1 - {x}^{2})}^{2}{(1 - {x}^{3})}^{3}\ldots }}$$

for two-dimensional (plane) partitions, it is quite natural to ask about higher-dimensional partitions. In particular, a solid partition of n is a three-dimensional array $\pi = (\pi _{ijk})_{i,j,k\geq 1}$ of nonnegative integers, weakly decreasing in each of the three coordinate directions, and with elements summing to n. Let sol(n) denote the number of solid partitions of n. It is easy to see that for any integer sequence a ₀ = 1, a ₁, $a_{2},\ldots$, there are unique integers b ₁, $b_{2},\ldots$ for which

$$\displaystyle{\sum _{n\geq 0}a_{n}{x}^{n} =\prod _{ i\geq 1}{(1 - {x}^{i})}^{-b_{i} }.}$$

For the case $a_{n} =\mathrm{ sol}(n)$, we have

$$\displaystyle{b_{1} = 1,b_{2} = 3,b_{3} = 6,b_{4} = 10,b_{5} = 15,}$$

which looks quite promising. Alas, the sequence of exponents continues

$$\displaystyle{20,26,34,46,68,97,120,112,23,-186,-496,-735,-531,779,\ldots.}$$

The problem of enumerating solid partitions remains open and is considered most likely to be hopeless.

Notes for Chap. 8

SYT were first enumerated by P.A. MacMahon [74, p. 175] (see also [75, Sect. 103]). MacMahon formulated his result in terms of “generalized ballot sequences” or “lattice permutations” rather than SYT, but they are easily seen to be equivalent. He stated the result not in terms of the products of hook lengths as in Theorem 8.1, but as a more complicated product formula. The formulation in terms of hook lengths is due to J.S. Frame and appears first in the paper [38, Theorem 1] of Frame, Robinson, and R.M. Thrall; hence it is sometimes called the “Frame-Robinson-Thrall hook-length formula.” (The actual definition of SYT is due to A. Young [122, p. 258].)

Independently of MacMahon, F.G. Frobenius [41, Eq. (6)] obtained the same formula for the degree of the irreducible character ${\chi }^{\lambda }$ of $\mathfrak{S}_{n}$ as MacMahon obtained for the number of lattice permutations of type λ. Frobenius was apparently unaware of the combinatorial significance of deg χ ^λ, but Young showed in [122, pp. 260–261] that degχ ^λ was the number of SYT of shape λ, thereby giving an independent proof of MacMahon’s result. (Young also provided his own proof of MacMahon’s result in [122, Theorem II].)

A number of other proofs of the hook-length formula were subsequently found. C. Greene et al. [48] gave an elegant probabilistic proof. A proof of A. Hillman and R. Grassl [57] shows very clearly the role of hook lengths, though the proof is not completely bijective. A bijective version was later given by C.F. Krattenthaler [64]. Completely bijective proofs of the hook-length formula were first given by D.S. Franzblau and D. Zeilberger [39] and by J.B. Remmel [93]. An exceptionally elegant bijective proof was later found by J.-C. Novelli et al. [80].

The use of the operators U and D to count walks in the Hasse diagram of Young’s lattice was developed independently, in a more general context, by S. Fomin [36, 37] and R. Stanley [104, 106]. See also [107, Sect. 3.21] for a short exposition.

The RSK algorithm (known by a variety of other names, either “correspondence” or “algorithm” in connection with some subset of the names Robinson, Schensted, and Knuth) was first described, in a rather vague form, by G. de B. Robinson [94, Sect. 5], as a tool in an attempted proof of a result now known as the “Littlewood–Richardson Rule.” The RSK algorithm was later rediscovered by C.E. Schensted (see below), but no one actually analyzed Robinson’s work until this was done by M. van Leeuwen [120, Sect. 7]. It is interesting to note that Robinson says in a footnote on page 754 that “I am indebted for this association I to Mr. D.E. Littlewood.” Van Leeuwen’s analysis makes it clear that “association I” gives the recording tableau Q of the RSK algorithm $\pi { \mathrm{RSK} \atop \rightarrow } (P,Q)$. Thus it might be correct to say that if $\pi \in \mathfrak{S}_{n}$ and $\pi { \mathrm{RSK} \atop \rightarrow } (P,Q)$, then the definition of P is due to Robinson, while the definition of Q is due to Littlewood.

No further work related to Robinson’s construction was done until Schensted published his seminal paper [97] in 1961. (For some information about the unusual life of Schensted, see [5].) Schensted’s purpose was the enumeration of permutations in $\mathfrak{S}_{n}$ according to the length of their longest increasing and decreasing subsequences. According to Knuth [65, p. 726], the connection between the work of Robinson and that of Schensted was first pointed out by M.-P. Schützenberger, though as mentioned above the first person to describe this connection precisely was van Leeuwen.

Plane partitions were discovered by MacMahon in a series of papers which were not appreciated until much later. (See MacMahon’s book [75, Sects. IX and X] for an exposition of his results.) MacMahon’s first paper dealing with plane partitions was [73]. In Article 43 of this paper he gives the definition of a plane partition (though not yet with that name). In Article 51 he conjectures that the generating function for plane partitions is the product

$$\displaystyle{{(1 - x)}^{-1}\,{(1 - {x}^{2})}^{-2}\,{(1 - {x}^{3})}^{-3}\,{(1 - {x}^{4})}^{-4}\cdots }$$

(our Eq. (8.23)). In Article 52 he conjectures our Eq. (8.22) and Theorem 8.18, finally culminating in a conjectured generating function for plane partitions of n with at most r rows, at most s columns, and with largest part at most t. (See Exercise 34.) MacMahon goes on in Articles 56–62 to prove his conjecture in the case of plane partitions with at most 2 rows and s columns (the case r = 2 of our Theorem 8.18), mentioning on page 662 that an independent solution was obtained by A.R. Forsyth. (Though a publication reference is given to Forsyth’s paper, apparently it never actually appeared.)

We will not attempt to describe MacMahon’s subsequent work on plane partitions, except to say that the culmination of his work appears in [75, Art. 495], in which he proves his main conjecture from his first paper [73] on plane partitions, viz., our Exercise 34. MacMahon’s proof is quite lengthy and indirect.

In 1972 E.A. Bender and D.E. Knuth [6] showed the connection between the theory of symmetric functions and the enumeration of plane partitions. They gave simple proofs based on the RSK algorithm of many results involving plane partitions, including the first bijective proof (the same proof that we give) of our Theorem 8.18.

For further aspects of Young tableaux and the related topics of symmetric functions, representation theory of the symmetric group, Grassmann varieties, etc., see the expositions of W.E. Fulton [42], B.E. Sagan [96], and R. Stanley [108, Chap. 7].

Exercises for Chap. 8

• 1. Draw all the SYT of shape (4, 2).

• 2. Using the hook-length formula, show that the number of SYT of shape (n, n) is the Catalan number $C_{n} = \frac{1} {n+1}\left ({ 2n \atop n} \right )$.

• 3. How many maximal chains are in the poset L(4, 4), where L(m, n) is defined in Chap. 6? Express your answer in a form involving products and quotients of integers (no sums).

• 4. A corner square of a partition λ is a square in the Young diagram of λ whose removal results in the Young diagram of another partition (with the same upper-left corner). Let c(λ) denote the number of corner squares (or distinct parts) of the partition λ. For instance, c(5, 5, 4, 2, 2, 2, 1, 1) = 4. (The distinct parts are 5, 4, 2, 1.) Show that

  $$\displaystyle{\sum _{\lambda \vdash n}c(\lambda ) = p(0) + p(1) + \cdots + p(n - 1),}$$

  where p(i) denotes the number of partitions of i (with p(0) = 1). Try to give an elegant combinatorial proof.

• 5. Show that the number of odd hook lengths minus the number of even hook lengths of a partition λ is a triangular number (a number of the form k(k + 1) ∕ 2).

• 6. (moderately difficult) Show that the total number of SYT with n entries and at most two rows is $\left ({ n \atop \lfloor n/2\rfloor } \right )$. Equivalently,

  $$\displaystyle{\sum _{i=0}^{\lfloor n/2\rfloor }{f}^{(n-i,i)} = \left ({ n \atop \lfloor n/2\rfloor } \right ).}$$

  Try to give an elegant combinatorial proof.

• 7. (difficult) (*) Let f(n) be the number of partitions λ of 2n whose Young diagram can be covered with n nonoverlapping dominos (i.e., two squares with a common edge). For instance, the figure below shows a domino covering of the partition 43221.

  

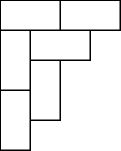
  Let

  $$\displaystyle{F(x) =\sum _{n\geq 0}f(n){x}^{n} = 1 + 2x + 5{x}^{2} + 10{x}^{3} + 20{x}^{4} + 36{x}^{5} + \cdots \,.}$$

  Show that

  $$\displaystyle{F(x) =\prod _{n\geq 1}{(1 - {x}^{n})}^{-2}.}$$

• 8. (difficult) Let λ be a partition. Let m _k (λ) denote the number of parts of λ that are equal to k, and let η _k (λ) be the number of hooks of length k of λ. Show that

  $$\displaystyle{\sum _{\lambda \vdash n}\eta _{k}(\lambda ) = k\sum _{\lambda \vdash n}m_{k}(\lambda ).}$$

• 9. (moderately difficult) Let μ be a partition, and let A _μ be the infinite shape consisting of the quadrant Q = { (i, j) : i < 0,  j > 0} with the shape μ removed from the lower right-hand corner. Thus every square of A _μ has a finite hook and hence a hook length. For instance, when μ = (3, 1) we get the diagram

  

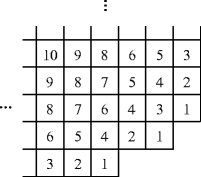
  Show that the multiset of hook lengths of A _μ is equal to the union of the multiset of hook lengths of Q (explicitly given by $\{{1}^{1},{2}^{2},{3}^{3},\ldots \}$) and the multiset of hook lengths of μ.

• 10. In how many ways can we begin with the empty partition ∅, then add 2n squares one at a time (always keeping a partition), then remove n squares one at a time, then add n squares one at a time, and finally remove 2n squares one at a time, ending up at ∅?

• 11. (difficult) Fix n. Show that the number of partitions λ ⊢ n for which f ^λ is odd is equal to ${2}^{k_{1}+k_{2}+\ldots }$, where $k_{1} < k_{2} < \cdots$ and $n = {2}^{k_{1}} + {2}^{k_{2}} + \cdots$ (the binary expansion of n). For instance, $75 = {2}^{0} + {2}^{1} + {2}^{3} + {2}^{6}$, so the number of partitions λ of 75 for which f ^λ is odd is 2^{6 + 3 + 1 + 0} = 1024.

• 12. Let U and D be the linear transformations associated with Young’s lattice. Write D ² U ² and D ³ U ³ in the form $\sum a_{ij}{U}^{i}{D}^{j}$.

• 13. Let U and D be the linear transformations associated with Young’s lattice. Suppose that f is some (noncommutative) polynomial in U and D satisfying f(U, D) = 0, e.g., f(U, D) = DU − UD − I. Let $i = \sqrt{-1}$. Show that f(iD, iU) = 0.

• 14. (*) Show that

  $$\displaystyle{ {U}^{n}{D}^{n} = (UD - (n - 1)I)(UD - (n - 2)I)\cdots (UD - I)UD, }$$

  (8.24)

  where U and D are the linear transformations associated with Young’s lattice (and I is the identity transformation), and where both sides of (8.24) operate on the vector space $\mathbb{R}Y _{j}$ (for some fixed j).

• 15. (difficult) Give a bijective proof of Corollary 8.8, i.e., $\beta (2m,\emptyset ) = 1 \cdot 3 \cdot 5\cdots (2m - 1)$. Your proof should be an analogue of the RSK algorithm. To start with, note that [why?] 1 ⋅3 ⋅5⋯(2m − 1) is the number of complete matchings of [2m], i.e., the number of graphs on the vertex set [2m] with m edges such that every vertex is incident to exactly one edge.

• 16. Fix a partition λ ⊢ n − 1. Find a simple formula for the sum $t(\lambda ) =\sum _{\mu \gtrdot \lambda }{f}^{\mu }$ in terms of f ^λ. The sum ranges over all partitions μ that cover λ (i.e., μ > λ and nothing is in between, so $\mu \vdash n$) in Young’s lattice Y. Give a simple proof using linear algebra rather than a combinatorial proof.

• 17.

  • (a) (*) The Bell numberB(n) is defined to be the number of partitions of an n-element set S, i.e., the number of sets $\{B_{1},\ldots,B_{k}\}$ where B _i ≠∅, $B_{i} \cap B_{j} = \emptyset$ if i≠j, and $\bigcup B_{i} = S$. Find a simple formula for the generating function

    $$\displaystyle{F(x) =\sum _{n\geq 0}B(n)\frac{{x}^{n}} {n!} = 1 + x + 2\frac{{x}^{2}} {2!} + 5\frac{{x}^{3}} {3!} + 15\frac{{x}^{4}} {4!} + \cdots \,.}$$

  • (b) (moderately difficult) Let f(n) be the number of ways to move from the empty partition ∅ to ∅ in n steps, where each step consists of either (i) adding a box to the Young diagram, (ii) removing a box, or (iii) adding and then removing a box, always keeping the diagram of a partition (even in the middle of a step of type (iii)). For instance, f(3) = 5, corresponding to the five sequences

    $$\displaystyle{\begin{array}{ccccc} \emptyset &(1,\emptyset )& (1,\emptyset ) &(1,\emptyset ) \\ \emptyset &(1,\emptyset )& 1 & \emptyset \\ \emptyset & 1 & (2,1) & \emptyset \\ \emptyset & 1 &(11,1)& \emptyset \\ \emptyset & 1 & \emptyset &(1,\emptyset )\end{array} }$$

    Find (and prove) a formula for f(n) in terms of Bell numbers.

• 18. (difficult) (*) For n, k ≥ 0 let κ(n → n + k → n) denote the number of closed walks in Y that start at level n, go up k steps to level n + k, and then go down k steps to level n. Thus for instance $\kappa (n \rightarrow n + 1 \rightarrow n)$ is the number of cover relations between levels n and n + 1. Show that

  $$\displaystyle{\sum _{n\geq 0}\kappa (n \rightarrow n + k \rightarrow n){q}^{n} = k!\,{(1 - q)}^{-k}F(Y,q).}$$

  Here F(Y, q) is the rank-generating function of Y, which by Proposition 8.14 (letting s → ∞) is given by

  $$\displaystyle{F(Y,q) =\prod _{i\geq 1}{(1 - {q}^{i})}^{-1}.}$$

• 19. Let X denote the formal sum of all elements of Young’s lattice Y. The operators U and D still act in the usual way on X, producing infinite linear combinations of elements of Y. For instance, the coefficient of the partition (3, 1) in DX is 3, coming from applying D to (4, 1), (3, 2), and (3, 1, 1).

  • (a) Show that DX = (U + I)X, where as usual I denotes the identity linear transformation.

  • (b) Express the coefficient s _n of ∅ (the empty partition) in D ⁿ X in terms of the numbers f ^λ for $\lambda \vdash n$. (For instance, $s_{0} = s_{1} = 1,s_{2} = 2,s_{3} = 4$.)

  • (c) Show that

    $$\displaystyle{{D}^{n+1}X = (U{D}^{n} + {D}^{n} + n{D}^{n-1})X,\ \ n \geq 0,}$$

    where D ^− 1 = 0, D ⁰ = I.

  • (d) Find a simple recurrence relation satisfied by s _n .

  • (e) Find a simple formula for the generating function

    $$\displaystyle{F(x) =\sum _{n\geq 0}s_{n}\frac{{x}^{n}} {n!}.}$$

  • (f) Show that s _n is the number of involutions in $\mathfrak{S}_{n}$, i.e., the number of elements $\pi \in \mathfrak{S}_{n}$ satisfying ${\pi }^{2} =\iota$.

  • (g) (quite difficult) Show that if $\pi \in \mathfrak{S}_{n}$ and $\pi { \mathrm{RSK} \atop \rightarrow } (P,Q)$, then ${\pi }^{-1}{ \mathrm{RSK} \atop \rightarrow } (Q,P)$.

  • (h) Deduce (f) from (g).

• 20.

  • (a) Consider the linear transformation $U_{n-1}D_{n}: \mathbb{R}Y _{n} \rightarrow \mathbb{R}Y _{n}$. Show that its eigenvalues are the integers i with multiplicity p(n − i) − p(n − i − 1), for 0 ≤ i ≤ n − 2 and i = n.

  • (b) (*) Use (a) to give another proof of Theorem 8.9.

• 21.

  • (a) (moderately difficult) Let Y _{[j − 2, j]} denote the Hasse diagram of the restriction of Young’s lattice Y to the levels j − 2, j − 1, j. Let p(n) denote the number of partitions of n, and write Δp(n) = p(n) − p(n − 1). Show that the characteristic polynomial of the adjacency matrix of the graph Y _{[j − 2, j]} is given by

    $$\displaystyle{\pm {x}^{\Delta p(j)}{({x}^{2} - 1)}^{\Delta p(j-1)}\prod _{ s=2}^{j}{({x}^{3} - (2s - 1)x)}^{\Delta p(j-1)},}$$

    where the sign is ${(-1)}^{\#Y _{[j-2,j]} } = {(-1)}^{p(j-2)+p(j-1)+p(j)}$.

  • (b) (difficult) Extend to Y _{[j − i, j]} for any i ≥ 0. Express your answer in terms of the characteristic polynomial of matrices of the form

    $$\displaystyle{\left [\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0\quad &a\quad & 0 \quad &\quad &\quad &0\quad &0\\ 1\quad &0\quad &a + 1\quad &\quad &\quad &0\quad &0 \\ 0\quad &1\quad & 0 \quad &\quad &\ddots\quad &0\quad &0\\ \quad & \quad & \quad &\ddots\quad \\ \quad & \quad & \ddots \quad &\quad &\quad &0\quad &b \\ \quad & \quad & \quad &\quad &\quad &1\quad &0\end{array} \right ].}$$

• 22. (moderately difficult)

  • (a) Let U and D be operators (or just noncommutative variables) satisfying DU − UD = 1. Show that for any power series $f(U) =\sum a_{n}{U}^{n}$ whose coefficients a _n are real numbers, we have

    $$\displaystyle{{e}^{Dt}f(U) = f(U + t){e}^{Dt}.}$$

    In particular,

    $$\displaystyle{ {e}^{Dt}{e}^{U} = {e}^{t+U}{e}^{Dt}. }$$

    (8.25)

    Here t is a variable (indeterminate) commuting with U and D. Regard both sides as power series in t whose coefficients are (noncommutative) polynomials in U and D. Thus for instance

    $$\displaystyle\begin{array}{rcl}{ e}^{Dt}{e}^{U}& =& \left (\sum _{ m\geq 0}\frac{{D}^{n}{t}^{n}} {n!} \right )\left (\sum _{n\geq 0}\frac{{U}^{n}} {n!} \right ) {}\\ & =& \sum _{m,n\geq 0}\frac{{D}^{m}{U}^{n}{t}^{m}} {m!\,n!}. {}\\ \end{array}$$

  • (b) Show that ${e}^{(U+D)t} = {e}^{\frac{1} {2} {t}^{2}+Ut }{e}^{Dt}$.

• 23. Let w be a balanced word in U and D, i.e., the same number of U’s as D’s. For instance, UUDUDDDU is balanced. Regard U and D as linear transformations on $\mathbb{R}Y$ in the usual way. A balanced word thus takes the space $\mathbb{R}Y _{n}$ to itself, where Y _n is the nth level of Young’s lattice Y. Show that the element $E_{n} =\sum _{\lambda \vdash n}{f}^{\lambda }\lambda \in \mathbb{R}Y _{n}$ is an eigenvector for w, and find the eigenvalue.

• 24. (*) Prove that any two balanced words (as defined in the previous exercise) commute.

• 25. Define a graded poset Z inductively as follows. The bottom level Z ₀ consists of a single element. Assume that we have constructed the poset up to level n. First “reflect” Z _n − 1 through Z _n . More precisely, for each element x ∈ Z _n − 1, let x′ be a new element of Z _n + 1, with $x^{\prime} \gtrdot y$ (where y ∈ Z _n ) if and only if $y \gtrdot x$. Then for each element y ∈ Z _n , let y′ be a new element of Z _n + 1 covering y (and covering no other elements of Z _n ). Figure 8.1 shows the poset Z up to level five. The cover relations obtained by the reflection construction are shown by solid lines, while those of the form $y^{\prime} \gtrdot y$ are shown by broken lines.

  • (a) Show that $\#Z_{n} = F_{n+1}$ (a Fibonacci number), so the rank-generating function of Z is given by

    $$\displaystyle{F(Z,q) = \frac{1} {1 - q - {q}^{2}}.}$$

  • (b) Define $U_{i}: \mathbb{R}Z_{i} \rightarrow \mathbb{R}Z_{i+1}$ and $D_{i}: \mathbb{R}Z_{i} \rightarrow \mathbb{R}Z_{i-1}$ exactly as we did for Y, namely, for x ∈ Z _i we have

    $$\displaystyle\begin{array}{rcl} U_{i}(x)& =& \sum _{y\gtrdot x}y, {}\\ D_{i}(x)& =& \sum _{y\lessdot x}y. {}\\ \end{array}$$

    Show that $D_{i+1}U_{i} - U_{i-1}D_{i} = I_{i}$. Thus all the results we have obtained for Y based on this commutation relation also hold for Z! (For results involving p(n), we need only replace p(n) by F _n + 1.)

  Fig. 8.1

  

  The poset Z up to level 5

• 26.

  • (a) Suppose that $\pi \in \mathfrak{S}_{n}$ and $\pi { \mathrm{RSK} \atop \rightarrow } (P,Q)$. Let f(π) be the largest integer k for which $1,2,\ldots,k$ all appear in the first row of P. Find a simple formula for the number of permutations $\pi \in \mathfrak{S}_{n}$ for which f(π) = k.

  • (b) Let E(n) denote the expected value of f(π) for $\pi \in \mathfrak{S}_{n}$, i.e.,

    $$\displaystyle{E(n) = \frac{1} {n!}\sum _{\pi \in \mathfrak{S}_{n}}f(\pi ).}$$

    Find lim _{n → ∞} E(n).

• 27.

  • (a) An increasing subsequence of a permutation $a_{1}a_{2}\cdots a_{n} \in \mathfrak{S}_{n}$ is a subsequence $a_{i_{1}}a_{i_{2}}\cdots a_{i_{j}}$ such that $a_{i_{1}} < a_{i_{2}} < \cdots < a_{i_{j}}$. For instance, 2367 is an increasing subsequence of the permutation 52386417. Suppose that the permutation $w \in \mathfrak{S}_{n}$ is sent into an SYT of shape $\lambda = (\lambda _{1},\lambda _{2},\ldots )$ under the RSK algorithm. Show that λ ₁ is the length of the longest increasing subsequence of w.

  • (b) (much harder) Define decreasing subsequence similarly to increasing subsequence. Show that λ′ ₁ (the number of parts of λ) is equal to the length of the longest decreasing subsequence of λ.

  • (c) Assuming (a) and (b), show that for m, n ≥ 1, a permutation $w \in \mathfrak{S}_{mn+1}$ has an increasing subsequence of length m + 1 or a decreasing subsequence of length n + 1.

  • (d) How many permutations $w \in \mathfrak{S}_{mn}$ have longest increasing subsequence of length m and longest decreasing subsequence of length n? (Use the hook-length formula to obtain a simple explicit answer.)

• 28. Write down the 13 plane partitions of 4 and the 24 plane partitions of 5.

• 29. Prove the statement preceding Lemma 8.17 that in the bijection $A{ \mathrm{RS{K}^{^{\prime}}} \atop \rightarrow } (P,Q)$, equal elements of Q are inserted from left to right.

• 30. Let A be the r ×s matrix of all 1’s. Describe the plane partition π′(A).

• 31.

  • (a) Find the $\mathbb{N}$-matrix A for which

    $$\displaystyle{\pi ^{\prime}(A) = \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 6\quad &4\quad &4\quad &3\quad &3 \\ 5\quad &3\quad &3\quad &2\quad \\ 3\quad &2\quad &1\quad \end{array}.}$$

  • (b) What message is conveyed by the nonzero entries of A?

• 32.

  • (a) (quite difficult) Let A be an r ×s $\mathbb{N}$-matrix, and let $A{ \mathrm{RS{K}^{^{\prime}}} \atop \rightarrow } (P,Q)$. If A ^t denotes the transpose of A, then show that ${A}^{t}{ \mathrm{RS{K}^{^{\prime}}} \atop \rightarrow } (Q,P)$.

    Note. This result is quite difficult to prove from first principles. If you can do Exercise 19(g), then the present exercise is a straightforward modification. In fact, it is possible to deduce the present exercise from Exercise 19(g).

  • (b) A plane partition $\pi = (\pi _{ij})$ is symmetric if $\pi _{ij} =\pi _{ji}$ for all i and j. Let s _r (n) denote the number of symmetric plane partitions of n with at most r rows. Assuming (a), show that

    $$\displaystyle{\sum _{n\geq 0}s_{r}(n){x}^{n} =\prod _{ i=1}^{r}{\left (1 - {x}^{2i-1}\right )}^{-1} \cdot \prod _{ 1\leq i<j\leq r}{\left (1 - {x}^{2(i+j-1)}\right )}^{-1}.}$$

  • (c) Let s(n) denote the total number of symmetric plane partitions of n. Let r → ∞ in (b) to deduce that

    $$\displaystyle{\sum _{n\geq 0}s(n){x}^{n} =\prod _{ i\geq 1} \frac{1} {(1 - {x}^{2i-1}){(1 - {x}^{2i})}^{\lfloor i/2\rfloor }}.}$$

  • (d) (very difficult; cannot be done using RSK) Let s _rt (n) denote the number of symmetric plane partitions of n with at most r rows and with largest part at most t. Show that

    $$\displaystyle{\sum _{n\geq 0}s_{rt}(n){x}^{n} =\prod _{ 1\leq i<j\leq r}\prod _{k=1}^{t}\frac{1 - {x}^{(2-\delta _{ij})(i+j+k-1)}} {1 - {x}^{(2-\delta _{ij})(i+j+k-2)}}.}$$

• 33. The trace of a plane partition π = (π _ij ) is defined as tr$(\pi ) =\sum _{i}\pi _{ii}$. Let $\mathrm{pp}(n,k)$ denote the number of plane partitions of n with trace k. Show that

  $$\displaystyle{\sum _{n\geq 0}\sum _{k\geq 0}\mathrm{pp}(n,k){q}^{k}{x}^{n} =\prod _{ i\geq 1}{(1 - q{x}^{i})}^{-i}.}$$

• 34. (very difficult; cannot be done using RSK) Let $\mathrm{pp}_{rst}(n)$ be the number of plane partitions of n with at most r rows, at most s columns, and with largest part at most t. Show that

  $$\displaystyle{\sum _{n\geq 0}\mathrm{pp}_{rst}(n){x}^{n} =\prod _{ i=1}^{r}\prod _{ j=1}^{s}\prod _{ k=1}^{t}\frac{1 - {x}^{i+j+k-1}} {1 - {x}^{i+j+k-2}}.}$$

• 35. Let f(n) denote the number of solid partitions of n with largest part at most 1. Find the generating function $F(x) =\sum _{n\geq 0}f(n){x}^{n}$.