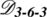Abstract
A general strategy was presented in 2009 by Yamaleev and Carpenter (J. Comput. Phys. 228(11):4248–4272, 2009; J. Comput. Phys. 228(8):3025–3047, 2009), for constructing Energy Stable Weighted Essentially Non-Oscillatory (ESWENO) finite-difference schemes on periodic domains. Fisher et al. (J. Comput. Phys. 230(10):3727–3752, 2011) provided boundary closures for the fourth-order ESWENO scheme that maintain, the WENO stencil biasing properties and satisfy the summation-by-parts (SBP) operator convention, thereby ensuring stability in an L 2 norm. Herein, the general capability of finite-domain schemes is extended by providing closures for the sixth-order case. Third-order and fifth-order boundary closures are developed that are stable in diagonal and block norms, respectively, and achieve fourth- and sixth-order global accuracy for hyperbolic systems. A novel set of nonuniform flux interpolation points is necessary near the boundaries to simultaneously achieve (1) accuracy, (2) the SBP convention, and (3) WENO stencil biasing mechanics. Complete implementation details for the diagonal-norm sixth-order operator are provided as well as examples that demonstrate shock capturing and multi-domain capabilities.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Stencil biasing across block interfaces is still an area of active development. Maturity is approximately equivalent to that of state-of-the-are finite-element WENO formulations.
- 2.
The r={L2,L1,R1,R2} nomenclature identifies the origin of the data relative to the interface position.
- 3.
Note that the dimensions of the even indexed Λ i are (N×N), while the odd-indexed Λ i have dimensions (N+1×N+1). This is the result of the difference matrix Δ having dimensions [N×(N+1)].
- 4.
Equation (15) describes the role of the parameter ε in the WENO stencil biasing mechanics. The parameter determines the amplitude of oscillation that the biasing mechanics can detect. Using
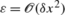 permits larger oscillations in the solution.
permits larger oscillations in the solution. - 5.
For applications where the solution changes drastically during simulation, ε can be rescaled as necessary.
References
R. Borges, M. Carmona, B. Costa, and W. S. Don. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws. Journal of Computational Physics, 227(6):3191–3211, 2008.
M. H. Carpenter, D. Gottlieb, and S. Abarbanel. Time-stable boundary conditions for finite-difference schemes solving hyperbolic systems: Methodology and application to high-order compact schemes. Journal of Computational Physics, 111(2):220–236, 1994.
M. H. Carpenter and C. A. Kennedy. Fourth-order 2n-storage Runge-Kutta schemes. Technical Report TM 109112, NASA, 1994.
M. H. Carpenter, J. Nordström, and D. Gottlieb. A stable and conservative interface treatment of arbitrary spatial accuracy. Journal of Computational Physics, 148(2):341–365, 1999.
M. H. Carpenter, J. Nordström, and D. Gottlieb. Revisiting and extending interface penalties for multi-domain summation-by-parts operators. Technical Report TM 214892, NASA, 2007.
M. H. Carpenter, J. Nordström, and D. Gottlieb. Revisiting and extending interface penalties for multi-domain summation-by-parts operators. Journal of Scientific Computing, 45(1–3):118–150, 2010.
J. Casper and M. H. Carpenter. Computational considerations for the simulation of shock-induced sound. SIAM Journal on Scientific Computing, 19(3):813–828, 1998.
B. Cockburn, C. Johnson, C.-W. Shu, and E. Tadmor. Advanced Numerical Approximation of Nonlinear Hyperbolic Equations. Springer, Berlin, 1998.
G. Erlebacher, M. Hussaini, and C.-W. Shu. Interaction of a shock with a longitudinal vortex. Journal of Fluid Mechanics, 337:129–153, 1997.
T. C. Fisher, M. H. Carpenter, N. K. Yamaleev, and S. H. Frankel. Boundary closures for fourth-order energy stable weighted essentially non-oscillatory finite-difference schemes. Journal of Computational Physics, 230(10):3727–3752, 2011.
B. Gustaffson. High Order Finite Difference Methods for Time Dependent PDE. Springer, Berlin, 2008.
B. Gustafsson. The convergence rate for difference approximations to mixed initial boundary value problems. Mathematics of Computation, 29:396–406, 1975.
G. Jiang and C.-W. Shu. Efficient implementation of weighted ENO schemes. Journal of Computational Physics, 126(1):202–228, 1996.
A. Kitson, R. I. McLachlan, and N. Robidoux. Skew-adjoint finite difference methods on nonuniform grids. New Zealand Journal of Mathematics, 32(2):139–159, 2003.
H.-O. Kreiss and G. Scherer. Finite element and finite difference methods for hyperbolic partial differential equations. In Mathematical Aspects of Finite Elements in Partial Differential Equations, pages 195–212. Academic Press, San Diego, 1974.
P. Lax and M. Mock. The computation of discontinuous solutions of linear hyperbolic equations. Communications in Pure and Applied Mathematics, 31:423–430, 1978.
M. Martin, E. Taylor, M. Wu, and V. Weris. A bandwidth-optimized WENO scheme for the effective direct numerical simulation of compressible turbulence. Journal of Computational Physics, 220(1):270–289, 2006.
K. Mattsson. Summation by parts operators for finite difference approximations of second-derivatives with variable coefficients. Journal of Scientific Computing, 29(1):1–33, 2011.
R. I. McLachlan and N. Robidoux. EQUADIFF 99. In Antisymmetry, Pseudospectral Methods, and Conservative PDEs, pages 994–999. World Scientific, Singapore, 2000.
J. Nordström. Conservative finite difference formulations, variable coefficients, energy estimates and artificial dissipation. Journal of Scientific Computing, 29(3):375–404, 2006.
J. Nordström and M. H. Carpenter. Boundary and interface conditions for high-order finite-difference methods applied to the Euler and Navier-Stokes equations. Journal of Computational Physics, 148(2):621–645, 1999.
J. Nordström, J. Gong, E. van der Weide, and M. Svärd. A stable and conservative high order multi-block method for the compressible Navier-stokes equation. Journal of Computational Physics, 228(24):9020–9035, 2009.
C.-W. Shu. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. In Advanced Numerical Approximation of Nonlinear Hyperbolic Equations: Lecture Notes in Mathematics, volume 1697, pages 325–432. Springer, Berlin, 1998.
B. Strand. Summation by parts for finite difference approximations for d/dx. Journal of Computational Physics, 110(1):47–67, 1994.
M. Svärd and J. Nordström. On the order of accuracy for difference approximations of initial-boundary value problems. Journal of Computational Physics, 218(1):333–352, 2006.
N. K. Yamaleev and M. H. Carpenter. A systematic methodology for constructing high-order energy stable WENO schemes. Journal of Computational Physics, 228(11):4248–4272, 2009.
N. K. Yamaleev and M. H. Carpenter. Third-order energy stable WENO scheme. Journal of Computational Physics, 228(8):3025–3047, 2009.
S. Zhang, S. Jiang, Y. Zhang, and C. Shu. The mechanism of sound generation in the interaction between a shock wave and two counter-rotating vortices. Physics of Fluids, 21:076101, 2009.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
1.1 8.1 Implementation of WENO
The nonlinear WENO scheme is defined as

The fluxes are constructed by using the formula
The expressions for \(\bar{f}_{j}\) at the six boundary closure points are slightly more complicated but conform to the same matrix conventions,
where n b is the number of flux terms in each boundary flux.
The nonlinear weights \(\bar{w}^{(r)}\) are defined by
The coefficients \(\bar{d}_{j}^{(r)}\) are the target weights of the candidate stencils, and \(\bar{\beta}_{j}^{(r)}\) and \(\bar{\tau}_{j}\) are the smoothness indicators.
The smoothness indicators \(\bar{\beta}_{j}^{(r)}\) have the same form at all flux points, although they may not all be defined near the boundaries. Experimentation has determined that the choice of f affects the solution smoothness and dissipation properties, and that the best practice is to base the smoothness indicator on the characteristic variables rather than the characteristic fluxes. The interior smoothness indicators
The indicators \(\bar{\beta}^{L3}\) and \(\bar{\beta}^{R3}\) (needed only near boundaries) as well as the \(\bar{\beta}^{r}\) stencil coefficients used near the boundaries are included in Appendix 8.3.
To guarantee that the downwind stencil weight does not exceed that of the central or upwind weights, the downwind smoothness indicator is modified by using the expression
where k is an even integer, and n s is the number of distinct interpolants contributing to the flux f j .
An additional stencil biasing parameter, \(\bar{\tau}_{j}\), is needed for the ESWENO scheme. Here, \(\bar{\tau}_{j}\) is a quadratic function of the sum of fourth-order undivided differences that are available on the stencil for \(\bar{f}_{j}\) (see Fig. 1),

At the points \(\bar{x}_{1}\) and \(\bar{x}_{2}\), \(\bar{\tau}_{j}\) is constructed from a single fourth-order undivided difference, biased toward the interior of the domain as
The \(\bar{\tau}_{j}\) is biased in a mirrored fashion at \(\bar {x}_{N-2}\) and \(\bar{x}_{N-1}\).
The parameter ε is a function of the number of points in the discretization:
where ∥f 0∥ and ∥f 0∥′ represent a norm of the flux and the gradient of the flux, respectively, as determined using initial conditions but excluding points near discontinuities.Footnote 5
1.2 8.2 Recipe
Consider the Euler equations U t +F(U) x =0. A recipe for calculating the gradient term F(U) x using a sixth-order ESWENO scheme is summarized below.
-
1.
Construct the convective flux F at solution points (x) according to the governing differential equations.
-
2.
Construct the flux Jacobian matrices: \(A = \frac{\partial F}{\partial U}\) at the flux points (\(\bar{\mathbf{x}}\)) by using the Roe-averaged variables that are formed from nearest neighbor solution point data. Form the eigenvector decomposition A=SϒS −1, where S is the matrix of right eigenvectors and ϒ is the diagonal matrix of eigenvalues.
-
3.
For the flux point \(\bar{x}_{j}\), use the eigenvector matrix \(\bar{S}^{-1}_{j}\) to transform the solution and the flux at all points x into characteristic form \(U_{c} = \bar{S}^{-1} U ; F_{c}(U) = \bar{S}^{-1} F(U) = \varUpsilon U_{c}\).
Remark Forming the characteristic variables and fluxes is only necessary for nodal points that are located in the stencil of a given flux point. The presentation herein assumes that the transformed fluxes and variables are available at all points but can be reduced to improve performance.
-
4.
Form the Lax-Friedrichs characteristic fluxes \(\mathbf{f}_{\mathbf{c}}^{\pm}=\frac{1}{2} (F_{c} \pm\varUpsilon_{max} U_{c} )\), where ϒ max is a diagonal matrix of the maximum local eigenvalues contained within each stencil.
-
5.
Perform interpolations on each candidate stencil,
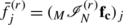 .
. -
6.
Calculate the stencil biasing parameters:
-
7.
Calculate and normalize the weights using the stencil biasing parameters and the target weights in (70) (see (15) in text).
-
8.
Calculate Λ i from the weights by using (88) through (91) for the diagonal-norm scheme.
-
9.
Modify the diagonal of Λ i to be smoothly positive according to (32).
-
10.
Calculate the WENO flux from the weights and candidate interpolations by using (68) (see (20) in the text).
-
11.
Calculate the energy stable flux \(\bar{\boldsymbol{\psi}}\) from (33).
-
12.
Reconstruct the fluxes in characteristic space, \(\bar{f}_{j}=\bar{f}^{+}_{j}+\bar{f}_{j}^{-}\) and \(\psi_{j}=\psi_{j}^{+}+\psi_{j}^{-}\), and then transform the fluxes back to physical space by using \(\hat{f}_{j} = S (\bar{f}_{j} + \psi_{j} )\).
-
13.
After calculating the ESWENO interpolation at all flux points, calculate the gradient using the inverse of the
 norm, as in (34).
norm, as in (34).
Remark
Note that all of the presented equations are for the forward-propagating waves, \(\bar{f}_{j}^{+}\). The equations for interpolation of backward-propagating waves (\(\bar{f}_{j}^{-}\)) are found in exactly the same manner, except that the downwind stencil in (72) is the far left instead of the far right stencil. The Λ i terms are to be negative instead of positive; therefore, we use
1.3 8.3 Sixth-Order Diagonal-Norm Operator: 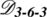
1.3.1 8.3.1 Differentiation Matrix
The upper left matrix quadrant of the target SBP differentiation operator  can be written in the form
can be written in the form

The matrix elements in the lower right quadrant are structurally equivalent relative to the outflow boundary, but with the opposite sign. The diagonal mass matrix  is
is

The skew-symmetric matrix  follows immediately from
follows immediately from  .
.
The distribution the flux points \(\bar{\mathbf{x}}\) as described in Lemma 1 follows immediately from the norm  and can be written as
and can be written as
where
Then, the vector \({\varDelta }\bar{\mathbf{x}}\) is the reciprocal of the diagonal elements of  . The product
. The product  is trivially the identity vector 1 because
is trivially the identity vector 1 because  is a diagonal matrix. Note that all integer coefficients are exact. Case should be taken to ensure that the rational coefficients retain the full working precision of the coding language (e.g. 64 bit arithmetic).
is a diagonal matrix. Note that all integer coefficients are exact. Case should be taken to ensure that the rational coefficients retain the full working precision of the coding language (e.g. 64 bit arithmetic).
1.3.2 8.3.2 Interpolation Operators
The tri-diagonal interpolation matrices  , r={L4,L3,L2,L1,R1,R2,R3,R4} for the ESWENO3-6-3 scheme, presented in compressed format using the arrays I
r
, r={L4,L3,L2,L1,R1,R2,R3,R4}, are given by
, r={L4,L3,L2,L1,R1,R2,R3,R4} for the ESWENO3-6-3 scheme, presented in compressed format using the arrays I
r
, r={L4,L3,L2,L1,R1,R2,R3,R4}, are given by


The interpolants I r , r={R1,R2,R3,R4} are mirror images of I r , r={L1,L2,L3,L4}. For example, the interpolants I r , r={R1,R2} are given by
Reconstructing  from the data I
r
is accomplished by populating the appropriate diagonals in the interpolation matrices. The middle column of I
r coincides with the diagonal of
from the data I
r
is accomplished by populating the appropriate diagonals in the interpolation matrices. The middle column of I
r coincides with the diagonal of  , r={L4,L3,L2,L1,R1,R2,R3,R4} that is shifted {−4,−3,−2,−1,0,1,2,3} relative to the main diagonal.
, r={L4,L3,L2,L1,R1,R2,R3,R4} that is shifted {−4,−3,−2,−1,0,1,2,3} relative to the main diagonal.
1.3.3 8.3.3 Target Weights
The target weights for the five interpolation stencils are
For brevity, the last two columns are excluded from the table. Recognizing the relationship between columns 4 and 7 (and 5 and 6), columns 6 and 7 can be recovered from the mirror images of columns 1 and 2, respectively. Note that the WENO/ESWENO3-6-3 scheme requires the inclusion of two extra stencils near each boundary.
1.3.4 8.3.4 Smoothness Indicators Coefficients
The smoothness indicators \(\bar{\beta}^{r}\) measure the smoothness of the data used by each interpolant. This is accomplished by comparing the L 2 of the undivided first and second derivatives, evaluated at the flux point \({\bar{x}}_{j}\).
The leading order truncation term is identical in all cases. For example, the interior terms
The coefficients needed for the first derivative term \({\delta x} \frac{\partial}{\partial x}\) in the smoothness indicators throughout the spatial domain can be expressed as follows.


The coefficients needed for the first derivative term \({\delta x} \frac{\partial}{\partial x}\) in the rightward biased stencils (r=R1,R2,R3,R4) are the mirror images of those used for leftward biased stencils (r=L1,L2,L3,L4).
The second derivative stencil coefficients are always
1.3.5 8.3.5 Energy-Stable Terms
The stabilization matrix Diag(Λ 0) is identically zero for the ESWENO3-6-3 scheme (as it is with every consistent scheme). The nonzero terms of the diagonal matrices Λ i , i=1,5 are




Rights and permissions
Copyright information
© 2013 Springer Science+Business Media New York
About this chapter
Cite this chapter
Carpenter, M.H., Fisher, T.C., Yamaleev, N.K. (2013). Boundary Closures for Sixth-Order Energy-Stable Weighted Essentially Non-Oscillatory Finite-Difference Schemes. In: Melnik, R., Kotsireas, I. (eds) Advances in Applied Mathematics, Modeling, and Computational Science. Fields Institute Communications, vol 66. Springer, Boston, MA. https://doi.org/10.1007/978-1-4614-5389-5_6
Download citation
DOI: https://doi.org/10.1007/978-1-4614-5389-5_6
Publisher Name: Springer, Boston, MA
Print ISBN: 978-1-4614-5388-8
Online ISBN: 978-1-4614-5389-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


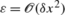 permits larger oscillations in the solution.
permits larger oscillations in the solution.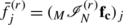 .
. norm, as in (
norm, as in (