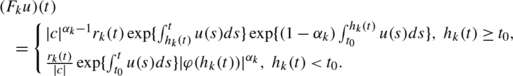Nonlinear Models—Modifications of Delay Logistic Equations

Abstract

Logistic equations have numerous applications, especially in population dynamics. In Chap. 11, several modifications of delay logistic equations are considered, in particular, both additive and multiplicative generalizations.

In the study of the nonoscillation properties of nonlinear equations usually one of the following three methods is applied: first, a differential equation can be transformed into an operator equation with the following property: if the operator equation has a nonnegative solution, then the differential equation has a nonoscillatory solution, second, for the relevant operator equation either the Schauder Fixed-Point Theorem is applied, or convergence of monotone approximations to a solution is demonstrated, and, third, the connection of oscillation properties of nonlinear and linear delay differential equations can be employed. In this chapter, all the three methods are used. In the most difficult superlinear case the differential equation is transformed into an operator equation which incorporates both an increasing and a decreasing operators.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

11.1 Introduction

In this chapter, we study several nonlinear delay differential equations for which the linearization method of the previous chapter cannot be applied.

The delay logistic equation

$$ \dot{y}(t)= r(t)y(t) \biggl( 1-\frac{y(h(t))}{K} \biggr),\ h(t)\leq t,$$

(11.1.1)

is known as Hutchinson’s equation if r and K are positive constants and h(t)=t−τ for a positive constant τ. Hutchinson’s equation was investigated by several authors, see, for example, [213, 214, 285, 334]. Delay logistic equation (11.1.1) was studied by Gopalsamy and Zhang [167, 354], who gave sufficient conditions for oscillation and nonoscillation of (11.1.1).

Publications [12, 154, 175, 176, 192, 237, 244, 255, 296, 330, 340] are devoted to various generalizations of logistic equation (11.1.1). For example, in [12, 154, 237] the authors considered the equation

$$ \dot{y}(t)= r(t)y(t) \biggl( 1-\frac{y(h(t))}{K} \biggr) \biggl \vert 1-\frac{y(h(t))}{K}\biggr \vert ^{\alpha-1},$$

(11.1.2)

where α<1 (sublinear case) or α>1 (superlinear case).

In this chapter, we study (11.1.2) with several delays,

$$ \dot{y}(t)= \sum_{k=1}^mr_k(t)y(t) \biggl( 1-\frac{y(h_k(t))}{K} \biggr) \biggl \vert 1-\frac{y(h_k(t))}{K}\biggr \vert ^{\alpha_k-1}.$$

(11.1.3)

We consider the cases α _k ≤1, k=1,⋯,m, α _k ≥1, k=1,⋯,m and also the three mixed cases for m=2. The case α _k =1, k=1,⋯,m was considered in the previous chapter.

Delay logistic equation (11.1.1) assumes both additive and multiplicative generalizations. For example, in [175] the authors considered the multiplicative logistic equation

$$\dot{y}(t)= r(t)y(t) \Biggl( 1-\prod_{k=1}^m\frac{y(h_k(t))}{K} \Biggr).$$

In [90, 336], oscillation properties of the nonlinear delay equation

$$\dot{y}(t)+a(t)y(t) + b(t)\prod_{k=1}^m\biggl( \frac{y(h_k(t))}{K} \biggr)^{\alpha_k} =0,\ \sum _{k=1}^m\alpha_k=1,$$

were studied. In [265], the authors considered the nonlinear neutral multiplicative differential equation

$$\frac{d}{dt}\bigl[r(t)-c(t)x(t-r)\bigr]+p(t)\prod _{k=1}^m \bigl[x(t-r_k)\bigr]^{\alpha _k} =0,$$

where also $\sum_{k=1}^{m}\alpha_{k}=1$.

In this chapter, we consider the generalized logistic equation where the sum in (11.1.3) is replaced by a product:

$$ \dot{y}(t)= \prod_{k=1}^mr(t)y(t) \biggl( 1-\frac{y(h_k(t))}{K} \biggr) \biggl \vert 1-\frac{y(h_k(t))}{K}\biggr \vert ^{\alpha_k-1},\ \sum_{k=1}^m\alpha_k=1.$$

(11.1.4)

It is interesting to discuss here some methods that are applied to obtain nonoscillation and oscillation results for the delay logistic equations and their generalizations.

Usually a differential equation is transformed into an operator equation with the following property: if the operator equation has a nonnegative solution, then the differential equation has a nonoscillatory solution. For the operator equation, either the Schauder Fixed-Point Theorem is applied, convergence of monotone approximations to a solution is demonstrated or the connection of oscillation properties of the nonlinear logistic equation and a linear delay differential equation is employed.

Here we use all three methods mentioned above. We do not assume that the parameters of (11.1.3) are continuous functions. Hence, unlike most known results, we have to apply the Schauder Fixed-Point Theorem in the space L _∞ of Lebesgue measurable and locally essentially bounded functions. In the most difficult superlinear case, we transform the differential equation into an operator equation,

$$u=Au Bu,$$

where the operator A is monotonically increasing and B is monotonically decreasing. We prove that there exist two functions v, w, where 0≤v(t)≤w(t), such that

$$v(t)\leq(Av) (t) (Bw) (t),\ w(t)\geq(Aw) (t) (Bv) (t).$$

Then the operator Tu=AuBu maps the interval v(t)≤u(t)≤w(t) into itself, and therefore we can use the Schauder Fixed-Point Theorem.

The chapter is organized as follows. In Sect. 11.2, we study the generalized logistic equation with several delays (11.1.3). For this equation, we consider the cases of sublinear and superlinear equations and also mixed equations that contain both sublinear and superlinear terms. Section 11.3 includes investigation of nonoscillation properties for the multiplicative delay logistic equation (11.1.4), which contains a product of logistic terms. Section 11.4 provides discussion and states some open problems.

11.2 Generalized Logistic Equation with Several Delays

11.2.1 Preliminaries

Consider the scalar delay differential equation

$$ \dot{x}(t)=-\bigl(1+x(t)\bigr)\sum_{k=1}^mr_k(t)x\bigl(h_k(t)\bigr)\bigl|x\bigl(h_k(t)\bigr)\bigr|^{\alpha_k-1} ,\ t\geq0,$$

(11.2.1)

under the following assumptions:

• (a1) r _k , k=1,⋯,m, are Lebesgue measurable locally essentially bounded functions, r _k (t)≥0.

• (a2) h _k :[0,∞)→ℝ are Lebesgue measurable functions, h _k (t)≤t, lim _t→∞ h _k (t)=∞, k=1,⋯,m, and α _k >0, k=1,2,⋯,m are real numbers.

Together with (11.2.1), we consider for each t ₀≥0 the initial value problem

$$ \dot{x}(t)=-\bigl(1+x(t)\bigr)\sum_{k=1}^mr_k(t)x\bigl(h_k(t)\bigr)\bigl|x\bigl(h_k(t)\bigr)\bigr|^{\alpha_k-1},\ t\geq t_0,$$

(11.2.2)

$$ x(t)=\varphi(t), \ t<t_0,\ x(t_0)=x_0.$$

(11.2.3)

We also assume that the following hypothesis holds:

• (a3) φ:(−∞,t ₀)→ℝ is a Borel measurable bounded function.

Definition 11.1

A function x:ℝ→ℝ absolutely continuous in each interval [t ₀,b] is called a solution of problem (11.2.2), (11.2.3) if it satisfies (11.2.2) for almost all t∈[t ₀,∞) and equalities (11.2.3) for t≤t ₀.

Equation (11.2.1) is obtained from the generalized logistic equation

$$ \dot{y}(t)= \sum_{k=1}^mr_k(t)y(t) \biggl( 1-\frac{y(h_k(t))}{K} \biggr) \biggl \vert 1-\frac{y(h_k(t))}{K} \biggr \vert ^{\alpha_k-1}$$

(11.2.4)

using the substitution

$$y=K(1+x).$$

Let us note that all solutions of (11.2.4) with a positive initial value and a nonnegative initial function are positive by Theorem B.17. Since for the logistic equation y(t)>0 we will consider only such solutions of (11.2.1) for which the inequality

$$x(t)>-1$$

holds.

11.2.2 Sublinear Case α _k <1, k=1,⋯,m

Together with (11.2.1), consider the differential inequalities

$$ \dot{x}(t)\leq-\bigl(1+x(t)\bigr)\sum_{k=1}^mr_k(t)x\bigl(h_k(t)\bigr)\bigl|x\bigl(h_k(t)\bigr)\bigr|^{\alpha _k -1} ,\ t\geq0,$$

(11.2.5)

$$ \dot{x}(t)\geq-\bigl(1+x(t)\bigr)\sum_{k=1}^mr_k(t)x\bigl(h_k(t)\bigr)\bigl|x\bigl(h_k(t)\bigr)\bigr|^{\alpha_k -1} ,\ t\geq0.$$

(11.2.6)

As was mentioned before, only such solutions of (11.2.1), (11.2.5) and (11.2.6) for which the condition

$$ 1+x(t)>0$$

(11.2.7)

holds are considered.

Theorem 11.1

The following statements are equivalent:

• 1. Either inequality (11.2.5) has an eventually positive solution or inequality (11.2.6) has an eventually negative solution satisfying −1<x(t)<0.

• 2. There exist a point t ₀≥0, number c and function φ:(−∞,t ₀)→ℝ with either φ(t)≥0, c>0 or −1<φ(t)≤0, −1<c<0, such that the inequality

  $$ u(t)\geq \biggl( 1+c\exp \biggl\{-\int_{t_0}^tu(s)ds \biggr\} \biggr) \sum_{k=1}^m(F_ku) (t)$$

  (11.2.8)

  has a nonnegative solution locally integrable on [t ₀,∞), where operators F _k are defined as

  

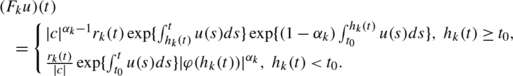
• 3. Equation (11.2.1) has a nonoscillatory solution.

Proof

1)⇒2) Let x be a solution of (11.2.5) and x(t)>0 for t≥t ₁. Then there exists t ₀≥t ₁ such that h _k (t)≥t ₁ for t≥t ₀, k=1,⋯,m. Denote φ(t)=x(t), t<t ₀ and c=x(t ₀). Then φ(t)>0, c>0.

Let $u(t)=-\frac{\dot{x}(t)}{x(t)}$, t≥t ₀. For the solution x(t) of (11.2.5), we have $\dot{x}(t)\leq 0$, t≥t ₀ and consequently u(t)≥0. We can now rewrite x in the form

$$ x(t) = \left \{ \begin{array}{ll}c\exp\{-\int_{t_0}^t u(s)ds \}, & t\geq t_0,\\\noalign{\vspace{3pt}}\varphi(t), & t<t_0.\end{array} \right .$$

(11.2.9)

By substituting x in (11.2.5), we obtain inequality (11.2.8). Similarly (11.2.8) can be obtained if −1<x(t)<0 is a solution of (11.2.6).

2)⇒3) Let u ₀ be a nonnegative solution of inequality (11.2.8) with −1<φ(t)≤0, −1<c<0. For the sequence {u _n } denoted by

$$ u_{n}(t)= \biggl( 1+c\exp \biggl\{ -\int _{t_0}^t u_{n-1}(s)ds \biggr\} \biggr)\sum_{k=1}^m (F_ku_{n-1})(t),$$

(11.2.10)

inequality (11.2.8) implies u ₁(t)≤u ₀(t). By induction, we can prove

$$0\leq u_{n} (t) \leq u_{n-1}(t)\leq u_0(t).$$

There exists a pointwise limit of the nonincreasing nonnegative sequence u _n (t). Let u(t)=lim _n→∞ u _n (t). Then, by the Lebesgue convergence theorem, u(t) is locally integrable and

$$\lim_{n\rightarrow\infty} ( F_ku_n ) (t) =(F_ku) (t),\ k=1,\cdots,m.$$

Thus (11.2.10) implies

$$u(t)= \biggl( 1+c\exp \biggl\{ -\int_{t_0}^tu(s)ds \biggr\} \biggr) \sum_{k=1}^m (F_ku) (t).$$

Hence the function x defined by equality (11.2.9) is an eventually negative solution of (11.2.1).

Further, let u ₀ be a nonnegative solution of inequality (11.2.8) with φ(t)≥0 and c>0. If inequality (11.2.8) holds for some φ, then it holds also for φ≡0, so we can assume that φ≡0.

If 0<c<1, then denoting c ₀=−c we obtain that u ₀ is also a solution of (11.2.8) with c ₀, φ≡0 instead of c, φ(t). From the previous case, it follows that there exists an eventually negative solution of (11.2.1).

Next, suppose that c≥1. From (11.2.8), we have

where the sum includes only the terms for which h _k (t)≥t ₀.

There exists 0<d≤1 such that $c^{\alpha_{k}}>d^{\alpha_{k}-1},k=1,\cdots,m$ if c>1 and d=c=1 if c=1.

Hence $u(t)\geq\sum_{k=1}^{m} (F_{k} u)(t)$, where c in the definition of F _k is replaced by d and φ≡0. Denote c ₀=−d. Then inequality (11.2.8) holds for −1<c ₀<0 and φ≡0. As was proven above, there exists a nonnegative function u(t) such that

$$x(t)=c_0\exp \biggl\{ - \int_{t_0}^tu_0(s)ds \biggr\} ,\ t\geq0,\ x(t)=0,\ t<t_0,$$

is an eventually negative solution of (11.2.1).

Implication 3)⇒1) is evident. □

Corollary 11.1

Suppose that there exist t ₀ and A>1 such that the inequality

$$ u(t)\geq A\sum_{k=1}^mr_k(t)\exp \biggl\{ \int_{h_k(t)}^tu(s)ds \biggr\} \exp \biggl\{(1-\alpha_k) \int_{t_0}^{h_k(t)}u(s)ds \biggr\} ,\ t\geq t_0,$$

(11.2.11)

has a nonnegative locally integrable solution, where the sum contains only such terms for which h _k (t)≥t ₀. Then (11.2.1) has a nonoscillatory solution.

Proof

The corollary follows from statement 2) of Theorem 11.1 if we assume φ≡0 and −1<c<0 such that $|c|^{\alpha_{k}-1}<A$, k=1,⋯,m. □

Corollary 11.2

If there exists an eventually positive solution of (11.2.1), then there exists an eventually negative solution of (11.2.1).

Proof

This result follows from the proof of Theorem 11.1. □

Remark 11.1

Theorem 11.1 and its corollaries remain valid if for some or all indices k we have α _k =1.

Theorem 11.2

There exists a nonoscillatory solution of (11.2.1) if and only if

$$\int_0^{\infty} r_k(t) dt <\infty,\ k=1,\cdots,m.$$

Proof

Let

$$\int_0^{\infty} r_k(t) dt <\infty,\ k=1,\cdots,m.$$

Then there exists t ₀ and A>1 such that $A\exp\{2\int_{t_{0}}^{\infty} \sum_{k=1}^{m} r_{k}(s)ds \}<2$. For any nonnegative u, u(t)=0, for t<t ₀ we have

Let $u(t)= 2\sum_{k=1}^{m} r_{k}(t)$, t≥t ₀. Then u is a solution of inequality (11.2.11). Corollary 11.1 implies that (11.2.1) has a nonoscillatory solution.

Suppose now that for some i, 1≤i≤m, we have $\int_{0}^{\infty} r_{i}(t) dt =\infty$. Let x be a positive or negative solution of (11.2.1) for t≥t ₁. There exists t ₀≥t ₁ such that h _k (t)≥t ₁, t≥t ₀, k=1,⋯,m. Let $u(t)=-\frac{\dot{x}(t)}{x(t)}$, t≥t ₀. Then u(t)≥0. We can now rewrite x in the form (11.2.10), where c=x(t ₀), φ(t)=x(t), t<t ₀. Since we consider only solutions x(t)>−1, we have c>−1.

By substituting x in (11.2.1), we obtain for t≥t ₀ the equality

$$u(t)= \biggl( 1+c\exp \biggl\{-\int_{t_0}^tu(s)ds \biggr\} \biggr) \sum_{k=1}^m(F_ku) (t),$$

which corresponds to inequality (11.2.8).

There exists t ₂>t ₀ such that h _k (t)≥t ₀ for t≥t ₂. Then, for t≥t ₂ we have

$$u(t)\geq\min\{1, 1+c\}|c|^{\alpha_i-1}r_i(t) \exp \biggl\{(1-\alpha_i)\int_{t_1}^t u(s)ds \biggr\}.$$

Hence

$$r_i(t)\leq\frac{|c|^{1-\alpha_i}}{ \min\{1, 1+c\}}u(t) \exp \biggl\{-(1-\alpha_i)\int_{t_1}^t u(s)ds \biggr\},\ t\geq t_2,$$

which implies

Thus $\int_{t_{1}}^{\infty} a_{i}(s)ds <\infty$, which gives a contradiction. Hence all the solutions of (11.2.1) are oscillatory. □

Remark 11.2

The sufficient part (“if”) of Theorem 11.2 remains true if some or all α _k are equal to one.

11.2.3 Superlinear Case α _k >1, k=1,⋯,m

Theorem 11.3

Suppose that for some ε>0 there exists a nonoscillatory solution of the linear delay differential equation

$$ \dot{x}(t)=-\varepsilon\sum_{k=1}^mr_k(t)x\bigl(h_k(t)\bigr).$$

(11.2.12)

Then there exists a nonoscillatory solution of (11.2.1).

Proof

Let t ₀≥0, c and φ:(−∞,t ₀)→ℝ be such that −1<c<0, φ(t)≤0, $|\varphi(t)|<|c|<{\varepsilon}^{1 / (\alpha_{k}-1)}$, k=1,⋯,m, and hence c≤φ(t)≤0. Theorem 2.22 implies that initial value problem (11.2.12), (11.2.3) with initial function φ and initial value x ₀=c has a negative solution x ₀(t)<0. Denote

$$w_0(t)=-\frac{\dot{x}_0(t)}{x_0(t)}.$$

Then w ₀(t)≥0 and $x_{0}(t)=c\exp\{-\int_{t_{0}}^{t} w_{0}(s)ds\}$, t≥t ₀.

After substituting x ₀ into (11.2.12), we have

$$w_0(t)=\varepsilon\sum_{k=1}^mr_k(t) \times \left \{ \begin{array}{ll} {\exp \{\int_{h_k(t)}^tw_0(s)ds \}},& h_k(t)\geq t_0, \\\noalign{\vspace{3pt}}{\exp \{\int_{t_0}^t w_0(s)ds \}\frac {\varphi (h_k(t))}{c}},&h_k(t)<t_0.\end{array} \right .$$

Consider now the two sequences

where w ₀ was defined above and v ₀=0.

We have $|\varphi(h_{k}(t))|^{\alpha_{k}-1}<|c|^{\alpha_{k}-1}<\varepsilon$ and $1+c\exp \{-\int_{t_{0}}^{t} w_{0}(s)\,ds \} < 1$. Then w ₁(t)≤w ₀(t), v ₁(t)≥v ₀(t)=0 and w ₀(t)≥v ₀(t). Hence, by induction,

$$0\leq w_n(t)\leq w_{n-1}(t)\leq\cdots\leq w_0(t),\ v_n(t)\geq v_{n-1}(t)\geq\cdots\geq v_0(t)= 0,$$

and v _n (t)≤w _n (t)≤w ₀(t).

There exist pointwise limits of the nonincreasing nonnegative sequence w _n (t) and of the bounded nondecreasing sequence v _n (t). If we denote w(t)=lim _n→∞ w _n (t) and v(t)=lim _n→∞ v _n (t), then by the Lebesgue monotone convergence theorem (see Theorem A.1) we conclude that

(11.2.13)

and

(11.2.14)

Denote the operator T:L _∞[a,b]→:L _∞[a,b] by the equality

Equalities (11.2.13), (11.2.14) imply that for every function u from the interval v≤u≤w we have v≤Tu≤w. Theorem A.6 implies that operator T is a compact operator in the space L _∞[t ₀,b] for every b>t ₀. Then, by the Schauder Fixed-Point Theorem (see Theorem A.15) there exists a nonnegative solution of equation u=Tu.

Thus x(t) defined as

$$x(t)= \left \{ \begin{array}{ll} { c\exp \{-\int_{t_0}^tu(s)ds \}}, & t\geq t_0,\\\noalign{\vspace{3pt}}\varphi(t), & t<t_0.\end{array} \right .$$

is a negative solution of (11.2.1), which completes the proof. □

Corollary 11.3

If

$$ \limsup_{t\rightarrow\infty} \int_{\min_k\{h_k(t)\}}^t\sum_{i=1}^m r_i(s)ds<\infty,$$

(11.2.15)

then (11.2.1) has a nonoscillatory solution.

Proof

Inequality (11.2.15) yields that for some ε>0

$$\limsup_{t\rightarrow\infty} \int_{\min_k\{h_k(t)\}}^t \sum _{k=1}^m \varepsilon r_k(s)ds<\frac{1}{e}.$$

Theorems 2.7 and 11.3 imply that (11.2.1) has a nonoscillatory solution. □

Next, consider the case where some α _k can equal one.

Theorem 11.4

Let {1,⋯,m}=I∪J, where α _k >1, k∈I, α _k =1, k∈J. Suppose that for some ε>0 there exists a nonoscillatory solution of the linear delay differential equation

$$ \dot{x}(t)=-\varepsilon\sum_{k\in I}r_k(t)x\bigl(h_k(t)\bigr) -\sum _{k\in J} r_k(t)x\bigl(h_k(t)\bigr).$$

(11.2.16)

Then there exists a nonoscillatory solution of (11.2.1).

Corollary 11.4

If

$$\limsup_{t\rightarrow\infty} \int_{\min_{k\in I}\{h_k(t)\}}^t\sum _{i\in I} r_i(s)ds<\infty ,$$

$$\limsup_{t\rightarrow\infty} \int_{\min_{k\in J}\{h_k(t)\}}^t\sum _{i\in J} r_i(s)ds<\frac{1}{e} ,$$

then (11.2.1) has a nonoscillatory solution.

The proof of Theorem 11.4 and its corollary is similar to the proof of the previous theorem and its corollary.

11.2.4 Mixed Cases

For simplicity, we consider in this section model (11.2.1) with m=2; i.e., the equation

(11.2.17)

General equation (11.2.1) can be studied in a similar way.

I. Case α ₁<1=α ₂.

Theorem 11.5

Let α ₁<1=α ₂ and all solutions of at least one of the equations

$$ \dot{x}(t)=-\bigl(1+x(t)\bigr) r_1(t)x\bigl(h_1(t)\bigr)\bigl|x\bigl(h_1(t)\bigr)\bigr|^{\alpha_1 -1},$$

(11.2.18)

$$ \dot{x}(t)=-\bigl(1+x(t)\bigr) r_2(t)x\bigl(h_2(t)\bigr),$$

(11.2.19)

be oscillatory. Then all solutions of (11.2.17) are also oscillatory.

Proof

Suppose there exists a nonoscillatory solution x of (11.2.17). If x is an eventually positive solution of (11.2.17), then there exists t ₀≥0 such that

$$\dot{x}(t)\leq-\bigl(1+x(t)\bigr) r_1(t)x\bigl(h_1(t)\bigr)\bigl|x\bigl(h_1(t)\bigr)\bigr|^{\alpha_1 -1} ,\ t\geq t_0,$$

and

$$\dot{x}(t)\leq-\bigl(1+x(t)\bigr) r_2(t)x\bigl(h_2(t)\bigr) ,\ t\geq t_0.$$

Theorem 11.1 and Remark 11.1 imply that (11.2.18) and (11.2.19) have nonoscillatory solutions, which gives a contradiction.

The case where (11.2.1) has an eventually negative solution is similar. □

Corollary 11.5

Let m=2, α ₁<1=α ₂. If

$$\mbox{\textit{either} } \int_0^{\infty}r_1(s)ds =\infty\mbox{ \textit{or} } \liminf_{t\rightarrow\infty} \int _{h_2(t)}^t r_2(s)ds>\frac{1}{e},$$

then all the solutions of (11.2.17) are oscillatory.

Proof

The result follows from Theorems 11.2 and 10.4. □

Theorem 11.6

Let α ₁<1=α ₂. If in addition

$$\int_0^{\infty} r_k(s)ds <\infty,\ k=1,2,$$

then there exists a nonoscillatory solution of (11.2.17).

Proof

The result follows from Remark 11.2 and Theorem 11.2. □

II. Case α ₁>1=α ₂.

Theorem 11.7

Let α ₁>1=α ₂. Suppose that for some ε>0 there exists a nonoscillatory solution of the linear equation

$$ \dot{x}(t)=-\varepsilon r_1(t)x\bigl(h_1(t)\bigr)- r_2(t)x\bigl(h_2(t)\bigr) .$$

(11.2.20)

Then there exists a nonoscillatory solution of (11.2.17).

Proof

The proof is similar to the proof of Theorem 11.4. □

Corollary 11.6

Let α ₁>1=α ₂. If

$$\limsup_{t\rightarrow\infty} \int_{\min\{h_1(t),h_2(t)\}}^tr_1(s)ds <\infty\mbox{ \textit{and} } \limsup_{t\rightarrow\infty} \int _{\min\{h_1(t),h_2(t)\}}^t r_2(s)ds<\frac{1}{e},$$

then there exists a nonoscillatory solution of (11.2.17).

Proof

The proof follows from Corollary 11.4 for the case m=2. □

III. Case α ₁>1>α ₂.

Theorem 11.8

Let α ₁>1>α ₂. Suppose there exists a nonoscillatory solution of (11.2.17) with α ₁=1>α ₂. Then there exists a nonoscillatory solution of (11.2.17) with α ₁>1>α ₂.

Proof

As in the proof of Theorem 11.1 (see also Remark 11.1), there exist t ₀, c and φ satisfying t ₀≥0, −1<c<0, −1<φ(t)≤0 such that (11.2.1), (11.2.3) with m=2, α ₁=1>α ₂ has a negative solution x ₀(t). Denote $w_{0}(t)=-\frac{\dot{x_{0}}(t)}{x_{0}(t)}$. Then w ₀(t)≥0 and $x_{0}(t)=c\exp\{-\int_{t_{0}}^{t} w_{0}(s)ds\}$, t≥t ₀, where c=x ₀(t ₀).

By substituting x ₀ into (11.2.1) with α ₁=1>α ₂, we have

where α ₁=1. Then, for α ₁>1>α ₂, we have

where the sum contains only such terms for which h _k (t)≥t ₀. Let v ₀(t)≡0 and consider the two sequences

and

Then, as in the proof of Theorem 11.5, we obtain

$$0\leq w_n(t)\leq w_{n-1}(t)\leq\cdots\leq w_0(t),\ v_n(t)\geq v_{n-1}(t)\geq\cdots\geq v_0(t)= 0,$$

and w _n (t)≥v _n (t). Then there exist w(t)=lim _n→∞ w _n (t) and v(t)=lim _n→∞ v _n (t). Hence by the Schauder Fixed-Point Theorem there is u satisfying v≤u≤w, which is a solution of the equation

Then

$$x(t)= \left\{ \begin{array}{ll} c\exp\{-\int_{t_0}^t u(s)ds\}, & t\geq t_0,\\\noalign{\vspace{3pt}}0, & t<t_0,\end{array} \right .$$

is a negative solution of (11.2.17), (11.2.3) with x(t ₀)=c, φ≡0, which completes the proof. □

Corollary 11.7

Let α ₁>1>α ₂. If

$$\int_0^{\infty} r_k(s)ds<\infty,\ k=1,2,$$

then there exists a nonoscillatory solution of (11.2.17).

11.2.5 Generalized Logistic Equation—Main Results

The main purpose of this section is to study oscillation of the generalized logistic equation about the unique positive equilibrium.

Consider

$$ \dot{y}(t)= \sum_{k=1}^mr_k(t)y(t) \biggl( 1-\frac{y(h_k(t))}{K} \biggr) \biggl \vert 1-\frac{y(h_k(t))}{K} \biggr \vert ^{\alpha_k-1},$$

(11.2.21)

where r _k , h _k , α _k satisfy conditions (a1) and (a2), K>0 and the initial function ψ satisfies (a3) with the initial condition

$$ y(t)=\psi(t) ,\ t< t_0,\ y(t_0)=y_0.$$

(11.2.22)

In this section we assume that the initial conditions satisfy

• (a4) y ₀>0, ψ(t)≥0, t<t ₀.

By Theorem B.17, there exists a unique positive solution of problem (11.2.21), (11.2.22).

Definition 11.2

A positive solution y of (11.2.21) is said to be oscillatory about K if there exists a sequence t _n , t _n →∞ such that y(t _n )−K=0, n=1,2,⋯ ; y is nonoscillatory about K if there exists T≥t ₀ such that |y(t)−K|>0 for t≥T. A solution y is eventually positive (eventually negative) about K if y−K is eventually positive (eventually negative).

Suppose y is a positive solution of (11.2.21), and define x as $x=\frac{y}{K}-1$. Then x is a solution of (11.2.1) such that 1+x>0.

Hence oscillation (or nonoscillation) of y about K is equivalent to oscillation (nonoscillation) of x.

By applying Theorems 11.1–11.8, we obtain the following results for (11.2.21).

Theorem 11.9

Let α _k <1, k=1,⋯,m. There exists a solution of (11.2.21) nonoscillatory about K if and only if

$$\int_0^{\infty} r_k(t) dt <\infty,\ k=1,\cdots,m.$$

Theorem 11.10

Let α _k >1, k=1,⋯,m.

If

$$\limsup_{t\rightarrow\infty} \int_{\min_k\{h_k(t)\}}^t\sum _{i=1}^m r_i(s)ds<\infty,$$

then (11.2.21) has a solution nonoscillatory about K.

Remark 11.3

If m=1 and the parameters of (11.2.21) are continuous functions, then the results of Theorems 11.9 and 11.10 were first obtained in [12, 237].

Theorem 11.11

Let m=2, α ₁<1=α ₂. If either

$$\int_0^{\infty} r_1(s)ds =\infty $$

or

$$\liminf_{t\rightarrow\infty} \int_{h_2(t)}^tr_2(s)ds>\frac{1}{e} ,$$

then all solutions of (11.2.21) are oscillatory about K.

If

$$\int_0^{\infty} r_k(s)ds <\infty,\ k=1,2,$$

then there exists a solution of (11.2.21) nonoscillatory about K.

Theorem 11.12

Let m=2, α ₁>1=α ₂.

If

$$\limsup_{t\rightarrow\infty} \int_{\min\{h_1(t),h_2(t)\}}^tr_1(s)ds <\infty,\ \limsup_{t\rightarrow\infty} \int _{\min\{h_1(t),h_2(t)\}}^t r_2(s)ds<\frac{1}{e} ,$$

then there exists a solution of (11.2.21) nonoscillatory about K.

Theorem 11.13

Let m=2, α ₁>1>α ₂.

If

$$\int_0^{\infty} r_k(s)ds <\infty,\ k=1,2,$$

then there exists a solution of (11.2.21) nonoscillatory about K.

11.3 Multiplicative Delay Logistic Equation

11.3.1 Preliminaries

In this section, the scalar multiplicative delay differential equation

$$ \dot{x}(t)=-r(t) \bigl(1+x(t)\bigr)\prod _{k=1}^m x\bigl(h_k(t)\bigr)\bigl|x\bigl(h_k(t)\bigr)\bigr|^{\alpha_k-1} ,\ t\geq0,$$

(11.3.1)

is considered under the following assumptions:

• (b1) r is a Lebesgue measurable locally essentially bounded function, r(t)≥0;

• (b2) h _k :[0,∞)→ℝ are Lebesgue measurable functions, h _k (t)≤t, lim _t→∞ h _k (t)=∞, k=1,⋯,m, α _k >0, k=1,2,⋯,m, are real numbers and $\sum_{k=1}^{m}\alpha_{k}=1$.

Equation (11.3.1) is obtained from the multiplicative delay logistic equation

$$ \dot{y}(t)= r(t)y(t)\prod_{k=1}^m\biggl( 1-\frac{y(h_k(t))}{K} \biggr) \biggl \vert 1-\frac{y(h_k(t))}{K} \biggr \vert ^{\alpha_k-1}$$

(11.3.2)

by the substitution y(t)=1+x(t). Let us note that all solutions of (11.3.2) with positive initial conditions are positive by Theorem B.17, so x(t)>−1 as far as the initial values satisfy the inequalities

$$x(t) \geq-1,\ t \leq t_0,\ x(t_0)>-1.$$

Together with (11.3.1), we consider for each t ₀≥0 the initial value problem

$$ \dot{x}(t)=-r(t) \bigl(1+x(t)\bigr)\prod _{k=1}^m x\bigl(h_k(t)\bigr)\bigl|x\bigl(h_k(t)\bigr)\bigr|^{\alpha_k-1},\ t\geq t_0,$$

(11.3.3)

$$ x(t)=\varphi(t),\ t<t_0,\ x(t_0)=x_0.$$

(11.3.4)

We also assume that the following hypothesis holds:

• (b3) φ:(−∞,t ₀)→ℝ is a Borel measurable bounded function.

Definition 11.3

A function x:ℝ→ℝ absolutely continuous in each interval [t ₀,b] is called a solution of problem (11.3.3), (11.3.4) if it satisfies (11.3.3) for almost all t∈[t ₀,∞) and equalities (11.3.4) for t≤t ₀.

11.3.2 Nonoscillation Criteria

Together with (11.3.1), consider the differential inequalities

$$ \dot{x}(t)\leq-r(t) \bigl(1+x(t)\bigr)\prod _{k=1}^m x\bigl(h_k(t)\bigr)\bigl|x\bigl(h_k(t)\bigr)\bigr|^{\alpha _k -1} ,\ t\geq0,$$

(11.3.5)

$$ \dot{x}(t)\geq-r(t) \bigl(1+x(t)\bigr)\prod _{k=1}^m x\bigl(h_k(t)\bigr)\bigl|x\bigl(h_k(t)\bigr)\bigr|^{\alpha_k -1} ,\ t\geq0.$$

(11.3.6)

In this section, we assume that (b1)–(b3) hold and consider only such solutions of (11.3.1), (11.3.5) and (11.3.6) for which the following condition holds:

$$ 1+x(t)>0.$$

(11.3.7)

Theorem 11.14

The following statements are equivalent:

• 1. Either inequality (11.3.5) has an eventually positive solution or inequality (11.3.6) has an eventually negative solution.

• 2. There exist t ₀≥0, −∞<c<∞, φ:(−∞,t ₀)→ℝ, either φ(t)≥0, c>0, or φ(t)≤0, −1<c<0, such that the inequality

  $$ u(t)\geq r(t) \biggl( 1+c\exp \biggl\{-\int_{t_0}^tu(s)ds \biggr\} \biggr)\prod_{k=1}^m (F_ku) (t)$$

  (11.3.8)

  has a nonnegative locally integrable solution on [t ₀,∞), where

  $$(F_ku) (t)= \left\{ \begin{array}{ll}{\exp \{\alpha_k\int_{h_k(t)}^t u(s)ds \} },&h_k(t)\geq t_0,\\\noalign{\vspace{3pt}}{\frac{1}{|c|^{\alpha_k}}\exp \{\alpha_k\int_{t_0}^tu(s)ds\}{|\varphi(h_k(t))|}^{\alpha_k} }, &h_k(t)<t_0,\end{array} \right .$$

• 3. Equation (11.3.1) has a nonoscillatory solution.

Proof

1)⇒2) Let x be a solution of (11.3.5) and x(t)>0 for t≥t ₁. Then there exists t ₀≥t ₁ such that h _k (t)≥t ₁ for t≥t ₀, k=1,⋯,m. Denote φ(t)=x(t), t<t ₀ and c=x(t ₀), c>0.

Let $u(t)=-\frac{\dot{x}(t)}{x(t)}$, t≥t ₀. For the solution x(t) of (11.3.5), we have $\dot{x}(t)\leq 0$, t≥t ₀, and consequently u(t)≥0. The solution x(t) can be rewritten in the form

$$ x(t) = \left\{ \begin{array}{ll}c\exp\{-\int_{t_0}^t u(s)ds \}, & t\geq t_0,\\\noalign{\vspace{3pt}}\varphi(t), & t<t_0.\end{array} \right .$$

(11.3.9)

After substituting x defined by (11.3.9) into inequality (11.3.5), we obtain (11.3.8).

Similarly, (11.3.8) can be obtained if x(t)<0 is a solution of (11.3.6).

2)⇒3) Let u ₀ be a nonnegative solution of inequality (11.3.8) with φ(t)≤0, −1<c<0. For the sequence {u _n } denoted by

$$ u_{n}(t)=r(t) \biggl( 1+c\exp \biggl\{ -\int _{t_0}^t u_{n-1}(s)ds \biggr\} \biggr)\prod_{k=1}^m (F_ku_{n-1})(t),$$

(11.3.10)

inequality (11.3.8) implies 0≤u ₁(t)≤u ₀(t). Since the right-hand side in (11.3.8) is a nondecreasing operator in u, the inequalities

$$0\leq u_{n} (t) \leq u_{n-1}(t)\leq u_0(t)$$

can be easily obtained by induction.

Thus there exists a pointwise limit of the nonincreasing nonnegative sequence u _n (t). Let u(t)=lim _n→∞ u _n (t). By the Lebesgue monotone convergence theorem, u(t) is locally integrable and

$$\lim_{n\rightarrow\infty} ( F_ku_n ) (t) =(F_ku) (t),\ k=1,\cdots,m.$$

Thus (11.3.10) implies

$$u(t)= r(t) \biggl( 1+c\exp \biggl\{ -\int_{t_0}^tu(s)ds \biggr\} \biggr)\prod_{k=1}^m (F_ku) (t),$$

and hence the function x defined by equality (11.3.9) is an eventually negative solution of (11.3.1).

The case where u ₀ is a nonnegative solution of inequality (11.3.8) with φ(t)≥0, c>0, is considered similarly to the proof of Theorem 11.1.

Implication 3)⇒1) is evident. □

The proof of Theorem 11.14 yields the following statement.

Corollary 11.8

If there exists an eventually positive solution of (11.3.1), then there exists an eventually negative solution of (11.3.1).

Theorem 11.15

If there exists a nonoscillatory solution of the linear equation

$$ \dot{x}(t)+r(t)\sum_{k=1}^mx\bigl(h_k(t)\bigr)=0,$$

(11.3.11)

then there is a nonoscillatory solution of (11.3.1).

Proof

Suppose that linear equation (11.3.11) has a nonoscillatory solution. Theorem 2.1 implies that for some t ₀≥0 there exists a solution u(t), nonnegative locally integrable on t≥t ₀, of the inequality

$$u(t)\geq r(t)\exp \Biggl\{ \sum_{k=1}^m\int_{h_k(t)}^t u(s)ds \Biggr\},\ t \geq t_0,$$

and hence

$$ u(t)\geq r(t)\exp \Biggl\{ \sum_{k=1}^m\alpha_k\int_{h_k(t)}^t u(s)ds \Biggr \},\ t \geq t_0,$$

(11.3.12)

where the sum contains only terms for which h _k (t)≥t ₀.

Then u is also a solution of the inequality

$$u(t)\geq r(t) \biggl( 1+c\exp \biggl\{-\int_{t_0}^tu(s)ds \biggr\} \biggr) \prod_{k=1}^m \exp \biggl\{\alpha_k\int_{h_k(t)}^t u(s)ds\biggr\}$$

for any −1<c<0. The implication 2)⇒3) in Theorem 11.14 implies the statement of the theorem if we assume φ≡0. □

Corollary 11.9

If

$$\limsup_{t\rightarrow\infty} \int_{\min_{ k} h_k(t)}^t r(s)ds <\frac{1}{e},$$

then (11.3.1) has a nonoscillatory solution.

Proof

The proof follows from Theorems 11.15 and 2.7. □

Theorem 11.16

If for some ε>0 all solutions of the linear equation

$$ \dot{x}(t)+(1-\varepsilon)r(t)\sum_{k=1}^m\alpha_k x\bigl(h_k(t)\bigr)=0$$

(11.3.13)

are oscillatory, then all solutions of (11.3.1) are also oscillatory.

Proof

If there exists a nonoscillatory solution of (11.3.1), then for some t ₀ by Theorem 11.14 there is a nonnegative solution u of inequality (11.3.8) for c>−1. We can assume that φ≡0. There exists t ₁≥t ₀ such that h _k (t)≥t ₀, t≥t ₁, k=1,⋯,m.

We have u(t)≥min{1,1+c}r(t), t≥t ₁. Let $\int_{0}^{\infty} r(s)ds <\infty$. Then, by Corollary 2.6, (11.3.1) has a nonoscillatory solution, which contradicts the theorem assumption.

Thus $\int_{0}^{\infty} r(s)ds =\infty$, and so $\int_{0}^{\infty} u(s)ds=\infty$. Hence there exist t ₂≥t ₀ and ε>0 such that

$$1+c\exp \biggl\{ -\int_{t_0}^t u(s)ds \biggr\}>1-\varepsilon,\ t\geq t_2,$$

which implies

$$u(t)\geq(1-\varepsilon)r(t)\sum_{k=1}^m\exp \biggl\{\alpha_k \int_{h_k(t)}^tu(s) ds \biggr\},\ t\geq t_2.$$

Theorem 2.1 yields that (11.3.13) has a nonoscillatory solution, which leads to a contradiction. □

Corollary 11.10

If

$$\liminf_{t\rightarrow\infty} \int_{\max_{ k}h_k(t)}^t r(s)ds >\frac{1}{e},$$

then all solutions of (11.3.1) are oscillatory.

11.3.3 Multiplicative Logistic Equation—Main Results

In this section, we consider the equation

$$ \dot{y}(t)= r(t)y(t)\prod_{k=1}^m\biggl( 1-\frac{y(h_k(t))}{K} \biggr) \biggl \vert 1-\frac{y(h_k(t))}{K} \biggr \vert ^{\alpha_k-1}$$

(11.3.14)

with the unique positive equilibrium K and also the differential inequalities

$$ \dot{y}(t)\geq r(t)y(t)\prod_{k=1}^m\biggl( 1-\frac{y(h_k(t))}{K} \biggr) \biggl \vert 1-\frac{y(h_k(t))}{K} \biggr \vert ^{\alpha_k-1},$$

(11.3.15)

$$ \dot{y}(t)\leq r(t)y(t)\prod_{k=1}^m\biggl( 1-\frac{y(h_k(t))}{K} \biggr) \biggl \vert 1-\frac{y(h_k(t))}{K} \biggr \vert ^{\alpha_k-1},$$

(11.3.16)

where r _k , h _k , α _k satisfy conditions (b1) and (b2), K>0. Equation (11.3.14) will be considered with the initial condition

$$ y(t)=\psi(t) ,\ t< t_0,\ y(t_0)=y_0,$$

(11.3.17)

where the initial function ψ satisfies (b3).

In this section, we assume that an additional condition,

• (b4) y ₀>0, ψ(t)≥0, t<t ₀,

holds. By Theorem B.17, there exists a unique positive solution of (11.3.14), (11.3.17).

Definition 11.4

A positive solution y of (11.3.14), (11.3.17) is oscillatory about K if there exists a sequence t _n , t _n →∞, such that y(t _n )−K=0, n=1,2,⋯ ; y is nonoscillatory about K if there exists T≥t ₀ such that |y(t)−K|>0 for t≥T.

Let y be a positive solution of (11.3.14) and define x as $x=\frac{y}{K}-1$. Then x is a solution of (11.3.1) such that 1+x>0. Hence oscillation (or nonoscillation) of y about K is equivalent to oscillation (nonoscillation) of x.

The same equivalence connects the pairs of differential inequalities (11.3.5), (11.3.15) and (11.3.6), (11.3.16), respectively.

By applying Theorems 11.14–11.16, we obtain the following results for (11.3.14).

Theorem 11.17

The following statements are equivalent:

• 1. Either inequality (11.3.15) has a solution eventually greater than K or inequality (11.3.16) has a solution eventually less than K.

• 2. There exist t ₀≥0, φ:(−∞,t ₀)→ℝ, either φ(t)≥0, c>0 or φ(t)≤0, 1<c<0, such that inequality (11.3.8) has a nonnegative solution locally integrable on [t ₀,∞).

• 3. Equation (11.3.14) has a solution nonoscillatory about K.

Corollary 11.11

Suppose that for functions p(t) and g _k (t) conditions (b1) and (b2) hold.

If p(t)≤r(t), g _k (t)≥h _k (t) and (11.3.14) has a solution nonoscillatory about K, then the equation

$$ \dot{y}(t)= p(t)y(t)\prod_{k=1}^m\biggl( 1-\frac{y(g_k(t))}{K} \biggr) \biggl \vert 1-\frac{y(g_k(t))}{K} \biggr \vert ^{\alpha_k-1}$$

(11.3.18)

has a solution nonoscillatory about K.

If p(t)≥r(t), g _k (t)≤h _k (t) and all solutions of (11.3.14) are oscillatory about K, then all the solutions of (11.3.18) are also oscillatory about K.

Proof

Let p(t)≤r(t), g _k (t)≥h _k (t), and suppose that (11.3.14) has a solution nonoscillatory about K. Theorem 11.14 implies that inequality (11.3.8) has a nonnegative solution u, and u is also a nonnegative solution of the inequality (11.3.8), where r and h _k are replaced by p and g _k , respectively. Hence, again by Theorem 11.14, (11.3.18) has a nonoscillatory solution.

The second assertion of the theorem is a consequence of the first one. □

Theorem 11.18

If there exists a nonoscillatory solution of linear equation (11.3.11), then there exists a solution of (11.3.14) nonoscillatory about K.

Corollary 11.12

If

$$\limsup_{t\rightarrow\infty} \int_{\min_{ k} h_k(t)}^t r(s)ds <\frac{1}{e} ,$$

then (11.3.14) has a solution nonoscillatory about K.

Theorem 11.19

If for some ε>0 all solutions of linear equation (11.3.13) are oscillatory, then all solutions of (11.3.14) are oscillatory about K.

Corollary 11.13

If

$$\liminf_{t\rightarrow\infty} \int_{\max_{ k}h_k(t)}^t r(s)ds >\frac{1}{e},$$

then all the solutions of (11.3.14) are oscillatory about K.

11.4 Discussion and Open Problems

All the results of this chapter are obtained under the assumption that coefficients, delays and initial functions are arbitrarily measurable, and not necessarily continuous, functions. It is important to avoid a usual constraint that the parameters are continuous since in many interesting applications they are not continuous. In addition, in [193] the authors proved that oscillation properties of a difference equation can be derived from oscillation properties of some delay differential equation with discontinuous delays. In Chap. 12, it will be shown that we can study oscillation of nonimpulsive delay equations with discontinuous coefficients rather than oscillation of an impulsive delay equation. We also note here the paper [175], where the parameters of the logistic equation were not assumed to be continuous functions.

Some other nonoscillation results for nonlinear delay differential equations can be found in [294]. The results of this chapter were published in the papers [47, 49].

Finally, let us present some open problems and topics for research and discussion.

• 1. Find necessary and/or sufficient oscillation conditions for (11.1.3) in the case where all or some of α _k >1.

• 2. Prove or disprove the inverse statement to Corollary 11.2: existence of an eventually negative solution implies existence of an eventually positive solution.

• 3. Consider the following generalizations of the logistic equation with concentrated delays:

  • the integrodifferential equations

    $$\dot{y}(t)=y(t)\sum_{k=1}^m \int _{h_k(t)}^t M_k(t,s) \biggl( 1-\frac{y(s)}{K} \biggr) \biggl \vert 1-\frac{y(s)}{K} \biggr \vert ^{\alpha_k-1}ds;$$

  • equations of a mixed type containing terms with a concentrated delay and also integral terms;

  • the equations with a distributed delay

    $$\dot{y}(t)=y(t)\sum_{k=1}^m \int _{-\infty}^t \biggl( 1-\frac{y(s)}{K} \biggr)\biggl \vert 1-\frac{y(s)}{K} \biggr \vert ^{\alpha_k-1}d_sR_k(t,s).$$

• 4. Consider the following multiplicative delay logistic equations:

  • the integrodifferential equations

    $$\dot{y}(t)= y(t)\int_{-\infty}^t\prod _{k=1}^m L_k(t,s) \biggl( 1-\frac {y(s)}{K} \biggr) \biggl \vert 1-\frac{y(s)}{K} \biggr \vert ^{\alpha_k-1}ds,$$
    $$\dot{y}(t)= y(t)\prod_{k=1}^m\int _{h_k(t)}^t L_k(t,s) \biggl( 1-\frac {y(s)}{K} \biggr) \biggl \vert 1-\frac{y(s)}{K} \biggr \vert ^{\alpha_k-1}ds;$$

  • equations of a mixed type containing concentrated delay terms and integral terms;

  • the equations with a distributed delay

    $$\dot{y}(t)= y(t)\int_{-\infty}^t\prod _{k=1}^m \biggl( 1-\frac{y(s)}{K} \biggr) \biggl \vert 1-\frac{y(s)}{K} \biggr \vert ^{\alpha_k-1}d_sR_k(t,s),$$
    $$\dot{y}(t)= y(t)\prod_{k=1}^m\int _{h_k(t)}^t \biggl( 1-\frac{y(s)}{K} \biggr)\biggl \vert 1-\frac{y(s)}{K} \biggr \vert ^{\alpha_k-1}d_sR_k(t,s).$$

• 5. Prove or disprove:

  If r _k (t)≥r ₀>0, then any solution of (11.2.21) nonoscillatory about K tends to K.

• 6. Prove or disprove:

  If r _k (t)≥r ₀>0, then any solution of (11.3.14) nonoscillatory about K tends to K.

• 7. Consider oscillation and nonoscillation properties of (11.2.21) with positive and negative coefficients r _k (t) and with oscillatory coefficients.

• 8. Consider oscillation and nonoscillation properties of (11.3.14) without the assumption that $\sum_{k=1}^{m} \alpha_{k} =1$.