Abstract
The basics of kernel methods and their position in the generalized data-driven fault diagnostic framework are reviewed. The review starts out with statistical learning theory, covering concepts such as loss functions, overfitting and structural and empirical risk minimization. This is followed by linear margin classifiers, kernels and support vector machines. Transductive support vector machines are discussed and illustrated by way of an example related to multivariate image analysis of coal particles on conveyor belts. Finally, unsupervised kernel methods, such as kernel principal component analysis, are considered in detail, analogous to the application of linear principal component analysis in multivariate statistical process control. Fault diagnosis in a simulated nonlinear system by the use of kernel principal component analysis is included as an example to illustrate the concepts.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
As long as the data points are not situated exactly on a linear hyperplane.
- 2.
The general formulation of constrained optimization problems states the inequality constraints as less than or equal to zero. For ease of visualization and generalization to SVM, inequality constraints are stated here as larger than or equal to zero, without loss of generality.
- 3.
For the progression of the ridge regression explanation, the general statistical nomenclature of x for independent variables and y for dependent variables will be used. KPCA reconstruction by learning has the input space
 as output, and the KPCA feature space
as output, and the KPCA feature space 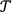 as input. The KPCA nomenclature will be returned to once the ridge regression explanation is completed.
as input. The KPCA nomenclature will be returned to once the ridge regression explanation is completed.
References
Belousov, A. I., Verzakov, S. A., & von Frese, J. (2002). Applicational aspects of support vector machines. Journal of Chemometrics, 16(8–10), 482–489.
Berk, R. A. (2008). Statistical learning from a regression perspective (1st ed.). New York: Springer.
Boser, B. E., Guyon, I. M., & Vapnik, V. N. (1992). A training algorithm for optimal margin classifiers. In Proceedings of the fifth annual workshop on Computational Learning Theory – COLT’92. The 5th annual workshop (pp. 144–152), Pittsburgh, PA, USA. Available at: http://portal.acm.org/citation.cfm?doid=130385.130401. Accessed 27 May 2011.
Boyd, S., & Vandenberghe, L. (2004). Convex optimization. Cambridge/New York: Cambridge University Press.
Burges, C. J. C. (1998). A tutorial on support vector machines for pattern recognition. Data Mining and Knowledge Discovery, 2(2), 121–167.
Chapelle, O., & Zien, A. (2005). Semi-supervised classification by low-density separation. In Proceedings of the 10th international workshop on Artificial Intelligence and Statistics (pp. 57–64).
Cortes, C., & Vapnik, V. (1995). Support vector networks. Machine Learning, 20(3), 273–297.
Cover, T. M. (1965). Geometrical and statistical properties of systems of linear inequalities with applications in pattern recognition. IEEE Transactions on Electronic Computers, EC-14(3), 326–334.
Dong, D., & McAvoy, T. J. (1992). Nonlinear principal component analysis – Based on principal curves and neural networks. Computers and Chemical Engineering, 16, 313–328.
Fisher, R. A. (1936). The use of multiple measurements in taxonomic problems. Annals of Eugenics, 7, 179–188.
Franc, V., Schlesinger, M. I., & Hlavac, V. (2008). Statistical pattern recognition toolbox for Matlab. Available at: http://cmp.felk.cvut.cz/cmp/software/stprtool/. Accessed 12 Dec 2011.
Hastie, T., & Stuetzle, W. (1989). Principal curves. Journal of the American Statistical Association, 84, 502–516.
Hotelling, H. (1933). Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology, 24(6), 417–441. Available at: Accessed 13 Apr 2011.
Hsieh, W. (2009). Machine learning methods in the environmental sciences: Neural networks and kernels. Cambridge/New York: Cambridge University Press.
Jemwa, G. T., & Aldrich, C. (2006). Kernel-based fault diagnosis on mineral processing plants. Minerals Engineering, 19(11), 1149–1162.
Jemwa, G. T., & Aldrich, C. (2012). Estimating size fraction categories of coal particles on conveyor belts using image texture modelling methods. Expert Systems with Applications, 39(9), 7947–7960.
Kaartinen, J., Hätönen, J., Hyötyniemi, H., & Miettunen, J. (2006). Machine-visionbasedcontrol of zinc flotation – A case study. Control Engineering Practice, 14, 1455–1466.
Kwok, J. T.-Y., & Tsang, I. W.-H. (2004). The pre-image problem in kernel methods. IEEE Transactions on Neural Networks, 15(6), 1517–1525. Available at: Accessed 19 Aug 2011.
Mika, S., Schölkopf, B., Smola, A., Müller, K.-R., Scholz, M., & Rätsch, G. (1999). Kernel PCA and de-noising in feature spaces. In Advances in neural information processing systems 11 (pp. 536–542). Cambridge: MIT Press.
Moolman, D. W., Aldrich, C., van Deventer, J. S. J., & Stange, W. W. (1995). The classification offroth structures in a copper flotation plant by means of a neural net. International Journal of Mineral Processing, 43, 23–30.
Müller, K.-R., Mika, S., Ratsch, G., Tsuda, K., & Scholkopf, B. (2001). An introduction to kernel-based learning algorithms. IEEE Transactions on Neural Networks, 12(2), 181–201.
Schölkopf, B., & Smola, A. J. (2001). Learning with kernels: Support vector machines, regularization, optimization, and beyond (1st ed.). Cambridge: MIT Press.
Schölkopf, B., Smola, A., & Müller, K.-R. (1998). Nonlinear component analysis as a kernel eigenvalue problem. Neural Computation, 10(5), 1299–1319.
Schölkopf, B., Mika, S., Burges, C. J. C., Knirsch, P., Muller, K.-R., Ratsch, G., & Smola, A. J. (1999). Input space versus feature space in kernel-based methods. IEEE Transactions on Neural Networks, 10(5), 1000–1017. Available at: Accessed 19 Aug 2011.
Schölkopf, B., Platt, J. C., Shawe-Taylor, J., Smola, A. J., & Williamson, R. C. (2001). Estimating the support of a high-dimensional distribution. Neural Computation, 13(7), 1443–1471. Available at: Accessed 30 May 2011.
Shawe-Taylor, J., & Cristianini, N. (2004). Kernel methods for pattern analysis. Cambridge: Cambridge University Press.
Smola, A. J., & Schölkopf, B. (2000). Sparse greedy matrix approximation for machine learning. In Proceedings of the seventeenth International Conference on Machine Learning. ICML’00 (pp. 911–918). San Francisco: Morgan Kaufmann Publishers Inc.. Available at: http://dl.acm.org/citation.cfm?id=645529.657980.
Smola, A. J., & Schölkopf, B. (2004). A tutorial on support vector regression. Statistics and Computing, 14(3), 199–222. Available at: Accessed 30 May 2011.
Smola, A. J., Mangasarian, O. L., & Schölkopf, B. (1999). Sparse kernel feature analysis. Madison: Data Mining Institute.
Tessier, J., Duchesne, C., & Bartolacci, G. (2007). A machine vision approach to on-line estimation of run-of-mine ore composition on conveyor belts. Minerals Engineering, 20(12), 1129–1144.
Tipping, M. (2001). Sparse kernel principal component analysis. In T. K. Leen, T. G. Dietterich, & V. Tresp (Eds.), Advances in neural information processing systems (Neural Information Processing Systems 13 (NIPS 2000), pp. 633–639). Cambridge, MA: MIT Press.
Vapnik, V. (2006). Transductive inference and semi-supervisedlearning. In O. Chapelle, B. Schölkopf, & A. Zien (Eds.), Semi-supervised learning (pp. 453–472). Cambridge, MA: MIT Press.
Author information
Authors and Affiliations
Nomenclature
Nomenclature
Symbol | Description |
|---|---|
\( \tilde{\mathrm{x}} \) | Point satisfying all inequality constraints of an optimization problem |
\( {K_{ij }} \) | Element of Gram matrix in ith row and jth column |
\( {N_{SV }} \) | Number of support vectors in a training data set |
\( {R_e}(f) \) | Empirical risk of overfitting function f |
\( {f_0}(\mathbf{x}) \) | Objective function in an optimization problem |
\( {f_0}(\tilde{\mathbf{x}} ) \) | Objective function value at point where all inequality constraints of optimization problem are satisfied |
\( f_0^{*} \) | Optimal value of objective function |
\( {m_G}(\mathbf{x},y) \) | Geometrical margin, i.e. the distance of a point x with associated label y from a separating hyperplane defined by parameters w and b |
\( {\xi_i} \) | ith slack variable of an optimization problem |
C p * | Optimal parameter in a kernel function |
C q | Parameter in a kernel function |
D | Diameter of sphere enclosing a set of (training) data |
D s | Diameter of smallest sphere enclosing a set of (training) data |
\( \mathcal{F} \) | Function space, class of functions |
f* | Function associated with lowest risk bound |
h | Capacity parameter of a model, such as VC dimension |
\( \mathcal{H} \) | Feature space |
K | Gram matrix |
L(y, f(x)) | Loss function |
M | Dimensionality of input space |
m | Margin or shortest distance between two separating hyperplanes |
P(x, y) | Joint probability distribution between x and y |
Q | Arbitrary number of parameters |
δ | Confidence |
ξ | Vector of slack variables |
ρ | Bias defining location of a hyperplane |
σ | Width of Gaussian kernel |
\( \varPhi (\mathbf{x}) \) | Mapping function from space |
C | Covariance matrix of mean-centred data matrix X |
v | Arbitrary vector |
\( L(\tilde{\mathbf{x}}, \propto ) \) | Lagrangian function value at point where all inequality constraints of optimization problem are satisfied |
\( L(\mathbf{x},\propto ) \) | Lagrangian function |
N | Number of samples in a training data set |
R(f) | Risk of overfitting function f |
C(h, N, δ) | Capacity of a model |
\( g(\propto ) \) | Lagrangian dual function |
\( k(\mathbf{x},{\mathbf{x}}^{\prime}) \) | Kernel function |
\( m(\mathbf{w},b) \) | Margin of a separating hyperplane |
| Principal component score space |
| Vector space of x |
∝ | Vector of Lagrangian multipliers |
θ | Angle |
κ | Sigmoidal kernel parameter |
v | Parameter in the optimization of a soft margin classifier |
ρ | Parameter in the optimization of a soft margin classifier |
\( \vartheta \) | Sigmoidal kernel parameter |
Rights and permissions
Copyright information
© 2013 Springer-Verlag London
About this chapter
Cite this chapter
Aldrich, C., Auret, L. (2013). Statistical Learning Theory and Kernel-Based Methods. In: Unsupervised Process Monitoring and Fault Diagnosis with Machine Learning Methods. Advances in Computer Vision and Pattern Recognition. Springer, London. https://doi.org/10.1007/978-1-4471-5185-2_4
Download citation
DOI: https://doi.org/10.1007/978-1-4471-5185-2_4
Published:
Publisher Name: Springer, London
Print ISBN: 978-1-4471-5184-5
Online ISBN: 978-1-4471-5185-2
eBook Packages: Computer ScienceComputer Science (R0)


 as output, and the KPCA feature space
as output, and the KPCA feature space 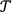 as input. The KPCA nomenclature will be returned to once the ridge regression explanation is completed.
as input. The KPCA nomenclature will be returned to once the ridge regression explanation is completed.