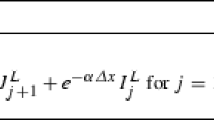Abstract
A new method, “wave confinement” (WC), is developed to efficiently solve the scalar wave equation on a discretized domain. This method is similar to the originally developed method, “vorticity confinement,” which is used to solve a vast range of fluid dynamics problems [StWePu95]. WC involves modifying the discretized wave equation by adding a nonlinear term to generate traveling “dissipative solitary” waves that are stable to perturbations due to numerical effects, such as dissipation and dispersion. As the present study involves treating thin waves propagating long distances, on feasible computational grids, the propagating functions cannot be more than 2–3 cells wide. In these cases, since the accuracy of conventional higher-order schemes increases only as the number of points across the pulse becomes relatively large, they are not useful. Often, for these cases, the main quantities of interest in the far field are the integrated amplitude and the motion of the centroid surfaces (which we use to represent wave fronts), rather than the details of the internal structure of the pulse. For realistic problems, these pulse surfaces can have multiple sources and scattering surfaces, propagate through regions with a varying refraction index, and have complex topology. Accordingly, we only consider Eulerian methods, where such general surface topologies can automatically be treated with no need for complex “surface fitting” or adaptive grids.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Cahn, J.W., Hilliard, J.E.: Free energy of a nonuniform system. J. Chemical Phys., 28, 258–267 (1983).
Lax, P.: Hyperbolic systems of conservation laws. II. Comm. Pure Appl. Math., 10, 537–566 (1958).
Rosenau, P., Hyman, M.J., Stanley, M.: Multidimensional compactons. Phys. Review Lett., 98, article 24101 (2007).
Smolarkiewicz, P.A.: A simple positive definite advection scheme with small implicit diffusion. Monthly Weather Revue, 111, 479–486 (1983).
Steinhoff, J., Wenren, Y., Puskas, E.: Computation of short acoustic pulses, in Proceedings Sixth Internat. Symp. CFD, (1995).
Steinhoff, J., Dietz, W., Haas, S., Xiao, M., Lynn, N., Fan, M.: Simulating small scale features in fluid dynamics and acoustics as nonlinear solitary waves. AIAA, 2003–0078 (2003).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2010 Birkhäuser Boston
About this chapter
Cite this chapter
Steinhoff, J., Chitta, S. (2010). Long-Time Solution of the Wave Equation Using Nonlinear Dissipative Structures. In: Constanda, C., Pérez, M. (eds) Integral Methods in Science and Engineering, Volume 2. Birkhäuser Boston. https://doi.org/10.1007/978-0-8176-4897-8_32
Download citation
DOI: https://doi.org/10.1007/978-0-8176-4897-8_32
Published:
Publisher Name: Birkhäuser Boston
Print ISBN: 978-0-8176-4896-1
Online ISBN: 978-0-8176-4897-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)