Abstract
In the spring of 1880, not long before leaving for Europe on scientific business for the United States Coast and Geodetic Survey, Charles Peirce sent a paper entitled “On the Algebra of Logic” to The American Journal of Mathematics 1 (hereafter referred to as AJM-1880; I will similarly refer to two other papers published in that journal). Peirce had just taken up a lectureship at The Johns Hopkins University and in November 1879 wrote to his father that he was taking great pains with his lectures. But Peirce retained his assistant-ship in the Coast Survey and for the next 5 years conducted two careers, one as a lecturer in logic at The Johns Hopkins, the other as a scientist, already with 20 years of service for the Coast Survey, where since 1872 he had been in charge of measuring gravity. During those years Peirce was a frequent commuter on the B & O Railroad between Baltimore and Washington.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Notes
“On the Algebra of Logic,” American Journal of Mathematics 3 (1880), 15–57. “On the Algebra of Logic” is included in the Collected Papers of Charles Sanders Peirce(CP 3.154-251) and will be published in volume 4 of the Writings of Charles S. Peirce. Throughout these notes abbreviated references will be made to four sources: (1) Collected Papers of Charles Sanders Peirce, vol. 3, eds. Charles Hartshorne and Paul Weiss, Cambridge, Mass., Harvard University Press, 1933; (2) Writings of Charles S. Peirce, vol. 2, eds. Moore, Fisch, Kloesel, Roberts, and Ziegler, Bloomington, Indiana University Press, 1984; (3) New Elements of Mathematics by Charles S. Peirce, vol. III-l, ed. Carolyn Eisele, The Hague, Mouton, 1976; and (4) The Charles S. Peirce Papers at the Houghton Library of Harvard University. In references to the Collected Papers I will give volume and paragraph numbers (CP 3.xyz), for Writings I will give volume and page (W2.xyz), for New Elements, volume and page (NEIII-l.xyz), and for the Peirce Papers I will give manuscript numbers according to the Robin Catalogue and page numbers as assigned by the Institute for Studies in Pragmaticism, Lubbock, Texas (MS xyz, p. #).
Arthur N. Prior, “The Algebra of the Copula,” Studies in the Philosophy of Charles Sanders Peirce, Second Series, eds. Edward C. Moore and Richard S. Robin, University of Massachusetts Press (1964), 79–94. In Prior’s opinion Peirce did not quite achieve his purpose, although he did take a definite step forward.
Peirce’s comparison of syllogistic with Boole’s algebra of logic was underway by 1865 when he gave a series of lectures at Harvard entitled “On the Logic of Science.” Those lectures appear in the first volume of the new edition of Peirce’s writings, The Writings of Charles S. Peirce 1857–1866 (see especially the sixth lecture, pp. 223–239).
See Prior for an account of the success of Peirce’s 1880 logic. It is not universally agreed that Peirce’s purpose was to construct a propositional logic per se. For criticism of Prior’s account see Randall R. Dipert, “Peirce’s Propositional Logic,” Review of Metaphysics 34 (March 1981), 569–595.
In 1880 Peirce thought that to establish theoremhood a statement had to be derived by accepted rules from pedigreed laws (in 1880 the best pedigree from Peirce’s standpoint seems to have been an undisputed descent from syllogistic), while in 1885 he admitted as “theorems” (logical truths) statements shown to be necessary by truth-function analysis. Without explicitly saying so, Peirce seems to have expanded his conception of validity to include what is now often called “semantic validity.” See Susan Haack, Philosophy of Logics (Cambridge University Press, 1978, pp. 13–14) for a brief account of the syntactic-semantic distinction.
After Peter of Spain a term is said to be distributed when it is taken universally and to be undistributed if it is not taken universally. In the statement “All men are mortal,” the term “men” is distributed because its reference is to every man, but “mortal” is undistributed because its reference is not to every mortal. In general, for traditional Aristotelean logic, we can classify the four propositional forms by the status of their subject and predicate terms with reference to distribution. (Baldwin’s Dictionary of Philosophy and Psychology, Vol. 1, “Distribution,” by R. Adamson, p. 289.)
Boole gives an early general definition of distribution on p. 34 of The Laws of Thought (Dover, 1958). See also The Mathematical Analysis of Logic (1847), pp. 16–17.
Euclid’s principle (II, 1) was given as follows: “If there be two straight lines, and one of them be cut into any number of segments whatever, the rectangle contained by the two straight lines is equal to the rectangles contained by the uncut straight line and each of the segments.” (Euclid’s Elements, Dover, I, 375.) Suppose we have a rectangle with one side of length x and with an adjacent side of length w. For the simplest application of Euclid’s principle we shall suppose that side w is divided into two segments of lengths y and z. Thus w = y + z. According to Euclid’s principle the area of the rectangle xw is equal to the sum of the areas of the rectangles xy and xz. Since w = y + z, we can characterize this simplest case of Euclid’s principle as x(y + z) = xy + xz, which is the law of distribution for the algebra of mathematics. Euclid’s demonstration of II, 1 is given and discussed by Hogben in Mathematics for the Million, 135ff. In 1888 David Hilbert published his Grundlagen in which he, following others, completed Euclid’s Elements. Hilbert’s proof of the distributive law for multiplication appears in Beth’s The Foundations of Mathematics, p. 146.
Heron lived in the third century A.D. and wrote a systematic commentary of the Elements. See Heath, Dover, 20ff., for an examination of the evidence for dating Heron’s commentary. Heath indicates that Heron expressed the law of distribution in a formula equivalent to the standard algebraic expression a(b + c + d) = ab + ac + ad. Heath attributes this information to the commentary of an-Nairizi (ed. Curtze, p. 89). See Heath, Dover I, 373. However, the signs “+” and “×” as symbols of addition and multiplication did not make their appearance until about the fifteenth century, and there do not seem to have been any previous commonly accepted symbols for these operations. See Hogben, Mathematics for the Million, pp. 306–307.
American Journal of Mathematics 4 (1881), 85–95; CP 3.252-288.
For the demonstration of Peirce’s priority in this achievement see Paul Bartram Shields’s dissertation, Charles S. Peirce on the Logic of Number (Fordham University, 1981).
Boole, The Laws of Thought, p. 10.
Boole, The Laws of Thought, p. 37; see also p. 166.
See Boole’s The Mathematical Analysis of Logic, p. 18, and The Laws of Thought, p. 37. This special law of logic appears to have been recognized by Leibniz: see his “Study in the Logical Calculus,” written in the early 1690s, and published in Loemker’s Philosophical Papers and Letters of Leibniz, pp. 380–81.
The conception of duality that follows should be distinguished from that associated with Boole’s law of duality, x(1 − x) = 0, which is a form of the law of noncontradiction. See Boole’s Laws of Thought (Dover), pp. 49–51.
Originally published in the Zeitschrift für Mathematik und Physik 25 (1880), 81–94. Republished in translation by Victor H. Dudman in Southern Journal of Philosophy 1 (1969), 139–150. In The Johns Hopkins University Circular for April 1880, p. 49, Schroder was reported to have made an earlier reference to Peirce’s priority in Leo Koenigsberger’s Repertorium der literarischen arbeiten aus dent gebiete der reinen und angewandten mathematik (Leipzig: B.G. Teubner, 1877–79).
See, for example, Marcel Rueff and Max Jeger, Sets and Boolean Algebra, Allen and Unwin, London, 1970, p. 21.
Arthur N. Prior, in the paper cited in note 2, interprets the nonrelative logic of AJM-1880 as an axiomatic system, although he remarks that Peirce’s “metalogic is... loosely stated, and has something in common with systems of natural deduction” (p. 79). Instead of introducing axioms Peirce identified some fundamental rules of inference, some given as definitions, and a rule (Part 1, §4(2)) for conditionalizing his rules. He did not, however, prove the rule of conditionalization as a theorem, although he did later (in 1898) for his system of Existential Graphs. (See Don D. Roberts, “The Existential Graphs and Natural Deduction,” Moore and Robin, pp. 113–114.)
CP 3.198ff.
An abstract of Schroder’s paper was printed in the Report of the Fifty-Third Meeting of the British Association for the Advancement of Science, held at Southport in September 1883. (London: John Murray, 1884.) Either Schroder or his printer appear to have transposed the formulas in expressing which can and which cannot be proved. Peirce always identified a(b + c)-< ab + ac and its dual (a + b)(a + c)-< a + bc as the contentious formulas. In any case, Schroder announced to the world that Peirce had failed in his 1880 construction. Schröder’s full discussion of this matter can be found in his Vorlesungen über die Algebra der Logik, Bd. 1, §12. a(b + c) = ab + ac appears as an axiom in Schröder’s 1877 Der Operationskreis des Logikkalkuls, (pp. 9–10).
Edward V. Huntington, “Sets of Independent Postulates for the Algebra of Logic,” Transactions of the American Mathematical Society 5 (1904), 288–309. See p. 291n.
Prior, p. 79. Prior refers to De Morgan’s article “Syllogism” in the English Cyclopaedia (1861).
John Venn in his Symbolic Logic, p. 93 (Chelsea reprint of 1894 second edition), noted that the rule equating the proposition “xy is a or b” with “xā is \( \bar y \) or b” is “sometimes called Peirce’s rule.” Venn also gave a more general statement of this rule. I have found no evidence that the name, “Peirce’s rule,” has been carried forward to denote this, or any other, proposition or rule.
Whenever I use the rule of a theorem to justify a step in the proofs that follow, I am abbreviating the proof by omitting a statement of the theorem and an application of MP. See Prior, p. 93, re Peirce’s implicit use of the rule that (p and q ∴ r) is of the same validity as, and interderivable with ((p × q) ∴ r).
See MS 575, p. 21. MS 575 will be remarked on toward the end of this chapter.
Whately, Elements, 114.
A good beginning for understanding the problems of Peirce’s logic in the light of the developments following Principia Mathematica is Randall R. Dipert’s dissertation “Development and Crisis in Late Boolean Logic: the Deductive Logics of Peirce, Jevons, and Schroder” (Indiana University, 1978).
MS 527, pp. 13, 15.
Studies in Logic, By Members of The Johns Hopkins University. Edited by C.S. Peirce, Boston: Little, Brown, and Company. Reprinted in 1983 by John Benjamins Publishing Company.
MS 527, p. 12. Mitchell also used this disjunctive definition of implication. Peirce does not appear to have been familiar at this time with the propositional logic of the Megarian and early Stoic logicians, although he knew of it by way of the Epicurean critiques. His student, Allen Marquand, lists Zeller’s 1880 Stoics, Epicureans, and Sceptics as a reference in his “The Logic of the Epicureans” which appeared in Studies in Logic. Epicurean logic, particularly that of Philodemus, was the subject of Marquand’s doctoral thesis for The Johns Hopkins University, for which Peirce was his advisor.
“On the Algebra of Logic: A Contribution to the Philosophy of Notation,” The American Journal of Mathematics 7 (1885) 180–220; CP 3.359-403. Peirce “proved” his fifth icon by a short truth-table method. (See MS S527, pp. 2 and 14, for early appearances of Peirce’s law.) Łukasiewicz may have been the first to refer to the fifth icon as “Peirce’s Law.” (See J. Łukasiewicz, Selected Works, ed. L. Borkowski, Amsterdam: North-Holland Pub. Co. (1970), p. 296.) The importance of “Peirce’s law” for the development of modern logic is widely recognized. According to Hao Wang “it is now a familiar result that it is necessary to add Peirce’s law... to render the positive implicational calculus classically complete” (From Frege to Gödei. A Source Book in Mathematical Logic, 1879–1931, ed. Jean van Heijenoort, p. 416). A more obscure, though interesting, reference to “Peirce’s law” (without reference to Peirce) was made by Bertrand Russell in a letter to Frege (12.12.1904: Philosophical and Mathematical Correspondence, Gottlob Frege, eds. Gabriel, Hermes, Kambartel, Thiel, and Veraart, Chicago, University of Chicago Press, 1980, p. 168): For negation I use as a primitive law:
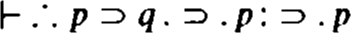 which is hardly self-evident. Russell called this formula the “principle of reduction.” His remark is curiously similar in manner of presentation to Peirce’s own statement in AJM-1885, a paper Russell appears to have been acquainted with. See Atwell R. Turquette’s “Peirce’s Icons for Deductive Logic” (Studies, pp. 95–108; see note 2 above) for an assessment of AJM-1885. Turquette gives many helpful interpretative suggestions.
which is hardly self-evident. Russell called this formula the “principle of reduction.” His remark is curiously similar in manner of presentation to Peirce’s own statement in AJM-1885, a paper Russell appears to have been acquainted with. See Atwell R. Turquette’s “Peirce’s Icons for Deductive Logic” (Studies, pp. 95–108; see note 2 above) for an assessment of AJM-1885. Turquette gives many helpful interpretative suggestions.Huntington, p. 300n. See CP 3.200n.
Henry H. Crapo and Don D. Roberts, Abstract of “Peirce Algebras and The Distributivity Scandal.” Journal of Symbolic Logic 34 (1969), 153–154. Peirce’s proof, and the significance of AJM-1880 for the development of lattice theory, is discussed in Crapo’s Lattice Theory, University of Waterloo, 1966.
Frege is often credited with the discovery of the modern quantifier, and the 1879 publication of his Begriffsschrift, at least 4 years before the publication of a paper by Peirce that might be argued to contain modern quantification theory (Note B in Studies in Logic) and 6 years before AJM-1885, is strong prima facie evidence for Frege’s priority. But Hilary Putnam, in a recent paper about Peirce as a logician (“Peirce the Logician,” Historia Mathematica 9, no. 3, August, 1982) distinguishes between discovery that is historically first and discovery that is effective in the sense that it initiates a line of research. He says that Frege discovered the quantifier in the first sense but that Peirce and his students were its discoverers in the second sense.
O.H. Mitchell, “On a New Algebra of Logic,” Studies in Logic, pp. 72–106. Peirce frequently remarked on the importance and originality of Mitchell’s work; see, for example, MS 527 and CP 3.363. Besides its importance for the development of quantification theory, Mitchell’s work raised doubts for Peirce about the wisdom of basing his logic on implication.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2008 Birkhäuser Boston
About this chapter
Cite this chapter
Houser, N. (2008). Peirce and the Law of Distribution. In: Drucker, T. (eds) Perspectives on the History of Mathematical Logic. Birkhäuser Boston. https://doi.org/10.1007/978-0-8176-4769-8_2
Download citation
DOI: https://doi.org/10.1007/978-0-8176-4769-8_2
Publisher Name: Birkhäuser Boston
Print ISBN: 978-0-8176-4768-1
Online ISBN: 978-0-8176-4769-8
eBook Packages: Springer Book Archive


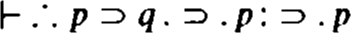 which is hardly self-evident. Russell called this formula the “principle of reduction.” His remark is curiously similar in manner of presentation to Peirce’s own statement in AJM-1885, a paper Russell appears to have been acquainted with. See Atwell R. Turquette’s “Peirce’s Icons for Deductive Logic” (Studies, pp. 95–108; see note 2 above) for an assessment of AJM-1885. Turquette gives many helpful interpretative suggestions.
which is hardly self-evident. Russell called this formula the “principle of reduction.” His remark is curiously similar in manner of presentation to Peirce’s own statement in AJM-1885, a paper Russell appears to have been acquainted with. See Atwell R. Turquette’s “Peirce’s Icons for Deductive Logic” (Studies, pp. 95–108; see note 2 above) for an assessment of AJM-1885. Turquette gives many helpful interpretative suggestions.