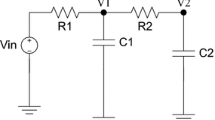
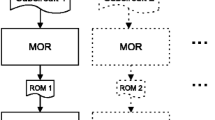
Analysis and verification environments for next-generation nano-scale RFIC designs must be able to cope with increasing design complexity and to account for new effects, such as process variations and Electromagnetic (EM) couplings. Designed-in passives, substrate, interconnect and devices can no longer be treated in isolation as the interactions between them are becoming more relevant to the behavior of the complete system. At the same time variations in process parameters lead to small changes in the device characteristics that may directly affect system performance. These two effects, however, cannot be treated separately as the process variations that modify the physical parameters of the devices also affect those same EM couplings. Accurately capturing the effects of process variations as well as the relevant EM coupling effects requires detailed models that become very expensive to simulate. Reduction techniques able to handle parametric descriptions of linear systems are necessary in order to obtain better simulation performance. In this work we discuss parametric Model Order Reduction techniques based on Structure-Preserving formulations that are able to exploit the hierarchical system representation of designed-in blocks, substrate and interconnect, in order to obtain more efficient simulation models.
Chapter PDF
Similar content being viewed by others
Keywords
- Singular Value Decomposition
- Model Order Reduction
- Krylov Subspace
- Moment Match
- Congruence Transformation
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Antoulas, A.C.: Approximation of Large-Scale Dynamical Systems. Society for Industrial and Applied Mathematics, Philadelphia, PA, USA (2005)
Moore, B.: Principal Component Analysis in Linear Systems: Controllability, Observability, and Model Reduction. IEEE Transactions on Automatic Control AC-26 (1981) 17–32
Phillips, J., Daniel, L., Silveira, L.M.: Guaranteed passive balancing transformations for model order reduction. In: 39th ACM/IEEE Design Automation Conference, New Orleans, Louisiana (2002) 52–57
Li, J.R., Wang, F., White, J.: Efficient model reduction of interconnect via approximate system grammians. In: International Conference on Computer Aided-Design, San Jose, CA (1999) 380–383
Jaimoukha, I.M., Kasenally, E.M.: Krylov subspace methods for solving large Lyapunov equations. SIAM Journal on Numerical Analysis 31 (1994) 227–251
Kamon, M., Wang, F., White, J.: Generating nearly optimally compact models from Krylov-subspace based reduced-order models. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing 47 (2000) 239–248
Feldmann, P., Freund, R.W.: Efficient linear circuit analysis by Padé approximation via the Lanczos process. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 14 (1995) 639–649
Odabasioglu, A., Celik, M., Pileggi, L.T.: PRIMA: passive reduced-order interconnect macromodeling algorithm. IEEE Trans. Computer-Aided Design 17 (1998) 645–654
Phillips, J.R., Silveira, L.M.: Poor Man’s TBR: A simple model reduction scheme. IEEE Trans. Computer-Aided Design 24 (2005) 43–55
Elfadel, I.M., Ling, D.L.: A block rational arnoldi algorithm for multipoint passive modelorder reduction of multiport rlc networks. In: International Conference on Computer Aided-Design, San Jose, California (1997) 66–71
Daniel, L., Siong, O.C., Low, S.C., Lee, K.H., White, J.K.: A multiparameter moment-matching model-reduction approach for generating geometrically parametrized interconnect performance models. IEEE Trans. Computer-Aided Design 23 (2004) 678–693
Li, P., Liu, F., Li, X., Pileggi, L., Nassif, S.: Modeling interconnect variability using efficient parametric model order reduction. In: Proc. Design, Automation and Test in Europe Conference and Exhibition. (2005)
Gunupudi, P., Khazaka, R., Nakhla, M., Smy, T., Celo, D.: Passive parameterized time-domain macromodels for high-speed transmission-line networks. IEEE Trans. On Microwave Theory and Techniques 51 (2003) 2347–2354
Li, X., Li, P., Pileggi, L.: Parameterized interconnect order reduction with Explicit-and-Implicit multi-Parameter moment matching for Inter/Intra-Die variations. In: International Conference on Computer Aided-Design, San Jose, CA (2005) 806–812
Zhu, Z., Phillips, J.: Random sampling of moment graph: a stochastic krylov-reduction algorithm. In: Proc. Design, Automation and Test in Europe Conference and Exhibition, Nice, France (2007) 1502–1507
Li, Y.T., Bai, Z., Su, Y., Zeng, X.: Parameterized model order reduction via a two-directional arnoldi process. In: International Conference on Computer Aided-Design, San Jose, CA, USA (2007) 868–873
Phillips, J.: Variational interconnect analysis via PMTBR. In: International Conference on Computer Aided-Design, San Jose, CA, USA (2004) 872–879
Vandendorpe, A., Dooren, P.V.: Model reduction of interconnected systems. In: Proc. of 16th International Symposium on Mathematical Theory of Networks and Systems (MTNS 2004), Leuven, Belgium (2004) THP3–4
Freund, R.W.: Sprim: Structure-preserving reduced-order interconnect macro-modeling. In: International Conference on Computer Aided-Design, San Jose, CA. U.S.A (2004) 80–87
Yu, H., He, L., Tan, S.X.D.: Block structure preserving model order reduction. In: BMAS - IEEE Behavioral Modeling and Simulation Wokshop. (2005) 1–6
Li, R.C., Bai, Z.: Structure-preserving model reduction using a krylov subspace projection fomulation. Comm. Math. Sci. 3 (2005) 179–199
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
Copyright information
© 2009 Springer-Verlag US
About this chapter
Cite this chapter
Villena, J., Schilders, W., Miguel Silveira, L. (2009). Parametric Structure-Preserving Model Order Reduction. In: VLSI-SoC: Advanced Topics on Systems on a Chip. IFIP International Federation for Information Processing, vol 291. Springer, Boston, MA. https://doi.org/10.1007/978-0-387-89558-1_5
Download citation
DOI: https://doi.org/10.1007/978-0-387-89558-1_5
Published:
Publisher Name: Springer, Boston, MA
Print ISBN: 978-0-387-89557-4
Online ISBN: 978-0-387-89558-1
eBook Packages: Computer ScienceComputer Science (R0)