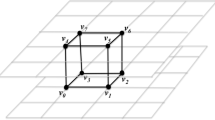
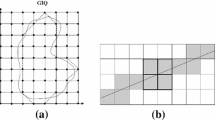
Abstract
In this article, we present a new process for defining and building the set of configurations of Marching-Cubes algorithms. Our aim is to extract a topologically correct isosurface from a volumetric image. Our approach exploits the underlying discrete topology of voxels. Our main contribution is to provide a formal proof of the validity of the generated isosurface. The generated isosurface is a closed, oriented surface without singularity with no self-intersection. Furthermore, we demonstrate that it separates the foreground from the background. Finally we show that the graph defining the isosurface is closely linked to the surfel-adjacency graph of the digital surface of the same image.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
J.-H. Chuang and W.-C. Lee. Efficient Generation of Isosurfaces in Volume Rendering. Computer & Graphics, 19(6):805–813, 1995.
M.J. Dürst. Additionnal Reference to Marching Cubes. Computer Graphics, 22(2):72–73, 1988.
J. Françon. Discrete Combinatorial Surfaces. CVGIP: Graphical Models and Image Processing, 57(1):20–26, January 1995.
G.T. Herman. “Discrete Multidimensional Jordan Surfaces”. CVGIP, 54(6):507–515, November 1992.
T.Y. Kong and J.K. Udupa. A justification of a fast surface tracking algorithm. CVGIP: Graphical Models and Image Processing, 54(6):507–515, November 1992.
J-O. Lachaud and A. Montanvert. “Volumic Segmentation using Hierarchical Representation and Triangulated Surface”. In 6th European Conference on Computer Vision, pages 137–146, Cambridge, UK, April 1996.
J.O. Lachaud. “Topologically Defined Isosurfaces”. Research Report 96-20, LIP 3-ENS Lyon, France, 1996.
W. E. Lorensen and H. E. Cline. “Marching Cubes: A High Resolution 3D Surface Construction Algorithm”. Computer Graphics, 21:163–169, January 1987.
S. Miguet and J-M. Nicod. “A load-balanced parallel implementation of the Marching-Cube algorithm”. In HPCS, July 1995.
S. Miguet and L. Perroton. “Discrete surfaces of 26-connected sets of voxels”. In 5th Discrete Geometry for Computer Imagery, September 1995.
G.M. Nielson and B. Hamman. The Asymptotic Decider: Resolving the Ambiguity in Marching Cubes. In IEEE, editor, Visualization'91, pages 83–90, San Diego, 1991.
L. Perroton. A 26-connected object surface tracking algorithm. Géométrie discrète en imagerie, fondements et applications, 1:1–10, September 1993.
S. Röll, A. Haase, and M. von Kienlin. “Fast Generation of Leakproof Surfaces from Well-Defined Objects by a Modified Marching Cubes Algorithm”. Computer Graphics Forum, 14(2):127–138, January 1995.
A. Rosenfeld, T.Y. Kong, and A.Y. Wu. “Digital Surfaces”. CVGIP, 53(4):305–312, July 1991.
J.K. Udupa. Multidimensional Digital Boundaries. CVGIP: Graphical Models and Image Processing, 56(4):311–323, July 1994.
A. van Gelder and J. Wilhelms. Topological Considerations in Isosurface Generation. ACM Transactions on Graphics, 13(4):337–375, October 1994.
J. Wilhelms and A. van Gelder. Octrees for Faster Isosurface Generation. ACM Transactions on Graphics, 11(3):201–227, July 1992.
G. Wyvill, C. McPheeters, and B. Wyvill. Data Structure for Soft Objects. The visual Computer, 2:227–234, 1986.
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 1996 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Lachaud, JO. (1996). Topologically defined isosurfaces. In: Miguet, S., Montanvert, A., Ubéda, S. (eds) Discrete Geometry for Computer Imagery. DGCI 1996. Lecture Notes in Computer Science, vol 1176. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-62005-2_21
Download citation
DOI: https://doi.org/10.1007/3-540-62005-2_21
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-62005-1
Online ISBN: 978-3-540-49595-6
eBook Packages: Springer Book Archive