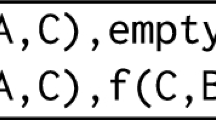Abstract
In this paper, we identify a class of polynomial-time learnable logic programs. These programs can be learned from examples in an incremental fashion using the already defined predicates as background knowledge. Our class properly contains the class of innermost simple programs of [20] and the class of hereditary programs of [12,13]. Standard programs for multiplication, quick-sort, reverse and merge are a few examples of programs that can be handled by our results but not by the earlier results of [12, 13, 20].
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
G. Aguzzi and U. Modigliani (1993), Proving termination of logic programs by transforming them into equivalent term rewriting systems, Proc. of FST&TCS'93, LNCS 761, pp. 114–124.
S. Arikawa, S. Miyano, A. Shinohara, T. Shinohara and A. Yamamoto (1992), Algorithmic learning theory and elementary formal systems, IEICE Trans. Inf. & Sys. E75-D, pp. 405–414.
A. Blumer, A. Ehrenfeucht, D. Haussler and M.K. Warmuth (1989), Learnability and Vapnik-Chervonenkis dimension, JACM 36, pp. 929–965.
P.G. Bosco, E. Giovannetti and C. Moiso (1988), Narrowing vs. SLD-resolution, Theoretical Computer Science 59, pp. 3–23.
S. Dzeroski, S. Muggleton and S. Russel (1992), PAC-learnability of determinate logic programs, Proc. of COLT'92, pp. 128–135.
M. Hanus (1994), The integration of functions into logic programming: a survey, J. Logic Prog. 19/20, pp. 583–628.
J.-M. Hullot (1980), Canonical forms and unification, Proc. of CADE'80, LNCS 87, pp. 318–334.
K. Ito and A. Yamamoto (1992), Polynomial-time MAT learning of multilinear logic programs, Proc. of ALT'92, LNAI 743, pp. 63–74.
M.R.K. Krishna Rao, D. Kapur and R.K. Shyamasundar (1991), A Transformational methodology for proving termination of logic programs, Proc. of CSL'91, LNCS 626, pp. 213–226.
M.R.K. Krishna Rao, D. Kapur and R.K. Shyamasundar (1993), Proving termination of GHC programs, Proc. of ICLP'93, pp. 720–736.
J. W. Lloyd (1987), Foundations of Logic Programming, Springer-Verlag.
S. Miyano, A. Shinohara and T. Shinohara (1991), Which classes of elementary formal systems are polynomial-time learnable?, Proc. of ALT'91, pp. 139–150.
S. Miyano, A. Shinohara and T. Shinohara (1993), Learning elementary formal systems and an application to discovering motifs in proteins, Tech. Rep. RIFIS-TR-CS-37, RIFIS, Kyushu University.
S. Muggleton and L. De Raedt (1994), Inductive logic programming: theory and methods, J. Logic Prog. 19/20, pp. 629–679.
B.K. Natarajan (1991), Machine Learning: A Theoretical Approach, Morgan-Kaufmann.
Y. Sakakibara (1990), Inductive inference of logic programs based on algebraic semantics, New Gen. Comp. 7, pp. 365–380.
E. Shapiro (1981), Inductive inference of theories from facts, Tech. Rep., Yale Univ.
E. Shapiro (1983), Algorithmic Program Debugging, MIT Press.
R.K. Shyamasundar, M.R.K. Krishna Rao and D. Kapur (1992), Rewriting concepts in the study of termination of logic Programs, Proc. of ALPUK'92 conf. (edited by K. Broda), Workshops in Computing series, pp. 3–20, Springer-Verlag.
A. Yamamoto (1993), Generalized unification as background knowledge in learning logic programs, Proc. of ALT'93, LNAI 744, pp. 111–122. Revised version appears as Learning logic programs using definite equality theories as background knowledge, IEICE Trans. Inf. & Syst. E78-D, May 1995, pp. 539–544.
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 1995 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Rao, M.R.K.K. (1995). Incremental learning of logic programs. In: Jantke, K.P., Shinohara, T., Zeugmann, T. (eds) Algorithmic Learning Theory. ALT 1995. Lecture Notes in Computer Science, vol 997. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-60454-5_31
Download citation
DOI: https://doi.org/10.1007/3-540-60454-5_31
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-60454-9
Online ISBN: 978-3-540-47470-8
eBook Packages: Springer Book Archive