Abstract
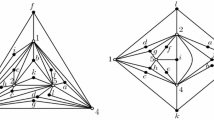
We define the geometric thickness of a graph to be the smallest number of layers such that we can draw the graph in the plane with straight-line edges and assign each edge to a layer so that no two edges on the same layer cross. The geometric thickness lies between two previously studied quantities, the (graph-theoretical) thickness and the book thickness. We investigate the geometric thickness of the family of complete graphs, K n . We show that the geometric thickness of K n lies between ⌈(n/5.646) +0.342⌉ and ⌈n/4⌉, and we give exact values of the geometric thickness of K n for n ≤ 12 and n ∈ 15,16.
Supported by NSF Grants CDA-9617349 and CCR-9703572.
Supported by NSF Grant CCR-9258355 and matching funds from Xerox Corp.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
V. B. Alekseev and V. S. Gončakov. The thickness of an arbitrary complete graph. Math USSR Sbornik, 30(2):187–202, 1976.
L. W. Beineke. The decomposition of complete graphs into planar subgraphs. In F. Harary, editor, Graph Theory and Theoretical Physics, chapter 4, pages 139–153. Academic Press, London, UK, 1967.
L. W. Beineke and F. Harary. The thickness of the complete graph. Canadian Journal of Mathematics, 17:850–859, 1965.
F. Bernhart and P. C. Kainen. The book thickness of a graph. Journal of Combinatorial Theory Series B, 27:320–331, 1979.
R. Cimikowski. On heuristics for determining the thickness of a graph. Information Sciences, 85:87–98, 1995.
A. M. Dean, J. P. Hutchinson, and E. R. Scheinerman. On the thickness and arboricity of a graph. Journal of Combinatorial Theory Series B, 52:147–151, 1991.
J. H. Halton. On the thickness of graphs of given degree. Information Sciences, 54:219–238, 1991.
N. Hartsfield and G. Ringel. Pearls in Graph Theory. Academic Press, Boston, MA, 1990.
B. Jackson and G. Ringel. Plane constructions for graphs, networks, and maps: Measurements of planarity. In G. Hammer and Pallaschke D, editors, Selected Topics in Operations Research and Mathematical Economics: Proceedings of the 8th Symposium on Operations Research, pages 315–324, Karlsruhe, West Germany, August 1983. Springer-Verlag Lecture Notes in Economics and Mathematical Systems 226.
P. C. Kainen. Thickness and coarseness of graphs. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg, 39:88–95, 1973.
A. Mansfield. Determining the thickness of a graph is NP-hard. Mathematical Proceedings of the Cambridge Philosophical Society, 93(9):9–23, 1983.
J. Mayer. Decomposition de K16 en trois graphes planaires. Journal of Combinatorial Theory Series B, 13:71, 1972.
J. Vasak. The thickness of the complete graph having 6m + 4 points. Manuscript. Cited in [8, 9].
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1998 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Dillencourt, M.B., Eppstein, D., Hirschberg, D. (1998). Geometric Thickness of Complete Graphs. In: Whitesides, S.H. (eds) Graph Drawing. GD 1998. Lecture Notes in Computer Science, vol 1547. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-37623-2_8
Download citation
DOI: https://doi.org/10.1007/3-540-37623-2_8
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-65473-5
Online ISBN: 978-3-540-37623-1
eBook Packages: Springer Book Archive