Abstract
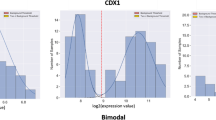
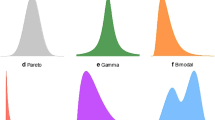
We propose a novel mixture probability model for the probability distribution function (PDF) of microarray signals, which comprises a noise and a signal component. The noise term, due to non-specific mRNA hybridization, is given by a lognormal distribution; and the true signal, from specific mRNA hybridization, is described by the generalized Pareto-gamma (GPG) function. The model, applied to expression data of 251 human breast cancer tumors on the Affymetrix microarray platform, yields accurate fits for all tumor samples. We observe that (i) high aggressive cancers have, in general, broader right tails in the GPG than low aggressive cancers; (ii) the exponent parameter value of the GPG distribution is not constant and correlates strongly with ~4000 expressed genes and several "gold standard" clinical risk factors. These results can not be obtained from so-called “scale-free network” models. We conclude that an accurate parameterization of scale-dependent GPG function could provide robust prognostic benefits for cancer patients.
Chapter PDF
Similar content being viewed by others
Keywords
- Lognormal Distribution
- Probability Distribution Function
- Clinical Risk Factor
- Pareto Distribution
- Empirical Distribution Function
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Anderson, T.W., Darling, D.A.: Asymptotic theory of certain ‘goodness-of-fit’ criteria based on stochastic processes. Ann. Math. Stat. 23, 193–212 (1952)
Furusawa, C., Kaneko, K.: Zipf’s law in gene expression. Phys. Rev. Lett. 90(8), 88–102 (2003)
Hoyle, D.C., Rattray, M., Jupp, R., Brass, A.: Making sense of microarray data distributions. Bioinformatics 18(4), 576–584 (2002)
Dozmorov, I., et al.: Neurokinin 1 receptors and neprilysin modulation of mouse bladder gene regulation. Physiol. Genomics 12, 239–250 (2003)
Ivshina, A.V., et al.: Genetic reclassification of histologic grade delineates new clinical subtypes of breast cancer. In: Liu, E.T., Colman, A.,C., Harris, C., Nishikawa, S.-I., Reddel, R. (eds.) Stem cells, Senescence and Cancer. Keystone Symposia on Mol. Biol., Singapore, p. 76 (October 2005)
Johnson, N.L., Kotz, S., Balakrishnan, N.: Continuous Univariate Distributions, 2nd edn., vol. 1 and 2. Wiley-Interscience, Chichester (1993)
Konishi, T.: Three-parameter lognormal distribution ubiquitously found in cDNA microarray data and its application to parametric data treatment. BMC Bioinformatics 13(5), 5 (2004)
Kuznetsov, V.A.: Distribution associated with stochastic processes of gene expression in a single eukaryotic. EURASIP J. App. Signal Processing 4, 258–296 (2001)
Kuznetsov, V.A.: Mathematical Analysis and Modeling of SAGE Transcriptome, pp. 139–179. Horizon Science Press (2005)
Kuznetsov, V.A., Knott, G.D., Bonner, R.F.: General statistics of stochastic process of gene expression in eukaryotic cells. Genetics 161(3), 1321–1332 (2002)
Li, W., Yang, Y.: Zipf’s law in importance of genes for cancer classification using microarray data. J. Theor. Biol. 219(4), 539–551 (2002)
Metropolis, N., Rosenbluth, A.W., Rosenbluth, M.H., Teller, A.H., Teller, E.: Equation of state calculations by fast computing machines. J. Chem. Phys. 21(6), 1087–1092 (1953)
Michiels, S., Koscielny, S., Hill, C.: Prediction of cancer outcome with microarrays: a multiple random validation strategy. Lancet 365(9458), 488–492 (2005)
Pareto, V.: Cours d’economie Politique, vol. II. F. Rouge, Lausanne (1897)
Reis-Filho, J.S., Westbury, C., Pierga, J.Y.: The impact of expression profiling on prognostic and predictive testing in breast cancer. J. Clin. Pathol. 59(3), 225–231 (2006)
Stephens, M.A.: Statistics for goodness of fit and some comparisons. J. Amer. Stat. Ass. 23, 193–197 (1974)
Ueda, H.R., et al.: Universality and flexibility in gene expression from bacteria to human. PNAS 101(11), 3765–3769 (2004)
Zucchi, I., Mento, E., Kuznetsov, V.A., et al.: Gene expression profiles of epithelial cells microscopically isolated from a breast-invasive ductal carcinoma and a nodal metastasis. Proc. Natl. Acad. Sci. USA 101(52), 18147–18152 (2004)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2006 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Chua, A.L.S., Ivshina, A.V., Kuznetsov, V.A. (2006). Pareto-Gamma Statistic Reveals Global Rescaling in Transcriptomes of Low and High Aggressive Breast Cancer Phenotypes. In: Rajapakse, J.C., Wong, L., Acharya, R. (eds) Pattern Recognition in Bioinformatics. PRIB 2006. Lecture Notes in Computer Science(), vol 4146. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11818564_7
Download citation
DOI: https://doi.org/10.1007/11818564_7
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-37446-6
Online ISBN: 978-3-540-37447-3
eBook Packages: Computer ScienceComputer Science (R0)