Abstract
We perform a concrete security treatment of digital signature schemes obtained from canonical identification schemes via the Fiat-Shamir transform. If the identification scheme is random self-reducible and satisfies the weakest possible security notion (hardness of key-recoverability), then the signature scheme obtained via Fiat-Shamir is unforgeable against chosen-message attacks in the multi-user setting. Our security reduction is in the random oracle model and loses a factor of roughly \(Q_h\), the number of hash queries. Previous reductions incorporated an additional multiplicative loss of N, the number of users in the system. Our analysis is done in small steps via intermediate security notions, and all our implications have relatively simple proofs. Furthermore, for each step, we show the optimality of the given reduction in terms of model assumptions and tightness.
As an important application of our framework, we obtain a concrete security treatment for Schnorr signatures in the multi-user setting.
E. Kiltz—Supported in part by ERC Project ERCC (FP7/615074).
D. Masny—Supported by the DFG Research Training Group GRK 1817/1.
J. Pan—Supported by the DFG Research Training Group GRK 1817/1 and by the DFG grant HO 4534/4-1.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Canonical Identification Schemes and the Fiat-Shamir Transform. A canonical identification scheme \({\mathsf {ID}}\) as formalized by Abdalla et al. [1] is a three-move public-key authentication protocol of a specific form. The prover (holding the secret-key) sends a commitment \(R\) to the verifier. The verifier (holding the public-key) returns a random challenge \(h\), uniformly chosen from a set \(\mathsf {ChSet}\) (of exponential size). The prover sends a response \(s\). Finally, using the verification algorithm, the verifier publicly checks correctness of the transcript \((R, h,s)\). There is a large number of canonical identification schemes known (e.g. [13, 15, 20, 28, 29, 31, 34, 36, 38, 39, 42], the most popular among them being the scheme by Schnorr [42]. The Fiat-Shamir method [20] transforms any such canonical identification scheme into a digital signature scheme \({\mathsf {SIG}}[{\mathsf {ID}}]\) using a hash function.
Digital Signatures in the Multi-User Setting. When it comes to security of digital signature schemes, in the literature almost exclusively the standard security notion of unforgeability against chosen message attacks (\({\mathsf {UF\text{- }CMA}}\)) [30] is considered. This is a single-user setting, where an adversary obtains one single public-key and it is said to break the scheme’s security if he can produce (after obtaining \(Q_s\) many signatures on messages of his choice) a valid forgery, i.e. a message-signature pair that verifies on the given public-key. However, in the real world the attacker is usually confronted with many public-keys and presumably he is happy if he can produce a valid forgery under any of the given public-keys. This scenario is captured in the multi-user setting for signatures schemes. Concretely, in multi-user unforgeability against chosen message attacks (\({{\mathsf {MU\text{- }UF\text{- }CMA}}}\)) the attacker obtains N independent public-keys and is said to break the scheme’s security if he can produce (after obtaining \(Q_s\) many signatures on public-keys of his choice) a valid forgery that verifies under any of the public-keys.
There are essentially two reasons why one typically only analyzes signatures in the single-user setting. First, the single-user security notion and consequently their analysis are simpler. Second, there exists a simple generic security reduction [25] between multi-user security and standard single-user security. Namely, for any signature system, attacking the scheme in the multi-user setting with N public-keys cannot increase the attacker’s success ratio (i.e., the quotient of its success probability and its running time) by a factor more than N compared to attacking the scheme in the single-user setting. As the number of public-keys N is bounded by a polynomial, asymptotically, the single-user and the multi-user setting are equivalent. However, the security reduction is not tight: it has a loss of a non-constant factor N. This is clearly not satisfactory as in complex environments one can easily assume the existence of at least \(N=2^{30}\) (\(\approx \) 1 billion) public-keys, thereby increasing the upper bound on the attacker’s success ratio by a factor of \(2^{30}\). For example, if we assume the best algorithm breaking the single-user security having success ratio \(\rho =2^{-80}\), then it can only be argued that the best algorithm breaking the multi-user security has success ratio \(\rho '=2^{-80} \cdot 2^{30} = 2^{-50}\), which is not a safe security margin that defends against today’s attackers.
Tightness. Generally, we call a security implication between two problems tight [9], if the success ratio \(\rho \) of any adversary attacking the first problem cannot decease by more than a small constant factor compared to the success ratio \(\rho '\) of any adversary attacking the second problem [7, 26]. Here the success ratio \(\rho \) is defined as the quotient between the adversary’s success probability and its running time. We note that this notion of tightness is slightly weaker than requiring that both, success probability and running time, cannot decrease by more than a small constant factor (called strong tightness in [26]). However, the main goal of a concrete security analysis is to derive parameters provably guaranteeing k-bit security. As the term k-bit security is commonly defined as the non-existence of any adversary that breaks the scheme with a success ratio better than \(2^{-k}\) (see, e.g., [7, 18]), our definition of tightness is sufficient for this purpose.
1.1 Our Contributions
This work contains a concrete and modular security analysis of signatures \({\mathsf {SIG}}[{\mathsf {ID}}]\) obtained via the Fiat-Shamir transform. Throughout this paper we assume that our identification schemes \({\mathsf {ID}}\) are \(\varSigma \)-protocols, i.e. they are honest-verifier zero-knowledge (\(\mathsf {HVZK}\)), have special soundness (\(\mathsf {SS}\)), and commitments \(R\) are sampled at random from a sufficiently large set. For some of our tight implications we furthermore require \({\mathsf {ID}}\) to be random self-reducible (\(\mathsf {RSR}\)), a property we formally define in Definition 5. Most known canonical identification schemes satisfy the above properties.
Security Notions. For identification schemes we consider \(\mathsf {XXX}\text{- }\mathsf {YYY}\) security, where \(\mathsf {XXX}\in \{\mathsf {KR},\mathsf {IMP},\mathsf {PIMP}\}\) denotes the attacker’s goal and \(\mathsf {YYY}\in \{\mathsf {KOA},\mathsf {PA}\}\) the attacker’s capabilities. If the attacker’s goals defined as follows: in key-recovery (\(\mathsf {KR}\)), it tries to compute a valid secret-key; in impersonation (\(\mathsf {IMP}\)), it tries to impersonate a prover by convincing an honest verifier; parallel impersonation (\(\mathsf {PIMP}\)) is a parallel version of \(\mathsf {IMP}\), where the adversary tries to convince a verifier in one of \(Q_\textsc {Ch}\) many parallel sessions. The attacker’s capabilities are defined as follows: in a key-only attack \((\mathsf {KOA})\), the adversary is only given the public-key; in a passive attack (\(\mathsf {PA}\)), the adversary is provided with valid transcripts between an honest prover and verifier. In total, we obtain \(3 \times 2 =6\) different security notions that were all previously considered in the literature [1, 37, 41], except \(\mathsf {PIMP}\text{- }\mathsf {YYY}\) security.
Overview. We show via a chain of implications that \(\mathsf {KR}\text{- }\mathsf {KOA}\)-security (the weakest possible security notion for \({\mathsf {ID}}\) where the adversary has to compute a secret-key from a given public-key without any further oracle access) implies multi-user unforgeability against chosen message attacks (\({{\mathsf {MU\text{- }UF\text{- }CMA}}} \)) of \({\mathsf {SIG}}[{\mathsf {ID}}]\). The diagram in Fig. 1 summarizes our results. All implications are optimal in terms of tightness and model requirements in the following sense. If one implication makes use of a special model requirement, we prove its impossibility without this requirement. For example, our implication \(\mathsf {PIMP}\text{- }\mathsf {KOA}\xrightarrow {} {\mathsf {UF\text{- }KOA}}\) requires the random oracle model [8] (with its well-known deficiencies [17]) and we show that the non-programmable random oracle model [22] is not sufficient to prove the same implication. Exactly one of our implications, namely \(\mathsf {IMP}\text{- }\mathsf {KOA}\xrightarrow {} \mathsf {PIMP}\text{- }\mathsf {KOA}\) is non-tight, and we prove the impossibility of such a tight implication. We now discuss the implications from Fig. 1 in more detail.
From Identification to Single User Security for Signatures. Our first main theorem can be informally stated as follows.
Overview of our notions and results for canonical identification schemes \({\mathsf {ID}}\) and their implied signature schemes \({\mathsf {SIG}}[{\mathsf {ID}}]\). \(\mathsf {X} \xrightarrow {\text {Z}} \mathsf {Y}\) means that \(\mathsf {X}\)-security implies \(\mathsf {Y}\)-security under condition Z. Trivial implications are denoted with dashed arrows. All implications are tight except the one marked with “loss Q”. The conditions are: rew. (reduction rewinds), loss Q (reduction loses a factor of Q), PRO (reduction is in the programmable random oracle model), \(\mathsf {SS}\) (reduction uses special soundness), and \(\mathsf {RSR}\) (reduction uses random self-reducibility for tightness). All implications from top to bottom require \(\mathsf {HVZK}\).  means that \(\mathsf {X}\)-security does not imply \(\mathsf {Y}\)-security if only condition Z is fulfilled. The conditions are: non-rew. (reduction does not rewind), loss \(<Q\) (reduction loses a factor smaller than Q), and \(\text {NPRO}\) (reduction is in the non-programmable random oracle model).
means that \(\mathsf {X}\)-security does not imply \(\mathsf {Y}\)-security if only condition Z is fulfilled. The conditions are: non-rew. (reduction does not rewind), loss \(<Q\) (reduction loses a factor smaller than Q), and \(\text {NPRO}\) (reduction is in the non-programmable random oracle model).
Theorem 1
If the identification scheme is \(\mathsf {KR}\text{- }\mathsf {KOA}\)-secure against any adversary having success ratio \(\rho \), then \({\mathsf {SIG}}[{\mathsf {ID}}]\) is \({\mathsf {UF\text{- }CMA}}\)-secure in the random oracle model against any adversary having success ratio \(\rho ' \approx \rho /Q_h\), where \(Q_h\) is the maximal number of the adversary’s random oracle queries.
The proof of this theorem is obtained by combining four independent Lemmas 3, 4, 5, and 6 via intermediate security notions \(\mathsf {IMP}\text{- }\mathsf {KOA}\), \(\mathsf {PIMP}\text{- }\mathsf {KOA}\), and \({\mathsf {UF\text{- }KOA}}\) Footnote 1 security, see Fig. 1. We certainly do not claim any novelty of the above lemmas, nor a new proof technique. For example, the implication \(\mathsf {IMP}\text{- }\mathsf {KOA}\rightarrow {\mathsf {UF\text{- }CMA}}\) is already explicitly contained in [37] (and implicitly in the seminal paper by Pointcheval and Stern [41]). However, by our specific choice of the intermediate security notions, all four proofs are simple and intuitive. In particular, unlike previous proofs, none of our proofs requires the full power of the Forking Lemma [5, 41]. At the core of Lemma 3 (\(\mathsf {KR}\text{- }\mathsf {KOA}\rightarrow \mathsf {IMP}\text{- }\mathsf {KOA}\)) we use a new Multi-Instance Reset Lemma (Lemma 1) which is a generalization of Bellare and Palacio’s (Single-Instance) Reset Lemma [6] and may be of independent interest. The key to simplicity is the fact that \(\mathsf {IMP}\text{- }\mathsf {KOA}\) security only deals with one single impersonation session, which greatly simplifies the probability analysis. Even though the reduction uses rewinding, the \(\mathsf {RSR}\) property makes the implication \(\mathsf {KR}\text{- }\mathsf {KOA}\rightarrow \mathsf {IMP}\text{- }\mathsf {KOA}\) tight. We view identifying the intermediate security notions that allow for simple proofs as a conceptual contribution. Our result show that \(\mathsf {IMP}\text{- }\mathsf {KOA}\) and \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) security can be seen as the tightness barrier for identification schemes in the sense that \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) is the weakest of our notions for \({\mathsf {ID}}\) that is tightly equivalent to (multi-user) \({\mathsf {UF\text{- }CMA}}\) security of \({\mathsf {SIG}}[{\mathsf {ID}}]\) in the random oracle model, whereas \(\mathsf {IMP}\text{- }\mathsf {KOA}\) is tightly equivalent to \(\mathsf {KR}\text{- }\mathsf {KOA}\).
One particular advantage of our modular approach is that we are able to prove optimality of all four implications via meta-reductions (Lemmas 9, 10, 11, and 12). Lemma 10 proving the impossibility of a tight reduction between \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) and \(\mathsf {IMP}\text{- }\mathsf {KOA}\) security is a generalization of Seurin’s impossibility result to canonical identification schemes [43]; Lemmas 11 and 12 proving the impossibility of a reduction in the non-programmable random oracle model between \(\mathsf {PIMP}\text{- }\mathsf {KOA}\), \({\mathsf {UF\text{- }KOA}}\), and \({\mathsf {UF\text{- }CMA}}\) can be considered as a fine-grained version of a general impossibility result by Fukumitsu and Hasegawa [24] who only consider the implication \(\mathsf {IMP}\text{- }\mathsf {PA}\rightarrow {\mathsf {UF\text{- }CMA}}\); All our impossibility results assume the reductions to be key-preserving [40] and are conditional in the sense that the existence of a reduction would imply that \({\mathsf {ID}}\) does not satisfy some other natural security property (that is believed to hold).
From Single-User to Multi-User Security for Signatures. Our second main theorem can be informally stated as follows.
Theorem 2
If \({\mathsf {ID}}\) is \({\mathsf {UF\text{- }KOA}}\)-secure against any adversary having success ratio \(\rho \), then it is \({{\mathsf {MU\text{- }UF\text{- }CMA}}} \)-secure in the random oracle model against any adversary having success ratio \(\rho '\approx \rho /4\), independent of the number of users N in the multi-user scenario.
This theorem improves the bound implied by previous generic reductions [25] by a factor of N. Following our modular approach, the theorem is proved in two steps via Lemmas 7 and 8. Lemma 7 proves that \({\mathsf {UF\text{- }KOA}}\) tightly implies \({\mathsf {MU\text{- }UF\text{- }KOA}}\). Tightness stems from the \(\mathsf {RSR}\) property, meaning that from a given public key \(pk\) we can derive properly distributed \(pk_1, \ldots , pk_N\) such that any signature \(\sigma \) which is valid under \(pk\) can be transformed into a signature \(\sigma _i\) which is valid under \(pk_i\) and vice-versa.
Lemma 8 is our main technical contribution and proves \({\mathsf {MU\text{- }UF\text{- }KOA}}\rightarrow {{\mathsf {MU\text{- }UF\text{- }CMA}}} \) in the programmable random oracle model, again with a tight reduction. One is tempted to believe that it can be proved the same way as in the single user setting (i.e., the same way as \({\mathsf {UF\text{- }KOA}}\rightarrow {\mathsf {UF\text{- }CMA}}\)). In the single user setting, the reduction simulates signatures on \({m}_j\) using the \(\mathsf {HVZK}\) property to obtain a valid transcript \((R_j, h_j, s_j)\) and programs the random oracle as \(H(R_j,{m}_j):=h_j\). However, in the \({\mathsf {MU\text{- }UF\text{- }KOA}}\) experiment an adversary can ask for a signature under \(pk_1\) on message \({m}\) which makes the reduction program the random oracle \(H(R_1,{m}):=h_1\). Now, if the adversary submits a forgery \((R_1, s_2)\) under \(pk_2\) on the same message \({m}\), the reduction cannot use this forgery to break the \({\mathsf {MU\text{- }UF\text{- }KOA}}\) experiment because the random oracle \(H(R_1,{m})\) was externally defined by the reduction. Hence, for the \({\mathsf {MU\text{- }UF\text{- }KOA}}\) experiment, \({m}, (R_1, s_2)\) does not constitute a valid forgery. In order to circumvent the above problem we make a simple probabilistic argument. In our reduction, about one half of the multi-user public-keys are coming from the \({\mathsf {MU\text{- }UF\text{- }KOA}}\) experiment, for the other half the reduction knows the corresponding secret-keys. Which secret-keys are known is hidden from the adversary’s view. Now, if the multi-user adversary first obtains a signature on message \({m}\) under \(pk_1\) and then submits a forgery on the same message \({m}\) under \(pk_2\), the reduction hopes for the good case that one of the public-keys comes from the \({\mathsf {MU\text{- }UF\text{- }KOA}}\) experiment and the other one is known. This happens with probability 1 / 4 which is precisely the loss of our new reduction.
1.2 Example Instantiations
Schnorr Signatures. One of the most important and signature schemes in the discrete logarithm setting is the Schnorr signature scheme [42]. It is obtained via the Fiat-Shamir transform applied to the Schnorr identification protocol. The recent expiry of the patent in 2008 has triggered a number of initiatives to obtain standardized versions of it.
Theorems 1 and 2 can be used to derive a concrete security bound for strong multi-user \({{\mathsf {MU\text{- }UF\text{- }CMA}}} \)-security of Schnorr signatures in the random oracle model from the \(\mathsf {DLOG}\) problem.Footnote 2 Our reduction loses a factor of roughly \(Q_h\), the number of random oracle queries. This improves previous bounds by a factor of N, the number of users in the system. We derive concrete example parameters for a provably secure instantiation. Figure 1 shows that \(\mathsf {DLOG}\) is tightly equivalent to \(\mathsf {IMP}\text{- }\mathsf {KOA}\)-security and \(\mathsf {PIMP}\text{- }\mathsf {KOA}\)-security is tightly equivalent to \({{\mathsf {MU\text{- }UF\text{- }CMA}}} \)-security, meaning the tightness barrier for Schnorr lies precisely between \(\mathsf {IMP}\text{- }\mathsf {KOA}\) and \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) security.
Katz-Wang Signatures. The Chaum-Pedersen identification scheme [19] is a double-generator version of Schnorr. It is at least as secure as Schnorr which means one cannot hope for a tight proof under the \(\mathsf {DLOG}\) assumption. However, we can use a simple argument from [29, 34] for a tight security proof of its \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) security under the (stronger) Decision Diffie-Hellman Assumption. The resulting signature scheme is known as the Katz-Wang signature scheme [34] and our framework yields a tight proof of its strong \({{\mathsf {MU\text{- }UF\text{- }CMA}}} \)-security. Again, this improves previous bounds by a factor of N, the number of users in the system.
Guillou-Quisquater Signatures. Another canonical identification scheme of interest with the required properties is the one by Guillou-Quisquater [31]. Similar to Katz-Wang, for the Guillou-Quisquater scheme, we can use an argument from [2] for a tight proof of \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) security under the Phi-hiding assumption. Alternatively, we can give a proof with loss \(Q_h\) under the Factoring assumption. Our framework also shows that this loss is unavoidable. Details are shown in the full version [35].
1.3 Related Work
Single-User Security. There have been many different works addressing the single-user security of Fiat-Shamir based signature schemes \({\mathsf {SIG}}[{\mathsf {ID}}]\). In pioneering work, Pointcheval and Stern [41] introduced the Forking Lemma as a tool to prove \({\mathsf {UF\text{- }CMA}}\) security of \({\mathsf {SIG}}[{\mathsf {ID}}]\) from \(\mathsf {HVZK}\), \(\mathsf {SS}\) and \(\mathsf {KR}\text{- }\mathsf {KOA}\)-security. Ohta and Okamoto [37] gave an alternative proof from \(\mathsf {IMP}\text{- }\mathsf {KOA}\) security and \(\mathsf {HVZK}\). Abdalla et al. [1] prove the equivalence of \(\mathsf {IMP}\text{- }\mathsf {PA}\)-security of \({\mathsf {ID}}\) and \({\mathsf {UF\text{- }CMA}}\) security of \({\mathsf {SIG}}[{\mathsf {ID}}]\) in the random oracle model. All above results incorporate a security loss of at least \(Q_h\) and can be seen as a special case of our framework. Furthermore, [6] consider stronger security notions (e.g., \(\mathsf {IMP}\text{- }\mathsf {AA}\) and man-in-the middle security) for the Schnorr and GQ identification schemes. Abdalla et al. [3] show that lossy identification schemes tightly imply \({\mathsf {UF\text{- }CMA}}\)-secure signatures in the random oracle model from decisional assumptions. Our Multi-Instance Reset Lemma (Lemma 1) is a generalization to the Reset Lemma of Bellare and Palacio [6].
Multi-user security. To mitigate the generic security loss problem in the multi-user setting for the special case of Schnorr’s signature scheme, Galbraith, Malone-Lee, and Smart (GMLS) proved [25] a tight reduction, namely that attacking the Schnorr signatures in the multi-user setting with N public-keys provably cannot decrease (by more than a small constant factor) the attacker’s success ratio compared to attacking the scheme in the single-user setting. Unfortunately, Bernstein [11] recently pointed out an error in the GMLS proof leaving a tight security reduction for Schnorr signatures as an open problem. Even worse, Bernstein identifies an “apparently insurmountable obstacle to the claimed [GMLS] theorem”. Section 4.3 of [11] further expands on the insurmountable obstacle. Our Theorem 2 shows there is such a tight security reduction for Schnorr signatures if one is willing to rely on the random oracle model. Additionally, in [35] we also prove an alternative tight reduction in the standard model which assumes strong \({\mathsf {UF\text{- }CMA}}\) security. (\(\mathsf {Schnorr}\) is generally believed to be strongly \({\mathsf {UF\text{- }CMA}}\) secure and this is provably equivalent to \({\mathsf {UF\text{- }CMA}}\) security in the random oracle model.) Proving the original GMLS theorem (i.e., without random oracles and from standard \({\mathsf {UF\text{- }CMA}}\) security) remains an open problem.
Impossibility Results. In terms of impossibility results, Seurin [43], building on earlier work of [27, 40], proves that there is no tight reduction from the (one-more) discrete logarithm assumption to \({\mathsf {UF\text{- }KOA}}\)-security of Schnorr signatures. A more recent result by [23] even excludes a reduction from any non-interactive assumption.Footnote 3 Fukumitsu and Hasegawa [24], generalizing earlier work on Schnorr signatures [21, 40], prove that \({\mathsf {SIG}}[{\mathsf {ID}}]\) cannot be proved secure in the non-programmable random oracle model only assuming \(\mathsf {IMP}\text{- }\mathsf {PA}\) security of \({\mathsf {ID}}\).
Schnorr signatures vs. Key-Prefixed Schnorr signatures. After identifying the error in the GMLS proof, Bernstein [11] uses the lack of a tight security reduction for Schnorr’s signature scheme as a motivation to promote a “key-prefixed” modification to Schnorr’s signature scheme which includes the verifier’s public-key in the hash function. The EdDSA signature scheme by Bernstein et al. [12] is essentially a key-prefixing variant of Schnorr’s signature scheme. (In the context of security in a multi-user setting, key-prefixing was considered before, e.g., in [14].) In [12] key-prefixing is advertized as “an inexpensive way to alleviate concerns that several public keys could be attacked simultaneously.” Indeed, Bernstein [11] proves that single-user security of the original Schnorr signatures scheme tightly implies multi-user security of the key-prefixed variant of the scheme. That is, the key-prefixed variant has the advantage of a standard model proof of its tight multi-user security, whereas for standard Schnorr signatures one has to assume strong security or rely on the random oracle model.
The TLS standard used to secure HTTPS connections is maintained by the Internet Engineering Task Force (IETF) which delegates research questions to the Internet Research Task Force (IRTF). Cryptographic research questions are usually discussed in the Crypto Forum Research Group (CFRG) mailing list. In the last months the CFRG discussed the issue of key-prefixing.
Key-prefixing comes with the disadvantage that the entire public-key has to be available at the time of signing. Specifically, in a CFRG message from September 2015 Hamburg [32] argues “having to hold the public key along with the private key can be annoying” and “can matter for constrained devices”. Independent of efficiency, we believe that a cryptographic protocol should be as light as possible and prefixing (just as any other component) should only be included if its presence is justified. Naturally, in light of the GMLS proof, Hamburg [32] and Struik [44] (among others) recommended against key prefixing for Schnorr. Shortly after, Bernstein [10] identifies the error in the GMLS theorem and posts a tight security proof for the key-prefixed variant of Schnorr signatures. In what happens next, the participant of the CFRG mailing list switched their minds and mutually agree that key-prefixing should be preferred, despite of its previously discussed disadvantages. Specifically, Brown writes about Schnorr signatures that “this justifies a MUST for inclusion of the public key in the message of the classic signature” [16]. As a consequence, key-prefixing is contained in the current draft for EdDSA [33]. In the light of our new results, we recommend to reconsider this decision.
2 Definitions
2.1 Preliminaries
For an integer p, define \([p]:= \{1,\ldots , p\}\) and \(\mathbb {Z}_p\) as the residual ring \(\mathbb {Z}/p\mathbb {Z}\). If A is a set, then  denotes picking a from A according to the uniform distribution. All our algorithms are probabilistic polynomial time unless stated otherwise. If \({\mathsf {A}}\) is an algorithm, then
denotes picking a from A according to the uniform distribution. All our algorithms are probabilistic polynomial time unless stated otherwise. If \({\mathsf {A}}\) is an algorithm, then  denotes the random variable which is defined as the output of \(\mathcal {A}\) on input b. To make the randomness explicit, we use the notation \(a := {\mathsf {(}}A)(b; \rho )\) meaning that the algorithm is executed on input b and randomness \(\rho \). Note that \({\mathsf {A}}\)’s execution is now deterministic.
denotes the random variable which is defined as the output of \(\mathcal {A}\) on input b. To make the randomness explicit, we use the notation \(a := {\mathsf {(}}A)(b; \rho )\) meaning that the algorithm is executed on input b and randomness \(\rho \). Note that \({\mathsf {A}}\)’s execution is now deterministic.
2.2 Canonical Identification Schemes
A canonical identification scheme \({\mathsf {ID}}\) is a three-move protocol of the form depicted in Fig. 2. The prover’s first message \(R\) is called commitment, the verifier selects a uniform challenge \(h\) from set \(\mathsf {ChSet}\), and, upon receiving a response \(s\) from the prover, makes a deterministic decision.
Definition 1
(Canonical Identification Scheme). A canonical identification scheme \({\mathsf {ID}}\) is defined as a tuple of algorithms \({\mathsf {ID}}:=({\mathsf {IGen}},{\mathsf {P}},\mathsf {ChSet},{\mathsf {V}})\).
-
The key generation algorithm \({\mathsf {IGen}}\) takes system parameters \(\mathsf {par}\) as input and returns public and secret key \((pk, sk)\). We assume that \(pk\) defines \(\mathsf {ChSet}\), the set of challenges.
-
The prover algorithm \({\mathsf {P}}=({\mathsf {P}}_1,{\mathsf {P}}_2)\) is split into two algorithms. \({\mathsf {P}}_1\) takes as input the secret key \(sk\) and returns a commitment \(R\) and a state \( St \); \({\mathsf {P}}_2\) takes as input the secret key \(sk\), a commitment \(R\), a challenge \(h\), and a state \( St \) and returns a response \(s\).
-
The verifier algorithm \({\mathsf {V}}\) takes the public key \(pk\) and the conversation transcript as input and outputs a deterministic decision, 1 (acceptance) or 0 (rejection).
We require that for all \((pk,sk) \in {\mathsf {IGen}}(\mathsf {par})\), all \((R, St ) \in {\mathsf {P}}_1(sk)\), all \(h\in \mathsf {ChSet}\) and all \(s\in {\mathsf {P}}_2(sk,R,h, St )\), we have \({\mathsf {V}}(pk, R, h,s)=1\).
We make a couple of useful definitions. An identification scheme \({\mathsf {ID}}\) is called unique if for all \((pk,sk) \in {\mathsf {IGen}}(\mathsf {par})\), \((R, St ) \in {\mathsf {P}}_1(sk)\), \(h\in \mathsf {ChSet}\), there exists at most one response \(s\in \{0,1\}^*\) such that \({\mathsf {V}}(pk, R, h,s)=1\). A transcript is a three-tuple \((R,h,s)\). It is called valid (with respect to public-key \(pk\)) if \({\mathsf {V}}(pk, R, h,s)=1\). Furthermore, it is called real, if it is the output of a real interaction between prover and verifier as depicted in Fig. 2. A canonical identification schemes \({\mathsf {ID}}\) has \(\alpha \) bits of min-entropy, if for all \((pk,sk) \in {\mathsf {IGen}}(\mathsf {par})\), the commitment generated by the prover algorithm is chosen from a distribution with at least \(\alpha \) bits of min-entropy. That is, for all strings \(R'\) we have \(\Pr [R=R'] \le 2^{-\alpha }\), if  was honestly generated by the prover.
was honestly generated by the prover.
We now define (parallel) impersonation against key-only attack (\(\mathsf {KOA}\)), passive attack (\(\mathsf {PA}\)), and active attack \((\mathsf {AA})\).
Definition 2
((Parallel) Impersonation). Let \(\mathsf {YYY}\in \{\mathsf {KOA},\mathsf {PA},\mathsf {AA}\}\). A canonical identification \({\mathsf {ID}}\) is said to be \((t, \varepsilon , Q_\textsc {Ch},Q_\textsc {O})\)-\(\mathsf {PIMP}\)-\(\mathsf {YYY}\) secure (parallel impersonation against \(\mathsf {YYY}\) attacks) if for all adversaries \(\mathcal {A}\) running in time at most t and making at most \(Q_\textsc {Ch}\) queries to the challenge oracle \(\textsc {Ch}\) and \(Q_\textsc {O}\) queries to oracle \(\textsc {O}\),

where on the i-th query \(\textsc {Ch}(R_i)\) (\(i \in [Q_\textsc {Ch}]\)), the challenge oracle returns  Footnote 4 Depending on \(\mathsf {YYY}\), oracle \(\textsc {O}\) is defined as follows.
Footnote 4 Depending on \(\mathsf {YYY}\), oracle \(\textsc {O}\) is defined as follows.
-
If \(\mathsf {YYY}=\mathsf {KOA}\) (key-only attack), then \(\textsc {O}\) always returns \(\perp \).
-
If \(\mathsf {YYY}=\mathsf {PA}\) (passive attack), then \(\textsc {O}:= \textsc {Tran}\), where on the j-th empty query \(\textsc {Tran}(\epsilon )\) (\(j \in Q_\textsc {O}\)), the transcript oracle returns a real transcript \((R'_j,h'_j,s'_j)\) to \(\mathcal {A}\), where
 .
. -
If \(\mathsf {YYY}=\mathsf {AA}\) (active attack), then \(\textsc {O}:= \textsc {Prover}=(\textsc {Prover}_1,\textsc {Prover}_2)\), where on the j-th query \(\textsc {Prover}_1(\epsilon )\) (\(j \in Q_\textsc {O}\)), the prover oracle returns
 to \(\mathcal {A}\); on query \(\textsc {Prover}_2(j, h'_{j})\), the oracle returns
to \(\mathcal {A}\); on query \(\textsc {Prover}_2(j, h'_{j})\), the oracle returns  , if \(R'_{j}\) is already defined (and \(\perp \) otherwise).
, if \(R'_{j}\) is already defined (and \(\perp \) otherwise).
If \(\mathsf {YYY}=\mathsf {KOA}\), then the parameter \(Q_\textsc {O}\) is not used and we simply speak of \((t,\varepsilon ,Q_\textsc {Ch})\)-\(\mathsf {PIMP}\text{- }\mathsf {KOA}\). Moreover, \((t,\varepsilon ,Q_\textsc {O})\)-\(\mathsf {IMP}\text{- }\mathsf {YYY}\) (impersonation against \(\mathsf {YYY}\) attack) security is defined as \((t,\varepsilon ,1,Q_\textsc {O})\)-\(\mathsf {PIMP}\text{- }\mathsf {YYY}\) security, i.e., the adversary is only allowed \(Q_\textsc {Ch}=1\) query to the \(\textsc {Ch}\) oracle.
Definition 3
(Key-recovery). Let \(\mathsf {YYY}\in \{\mathsf {KOA},\mathsf {PA},\mathsf {AA}\}\). A canonical identification \({\mathsf {ID}}\) is said to be \((t, \varepsilon )\)-\(\mathsf {KR}\text{- }\mathsf {YYY}\) secure (key recovery under \(\mathsf {YYY}\) attack) if for all adversaries \(\mathcal {A}\) running in time at most t,

where depending on \(\mathsf {YYY}\) oracle \(\textsc {O}\) is defined as in Definition 2. The winning condition \((sk^*,pk) \in {\mathsf {IGen}}(\mathsf {par})\) means that the tuple \((sk^*,pk)\) is in the support of \({\mathsf {IGen}}(\mathsf {par})\), i.e., that \(\mathcal {A}\) outputs a valid secret-key \(sk^*\) with respect to \(pk\).
Definition 4
(Special Soundness). A canonical identification \({\mathsf {ID}}\) is said to be \(\mathsf {SS}\) (special sound) if there exists an extractor algorithm \({\mathsf {Ext}}\) such that, for all \((pk,sk)\in {\mathsf {IGen}}(\mathsf {par})\), given any two accepting transcripts \((R,h,s)\) and \((R,h',s')\) (where \(h\ne h'\)), we have  .
.
Definition 5
(Random Self-reducibility). A canonical identification \({\mathsf {ID}}\) is said to be \(\mathsf {RSR}\) (random self-reducible) if there is an algorithm \({\mathsf {Rerand}}\) and two deterministic algorithms \({\mathsf {Tran}}\) and \({\mathsf {Derand}}\) such that, for all \((pk,sk) \in {\mathsf {IGen}}(\mathsf {par})\):
-
\(pk'\) and \(pk''\) have the same distribution, where
 is the rerandomized key-pair and
is the rerandomized key-pair and  is a freshly generated key-pair.
is a freshly generated key-pair. -
For all \((pk',\tau ') \in {\mathsf {Rerand}}(pk)\), all \((pk',sk') \in {\mathsf {IGen}}(\mathsf {par})\), and \(sk^* = {\mathsf {Derand}}(pk,pk',sk',\tau ')\), we have \((pk,sk^*) \in {\mathsf {IGen}}(\mathsf {par})\), i.e., \({\mathsf {Derand}}\) returns a valid secret-key \(sk^*\) with respect to \(pk\), given any valid \(sk'\) for \(pk'\).
-
For all \((pk',\tau ') \in {\mathsf {Rerand}}(pk)\), all transcripts \((R',h',s')\) that are valid with respect to \(pk'\), the transcript \((R',h',s:={\mathsf {Tran}}(pk,pk',\tau ',(R',h',s')))\) is valid with respect to \(pk\).
Definition 6
(Honest-verifier Zero-knowledge). A canonical identification \({\mathsf {ID}}\) is said to be (perfect) \(\mathsf {HVZK}\) (honest-verifier zero-knowledge) if there exists an algorithm \(\mathsf {Sim}\) that, given public key \(pk\), outputs \((R,h,s)\) such that \((R,h,s)\) is a real (i.e., properly distributed) transcript with respect to \(pk\).
2.3 Digital Signatures
We now define syntax and security of a digital signature scheme. Let \(\mathsf {par}\) be common system parameters shared among all participants.
Definition 7
(Digital Signature). A digital signature scheme \({\mathsf {SIG}}\) is defined as a triple of algorithms \({\mathsf {SIG}}= ({\mathsf {Gen}}, {\mathsf {Sign}}, {\mathsf {Ver}})\).
-
The key generation algorithm \({\mathsf {Gen}}(\mathsf {par})\) returns the public and secret keys \((pk,sk)\).
-
The signing algorithm \({\mathsf {Sign}}(sk,{m})\) returns a signature \(\sigma \).
-
The deterministic verification algorithm \({\mathsf {Ver}}(pk, {m},\sigma )\) returns 1 (accept) or 0 (reject).
We require that for all \((pk,sk)\in {\mathsf {Gen}}(\mathsf {par})\), all messages \({m}\in \{0,1\}^*\), we have \({\mathsf {Ver}}(pk,{m},{\mathsf {Sign}}(sk,{m}))=1\).
Definition 8
(Multi-user Security). A signature scheme \({\mathsf {SIG}}\) is said to be \((t,\varepsilon ,N,Q_s)\)-\({\mathsf {MU\text{- }SUF\text{- }CMA}}\) secure (multi-user strongly unforgeable against chosen message attacks) if for all adversaries \(\mathcal {A}\) running in time at most t and making at most \(Q_s\) queries to the signing oracle,

where on the j-th query \((i_j,{m}_j)\in [N] \times \{0,1\}^*\) (\(j \in [Q_s]\)) the signing oracle \(\textsc {Sign}\) returns  to \(\mathcal {A}\), i.e., a signature on message \(m_j\) under public-key \(pk_{i_j}\).
to \(\mathcal {A}\), i.e., a signature on message \(m_j\) under public-key \(pk_{i_j}\).
We stress that an adversary in particular breaks multi-user security if he asks for a signature on message \({m}\) under \(pk_1\) and submits a valid forgery on the same message \({m}\) under \(pk_2\).
The first condition in the probability statement of Definition 8 is called the correctness condition, the second condition is called the freshness condition. Definition 8 covers strong security in the sense that a new signature on a previously queried message is considered as a fresh forgery. For standard (non-strong) \({{\mathsf {MU\text{- }UF\text{- }CMA}}} \) security (multi-user unforgeablility against chosen message attack) we modify the freshness condition in the experiment to \((i^*,{m}^*) \notin \{(i_j, {m}_j, ) \mid j \in [Q_s]\}\), i.e., to break the scheme the adversary has to come up with a signature on a message-key pair which has not been queried to the signing oracle. We also define \((t, \varepsilon ,N)\)-\({\mathsf {MU\text{- }UF\text{- }KOA}}\) security (multi-user unforgeability against key only attack) as \((t,\varepsilon ,N,0)\)-\({{\mathsf {MU\text{- }UF\text{- }CMA}}} \) security, i.e. \(Q_s=0\), the adversary is not allowed to make any signing query.
Definition 9
(Single-user Security). In the single-user setting, i.e. \(N=1\) users, \((t,\varepsilon ,Q_s)\)-\({\mathsf {SUF\text{- }CMA}}\) security (strong unforgeablility against chosen message attacks) is defined as \((t,\varepsilon ,1,Q_s)\)-\({\mathsf {MU\text{- }SUF\text{- }CMA}}\) security. Similarly, standard (non-strong) \((t,\varepsilon ,Q_s)\)-\({\mathsf {UF\text{- }CMA}}\) security (unforgeablility against chosen message attack) is defined as \((t,\varepsilon ,1,Q_s)\)-\({{\mathsf {MU\text{- }UF\text{- }CMA}}} \) security. Further, \((t,\varepsilon )\)-\(\mathsf {UF}\)-\(\mathsf {KOA}\) security (unforgeablility against key-only attack) is defined as \((t,\varepsilon ,1,0)\)-\(\mathsf {MU \text{- }SUF}\)-\( \mathsf {CMA}\) security, i.e., \(N=1\) users and \(Q_s=0\) signing queries.
Security in the random oracle model. The security of identification and signature schemes containing a hash function can be analyzed in the random oracle model [8]. In this model hash values can only be accessed by an adversary through queries to an oracle H. On input x this oracle returns a uniformly random output H(x) which is consistent with previous queries for input x. Using the random oracle model, the maximal number of queries to H becomes a parameter in the concrete security notions. For example, for \((t,\varepsilon ,N,Q_s,Q_h)\)-\({\mathsf {MU\text{- }SUF\text{- }CMA}}\) security we consider all adversaries making at most \(Q_h\) queries to the random oracle. We make the convention that each query to the random oracle made during a signing query is counted as the adversary’s random oracle query, meaning \(Q_h \ge Q_s\).
2.4 Signatures from Identification Schemes
Let \({\mathsf {ID}}:=({\mathsf {IGen}},{\mathsf {P}},\mathsf {ChSet},{\mathsf {V}})\) be a canonical identification scheme. By the generalized Fiat-Shamir transformation [6], the signature scheme \({\mathsf {SIG}}[{\mathsf {ID}}]:=({\mathsf {Gen}},{\mathsf {Sign}}, {\mathsf {Ver}})\) from \({\mathsf {ID}}\) is defined as follows. \(\mathsf {par}\) contains the system parameters of \({\mathsf {ID}}\) and a hash function \(H:\{0,1\}^* \rightarrow \mathsf {ChSet}\).

In some variants of the Fiat-Shamir transform, the hash additionally inputs some public parameters, for example \(h=H(pk,R,{m})\).
We call \({\mathsf {ID}}\) commitment-recoverable, if \({\mathsf {V}}(pk,R,h,s)\) first recomputes \(R' = {\mathsf {V}}'(pk,h,s)\) and then outputs 1 iff \(R' = R\). For commitment-recoverable \({\mathsf {ID}}\), we can define an alternative Fiat-Shamir transformation \({\mathsf {SIG}}'[{\mathsf {ID}}]:=({\mathsf {Gen}},{\mathsf {Sign}}',{\mathsf {Ver}}')\), where \({\mathsf {Gen}}\) is as in \({\mathsf {SIG}}[{\mathsf {ID}}]\). Algorithm \({\mathsf {Sign}}'(sk,{m})\) is defined as \({\mathsf {Sign}}(sk,{m})\) with the modified output \(\sigma ' = (h,s)\). Algorithm \({\mathsf {Ver}}'(pk,{m},\sigma ')\) first parses \(\sigma '=(h,s)\), then recomputes the commitment as \(R' := {\mathsf {V}}'(pk,h,s)\), and finally returns 1 iff \(H(R',{m})=h\).
Since \(\sigma =(R,s)\) can be publicly transformed into \(\sigma '=(h,s)\) and vice-cersa, \({\mathsf {SIG}}[{\mathsf {ID}}]\) and \({\mathsf {SIG}}'[{\mathsf {ID}}]\) are equivalent in terms of security. On the one hand, the alternative Fiat-Shamir transform yields shorter signatures if \(h\in \mathsf {ChSet}\) has a smaller representation size than response s. On the other hand, signatures of the Fiat-Shamir transform maintain their algebraic structure which in some cases enables useful properties such as batch verification.
3 Security Implications
In this section we will prove the following two main results.
Theorem 3
(Main Theorem 1 ). Suppose \({\mathsf {ID}}\) is \(\mathsf {SS}\), \(\mathsf {HVZK}\), \(\mathsf {RSR}\) and has \(\alpha \) bit min-entropy. If \({\mathsf {ID}}\) is \((t,\varepsilon )\)-\(\mathsf {KR}\text{- }\mathsf {KOA}\) secure then \({\mathsf {SIG}}[{\mathsf {ID}}]\) is \((t',\varepsilon ',Q_s,Q_h)\)-\({\mathsf {UF\text{- }CMA}}\)-secure and \((t'',\varepsilon '',N,Q_s,Q_h)\)-\({{\mathsf {MU\text{- }UF\text{- }CMA}}} \)-secure in the programmable random oracle model, where
The proof of Theorem 3 is obtained by combining Lemmas 3–8 below and using \(Q_h \le t'-1\).
Theorem 4
(Main Theorem 2 ). Suppose \({\mathsf {SIG}}[{\mathsf {ID}}]\) is \(\mathsf {HVZK}\), \(\mathsf {RSR}\) and has \(\alpha \) bit min-entropy. If \({\mathsf {SIG}}[{\mathsf {ID}}]\) is \((t,\varepsilon ,Q_h+Q_s)\)-\({\mathsf {UF\text{- }KOA}}\) secure then \({\mathsf {SIG}}[{\mathsf {ID}}]\) is \((t',\varepsilon ',N,Q_s,Q_h)\)-\({{\mathsf {MU\text{- }UF\text{- }CMA}}} \) secure in the programmable random oracle model, where
and \(Q_s\), \(Q_h\) are upper bounds on the number of signing and hash queries in the \({{\mathsf {MU\text{- }UF\text{- }CMA}}} \) experiment, respectively.
The proof of Theorem 4 is obtained by combining Lemmas 7 and 8 below.
Here we present the proofs of Lemmas 1 and 3 (a new Multi-Instance Reset Lemma and an application of it), Lemmas 7 and 8 (the implication of “\({\mathsf {UF\text{- }KOA}}\xrightarrow {} {{\mathsf {MU\text{- }UF\text{- }CMA}}} \)”), which are the main contributions of this paper. All remaining proofs are deferred to [35].
3.1 Multi-Instance Reset Lemma
We first state a new reset lemma that we will later use in the proof of Theorem 3. It is presented in the style of Bellare and Neven’s General Forking Lemma [5] and does not talk about signatures or identification protocols. It is a generalization to many parallel instances of the Reset Lemma [6], which is obtained by setting \(N=1\).
Lemma 1
(Multi-Instance Reset Lemma). Fix an integer \(N \ge 1\) and a non-empty set H. Let \(\mathcal {C}\) be a randomized algorithm that on input (I, h) returns a pair \((b,\sigma )\), where b is a bit and \(\sigma \) is called the side output. Let \({\mathsf {IG}}\) be a randomized algorithm that we call the input generator. The accepting probability of \(\mathcal {C}\) is defined as

The (multi-instance) reset algorithm \(\mathcal {R}_\mathcal {C}\) associated to \(\mathcal {C}\) is the randomized algorithm that takes input \(I_1, \ldots , I_N\) and proceeds as follows.

Let  . Then
. Then
Proof
For fixed instance I and coins \(\rho \), we define the probabilities

As for fixed \(I, \rho \), the two events \(b=1\) and \(b'=1\) are independent and we obtain
where the additive factor \(\frac{1}{|H|}\) accounts for the fact that \(\Pr [h'=h]=1/|H|\). With the expectation taken over  and random coins \(\rho \), we bound
and random coins \(\rho \), we bound
Above, we used (1), Jensen’s inequalityFootnote 5 applied to the convex function \(\varphi (X):=X\cdot (X-1/|H|)\), and the fact that \(\mathsf {acc}=\mathsf {E}_{I,\rho }[ \mathsf {acc}(I,\rho )]\).
Next, consider the random variables \(b_{i^*}\) and \(b_j'\) (\(j \in [N]\)) as defined during in the execution of \(\mathcal {R}_\mathcal {A}(I_1, \ldots , I_N)\). Using \(\mathsf {acc}=\Pr [b_{i^*}=1]\) and \(\Pr [b_j'=1 \wedge b_{i^*}=1] = \mathsf {E}_{I_{i^*},\rho _{i^*}}\left[ \mathsf {res}(I_{i^*},\rho _{i^*}) \right] \), we obtain
Finally, we bound

and

to establish

This completes the proof. \(\square \)
3.2 Proof of the Main Theorems
Lemma 2
( \(\mathsf {XXX}\text{- }\mathsf {KOA}\xrightarrow {} \mathsf {XXX}\text{- }\mathsf {PA}\) ). Let \(\mathsf {XXX}\in \{\mathsf {KR},\mathsf {IMP},\mathsf {PIMP}\}\). If \({\mathsf {ID}}\) is \((t,\varepsilon ,Q_\textsc {Ch})\)-\(\mathsf {XXX}\text{- }\mathsf {KOA}\) secure and \(\mathsf {HVZK}\), then \({\mathsf {ID}}\) is \((\approx t,\varepsilon ,Q_\textsc {Ch},Q_\textsc {O})\)-\(\mathsf {XXX}\text{- }\mathsf {PA}\) secure.
The proof is given in the full version [35].
Lemma 3 below proving that \(\mathsf {KR}\text{- }\mathsf {KOA}\) tightly implies \(\mathsf {IMP}\text{- }\mathsf {KOA}\) uses the Multi-Instance Reset Lemma and that takes advantage of \({\mathsf {ID}}\)’s random self-reducibility (\(\mathsf {RSR}\)).
Lemma 3
( \(\mathsf {KR}\text{- }\mathsf {KOA}\xrightarrow {\mathbf{rewinding}} \mathsf {IMP}\text{- }\mathsf {KOA}\) ). If \({\mathsf {ID}}\) is \((t,\varepsilon )\)-\(\mathsf {KR}\text{- }\mathsf {KOA}\) secure, \(\mathsf {SS}\) and \(\mathsf {RSR}\), then \({\mathsf {ID}}\) is \((t',\varepsilon ')\)-\(\mathsf {IMP}\text{- }\mathsf {KOA}\) secure, where for any \(N \ge 1\),
In particular, the two success ratios are related as
We remark that without \(\mathsf {RSR}\), we can still obtain the weaker bounds \(\varepsilon \ge \varepsilon ' (\varepsilon '-\frac{1}{|\mathsf {ChSet}|})\), \(t\approx 2t'\).
Proof
We first show how to derive (3) from (2). If \(\varepsilon ' \le 1/|\mathsf {ChSet}|\), then (3) holds trivially. Assuming \(\varepsilon ' > 1/|\mathsf {ChSet}|\), we set \(N:=(\varepsilon '-1/|\mathsf {ChSet}|)^{-1}\) to obtain \(t\approx 2t'/(\varepsilon '-1/|\mathsf {ChSet}|)\) and \(\varepsilon \ge (1-\frac{1}{e})^2 \ge \frac{1}{3}\). Dividing \(\varepsilon \) by t yields (3).
To prove (2), let \(\mathcal {A}\) be an adversary against the \((t',\varepsilon ')\)-\(\mathsf {IMP}\text{- }\mathsf {KOA}\)-security of \({\mathsf {ID}}\). We now build an adversary \(\mathcal {B}\) against the \((t,\varepsilon )\)-\(\mathsf {KR}\text{- }\mathsf {KOA}\) security of \({\mathsf {ID}}\), with \((t,\varepsilon )\) as claimed in (2).
We use the Multi-Instance Reset Lemma (Lemma 1), where \(H:=\mathsf {ChSet}\) and \({\mathsf {IG}}\) runs  and returns \(pk\) as instance I. We first define adversary \(\mathcal {C}(pk,h; \rho )\) that executes \(\mathcal {A}(pk;\rho )\), answers \(\mathcal {A}\)’s single query R with h, and finally receives s from \(\mathcal {A}\). If transcript (R, h, s) is valid with respect to \(pk\) (i.e., \({\mathsf {V}}(pk,R,h,s)=1)\)), \(\mathcal {C}\) returns \((b=1, \sigma =(R,h,s))\); otherwise, it returns \((b=0, \epsilon )\). By construction, \(\mathcal {C}\) returns \(b=1\) iff \(\mathcal {A}\) is successful: \(\mathsf {acc}=\varepsilon '.\)
and returns \(pk\) as instance I. We first define adversary \(\mathcal {C}(pk,h; \rho )\) that executes \(\mathcal {A}(pk;\rho )\), answers \(\mathcal {A}\)’s single query R with h, and finally receives s from \(\mathcal {A}\). If transcript (R, h, s) is valid with respect to \(pk\) (i.e., \({\mathsf {V}}(pk,R,h,s)=1)\)), \(\mathcal {C}\) returns \((b=1, \sigma =(R,h,s))\); otherwise, it returns \((b=0, \epsilon )\). By construction, \(\mathcal {C}\) returns \(b=1\) iff \(\mathcal {A}\) is successful: \(\mathsf {acc}=\varepsilon '.\)
Adversary \(\mathcal {B}\) is defined as follows. For each \(i\in [N]\), it uses the \(\mathsf {RSR}\) property of \({\mathsf {ID}}\) to generate a fresh public key/trapdoor pair  Next, it runs
Next, it runs  with \(\mathcal {C}\) defined above. If \(i^* \ge 1\), then both transcripts \(\sigma =(R,h,s)\) and \(\sigma '=(R,h',s')\) are valid with respect to \(pk_{i^*}\) and \(h\ne h'\). \(\mathcal {B}\) uses the \(\mathsf {SS}\) property of \({\mathsf {ID}}\) and computes \(sk_{i^*}\leftarrow {\mathsf {Ext}}(pk_{i^*},R,h,s,h',s')\). Finally, using the \(\mathsf {RSR}\) property of \({\mathsf {ID}}\), it returns \(sk={\mathsf {Derand}}(pk_{i^*},sk_{i^*}, \tau _{i^*})\) and terminates. By construction, \(\mathcal {B}\) is successful iff \(\mathcal {R}_\mathcal {C}\) is. By Lemma 1 we can bound \(\mathcal {B}\)’s success probability as
with \(\mathcal {C}\) defined above. If \(i^* \ge 1\), then both transcripts \(\sigma =(R,h,s)\) and \(\sigma '=(R,h',s')\) are valid with respect to \(pk_{i^*}\) and \(h\ne h'\). \(\mathcal {B}\) uses the \(\mathsf {SS}\) property of \({\mathsf {ID}}\) and computes \(sk_{i^*}\leftarrow {\mathsf {Ext}}(pk_{i^*},R,h,s,h',s')\). Finally, using the \(\mathsf {RSR}\) property of \({\mathsf {ID}}\), it returns \(sk={\mathsf {Derand}}(pk_{i^*},sk_{i^*}, \tau _{i^*})\) and terminates. By construction, \(\mathcal {B}\) is successful iff \(\mathcal {R}_\mathcal {C}\) is. By Lemma 1 we can bound \(\mathcal {B}\)’s success probability as
The running time \(t\) of \(\mathcal {B}\) is that of \(\mathcal {R}_\mathcal {C}\), meaning \(2 Nt'\) plus the N times the time to run the \({\mathsf {Rerand}}\) and \({\mathsf {Derand}}\) algorithms of \(\mathsf {RSR}\) plus the time to run the \({\mathsf {Ext}}\) algorithm of \(\mathsf {SS}\). We write \(t\approx 2Nt'\) to indicate that this is the dominating running time of \(\mathcal {B}\). \(\square \)
Lemma 4
( \(\mathsf {IMP}\text{- }\mathsf {KOA}\xrightarrow {\mathbf{loss\,}Q} \mathsf {PIMP}\text{- }\mathsf {KOA}\) ). If \({\mathsf {ID}}\) is \((t,\varepsilon )\)-\(\mathsf {IMP}\text{- }\mathsf {KOA}\) secure, then \({\mathsf {ID}}\) is \((t',\varepsilon ',Q_\textsc {Ch})\)-\(\mathsf {PIMP}\text{- }\mathsf {KOA}\) secure, where
The proof is given in the full version [35].
Lemma 5
( \(\mathsf {PIMP}\text{- }\mathsf {KOA}\xrightarrow {\mathbf{PRO}} {\mathsf {UF\text{- }KOA}}\) ). If \({\mathsf {ID}}\) is \((t,\varepsilon ,Q_\textsc {Ch})\)-\(\mathsf {PIMP}\text{- }\mathsf {KOA}\) secure, then \({\mathsf {SIG}}[{\mathsf {ID}}]\) is \((t',\varepsilon ',Q_h)\)-\({\mathsf {UF\text{- }KOA}}\) secure in the programmable random oracle model, where
The proof is given in the full version [35].
The following lemma is a special case of Lemma 8 (with a slightly improved bound).
Lemma 6
( \({\mathsf {UF\text{- }KOA}}\xrightarrow {\mathbf{PRO}} {\mathsf {UF\text{- }CMA}}\) ). Suppose \({\mathsf {ID}}\) is \(\mathsf {HVZK}\) and has \(\alpha \) bit min-entropy. If \({\mathsf {SIG}}[{\mathsf {ID}}]\) is \((t,\varepsilon ,Q_h)\)-\({\mathsf {UF\text{- }KOA}}\) secure, then \({\mathsf {SIG}}[{\mathsf {ID}}]\) is \((t',\varepsilon ',Q_s,Q_h)\)-\({\mathsf {UF\text{- }CMA}}\) secure in the programmable random oracle model, where
and \(Q_s\), \(Q_h\) are upper bounds on the number of signing and hash queries in the \({\mathsf {UF\text{- }CMA}}\) experiment, respectively.
Lemma 7
( \({\mathsf {UF\text{- }KOA}}\xrightarrow {\mathbf{RSR}} {\mathsf {MU\text{- }UF\text{- }KOA}}\) ). Suppose \({\mathsf {ID}}\) is \(\mathsf {RSR}\). If \({\mathsf {SIG}}[{\mathsf {ID}}]\) is \((t,\varepsilon )\)-\({\mathsf {UF\text{- }KOA}}\) secure, then \({\mathsf {SIG}}[{\mathsf {ID}}]\) is \((t',\varepsilon ',N)\)-\({\mathsf {MU\text{- }UF\text{- }KOA}}\) secure, where
Note that without the \(\mathsf {RSR}\) property one can use the generic bounds from [25] to obtain a non-tight bound with a loss of N.
Proof
Let \(\mathcal {A}\) be an algorithm that breaks \((t',\varepsilon ',N)\)-\({\mathsf {MU\text{- }UF\text{- }KOA}}\) security of \({\mathsf {SIG}}[{\mathsf {ID}}]\). We will describe an adversary \(\mathcal {B}\) invoking \(\mathcal {A}\) that breaks \((t,\varepsilon )\)-\({\mathsf {UF\text{- }KOA}}\) security of \({\mathsf {SIG}}[{\mathsf {ID}}]\) with \((t,\varepsilon )\) as stated in the lemma. Adversary \(\mathcal {B}\) is executed in the \({\mathsf {UF\text{- }KOA}}\) experiment and obtains a public-key \(pk\).
Simulation of public-keys input to \(\mathcal {A}\). For each \(i \in [N]\), \(\mathcal {B}\) generates  by using the \(\mathsf {RSR}\) property of \({\mathsf {ID}}\). Then \(\mathcal {B}\) runs \(\mathcal {A}\) on input \((pk_1,\ldots , pk_N)\).
by using the \(\mathsf {RSR}\) property of \({\mathsf {ID}}\). Then \(\mathcal {B}\) runs \(\mathcal {A}\) on input \((pk_1,\ldots , pk_N)\).
Forgery. Eventually, \(\mathcal {A}\) will submit its forgery \((i^*,{m}^*,\sigma ^*:=(R^*,s^*))\) in the \({\mathsf {MU\text{- }UF\text{- }KOA}}\) experiment. \(\mathcal {B}\) computes \(h^*=H({m}^*,R^*)\) and runs  . By the \(\mathsf {RSR}\) property of \({\mathsf {ID}}\), the random variables \((pk,R^*, h^*,s)\) and \((pk_{i^*},R^*,h^*,s^*)\) are identically distributed. If \(\sigma ^*\) is a valid signature on message \({m}^*\) under \(pk_{i^*}\), then \((R^*,s)\) is also a valid signature on \({m}^*\) under \(pk\). Thus, we have \(\varepsilon =\varepsilon '\). The running time \(t\) of \(\mathcal {B}\) is \(t'\) plus the N times the time to run the \({\mathsf {Rerand}}\) and \({\mathsf {Tran}}\) algorithms of \(\mathsf {RSR}\). We again write \(t\approx t'\). \(\square \)
. By the \(\mathsf {RSR}\) property of \({\mathsf {ID}}\), the random variables \((pk,R^*, h^*,s)\) and \((pk_{i^*},R^*,h^*,s^*)\) are identically distributed. If \(\sigma ^*\) is a valid signature on message \({m}^*\) under \(pk_{i^*}\), then \((R^*,s)\) is also a valid signature on \({m}^*\) under \(pk\). Thus, we have \(\varepsilon =\varepsilon '\). The running time \(t\) of \(\mathcal {B}\) is \(t'\) plus the N times the time to run the \({\mathsf {Rerand}}\) and \({\mathsf {Tran}}\) algorithms of \(\mathsf {RSR}\). We again write \(t\approx t'\). \(\square \)
Lemma 8
( \({\mathsf {MU\text{- }UF\text{- }KOA}}\xrightarrow {\mathbf{PRO}} {{\mathsf {MU\text{- }UF\text{- }CMA}}} \) ). Suppose \({\mathsf {ID}}\) is \(\mathsf {HVZK}\) and has \(\alpha \) bit min-entropy. If \({\mathsf {SIG}}[{\mathsf {ID}}]\) is \((t,\varepsilon ,N,Q_h)\)-\({\mathsf {MU\text{- }UF\text{- }KOA}}\) secure, then \({\mathsf {SIG}}[{\mathsf {ID}}]\) is \((t',\varepsilon ',N,Q_s,Q_h)\)-\({{\mathsf {MU\text{- }UF\text{- }CMA}}} \) secure in the programmable random oracle model, where
and N is the number of users and \(Q_s\) and \(Q_h\) are upper bounds on the number of signing and hash queries in the \({{\mathsf {MU\text{- }UF\text{- }CMA}}} \) experiment, respectively.
Proof
Let \(\mathcal {A}\) be an algorithm that breaks \((t',\varepsilon ',N,Q_s,Q_h)\)-\({{\mathsf {MU\text{- }UF\text{- }CMA}}} \) security of \({\mathsf {SIG}}[{\mathsf {ID}}]\). We will describe an adversary \(\mathcal {B}\) invoking \(\mathcal {A}\) that breaks \((t,\varepsilon ,N,Q_h)\)-\({\mathsf {MU\text{- }UF\text{- }KOA}}\) security of \({\mathsf {SIG}}[{\mathsf {ID}}]\) with \((t,\varepsilon )\) as stated in the lemma. Adversary \(\mathcal {B}\) is executed in the \({\mathsf {MU\text{- }UF\text{- }KOA}}\) experiment and obtains public-keys \((pk_1,\ldots , pk_N)\), and has access to a random oracle H.
Preparation of public-keys. For each \(i \in [N]\), adversary \(\mathcal {B}\) picks a secret bit  . If \(b_i=1\) then \(\mathcal {B}\) defines \(pk'_i:=pk_i\), else \(\mathcal {B}\) generates the key-pair
. If \(b_i=1\) then \(\mathcal {B}\) defines \(pk'_i:=pk_i\), else \(\mathcal {B}\) generates the key-pair  itself. We note that all simulated public-keys are correctly distributed.
itself. We note that all simulated public-keys are correctly distributed.
Adversary \(\mathcal {B}\) runs \(\mathcal {A}\) on input \((pk'_1,\ldots ,pk'_N)\) answering hash queries to random oracle \(H'\) and signing queries as follows.
Simulation of hash queries. A hash query \(H'(R,{m})\) is answered by \(\mathcal {B}\) by querying its own hash oracle \(H(R,{m})\) and returning its answer.
Simulation of signing queries. On \(\mathcal {A}\)’s j-th signature query \((i_j,{m}_j)\), \(\mathcal {B}\) returns a signature \(\sigma _j\) on message \({m}_j\) under \(pk_{i_j}\) according to the following case distinction.
-
Case A: \(b_{i_j}=0\). In that case \(sk'_{i_j}\) is known to \(\mathcal {B}\) and the signature is computed as
 . Note that this involves \(\mathcal {B}\) making a hash query and defining \(H'(R_j,{m}_j):=H(R_j,{m}_j)\).
. Note that this involves \(\mathcal {B}\) making a hash query and defining \(H'(R_j,{m}_j):=H(R_j,{m}_j)\). -
Case B: \(b_{i_j} = 1\). In that case \(sk'_{i_j}\) is unknown to \(\mathcal {B}\) and the signature is computed using the \(\mathsf {HVZK}\) property of \({\mathsf {ID}}\). Concretely, \(\mathcal {B}\) runs
 . If hash value \(H'(R_j,{m}_j)\) was already defined (via one of \(\mathcal {A}\)’s hash/signing queries) and \(H'(R_j,{m}_j) \ne h_j\), \(\mathcal {B}\) aborts. Otherwise, it defines the random oracle $$\begin{aligned} H'(R_j,{m}_j):=h_j \end{aligned}$$(4)
. If hash value \(H'(R_j,{m}_j)\) was already defined (via one of \(\mathcal {A}\)’s hash/signing queries) and \(H'(R_j,{m}_j) \ne h_j\), \(\mathcal {B}\) aborts. Otherwise, it defines the random oracle $$\begin{aligned} H'(R_j,{m}_j):=h_j \end{aligned}$$(4)and returns \(\sigma _j := (R_j,s_j)\), which is a correctly distributed valid signatures on \({m}_j\) under \(pk_{i_j}\). Note that by (4), \(\mathcal {B}\) makes H and \(H'\) inconsistent, i.e., we have \(H(R_j,{m}_j) \ne H'(R_j,{m}_j)\) with high probability. Also note that for each signing query, \(\mathcal {B}\) aborts with probability at most \(Q_h/2^\alpha \) because \(R_j\) has min-entropy \(\alpha \). Since the number of signing queries is bounded by \(Q_s\), \(\mathcal {B}\) aborts overall with probability at most \(Q_hQ_s/2^\alpha \).
Forgery. Eventually, \(\mathcal {A}\) will submit its forgery \((i^*,{m}^*,\sigma ^*:=(R^*,s^*))\). We assume that it is a valid forgery in the \({{\mathsf {MU\text{- }UF\text{- }CMA}}} \) experiment, i.e., for \(h^* = H'(R^*,{m}^*)\) we have \({\mathsf {V}}(pk'_{i^*}, R^*,h^*,s^*)=1\). Furthermore, it satisfies the freshness condition, i.e.,
After receiving \(\mathcal {A}\)’s forgery, \(\mathcal {B}\) computes a forgery for the \({\mathsf {MU\text{- }UF\text{- }KOA}}\) experiment according to the following case distinction.
-
Case 1: There exists a \(j \in [Q_s]\) such that \(({m}^*,R^*)=({m}_j,R_j)\). (If there is more than one j, fix any of them.) In that case we have and \(h^*=h_j\) and furthermore \(i^* \ne i_j\) by the freshness condition (5).
-
Case 1a: \((b_{i^*}=1)\) and \((b_{i_j}=0)\). Then the hash value \(h^*=H'(R^*,{m}^*)\) was not programmed by \(\mathcal {B}\) in (4). That means \(h^*=H'(R^*,{m}^*)=H(R^*,{m}^*)\) and \(\mathcal {B}\) returns \((i^*,{m}^*,(R^*,s^*))\) as a valid forgery to its \({\mathsf {MU\text{- }UF\text{- }KOA}}\) experiment.
-
Case 1b: \((b_{i^*}=b_{i_j})\) or \((b_{i^*}=0 \wedge b_{i_j}=1)\). Then \(\mathcal {B}\) aborts.
Note that in case 1 we always have \(i^* \ne i_j\) and therefore \(\mathcal {B}\) does not abort with probability 1 / 4 in which case it outputs a valid forgery.
-
-
Case 2: For all \(j \in [Q_s]\) we have: \(({m}^*,R^*) \ne ({m}_j,R_j)\).
-
Case 2a: \(b_{i^*}=1\). Then the hash value \(h^*=H'(R^*,{m}^*)\) was not programmed by \(\mathcal {B}\) in (4). That means \(h^*=H'(R^*,{m}^*)=H(R^*,{m}^*)\) and \(\mathcal {B}\) returns \((i^*,{m}^*,(R^*,s^*))\) as a valid forgery to its \({\mathsf {MU\text{- }UF\text{- }KOA}}\) experiment.
-
Case 2b: \(b_{i^*}=0\). Then \(\mathcal {B}\) aborts.
Note that in case 2, \(\mathcal {B}\) does not abort with probability 1 / 2 in which case it outputs a valid forgery.
-
Overall, \(\mathcal {B}\) returns a valid forgery of \({\mathsf {MU\text{- }UF\text{- }KOA}}\) experiment with probability
The running time of \(\mathcal {B}\) is that of \(\mathcal {A}\) plus the \(Q_s\) executions of \(\mathsf {Sim}\). We write \(t' \approx t\). This completes the proof. \(\square \)
If \(s\) in \({\mathsf {ID}}\) is uniquely defined by \((pk,R,h)\) (e.g., as in the Schnorr identification scheme), then one can show the above proof even implies \({\mathsf {MU\text{- }SUF\text{- }CMA}}\) security of \({\mathsf {SIG}}[{\mathsf {ID}}]\). The simulation of hash and signing queries is the same as in the above proof. Let \((i^*,{m}^*,R^*,s^*)\) be \(\mathcal {A}\)’s forgery. The freshness condition of the \({\mathsf {MU\text{- }SUF\text{- }CMA}}\) experiment says that \((i^*,{m}^*,R^*,s^*) \notin \{(i_j,{m}_j,R_j,s_j): j \in [Q_s]\}\). Together with the uniqueness of \({\mathsf {ID}}\), this implies \((i^*,{m}^*,R^*) \notin \{(i_j,{m}_j,R_j): j \in [Q_s]\}\). If \((i^*,{m}^*) \not \in \{(i_j,{m}_j) : j \in [Q_s]\}\), then \(\mathcal {B}\) can break \({\mathsf {MU\text{- }UF\text{- }KOA}}\) security by the same case distinction as in the proof above. Otherwise, we have \(R^* \notin \{R_j: j \in [Q_s] \}\), in which case we can argue as in case 2.
4 Impossibility Results
In this section, we show that Theorems 3 and 4 from the previous section are optimal in the sense that the security reduction requires: rewinding (Lemma 9), security loss of at least O(Q) (Lemma 10) and programmability of random oracles (Lemmas 11 and 12).
Let \(\mathsf {X}\) and \(\mathsf {Y}\) be some hard cryptographic problems, defined through a (possibly) interactive experiment. A black-box reduction \(\mathcal {R}\) from \(\mathsf {X}\) to \(\mathsf {Y}\) is an algorithm that, given black-box access to an adversary \(\mathcal {A}\) breaking problem \(\mathsf {Y}\), breaks problem \(\mathsf {X}\). If \(\mathsf {X}\) and \(\mathsf {Y}\) are security notions for identification or signatures schemes, then a reduction \(\mathcal {R}\) is called key-preserving, if \(\mathcal {R}\) only makes calls to \(\mathcal {A}\) with the same \(pk\) that it obtained by its own problem \(\mathsf {X}\). All our reductions considered in this section are key-preserving. All proofs from this section are given in the full version [35].
Lemma 9
 If there is a key-preserving reduction \(\mathcal {R}\) that \((t_\mathcal {R},\varepsilon _\mathcal {R})\)-breaks \(\mathsf {KR}\text{- }\mathsf {KOA}\) security of \({\mathsf {ID}}\) with one-time black-box access to an adversary \(\mathcal {A}\) that \((t_\mathcal {A},\varepsilon _\mathcal {A})\)-breaks \(\mathsf {IMP}\text{- }\mathsf {KOA}\) security of \({\mathsf {ID}}\), then there exists an algorithm \(\mathcal {M}\) that \((t_\mathcal {M},\varepsilon _\mathcal {M},Q_\textsc {O})\)-breaks \(\mathsf {IMP}\text{- }\mathsf {AA}\) security of \({\mathsf {ID}}\), where
If there is a key-preserving reduction \(\mathcal {R}\) that \((t_\mathcal {R},\varepsilon _\mathcal {R})\)-breaks \(\mathsf {KR}\text{- }\mathsf {KOA}\) security of \({\mathsf {ID}}\) with one-time black-box access to an adversary \(\mathcal {A}\) that \((t_\mathcal {A},\varepsilon _\mathcal {A})\)-breaks \(\mathsf {IMP}\text{- }\mathsf {KOA}\) security of \({\mathsf {ID}}\), then there exists an algorithm \(\mathcal {M}\) that \((t_\mathcal {M},\varepsilon _\mathcal {M},Q_\textsc {O})\)-breaks \(\mathsf {IMP}\text{- }\mathsf {AA}\) security of \({\mathsf {ID}}\), where
For our next impossibility result, we will require the following definition for identification schemes.
Definition 10
(Concurrent (Weak) Impersonation against Man-in-the-Middle Attacks). A canonical identification \({\mathsf {ID}}\) is said to be \((t, \varepsilon , Q_\textsc {Ch},Q_\textsc {O})\)-\(\mathsf {IMP}\text{- }\mathsf {MIM}\) secure (impersonation against man-in-the-middle attacks) if for all adversaries \(\mathcal {A}\) running in time at most t and adaptively making at most \(Q_\textsc {O}\) queries to the prover oracle \(\textsc {Prover}\) and \(Q_\textsc {Ch}\) queries to the challenge oracle \(\textsc {Ch}\),

where oracles \(\textsc {Prover}\) and \(\textsc {Ch}\) are defined as in Definition 2. We define weak impersonation against man-in-the-middle attack (\(\mathsf {wIMP}\text{- }\mathsf {MIM}\)) by restricting \(R_{i^*} \in \{R'_1,\ldots ,R'_{Q_\textsc {O}} \}\).
We remark that \(\mathsf {wIMP}\text{- }\mathsf {MIM}\) is a non-standard definition without any practical relevance, but it will only be used for showing negative results. The following generalizes a result by Seurin [43] to canonical identification schemes.
Lemma 10
 Suppose that \({\mathsf {ID}}\) has \(\alpha \) bit min-entropy and there is a key-preserving reduction \(\mathcal {R}\) that \((t_\mathcal {R},\varepsilon _\mathcal {R})\)-breaks \(\mathsf {IMP}\text{- }\mathsf {KOA}\) security of \({\mathsf {ID}}\) with n
-time black-box access to an adversary \(\mathcal {A}\) that \((t_\mathcal {A},\varepsilon _\mathcal {A},Q_\textsc {Ch})\)-breaks \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) security of \({\mathsf {ID}}\). Then there exists an algorithm \(\mathcal {M}\) that \((t_\mathcal {M},\varepsilon _\mathcal {M}, 1, Q_\textsc {O}=nQ_\textsc {Ch})\)-breaks \(\mathsf {IMP}\text{- }\mathsf {MIM}\) security of \({\mathsf {ID}}\), where
Suppose that \({\mathsf {ID}}\) has \(\alpha \) bit min-entropy and there is a key-preserving reduction \(\mathcal {R}\) that \((t_\mathcal {R},\varepsilon _\mathcal {R})\)-breaks \(\mathsf {IMP}\text{- }\mathsf {KOA}\) security of \({\mathsf {ID}}\) with n
-time black-box access to an adversary \(\mathcal {A}\) that \((t_\mathcal {A},\varepsilon _\mathcal {A},Q_\textsc {Ch})\)-breaks \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) security of \({\mathsf {ID}}\). Then there exists an algorithm \(\mathcal {M}\) that \((t_\mathcal {M},\varepsilon _\mathcal {M}, 1, Q_\textsc {O}=nQ_\textsc {Ch})\)-breaks \(\mathsf {IMP}\text{- }\mathsf {MIM}\) security of \({\mathsf {ID}}\), where
For a precise analysis of the function \(\ln \big ((1-\varepsilon _{\mathcal {A}})^{-1} \big )\), we refer to [43]. For our purpose, it is sufficient that for a concrete choice of \(\varepsilon _{\mathcal {A}}\), there is a constant c such that \(c\cdot \varepsilon _{\mathcal {A}}=\ln \big ((1-\varepsilon _{\mathcal {A}})^{-1} \big )\). Hence Lemma 10 gives roughly \(\varepsilon _\mathcal {M}\ge \varepsilon _\mathcal {R}-(c\cdot n/Q_\textsc {Ch})\cdot \varepsilon _{\mathcal {A}}\) for a suitable choice of \(\varepsilon _{\mathcal {A}}\). Therefore \(\varepsilon _\mathcal {R}\) can be at most \((c\cdot n/Q_\textsc {Ch})\cdot \varepsilon _{\mathcal {A}}\). Otherwise \(\mathcal {M}\) would break \(\mathsf {IMP}\text{- }\mathsf {MIM}\) security of \({\mathsf {ID}}\) with \(\varepsilon _\mathcal {M}> 0\).
In the proof of Lemma 10 (cf. [35]), the meta-reduction just forwards all \(R_{j,i}\) received during the Man-in-the-Middle attack and \(R\) sent by \(\mathcal {R}\). So if \(\mathcal {R}\) is furthermore randomness-preserving, i.e., it chooses \(R\in \{R_{1,1},\ldots ,R_{n,Q_\textsc {Ch}}\}\), then \(\mathcal {M}\) attacks \(\mathsf {wIMP}\text{- }\mathsf {MIM}\)-security of \({\mathsf {ID}}\). This observation (formalized in the following corollary) is important since the Schnorr identification scheme is \(\mathsf {wIMP}\text{- }\mathsf {MIM}\) but not \(\mathsf {IMP}\text{- }\mathsf {MIM}\)-secure.
Corollary 1
If \({\mathsf {ID}}\) has \(\alpha \) bit min-entropy and there exists a key- and randomness-preserving reduction \(\mathcal {R}\) that \((t_\mathcal {R},\varepsilon _\mathcal {R})\)-breaks \(\mathsf {IMP}\text{- }\mathsf {KOA}\) security of \({\mathsf {ID}}\) with n -time black-box access to an adversary \(\mathcal {A}\) that \((t_\mathcal {A},\varepsilon _\mathcal {A}, Q_\textsc {Ch})\)-breaks \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) security of \({\mathsf {ID}}\), then there exists an algorithm \(\mathcal {M}\) that \((t_\mathcal {M},\varepsilon _\mathcal {M},1, Q_\textsc {O}=nQ_\textsc {Ch})\)-breaks \(\mathsf {wIMP}\text{- }\mathsf {MIM}\) security of \({\mathsf {ID}}\), where
Lemma 11
 If there exists a key-preserving reduction \(\mathcal {R}\) in the non-programmable random oracle (NPRO) model that \((t_\mathcal {R},\varepsilon _\mathcal {R})\)-breaks \(\mathsf {IMP}\text{- }\mathsf {KOA}\) security of \({\mathsf {ID}}\) with n-time black-box access to an adversary \(\mathcal {A}\) that \((t_\mathcal {A},\varepsilon _\mathcal {A}, Q_h)\)-breaks \({\mathsf {UF\text{- }KOA}}\) security of \({\mathsf {SIG}}[{\mathsf {ID}}]\), then there exists an algorithm \(\mathcal {M}\) that \((t_\mathcal {M},\varepsilon _\mathcal {M},1)\)-breaks \(\mathsf {IMP}\text{- }\mathsf {AA}\)-security of \({\mathsf {ID}}\), where
If there exists a key-preserving reduction \(\mathcal {R}\) in the non-programmable random oracle (NPRO) model that \((t_\mathcal {R},\varepsilon _\mathcal {R})\)-breaks \(\mathsf {IMP}\text{- }\mathsf {KOA}\) security of \({\mathsf {ID}}\) with n-time black-box access to an adversary \(\mathcal {A}\) that \((t_\mathcal {A},\varepsilon _\mathcal {A}, Q_h)\)-breaks \({\mathsf {UF\text{- }KOA}}\) security of \({\mathsf {SIG}}[{\mathsf {ID}}]\), then there exists an algorithm \(\mathcal {M}\) that \((t_\mathcal {M},\varepsilon _\mathcal {M},1)\)-breaks \(\mathsf {IMP}\text{- }\mathsf {AA}\)-security of \({\mathsf {ID}}\), where
By Lemmas 4 and 11 implies that there is no reduction from \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) to \({\mathsf {UF\text{- }KOA}}\) in the non-programmable random oracle model.
The following simple lemma actually holds for any signature scheme \({\mathsf {SIG}}\).
Lemma 12
 Suppose that there is a key-preserving reduction \(\mathcal {R}\) in the non-programmable random oracle (NPRO) model that \((t_\mathcal {R},\varepsilon _\mathcal {R}, Q_h)\)-breaks \({\mathsf {UF\text{- }KOA}}\) security of \({\mathsf {SIG}}\) with n-time black-box access to an adversary \(\mathcal {A}\) that \((t_\mathcal {A},\varepsilon _\mathcal {A},Q_s,Q_h)\)-breaks \({\mathsf {UF\text{- }CMA}}\) security of \({\mathsf {SIG}}\). Then there exists an algorithm \(\mathcal {M}\) that \((t_\mathcal {M},\varepsilon _\mathcal {M})\)-breaks \({\mathsf {UF\text{- }KOA}}\) security of \({\mathsf {SIG}}\), where
Suppose that there is a key-preserving reduction \(\mathcal {R}\) in the non-programmable random oracle (NPRO) model that \((t_\mathcal {R},\varepsilon _\mathcal {R}, Q_h)\)-breaks \({\mathsf {UF\text{- }KOA}}\) security of \({\mathsf {SIG}}\) with n-time black-box access to an adversary \(\mathcal {A}\) that \((t_\mathcal {A},\varepsilon _\mathcal {A},Q_s,Q_h)\)-breaks \({\mathsf {UF\text{- }CMA}}\) security of \({\mathsf {SIG}}\). Then there exists an algorithm \(\mathcal {M}\) that \((t_\mathcal {M},\varepsilon _\mathcal {M})\)-breaks \({\mathsf {UF\text{- }KOA}}\) security of \({\mathsf {SIG}}\), where
Remark 1
All the reductions considered in this section are key-preserving which is the main restriction of our results. If \(pk\) and R are elements from some multiplicative group \(\mathbb {G}\) of prime order p, then we can extend our previous techniques to exclude the larger class of algebraic reductions. A reduction is algebraic, if for all group elements h output by the reduction, their respective representation is known. That is, if at some point of its execution the reduction holds group elements \(g_1, \ldots , g_n \in \mathbb {G}\) and outputs a new group element h, then it also knows it representation meaning it also outputs \((\alpha _1, \ldots , \alpha _n) \in \mathbb {Z}_p^n\) satisfying \(h = \prod g_i^{\alpha _i}\). Note that key-preserving and randomness-preserving reductions are a special case of algebraic reductions.
5 Instantiations
In this section we consider two important identification schemes, namely the ones by Schnorr [42] and by Katz-Wang [19, 34]. We use our framework to derive tight security bounds and concrete parameters for the corresponding Schnorr/Katz-Wang signature schemes. In the full version [35] we discuss one more identification scheme, namely the one by Guillou-Quisquater [31].
5.1 Schnorr Identification/Signature Scheme
Schnorr’s Identification Scheme. The well-known Schnorr’s identification scheme is one of the most important instantiations of our framework. For completeness we show that Schnorr’s identification has large min-entropy, special soundness (\(\mathsf {SS}\)), honest-verifier zero-knowledge (\(\mathsf {HVZK}\)), random-self reducibility (\(\mathsf {RSR}\)) and key-recovery security (\(\mathsf {KR}\text{- }\mathsf {KOA}\)) based on the discrete logarithm problem (\(\mathsf {DLOG}\)). Moreover, based on the one-more discrete logarithm problem (\(\mathsf {OMDL}\)), Schnorr’s identification is actively secure (\(\mathsf {IMP}\text{- }\mathsf {AA}\)) and weakly secure against man-in-the-middle attack (\(\mathsf {wIMP}\text{- }\mathsf {MIM}\)).
Let \(\mathsf {par}:=( p, g,\mathbb {G})\) be a set of system parameters, where \(\mathbb {G}=\langle g\rangle \) is a cyclic group of prime order p with a hard discrete logarithm problem. Examples of groups \(\mathbb {G}\) include appropriate subgroups of certain elliptic curve groups, or subgroups of \(\mathbb {Z}_{q}^*\). The Schnorr identification scheme \({\mathsf {ID}}_{{\mathsf {S}}}:=({\mathsf {IGen}},{\mathsf {P}},\mathsf {ChSet},{\mathsf {V}})\) is defined as follows.

We recall the \(\mathsf {DLOG}\) assumption.
Definition 11
(Discrete Logarithm Assumption). The discrete logarithm problem \(\mathsf {DLOG}\) is \((t, \varepsilon )\)-hard in \(\mathsf {par}=( p, g,\mathbb {G})\) if for all adversaries \(\mathcal {A}\) running in time at most t, 
Lemma 13
\({\mathsf {ID}}_{{\mathsf {S}}}\) is a canonical identification with \(\alpha =\log p\) bit min-entropy and it is unique, has special soundness (\(\mathsf {SS}\)), honest-verifier zero-knowledge (\(\mathsf {HVZK}\)) and is random-self reducible (\(\mathsf {RSR}\)). Moreover, if \(\mathsf {DLOG}\) is \((t,\varepsilon )\)-hard in \(\mathsf {par}=(p, g,\mathbb {G})\) then \({\mathsf {ID}}_{{\mathsf {S}}}\) is \((t,\varepsilon )\)-\(\mathsf {KR}\text{- }\mathsf {KOA}\) secure.
Proof
The correctness of \({\mathsf {ID}}_{{\mathsf {S}}}\) is straightforward to verify. We note that R in  is uniformly random over \(\mathbb {G}\). Hence, \({\mathsf {ID}}_{{\mathsf {S}}}\) has \(\log |\mathbb {G}|=\log p\) bit min-entropy. We show the other properties as follows.
is uniformly random over \(\mathbb {G}\). Hence, \({\mathsf {ID}}_{{\mathsf {S}}}\) has \(\log |\mathbb {G}|=\log p\) bit min-entropy. We show the other properties as follows.
Uniqueness. For all \((X,x)\in {\mathsf {IGen}}(\mathsf {par})\), \((R:=g^r, St :=r) \in {\mathsf {P}}_1(sk)\) and \(h\in \{0,1\}^n\), the value \(s \in \mathbb {Z}_p\) satisfying \(g^s = X^hR \Leftrightarrow s = xh+r\) is uniquely defined.
Special Soundness (\(\mathsf {SS}\)). Given two accepting transcripts \((R,h,s)\) and \((R, h', s')\) with \(h\ne h'\), we define an extractor algorithm \({\mathsf {Ext}}(X,R,h,s,h',s'):=x^*:={(s-s')}/{(h-h')}\) such that, for all \((X:=g^x,x) \in {\mathsf {IGen}}(\mathsf {par}) \), we have \(\Pr [g^{x^*}=X]=1\), since we have \(R=g^sX^{-h}=g^{s'} X^{-h'}\) and then \(X=g^{{(s-s')}/{(h-h')}}\).
Honest-verifier Zero-knowledge (\(\mathsf {HVZK}\)). Given public key X, we let \(\mathsf {Sim}(X)\) first sample  and then output \((R:=g^s X^{-h},h,s)\). Clearly, (R, h, s) is a real transcript, since s is uniformly random over \(\mathbb {Z}_p\) and R is the unique value satisfying \(R=g^s X^{-h}\).
and then output \((R:=g^s X^{-h},h,s)\). Clearly, (R, h, s) is a real transcript, since s is uniformly random over \(\mathbb {Z}_p\) and R is the unique value satisfying \(R=g^s X^{-h}\).
Random-self Reducibility (\(\mathsf {RSR}\)). Algorithm \({\mathsf {Rerand}}\) and two deterministic algorithm \({\mathsf {Derand}}\) and \({\mathsf {Tran}}\) are defined as follows:
-
\({\mathsf {Rerand}}(X)\) chooses
 and outputs \((X':=X\cdot g^{\tau '},\tau ')\). We have that, for all \((X,x)\in {\mathsf {IGen}}(\mathsf {par})\), \(X'\) is uniform and has the same distribution as \(X''\), where
and outputs \((X':=X\cdot g^{\tau '},\tau ')\). We have that, for all \((X,x)\in {\mathsf {IGen}}(\mathsf {par})\), \(X'\) is uniform and has the same distribution as \(X''\), where  .
. -
\({\mathsf {Derand}}(X,X',x',\tau ')\) outputs \(x^*=x'-\tau '\). We have, for all
 and \((X',x')\in {\mathsf {IGen}}(\mathsf {par})\), \(X'=g^{x'}\) and \(x'=x+\tau '\) and thus \(x^*=x\).
and \((X',x')\in {\mathsf {IGen}}(\mathsf {par})\), \(X'=g^{x'}\) and \(x'=x+\tau '\) and thus \(x^*=x\). -
\({\mathsf {Tran}}(X,X',\tau ',(R',h',s'))\) outputs \(s=s'-\tau ' \cdot h'\). We have, for all \((X',\tau ') \in {\mathsf {Rerand}}(X:=g^x)\), if \((R',h',s')\) is valid with respect to \(X':=g^{x+\tau '}\) then \(s=s'-\tau ' \cdot h'= (x+\tau ')h' + r -\tau ' \cdot h'=xh'+r\) and \((R',h',s)\) is valid with respect to X.
Key-recovery against Key-only Attack (\(\mathsf {KR}\text{- }\mathsf {KOA}\)). \(\mathsf {KR}\text{- }\mathsf {KOA}\)-security for \({\mathsf {ID}}\) is exactly the \(\mathsf {DLOG}\) assumption. \(\square \)
Under the one-more discrete logarithm assumption [4], \({\mathsf {ID}}_{{\mathsf {S}}}\) is \(\mathsf {IMP}\text{- }\mathsf {AA}\) secure [6] and in the full version [35] we show that \({\mathsf {ID}}_{{\mathsf {S}}}\) is weakly \(\mathsf {IMP}\text{- }\mathsf {MIM}\) secure.
We now define the Q-interactive discrete-logarithm problem which precisely models \(\mathsf {PIMP}\text{- }\mathsf {KOA}\)-security for \({\mathsf {ID}}_{{\mathsf {S}}}\), where \(Q=Q_\textsc {O}\) is the number of parallel impersonation rounds.
Definition 12
( \(Q\text{- }\mathsf {IDLOG}\) ). The interactive discrete-logarithm assumption \(Q\text{- }\mathsf {IDLOG}\) is said to be \((t, \varepsilon )\)-hard in \(\mathsf {par}=(p, g,\mathbb {G})\) if for all adversaries \(\mathcal {A}\) running in time at most t and making at most Q queries to the challenge oracle \(\textsc {Ch}\),

where on the i-th query \(\textsc {Ch}(g^{r_i})\) (\(i \in [Q]\)), the challenge oracle returns  to \(\mathcal {A}\).
to \(\mathcal {A}\).
In [35] we prove that in the generic group model, the \(Q\text{- }\mathsf {IDLOG}\) problem in groups of prime-order p is at least \((t,2t^2/p)\)-hard. Note that the bound is independent of Q.
Schnorr’s Signature Scheme. Let \(H:\{0,1\}^* \rightarrow \{0,1\}^n\) be a hash function with \(n < \log _2(p)\). As \({\mathsf {ID}}_{{\mathsf {S}}}\) is commitment-recoverable we can use the alternative Fiat-Shamir transformation to obtain the Schnorr signature scheme \(\mathsf {Schnorr}:=(\mathsf {Gen},\mathsf {Sign},\mathsf {Ver})\).

The \(\mathsf {DLOG}\) problem is tightly equivalent to the \(1\text{- }\mathsf {IDLOG}\) problem by Lemma 3. Assuming the \(\mathsf {OMDL}\) problem is hard, \(\mathsf {Schnorr}\) is \(\mathsf {wIMP}\text{- }\mathsf {MIM}\)-secure and by Corollary 1 there cannot exist a tight implication \(1\text{- }\mathsf {IDLOG} \rightarrow Q\text{- }\mathsf {IDLOG}\) meaning the bound from Lemma 4 is optimal. By Lemmas 5 and 6, the \(Q\text{- }\mathsf {IDLOG}\) problem is tightly equivalent to \({\mathsf {SUF\text{- }CMA}}\)-security of \(\mathsf {Schnorr}\) in the programmable ROM. The latter is only tightly equivalent to \({\mathsf {MU\text{- }SUF\text{- }CMA}}\)-security in the programmable ROM (via Lemmas 7 and 8). In the full version [35] we improve this by proving that \({\mathsf {SUF\text{- }CMA}}\) security is tightly equivalent to \({\mathsf {MU\text{- }SUF\text{- }CMA}}\)-security in the standard model. Figure 3 summarizes the modular security implications for \(\mathsf {Schnorr}\).
We derive the following concrete security implications.
Lemma 14
If \(\mathsf {DLOG}\) is \((t,\varepsilon )\)-hard in \(\mathsf {par}=( p, g,\mathbb {G})\) then \(\mathsf {Schnorr}\) is \((t',\varepsilon ',Q_s,Q_h)\)-\({\mathsf {SUF\text{- }CMA}}\) secure and \((t'',\varepsilon '',N,Q_s,Q_h)\)-\({\mathsf {MU\text{- }SUF\text{- }CMA}}\) secure in the programmable random oracle model, where
Lemma 15
If \(Q_h\text{- }\mathsf {IDLOG}\) is \((t,\varepsilon )\)-hard in \(\mathsf {par}\) then \(\mathsf {Schnorr}\) is \((t',\varepsilon ',N,Q_s,Q_h)\)-\({\mathsf {MU\text{- }SUF\text{- }CMA}}\) secure in the programmable random oracle model, where
We leave it an open problem to come up with a more natural hard problem over \(\mathsf {par}\) that tightly implies \(Q\text{- }\mathsf {IDLOG}\) (and hence \({\mathsf {MU\text{- }SUF\text{- }CMA}}\)-security of \(\mathsf {Schnorr}\)). Note that according to [23], the hard problem has to have at least one round of interaction.
The interpretation for the multi-user security of \(\mathsf {Schnorr}\) over elliptic-curve groups is as follows. It is well-known that a group of order p providing k-bits security against the \(\mathsf {DLOG}\) problem requires \(\log p \ge 2k\). If one requires provable security guarantees for \(\mathsf {Schnorr}\) under \(\mathsf {DLOG}\), then one has to increase the group size by \(\approx \log (Q_h)\) bits. Reasonable upper bounds for \(\log Q_h\) are between 40 and 80. However, the generic lower bound for the \(Q\text{- }\mathsf {IDLOG}\) problem indicates that the only way to attack \(\mathsf {Schnorr}\) in the sense of \({\mathsf {UF\text{- }KOA}}\) (and hence to attack \(Q\text{- }\mathsf {IDLOG}\)) is to break the \(\mathsf {DLOG}\) problem. In that case using groups with \(\log p \approx 2k\) already gives provable security guarantees for \(\mathsf {Schnorr}\).
5.2 Chaum-Pedersen Identification/Katz-Wang Signature Scheme
Chaum-Pedersen Identification Scheme. Let \(\mathsf {par}:=( p, g_1,g_2,\mathbb {G})\) be a set of system parameters, where \(\mathbb {G}=\langle g_1\rangle =\langle g_2\rangle \) is a cyclic group of prime order p. The Chaum-Pedersen identification scheme \({\mathsf {ID}}_{{\mathsf {CP}}}:=({\mathsf {IGen}},{\mathsf {P}},\mathsf {ChSet},{\mathsf {V}})\) is defined as follows.

We recall the \(\mathsf {DDH}\) assumption.
Definition 13
(Decision Diffie-Hellman Assumption). The Decision Diffie-Hellman problem \(\mathsf {DDH}\) is \((t, \varepsilon )\)-hard in \(\mathsf {par}=( p, g_1, g_2,\mathbb {G})\) if for all adversaries \(\mathcal {A}\) running in time at most t,

Clearly, all security results of Schnorr carry over to the Chaum-Pedersen identification scheme, i.e., \({\mathsf {ID}}_{{\mathsf {CP}}}\) is at least as secure as \({\mathsf {ID}}_{{\mathsf {S}}}\). That also means that we cannot hope for tight \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) security from the \(\mathsf {DLOG}\) assumption. Instead, for the Chaum-Pedersen identification scheme, we give a direct tight proof of \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) security under the \(\mathsf {DDH}\) assumption which we extracted from [34].
Lemma 16
\({\mathsf {ID}}_{{\mathsf {CP}}}\) is a canonical identification scheme with \(\alpha =\log p\) bit min-entropy and it is unique, has special soundness (\(\mathsf {SS}\)), honest-verifier zero-knowledge (\(\mathsf {HVZK}\)) and is random-self reducible (\(\mathsf {RSR}\)). Moreover, if \(\mathsf {DDH}\) is \((t,\varepsilon )\)-hard in \(\mathsf {par}=( p, g_1,g_2,\mathbb {G})\) then \({\mathsf {ID}}_{{\mathsf {CP}}}\) is \((t',\varepsilon ',Q_\textsc {Ch})\)-\(\mathsf {PIMP}\text{- }\mathsf {KOA}\) secure, where \(t \approx t'\) and \(\varepsilon \ge \varepsilon ' -Q_\textsc {Ch}/2^n\).
Proof
The proof of \(\mathsf {SS}\), \(\mathsf {HVZK}\), uniqueness, and \(\mathsf {RSR}\) is the same as in \({\mathsf {ID}}_{{\mathsf {S}}}\).
To prove \(\mathsf {PIMP}\text{- }\mathsf {KOA}\)-security under \(\mathsf {DDH}\), let \(\mathcal {A}\) be an adversary that \((t',\varepsilon ',Q_\textsc {Ch})\)-breaks \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) security. We build an adversary \(\mathcal {B}\) against the (\(t,\varepsilon \))-hardness of \(\mathsf {DDH}\) as follows. Adversary \(\mathcal {B}\) inputs \((X_1, X_2)\) and defines \(pk:=(X_1, X_2)\). On the i-th challenge query \(\textsc {Ch}(R_{i,1},R_{i,2})\), it returns  . Eventually, \(\mathcal {A}\) returns \(i^* \in [Q_\textsc {Ch}]\) and \(s_{i^*}\) and terminates. Finally, \(\mathcal {B}\) outputs \(d:={\mathsf {V}}(pk,R_{i^*},h_{i^*}, s_{i^*})\).
. Eventually, \(\mathcal {A}\) returns \(i^* \in [Q_\textsc {Ch}]\) and \(s_{i^*}\) and terminates. Finally, \(\mathcal {B}\) outputs \(d:={\mathsf {V}}(pk,R_{i^*},h_{i^*}, s_{i^*})\).
Analysis of \(\mathcal {B}\). If \((X_1, X_2) = (g_1^x, g_2^x)\), then \(\mathcal {B}\) perfectly simulates the \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) game and hence \(\Pr [d=1 \mid (X_1, X_2) = (g_1^x, g_2^x)] = \varepsilon '\). If \((X_1, X_2) = (g_1^{x_1}, g_2^{x_2})\) with \(x_1 \ne x_2\), then we claim that even a computationally unbounded \(\mathcal {A}\) can only win with probability \(Q_\textsc {Ch}/2^n\), i.e., \(\Pr [d=1 \mid (X_1, X_2) = (g_1^{x_1}, g_2^{x_2})] \le Q_\textsc {Ch}/2^n\).
It remains to prove the claim. For each index \(i \in [Q_\textsc {Ch}]\), \(\mathcal {A}\) first commits to \(R_{i,1}= g_1^{r_{i,1}}\) and \(R_{i,2}= g_2^{r_{i,2}}\) (for arbitrary \(r_{i,1}, r_{i,2} \in \mathbb {Z}_p\)) and can only win if there exists an \(s_i \in \mathbb {Z}_p\) such that
where  is chosen independently of \(r_{i,1}, r_{i,2}\). This happens with probability at most \(1/2^n\), so by the union bound we obtain the bound \(Q_\textsc {Ch}/2^n\), as claimed. \(\square \)
is chosen independently of \(r_{i,1}, r_{i,2}\). This happens with probability at most \(1/2^n\), so by the union bound we obtain the bound \(Q_\textsc {Ch}/2^n\), as claimed. \(\square \)
Katz-Wang Signature Scheme. Let \(H:\{0,1\}^* \rightarrow \{0,1\}^n\) be a hash function with \(n < \log _2(p)\). As \({\mathsf {ID}}_{{\mathsf {CP}}}\) is commitment-recoverable we can use the alternative Fiat-Shamir transformation to obtain a signature scheme which is known as the Katz-Wang signature scheme \(\mathsf {KW}:=(\mathsf {Gen},\mathsf {Sign},\mathsf {Ver})\).

By our results we obtain the following concrete security statements, where the first bound matches [34, Theorem1].
Lemma 17
If \(\mathsf {DDH}\) is \((t,\varepsilon )\)-hard in \(\mathsf {par}=( p, g_1, g_2,\mathbb {G})\) then \(\mathsf {KW}\) is \((t',\varepsilon ',Q_s,Q_h)\)-\({\mathsf {SUF\text{- }CMA}}\) secure and \((t'',\varepsilon '',N,Q_s,Q_h)\)-\({\mathsf {MU\text{- }SUF\text{- }CMA}}\) secure in the programmable random oracle model, where
Notes
- 1.
Unforgeability against key-only attack (\({\mathsf {UF\text{- }KOA}}\) security) is the same as standard \({\mathsf {UF\text{- }CMA}}\) security, but the adversary is not allowed to ask any signing query.
- 2.
We can even prove strong \({{\mathsf {MU\text{- }UF\text{- }CMA}}} \) security of Schnorr signatures in the sense that a new signature on a previously signed message already counts as a valid forgery.
- 3.
The main result of the published paper [23] even excludes reduction from any interactive assumption (with special algebraic properties), but the proof turned out to be flawed.
- 4.
On two queries \(\textsc {Ch}(R_i)\) and \(\textsc {Ch}(R_{i'})\) with the same input \(R_i = R_{i'}\) the oracle returns two independent random challenges
 and
and 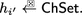 .
. - 5.
Jensen’s inequality states that if \(\varphi \) is a convex function and X is a random variable, then \(\mathsf {E}[\varphi (X)] \ge \varphi (\mathsf {E}[X])\).
References
Abdalla, M., An, J.H., Bellare, M., Namprempre, C.: From identification to signatures via the Fiat-Shamir transform: minimizing assumptions for security and forward-security. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 418–433. Springer, Heidelberg (2002)
Abdalla, M., Ben Hamouda, F., Pointcheval, D.: Tighter reductions for forward-secure signature schemes. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 292–311. Springer, Heidelberg (2013)
Abdalla, M., Fouque, P.-A., Lyubashevsky, V., Tibouchi, M.: Tightly-secure signatures from lossy identification schemes. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 572–590. Springer, Heidelberg (2012)
Bellare, M., Namprempre, C., Pointcheval, D., Semanko, M.: The one-more-RSA-inversion problems and the security of Chaum’s blind signature scheme. J. Cryptology 16(3), 185–215 (2003)
Bellare, M., Neven, G.: Multi-signatures in the plain public-key model and a general forking lemma. In: Juels, A., Wright, R.N., Vimercati, S. (eds.) ACM CCS 2006, pp. 390–399. ACM Press, October/November 2006
Bellare, M., Palacio, A.: GQ and schnorr identification schemes: proofs of security against impersonation under active and concurrent attacks. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 162–177. Springer, Heidelberg (2002)
Bellare, M., Ristenpart, T.: Simulation without the artificial abort: simplified proof and improved concrete security for Waters’ IBE scheme. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 407–424. Springer, Heidelberg (2009)
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: Ashby, V. (ed.) ACM CCS 1993, pp. 62–73. ACM Press, November 1993
Bellare, M., Rogaway, P.: The exact security of digital signatures - how to sign with RSA and Rabin. In: Maurer, U.M. (ed.) EUROCRYPT 1996. LNCS, vol. 1070, pp. 399–416. Springer, Heidelberg (1996)
Bernstein, D.: [Cfrg] key as message prefix \(=>\) multi-key security. https://mailarchive.ietf.org/arch/msg/cfrg/44gJyZlZ7-myJqWkChhpEF1KE9M, 2015
Bernstein, D.J.: Multi-user Schnorr security, revisited. Cryptology ePrint Archive, Report 2015/996, 2015. http://eprint.iacr.org/
Bernstein, D.J., Duif, N., Lange, T., Schwabe, P., Yang, B.-Y.: High-speed high-security signatures. In: Preneel, B., Takagi, T. (eds.) CHES 2011. LNCS, vol. 6917, pp. 124–142. Springer, Heidelberg (2011)
Beth, T.: Efficient zero-knowledged identification scheme for smart cards. In: Günther, C.G. (ed.) EUROCRYPT 1988. LNCS, vol. 330, pp. 77–84. Springer, Heidelberg (1988)
Boneh, D., Gentry, C., Lynn, B., Shacham, H.: Aggregate and verifiably encrypted signatures from bilinear maps. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 416–432. Springer, Heidelberg (2003)
Brickell, E.F., McCurley, K.S.: An interactive identification scheme based on discrete logarithms and factoring. In: Damgård, I.B. (ed.) EUROCRYPT 1990. LNCS, vol. 473, pp. 63–71. Springer, Heidelberg (1991)
Brown, D.: [Cfrg] key as message prefix \(=>\) multi-key security. http://www.ietf.org/mail-archive/web/cfrg/current/msg07336.html, 2015
Canetti, R., Goldreich, O., Halevi, S.: The random oracle methodology, revisited (preliminary version). In: 30th ACM STOC, pp. 209–218. ACM Press, May 1998
Chatterjee, S., Koblitz, N., Menezes, A., Sarkar, P.: Another look at tightness II: practical issues in cryptography. Cryptology ePrint Archive, Report 2016/360 (2016). http://eprint.iacr.org/
Chaum, D., Pedersen, T.P.: Wallet databases with observers. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 89–105. Springer, Heidelberg (1993)
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987)
Fischlin, M., Fleischhacker, N.: Limitations of the meta-reduction technique: the case of schnorr signatures. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 444–460. Springer, Heidelberg (2013)
Fischlin, M., Lehmann, A., Ristenpart, T., Shrimpton, T., Stam, M., Tessaro, S.: Random oracles with(out) programmability. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 303–320. Springer, Heidelberg (2010)
Fleischhacker, N., Jager, T., Schröder, D.: On tight security proofs for schnorr signatures. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 512–531. Springer, Heidelberg (2014)
Fukumitsu, M., Hasegawa, S.: Black-box separations on Fiat-shamir-type signatures in the non-programmable random oracle model. In: López, J., Mitchell, C.J. (eds.) ISC 2015. LNCS, vol. 9290, pp. 3–20. Springer, Heidelberg (2015)
Galbraith, S.D., Malone-Lee, J., Smart, N.P.: Public key signatures in the multi-user setting. Inf. Process. Lett. 83(5), 263–266 (2002)
Galindo, D.: The exact security of pairing based encryption and signature schemes. Based on a talk at Workshop on Provable Security, INRIA, Paris (2004). http://www.dgalindo.es/galindoEcrypt.pdf
Garg, S., Bhaskar, R., Lokam, S.V.: Improved bounds on security reductions for discrete log based signatures. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 93–107. Springer, Heidelberg (2008)
Girault, M.: An identity-based identification scheme based on discrete logarithms modulo a composite number. In: Damgård, I.B. (ed.) EUROCRYPT 1990. LNCS, vol. 473, pp. 481–486. Springer, Heidelberg (1991)
Goh, E.-J., Jarecki, S., Katz, J., Wang, N.: Efficient signature schemes with tight reductions to the Diffie-Hellman problems. J. Cryptology 20(4), 493–514 (2007)
Goldwasser, S., Micali, S., Rivest, R.L.: A digital signature scheme secure against adaptive chosen-message attacks. SIAM J. Comput. 17(2), 281–308 (1988)
Guillou, L.C., Quisquater, J.-J.: A “Paradoxical” identity-based signature scheme resulting from zero-knowledge. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 216–231. Springer, Heidelberg (1990)
Hamburg, M.: Re: [Cfrg] EC signature: next steps (2015). https://mailarchive.ietf.org/arch/msg/cfrg/af170b6OrLyNZUHBMOPWxcDrVRI
Josefsson, S., Liusvaara, I.: Edwards-curve digital signature algorithm (EdDSA), 7 October 2015. https://tools.ietf.org/html/draft-irtf-cfrg-eddsa-00
Katz, J., Wang, N.: Efficiency improvements for signature schemes with tight security reductions. In: Jajodia, S., Atluri, V., Jaeger, T. (eds.) ACM CCS 2003, pp. 155–164. ACM Press, October 2003
Kiltz, E., Masny, D., Pan, J.: Optimal security proofs for signatures from identification schemes. Cryptology ePrint Archive, Report 2016/191 (2016). http://eprint.iacr.org/
Micali, S., Shamir, A.: An improvement of the Fiat-Shamir identification and signature scheme. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 244–247. Springer, Heidelberg (1990)
Ohta, K., Okamoto, T.: On concrete security treatment of signatures derived from identification. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 354–369. Springer, Heidelberg (1998)
Okamoto, T.: Provably secure and practical identification schemes and corresponding signature schemes. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 31–53. Springer, Heidelberg (1993)
Ong, H., Schnorr, C.-P.: Fast signature generation with a Fiat-Shamir-like scheme. In: Damgård, I.B. (ed.) EUROCRYPT 1990. LNCS, vol. 473, pp. 432–440. Springer, Heidelberg (1991)
Paillier, P., Vergnaud, D.: Discrete-log-based signatures may not be equivalent to discrete log. In: Roy, B. (ed.) ASIACRYPT 2005. LNCS, vol. 3788, pp. 1–20. Springer, Heidelberg (2005)
Pointcheval, D., Stern, J.: Security arguments for digital signatures and blind signatures. J. Cryptology 13(3), 361–396 (2000)
Schnorr, C.-P.: Efficient signature generation by smart cards. J. Cryptology 4(3), 161–174 (1991)
Seurin, Y.: On the exact security of schnorr-type signatures in the random oracle model. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 554–571. Springer, Heidelberg (2012)
Struik, R.: Re: [Cfrg] EC signature: next steps (2015). https://mailarchive.ietf.org/arch/msg/cfrg/TOWH1DSzB-PfDGK8qEXtF3iC6Vc
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Kiltz, E., Masny, D., Pan, J. (2016). Optimal Security Proofs for Signatures from Identification Schemes. In: Robshaw, M., Katz, J. (eds) Advances in Cryptology – CRYPTO 2016. CRYPTO 2016. Lecture Notes in Computer Science(), vol 9815. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53008-5_2
Download citation
DOI: https://doi.org/10.1007/978-3-662-53008-5_2
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53007-8
Online ISBN: 978-3-662-53008-5
eBook Packages: Computer ScienceComputer Science (R0)




 .
. to
to  , if
, if  is the rerandomized key-pair and
is the rerandomized key-pair and  is a freshly generated key-pair.
is a freshly generated key-pair. . Note that this involves
. Note that this involves  . If hash value
. If hash value  and outputs
and outputs  .
. and
and 
 and
and 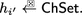 .
.