Abstract
The computational abilities of ancient Indian mathematicians are well known. The paper deals with the second-order interpolation schemes found in a few astronomical works of India.
Indian Journal of History of Science, Vol. 4, Nos. 1 & 2 (1969), pp. 86–98.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
However, these arguments are not adequate, since the true functional difference, corresponding to the residual arc, is \( \frac{\theta }{h} \cdot D_{t} \) (and not simply \( D_{t} \)) which will be zero (as it ought to be) when \( \theta = 0 \), whether \( D_{t} \) is taken \( D_{p} \) or \( \frac{1}{2}(D_{p} + D_{p + 1} ) \) there.
- 2.
In the published article, the reading was:
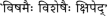 . This has been refined in consultation with the source work. (–ed.).
. This has been refined in consultation with the source work. (–ed.). - 3.
That is, the first, second, third rāśi rules of sines are to be used, respectively, for third, second, first rāśi in case of versed sines.
- 4.
The author of the present paper proposes to publish a separate article about Govindasvāmin’s computations of Indian sines.
- 5.
In the published article the reading was:
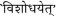 . This has been refined in consultation with the source work. (–ed.).
. This has been refined in consultation with the source work. (–ed.). - 6.
We have changed the printed
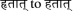 for an obvious reason. (–ed.).
for an obvious reason. (–ed.). - 7.
In the published article the reading was:
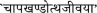 . This has been refined in consultation with the source work. (–ed.).
. This has been refined in consultation with the source work. (–ed.).
Abbreviations
- a :
-
the argument, circular arc measured in angular units; anomaly.
- a1, a2 etc.:
-
successive unequidistant values of a.
- h :
-
equal (common) arcual interval; elemental arc.
- h1, h2, etc.:
-
unequal arcual intervals (gatis); \( \begin{aligned} h_{1} & = a_{1} ; \\ h_{2} & = a_{2} - a_{1} ; \\ h_{3} & = a_{3} - a_{2} ,{\text{etc}}. \\ \end{aligned} \)
- R :
-
sinus totus (radius).
- R sin a, R cos a,:
-
.
- R versin a:
-
Indian sine, cosine and versed sine of the arc a
- f(a) :
-
the functional value of sine, versed sine or certain astronomical function called ‘equation’ (phala).
- p, q:
-
positive integers; \( x = p \cdot h \) or \( a_{p} \); arc passed over, such that \( f(x) \) is known.
- \( \theta \) :
-
residual arc such that \( f(x + \theta ) \) is required to be interpolated, \( \theta \) being positive and less than h or \( h_{p + 1} \).
- n :
-
\( \frac{\theta }{h} \).
- D1, D2, etc.:
-
tabulated functional differences;
\( \begin{aligned} D_{1} & = f(a_{1} )\,{\text{or}}\,f(h) \\ D_{2} & = f(a_{2} ) - f(a_{1} )\,{\text{or}}\,f(2h) - f(h) \\ D_{3} & = f(a_{3} ) - f(a_{2} )\,{\text{or}}\,f(3h) - f(2h),{\text{etc}}. \\ \end{aligned} \)
- \( \Delta \) :
-
first-order forward difference operator;
\( \begin{aligned} \Delta f(a) & = f(a + h) - f(a); \\ \Delta f(a_{q} ) & = f(a_{q + 1} ) - f(a_{q} ); \\ \Delta f(x) & = D_{p + 1} . \\ \end{aligned} \)
- \( \Delta^{2} \) :
-
second-order difference operator.
- hp, hp+1:
-
argumental intervals just passed over (last or bhukta-gati) and yet to be passed over (current or bhogya-gati), respectively.
- Dp, Dp+1:
-
the corresponding tabulated functional differences passed over (bhukta-khaṇḍa or gatiphala) and to be passed over (bhogya-khaṇḍa or gatiphala), respectively.
- D t :
-
the envisaged true (sphuṭa) value of the functional difference to be passed over.
- Z p :
-
‘adjusted’ value of the functional difference passed over in case of unequal intervals
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Singapore Pte Ltd.
About this chapter
Cite this chapter
Ramasubramanian, K. (2019). Second-Order Interpolation in Indian Mathematics up to the Fifteenth Century. In: Ramasubramanian, K. (eds) Gaṇitānanda. Springer, Singapore. https://doi.org/10.1007/978-981-13-1229-8_27
Download citation
DOI: https://doi.org/10.1007/978-981-13-1229-8_27
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-13-1228-1
Online ISBN: 978-981-13-1229-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


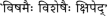 . This has been refined in consultation with the source work. (–ed.).
. This has been refined in consultation with the source work. (–ed.).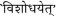 . This has been refined in consultation with the source work. (–ed.).
. This has been refined in consultation with the source work. (–ed.).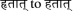 for an obvious reason. (–ed.).
for an obvious reason. (–ed.).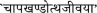 . This has been refined in consultation with the source work. (–ed.).
. This has been refined in consultation with the source work. (–ed.).