6.1 Introduction

After around 70 years of the seminal work of Norbert Wiener “Cybernetics: or the Control and Communication in the Animal and the Machine” [1], Wiener’s great thinking still presents fundamental impacts to many folds of the human society in the era of networking world and Big Data today, ranging from modelling and feedback-loop analysis to stability and control of categories of systems and subjects, whatever large-scale or simply structured, linear or nonlinear, low dimensional or extremely high dimensional. The communications among humans and machines in the eyes of Norbert Wiener in 1950s were generally assumed as point-to-point or neglected as regularly structured in the scope of classic graph theory [2, 3]. Afterwards, Erdős and Rényi extended the graph description with uncertainty and randomness, and proposed the random graph theory in 1960s [4]. In the following decades the flourishing information and communication techniques have pushed the whole human society to a networking village of today, while the understanding of dominant yet hidden connectivity patterns of the communications among humans and machines were not revisited until recently.

The discovery of small-world and scale-free features in 1998–1999 has been verified in ubiquitous complex networks [5, 6], which have attracted the world-wide attention to the new emergence of network science. The popular concerns cover not only the topological complexity of a large-scale complex network system but also the interdependence between the infrastructure and the collective performance of such networks [7–10]. Typically, from the viewpoint of system and control, the precise mathematic description and appropriate models of a complex network play a significant role to achieve the desirable performance in return. However, in the situations of large-scale spatial prevalence of diseases in human populations, for example, such a solution may be infeasible if the availability of accurate data collections is far from sufficiently satisfactory.

Nevertheless the global outbreaks of prevalent infectious diseases in recent decades have led to great social, economic, and public health loss [11–14], which is partially due to the urbanization process and, in particular, the wide-establishment of long-distance public transportation networks (e.g., world-wide air-line web) and urban public commuting systems (e.g., subway and metro networks) to facilitate the dissemination of pathogens accompanied with passengers [15, 16]. Academia has witnessed that prediction and control of epidemic dynamics in networks as a flourishing research topic with interdisciplinary approaches [17–20]. However, more challenging problems arising from the epidemic prevalence on a meta-population network have not received adequate attentions, such as identifying the parameters of epidemic network systems and the epidemic invasion pathways on a meta-population network, which, ignored previously, certainly play important roles in evaluating the intensity of outbreak of epidemics among human patches/populations.

Assume the seed of a disease/virus as the input signal to the whole human population system, and the observed patient samples as the system output. Then, the spatial invasion of the disease inside the human population is obscure as a black box to be identified, and this system combines many factors such as human mobility patterns (commuting and long-distance traveling) and mathematical epidemiology as well. Therefore, identifying such an epidemic process with the interplay of complex networks and the human population is a challenge to public health-care administrative agency when predicting the large-scale spatial prevalence of a disease and announcing counter strategies.

The theory of system identification has been used to estimate the epidemic parameters of a complex system which are described by ordinary differential equations (ODE) such as HIV/AIDS epidemic dynamics [21]. Another related topic is inferring network topology by utilizing the information about a dynamics process on networks [22, 23]. Note that system identification and network inference techniques are not fit to handle the epidemic process on meta-population networks which are stochastic, high-dimensional, and multi-scale. Besides, source identification on complex networks is a close and popular topic. Some source identification algorithms [24, 25] have been designed for information/contact networks, but they are not feasible in identifying the invasion processes on meta-population networks.

Many instructive methods have also been proposed to explore the spatial spread of an epidemic process on meta-population networks. Maeno [26] inferred the epidemic network between eleven countries and areas during SARS in 2003 by analysing the epidemic time series. Reference [27] extracted the most likely epidemic transmission trees of the 1918 influenza pandemic in England, Wales and the United States. Some methods based on machine learning were also proposed to infer the epidemic networks from surveillance data [28–30]. Gautreau et al. presented a measure of the average arrival time to characterize the minimum-distance path from subpopulation i to subpopulation j over all possible paths [31], and the average arrival time-based shortest path tree is constructed by assembling all the shortest paths from the seed subpopulation to any other subpopulation in a networked meta-population. Balcan et al. proposed a Monte Carlo maximum likelihood method to produce a most likely infection tree [32]. They constructed the minimum spanning tree from the seed subpopulation to minimize the distance. Recently, Brockmann and Helbing [15] proposed a new concept called “effective distance” to predict the disease arrival time. From node/location i to node/location j, the effective distance D ij is defined as the minimum sum of effective lengths over all reachable branches along this path. The set of shortest paths to all other nodes from seed node i constitutes a shortest path tree, illustrating the most probable paths from the root to other nodes. On the other hand, approaches based on machine learning such as genetic algorithm [28–30] has been used to extract epidemic transmission networks.

Note that some of the above works didn’t distinguish epidemic transmission network and invasion pathways/trees. In fact, these two concepts are a bit different, and very few work has discussed the parameter identification of a meta-population network system. Here a natural problem poses itself that whether the parameters and epidemic invasion process can be identified from the infection data of populations and network topology? To get a better understanding of how the contagion diffuses via an invasion process on network, more topics deserve further efforts: (i) So far, there are few works on identification of parameters of a meta-population network which an epidemic is occurring on. New questions such as the following ones are raised: How to use the data from the limited epidemic realizations to infer the system parameters as accurate as possible? Does a more appropriate model of individual mobility exist? (ii) Identification of spatial invasion pathways is to uncover the channels by which the hosts transmit viruses in a spatially structured population with the infection data. In a large-scale meta-population network, the complex pattern of pathways challenges the methodology to identify the epidemic invasion pathways in a meta-population network.

In this chapter, we review our series of work in recent years [33–37] on identifying parameters of the susceptible-infected model and spatial invasion pathways on a meta-population network as well as the minimal case of two-subpopulation version, which may also extend to the prediction of spatial epidemics as well. The remainder of this chapter is arranged as follows. Section 6.2 gives the detailed description of preliminaries. Section 6.3 introduces the parameter identification of epidemic models on a meta-population network. Section 6.4 contributes the inference of epidemic invasion pathways in a meta-population network with both methodologically and example verifications. In Sect. 6.5, extending the steps of the previous sections, the prediction of spatial epidemic transmission comes with several feasible methods. Finally, Sect. 6.6 concludes the whole chapter with outlook in future research.

6.2 Preliminary

A meta-population network, which was originated from the meta-population model proposed by Richard Levins [38] to explore spatial ecology, embeds public transportation networking systems to model and uncover nontrivial patterns of spatial prevalence of global infectious diseases in the past years [15, 31, 32, 39, 40]. In this section, we introduce the meta-population network model and the susceptible-infected (SI) compartment epidemic dynamic as well. In this chapter, we consider the discrete-time dynamics.

6.2.1 The Compartment Model with SI Reaction Dynamics

The well-known susceptible-infected (SI) compartment model (Fig. 6.1), which is the simplest version in the epidemic compartment family, generally describes the early stage of prevalence of viruses/pathogen [24, 25, 41], especially in the situation of non-recovery. In such a population, the states of individuals are stratified into two compartments (classes): susceptible to the infection of the pathogen; and infected by the pathogen. Generally, we assume that all individuals are homogenously mixing in the population. The state transition of an individual between two compartments is governed by the following reaction process: When a susceptible individual meets (i.e., has the contacts) with an infected individual in a unit time, the susceptible individual will be infected with an infection rate β.

Fig. 6.1
figure 1

Schematic illustration of the SI compartment model, where β denotes the infection rate

Full size image

6.2.2 The Two-Subpopulation Version of a Meta-population Network

Before describing a general meta-population network, we first introduce a minimal meta-population network containing two subpopulations (labelled as 1 and 2 as shown in Fig. 6.2) with SI epidemic compartments. We assume the infection process evolves as a discrete-time system, and subpopulation 1 is infected initially (In this case of simulation, we assume 1 individual is infected among all 10,000 individuals in subpopulation 1). During each time step, the reaction takes place in each subpopulation if it contains two classes of individuals (susceptible and infected). Denote p 12 (p 21) the diffusion rate of individuals transferring from subpopulation 1 to 2 (2 to 1), which are often not symmetric, i.e., p 12 ≠ p 21. Besides, an individual in subpopulation 1 (2) chooses jumping to subpopulation 2 (1) at diffusion rate p 12 (p 21), i.e., the so-called diffusion process. Therefore, the probability an individual stays in subpopulation 1 (2) is 1 − p 12 (1 − p 21).

Fig. 6.2
figure 2

Schematic representation of a minimal meta-population network with the SI model. At initial time, subpopulation 1 is infected (containing at least one infected individual (red)), and subpopulation 2 is susceptible (all are susceptible individuals (blue)) (From Wang et al. [33])

Full size image

Therefore, without considering the diffusion of new increment of infected individuals after reaction, the whole evolution dynamics is described as

$$\displaystyle{ \left \{\begin{array}{ll} \langle I_{1}(t + 1) - I_{1}(t)\rangle = \beta I_{1}(t) \dfrac{S_{1}(t)} {N_{1}(t)} + p_{21}I_{2}(t) - p_{12}I_{1}(t), \\ \langle I_{2}(t + 1) - I_{2}(t)\rangle = \beta I_{2}(t) \dfrac{S_{2}(t)} {N_{2}(t)} + p_{12}I_{1}(t) - p_{21}I_{2}(t), \end{array} \right. }$$
(6.1)

where 〈 ⋅ 〉 represents the expectation of the corresponding terms, N 1(t) (N 2(t)) denotes the number of individuals in subpopulation 1 (2) at time t, I 1(t) (I 2(t)) denotes the number of infected individuals in subpopulation 1 (2), S 1(t) (S 2(t)) denotes the number of susceptible individuals in subpopulation 1 (2). The first term of the right-hand side (RHS) in Eq. (6.1) represents the new increment of infected individuals \(\langle \varDelta _{R}I_{i}(t)\rangle = \beta I_{i}(t) \frac{S_{i}(t)} {N_{i}(t)},i = 1,2\), after reaction from t to t + 1. The second and third terms of RHS in Eq. (6.1) represent the diffusion of infected individuals in the diffusion process. As mentioned above, we do not consider the diffusion of new increment of infected individuals after reaction in this case. Besides, the evolution of susceptible individuals is similar with the infected individuals.

6.2.3 The General Description of a Meta-population Network

Extending the minimal version as two subpopulations to the general case of a meta-population network, we divide the whole population (generally, such a population covers a large-scale spatial region of a country or the whole world) into a number of subpopulations. In a meta-population network, a subpopulation is connected with others via a public transportation network, e.g., the air-line web, the high-way web to form the backbone of such a meta-population network. A subpopulation as a node in the network contains a number of individuals homogeneously mixed, and individuals travel between two subpopulations (nodes) via the public transportation means (edge) with some (fixed) diffusion rate. All edges are directed.

With the SI dynamics, the disease propagates in subpopulations and spreads among neighbouring subpopulations via the reaction-diffusion process in a unit time, as illustrated in Fig. 6.3. Denote N the number of subpopulations (nodes) of a meta-population network, and N i (t) = S i (t) + I i (t) is the population size of subpopulation i at time t, where S i (t) is the number of susceptible individuals, and I i (t) is the number of infected individuals of subpopulation i at time t, respectively. Therefore, the intra-population epidemic dynamics in subpopulation i is governed by the SI model. Per unit time, the risk of infection of a susceptible individual within subpopulation i is characterized by λ i (t) = βI i (t)∕N i (t) during the reaction process. Denote the probability that an individual (S or I) of subpopulation i moves to its neighbouring subpopulation j as diffusion rate p ij , which describes the inter-population mobility dynamics. The symbol of diffusion rate \(0 \leq p_{ij} = \frac{\langle w_{ij}\rangle } {\langle N_{i}\rangle } <1\), where w ij is the number of individuals moving from subpopulation i to j per unit time (0 ≤ 〈w ij 〉 < 〈N i 〉).

Fig. 6.3
figure 3

Illustration of a networked meta-population model, which comprises six subpopulations that are coupled by the mobility of individuals. In each subpopulation, each individual can be in one of the two states (susceptible, infected), as shown in different colours. Grey ones represent susceptible subpopulations. Red ones represent infected subpopulations. Light red subpopulations denote less number of infected individuals than the dark red ones. Each individual can travel between the connected subpopulations. (a) A networked meta-population. (b) Two subpopulations (From Wang et al. [35])

Full size image

Therefore, if we do not consider the diffusion of new increment of infected individuals after the reaction process, the evolution of an infected subpopulation i is described as follows:

$$\displaystyle{ \begin{array}{llll} \langle I_{i}(t + 1) - I_{i}(t)\rangle = \beta I_{i}(t) \frac{S_{i}(t)} {N_{i}(t)} + \sum _{j=1,j\neq i}^{N}p_{ ji}I_{j}(t) -\sum _{j=1,j\neq i}^{N}p_{ ij}I_{i}(t), \end{array} }$$
(6.2)

which is investigated in Sect. 6.4.

When we consider the diffusion of new increment of infected individuals after the reaction, the evolution is described by

$$\displaystyle{ \begin{array}{lll} \hspace{-8.0pt}\langle I_{i}(t + 1) - I_{i}(t)\rangle =&\beta I_{i}(t)S_{i}(t)/N_{i}(t) \\ & +\sum _{j\neq i}\left \{p_{ji}[I_{j}(t) +\langle \varDelta _{R}I_{j}(t)\rangle ] - p_{ij}[I_{i}(t) +\langle \varDelta _{R}I_{i}(t)\rangle ]\right \},\end{array} }$$
(6.3)

where Δ R I j (t) is the increment of I j (t) after the reaction from t to t + 1. We give the extensive investigation of the dynamics given by Eq. (6.3) in Sect. 6.5.

We now discuss the individual mobility operator to handle the presence of stochasticity and independence of individual mobility, where the number of successful migration of individuals between adjacent subpopulations is quantified by a binomial or a multinomial process, respectively. If the focal subpopulation i only has one neighbouring subpopulation j, the number of individuals in a given compartment \(\mathcal{X}\) (\(\mathcal{X} \in \{ S,I\}\) and \(\sum _{\mathcal{X}}\mathcal{X}_{i} = N_{i}\)) transferred from i to j per unit time, \(\mathcal{T}_{ij}(\mathcal{X}_{i})\), is generated from a binomial distribution with probability p ij representing the diffusion rate and the number of trials \(\mathcal{X}_{i}\), i.e.,

$$\displaystyle{ Binomial(\mathcal{T}_{ij},\mathcal{X}_{i},p_{ij}) = \frac{\mathcal{X}_{i}!} {\mathcal{T}_{ij}!(\mathcal{X}_{i} -\mathcal{ T}_{ij})!}p_{ij}^{\mathcal{T}_{ij} }(1 - p_{ij})^{(\mathcal{X}_{i}-\mathcal{T}_{ij})}, }$$
(6.4)

where 1 − p ij denotes the probability of an individual staying in subpopulation i.

If the focal subpopulation i has multiple neighbouring subpopulations j 1, j 2, …, j k , with k representing i’s degree, the numbers of individuals in a given compartment \(\mathcal{X}\) moving from i to j 1, j 2, …, j k are generated from a multinomial distribution with probabilities \(p_{ij_{1}},p_{ij_{2}},\ldots,p_{ij_{k}}\) representing the diffusion rates on the edges emanated from subpopulation i and the number of trails \(\mathcal{X}_{i}\), i.e.,

$$\displaystyle{ \begin{array}{lll} &Multinominal(\{\mathcal{T}_{ij_{\ell}}\},\mathcal{X}_{i},\{p_{ij_{\ell}}\}) & \\ &\qquad = \frac{\mathcal{X}_{i}!} {\prod _{\ell}\mathcal{T}_{ij_{\ell}}!(\mathcal{X}_{i}-\sum _{\ell}\mathcal{T}_{ij_{\ell}})!}(\prod _{\ell}p_{ij_{\ell}}^{\mathcal{T}_{ij_{\ell}}})(1 -\sum _{\ell}p_{ ij_{\ell}})^{(\mathcal{X}_{i}-\sum _{\ell}\mathcal{T}_{ij_{\ell}})},& \end{array} }$$
(6.5)

where integer ℓ ∈ [1, k], term \(1 -\sum _{\ell}p_{ij_{\ell}}\) denotes the probability of an individual staying in subpopulation i.

6.3 Epidemic Parameter Identification

The epidemic parameters of a networked meta-population include the infection rate and diffusion rate, which play an important role in the SI dynamics, while the stochastic epidemic dynamics and the limit of available data make such an identification task more difficult. In this section, we review the method to identify both parameters for a two-subpopulation network and an estimation of infection rate for a general network version.

6.3.1 The Case of Two-Subpopulation Model

We first describe one realization of the invasion process evolving as follows. At the beginning, subpopulation 1 has been initialized with one infected individual in this case. When time evolves, the number of infected individuals I 1(t) of subpopulation 1 increases due to the SI reaction dynamics in this subpopulation. The epidemic arrival time (EAT) is defined as the first arrival time of infected individuals from an infected subpopulation moving to a neighbouring susceptible subpopulation. To address the EAT, some infected individual(s) will move (diffuse) to subpopulation 2, which finally succeed in infecting subpopulation 2. Therefore, recording the infection data (the number of infected individuals in subpopulation i at time t, i.e., I i (t), i = 1, 2) of each subpopulation as the available data, we need to identify the unknown infection rate β and diffusion rate p 12.

At the early stage of epidemic dynamics, we can approximate S i (t) ≈ N i (t), i = 1, 2 (I i (0) ≪ N i (0)) and therefore simplify Eq. (6.1) as

$$\displaystyle{ \langle I_{1}(t + 1) - I_{1}(t)\rangle +\langle I_{2}(t + 1) - I_{2}(t)\rangle \approx \beta (I_{1}(t) + I_{2}(t)). }$$
(6.6)

Denote I(t) the number of infected individuals in all subpopulations at time t, i.e., I(t) = I 1(t) + I 2(t). Traditionally, the RHS of the above equation accounts for an exponential growth of the number of infected individuals, and β is regarded as the Malthusian growth rate. Thus, we rewrite Eq. (6.6) in the compact form as I(t) ≈ e β(t−0) I(0). Considering ln[I(0)] ≪ ln[I(t)], (0 ≪ t), we have \(\beta \sim \frac{\ln [I(t)]} {t}\). Therefore, we estimate the infection rate β by fitting the slope of ln[I(t)].

We now discuss how to identify diffusion rate p 12. Repeat the invasion of subpopulation 2 from subpopulation 1 until we record the epidemic arrival time to subpopulation 2, i.e., the disease/virus finally lands in subpopulation 2 and starts the local infection. We investigate the period from the initial time (t = 0) to the epidemic arrival time (t EAT ) that the first \(\mathcal{H}\) individuals from subpopulation 1 invade subpopulation 2. From t EAT − 1 to t EAT , we get

$$\displaystyle{ \left \{\begin{array}{ll} \langle I_{1}(t_{EAT}) - I_{1}(t_{EAT} - 1)\rangle = \beta I_{1}(t_{EAT} - 1) - p_{12}I_{1}(t_{EAT} - 1), \\ \langle I_{2}(t_{EAT}) - I_{2}(t_{EAT} - 1)\rangle = p_{12}I_{1}(t_{EAT} - 1). \end{array} \right. }$$
(6.7)

The likelihood function about the first \(\mathcal{H}\) infected individuals from subpopulation 1 traveling to subpopulation 2 at time t EAT is

$$\displaystyle{ \text{P}(\mathcal{H},t_{EAT}-1) = C_{I_{1}(t_{EAT}-1)}^{\mathcal{H}}(1-p_{ 12})^{I_{1}(t_{EAT}-1)-\mathcal{H}}p_{ 12}^{\mathcal{H}}\times \prod _{ i=1}^{\eta -1}(1-p_{ 12})^{I_{1}(i)}, }$$
(6.8)

where t EAT − 1 = η, η(η ≥ 1) is an integer. If there are s (s ≥ 1) rounds of repeated realizations of invasion processes, the joint likelihood function is given by

$$\displaystyle\begin{array}{rcl} & & \text{P}(\mathcal{H}^{\{1\}},t_{ 1};\mathcal{H}^{\{2\}},t_{ 2};\cdots \,;\mathcal{H}^{\{s\}},t_{ s}) \\ & & \qquad = \text{P}(\mathcal{H}^{\{1\}},t_{ 1}) \times \text{P}(\mathcal{H}^{\{2\}},t_{ 2}) \times \cdots \text{P}(\mathcal{H}^{\{s\}},t_{ s}),{}\end{array}$$
(6.9)

where s is the number of rounds of repeated simulation realizations of epidemic invasion processes. Take the logarithm of Eq. (6.9), the joint likelihood function yields \(\text{L(P)} =\ln (\text{P}(\mathcal{H}^{\{1\}},t_{1};\mathcal{H}^{\{2\}},t_{2};\cdots \,;\mathcal{H}^{\{s\}},t_{s})).\)

Therefore, by means of the maximum likelihood estimation, we have \(\frac{d\text{L(P)}} {dp_{12}} = \frac{1} {p_{12}-1}(\sum _{i=1}^{s}(I_{ 1}^{\{i\}}(\eta _{ i}) -\mathcal{ H}^{\{i\}}) +\sum _{ i=1}^{s}\sum _{ j=1}^{\eta _{i}-1}I_{ 1}^{\{i\}}(j)) + \frac{1} {p_{12}} \sum _{i=1}^{s}\mathcal{H}^{\{i\}}\). Letting \(\frac{d\text{L(P)}} {dp_{12}} = 0\), we finally have

$$\displaystyle{ \begin{array}{llll} \hat{p}_{12} = \frac{\sum _{i=1}^{s}\mathcal{H}^{\{i\}}} {\sum _{i=1}^{s}\left [I_{1}^{\{i\}}(\eta _{i})-\mathcal{H}^{\{i\}}+\mathcal{H}^{\{i\}}+\sum _{j=1}^{\eta _{i}-1}I_{1}^{\{i\}}(j)\right ]} = \frac{\sum _{i=1}^{s}\mathcal{H}^{\{i\}}} {\sum _{i=1}^{s}\sum _{j=1}^{\eta _{i}}I_{1}^{\{i\}}(j)}, \end{array} }$$
(6.10)

where \(\hat{p}_{12}\) represents the estimation of diffusion rate p 12. 

6.3.2 The Case of a Meta-population Network

Mathematically, the estimation of diffusion rates requires the availability of a large number of epidemic realizations for a given meta-population network. However, the availability of such repeated data for emergent infectious diseases is rather limited in reality. Therefore, the estimation of diffusion rates in the general case of a meta-population network is infeasible due to the computational complexity and the limit of available data, which generally can be alternatively obtained from the statistics of public transportation section. The estimation of infection rate β in the general case of a meta-population network is addressed here.

Summing the number of infected individuals in Eq. (6.3) over all subpopulations i, we have ∑ i 〈I i (t + 1) − I i (t)〉 = ∑ i = 1 N βI i (t)S i (t)∕N i (t). Since I i (t) ≪ N i (t) at the early epidemic stage, it is simplified as ∑ i 〈I i (t + 1) − I i (t)〉 ≈ β∑ i I i (t). The term I i (t + 1) − I i (t) fluctuates around its mathematical expectation, and we have the approximation as

$$\displaystyle\begin{array}{rcl} \begin{array}{lll} \beta \sim \frac{\sum _{i}(I_{i}(t+1)-I_{i}(t))} {\sum _{i}I_{i}(t)}.\end{array} & &{}\end{array}$$
(6.11)

Thus, given all recorded times t 1, t 2, …, t m′, the infection rate \(\hat{\beta }\) is estimated as

$$\displaystyle\begin{array}{rcl} \begin{array}{lll} \hat{\beta } =\arg \mathop{ \min }\limits _{\beta ^{{\ast}}}\ \sum _{t=t_{1}}^{t_{m'}}\left \vert (I(t + 1) - I(t)) -\beta ^{{\ast}}I(t)\right \vert ^{2} = (X^{\top }X)^{-1}X^{\top }Y,\end{array} & &{}\end{array}$$
(6.12)

where X ⊤ represents the transposition of X, and \(X = \left [I(t_{1}),I(t_{2}),\ldots,I(t_{m'})\right ]^{-1}\), \(Y = \left [(I(t_{1} + 1) - I(t_{1})),(I(t_{2} + 1) - I(t_{2})),\ldots,(I(t_{m'} + 1) - I(t_{m'}))\right ]^{-1}\).

6.3.3 Example: Identifying the Diffusion Rate p 12

In this subsection, we only illustrate the identification performance of estimating diffusion rate p 12 on a two-subpopulation SI model as an example. A more general case (in the sense of an arbitrary number of subpopulations) of example of identification performance of infection rate β will be investigated in Sect. 6.5. In the two-subpopulation case, statistic information of p 12 is embedded in the surveillance infection data of the two subpopulations during the epidemic invasion process. As shown in Fig. 6.4, the estimation of p 12 approaches the real value if the number of realizations increase, and the estimation error \(\vert \hat{p}_{12} - p_{12}\vert\) is less than 5% of p 12. Finally the estimation of p 12 as \(\hat{p}_{12}\) tends to the real value.

Fig. 6.4
figure 4

The estimation error of diffusion rate p 12 versus the number of realizations of the invasion process, and the error finally converges to zero. \(\hat{p}_{12}\) is the estimated value of p 12. The actual value of diffusion rate p 12 is 0.01

Full size image

6.4 Identification of Invasion Pathways

During a real spatial cascade of an infectious disease, the spatial invasion pathways are the collection of directed transmission paths of an infectious disease rooted in the infected source subpopulation invading their susceptible neighbouring subpopulations. Actually, no one can predict such spatial invasion pathways to suppress the spreading processes at its infant prevalence. With the data availability of epidemic arrival time (EAT), i.e., the first invasion time discussed in the previous section, we may infer the patterns of invasion pathways.

Suppose one subpopulation is initially infected containing several infected individuals. As time evolves, the infected individuals of the seed subpopulation travel to the neighbouring subpopulations and try to infect their individuals. The successful invasion brings more invaded subpopulations with the cascade of infections. Therefore, the focus of interest is that when a subpopulation is invaded/infected by its m(m ≥ 2) infected neighbours with the available EAT data, how can we infer the culprit(s) and identify the invasion pathways in such a cascade infection? In the concerned situation, we assume that the surveillance infection data (the number of infected individuals of each subpopulation at each time t) is available as well as the topology of the meta-population network (including diffusion rates).

6.4.1 Invasion Partition and Types of Invasion Cases

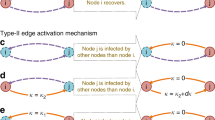
We categorize all candidates of invasion pathways via the so-called invasion partition (INP) into four types of invasion cases (INCs), as shown in Fig. 6.5. An invasion case contains two sets, i.e., \(\mathbb{S}\) and \(\mathbb{I}\). Subpopulations which are not infected at t EAT − 1 but infected at t EAT are put in set \(\mathbb{S}\), and their neighbours which are infected at t EAT − 1 are put in set \(\mathbb{I}\). All four types of invasion cases are defined.

  1. (i)

    I ↦ S: In this case, both \(\mathbb{I}\) and \(\mathbb{S}\) only have one subpopulation. That is to say, a susceptible subpopulation is infected at t EAT by the first arrival of infected individual(s) from its unique neighbouring infected subpopulation at t EAT − 1, and this infected subpopulation has no other newly infected neighbours at t EAT .

  2. (ii)

    I ↦ nS(n > 1): In this case, \(\mathbb{I}\) contains one infected subpopulation, and \(\mathbb{S}\) contains n(n > 1) subpopulations. That is to say, an infected subpopulation simultaneously infects its n(n > 1) susceptible neighbours, each of which has only one infected neighbouring subpopulation.

  3. (iii)

    mI ↦ S(m > 1): In this case, \(\mathbb{I}\) consists of m(m > 1) subpopulations, and \(\mathbb{S}\) only contains one single subpopulation. That is to say, a susceptible subpopulation is infected by the first arrival of infected individual(s) coming from its m(m > 1) infected neighbouring subpopulation, which has no other newly infected neighbours at this time.

  4. (iv)

    mI ↦ nS(m, n > 1): In this case, sets \(\mathbb{S}\) and \(\mathbb{I}\) both contain more than one subpopulation. The edges from \(\mathbb{I}\) to \(\mathbb{S}\) form a connected subgraph. Each previously susceptible subpopulation in \(\mathbb{S}\) is infected by the new arrival of infected individual(s) from at least one of the m infected subpopulations in \(\mathbb{I}\). Each subpopulation in \(\mathbb{I}\) has no other newly infected neighbours except the susbpopulations in \(\mathbb{S}\) at this time.

Fig. 6.5
figure 5

(a) Example of I ↦ S INC, in which the infected individuals of only one infected subpopulation invades one susceptible subpopulation. The infected subpopulation is represented in red, while the plain patch is the subpopulation that remains susceptible before time t EAT but will be infected between t EAT − 1 to t EAT due to the arrival of infected individuals from the upstream infected subpopulation. (b) Example of I ↦ nS INC, in which the infected individuals of only one infected subpopulation invades n(n ≥ 2) susceptible subpopulations. (c) Example of mI ↦ S INC, in which the infected individuals of m infected subpopulations invade one susceptible subpopulation. (d) Example of mI ↦ nS INC, in which the infected individuals of m(m ≥ 2) infected subpopulations invade n(n ≥ 2) susceptible subpopulations (From Wang et al. [35])

Full size image

Figure 6.5 illustrates such four types of invasion cases as I ↦ S, mI ↦ nS(n > 1), mI ↦ S(m > 1) and mI ↦ nS(m, n > 1). Besides, we define the directed edges from infected subpopulation i in \(\mathbb{I}\) to susceptible subpopulations in \(\mathbb{S}\) as invasion edges, which are the candidates of invasion pathways. Therefore, we define a decomposition procedure invasion partition (INP) to achieve the task of dividing subpopulations and edges into such invasion cases. As summarized in Algorithm 1, we propose a heuristic algorithm to achieve the INP task.

Algorithm 1 Invasion Partition (INP)

1: At an epidemic arrival time, collect all newly infected subpopulations as initial \(\mathbb{S}\) and their previously infected neighbours as \(\mathbb{I}\);

2: Start with an arbitrary element S i in set \(\mathbb{S}\), to compose the initial \(\mathbb{S}^{{\ast}}\);

3: Find all neighbors of S i in set \(\mathbb{I}\) to compose the set \(\mathbb{I}^{{\ast}}\);

4: For each new member in \(\mathbb{I}^{{\ast}}\), find its new neighbours in the \(\mathbb{S}\) to update \(\mathbb{S}^{{\ast}}\) if any;

5: For each new member in \(\mathbb{S}^{{\ast}}\), find its new neighbours in the \(\mathbb{I}\) to update \(\mathbb{I}^{{\ast}}\) if any;

6: Repeat the above two steps until we cannot find any new neighbours in \(\mathbb{S}\) and \(\mathbb{I}\), we get an invasion case consisting of \(\mathbb{I}^{{\ast}}\) and \(\mathbb{S}^{{\ast}}\), then update the \(\mathbb{S}\) and \(\mathbb{I}\);

7: Repeat steps 2–6 to get new invasion cases until there are no elements in \(\mathbb{S}\).

6.4.2 Observability of a Subpopulation and an Edge

We further classify the observability of a subpopulation and an edge. Observability of a subpopulation is defined by comparing the number of infected individuals of subpopulation i at time t EAT − 1 and t EAT , which reflects the information held for the inference of relevant invasion pathway. Observability of an directed edge emanated from an infected subpopulation can be defined by the types of subpopulations it connects to.

  1. (i)

    Observable Subpopulation: From t EAT − 1 to t EAT , subpopulation i is an observable subpopulation if it experiences one of the following three state transitions. The first is S i → I i , which indicates that this subpopulation has been infected (for the first time) during this period by infected individuals (because I i (t) is available). The second is I i → S i . We know how many infected individuals diffused from this subpopulation in this case. The third is S i → S i . This case represents subpopulation i keeps its susceptible status.

  2. (ii)

    Partially Observable Subpopulation: The number of infected individuals of an infected subpopulation may decrease, that is to say I i (t EAT ) < I i (t EAT − 1) and I i (t EAT ) > 0. We call subpopulation i is a partially observable subpopulation, because we know at least ΔI i (t EAT ) = | I i (t EAT ) − I i (t EAT − 1) | infected individuals leave i.

  3. (iii)

    Unobservable Subpopulation: If the number of infected individuals does not decrease, i.e., I i (t EAT ) ≥ I i (t EAT − 1), it is difficult to judge whether and how many infected hosts leave subpopulation i. We call it unobservable subpopulation.

Here the observability of a subpopulation indicates the diffusion information of this subpopulation. Figure 6.6a–c illustrate the above cases. Together with the observability of a subpopulation, the directed edges emanated from an infected subpopulation (here denoted i) in set \(\mathbb{I}\) can be classified into three types, i.e., observable edges, partially observable edges and unobservable edges:

  1. (i)

    Observable Edges: Any directed edge from i to observable subpopulation j whose transition is S j → S j or I j → S j from t EAT − 1 to t EAT . This edge implies no infected hosts move from i.

  2. (ii)

    Partially Observable Edges: If an directed edge emanated from infected subpopulation i to a partially observable subpopulation, the edge is partially observable.

  3. (iii)

    Unobservable Edges: If infected subpopulation i connects with an unobservable subpopulation, this directed edge from i is an unobservable edge.

Fig. 6.6
figure 6

Illustration of subpopulation observability: (a) observable subpopulations, (b) partially observable subpopulation, and (c) unobservable subpopulation. Here time t is t EAT (From Wang et al. [35])

Full size image

6.4.3 Accurate Identification of Invasion Pathways

We now consider to accurately identify the invasion pathways. Among the four types of invasion cases (INCs), since the two types of INCs (I ↦ S and I ↦ nS, n ≥ 2) have the unique invasion edge(s) from the neighboring infected subpopulation, the invasion pathways therefore are easy to identify accurately. We only need concern the other two types of INCs, i.e., mI ↦ S and mI ↦ nS.

6.4.3.1 The Case of mI ↦ S (m > 1)

A representative mI ↦ S(m > 1) INC (Fig. 6.5c) consists of two sets. Set \(\mathbb{I} =\{ I_{1},I_{2},\ldots,I_{m}\}\) is composed of the infected subpopulations at t EAT − 1, and set \(\mathbb{S} =\{ S_{1}\}\) is composed of the susceptible subpopulation(s) at t EAT − 1 which are infected at t EAT . Assume subpopulation S 1 is infected at t EAT by the first arrival of \(\mathcal{H}\) infected individuals coming from some of the infected subpopulations in \(\mathbb{I}\), where \(\mathcal{H}\) is a positive integer.

Suppose \(\mathcal{H}_{i1}\) is the actual number of infected individuals travelling from an infected subpopulation I i in set \(\mathbb{I}\), and we have

$$\displaystyle{ \sum _{i=1}^{m}\mathcal{H}_{ i1} =\mathcal{ H}, }$$
(6.13)

where \(0 \leq \mathcal{ H}_{i1} \leq \mathcal{ H}\), \(\mathcal{H}_{i1} \leq I_{i}(t_{EAT} - 1)\), and 0 ≤ i ≤ m. \(\mathcal{H}\) is available from the infection data, while we do not know \(\mathcal{H}_{i1}\). To reach the unique solution of Eq. (6.13) which corresponds to a set of invasion pathways of mI ↦ S(m > 1), we give Theorem 1 to accurately identify the invasion pathways of INC mI ↦ S(m > 1).

Theorem 1.

The invasion pathways of the invasion case mI ↦ S(m > 1) can be accurately identified, given the following two conditions are satisfied: (1) among m possible sources illustrated in set \(\mathbb{I}\) , there are only m′(m′ ≤ m) partially observable subpopulations \(\mathbb{I}'\) , whose neighbouring subpopulations j (excluding the invasion destination S 1 ) only experience the transition S j → S j or I j → S j at that EAT, (2) \(\sum _{i\in \mathbb{I}'}\big[I_{i}(t_{EAT} - 1) - I_{i}(t_{EAT})\big] =\mathcal{ H}\) .

Proof.

According to the definition of observability, in an INC, the number of local infected individuals in an partially observable source i will be decreased by [I i (t EAT − 1) − I i (t EAT )] due to the movement of infected individuals. If the subpopulations j in the neighbourhood of i only experience the transition of S j → S j or I j → S j from t EAT − 1 to t EAT , they do not to receive the infected individuals from subpopulation i. Therefore, the newly infected subpopulation S 1 is the only destination for those infected individuals departing from the partially observable sources. Since m′ ≤ m, the second condition guarantees that Eq. (6.13) only has a unique solution, which corresponds to the accurate identification of invasion pathways of this invasion case. □

6.4.3.2 The Case of mI ↦ nS(m > 1, n > 1)

The final typical INC mI ↦ nS as shown in Fig. 6.5d includes set \(\mathbb{I} =\{ I_{i}\vert i = 1,2,\ldots,m\}\) and \(\mathbb{S} =\{ S_{i}\vert i = 1,2,\ldots,n\}\). Denote \(\{\mathcal{H}_{i}\vert i = 1,2,\ldots,n\}\) the number of the first arrival of infected individuals to susceptible subpopulation S i in set \(\mathbb{S}\), and U i (i = 1, 2, …, m) the subset of susceptible neighbouring subpopulations in set \(\mathbb{S}\) of infected subpopulation I i , and Y j (j = 1, 2, …, n) the subset of infected neighbouring subpopulations in set \(\mathbb{I}\) of susceptible subpopulation S j .

Define \(\sigma =\{\{\mathcal{ H}_{i1}\vert i \in Y _{1}\},\ldots,\{\mathcal{H}_{in}\vert i \in Y _{n}\}\}\) as a potential solution for the mI ↦ nS, if σ is subject to the following two conditions: (i)

$$\displaystyle\begin{array}{rcl} \sum _{i\in Y _{k}}\mathcal{H}_{ik} =\mathcal{ H}_{k},& &{}\end{array}$$
(6.14)

where \(\mathcal{H}_{ik}(\geq 0)\) is the number of infected hosts invading subpopulation S k from I i at t EAT ; (ii) For any \(\mathcal{H}_{ik}\), we have \(\sum _{k\in U_{i}}\mathcal{H}_{ik} \leq I_{i}(t_{EAT} - 1)\), where 1 ≤ i ≤ m, 1 ≤ k ≤ n.

Suppose an mI ↦ nS has M potential solutions, and \(\sigma _{j} =\{\{\mathcal{ H}_{i1}^{(j)}\vert i \in Y _{1}\},\ldots,\{\mathcal{H}_{in}^{(j)}\vert i \in Y _{n}\}\}\ (1 \leq j \leq M)\) represents one of the solutions.

Given some specific prerequisites (as the conditions of Theorem 2), Eq. (6.14) has a unique solution, which implies that the invasion pathway(s) can be identified accurately. Theorem 2 elucidates this scenario.

Theorem 2.

The invasion pathway(s) of the invasion case mI ↦ nS(m, n > 1) can be identified accurately, given the following three conditions are satisfied: (1) the number of invasion edges E in ≤ n + m, (2) the neighbouring subpopulations j of each subpopulation in set \(\mathbb{I}\) are with the transition S j → S j or I j → S j except their neighbouring subpopulations in set \(\mathbb{S}\) during t EAT − 1 to t EAT , (3) \(\sum _{i=1}^{m}\varDelta I_{i}(t_{EAT}) =\sum _{ k=1}^{n}\mathcal{H}_{k}\) .

Proof.

Since the number of infected individuals in the partially observable subpopulation i reduces at time t EAT , i.e., I i (t EAT ) < I i (t EAT − 1), I i (t EAT ) > 0, it is inevitable that a few infected individuals diffuse away from subpopulation i. Occurring the state transitions of S j → S j or I j → S j from t EAT − 1 to t EAT , subpopulations j in the neighbourhood of i (excluding the new infected subpopulation j) cannot receive infected individuals. Therefore, the only possible destination for those infected individuals is subpopulation S k in \(\mathbb{S}\).

The conditions E in ≤ n + m and \(\sum _{i=1}^{m}\varDelta I_{i}(t_{EAT}) =\sum _{ k=1}^{n}\mathcal{H}_{k}\) make the equations \(\sum _{i\in Y _{k}}\mathcal{H}_{ik} =\mathcal{ H}_{k}\) and \(\sum _{k\in U_{i}}\mathcal{H}_{ik} =\varDelta I_{i}(t_{EAT})\) have the unique solution \(\sigma =\{\{\mathcal{ H}_{i1}\vert i \in Y _{1}\},\ldots,\{\mathcal{H}_{in}\vert i \in Y _{n}\}\}\). The reason is that rank(A coef )=E in , where A coef is the coefficient matrix of equations \(\sum _{i\in Y _{k}}\mathcal{H}_{ik} =\mathcal{ H}_{k}\) and \(\sum _{k\in U_{i}}\mathcal{H}_{ik} =\varDelta I_{i}(t_{EAT})\). Thus the invasion pathway(s) of this mI ↦ nS(m, n > 1) can be identified accurately. □

6.4.4 Identification for Potential Invasion Pathways

Now we are in the position to construct the whole framework of identifying invasion pathways, namely, the invasion pathways identification (IPI) algorithm as summarized as below.

  1. (i)

    Invasion partition: Twhole invasion pathways is defined as the whole invasion pathways of an invasion process. At each EAT, we get four types of invasion cases (i.e. I ↦ S, I ↦ nS, mI ↦ S, mI ↦ nS(m > 1, n > 1)). Suppose Twhole invasion pathways is contained in all Λ INCs. Denote by \(\hat{a}_{i}\) the identified invasion pathways of INC i , which can be optimally solved by (stochastic) dynamic programming as

    $$\displaystyle\begin{array}{rcl} \mathrm{T}_{\text{whole invasion pathways}} =\mathrm{ opt}\sum _{i=1}^{\varLambda }\hat{a}_{ i},& & {}\end{array}$$
    (6.15)

    where “opt” represents the optimal solution via dynamic programming.

  2. (ii)

    Accurate identification: For the two cases of I ↦ S, I ↦ nS, it is easy to reach the accurate identification of invasion pathways. In the other two cases of mI ↦ S, mI ↦ nS, we first evaluate whether mI ↦ S or mI ↦ nS can be accurately identified or not. If yes, Theorems 1 and 2 work out the accurate identification.

  3. (iii)

    Identification of potential invasion pathways: If accurate identification is not feasible, we propose an efficient optimization method based on the maximum likelihood estimation to identify the most likely invasion pathways. We define the maximum likelihood (ML) estimator as

    $$\displaystyle\begin{array}{rcl} \hat{a}_{i} =\mathop{ \arg \max }\limits _{a_{i}\in INC_{i}}\ P(a_{i}\vert INC_{i}),& & {}\end{array}$$
    (6.16)

    where P(a i | INC i ) is the likelihood of uncovering the potential pathway a i , supposing the actual pathway is a i ∗. Therefore, we evaluate P(a i | INC i ) and choose the maximal likelihood one as a i ∗ from all potential pathways a i ∈ INC i .

  4. (iv)

    The whole spatial invasion pathways can be reconstructed by assembling all invasion cases chronologically.

Therefore, in the situations where accurate identification of invasion pathways is not feasible, e.g., the conditions of Theorems 1 and 2 are not satisfied, Eqs. (6.13) and (6.14) may have a number of potential solutions which correspond to a set of potential invasion pathways. Therefore, we propose the identification algorithm to infer the most likely pathways among all potential invasion pathways. Herein we unify mI ↦ S(m > 1) and mI ↦ nS(m > 1, n > 1) as mI ↦ nS(m > 1, n ≥ 1).

Denote \(\varOmega (\mathcal{H}_{kk_{\hslash }}^{(j)})\) the transfer estimator of infected subpopulation I k in \(\mathbb{I}\), k ℏ ∈ Y k . Here the transfer estimator is used to estimate the diffusion likelihood if I k diffuses \(\mathcal{H}_{kk_{\hslash }}^{(j)}\) infected individuals to \(S_{k_{\hslash }}\). Thus, the likelihood of potential solution σ j of an INC mI ↦ nS(m > 1, n ≥ 1) is presented by

$$\displaystyle\begin{array}{rcl} P(\sigma _{j}\vert INC_{mInS}) =\prod _{ k=1}^{m}\varOmega (\mathcal{H}_{ kk_{\hslash }}^{(j)})\Big/\sum _{ i=1}^{M}\prod _{ k=1}^{m}\varOmega (\mathcal{H}_{ kk_{\hslash }}^{(i)}),& &{}\end{array}$$
(6.17)

where M represents the number of solution σ j .

We now consider the events from t EAT − 1 to t EAT , and give some definitions. We assume an infected subpopulation I i in \(\mathbb{I}\) emanates k i edges in total, among which there are ρ i (1 ≤ ρ i ≤ n) invasion edge(s) labeled as 1, 2, …, ρ i with the corresponding diffusion rates p ℏ , ℏ ∈ [1, ρ i ], ℏ is an integer. We suppose \(\mathcal{H}_{ii_{\hslash }}\) infected hosts invade its neighbouring subpopulations in the subset {Y i = i ℏ } at t EAT . Assume there are ℓ i unobservable and partially observable edges, labelled as 1 + ρ i , …, ℓ i + ρ i . Along each unobservable or partially observable edge, the traveling rate is p ℓ , ℓ ∈ [1, ℓ i ], and x ℓ infected hosts leave I i . Accordingly, in total η i = ∑ ℓ x ℓ infected individuals leave I i through the unobservable and partially observable edges. Now there remain k i − ℓ i −ρ i observable edges, labelled as ℓ i + ρ i + 1, …, k i . Along each observable edge, the diffusion rate is \(p_{\aleph }\), integer \(\aleph \in [\ell_{i} +\rho _{i} + 1,k_{i}]\), and \(x_{\aleph }\) infected individuals leave I i . With probability \(\overline{p_{i}} = 1 -\sum _{\hslash }p_{\hslash } -\sum _{\ell}p_{\ell} -\sum _{\aleph }p_{\aleph }\), an infected individual keeps staying at subpopulation I i . There are \(\overline{x_{i}}\) infected individuals staying in subpopulation I i with probability \(\overline{p_{i}}\). Because I i connects the unobservable and partially observable infected subpopulations, we obtain \(\sum _{\ell}x_{\ell} + \overline{x_{i}} =\eta '\).

Therefore, we have the transfer likelihood estimator Ω of I i in the following three parts.

  1. (a)

    Unobservable Subpopulation I i : It is difficult to estimate whether and how many infected hosts move to which neighbours due to ΔI i (t EAT ) = I i (t EAT − 1) − I i (t EAT ) ≤ 0 (we have I i (t EAT − 1) ≤ I i (t EAT ) because unobservable subpopulation I i ). We write the transfer likelihood estimator of I i as

    $$\displaystyle{ \begin{array}{lll} \varOmega _{u}(\mathcal{H}_{ii_{\hslash }}) = P(\mathcal{H}_{ii_{\hslash }},p_{\hslash }, \hslash = [1,2,\ldots,\rho ];x_{\ell},p_{\ell},\ell= [1+\rho,2+\rho, \\ \ldots,l+\rho ];x_{\aleph },p_{\aleph },\aleph = [l +\rho +1,l +\rho +2,\ldots,k];\overline{x_{i}},\overline{p_{i}}).\end{array} }$$
    (6.18)

    With the definition of observable edges, the transfer likelihood estimator is simplified as

    $$\displaystyle{ \varOmega _{u} = \frac{I_{i}(t - 1)!} {\prod _{\hslash }\mathcal{H}_{ii_{\hslash }}!\eta _{i}^{{\prime}}!} \prod _{\hslash }p_{\hslash }^{H_{ii_{\hslash }} }\Big[\sum _{\ell}p_{\ell} + \overline{p_{i}}\Big]^{\eta _{i}^{{\prime}} }. }$$
    (6.19)
  2. (b)

    Observable Subpopulation I i  (I i → S i ): Given an I → S observable subpopulation I i , the infected individuals \(H_{i} =\{\mathcal{ H}_{ii_{\hslash }}\vert \hslash = 1,2,\ldots,\rho \}\) moved out of subpopulation I i to \(S_{i_{\hslash }}\) are all from the term of ΔI i (t EAT ). Therefore, its transfer likelihood estimator is derived as

    $$\displaystyle\begin{array}{rcl} & & \varOmega _{ob} = \frac{\varDelta I_{i}(t)!} {\prod _{\hslash }\mathcal{H}_{ii_{\hslash }}!(\varDelta I_{i}(t) -\sum _{\hslash }\mathcal{H}_{ii_{\hslash }})!}\prod _{\hslash }( \frac{p_{\hslash }} {\sum _{k=1}^{l+\rho }p_{k}})^{\mathcal{H}_{ii_{\hslash }}^{{\prime\prime}} }\cdot \\ && ( \frac{\sum _{\ell}p_{\ell}} {\sum _{j=1}^{l+\rho }p_{j}})^{\varDelta I_{i}(t)-\sum _{\hslash }\mathcal{H}_{ii_{\hslash }} }, {}\end{array}$$
    (6.20)

    where ΔI i (t EAT ) = I i (t EAT − 1) − I i (t EAT ) = I i (t EAT − 1) (we have I i (t EAT ) = 0 because observable subpopulation I i (I i → S i )).

  3. (c)

    Partially Observable Subpopulation I i : Because ΔI i (t EAT ) = I i (t EAT − 1) − I i (t EAT ) > 0, at least ΔI i (t EAT ) infected individuals leave subpopulation I i from t EAT − 1 to t EAT according to the definition of partially observable subpopulation. \(H_{i} =\{\mathcal{ H}_{ii_{\hslash }}\vert \hslash = 1,\ldots,\rho \}\) is decomposed into two subsets: \(H_{i}^{{\prime}} =\{\mathcal{ H}_{ii_{\hslash }}^{{\prime}}\vert \hslash = 1,\ldots,\rho \}\) and \(H_{i}^{{\prime\prime}} =\{\mathcal{ H}_{ii_{\hslash }}^{{\prime\prime}}\vert \hslash = 1,2,\ldots,\rho \}\), \(\mathcal{H}_{ii_{\hslash }}^{{\prime}} +\mathcal{ H}_{ii_{\hslash }}^{{\prime\prime}} =\mathcal{ H}_{ii_{\hslash }}\), where \(\mathcal{H}_{ii_{\hslash }}^{{\prime}}\geq 0,\mathcal{H}_{ii_{\hslash }}^{{\prime\prime}}\geq 0\). \(H_{i}^{{\prime}} =\{\mathcal{ H}_{ii_{\hslash }}^{{\prime}}\vert \hslash = 1,\ldots,\rho \}\) represents the set of infected individuals departing from I i (t EAT −Δt) −ΔI i (t EAT ), and \(H_{i}^{{\prime\prime}} =\{\mathcal{ H}_{ii_{\hslash }}^{{\prime\prime}}\vert \hslash = 1,\ldots,\rho \}\) denote the infected individuals departing from ΔI i (t EAT ). We then have the transfer likelihood estimator in the following two cases.

Case 1: :

\(\sum _{\hslash }\mathcal{H}_{ii_{\hslash }} \geq \varDelta I_{i}(t_{EAT})\)

The transfer likelihood estimator is

$$\displaystyle{ \varOmega _{pu} =\sum _{ \phi =0}^{\varDelta I_{i}(t_{EAT})}\sum _{ \sum \mathcal{H}_{ii_{\hslash }}^{{\prime\prime}}=\phi }P_{1}P_{2}, }$$
(6.21)

where

$$\displaystyle\begin{array}{rcl} \begin{array}{ll} P_{1} = \frac{\varDelta I_{i}(t_{EAT})!} {\prod _{\hslash }\mathcal{H}_{ii_{\hslash }}^{{\prime\prime}}!(\varDelta I_{i}(t_{EAT})-\phi )!}\prod _{\hslash }( \frac{p_{\hslash }} {\sum _{k=1}^{l+\rho }p_{k}})^{\mathcal{H}_{ii_{\hslash }}^{{\prime\prime}} }( \frac{\sum _{\ell}p_{\ell}} {\sum _{j=1}^{l+\rho }p_{j}})^{\varDelta I_{i}(t_{EAT})-\phi }, \end{array} & & {}\\ \end{array}$$
$$\displaystyle\begin{array}{rcl} P_{2}& =& \frac{(I_{i}(t_{EAT} -\varDelta t) -\varDelta I_{i}(t_{EAT}))!} {\prod _{\hslash }\mathcal{H}_{ii_{\hslash }}^{{\prime}}!(I_{i}(t_{EAT} -\varDelta t) -\varDelta I_{i}(t_{EAT}) -\sum _{\hslash }\mathcal{H}_{ii_{\hslash }}+\phi )!}\prod _{\hslash }p_{\hslash }^{\mathcal{H}_{ii_{\hslash }}^{{\prime}} } {}\\ & & \times (\sum _{\ell}p_{\ell} + \overline{p_{i}})^{I_{i}(t_{EAT}-\varDelta t)-\varDelta I_{i}(t_{EAT})-\sum _{\hslash }\mathcal{H}_{ii_{\hslash }}+\phi }. {}\\ \end{array}$$

Here, \(\phi =\sum _{\hslash }\mathcal{H^{{\prime\prime}}}_{ii_{\hslash }}(0 \leq \phi \leq \varDelta I_{i}(t_{EAT}))\), which represents the sum of infected individuals travelling from subpopulation I i to \(S_{i_{\hslash }}\). For a given ϕ, we need to enumerate all possible sets \(H_{i}^{{\prime\prime}} =\{\mathcal{ H}_{ii_{j}}^{{\prime\prime}}\vert j = 1,\ldots,\rho \}\) to calculate the Ω pu .

Case 2: :

\(\sum _{\hslash }\mathcal{H}_{ii_{\hslash }} <\varDelta I_{i}(t)\)

Denote \(\phi =\sum _{\hslash }\mathcal{H^{{\prime\prime}}}_{ii_{\hslash }}(0 \leq \phi \leq \sum _{\hslash }\mathcal{H}_{ii_{\hslash }})\). Similar to Case 1, we should enumerate all possible permutations of \(H_{i}^{{\prime\prime}} =\{\mathcal{ H}_{ii_{j}}^{{\prime\prime}}\vert j = 1,\ldots,\rho \}\) for a fixed ϕ. Therefore, in this case we have the transfer likelihood estimator of I i as

$$\displaystyle{ \varOmega _{pu} =\sum _{ \phi =0}^{\sum _{\hslash }\mathcal{H}_{ii_{\hslash }} }\sum _{\sum \mathcal{H}_{ii_{ \hslash }}^{{\prime\prime}}=\phi }P_{1}P_{2}, }$$
(6.22)

where P 1 and P 2 are the same as those in Eq. (6.21).

According to Eq. (6.17), the most likely invasion pathways for an INC mI ↦ nS(m > 1, n ≥ 1) are identified as

$$\displaystyle{ \begin{array}{ll} \hat{a}^{mI\mapsto nS} =\arg \mathop{ \max }\limits _{\sigma _{i}}\ P(\sigma _{i}\vert INC_{mI\mapsto nS}) =\arg \mathop{ \max }\limits _{a_{i}}\ P(a_{i}\vert INC_{mI\mapsto nS}). \end{array} }$$
(6.23)

If the number of the first arrival infected individuals \(\mathcal{H}_{ij} \geq 3\), multiple potential solutions may correspond to the same set of potential pathway(s). In this case, we merge the transfer likelihood of all potential solutions of this INC if they belong to the same invasion pathways. Then we find out the most likely invasion pathways corresponding to the maximum likelihood.

After identifying the potential invasion pathways, the whole invasion pathway Twhole invasion pathways can be reconstructed chronologically by assembling all INCs. Finally, we depict the IPI algorithm explicitly with the pseudocodes as outlined in Algorithm 2.

Algorithm 2 Invasion Pathways Identification (IPI)

1: Inputs: the time series of infection data I i (t) and topology of network G

2: Find all EAT data

3: for each EAT

4:    Invasion partition to find out the I ↦ S, I ↦ nS, mI ↦ S and mI ↦ nS.

5:    for each mI ↦ S or mI ↦ nS

6:           if it satisfies conditions of Th 1 or Th 2

7:             Compute the unique invasion pathway

8:           else It does not satisfy conditions of Th 1 or Th 2

9:             Find all M potential solutions σ j

10:           Compute the P(σ j | INC mI ↦ S ) or P(σ j | INC mI ↦ nS )

11:           Merge the P(σ j | INC mI ↦ S ) or P(σ j | INC mI ↦ nS ) of σ j corresponding to same pathway(s)

12:         end if

13:   end for

14:   Find invasion pathway a mI ↦ S or a mI ↦ nS that maximize P(σ j | INC mI ↦ S ) or P(σ j | INC mI ↦ nS )

15: end for

16: Reconstruct the whole invasion pathways (T) by assembling each invasion case chronologically

6.4.5 Identifiability of Invasion Pathways

We now evaluate the identifiability of invasion pathways of all invasion cases. Denote π the likelihood corresponding to the most likely pathways for a given invasion case. Therefore we have

$$\displaystyle\begin{array}{rcl} \pi (\sigma ) =\sup _{\sigma _{i}}\{P(\sigma _{i}\vert INC)\}.& &{}\end{array}$$
(6.24)

Property 1.

Given an invasion case ‘mI ↦ S’ or ‘mI ↦ nS’, \(P(\sigma _{j}\vert INC) = \frac{\prod _{k=1}^{m}\varOmega } {\sum _{i=1}^{M}\prod _{k=1}^{m}\varOmega }\), there must exist P min and P max satisfying

$$\displaystyle\begin{array}{rcl} P_{min} \leq \pi (\sigma ) \leq P_{max}.& &{}\end{array}$$
(6.25)

Proof.

Suppose that P(σ 1 | INC) ≤ … ≤ P(σ M | INC), where M is the number of potential solutions. Thus P max = (P(σ M | INC)∕P(σ 2 | INC) + … + P(σ M | INC)); Because π(σ) ≥ 1∕M, let P min = max{1∕M, P(σ M | INC)∕(P(σ 1 | INC) + ∑ j = 1 M P(σ j | INC))}. We have P min ≤ π(σ) ≤ P max . □

We define an entropy to characterize the likelihood vector of M potential pathways of an INC.

Definition 1 (Entropy of Likelihoods of M Potential Solutions).

Define the normalized entropy of transfer likelihood P(σ 1 | INC), …, P(σ M | INC) as

$$\displaystyle\begin{array}{rcl} \mathcal{S} = - \frac{1} {\log M}\sum _{i=1}^{M}P(\sigma _{ i}\vert INC)\log P(\sigma _{i}\vert INC).& &{}\end{array}$$
(6.26)

This likelihood entropy \(\mathcal{S}\) tells the information embedded in the likelihood vector of the potential solutions of a given INC.

Definition 2 (Identifiability of Invasion Pathways).

Define the identifiability of invasion pathways to characterize the feasibility to identify an invasion case as

$$\displaystyle\begin{array}{rcl} \varPi =\pi (\sigma )(1 -\mathcal{ S}).& &{}\end{array}$$
(6.27)

Definition 2 tells that the bigger π(σ) and the smaller entropy \(\mathcal{S}\), the easier to identify the epidemic invasion pathways for an invasion case.

6.4.6 Examples

We illustrate the performance of our proposed IPI algorithm to identify the invasion pathways, with the maximal connected component of the American airports network (AAN, Fig. 6.7) to form a meta-population network. Note that the data to construct the AAN was collected from the U.S. demographic statistical data and domestic air transportation [35, 43]. Here, the AAN is a weighted and directed graph having V = 404 nodes (airports) and E = 6480 weighted and directed edges representing flight routes. The weight of edge E ij is defined as diffusion rate \(p_{ij} = \frac{\langle w_{ij}\rangle } {\langle N_{i}\rangle }\), where 〈w ij 〉 is the daily amount of passengers of the flight from i to j, 〈N i 〉 is the population of serving areas [43] of airport i. The average degree of the AAN is 〈k〉 ≈ 16, and the range of degree k is [1,158]. The range of distributions of 〈w ij 〉 and p ij is [1, 9100] and [7. 4 × 10−8, 0. 03], respectively. The range of distribution of 〈N i 〉 is [6100, 1. 907 × 107], and the total population of the AAN is N total ≈ 0. 243 × 109, i.e., approximately the whole population of the United States of America. Therefore, the AAN as the sample of a meta-population network shows high heterogeneity of connectivity patterns, traffic capacities as well as the population distribution [43].

Fig. 6.7
figure 7

Illustration of an American airports network (From Brockmann et al. [42])

Full size image

To verify the performance of the proposed IPI algorithm, we select three methods  [15, 31, 32] as the benchmark for comparison, which generate the shortest path trees or minimum spanning trees of a meta-population network. In more detail, [31] generates the average-arrival-time-based (ARR) shortest path tree, and [15] generates the effective-distance-based (EFF) most probable paths, and [32] generates the Monte-Carlo-Maximum-Likelihood-based (MCML) most likely epidemic invasion tree.

We define the identifying accuracy as the ratio of the number of correctly identified invasion pathways by each method to the number of true invasion pathways. We also compute the accuracy of accumulative INCs of mI ↦ S and mI ↦ nS, which is defined as the ratio of the number of correctly identified invasion pathways by each method to the number of true invasion pathways in this INC. Besides, we also make the comparison of the identification accuracy at the early stage of epidemic dynamics, which is defined as the period when the first 50 subpopulation have been infected. In the top and middle panels of Fig. 6.8, we observe the whole identification accuracy and the early-stage identification accuracy, while the bottom panel of Fig. 6.8 presents the early and whole accumulative identification accuracy of mI ↦ S and mI ↦ nS through 20 independent realizations on the AAN, respectively. Here the whole identification accuracy means the identification accuracy of whole meta-population network has been infected. The seed subpopulation in all such independent realizations is set as the Sun Valley Airport in Bullhead City, Arizona. We clearly observe that the IPI algorithm is more accurate at identifying the invasion pathways than other benchmark methods.

Fig. 6.8
figure 8

(Top) The wholly identifying accuracy of the invasion pathways on the AAN with 20 rounds of independent realizations. (Middle) The identifying accuracy of the invasion pathways for the early stage (before infecting 50 subpopulations) on the AAN with 20 rounds of independent realizations. (Bottom) The accumulative identifying accuracy of invasion cases (mI ↦ S and mI ↦ nS) for the early stage and the whole invasion pathways on the AAN. Here “mIS” and “mInS” stand for mI ↦ S and mI ↦ nS, respectively (From Wang et al. [35])

Full size image

We then visualize the identified invasion pathways (the lower panel of Fig. 6.9) during the early stage of a realization compared with the actual invasion pathways (the upper panel of Fig. 6.9). The weights (diffusion rates) of invasion edges are shown by the thicknesses of lines, and arrows represent the directions of invasions. We observe that most of the invasion pathways are correctly identified to form the invasive backbone of this realization of an epidemic dynamics, while there still exist some wrongly identified pathways in some INCs, indicating the necessity of defining the identifiability of an INC.

Fig. 6.9
figure 9

Illustration of the actual invasion pathways (the upper panel) and the identified invasion pathways (the lower panel), during the early stage of a realization (before the appearance of 50 infected subpopulations) on the AAN. Subpopulation 1 is the seed (Sun Valley Airport in Bullhead City, Arizona) (From Wang et al. [35])

Full size image

We finally examine the identifiability of an invasion case. Figure 6.10 shows the entropy and identifiability of wrongly identified mI ↦ S of 20 independent realizations on the AAN. The smaller the identifiability of an invasion case is, the more prone it is to be wrongly identified. The identifiability depicts the wrongly identified mI ↦ S more reasonably than the likelihoods entropy. The frequency of identifiability of INCs descends obviously, but that of the likelihood entropy of INCs does not clearly ascend. This statistical result indicates that the identifiability Π has a better performance to distinguish whether an invasion case is difficult to identify or not than the distinction performance of the likelihood entropy, and also tells that why some invasion cases are easy to identify, whose Π are more than 0.5, and why some invasion cases are difficult to identify, whose Π are much less than 0.5. Here 0.5 is an empirical value.

Fig. 6.10
figure 10

Statistical analysis of the likelihoods entropy and identifiability of wrongly identified mI ↦ S in 20 realizations of epidemic spreading on the AAN (From Wang et al. [35])

Full size image

6.5 Predicting the Epidemic Transmission

As the final part of this chapter, we now move a step further to predict the early stage of an epidemic transmission. Suppose the epidemic process starts from the patient 0 subpopulation. This subpopulation invades and infects its neighbours, and the cascading transmission proceeds. At the early epidemic stage, the time series of the number of infected individuals in each subpopulation I i (t) (i.e., the infection data) is recorded. Assume the topology of the meta-population network (including population sizes and diffusion rates, as Sect. 6.4) and the time series of the recorded infection data I i (t) until time t are available, and the focus of interest in this section is to predict which subpopulations will be infected at time step t + 1. We consider the SI model with the diffusion of new increment of infected individuals after reaction (see Sect. 6.2 Eq. (6.3)).

6.5.1 A Prediction Algorithm

The growth of infected individuals in an infected subpopulation is governed by the infected rate β, while the diffusion process is ruled by the parameters of multinomial distribution. We first identify the infection rate β by using the method in Sect. 6.3.2, then estimate the increment Δ R I i (t) of I i (t) of subpopulation i after the reaction from t to t + 1. Statistically, 〈Δ R I i (t)〉 = βI i (t)S i (t)∕N i (t). To keep the population balance of each subpopulation, we assume 〈w ij 〉 = 〈w ji 〉, i.e., 〈N i (t)p ij 〉 = 〈N j (t)p ji 〉, where w ij is the number of individuals that have moved from subpopulation i to subpopulation j in a unit time (e.g., a day). Thus we have 〈N j (t)〉 = 〈N j (t + 1)〉. At the early stage, N j (t) ≈ S j (t), and N j (t) is included in the population information of each subpopulation of meta-population network. Therefore, we estimate Δ R I j (t) by Δ R I j (t) ≈ βI j (t)∕N j (t).

Next we give the algorithm predicting n(n ≥ 1) subpopulations infected from t to t + 1 during the diffusion process. At time step t, all susceptible subpopulations having at least one infected neighbouring subpopulation comprise set S. We discuss the two cases of n = 1 and n > 1 in the following, and Algorithm 3 presents the pseudocode for the prediction algorithm.

  1. (i)

    n = 1;

In this case, there is only one susceptible subpopulation infected at time t + 1. The likelihood \(\mathcal{L}_{i}(t + 1)\) that subpopulation i in set S is infected at time t + 1 is derived as

$$\displaystyle\begin{array}{rcl} \begin{array}{lll} \mathcal{L}_{i}(t + 1) =&1 - (1 - p_{1i})^{I_{1}(t)+\varDelta _{R}I_{i}(t)}(1 - p_{2i})^{I_{2}(t)+\varDelta _{R}I_{2}(t)} \\ & \ldots (1 - p_{mi})^{I_{m}(t)+\varDelta _{R}I_{m}(t)},\end{array} & &{}\end{array}$$
(6.28)

where m is the number of infected neighbouring subpopulations of i at time step t. We label infected neighbouring subpopulations of i as 1, 2, …, m.

Accordingly, the most likely infected subpopulation \(\hat{v}\) is predicted as

$$\displaystyle\begin{array}{rcl} \begin{array}{lll} \hat{v} =\arg \mathop{ \max }\limits _{i}\ \mathcal{L}_{i}\prod _{j\neq i,j\in \mathbf{S}}\mathcal{\overline{L}}_{j},\end{array} & &{}\end{array}$$
(6.29)

where \(\mathcal{\overline{L}}_{j} = 1 -\mathcal{ L}_{j}\).

  1. (ii)

    n ≥ 2;

The most likely n(n ≥ 2) infected subpopulations in S can be predicted as

$$\displaystyle\begin{array}{rcl} \begin{array}{lll} \hat{v}_{n} =\arg \mathop{ \max }\limits _{i_{k}}\ \mathcal{L}_{i_{1}}\mathcal{L}_{i_{2}}\ldots \mathcal{L}_{i_{n}}\prod _{j\neq i_{k},k=1,2,\ldots,n,j\in \mathbf{S}}\mathcal{\overline{L}}_{j}.\end{array} & &{}\end{array}$$
(6.30)

Algorithm 3 Prediction Algorithm

1: Inputs: time series of infection data I i (t) and topology of network G

2: Estimate the infection rate β

3: for each time step t

4:   find all possible candidate subpopulations (set S)

5:   compute the likelihood \(\mathcal{L}_{i}(t + 1)\) of each subpopulation i ∈ S

6:   rank all subpopulations i by their likelihoods \(\mathcal{L}_{i}(t + 1)\)

7: end for

8: Choose the subpopulation i corresponding to the maximal likelihood \(\mathcal{L}_{i}(t + 1)\) as the most likely infected i in the next time step

Note that the above method only presents the most likely infected subpopulations at the next time step. Generally, the number of possibly infected subpopulations increases sharply during the epidemic dynamics. In this case, the likelihood of the most likely infected subpopulation may be very small. Therefore, we shall rank the likelihoods and investigate the top ranking subpopulations, which help us to judge which subpopulations are prone to be infected. Let \(\mathcal{P}_{i} =\mathcal{ L}_{i}\prod _{j\neq i,j\in \mathbf{S}}\mathcal{\overline{L}}_{j}\) in Eq. (6.29). We define the infected likelihood vector \(\{\mathcal{P}_{1},\mathcal{P}_{2},\ldots,\mathcal{P}_{Z}\}\) of all Z candidate subpopulations in set S, where \(\mathcal{P}_{i}\) is the likelihood the susceptible subpopulation i gets infected in the next time step as Eq. (6.29), i = 1, 2, …, Z. Then we define the infected likelihood entropy \(\mathcal{E}\) as

$$\displaystyle\begin{array}{rcl} \begin{array}{lll} \mathcal{E} = -\frac{1} {\log M}\sum _{i=1}^{M}\mathcal{P}_{ i}\log \mathcal{P}_{i}.\end{array} & &{}\end{array}$$
(6.31)

This entropy tells the extent of prediction difficulty at each time step. The smaller \(\mathcal{E}\), the easier the prediction.

6.5.2 Examples

This time we select an artificial meta-population network as the simulation example of spatial epidemic prediction. We generate a scale-free network with the BA model [6], then design the diffusion rate of each edge. Note that empirically the diffusion rates [44] of air transportation networks depend on the degree of the nodes. We define the diffusion rate from node i to node j as

$$\displaystyle{ p_{ij} = \frac{b_{ij}k_{j}^{\hat{\theta }}} {\sum _{l}b_{il}k_{l}^{\hat{\theta }}}C, }$$
(6.32)

where b ij stands for the elements of the adjacency matrix (b ij = 1 if i connects to j, and b ij = 0 otherwise), C is a constant (C is assumed as available, and set as 0.005), and \(\hat{\theta }\) is a parameter. We assume that parameter θ follows the Gaussian distribution \(\theta \sim N(\hat{\theta },\delta ^{2}) = \frac{1} {\sqrt{2\pi }\delta }exp(-\frac{(\hat{\theta }-\theta )^{2}} {2\delta ^{2}} )\) for each subpopulation. By setting constant C and computing the population of each subpopulation at equilibrium, the polynomial regression is employed to evaluate parameters \(\hat{\theta }\) and δ 2 based on the empirical rule of \(T^{{\prime}}\sim k^{\beta ^{{\prime}} },\beta ^{{\prime}}\simeq 1.5 \pm 0.1\), (where T ′ = ∑ l w jl , and β ′ is approximately linear with \(\hat{\theta }\) (observed in simulations). Assume \(\hat{\theta }= a^{{\prime}}\beta ^{{\prime}} + b^{{\prime}}\), we can obtain \(\hat{\theta }\), where a ′, b ′ are parameters). Therefore we can determine the diffusion rate p ij along each edge. We set the whole BA meta-population network having 404 nodes (subpopulation), and fix 〈k〉 = 16 (m 0 ′ = 9, m ′ = 8) as the average degree of the BA meta-population network. The initial size of each subpopulation is N 1 = N 2 = ⋯ = N N = 6 × 105, and the total population of the whole meta-population network is N total = 6 × 105 × 404 = 2. 424 × 108.

As illustrated in Fig. 6.11, the estimation of β is close to the actual infection rate. We compare our prediction algorithm with the randomization prediction, i.e., we randomly choose a susceptible subpopulation in S as the most likely infected subpopulation at the next time step. Ranking distance is defined as the difference of rank of likelihood \(\mathcal{L}(t + 1)\) between the investigated two subpopulations i and j. In Fig. 6.12, “RankError” means the ranking distance of the corresponding infected likelihood between the predicted candidate and the actual infected subpopulation. “RandError” means the ranking distance of the corresponding infected likelihood between the randomly selected candidate and the actual infected subpopulation. As shown in Fig. 6.12, the subpopulations predicted by our algorithm are closer to the actual infected subpopulations at the next time step compared with those randomly selected subpopulations.

Fig. 6.11
figure 11

The estimation of the infection rate β on a BA meta-population network with 404 subpopulations. The actual value of β = 0. 05. Inset: The evolution of I(t) in a linear scale (From Wang et al. [36])

Full size image
Fig. 6.12
figure 12

(Top) The distribution of the RankError from t to t + 1 at the early stage of a realization (one run) of epidemic dynamics. (Bottom) The distribution of the RandError from t to t + 1 at the early stage of the same realization of epidemic dynamics. Here t + 1 is each time of prediction. In the realization, the infection rate β = 0. 05 (From Wang et al. [36])

Full size image

We further investigate why the accurate prediction of the infected subpopulation is difficult to achieve. At time step t, if any new subpopulation(s) will be infected in this realization at the next time step, t + 1 is called the prediction time. As shown in Fig. 6.13, we observe that the number of possible infected candidates Z increases sharply, and the infected likelihood entropy also increases (generally \(\mathcal{E}> 0.5\)) during the time evolution. Because the likelihoods of possibly infected subpopulations become more homogeneous as the infection prevails, indicating the infected likelihoods in the likelihood vector are not significantly different from each other, the infected likelihood entropy herein becomes large, suggesting the difficulty of accurately predicting the next infected subpopulation.

Fig. 6.13
figure 13

(Top) The evolution of the number of possibly infected candidates Z with each prediction time. (Bottom) The entropy of likelihoods vector. The epidemic realization is run on a BA meta-population network with 404 subpopulations with the infection rate β = 0. 05 (From Wang et al. [36])

Full size image

6.6 Outlook

As only a snapshot of the emergent frontier in the exciting network science, some latest advances on identification and prediction of epidemic meta-population networks have been introduced in this chapter. The future steps along this line may involve the following aspects: (1) The adaptiveness of humans deserves sufficient respect when facing the modelling, analyses and prediction of a large-scale spatial pandemic situation, and an appropriately designed role with the feedback-loop of human adaptiveness into such a complex networking system will be much appreciated. (2) The power of Big Data and cloud computing may help embed high-resolution records of human behavioural dynamics (including mobility, interaction and other non-private profiles) into the study. Nevertheless, abuse of data should be carefully avoided. (3) The verification even for the prediction of an infectious process requires the precise control means and public strategy in the viewpoints of not only mathematical results but also implementations in practice. Finally comes the end of this chapter, which may still stands at the beginning of the long journey in this exciting and challenging direction.