Elementare Geometrie

Kapitelvorwort

In diesem Kapitel wiederholen Sie die wichtigsten Sätze der Geometrie und die grundlegenden trigonometrischen Beziehungen, mit deren Hilfe Sie Strecken und Winkel berechnen können.

Appendices

Aufgaben

11.1

Für welche der Vierecke Parallelogramm, Raute, Rechteck, Quadrat, Drachen gilt die Aussage?

• a) Alle Winkel sind gleich groß.

• b) Die Diagonalen sind orthogonal.

• c) Die Diagonalen halbieren sich.

• d) Die Diagonalen sind gleich lang.

• e) Das Viereck hat im Allgemeinen keine Symmetrieachse.

11.2

Ein Viereck ist sowohl ein Parallelogramm als auch ein Drachen. Welche Aussagen sind richtig?

• a) Das Viereck ist ein Trapez.

• b) Das Viereck ist ein Quadrat.

• c) Das Viereck ist eine Raute.

• d) Das Viereck hat genau eine Symmetrieachse.

• e) Das Viereck ist punktsymmetrisch.

11.3

Berechnen Sie den Winkel $\alpha$.

11.4

Berechnen Sie den Winkel $\alpha$ und prüfen Sie, ob die Geraden $g$ und $h$ parallel sind.

11.5

Geben Sie für die skizzierte Strahlensatzfigur jeweils gleiche Streckenverhältnisse an.

• a) $\displaystyle\frac{d}{c}=\frac{\qquad}{\qquad}$

• b) $\displaystyle\frac{a+b}{a}=\frac{\qquad}{\qquad}=\frac{\qquad}{\qquad}$

• c) $\displaystyle\frac{e}{d}=\frac{\qquad}{\qquad}=\frac{\qquad}{\qquad}$

• d) $\displaystyle\frac{q}{r}=\frac{\qquad}{\qquad}=\frac{\qquad}{\qquad}$

• e) $\displaystyle\frac{r}{p}=\frac{\qquad}{\qquad}=\frac{\qquad}{\qquad}$

• f) $\displaystyle\frac{q}{d}=\frac{\qquad}{\qquad}=\frac{\qquad}{\qquad}$

11.6

• a) In der skizzierten Figur ist $h\parallel k$. Berechnen Sie die Streckenlängen $x$ und $y$.

• b) Ist die Gerade $g$ parallel zur Geraden $k$? Begründen Sie Ihre Aussage.

11.7

Ein $54\,\textnormal{m}$ hoher Fabrikschornstein wirft auf dem ebenen Erdboden einen 81m langen Schatten. Ein Stück unterhalb der Schornsteinspitze befindet sich ein eiserner Haken. Der Schatten des Hakens ist vom Schatten der Schornsteinspitze $13{,}5\,\textnormal{m}$ entfernt. Fertigen Sie eine Skizze an und berechnen Sie, in welcher Höhe über dem Erdboden sich der Haken befindet.

11.8

Berechnen Sie jeweils den Winkel $\alpha$.

a):

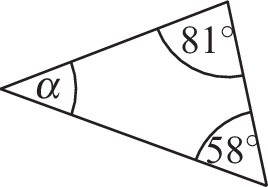
b):

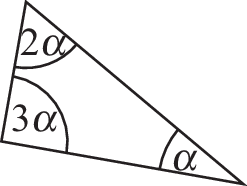
c) Drachen:

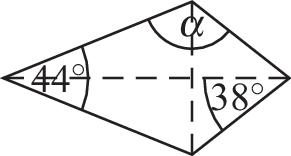
11.9

Berechnen Sie die Innenwinkel eines regelmäßigen Neunecks.

11.10

$M$ ist der gemeinsame Mittelpunkt der beiden Kreise. Begründen Sie, dass die Strecken ${AB}$ und ${CD}$ gleich lang sind.

11.11

• a) In einem rechtwinkligen Dreieck ist die Hypotenuse $13\,\textnormal{cm}$ und eine Kathete $5\,\textnormal{cm}$ lang. Berechnen Sie die Länge der zweiten Kathete.

• b) In einem rechtwinkligen Dreieck mit der Hypotenusenlänge $c$ gilt für die erste Kathete $a=\frac{1}{3}c$. Berechnen Sie die Länge der zweiten Kathete in Abhängigkeit von c.

11.12

Die Flächendiagonale eines Würfels ist $10\,\textnormal{cm}$ lang. Berechnen Sie die Länge seiner Raumdiagonalen.

11.13

Die Abbildung zeigt eine senkrechte quadratische Pyramide.

• a) Berechnen Sie die Höhe $h$ der Pyramide, wenn die Länge der Grundkante $a=100\,\textnormal{m}$ und die der Seitenkante $s=140\,\textnormal{m}$ beträgt.

• b) Bei manchen Pyramiden ist $a=s$. Stellen Sie eine Formel auf, mit der sich die Höhe $h$ direkt aus $a$ bzw. $s$ berechnen lässt.

11.14

Sind folgende Aussagen wahr oder falsch?

• a) Ein Kreis mit dem Radius $10\,\textnormal{cm}$ hat einen Flächeninhalt, der viermal so groß ist wie der Flächeninhalt eines Kreises mit dem Radius $5\,\textnormal{cm}$.

• b) Ein Kreis mit Radius $10\,\textnormal{cm}$ hat einen Umfang, der viermal so groß ist wie der Umfang eines Kreises mit dem Radius $5\,\textnormal{cm}$.

• c) Vier Kreise mit dem Radius $1\,\textnormal{m}$ haben zusammen den gleichen Umfang wie ein Kreis mit dem Radius $2\,\textnormal{m}$.

• d) Vergrößert man den Radius eines Kreises um $1\,\textnormal{m}$, so vergrößert sich sein Umfang um $1\,\textnormal{m}$.

• e) Verdoppelt man den Radius des Grundkreises eines Zylinders, so verdoppelt sich dabei auch sein Volumen.

• f) Verdoppelt man den Radius des Grundkreises eines Zylinders, so verdoppelt sich dabei auch sein Oberflächeninhalt.

• g) Halbiert man die Höhe eines Zylinders, so halbiert sich dabei auch sein Volumen.

• h) Verdoppelt man die Höhe eines Zylinders, so verdoppelt sich dabei auch sein Oberflächeninhalt.

11.15

Zeichen Sie in ein Koordinatensystem das Viereck $ABCD$ mit $A(1|3)$, $B(6|2)$, $C(4|6)$ und $D(1|5)$. Berechnen Sie den Flächeninhalt des Vierecks.

11.16

• a) Ein Kreis hat den Umfang $8\pi\,\textnormal{cm}$. Geben Sie seinen Flächeninhalt an.

• b) Ein Kreisausschnitt hat die Bogenlänge $3\pi\,\textnormal{m}$ und den Radius $2\,\textnormal{m}$. Berechnen Sie seinen Mittelpunktswinkel $\alpha$ im Gradmaß.

11.17

Einem Quadrat mit der Seitenlänge $10\,\textnormal{cm}$ wird ein Kreis einbeschrieben und ein Kreis umbeschrieben. Berechnen Sie den Flächeninhalt des dabei entstandenen Kreisrings.

11.18

Berechnen Sie den Flächeninhalt und den Umfang der grauen Figur, wenn das Quadrat die Seitenlänge $a$ hat.

11.19

Vier Bleikugeln mit dem Radius $1\,\textnormal{cm}$ werden eingeschmolzen; daraus wird eine neue Kugel gegossen.

• a) Berechnen Sie den Radius der neuen Kugel.

• b) Um wie viel Prozent ist die Oberfläche der neuen Kugel kleiner als die Oberflächen der vier kleinen Kugeln zusammen?

11.20

Ein hohler Würfel mit der äußeren Kantenlänge $10\,\textnormal{cm}$ hat als Begrenzungen Aluminiumplatten der Dicke $1\,\textnormal{cm}$.

• a) Berechnen Sie die Masse des Würfels (Dichte von Aluminium: $2{,}71\,\textnormal{g}/\textnormal{cm}^{3}$).

• b) Der Würfel wird ins Wasser geworfen. Schwimmt er oder geht er unter?

11.21

Ein gleichseitiges Dreieck mit der Seitenlänge $8\,\textnormal{cm}$ wird um eine seiner Symmetrieachsen gedreht, sodass ein Kegel entsteht.

• a) Berechnen Sie das Volumen und die Oberfläche dieses Kegels.

• b) Den Kegelmantel kann man als Kreisausschnitt in die Ebene abrollen. Berechnen Sie den Mittelpunktswinkel des abgerollten Kegelmantels.

11.22

Begründen Sie, warum der mit einem Taschenrechner berechnete Wert $\sin(0{,}49\pi)=0{,}02686$ nicht stimmen kann. Welcher Fehler wurde gemacht?

11.23

Jedes öffentliche Gebäude benötigt einen behindertengerechten Zugang, der mit einem Rollstuhl befahrbar ist. An einer Schule muss dafür eine Treppe mit drei Stufen à $20\,\textnormal{cm}$ Höhe durch eine Rampe überwunden werden. Eine solche Rampe darf maximal eine Steigung von $8\,\%$ haben. Berechnen Sie den Steigungswinkel und die kleinstmögliche Länge der Rampe.

11.24

Berechnen Sie die Länge der Strecke ${AC}$, wenn gilt:

$$\begin{aligned}\displaystyle\overline{AQ}&\displaystyle=5{,}0\,\textnormal{cm}&\displaystyle\overline{AB}&\displaystyle=3{,}0\,\textnormal{cm}&\displaystyle\overline{BP}&\displaystyle=1{,}0\,\textnormal{cm}\end{aligned}$$

11.25

Die beiden parallelen Seiten $a$ und $b$ eines gleichschenkligen Trapezes sind $a=8\,\textnormal{cm}$ und $b=14\,\textnormal{cm}$ lang. Die Höhe $h$ beträgt $4\,\textnormal{cm}$.

• a) Wie lang ist der Schenkel $s$?

• b) Wie groß ist der Winkel $\alpha$?

11.26

Ein Damm hat als Querschnitt ein gleichschenkliges Trapez. Der Böschungswinkel $\alpha$ beträgt $42^{\circ}$, die Länge der Böschung $s$ ist $12\,\textnormal{m}$, die untere Dammbreite beträgt $54\,\textnormal{m}$.

Berechnen Sie die Höhe des Damms und die Breite der Dammkrone.

11.27

Der Punkt $P(1|2)$ wird um den Ursprung $O$ gegen den Uhrzeigersinn um $80^{\circ}$ gedreht. Berechnen Sie den Winkel $\alpha$, den die Strecke ${OP}$ mit der $x$-Achse einschließt und die Koordinaten des gedrehten Punktes $P^{\prime}$.

11.28

• a) Geben Sie die Koordinaten des Punktes $P$ auf dem Einheitskreis an, der zum Winkel $x_{1}=\frac{\pi}{6}$ gehört.

• b) Bestimmen Sie einen weiteren Winkel $x_{2}$ ($x_{2}\in[0,2\pi]$) mit $\sin(x_{2})=\sin(x_{1})$.

• c) Bestimmen Sie einen weiteren Winkel $x_{3}$ ($x_{3}\in[0,2\pi]$) mit $\cos(x_{3})=\cos(x_{1})$.

Lösungen zu den Aufgaben

11.1

Die Aussage gilt für

• a) Rechteck, Quadrat

• b) Raute, Quadrat, Drachen

• c) Parallelogramm, Raute, Rechteck, Quadrat

• d) Rechteck, Quadrat

• e) Parallelogramm

11.2

Es sind nur die Aussagen a), c) und e) richtig.

11.3

$\alpha=55^{\circ}$

11.4

$\alpha=56^{\circ}$ (Scheitelwinkel), $\beta=180^{\circ}-73^{\circ}-56^{\circ}=51^{\circ}$ (Winkelsumme im Dreieck). Der Stufenwinkel zu $\beta$ ist $52^{\circ}$, also um $1^{\circ}$ größer, d. h., $g$ und $h$ sind nicht parallel.

11.5

• a) $\frac{d}{c}=\frac{a}{b}$

• b) $\frac{a+b}{a}=\frac{d+c}{d}=\frac{p}{q}$

• c) $\frac{e}{d}=\frac{f}{a}=\frac{r}{q}$

• d) $\frac{q}{r}=\frac{a}{f}=\frac{d}{e}$

• e) $\frac{r}{p}=\frac{e}{c+d}=\frac{f}{a+b}$

• f) $\frac{q}{d}=\frac{p}{c+d}=\frac{r}{e}$

11.6

• a) $x=\frac{4{,}2\cdot 3{,}6}{2{,}4}=6{,}3$; $y=\frac{2{,}4\cdot 3{,}5}{4{,}2}=2{,}0$

• b) Verhältnis auf dem 1. Strahl: $\frac{2{,}4}{0{,}8}=3$

  Verhältnis auf dem 2. Strahl: $\frac{3{,}6}{1{,}2}=3$

  Die Geraden sind also parallel.

11.7

Der Haken befindet sich 45 m über dem Erdboden.

11.8

• a) $\alpha=180^{\circ}-81^{\circ}-58^{\circ}=41^{\circ}$

• b) $6\alpha=180^{\circ}$, also $\alpha=30^{\circ}$

• c) $\alpha=180^{\circ}-38^{\circ}-22^{\circ}=120^{\circ}$

11.9

Größe eines Innenwinkels: $140^{\circ}$

11.10

Es gilt:

$$\begin{aligned}\displaystyle\overline{MD}&\displaystyle=\overline{MB}&\displaystyle&\displaystyle\textnormal{Radius des {\"a}u{\ss}eren Kreises}\\ \displaystyle\overline{MC}&\displaystyle=\overline{MA}&\displaystyle&\displaystyle\textnormal{Radius des inneren Kreises}\\ \displaystyle\sphericalangle DMC&\displaystyle=\sphericalangle AMB&\displaystyle&\displaystyle\textnormal{Scheitelwinkel}\end{aligned}$$

Nach dem Kongruenzsatz $sws$ sind die Dreiecke $MDC$ und $MAB$ kongruent. Also ist $\overline{AB}=\overline{CD}$.

11.11

• a) Länge der zweiten Kathete: 12 cm

• b) Länge der zweiten Kathete: $\sqrt{\frac{8}{9}c^{2}}=\frac{2}{3}\sqrt{2}c$

11.12

Kantenlänge des Würfels: $a=\sqrt{50}\,\textnormal{cm}=5\sqrt{2}\,\textnormal{cm}$

Länge der Raumdiagonalen: $5\sqrt{6}\,\textnormal{cm}\approx 12{,}2\,\textnormal{cm}$

11.13

• a) Die Höhe der Pyramide beträgt $\sqrt{14\,600}\,\textnormal{m}\approx 120{,}8\,\textnormal{m}$.

• b) Höhe der Pyramide: $\frac{a}{2}\sqrt{2}$

11.14

Richtig sind a) und g).

11.15

$$\begin{aligned}\displaystyle A_{\textnormal{ges}}&\displaystyle=A_{1}+A_{2}+A_{3}=\frac{1}{2}\overline{AD}\cdot h_{1}+\frac{1}{2}\overline{AE}\cdot h_{2}+\frac{1}{2}\overline{AE}\cdot h_{3}\\ \displaystyle&\displaystyle=\frac{1}{2}\cdot 2\cdot 3+\frac{1}{2}\cdot 4{,}5\cdot 3+\frac{1}{2}\cdot 4{,}5\cdot 1=12\end{aligned}$$

11.16

• a) $U=2\pi r=8\pi\ [\textnormal{cm}];\leavevmode\nobreak\ r=4\ [\textnormal{cm}]\leavevmode\nobreak\ \Rightarrow\leavevmode\nobreak\ A=\pi r^{2}=16\pi\ [\textnormal{cm}^{2}]$

• b) $3\pi=2\pi\cdot 2\cdot\frac{\alpha}{360^{\circ}}\Rightarrow\alpha=\frac{3}{4}\cdot 360^{\circ}=270^{\circ}$

11.17

Flächeninhalt des Kreisrings: $A=25\pi\ [\textnormal{cm}^{2}]$

11.18

Flächeninhalt: $A=a^{2}\cdot\left(1-\frac{\pi}{4}\right)\approx 0{,}215a^{2}$

Umfang: $U=\pi\cdot a$

11.19

• a) Volumen der vier Kugeln: $V_{\textnormal{ges}}=\frac{16}{3}\pi\ [\textnormal{cm}^{3}]$

  Radius $R$ der neuen Kugel: $R=\sqrt[3]{4}\ [\textnormal{cm}]\approx 1{,}59\ [\textnormal{cm}]$

• b) Oberfläche der vier kleinen Kugeln zusammen:

  $O_{\textnormal{ges}}=16\pi\ [\textnormal{cm}^{2}]$

  Oberfläche der großen Kugel:

  $O_{\textnormal{neu}}=8\pi\cdot\sqrt[3]{2}\ [\textnormal{cm}^{2}]$

  Differenz: $8\pi\cdot\left(2-\sqrt[3]{2}\right)\ [\textnormal{cm}^{2}]$

  Prozentuale Verkleinerung: $\approx 37\,\%$

11.20

• a) Volumen des Aluminiums: $488\,\textnormal{cm}^{3}$

  Masse des Aluminiums: $\approx 1\,322{,}5\,\textnormal{g}$

• b) Gewicht des Würfels: $G_{\textnormal{Al}}\approx 12{,}97\,\textnormal{N}$

  Auftrieb des völlig eingetauchten Würfels ($=$ Gewicht des von ihm verdrängten Wassers): $\approx 9{,}81\,\textnormal{N}$

  Da das Gewicht des Würfels größer ist als die auf ihn einwirkende Auftriebskraft, geht der Würfel unter.

11.21

• a) Das Volumen des Kegels beträgt $\frac{64}{3}\pi\cdot\sqrt{3}\,\textnormal{cm}^{3}\approx 116{,}1\,\textnormal{cm}^{3}$, die Oberfläche des Kegels beträgt $48\pi\,\textnormal{cm}^{2}\approx 150{,}8\,\textnormal{cm}^{2}$.

• b) Bogenlänge des Kreisausschnitts ($=$ Umfang des Grundkreises): $b=2\pi r=8\pi$ [cm]

  Radius des Kreisausschnitts: $s=8$ [cm]

  Mittelpunktswinkel: $\alpha=180^{\circ}$

11.22

$\sin(0{,}49\pi)\approx\sin\left(\frac{\pi}{2}\right)=1$, also ist der Wert von $0{,}02686$ viel zu klein. Fehler: Der Taschenrechner wurde nicht vom Grad- ins Bogenmaß umgestellt. Es ist $\sin(0{,}49\pi^{\circ})\approx 0{,}02686$.

11.23

Der Steigungswinkel der Rampe beträgt ca. $4{,}6^{\circ}$, ihre Länge ca. $7{,}524\,\textnormal{m}$.

11.24

$\overline{AC}=2{,}4\,\textnormal{cm}$

11.25

• a) Der Schenkel ist 5 cm lang.

• b) $\tan(\alpha)=\frac{4}{3}$, also $\alpha\approx 53{,}1^{\circ}$

11.26

Der Damm ist ca. 8 m hoch, die Dammkrone ca.  36,2 m lang.

11.27

$\tan(\alpha)=2$, also $\alpha\approx 63{,}43^{\circ}$; $P^{\prime}(-1{,}80|1{,}33)$

11.28

• a) $P\left(\frac{1}{2}\sqrt{3}|\frac{1}{2}\right)$

• b) $x_{2}=\frac{5}{6}\pi$

• c) $x_{3}=\frac{11}{6}\pi$

Ausführliche Lösungen zu den Aufgaben finden Sie im Online-Material.

tiny.cc/to5l1y