Abstract
We study verification problems for distributed systems communicating via unbounded FIFO channels. The number of processes of the system as well as the communication topology are not fixed a priori. Systems are given by parameterized communicating automata (PCAs) which can be run on any communication topology of bounded degree, with arbitrarily many processes. Such systems are Turing powerful so we concentrate on under-approximate verification. We extend the notion of split-width to behaviors of PCAs. We show that emptiness, reachability and model-checking problems of PCAs are decidable when restricted to behaviors of bounded split-width. Reachability and emptiness are Exptime-complete, but only polynomial in the size of the PCA. We also describe several concrete classes of bounded split-width, for which we prove similar results.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
We study verification problems for parameterized communicating automata (PCAs), which model distributed systems consisting of arbitrarily many identical processes, distributed on some communication topology. Each process runs a copy of the same finite automaton, that can send and receive messages from other processes through FIFO channels. Though the system may contain unboundedly many processes, we assume that each process may only communicate with a bounded number of other processes.
PCAs were introduced in [5] to study logical characterizations of parameterized systems. They extend communicating finite-state machines [8]. While the latter assume a fixed and known communication topology, a PCA can be run on any communication topology of bounded degree. Communicating finite-state machines are already Turing equivalent, and thus their verification is undecidable. The fact that PCAs can be run on arbitrarily large topologies induces other sources of undecidability. For instance, a Turing machine can be simulated on grid topologies by a PCA performing a bounded number of actions on each process. Thus, some restrictions on the topologies are necessary. Yet, even when fixing a simple class of topologies such as pipelines, and imposing rendez-vous synchronization, reachability of PCAs is undecidable [7].
In order to regain decidability, we focus on under-approximate verification. The idea is to restrict the verification problems to meaningful classes \(\mathcal {C}\) of finite behaviors. Typically, we are interested in the following problem: given a PCA \(\mathcal {S}\), is there a topology \(\mathcal {T}\) and a behavior in \(\mathcal {C}\) over \(\mathcal {T}\) on which \(\mathcal {S}\) reaches some local/global state? Our aim is to study under-approximation classes \(\mathcal {C}\) for which verification problems of PCAs becomes decidable. Even when we cannot cover all behaviors of a system with a decidable class, under-approximate verification is still very useful to detect bugs. Usually, the classes \(\mathcal {C} _i\) are parameterized and cover more and more behaviors when the parameter i increases.
The behaviors of PCAs are described by finite message sequence charts (MSC) [18], that is, graphs describing the communications between the different processes. Each node of the graph corresponds to an action performed by some process (sending or receiving a message), and the dependencies between the different actions are indicated by the edges of the graph. For model-checking, the specifications of our systems are typically given as monadic second order logic (MSO) or propositional dynamic logic (PDL) formulas over MSCs.
It is known that for any MSO definable class of bounded degree graphs, having a decidable MSO theory is equivalent to having bounded tree-width [9]. This applies to classes of MSCs, and characterizes decidability of MSO model-checking. However, showing a bound on tree-width is in general difficult. In the case of MSCs over a fixed architecture, an alternative notion called split-width has been introduced [1, 2]. Split-width is equivalent to tree-width on MSCs, but easier to use. It provides means to define uniform decision procedures, applying to many well-studied restrictions of communicating finite-state machines [10].
Following this approach, we generalize the definition of split-width, and we extend existing results over fixed architectures to the parameterized case. The idea of split-width is to decompose an MSC into atomic pieces, that is, pairs of matching send and receive events. This is done using two operations: splitting some edges between consecutive events of a same process, and dividing the resulting graph into disjoint components. Intuitively, an MSC has bounded split-width when this can be done while splitting a bounded number of edges at each step, on a bounded number of processes.
We show that emptiness and reachability of PCAs restricted to MSCs of bounded split-width are decidable. These problems are Exptime-complete but only polynomial in the size of the PCA. Our decision procedures are based on an interpretation of MSCs of bounded split-width into binary trees, and reductions to tree automata verification problems.
In the extended version [16] we also prove that model-checking restricted to bounded split-width is decidable. For MSO specifications, it has non-elementary complexity. However, the under-approximate model-checking is respectively Exptime-complete and 2-Exptime complete for CPDL (PDL with converse) and ICPDL (PDL with converse and intersection). In all cases, the problem is still polynomial in the size of the PCA.
Further, we give several examples of concrete classes of MSCs with bounded split-width, including existentially bounded or context-bounded behaviors, for which we show similar decidability and complexity results. Our approach based on split-width is generic since it can be easily adapted to other under-approximation classes.
Related Work. Various models of parameterized systems have been considered in the literature. In several cases, the assumptions of the model are sufficient to get decidability results without additional restrictions on the behaviors. Examples include token-passing systems [3, 15], models with a global store without locking [14], message-passing systems communicating synchronously via broadcast [12, 13], or rendez-vous [4]. An important distinction between the latter and PCAs is that PCAs use point-to-point communication: a process can distinguish between its neighbors, and specify the recipients of its messages. This makes the model more expressive, but also leads to undecidability.
The emptiness and model-checking problems for PCAs have been considered in [6, 7], respectively. Both papers assume rendez-vous synchronization, and a fixed class of topologies: pipelines, rings, or trees. Several notions of contexts are introduced, and decision procedures are described for the corresponding classes of context-bounded behaviors.
In the present paper, we also address context-bounded verification, but for unbounded FIFO channels and arbitrary topologies of bounded tree-width. In the general case of bounded split-width, we do not assume any restriction on the topology, but a bound on split-width already implies a bound on the tree-width of the communication topology.
Communicating finite-state machines (over fixed topologies) have been more extensively studied, and several restrictions are known to bring back decidability. Our work generalizes some of them to the parameterized setting, namely, context bounds (introduced in [19] for multi-stack concurrent systems), existential bounds [17], and bounded split-width [2].
Split-width was first introduced for multi-pushdown systems [11], and then generalized to communicating multi-pushdown systems [2].
Outline. In Sect. 2, we define topologies, PCAs, and MSCs. In Sect. 3, we introduce split-width. In Sect. 4, we give several examples of classes of bounded split-width, and state our results for the reachability problems of those classes. In Sect. 5, we present in more details the decision procedures leading to these results. In Sect. 6, we briefly present how they can be extended to decide model-checking problems, and discuss possible extensions of our model. Most proofs are omitted and can be found in the full version of the paper [16].
2 Parameterized Communicating Automata
We describe our formal model for communicating systems: we introduce topologies, MSCs, and parameterized communicating automata. Our definitions are taken from [5], except that we abstract away idle processes.
Topologies. We model distributed systems consisting of an unbounded number of processes. Each process is equipped with a bounded number of interfaces, through which it can communicate with other processes. A topology is a graph, describing the connections between the different processes (each of which is represented by a node in the graph, see example on the right). Throughout the paper, we assume a fixed nonempty finite set \(\mathcal {N} = \{a, b, \ldots \}\) of interface names (or, simply, interfaces).


Definition 1
A topology over \(\mathcal {N} \) is a pair  where P is the nonempty finite set of processes and
where P is the nonempty finite set of processes and  is the edge relation. We write
is the edge relation. We write  for
for  , which means that the a-interface of p is connected the b-interface of q. We require that, whenever
, which means that the a-interface of p is connected the b-interface of q. We require that, whenever  , the following hold:
, the following hold:
-
(a) \(p \ne q\) (there are no self loops),
-
(b)
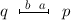 (adjacent processes are mutually connected), and
(adjacent processes are mutually connected), and -
(c) for all \(a',b' \in \mathcal {N} \) and \(q' \in P\) such that
 , we have \(a = a'\) iff \(q = q'\) (an interface is connected to at most one process, and two distinct interfaces are connected to distinct processes).
, we have \(a = a'\) iff \(q = q'\) (an interface is connected to at most one process, and two distinct interfaces are connected to distinct processes).
Message Sequence Charts. The possible behaviors of our systems are depicted as message sequence charts. A message sequence chart consists of a set of processes, and, for each process, of a sequence of events. Each event corresponds to an action of the process (sending or receiving a message through a given interface), and matching send and receive events are connected by a message edge. Events are labeled with elements of \(\varSigma \mathop {=}\limits ^\mathrm{{\tiny def}}\{a? \mid a \in \mathcal {N} \} \cup \{a! \mid a \in \mathcal {N} \}\), according to the type of action they execute.
Definition 2
A pre-message sequence chart (pre-MSC) over the set of interfaces \(\mathcal {N}\) is a tuple \(M = (P,E,\rightarrow ,\lhd ,\pi ,\lambda )\), where
-
P and E are nonempty finite sets of processes and events, respectively.
-
\(\pi : E \rightarrow P\) is a surjective map determining the location of an event. For \(p \in P\), we let \(E_p \mathop {=}\limits ^\mathrm{{\tiny def}}\{e \in E \mid \pi (e) = p\}\).
-
\(\lambda : E \rightarrow \varSigma \) associates with each event the type of action that it executes. We let \(E_? \mathop {=}\limits ^\mathrm{{\tiny def}}\{e \in E \mid \exists a \in \mathcal {N}. \lambda (e) = a?\}\), and \(E_! \mathop {=}\limits ^\mathrm{{\tiny def}}\{e \in E \mid \exists a \in \mathcal {N}. \lambda (e) = a!\}\).
-
\(\rightarrow \) is a union \(\bigcup _{p \in P} \rightarrow _{p}\), where each \({\rightarrow _p} \subseteq E_p \times E_p\) is the direct-successor relation of some total order on \(E_p\).
-
\({\lhd }\subseteq E_!\times E_?\) defines a bijection from \(E_!\) to \(E_?\). Moreover, for each \((e,f) \in \lhd \), \(\pi (e) \ne \pi (f)\).
Given such a pre-MSC, we define \(\mathcal {T} _M \mathop {=}\limits ^\mathrm{{\tiny def}}(P, \{(p,a,b,q) \in P \times \mathcal {N} ^2 \times P \mid \exists (e, f) \in E_p \times E_q.\, (e\lhd f \wedge \lambda (e) = a! \wedge \lambda (f) = b?) \text { or } (f\lhd e \wedge \lambda (e) = a? \wedge \lambda (f) = b!) \})\).
Not all pre-MSCs correspond to actual behaviors of systems (Fig. 2). To define MSCs, we additionally require that the events are coherently ordered, and that communications are compatible with some topology and follow a FIFO policy.
Definition 3
A message sequence chart (MSC) over \(\mathcal {N} \) is a pre-MSC \(M = (P, E, \rightarrow , \lhd , \pi , \lambda )\) such that the relation \({\le } \mathop {=}\limits ^\mathrm{{\tiny def}}{({\rightarrow } \cup {\lhd })^*}\) is a partial order, and:
-
\(\mathcal {T} _M\) as defined above is a topology, called the observable topology of M.
-
For all \(e_1 \lhd e_2\), \(f_1 \lhd f_2\) s.t. \(\pi (e_i) = \pi (f_i)\), we have \(e_1 \le f_1\) iff \(e_2 \le f_2\) (FIFO).
An MSC M is called compatible with a topology \(\mathcal {T} \) when \(\mathcal {T} _M\) is a subgraph of \(\mathcal {T} \). Intuitively, an MSC is compatible with a topology \(\mathcal {T} \) when it can be interpreted as a behavior over \(\mathcal {T} \), in which some processes may be inactive or may not use all their interfaces. We denote by \(\mathsf {MSC}\) the set of all MSCs over \(\mathcal {N}\), and by \(\mathsf {MSC}_{\mathcal {T}}\) the set of all MSCs compatible with a topology \(\mathcal {T}\).
Example 4
An example MSC is depicted in Fig. 1. The vertical lines represent the succession of events on a given process, and \(\lhd \)-edges are depicted by arrows.
Parameterized Communicating Automata. The idea is that each process of a topology runs one and the same automaton, whose transitions are labeled with actions of the form a!m, which emits a message m through interface a, or a?m, which receives m from interface a. The acceptance condition of a parameterized communicating automaton is given as a boolean combination of conditions of the form “at least n processes end in state s”, written \(\langle \# (s) \ge n \rangle \).
Definition 5
A parameterized communicating automaton (PCA) over \(\mathcal {N} \) is a tuple \(\mathcal {S} = (S,\iota , Msg ,\varDelta ,F)\) where S is the finite set of states, \(\iota \in S\) is the initial state, \( Msg \) is a nonempty finite set of messages, \(\varDelta \subseteq S \times (\varSigma \times Msg ) \times S\) is the transition relation, and F is the acceptance condition, a finite boolean combination of statements of the form \(\langle \# (s) \ge n \rangle \), with \(s \in S\) and \(n \in \mathbb {N} \).
The size |F| of the acceptance condition of \(\mathcal {S}\) is defined as the length of its encoding, where all integer values are written in binary.
Let \(M = (P, E, \rightarrow , \lhd , \pi , \lambda )\) be an MSC. A run of \(\mathcal {S} \) on M will be a mapping \(\rho : E \rightarrow S\) satisfying some requirements. Intuitively, \(\rho (e)\) is the local state of \(\pi (e)\) after executing e. To determine when \(\rho \) is a run, we define another mapping, \(\rho ^-: E \rightarrow S\), denoting the source state of a transition: whenever \(f \rightarrow e\), we let \(\rho ^-(e) = \rho (f)\); moreover, if e is \(\rightarrow \)-minimal, we let \(\rho ^-(e) = \iota \). With this, we say that \(\rho \) is a run of \(\mathcal {S} \) on M if, for all \((e,f) \in \mathord {\lhd }\), there is a message \(m \in Msg \) such that \((\rho ^-(e),(\lambda (e),m),\rho (e)) \in \varDelta \), and \((\rho ^-(f),(\lambda (f),m),\rho (f)) \in \varDelta \). A run \(\rho \) is accepting if it satisfies the acceptance condition. In particular, \(\rho \) satisfies \(\langle \# (s) \ge n \rangle \) when \(|\{e \in E \mid e \text { is } {\rightarrow }\text {-maximal and } \rho (e) = s\}| \ge n\).
The set of MSCs that allow for an accepting run is denoted by \(L(\mathcal {S})\). Given a topology \(\mathcal {T}\), we let \(L_\mathcal {T} (\mathcal {S}) = L(\mathcal {S}) \cap \mathsf {MSC} _\mathcal {T} \).
Remark 6
We could add labels from a finite alphabet to the events of MSCs and to the transitions of PCAs. Such labels can be handled similarly to the \(\lambda \)-labeling, and all our results can easily be adapted to this setting. Similarly, allowing internal transitions for PCAs would not add any technical difficulties.
Verification Problems. The non-emptiness problem asks, given a PCA \(\mathcal {S}\), whether its language \(L(\mathcal {S})\) is non empty; or in other words, whether \(L_\mathcal {T} (\mathcal {S}) \ne \varnothing \) for some topology \(\mathcal {T} \). The (local) reachability problem asks, given a PCA \(\mathcal {S}\) and a state s of \(\mathcal {S}\), whether there exists a run of \(\mathcal {S}\) in which some process reaches the state s. It can be seen as a special instance of the non-emptiness problem, by modifying the acceptance condition of \(\mathcal {S}\) to \(\langle \# (s) \ge 1 \rangle \).
Notice that the non-emptiness problem \(L_\mathcal {T} (\mathcal {S}) \ne \varnothing \) for a fixed topology \(\mathcal {T} \) is already undecidable, since two finite automata connected by two queues can easily simulate a Turing machine. Furthermore, many decidable restrictions over fixed topologies remain undecidable in the parameterized case: for instance, bounding the number of contexts, or even of actions, performed by each process, or imposing rendez-vous synchronization (even when restricted to pipeline topologies [7]). The idea is that the unbounded number of processes can be used to construct a PCA whose behaviors are grid-like MSCs of arbitrary height and width (see Figs. 3 and 4). It is then easy to encode runs of a Turing machine: the unbounded horizontal direction encodes the tape of the machine, and the vertical direction its evolution with time.
In the remaining of the paper, we will study several decidable underapproximations of the problem. For a family \((\mathcal {C} _i)_{i}\) of classes of MSCs (for the concrete families studied in Sect. 4, the index i is a tuple of integers), we define the problem \(\mathcal {C}\)-NonEmptiness as follows (and similarly, \(\mathcal {C}\)-Reachability):


3 Split-Width
In this section, we introduce the notion of split-width, and state our decidability result for MSCs of bounded split-width. The main motivation behind split-width is that it allows to design generic decision procedures that apply to many under-approximation classes, instead of having to develop for each class a specific decision procedure with its complexity. Several examples of classes of MSCs that are captured with split-width will be given in Sect. 4.
The idea of split-width is to decompose an MSC into atomic pieces consisting of a pair of matching send and receive events, using two operations: split (removing some process edges of the MSC), and divide (separating the resulting graph into two independent parts). This is described below as a two-player game. First, we introduce the notion of split MSC (an MSC missing process edges).
4-DST associated with the decomposition of Fig. 5 (Color figure online)
Definition 7
A split (pre-)MSC is a tuple \(M = (P, O, E, \rightarrow , \dashrightarrow , \lhd , \pi , \lambda )\), where \((P, E, {\rightarrow } \cup {\dashrightarrow }, \lhd , \pi , \lambda )\) is a (pre-)MSC, \({\dashrightarrow } \cap {\rightarrow } = \varnothing \), \(O \subseteq P\) is the set of open processes of M, and every split process is open, i.e., \(\{p \in P \mid {(E_p)^2} \cap {\dashrightarrow } \ne \varnothing \}\subseteq O \).
The \(\dashrightarrow \) edges are called elastic, and the \(\rightarrow \) edges rigid. Processes of \(P \setminus O\) are called closed. The intuition is that an open process of M is a process that may be missing some of its events or process edges, and an elastic edge represents a missing part of a process between two events. Any MSC can be seen as a split MSC, by taking \(O\) and \(\dashrightarrow \) empty.
A block of a split (pre-)MSC M is a maximal connected component of \((E,\rightarrow )\) on some open process. In particular, M has exactly \(|O | + |{\dashrightarrow }|\) blocks.
Several split MSCs are depicted in Fig. 5. Elastic edges are represented by red dotted lines. Open processes are indicated by dotted lines at their extremities. For instance, \(M'\) has one open process with 3 blocks, and \(M'_2\) has 2 open processes, with resp. 1 and 2 blocks.
We call splitting an edge of M the action of making elastic some rigid edge \(e \rightarrow f\) of M. The resulting split MSC is \(M' = (P, O \cup \{\pi (e)\}, E, {\rightarrow } \setminus \{(e,f)\}, {\dashrightarrow } \cup \{(e,f)\}, \lhd , \pi , \lambda )\). For instance in Fig. 5, \(M'\) is obtained by splitting two process edges of M.
We say that M can be divided into \(M_1 = (P_1, O _1, E_1, \rightarrow _1, \dashrightarrow _1, \pi _1, \lambda _1)\) and \(M_2 = (P_2, O _2, E_2, \rightarrow _2, \dashrightarrow _2, \pi _2, \lambda _2)\) when \(M_1\) and \(M_2\) are split (pre)-MSCs, and \(E = E_1 \uplus E_2\), \({\rightarrow } = {{\rightarrow _1} \uplus {\rightarrow _2}}\), \({\lhd } = {{\lhd _1} \uplus {\lhd _2}}\), \(\pi =\pi _1\uplus \pi _2\), \(\lambda =\lambda _1\uplus \lambda _2\), and for \(i \in \{1,2\}\), \(O _i = O \cap P_i\) and \({\dashrightarrow _i} \subseteq ({\rightarrow } \cup {\dashrightarrow })^+\). For instance, in Fig. 5, \(M'\) can be divided into \(M_1\) and \(M_2\). A connected component of M is a split MSC \(M_1 = (P_1, O _1, E_1, \rightarrow _1, \dashrightarrow _1, \pi _1, \lambda _1)\) such that \(E_1\) is a connected component of \((E, {\rightarrow } \cup {\lhd })\). Then, either \(M = M_1\) or M can be divided into \(M_1\) and some \(M_2\).
Split-Game. Let M be a split MSC with at most k blocks. A split-game with budget k on M is a two player game in which the existential player (Eve) tries to prove that M has split-width at most k, while the universal player (Adam) tries to disprove it. Eve begins by trying to disconnect M by splitting some of its process edges, with the condition that the resulting split MSC \(M'\) has at most k blocks. Adam then chooses a connected component \(M''\) of \(M'\), and the game resumes on \(M''\). Eve wins a play if it ends in an atomic MSC, i.e. a pair of matching send and receive events. She loses if she cannot disconnect a non-atomic MSC without introducing more than k blocks.
The split-width of an MSC M is the minimal k such that Eve wins the split-game with budget k on M. It is defined identically for pre-MSCs. We denote by \(\mathsf {SW} _k\) the set of MSCs of split-width at most k.
Example 8
Eve wins the split-game with budget 4 on M (see Fig. 5). She starts by splitting two process edges of M, which results in the split MSC \(M'\) with three blocks. \(M'\) has two connected components, \(M_1\) and \(M_2\), providing two choices for Adam. If he chooses \(M_2\), Eve wins by cutting the only remaining process edge: both connected components of the resulting \(M'_2\) are atomic. If he chooses \(M_1\), Eve split the middle process edge on the first process, which creates two more blocks, and results in a total of four blocks. \(M'_1\) has two isomorphic connected components, so Adam’s choices are all equivalent. Eve can then cut the two remaining process edges while still respecting her budget of four blocks.
Shuffle and Merge. One can also give a bottom-up description of split-width. The duals of the split and divide operations are called respectively merge ( ) and shuffle (\(\mathbin {{\sqcup }\mathchoice{}{}{}{}{\sqcup }}\)).
) and shuffle (\(\mathbin {{\sqcup }\mathchoice{}{}{}{}{\sqcup }}\)).  is the set of split MSCs that can be obtained by making some elastic edges of M rigid, and/or closing some of its open processes. \(M_1 \mathbin {{\sqcup }\mathchoice{}{}{}{}{\sqcup }}M_2\) is the set of split MSCs M such that M can be divided into \(M_1\) and \(M_2\).
is the set of split MSCs that can be obtained by making some elastic edges of M rigid, and/or closing some of its open processes. \(M_1 \mathbin {{\sqcup }\mathchoice{}{}{}{}{\sqcup }}M_2\) is the set of split MSCs M such that M can be divided into \(M_1\) and \(M_2\).
An MSC has split-width at most k when it can be obtain by combining atomic MSCs with shuffle and merge operations, while keeping the number of blocks at most k at each step.
Remark 9
The notion of open and closed processes is new. Our bound on the number of blocks (i.e. the number of open processes plus the number of elastic edges) replaces the bound on the number of elastic edges only that was used in [1, 2] for the split-width of MSCs over fixed architectures. When the topology \(\mathcal {T} \) is fixed, the two definitions are equivalent since the number of open processes is already bounded by the number of processes in \(\mathcal {T} \). This is no longer true in the parameterized case. For instance, the families of MSCs defined in Figs. 3 and 4 can be decomposed into atomic pieces while using only two elastic edges, but this introduces an unbounded number of open processes. In fact, they embed a grid, hence they should have unbounded width.
Remark 10
For MSCs, split-width is equivalent to tree-width and clique-width: there are linear bounds between the three measures (the proof is an easy adaptation from the non-parameterized case [10]). The motivation for introducing split-width rather than using existing measures on graphs is that it allows to take into account the specificities of MSCs, and is thus both simpler to understand and to use. In particular, using tree-width or clique-width would result in more involved automata constructions in Sect. 5.
Notice also that a bound on the split-width of an \(\mathsf {MSC}\) M induces a bound on the tree-width of the observable topology \(\mathcal {T} _M\) (See Theorem 20).
Decidability. The non-emptiness problem becomes decidable when restricted to MSCs of bounded split-width. Roughly, the proof goes as follows. First, we show that trees representing Eve’s winning strategies can be abstracted by trees over a finite alphabet (that depends only on the bound k on split-width). Then, we reduce the verification problems for PCAs to emptiness problems on tree automata. The details for these constructions will be given in Sect. 5. The proof is inspired from the non-parameterized case [2], and we show that the complexity remains the same in our setting.
Theorem 11
\(\mathsf {SW}\)-NonEmptiness is Exptime-complete, and only polynomial in the number of states and transitions of the input PCA.
4 Classes of Bounded Split-Width
The decision procedures based on split-width are generic and apply to various classes of MSCs (the main condition being that MSCs in the class have bounded split-width). When the topology is fixed, this covers many well-studied restrictions [10]. In this section, we give two examples of such classes that can be generalized to the parameterized setting: existentially bounded MSCs, and context-bounded MSCs. We also define a further extension of context-bounded MSCs, called tile-bounded MSCs, and show that it is equivalent to bounded split-width.
Existentially Bounded MSCs. M is called existentially k-bounded when there exists a linearization \(\le _\mathrm{lin}\) of its events (i.e. a total order extending \(\le \)) such that there are at most k process or message edges going out of any prefix of the linearization: for all \(g \in E\),
In the case of MSCs over a fixed topology, this is equivalent to bounding the number of pending messages at each prefix of the linearization, which is the usual definition of existentially bounded. This is no longer the case when considering topologies with an unbounded number of processes. For instance, the MSC of Fig. 3 is not existentially k-bounded. It is possible to find a linearization for which every prefix has at most one pending message, but it is not possible to simultaneously bound the number of non-terminated processes.
We denote by \(\mathsf {EB} _{k}\) the set of all existentially k-bounded MSCs over \(\mathcal {N}\).
Lemma 12
An existentially k-bounded MSC has split-width at most \(k+2\).
Proof
Eve’s strategy is as follows. She successively isolates the first events of the linearization by splitting the process edges originating from them, until a pair of matching send/receive events is disconnected. Adam chooses the remaining component, and Eve continues as before. In the split MSC obtained by isolating the first events \(e_1 <_\mathrm{lin} \ldots <_\mathrm{lin} e_i\) of the linearization and removing the disconnected messages, each block either consists of a single \(e_j~(1 \le j \le i)\), or only contains events that occur after \(e_i\) in the linearization, and is the last block on some open process. Blocks of the first kind are necessarily send events whose matching receive event occurs after \(e_i\), hence they correspond to pending messages at \(e_i\). Now consider a block of the second kind, and let f be its first event. Then f must occur after \(e_i\) in the linearization (otherwise, its block would be of the first kind). Moreover, since its process is open, there must be some \(e \in \{e_1, \ldots , e_i\}\) such that \(e \rightarrow f\) in the initial MSC. Hence, each block of the second kind correspond to a pending process edge at \(e_i\) (the edge \(e \rightarrow f\)). Thus, there are in total at most k blocks. Eve introduces at most two extra blocks when splitting a process edge. Hence she wins with budget \(k+2\). \(\square \)
Eve’s winning strategy results in a tree that is word-like [2, 10], i.e., at every binary node, one of the subtree is small (bounded size). Hence, we can use word automata instead of tree automata, resulting in a better complexity for the verification problems.
Theorem 13
\(\mathsf {EB}\)-NonEmptiness is Pspace-complete.
Context-Bounded MSCs. A context is an interval of events on a process, in which only one interface is accessed, and in a single direction (send or receive). More formally, let \(M =(P, E, \rightarrow , \lhd , \pi , \lambda )\) be an MSC. A context of M is a subset \(c = \{e_1, \ldots , e_n\}\) of E such that \(e_1 \rightarrow \cdots \rightarrow e_n\) and \(\lambda (e_i) = \lambda (e_j)\) for all i, j.
An MSC M is k-context bounded when for all \(p \in P\), there are contexts \(c_1, \ldots , c_i\) with \(i \le k\) such that \(E_p = c_1 \uplus \ldots \uplus c_i\). The class of k-context bounded MSCs has unbounded split-width. Actually, this is even the case for MSCs having a bounded number of events on every process (see Fig. 4). However, we obtain a bound on split-width when we additionally require that the topology has bounded tree-width.
Lemma 14
If M is a k-context-bounded MSC and \(\mathcal {T} _M\) has tree-width at most h, then M has split-width at most \(k(h+1)+2\).
We denote by \(\mathsf {CB} _{k,h}\) the set of all k-context bounded MSCs over topologies of tree-width at most h.
Theorem 15
\(\mathsf {CB}\)-NonEmptiness is Exptime-complete, and polynomial in the number of states and transitions of the input PCA.
Tile-Bounded MSCs. We can generalize the notion of contexts introduced above to tiles, which are independant parts of an MSC involving a bounded number of processes. In some sense, this section gives the link between fixed and parameterized topologies, when it comes to conditions ensuring decidability. Intuitively, an MSC with split-width at most k over an arbitrary topology (involving arbitrarily many processes) can be decomposed in tiles involving at most some fixed number (k) of processes. Moreover, each tile has bounded split-width and each process intersects at most some fixed number of tiles.
A k-tile is a split MSC T of split-width at most k and having only open processes. In particular, T has at most k blocks, hence at most k processes.
Let \(M = (P, E, \rightarrow , \lhd , \pi , \lambda )\) be an MSC. A \((k,\ell )\)
-tile-decomposition of M is a sequence \(T_1, \ldots , T_n\) of k-tiles such that  and every process \(p \in P\) is part of at most \(\ell \) tiles. An MSC is called \((k,\ell )\)
-tile-bounded when it admits some \((k,\ell )\)-tile-decomposition.
and every process \(p \in P\) is part of at most \(\ell \) tiles. An MSC is called \((k,\ell )\)
-tile-bounded when it admits some \((k,\ell )\)-tile-decomposition.
Example 16
A (5, 3)-decomposition with threetiles is depicted on the right. The first and the last process intersect with one tile, the middle one with 3 tiles and the other two processes intersect with two tiles. Tiles \(T_1\) and \(T_3\) have split-width exactly 5 (note that the first process is counted as open in \(T_1\)). Tile \(T_2\) tile has split-width 4.


Example 17
A k-context bounded MSC M (see page 11) admits a \((2k+2,2|\mathcal {N} |)\)-tile-decomposition. The tile decomposition is given by defining, for each pair of processes (p, q) connected in \(\mathcal {T} _M\), a tile \(T_{p,q}\) induced by the contexts of p in which it sends to q, and the contexts of q in which it receives from p. Notice that a tile needs not be a connected graph. In particular, each tile has at most 2k blocks, and can be decomposed by disconnecting one by one its messages, which introduces at most 2 extra blocks. Each process of M takes part in at most \(2|\mathcal {N} |\) tiles, one for each type (\(a!, a?, \ldots \)) of contexts it has.
We obtain the same results as for context-bounded MSCs. We denote by \(\mathsf {TB} _{k,\ell ,h}\) the set of \((k,\ell )\)-tile-bounded MSCs M such that \(\mathcal {T} _M\) has tree-width at most h.
Lemma 18
Let \(M \in \mathsf {TB} _{k,\ell ,h} \). Then M has split-width at most \(2k^2\ell ^2(h+1)\).
Theorem 19
\(\mathsf {TB}\)-NonEmptiness is Exptime-complete, and polynomial in the number of states and transitions of the input PCA.
In fact, such bounds are equivalent to bounding split-width, as shown by the theorem below.
Theorem 20
Let \(M \in \mathsf {SW} _k \). Then \(\mathcal {T} _M\) has tree-width at most \(k-1\), and M is \((k^2 + 2k, 3|\mathcal {N} |^k)\)-tile-bounded.
5 Tree Interpretation
We present the decision procedures leading to our complexity results. The general idea is to encode MSCs of bounded split-width into binary trees over a finite alphabet, and reduce our verification problems to problems on tree automata.
Split-Terms. The encoding of MSCs of bounded split-width into trees is based on the bottom-up description of split-width. Recall that an MSC has split-width at most k if it can be constructed by combining through shuffles and merges split MSCs with at most k blocks, the starting points being atomic MSCs. This construction can be described by a split-term, that is, a term over the following grammar:  (with \(a,b \in \mathcal {N} \)).
(with \(a,b \in \mathcal {N} \)).
However, since the merge and shuffle operations are ambiguous, a split-term may correspond to several MSCs. The next step is to disambiguate these operations by adding labels to the nodes of split-terms, describing respectively how the blocks of the children are shuffled, or which blocks are merged and which processes are closed.
Compared to the non-parameterized case [1, 2], the difficulty is that the number of processes may grow arbitrarily along the DST, instead of being fixed from the beginning – and we still need to use labels from a bounded domain. The solution comes from the distinction between open and closed processes, and the fact that the number of open processes stays bounded. Merge and shuffle operations only act on open processes: a merge makes some elastic edges rigid (which are all located on open processes, by definition), and/or closes some open processes. Similarly, a shuffle of two split MSCs \(M_1\) and \(M_2\) may only combine some pairs of open processes of \(M_1\) and \(M_2\) by shuffling their blocks and adding elastic edges between them. It simply takes the disjoint union of closed processes.
Thus, the disambiguated labels will focus on open processes. The idea is to describe how many blocks each process has after the operation, and the origin of each block.
A \(k\text {-}\) disambiguated split-term (k- DST ) is a split-term in which each internal node is labeled by a tuple of words \((w_p)_{1 \le p \le m}\) such that \(\sum _{p = 1}^{m} |w_p| \le k\), and
-
For a \(\mathbin {{\sqcup }\mathchoice{}{}{}{}{\sqcup }}\)-node, the word \(w_p \in \{B _\ell , B _r \}^+\) describes the composition of some open process, where \(B _\ell \) stands for a block coming from the left child, and \(B _r\) stands for a block coming from the right child (see for instance the label of \(n'\) in Fig. 6 which describes the origin of the 3 blocks of the open process of \(M'\) in Fig. 5).
-
For a
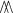 -node, the word \(w_p \in \{B _{i} \mid 1 \le i \le k\}^*\) describes how the blocks of the p-th open process of its child are merged: \(B _{i} \) stands for a block resulting from the merge of i consecutive blocks of the child. We use \(w_p=\varepsilon \) to indicate that process p is closed, merging all its blocks if any. For instance, in Figs. 5 and 6 the label \((B _{2}, B _{2})\) of node \(n_3\) indicates that on both process of \(M_3'\), the two blocks are merged in \(M_3\).
-node, the word \(w_p \in \{B _{i} \mid 1 \le i \le k\}^*\) describes how the blocks of the p-th open process of its child are merged: \(B _{i} \) stands for a block resulting from the merge of i consecutive blocks of the child. We use \(w_p=\varepsilon \) to indicate that process p is closed, merging all its blocks if any. For instance, in Figs. 5 and 6 the label \((B _{2}, B _{2})\) of node \(n_3\) indicates that on both process of \(M_3'\), the two blocks are merged in \(M_3\). -
For a \(\lhd \)-node, \(m\le 2\) and the word \(w_p \in \{B _!, B _? \}\) indicates that the p-th open process consists of the send (resp. receive) event. If \(m= 2\) then \(w_1 \ne w_2\). For instance, \(n_7\) is labeled \((B _!)\), which means that in \(M_7\) the process of the send event is open whereas the process of the receive event is closed.
We denote by \(\mathsf {DST}^k \) the set of all \(k\)-DSTs. A \(k\)-DST is called valid when the label of each node is coherent with the number of processes and blocks appearing in the label of its child/children. For instance, we cannot have \(w_p = B _{2} B _{1} \) at a  -node if its child does not have 3 blocks on process p.
-node if its child does not have 3 blocks on process p.
A valid \(k\)-DST t can be associated with a unique split pre-MSC (which is not necessarily a split MSC) \(M_{t} = (P, O, E, \rightarrow , \dashrightarrow , \lhd , \pi , \lambda )\), defined as follows. E is the set of leaves of t, and \(\lambda \) associates with a leaf e its label. We let \(e \lhd f\) whenever e and f are respectively the left and right children of a same \(\lhd \)-node.
To determine whether two leaves e and f are connected by a \(\rightarrow \)-edge, we proceed as follows. We track the block associated with leaf e, until reaching a  -node n in which it is merged with the block on its right (see example in green in Fig. 6). Similarly, we track the block associated with leaf f, until reaching a
-node n in which it is merged with the block on its right (see example in green in Fig. 6). Similarly, we track the block associated with leaf f, until reaching a  -node \(n'\) in which it is merged with the block on its left (in blue in Fig. 6). We set \(e \rightarrow f\) if \(n = n'\) and the blocks coincide. Similarly, we let \(e \dashrightarrow f\) when no merge ever occurs on the right of the block of e or on the left of the block of f, and at the root, the block of f is located just after the block of e.
-node \(n'\) in which it is merged with the block on its left (in blue in Fig. 6). We set \(e \rightarrow f\) if \(n = n'\) and the blocks coincide. Similarly, we let \(e \dashrightarrow f\) when no merge ever occurs on the right of the block of e or on the left of the block of f, and at the root, the block of f is located just after the block of e.
We identify processes with connected components of \((E, {\rightarrow } \cup {\dashrightarrow })\). To determine whether the process of an event e is open or closed, we walk up the tree remembering the process of e, until reaching a  -node in which it is closed, or the root (in which case it is open).
-node in which it is closed, or the root (in which case it is open).
For example, in Figs. 5 and 6 the split pre-MSC associated with the \(k\)-DST starting in node \(n_i\) (resp. \(n_i'\)) is \(M_i\) (resp. \(M_i'\)).
The next lemma states that the conditions for \(M_{t} \) to be an MSC can be checked by a tree automaton. We denote by \(\mathsf {DST}_{\mathsf {msc}}^{k}\) the set of all valid \(k\)-DSTs t such that \(M_{t} \) is an MSC.
Lemma 21
One can construct in space polynomial in k and \(|\mathcal {N} |\) a deterministic bottom-up tree automaton \(\mathcal {A} _\mathsf {msc}^k\) with \(2^{\mathcal {O}(| \mathcal {N} | k^4)}\) states s.t. \({L(\mathcal {A} _\mathsf {msc}^k) = \mathsf {DST}_{\mathsf {msc}}^{k}}\).
From PCAs to Tree Automata. Given a PCA, we can construct a tree automaton that accepts a tree \(t\in \mathsf {DST}_{\mathsf {msc}}^{k} \) iff \(M_{t} \) is accepted by the PCA.
Lemma 22
Let \(\mathcal {S} = (S,\iota , Msg ,\varDelta ,F)\) be a PCA, and \(k \in \mathbb {N} \). There is a bottom-up tree automaton \(\mathcal {A} ^k_{\mathcal {S}}\) of size \(|S|^{\mathcal {O}(k|F|^2)}\) such that \(L(\mathcal {A} ^k_{\mathcal {S}}) \cap \mathsf {DST}_{\mathsf {msc}}^{k} = \{t \in \mathsf {DST}_{\mathsf {msc}}^{k} \mid M_{t} \in L(\mathcal {S})\}\). It can be constructed in space polynomial in k and |F|, and logarithmic in |S| and \(|\varDelta |\).
Proof
\(\mathcal {A} ^k_{\mathcal {S}}\) guesses a run of \(\mathcal {S}\) on \(M_{t} \), and inductively checks that it is a valid accepting run. To do so, it remembers the states of \(\mathcal {S}\) before and after each block in the split MSC associated with the current subtree, that is, a pair \((\rho ^-, \rho ^+)\) of partial functions from [k] to S. (The blocks are numbered according to their position in the concatenation \(w_1w_2 \ldots w_{m}\) of the words in the label of the current node.) In addition, for each \(s \in S\) appearing in F, \(\mathcal {A} ^k_{\mathcal {S}}\) remembers the number \(n_s\) of closed processes that ends in state s, up to the maximal n such that \(\langle \# (s) \ge n \rangle \) appears in F. A state is accepting if it satisfies F.
At leaves, \(\mathcal {A} ^k_{\mathcal {S}}\) remembers the type of action executed (in \(\varSigma \)), and at a \(\lhd \)-node of the form \(a! \lhd b?\), it guesses a message m and transitions \(p \xrightarrow {a!m} p'\) and \(q \xrightarrow {b?m} q'\) of \(\mathcal {S}\). The functions \(\rho ^-\) and \(\rho ^+\) of the \(\lhd \)-node are initialized accordingly. For instance, after reading \(a! \lhd _{(B _!, B _?)} b?\) and guessing the transitions, \(\mathcal {A} ^k_{\mathcal {S}}\) goes to the state where \(\rho ^-(1) = p, \rho ^+(1) = p', \rho ^-(2) = q, \rho ^+(2) = q'\) and \(\rho ^-, \rho ^+\) are undefined elsewhere. After reading \(a! \lhd _{(B _?)} b?\), \(\mathcal {A} ^k_{\mathcal {S}}\) checks that \(p = \iota \) and increments \(n_{p'}\), and moves to state \(\rho ^-(1) = q, \rho ^+(1) = q'\).
The functions \(\rho ^-\) and \(\rho ^+\) are updated at each \(\mathbin {{\sqcup }\mathchoice{}{}{}{}{\sqcup }}\)- and  -node according to the renaming of the blocks. At a
-node according to the renaming of the blocks. At a  -node, \(\mathcal {A} ^k_{\mathcal {S}}\) checks than whenever two blocks b and \(b+1\) are merged, \(\rho ^+(b) = \rho ^-(b+1)\). It also checks that each process being closed starts in \(\iota \), and increments the counter \(n_s\) of its end state s (unless it has already reached its maximal value). \(\square \)
-node, \(\mathcal {A} ^k_{\mathcal {S}}\) checks than whenever two blocks b and \(b+1\) are merged, \(\rho ^+(b) = \rho ^-(b+1)\). It also checks that each process being closed starts in \(\iota \), and increments the counter \(n_s\) of its end state s (unless it has already reached its maximal value). \(\square \)
We then have \(L(\mathcal {S}) \cap \mathsf {SW} _k \ne \varnothing \) iff \(L(\mathcal {A} ^k_{\mathcal {S}} \cap \mathcal {A} _\mathsf {msc}^k) \ne \varnothing \), which leads to an algorithm in time polynomial in |S| and exponential in k, \(|\mathcal {N} |\) and |F| to decide the non-emptiness of \(L(\mathcal {S})\cap \mathsf {SW} _k \). This proves the upperbound of Theorem 11.
Classes of Bounded Split-With. The above decision procedure can be adapted for any class \(\mathcal {C} \) of MSCs of split-width at most k, provided we can construct an automaton \(\mathcal {A} _\mathcal {C} \) that accepts only encodings of MSCs in \(\mathcal {C} \), and at least one encoding for each \(M \in \mathcal {C} \). Under those assumptions, and given a PCA \(\mathcal {S}\), deciding whether \(L(\mathcal {S}) \cap \mathcal {C} = \varnothing \) e.g. reduces to deciding whether \(L(\mathcal {A} ^k_{\mathcal {S}} \cap \mathcal {A} _\mathsf {msc}^k \cap \mathcal {A} _\mathcal {C}) = \varnothing \).
This applies in particular to existentially bounded MSCs, and context- or tile-bounded MSCs over topologies of bounded tree-width. The construction of \(\mathcal {A} _\mathcal {C} \) is in all three cases based on the proof that \(\mathcal {C} \) has split-width at most k.
Note that this would also apply for instance to any class of bounded split-width that is recognized by a PCA.
6 Further Results
Model-Checking. The results presented in Sects. 3 and 5 can be generalized to model-checking problems (details can be found in [16]). Our most general decidability result states that the model-checking of PCAs against Monadic Second-Order (MSO) formulas is decidable. The idea is to construct, for a given specification \(\varphi \), a tree automaton \(\mathcal {A} ^k_{\varphi } \) that accepts a valid \(k\)-DST t iff \(M_{t} \) satisfies \(\varphi \). The bounded split-width model-checking problem then reduces to testing whether \(L(\mathcal {A} ^k_{\mathcal {S}} \cap \mathcal {A} ^k_{\lnot \varphi } \cap \mathcal {A} _\mathsf {msc}^k) = \varnothing \), and similarly for the other classes.
However, when the specification \(\varphi \) is given by an MSO formula, the construction of \(\mathcal {A} ^k_{\varphi }\) is non-elementary. Towards a better complexity, we study model checking against PDL specifications. PDL is both expressive (it subsumes most if not all temporal logics), easy to use and understand, and enjoys a very good complexity. We show that model-checking against PDL formulas is Exptime-complete, i.e., not harder than non-emptiness and reachability. It remains in Exptime when we extend PDL with converse (CPDL), and is 2-Exptime-complete for ICPDL (PDL with converse and intersection). A summary of our results is given in Fig. 7.
Multi-pushdown Processes. Our model could be extended by adding one or several stacks to processes, similarly to what is done in the case of fixed architectures [2]. We could also allow several FIFO channels between any pair of processes. This means relaxing the definition of topologies to allow loops or multiple edges, and similarly adapt the definition of MSCs. The definition of split-width and \(k\)-DSTs is the same, except that at \(\lhd \)-nodes, the send and receive events may be placed on the same process. Our decision procedures remain correct, with an additional check by \(\mathcal {A} _\mathsf {msc}^k\) of the LIFO conditions on the stacks. The results on existentially-bounded MSCs, context-bounded MSCs, or tile decompositions are also still valid.
References
Aiswarya, C., Gastin, P.: Reasoning about distributed systems: WYSIWYG (invited talk). In: FSTTCS 2014, LIPIcs, vol. 29, pp. 11–30. Leibniz-Zentrum für Informatik (2014)
Aiswarya, C., Gastin, P., Narayan Kumar, K.: Verifying communicating multi-pushdown systems via split-width. In: Cassez, F., Raskin, J.-F. (eds.) ATVA 2014. LNCS, vol. 8837, pp. 1–17. Springer, Heidelberg (2014)
Aminof, B., Jacobs, S., Khalimov, A., Rubin, S.: Parameterized model checking of token-passing systems. In: McMillan, K.L., Rival, X. (eds.) VMCAI 2014. LNCS, vol. 8318, pp. 262–281. Springer, Heidelberg (2014)
Aminof, B., Kotek, T., Rubin, S., Spegni, F., Veith, H.: Parameterized model checking of rendezvous systems. In: Baldan, P., Gorla, D. (eds.) CONCUR 2014. LNCS, vol. 8704, pp. 109–124. Springer, Heidelberg (2014)
Bollig, B.: Logic for communicating automata with parameterized topology. In: CSL-LICS 2014. ACM (2014)
Bollig, B., Gastin, P., Kumar, A.: Parameterized communicating automata: Complementation and model checking. In: FSTTCS 2014, LIPIcs, vol. 29, pp. 625–637 (2014)
Bollig, B., Gastin, P., Schubert, J.: Parameterized verification of communicating automata under context bounds. In: Ouaknine, J., Potapov, I., Worrell, J. (eds.) RP 2014. LNCS, vol. 8762, pp. 45–57. Springer, Heidelberg (2014)
Brand, D., Zafiropulo, P.: On communicating finite-state machines. J. ACM 30(2), 323–342 (1983)
Courcelle, B., Engelfriet, J.: Graph Structure and Monadic Second-Order Logic - A Language-Theoretic Approach. Encyclopedia of mathematics and its applications, vol. 138. Cambridge University Press, Cambridge (2012)
Cyriac, A.: Verification of Communicating Recursive Programs via Split-width. Ph.D. thesis, ENS Cachan (2014). http://www.lsv.ens-cachan.fr/~cyriac/download/Thesis_Aiswarya_Cyriac.pdf
Cyriac, A., Gastin, P., Kumar, K.N.: MSO decidability of multi-pushdown systems via split-width. In: Koutny, M., Ulidowski, I. (eds.) CONCUR 2012. LNCS, vol. 7454, pp. 547–561. Springer, Heidelberg (2012)
Delzanno, G., Sangnier, A., Zavattaro, G.: Parameterized verification of ad hoc networks. In: Gastin, P., Laroussinie, F. (eds.) CONCUR 2010. LNCS, vol. 6269, pp. 313–327. Springer, Heidelberg (2010)
Delzanno, G., Sangnier, A., Zavattaro, G.: On the power of cliques in the parameterized verification of ad hoc networks. In: Hofmann, M. (ed.) FOSSACS 2011. LNCS, vol. 6604, pp. 441–455. Springer, Heidelberg (2011)
Durand-Gasselin, A., Esparza, J., Ganty, P., Majumdar, R.: Model checking parameterized asynchronous shared-memory systems. In: Kroening, D., Păsăreanu, C.S. (eds.) CAV 2015. LNCS, vol. 9206, pp. 67–84. Springer, Heidelberg (2015)
Emerson, E.A., Namjoshi, K.S.: On reasoning about rings. Int. J. Found. Comput. Sci. 14(4), 527–550 (2003)
Fortin, M., Gastin, P.: Verification of parameterized communicating automata via split-width. Technical report, LSV, ENS Cachan (2016). http://www.lsv.ens-cachan.fr/~gastin/mes-publis.php
Genest, B., Kuske, D., Muscholl, A.: A Kleene theorem and model checking algorithms for existentially bounded communicating automata. Inf. Comput. 204(6), 920–956 (2006)
ITU-TS Recommendation Z.120anb: Formal Semantics of Message Sequence Charts (1998)
Qadeer, S., Rehof, J.: Context-bounded model checking of concurrent software. In: Halbwachs, N., Zuck, L.D. (eds.) TACAS 2005. LNCS, vol. 3440, pp. 93–107. Springer, Heidelberg (2005)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Fortin, M., Gastin, P. (2016). Verification of Parameterized Communicating Automata via Split-Width. In: Jacobs, B., Löding, C. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2016. Lecture Notes in Computer Science(), vol 9634. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49630-5_12
Download citation
DOI: https://doi.org/10.1007/978-3-662-49630-5_12
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49629-9
Online ISBN: 978-3-662-49630-5
eBook Packages: Computer ScienceComputer Science (R0)





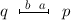 (adjacent processes are mutually connected), and
(adjacent processes are mutually connected), and , we have
, we have 











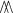 -node, the word
-node, the word 

