Abstract
This paper presents a shallow embedding of a probabilistic functional programming language in higher order logic. The language features monadic sequencing, recursion, random sampling, failures and failure handling, and black-box access to oracles. Oracles are probabilistic functions which maintain hidden state between different invocations. To that end, we propose generative probabilistic systems as the semantic domain in which the operators of the language are defined. We prove that these operators are parametric and derive a relational program logic for reasoning about programs from parametricity. Several examples demonstrate that our language is suitable for conducting cryptographic proofs.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
As cryptographic algorithms and protocols are becoming increasingly complicated, flaws in their security proofs are more likely to be overlooked. So, security vulnerabilities can remain undiscovered. The game playing technique [16, 29, 48] helps in structuring such proofs and can thus increase the level of confidence in their correctness. In this view, security notions are expressed as programs (called games) in the same language as the cryptographic algorithms and protocols. The proof then consists of transforming the program in several small steps until the desired properties obviously hold. To achieve high assurance, several frameworks [8, 14, 42] and a proof assistant [13] offer machine support in formalising algorithms and security notions and in checking such sequences of game transformations. This way, many cryptographic constructions have been mechanically proven secure, e.g., [6, 7, 43].
For security protocols such as TLS, Kerberos, and IPSec, only few mechanised security proofs in the computational model are available, e.g., [18, 21]. Instead, symbolic analysis tools [4, 19, 39, 47] dominate. They model protocol messages as terms in an algebra rather than bitstrings and assume that cryptography is perfect. Computational soundness (CS) results [1, 9, 25] bridge the gap between symbolic and computational models, but to our knowledge, they have never been mechanically checked. Yet, mechanising them is desirable for three reasons. First, the proofs are extremely technical with many case distinctions. A proof assistant can check that all cases are covered and no assumption is forgotten (as has happened in early CS works), and it provides automation for dealing with the easy cases. Second, computational soundness results need to be formalised only once per set of cryptographic primitives, not for every protocol to which the symbolic analyser is applied. That is, one mechanised proof yields trustworthy proofs for a whole class of protocols. Third, mechanisation supports the evolution of models and proofs. If a primitive is added or an assumption weakened as in [10], the proof assistant checks the proofs again and pinpoints where adaptations are needed.
Unfortunately, the existing frameworks are not suitable for formalising CS proofs. CertiCrypt [14] and Verypto [8] formalise stateful languages in the proof assistants Coq and Isabelle, respectively. Due to the deep embedding, program transformations always require a proof about the semantics and programs cannot easily reuse the existing libraries of the proof assistants. Therefore, formalising cryptographic arguments requires a very substantial effort. CertiCrypt’s successor EasyCrypt [13] provides much better automation using SMT solvers. Its logical foundation is higher order logic (HOL), but the reasoning infrastructure focuses on proofs in relational Hoare logic. However, substantial parts of CS proofs reason about the term algebra of the symbolic model for which EasyCrypt provides no support at all. The foundational cryptography framework (FCF) [42] alleviates CertiCrypt’s formalisation burden by taking a semi-shallow approach in Coq. For pure deterministic functions, the framework reuses the language of the logic; only probabilistic effects and interaction with oracles are modelled syntactically as monads. This saves considerable effort in comparison to CertiCrypt. Yet, the monadic language lacks features such as recursion and exceptions, which are desirable for CS, e.g., to implement probabilistic serialisers and parsers.
Contributions. We present a framework for cryptographic proofs formalised in higher order logic. It consists of a probabilistic functional programming language and a logic for reasoning about programs and probabilities. The language features monadic sequencing, recursion, random sampling, failures and their handling, and black-box access to oracles. Oracles are probabilistic functions that maintain hidden state between different invocations. We model the language shallowly, i.e., we define the operators directly in the semantic domain. Programs which need no access to oracles are interpreted in the monad of discrete subprobabilities (Sect. 2.2); recursive functions are defined in terms of a least fixpoint operator (Sect. 2.3). For programs with oracle access, we propose generative probabilistic systems as semantic domain, which supports corecursive definitions (Sect. 3.2). In particular, we define operators for composing programs with oracles and other programs. We have implemented the framework in the proof assistant Isabelle/HOL [41], but it could be formalised in any other HOL-based prover, too.
The shallow embedding offers three benefits. First, we can reuse all the existing infrastructure of the proof assistant, such as name binding, higher-order unification and the module system, but also definitional packages and existing libraries. Second, we obtain a rich equational theory directly on programs, i.e., without any intervening interpretation function. Equality is important as we can replace terms by equal terms in any context (by HOL’s substitution rule), i.e., there is no need for congruences. Consequently, proof automation can use the (conditional) equations directly for rewriting. Although no syntax is formalised in the logic, programs are still written as HOL terms. This suffices to guide syntax-directed proof tactics. Third, the language is not restricted to a fixed set of primitives. New operators can be defined in the semantic domain at any time.
Beyond equality, we provide a relational logic for reasoning about programs (Sects. 2.4 and 3.3). Relational parametricity [44, 50] has been our guide in that most rules follow from the fact that the operators are parametric. In particular, we demonstrate that several common reasoning principles in cryptographic proofs follow from parametricity. This approach ensures soundness of the logic by construction and can also guide the discovery of proof rules for new operators. Our logic is similar to those of the other tools. The novelty is that we follow a principled way in finding the rules and establishing soundness.
Three examples demonstrate that our framework is suitable for cryptographic proofs. We proved indistinguishability under chosen plaintext attacks (IND-CPA) for (i) Elgamal public-key encryption [27] in the standard model (Sects. 2.1 and 2.5), (ii) Hashed Elgamal encryption in the random oracle model (Sects. 3.1 and 3.4), and (iii) an encryption scheme based on pseudo-random functions [42]. The examples have been chosen to enable comparisons with the existing frameworks (see Sect. 4). They show that our framework leads to concise proofs with the level of proof automation being comparable to EasyCrypt’s, the current state of the art. This indicates that the framework scales to computational soundness results, although our examples are much simpler. Indeed, we have just started formalising a CS result, so this is only a first step. The framework and all examples and proofs have been formalised in Isabelle/HOL and are available online [37].
Preliminaries: HOL Notation. The meta-language HOL mostly uses everyday mathematical notation. Here, we present basic non-standard notation and a few types with their operations; further concepts will be introduced when needed.
HOL terms are simply typed lambda terms with let-polymorphism (we use Greek letters  for type variables). Types include in particular the type of truth values
for type variables). Types include in particular the type of truth values  and the singleton type
and the singleton type  with its only element
with its only element  and the space of total functions
and the space of total functions  . Type constructors are normally written postfix, e.g.,
. Type constructors are normally written postfix, e.g.,  denotes the type of finite lists of booleans, i.e., bitstrings. The notation
denotes the type of finite lists of booleans, i.e., bitstrings. The notation  means that the HOL term
means that the HOL term  has type
has type  .
.
Pairs (type  ) come with two projection functions
) come with two projection functions  and
and  , and the map function
, and the map function  . Tuples are identified with pairs nested to the right, i.e.,
. Tuples are identified with pairs nested to the right, i.e.,  is identical to
is identical to  and
and  to
to  . Dually,
. Dually,  denotes the disjoint sum of
denotes the disjoint sum of  and
and  ; the injections are
; the injections are  and
and  . Case distinctions on freely generated types use guard-like syntax. The map function
. Case distinctions on freely generated types use guard-like syntax. The map function  for disjoint sums, e.g., pattern matches on
for disjoint sums, e.g., pattern matches on  to apply the appropriate function:
to apply the appropriate function:  .
.
Sets (type  ) are isomorphic to predicates (type
) are isomorphic to predicates (type  ) via the bijections membership
) via the bijections membership  and set comprehension
and set comprehension  ; the empty set is
; the empty set is  . Binary relations are sets of pairs and written infix, i.e.,
. Binary relations are sets of pairs and written infix, i.e.,  denotes
denotes  . The relators
. The relators  and
and  lift relations component-wise to pairs and sums.
lift relations component-wise to pairs and sums.
The datatype  corresponds to the Haskell type Maybe. It adjoins a new element
corresponds to the Haskell type Maybe. It adjoins a new element  to
to  , all existing values in
, all existing values in  are prefixed by
are prefixed by  . Maps (partial functions) are modelled as functions of type
. Maps (partial functions) are modelled as functions of type  , where
, where  represents undefinedness and
represents undefinedness and  means that
means that  maps
maps  to
to  . The empty map
. The empty map  is undefined everywhere. Map update is defined as follows:
is undefined everywhere. Map update is defined as follows:  .
.
2 A Shallow Probabilistic Functional Language
Security notions in the computation model are expressed as games parametrised by an adversary. In formalising such games, we want to leverage as much of the prover’s infrastructure as possible. Therefore, we only model explicitly what cannot be expressed in the prover’s term language, namely probabilities and access to oracles. In this section, we focus on probabilities and show the framework in action on the example of Elgamal encryption (Sects. 2.1 and 2.5).
We model games as functions which return a discrete (sub)probability distribution over outcomes. Discrete subprobabilities strike a balance between expressiveness and ease of use. They provide a monadic structure for sequencing and failure (Sect. 2.2). Thus, games can be formulated naturally and control may be transferred non-locally in error cases such as invalid data produced by the adversary. They also host a fixpoint operator for defining recursive functions (Sect. 2.3). In contrast, measure-theoretic (sub)probability distributions clutter proofs with measurability requirements. For computational soundness, discrete subprobability distributions suffice. In Sect. 2.4, we prove that the operators are relationally parametric and derive a programming logic and common cryptographic reasoning principles from parametricity.
2.1 Example: Elgamal Encryption
In this section, we formalise Elgamal’s encryption scheme [27] to motivate the features of our language. In Sect. 2.5, we prove the scheme IND-CPA secure under the decisional Diffie-Hellman (DDH) assumption. We formally introduce the language only in Sect. 2.2. For now, an intuitive understanding sufficFes: monadic sequencing is written in Haskell-style do notation and  samples
samples  as a random element from the finite set
as a random element from the finite set  .
.
For the following, consider a fixed finite cyclic group  over the type
over the type  with generator
with generator  . We write
. We write  for group multiplication and
for group multiplication and  for exponentiation with natural numbers;
for exponentiation with natural numbers;  denotes the order of
denotes the order of  . In Elgamal, the public key is an arbitrary group element
. In Elgamal, the public key is an arbitrary group element  and the private key is the exponent
and the private key is the exponent  . The security of this scheme relies on the hardness of computing the discrete logarithm. The key generation algorithm
. The security of this scheme relies on the hardness of computing the discrete logarithm. The key generation algorithm  generates a new key pair by randomly sampling the exponent (Fig. 1b). Messages are group elements, too. To encrypt a message
generates a new key pair by randomly sampling the exponent (Fig. 1b). Messages are group elements, too. To encrypt a message  under the public key
under the public key  , the algorithm multiplies
, the algorithm multiplies  with
with  raised to a random power between
raised to a random power between  and the order of the group (Fig. 1a).
and the order of the group (Fig. 1a).
Elgamal’s encryption scheme produces ciphertexts that are indistinguishable under chosen plaintext attacks. Chosen plaintext attacks are formalised as the game  shown in Fig. 1c. An IND-CPA adversary
shown in Fig. 1c. An IND-CPA adversary  consists of two probabilistic functions
consists of two probabilistic functions  and
and  . Given a public key
. Given a public key  ,
,  chooses two plaintexts
chooses two plaintexts  and
and  . The game then encrypts one of them as determined by the random bit
. The game then encrypts one of them as determined by the random bit  (a coin flip) and gives the challenge ciphertext
(a coin flip) and gives the challenge ciphertext  to
to  and any arbitrary state information
and any arbitrary state information  produced by
produced by  . Then,
. Then,  produces a guess which of the two messages
produces a guess which of the two messages  decrypts to. Indistinguishability requires that the adversary cannot do significantly better than flipping a coin. This is measured by the IND-CPA advantage given by
decrypts to. Indistinguishability requires that the adversary cannot do significantly better than flipping a coin. This is measured by the IND-CPA advantage given by  . A concrete security theorem bounds the advantage by a quantity which is known or assumed to be small.
. A concrete security theorem bounds the advantage by a quantity which is known or assumed to be small.
If any step in the game fails,  behaves like a fair coin flip, i.e., the advantage is
behaves like a fair coin flip, i.e., the advantage is  in that case. This happens, e.g., if the plaintexts are invalid, i.e., not elements of the group, or the adversary does not produce plaintexts or a guess at all. (In an implementation, the latter could be detected using timeouts.)
in that case. This happens, e.g., if the plaintexts are invalid, i.e., not elements of the group, or the adversary does not produce plaintexts or a guess at all. (In an implementation, the latter could be detected using timeouts.)
The DDH assumption states that given two random group elements  and
and  , it is hard to distinguish
, it is hard to distinguish  from another random group element
from another random group element  . Formally, a DDH adversary
. Formally, a DDH adversary  is a probabilistic function that takes three group elements and outputs a Boolean. We model the two settings as two games
is a probabilistic function that takes three group elements and outputs a Boolean. We model the two settings as two games  and
and  parametrised by the adversary.
parametrised by the adversary.


The DDH advantage captures the difficulty of  distinguishing the two settings. It is defined as
distinguishing the two settings. It is defined as  . The DDH assumption states that the advantage is small, and in Sect. 2.5, we show that the IND-CPA advantage for Elgamal is bounded by the DDH advantage.
. The DDH assumption states that the advantage is small, and in Sect. 2.5, we show that the IND-CPA advantage for Elgamal is bounded by the DDH advantage.
2.2 The Monad of Discrete Subprobability Distributions
A discrete subprobability distribution is given by its subprobability mass function (spmf), i.e., a non-negative real-valued function which sums up to at most 1. We define the type  of all spmfsFootnote 1 over elementary events of type
of all spmfsFootnote 1 over elementary events of type  and use variables
and use variables  ,
,  for spmfs. We make applications of spmfs explicit using the operator
for spmfs. We make applications of spmfs explicit using the operator  . So,
. So,  denotes the subprobability mass that the spmf
denotes the subprobability mass that the spmf  assigns to the elementary event
assigns to the elementary event  . An event
. An event  is a set of elementary events; its subprobability
is a set of elementary events; its subprobability  is given by
is given by  . Moreover, the weight
. Moreover, the weight  of
of  is the total probability mass assigned by
is the total probability mass assigned by  , i.e.,
, i.e.,  . If
. If  is a probability distribution, i.e.,
is a probability distribution, i.e.,  , then we call
, then we call  lossless following [14] (notation
lossless following [14] (notation  ). The support
). The support  is countable by construction.
is countable by construction.
The type  hosts the polymorphic monad operations
hosts the polymorphic monad operations 
 and
and  given by
given by


In this paper and in our formalisation, we use Haskell-style do notation where  desugars to
desugars to  . The monad operations satisfy the usual monad laws: (i)
. The monad operations satisfy the usual monad laws: (i)  is associative and (ii)
is associative and (ii)  is neutral for
is neutral for  . In addition,
. In addition,  is commutative and constant elements cancel.
is commutative and constant elements cancel.


Here,  scales the subprobability masses of
scales the subprobability masses of  by
by  , i.e., \(\mathsf{scale}~r~p!x=r\,\cdot \) (p!x) for
, i.e., \(\mathsf{scale}~r~p!x=r\,\cdot \) (p!x) for  . In particular, if
. In particular, if  is lossless, then
is lossless, then  . The monad operations give rise to the functorial action \(\mathsf{map}_\mathsf{spmf}{:}{:}(\alpha \Rightarrow \beta )\Rightarrow \alpha \)
. The monad operations give rise to the functorial action \(\mathsf{map}_\mathsf{spmf}{:}{:}(\alpha \Rightarrow \beta )\Rightarrow \alpha \)
 given by
given by  .
.
For sampling, the monad provides an operation  which returns the uniform distribution over a finite set. There are three special cases worth mentioning. First, for a singleton set, we have
which returns the uniform distribution over a finite set. There are three special cases worth mentioning. First, for a singleton set, we have  . Second, as fair coin flips are particularly prominent in cryptographic games, we abbreviate
. Second, as fair coin flips are particularly prominent in cryptographic games, we abbreviate  with
with  . Third, in case of an empty set, we let
. Third, in case of an empty set, we let  denote the empty subprobability distribution
denote the empty subprobability distribution  which assigns no probability to any event at all, i.e.,
which assigns no probability to any event at all, i.e.,  for all
for all  . In combination with sequencing and recursion,
. In combination with sequencing and recursion,  is fairly expressive.
is fairly expressive.
For example, the Bernoulli distribution  , which returns
, which returns  with probability
with probability  for any
for any  , can be sampled from fair coin flips as shown on the right [32]. It can be used to define probabilistic choice.
, can be sampled from fair coin flips as shown on the right [32]. It can be used to define probabilistic choice.
Moreover, the subprobability monad contains a failure element, namely  . Failure aborts the current part of the program, as
. Failure aborts the current part of the program, as  propagates:
propagates:  . However, we hardly use
. However, we hardly use  in programs directly. It is more natural to define an assertion statement
in programs directly. It is more natural to define an assertion statement  . Assertions are useful in validating the inputs received from the adversary. For example, the assertion in the IND-CPA security game in Fig. 1c checks that the adversary
. Assertions are useful in validating the inputs received from the adversary. For example, the assertion in the IND-CPA security game in Fig. 1c checks that the adversary  produced valid plaintexts.
produced valid plaintexts.
Failures are handled using the statement  , which distributes the probability mass not assigned by
, which distributes the probability mass not assigned by  according to
according to  . Formally, it satisfies
. Formally, it satisfies  for all
for all  . Clearly, we have the equalities
. Clearly, we have the equalities  and
and  if
if  is lossless. Moreover,
is lossless. Moreover,  commutes with
commutes with  for lossless spmfs, i.e., we can enlarge or shrink the scope of the handler.
for lossless spmfs, i.e., we can enlarge or shrink the scope of the handler.


The IND-CPA game in Fig. 1c treats failures as fair coin flips. This is sound as the advantage is the probability of the outcome  less
less  .
.
This completes the exposition of the language primitives except for the fixpoint combinator (see Sect. 2.3). They suffice for all examples in this paper, but note that we are not restricted to this set of operations. If necessary, users can define their own discrete subprobability distribution on the spot thanks to the shallow embedding. Also remember that all the equation in this section are equalities inside the logic. Hence, we can use them for rewriting in any context, not just under a semantics interpretation as with a deep embedding.
2.3 Recursive Functions in the SPMF Monad
In this section, we consider the denotation of recursive functions in the spmf monad. As usual in programming languages, we interpret a recursive specification as the least fixpoint of the associated functional. In the case of spmf, the approximation order  is given by
is given by  [5]. In this order, every chain
[5]. In this order, every chain  has a least upper bound (lub)
has a least upper bound (lub)  which is taken pointwise:
which is taken pointwise:  where
where  denotes the supremum of a bounded set
denotes the supremum of a bounded set  of real numbers. Thus, the approximation order is a chain-complete partial order (ccpo) with least element
of real numbers. Thus, the approximation order is a chain-complete partial order (ccpo) with least element  (see Proposition 1 below).
(see Proposition 1 below).
By Tarski’s fixpoint theorem, every monotone function  on a ccpo has a least fixpoint
on a ccpo has a least fixpoint  , which is obtained by the least upper bound of the transfinite iteration of
, which is obtained by the least upper bound of the transfinite iteration of  starting at the least element. Therefore, we can define recursive functions as the least fixpoint of the associated (monotone) functional.
starting at the least element. Therefore, we can define recursive functions as the least fixpoint of the associated (monotone) functional.
Using Isabelle’s package for recursive monadic function definitions [34], we hide the internal construction via fixpoints from the user and automate the monotonicity proof. For example, the function  can be specified exactly as shown in Fig. 2. The monotonicity proof succeeds as
can be specified exactly as shown in Fig. 2. The monotonicity proof succeeds as  is monotone in both arguments. Namely, if
is monotone in both arguments. Namely, if  and
and  for all
for all  , then
, then  . In contrast,
. In contrast,  is monotone only in the second argument, but not in the first. For example,
is monotone only in the second argument, but not in the first. For example,  , but
, but 
 . Therefore, recursion is always possible through
. Therefore, recursion is always possible through  and
and  , but not in general through
, but not in general through  .
.
Proposition 1
The approximation order  is a chain-complete partial order.
is a chain-complete partial order.
Proof
We have to show that  is a partial order and that
is a partial order and that  is well-defined and the least upper bound for every chain
is well-defined and the least upper bound for every chain  , i.e., every set of spmfs all of whose elements are comparable in
, i.e., every set of spmfs all of whose elements are comparable in  . The difficult part is to show that
. The difficult part is to show that  is well-defined. In particular, we must show that the support of
is well-defined. In particular, we must show that the support of  is countable even if
is countable even if  is uncountable. Then, it is not hard to see that
is uncountable. Then, it is not hard to see that  sums up to at most 1.
sums up to at most 1.
Clearly, we have  . Yet, the union of an uncountable sequence of increasing countable sets need not be countable in general. In the following, we show that even for uncountable chains
. Yet, the union of an uncountable sequence of increasing countable sets need not be countable in general. In the following, we show that even for uncountable chains  of spmfs, the union of the supports remains countable. To that end, we identify a countable sub-sequence of
of spmfs, the union of the supports remains countable. To that end, we identify a countable sub-sequence of  whose lub has the same support. The key idea is that for
whose lub has the same support. The key idea is that for  -comparable spmfs
-comparable spmfs  and
and  , the order can be decided by looking only at the assigned probability masses, namely,
, the order can be decided by looking only at the assigned probability masses, namely,  iff
iff  . So suppose without loss of generality that
. So suppose without loss of generality that  does not contain a maximal element (otherwise, the lub is the maximal element and we are done). The set of assigned probability masses
does not contain a maximal element (otherwise, the lub is the maximal element and we are done). The set of assigned probability masses  has a supemum
has a supemum  , as
, as  bounds the set from above. The closure of
bounds the set from above. The closure of  contains the supremum
contains the supremum  , so
, so  must contain a countable increasing sequence which converges to
must contain a countable increasing sequence which converges to  . This sequence gives rise to a countable sub-sequence
. This sequence gives rise to a countable sub-sequence  of
of  , for which we show
, for which we show  . For any
. For any  , there is a
, there is a  such that
such that  , as the assigned probability masses in
, as the assigned probability masses in  converge to
converge to  from below and
from below and  is not maximal. Hence,
is not maximal. Hence,  as
as  and
and  are related in
are related in  , and therefore
, and therefore  as
as  is monotone.
is monotone.
The attentive reader might wonder why we need transfinite iteration for the fixpoint despite having shown that uncountable chains can be reduced to countable ones for the purpose of lubs. Countable fixpoint iteration, which defines the least fixpoint as  , does not suffice. (Here, function iteration is defined by
, does not suffice. (Here, function iteration is defined by  and
and  .) The reason is that the chain
.) The reason is that the chain  might stop before the least fixpoint is reached. Consider, e.g., the monotone spmf transformer
might stop before the least fixpoint is reached. Consider, e.g., the monotone spmf transformer  given below.
given below.


The countable iteration of f starting at  yields a sequence of spmfs which assign to
yields a sequence of spmfs which assign to  the masses 0,
the masses 0,  The least upper bound of this sequence assigns
The least upper bound of this sequence assigns  to
to  . That is, the iteration has not yet reached f’s fixed point, which assigns the mass 1 to
. That is, the iteration has not yet reached f’s fixed point, which assigns the mass 1 to  . This is because f is not (chain) continuous, i.e., it does not preserve lubs.
. This is because f is not (chain) continuous, i.e., it does not preserve lubs.
Overall, arbitrary chains and transfinite iteration are superior to ordinary fixpoint iteration in two ways. First, our fixpoint combinator can handle more functions, i.e., we can accept more recursive specifications. Second, the proof obligations that recursive specifications incur are simpler: monotonicity is usually easier to show than continuity.
2.4 Lifting and Parametricity
Game playing proofs transform games step by step. In each step, we have to bound the probability that the adversary can distinguish the original game from the transformed one. For some transformations, the equational theory suffices to prove the games equal—then, the probability is 0. Other transformations are justified by cryptographic assumptions. To bound the probability in such cases, our framework provides a relational logic for programs.
To that end, we first define an operation to lift relations over elementary events to relations over spmfs. With this lifting operator, our primitive operations are parametric. Then, we can derive the logic from parametricity.
Lifting. The lifting operation  transforms a binary relation R over elementary events into a relation over spmfs over these events. For lossless distributions, a number of definitions have appeared in the literature. We generalise the one from [30] as the relator associated with the natural transformation
transforms a binary relation R over elementary events into a relation over spmfs over these events. For lossless distributions, a number of definitions have appeared in the literature. We generalise the one from [30] as the relator associated with the natural transformation  [45]. Formally,
[45]. Formally,  relates the spmfs
relates the spmfs  and
and  iff there is an spmf
iff there is an spmf  such that (i)
such that (i)  , (ii)
, (ii)  , and (iii)
, and (iii)  , We call w a R-joint spmf of p and q.
, We call w a R-joint spmf of p and q.
This definition reformulates the one by Larsen and Skou [36] for lossless spmfs. They consider w as a non-negative weight function on the relation such that the marginals are the original distribution., i.e., w must satisfy (i)  whenever
whenever  , (ii)
, (ii)  for all x, and (iii)
for all x, and (iii)  for all y, Using the functorial structure of spmfs, our definition expresses the same conditions more abstractly without summations. In previous work [30], this led to considerably shorter proofs.
for all y, Using the functorial structure of spmfs, our definition expresses the same conditions more abstractly without summations. In previous work [30], this led to considerably shorter proofs.
Recently, Sack and Zhang [46] showed that if p and q are lossless, then


generalising Desharnais’ proof for the finite case [26]. In our formalisation, we assume the “if” direction of the equivalence. We have not yet proved it formally, as it relies on the max-flow min-cut theorem for countable networks [3], which itself requires a substantial formalisation effort. Still, we formally derive the following characterisation of  for arbitrary spmfs from this assumption.
for arbitrary spmfs from this assumption.
Lemma 1
(Characterisation of \({{{\mathbf {\mathsf{{rel}}}}}_{{\varvec{\mathsf{{ spmf}}}}}}\) ).
The following are equivalent for all R, p, and q.
-
(a)

-
(b)
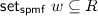 and
and 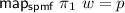 and
and 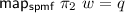 for some w
for some w
-
(c)
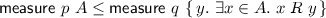 for all A and
for all A and 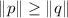
The relator enjoys a number of useful properties. For example, (i) it generalises equality, namely  , (ii) it distributes over relation composition, and (iii) it is monotone:
, (ii) it distributes over relation composition, and (iii) it is monotone:  implies
implies  if
if  whenever
whenever  and
and  and
and  .
.
Parametricity. The program logic describes the interaction between the spmf operations and the relator. As it turns out, relational parametricity [44, 50] helps us to find the rules and prove them sound.Footnote 2
Parametricity expresses that a polymorphic function does not inspect the values of type variables, but works uniformly for all instances. Relational parametricity formalises this as follows. Types are interpreted as relations and type constructors as relation transformers. A polymorphic function is (relationally) parametric iff it is related to itself in its type’s relation where type variables are interpreted as arbitrary relations. For spmfs, the relator  is the appropriate relation transformers. For example, parametricity for
is the appropriate relation transformers. For example, parametricity for  is expressed as
is expressed as  for all
for all  . Here, the relator
. Here, the relator  for the function space relates two functions f and g iff they transform relatedness in R into relatedness in S, i.e.,
for the function space relates two functions f and g iff they transform relatedness in R into relatedness in S, i.e.,  implies
implies  for all x and y.
for all x and y.
Wadler [50] proved that all functions of the polymorphic lambda calculus are parametric. He also demonstrated that adding polymorphic equality destroys this property. Higher order logic has polymorphic equality  and description operators, so not all HOL functions are parametric. Thus, parametricity is not a free theorem in our setting; we have to prove it. For
and description operators, so not all HOL functions are parametric. Thus, parametricity is not a free theorem in our setting; we have to prove it. For  , parametricity follows directly from unfolding the definitions and taking
, parametricity follows directly from unfolding the definitions and taking  as the joint spmf for
as the joint spmf for  and
and  for all
for all  . For
. For  , the parametricity statement is
, the parametricity statement is


The proof is similar to the one for  : after having unfolded the definitions, we take
: after having unfolded the definitions, we take  as the joint spmf for
as the joint spmf for  and
and  where w is the R-joint spmf for p and q and
where w is the R-joint spmf for p and q and  denotes the R’-joint spmf for f x and g y for all
denotes the R’-joint spmf for f x and g y for all  .
.
As function application preserves parametricity, any combination of parametric functions is parametric, too. For example, parametricity of  and
and  follows. Similarly,
follows. Similarly,  is parametric, too. Thus, this extends to whole probabilistic programs, which we will exploit in Sect. 3.4. Such parametricity proofs are highly automated in Isabelle [31, 35].
is parametric, too. Thus, this extends to whole probabilistic programs, which we will exploit in Sect. 3.4. Such parametricity proofs are highly automated in Isabelle [31, 35].
For reasoning about probabilistic programs, we derive more conventional rules by supplying some arguments. For example, we get the following rules for the monad operations. Note that parametricity dictates the shape of the rules.


However, not all functions are parametric. The function  , e.g., is not, because it relies on polymorphic equality: the cardinality of a set depends on the equality of elements. In detail, the relator for
, e.g., is not, because it relies on polymorphic equality: the cardinality of a set depends on the equality of elements. In detail, the relator for  relates two sets A and B iff R relates each element of A with one in B and vice versa; formally,
relates two sets A and B iff R relates each element of A with one in B and vice versa; formally,  and
and  . Now,
. Now,


holds if (and only if) the relation R respects equality, i.e.,  holds, where
holds, where  is the identity relation on Booleans (type
is the identity relation on Booleans (type  ). Interestingly, this restricted parametricity property is equivalent to optimistic sampling in cryptographic proofs. Namely, if f is injective on A, then
). Interestingly, this restricted parametricity property is equivalent to optimistic sampling in cryptographic proofs. Namely, if f is injective on A, then


where  denotes the image of A under f. This is one example of Wadler’s free theorems [50] in our context. If we specialise A to bitstrings of a given length and f to the bitwise exclusive or (xor) with a fixed bitstring, we obtain the well-known one-time-pad lemma:
denotes the image of A under f. This is one example of Wadler’s free theorems [50] in our context. If we specialise A to bitstrings of a given length and f to the bitwise exclusive or (xor) with a fixed bitstring, we obtain the well-known one-time-pad lemma:  where s is a bitstring of length n and
where s is a bitstring of length n and  denotes the set of all bitstrings of length n.
denotes the set of all bitstrings of length n.
Parametricity also connects the relator with probabilities of events. Recall that  denotes the probability of event A under the spmf p. The rule
denotes the probability of event A under the spmf p. The rule


follows directly from parametricity of  , namely
, namely


Here, the relator  treats sets as predicates, i.e.,
treats sets as predicates, i.e., 
 for all
for all  , and
, and  is the identity relation on real numbers.
is the identity relation on real numbers.
For example, this rule plays an important role in Bellare’s and Rogaway’s fundamental lemma [16]. Lacking syntax, we cannot express their syntactic condition in HOL. Borrowing ideas from EasyCrypt [13], we instead rephrase the condition in terms of the relator.
Lemma 2
(Fundamental lemma [13, 16]). Let A,  and B,
and B,  be events of two spmfs p and q, respectively, such that
be events of two spmfs p and q, respectively, such that


Then, the probability difference between A occurring in p and B in q is bounded by the probability of  in p, which equals
in p, which equals  ’s in q.
’s in q.


Optimistic sampling and the fundamental lemma have illustrated how cryptographic arguments follow from parametricity. But parametricity offers yet another point of view. Mitchell [40] uses parametricity to express representation independence, i.e., one can change the representation of data without affecting the overall result. In Sect. 3.4, we will exploit representation independence in the bridging steps of the game transformations.
The Fixpoint Combinator We have not yet covered one important building block of our probabilistic language in our analysis: the fixpoint combinator on spmfs. It turns out that it preserves parametricity.Footnote 3
Theorem 1
(Parametricity of spmf fixpoints).
If  and
and  are monotone w.r.t.
are monotone w.r.t.  and
and  , then
, then  .
.
To avoid higher-kinded types, the theorem generalises parametricity to the preservation of relatedness. In the typical use case, f and g are instances of the same polymorphic function.
We prove Theorem 1 by parallel induction on the two fixpoints. Both inductive cases are trivial. The base case requires  to be strict, i.e., it relates the least elements, which holds trivially. The step case is precisely the relatedness condition of f and g which the theorem assumes. The hard part consists of showing that parallel induction is a valid proof principle. To that end, we must show that
to be strict, i.e., it relates the least elements, which holds trivially. The step case is precisely the relatedness condition of f and g which the theorem assumes. The hard part consists of showing that parallel induction is a valid proof principle. To that end, we must show that  is admissible. A relation
is admissible. A relation  is admissible w.r.t. two ccpos iff for any chain
is admissible w.r.t. two ccpos iff for any chain  of pairs in the product ccpo (the ordering is component-wise), R relates the component-wise lubs of Y.
of pairs in the product ccpo (the ordering is component-wise), R relates the component-wise lubs of Y.
Proposition 2
 is admissible.
is admissible.
Proof
We exploit the characterisation of  in terms of
in terms of  . We must show
. We must show  for all chains Y of pairs in
for all chains Y of pairs in  . By the characterisation (Lemma 1), this holds by the following reasoning. The first and last step exploit that the lub commutes with
. By the characterisation (Lemma 1), this holds by the following reasoning. The first and last step exploit that the lub commutes with  , and the inequality follows from monotonicity of
, and the inequality follows from monotonicity of  and the characterisation of
and the characterisation of  for elements of the chain.
for elements of the chain.


Note that it is not clear how to prove admissibility via the characterisation in terms of joint spmfs. The issue is that the joint spmfs for the pairs in the chain need not form a chain themselves. So we cannot construct the joint spmf for the lubs as the lub of the joint spmfs.
Admissibility of relators is preserved by the function space (ordered point-wise) and products (ordered component-wise). Thus, analogues to Theorem 1 hold for fixpoints over  , etc. They are useful to show parametricity of (mutually) recursive probabilistic functions (Sect. 3.3) rather than recursively defined spmfs.
, etc. They are useful to show parametricity of (mutually) recursive probabilistic functions (Sect. 3.3) rather than recursively defined spmfs.
2.5 Security of Elgamal Encryption
We are now ready to prove Elgamal encryption (Sect. 2.1) IND-CPA secure under the decisional Diffie-Hellman (DDH) assumption. The security theorem bounds the IND-CPA advantage by the DDH advantage. For Elgamal, we prove


where the reduction  transforms an IND-CPA adversary into a DDH adversary as shown in Fig. 3.
transforms an IND-CPA adversary into a DDH adversary as shown in Fig. 3.
The proof consists of two steps. First, observe that 
 , because after the definitions have been unfolded, both sides are the same except for associativity and commutativity of
, because after the definitions have been unfolded, both sides are the same except for associativity and commutativity of  and the group law
and the group law  . Second, we show that
. Second, we show that  . Note that the message m is independent of
. Note that the message m is independent of  , which is sampled uniformly. Multiplication with a fixed group element m is a bijection on the carrier. By (4), we can omit the multiplication and the guess b’ becomes independent of b. Hence, the adversary has to guess a random bit, which is equivalent to flipping a coin.
, which is sampled uniformly. Multiplication with a fixed group element m is a bijection on the carrier. By (4), we can omit the multiplication and the guess b’ becomes independent of b. Hence, the adversary has to guess a random bit, which is equivalent to flipping a coin.
Formally, the second proof is broken up into three step. First, we rewrite the game using the identities about  , and
, and  such that we can apply (4) on the multiplication. Second, we rewrite the resulting game such that we can apply (4) once more on the equality test. Finally, we show that the irrelevant assignments cancel out. This holds even if the adversary is not lossless thanks to the surrounding
such that we can apply (4) on the multiplication. Second, we rewrite the resulting game such that we can apply (4) once more on the equality test. Finally, we show that the irrelevant assignments cancel out. This holds even if the adversary is not lossless thanks to the surrounding  . Thus, our statement does not need any technical side condition like losslessness of the adversary in CertiCrypt [14] and EasyCrypt [13].
. Thus, our statement does not need any technical side condition like losslessness of the adversary in CertiCrypt [14] and EasyCrypt [13].
Modules. Note that the definition of IND-CPA security does not depend on the Elgamal encryption scheme. In the formalisation, we abstract over the encryption scheme using Isabelle’s module system [11]. Like an ML-style functor, the IND-CPA module takes an encryption scheme and specialises the definitions of game and advantage and the proven theorems to the scheme. Similarly, the DDH assumption has its own module which takes the group as argument. This allows to reuse security definitions and cryptographic algorithms in different contexts. For Elgamal, we import the DDH module for the given group and the IND-CPA module for the Elgamal encryption scheme.
3 Adversaries with Oracle Access
In many security games, the adversary is granted black-box access to oracles. An oracle is a probabilistic function which maintains mutable state across different invocations, but the adversary must not get access to this state. In this section, we propose a new semantic domain for probabilistic functions with oracle access (Sect. 3.2). Like in Sect. 2.4, we derive reasoning rules from parametricity and explore the connection to bisimulations (Sect. 3.3). We motivate and illustrate the key features by formalising a hashed version of Elgamal encryption (HEG) in the random oracle model (ROM) [15] (Sect. 3.1) and verifying its security under the computational Diffie-Hellman (CDH) assumption (Sect. 3.4).
3.1 Example: Hashed Elgamal Encryption
Elgamal’s encryption scheme from Sect. 2.1 requires messages to be group elements, but often bitstrings of a given length are more convenient. Therefore, we consider a version of Elgamal encryption where a hash function H converts group elements into bitstring [48]. We model the hash function as a random oracle, which acts like a random function. In detail, we replace the multiplication with the group element  in Fig. 1a with the xor of its hash h; Fig. 4a shows the resulting encryption algorithm. The encryption algorithm obtains the hash by calling the oracle with a random group element.
in Fig. 1a with the xor of its hash h; Fig. 4a shows the resulting encryption algorithm. The encryption algorithm obtains the hash by calling the oracle with a random group element.
In Sect. 3.4, we prove that HEG is IND-CPA secure under the computational Diffie Hellman (CDH) assumption. For now, we explain how the formalisation changes. Figure 4c shows the new game for chosen plaintext attacks where the key generation algorithm, the encryption function and the adversary have access to an oracle. In comparison to Fig. 1c, the monad has changed: the game uses the new monad of generative probabilistic values (gpv) rather than spmf; see Sect. 3.2 for details. Accordingly, the coin flips  are embedded with the monad homomorphism
are embedded with the monad homomorphism  .
.
In one step of the security proof, we will have to keep track of the calls that the adversary has made. This is achieved by using the oracle transformation  in Fig. 4b. It forwards all calls x and records them in its local state X.
in Fig. 4b. It forwards all calls x and records them in its local state X.
As before, all these definitions live in different modules that abstract over the encryption scheme, group, and oracle. In fact, the programs in Fig. 4 are completely independent of the concrete oracle. We compose the game with the oracle only when we define the advantage. Thus, it now depends on an oracle  with initial state
with initial state  . Here,
. Here,  binds the oracle calls in
binds the oracle calls in  to the oracle
to the oracle  . It thus reduces a program with oracle access to one without, i.e., a spmf.
. It thus reduces a program with oracle access to one without, i.e., a spmf.
3.2 Generative Probabilistic Values
The example from the previous section determines a wish list of features for the language of probabilistic programs with oracle access: assertions and failure handling, calls to unspecified oracles, embedding of probabilistic programs without oracle access, and composition operators. In this section, we propose a semantic domain for probabilistic computations with oracle access and show how to express the above features in this domain.
We start by discussing why spmfs do not suffice. In our probabilistic language of spmfs, we can model an oracle as a function of type  , which takes a state and the arguments of the call and returns a subprobability distribution over the output and the new state. Unfortunately, we cannot model the adversary as a probabilistic program parametrised over the oracle and its initial state. Suppose we do. Then, its type has the shape
, which takes a state and the arguments of the call and returns a subprobability distribution over the output and the new state. Unfortunately, we cannot model the adversary as a probabilistic program parametrised over the oracle and its initial state. Suppose we do. Then, its type has the shape  . To hide the oracle state from the adversary despite passing it as an argument, we could require that the adversary be parametric in
. To hide the oracle state from the adversary despite passing it as an argument, we could require that the adversary be parametric in  . This expresses that the adversary behaves uniformly for all states, so it cannot inspect the state. Yet, we must also ensure that the adversary uses the state only linearly, i.e., it does not call the oracle twice with the same state. As we are not aware of a semantic characterisation of linearity, we cannot model the adversary like this.
. This expresses that the adversary behaves uniformly for all states, so it cannot inspect the state. Yet, we must also ensure that the adversary uses the state only linearly, i.e., it does not call the oracle twice with the same state. As we are not aware of a semantic characterisation of linearity, we cannot model the adversary like this.
Instead, we explicitly model the interactions between the adversary and the oracle. To that end, we propose the following algebraic codatatype of generative probabilistic values (gpv):Footnote 4


Conceptually, a gpv is a probabilistic system in which each state chooses probabilistically between failing, terminating with a result of type  , and continuing by producing an output
, and continuing by producing an output  and transitioning into a reactive probabilistic value (rpv), which waits for a non-deterministic response of the environment (e.g., the oracle) of type
and transitioning into a reactive probabilistic value (rpv), which waits for a non-deterministic response of the environment (e.g., the oracle) of type  . Upon reception, the rpv transitions to the generative successor state.
. Upon reception, the rpv transitions to the generative successor state.
As we are interested in a shallow embedding, the type  only models the observations (termination with result or failure and interaction with the environment) of the system rather than the whole system with the states. This yields a richer equational theory, i.e., we can prove more properties by rewriting without resorting to bisimulation arguments. Any probabilistic system with explicit states can be transformed into a gpv by identifying bisimilar states. The coiterator
only models the observations (termination with result or failure and interaction with the environment) of the system rather than the whole system with the states. This yields a richer equational theory, i.e., we can prove more properties by rewriting without resorting to bisimulation arguments. Any probabilistic system with explicit states can be transformed into a gpv by identifying bisimilar states. The coiterator  formalises this: given a probabilistic system and an initial state, it constructs the corresponding gpv.
formalises this: given a probabilistic system and an initial state, it constructs the corresponding gpv.
Basic Operations. The basic operations for gpv are the monadic functions  and
and  , calling an oracle
, calling an oracle  , sampling
, sampling  , exceptional termination
, exceptional termination  (from which we derive assertions
(from which we derive assertions  ) and failure handling
) and failure handling  . They can be implemented as shown in Fig. 5, where
. They can be implemented as shown in Fig. 5, where  and
and  and
and  is the identity and
is the identity and  the inverse of
the inverse of  . Note that
. Note that  and
and  can be defined by primitive corecursion.
can be defined by primitive corecursion.
The operations behave as expected. In particular,  and
and  satisfy the monad laws,
satisfy the monad laws,  propagates, and
propagates, and  is a monad homomorphism.
is a monad homomorphism.


The resulting equational theory is rich again, but not as rich as for spmfs. Commutativity (1) and cancellation (2), e.g., do not carry over to  in general.
in general.
Composition Operators. Two gpvs can be composed such that one (the callee) processes all the calls of the other (the caller). Thereby, the callee may issue further calls. In games, composition is mainly used to intercept and redirect the oracle calls of the adversary, i.e., the callee is an oracle transformation like  . Syntactically, composition corresponds to inlining the callee into the caller. If programs were modelled syntactically, implementing inlining would be trivial; but with a shallow approach, we cannot rely on syntax.
. Syntactically, composition corresponds to inlining the callee into the caller. If programs were modelled syntactically, implementing inlining would be trivial; but with a shallow approach, we cannot rely on syntax.


Instead, we define inlining by a combination of recursion and corecursion as shown in Fig. 6. The sequence diagram on the right illustrates what is happening in an example. The caller v issues calls of type  which return values of type
which return values of type  . The callee c is a function from
. The callee c is a function from  to a gpv which may issue further calls of type
to a gpv which may issue further calls of type  which return values of type
which return values of type  . The callee maintains its own state of type
. The callee maintains its own state of type  between invocations. Therefore, like oracles, the callee additionally takes a state as argument and the results of the gpv are the return values and the new states. The function
between invocations. Therefore, like oracles, the callee additionally takes a state as argument and the results of the gpv are the return values and the new states. The function  first calls the auxiliary function
first calls the auxiliary function  , which searches for the first call issued by the callee during a call by the caller. If
, which searches for the first call issued by the callee during a call by the caller. If  finds none, it returns the result x of the caller and the updated state \(s^{\prime }\) of the callee. Then,
finds none, it returns the result x of the caller and the updated state \(s^{\prime }\) of the callee. Then,  terminates with the same outcome. Otherwise,
terminates with the same outcome. Otherwise,  issues the call u and forwards the return value w to the rpv \(r^{\prime }\) of the callee, which may issue further calls (
issues the call u and forwards the return value w to the rpv \(r^{\prime }\) of the callee, which may issue further calls ( in the diagram). The result b of the callee is then fed to the rpv r of the caller and
in the diagram). The result b of the callee is then fed to the rpv r of the caller and  corecurses with the updated state \(s^{\prime }\) of the callee.
corecurses with the updated state \(s^{\prime }\) of the callee.
The function  recursively goes through the interactions between the caller and the callee. If the caller terminates with result x, there are no calls and the search terminates. Otherwise, the caller issues a call a and becomes the rpv r. In that case,
recursively goes through the interactions between the caller and the callee. If the caller terminates with result x, there are no calls and the search terminates. Otherwise, the caller issues a call a and becomes the rpv r. In that case,  analyses the callee under the argument a. If the callee returns b without issuing a call itself, the search continues recursively on r b. Otherwise, the first call is found and the search terminates.
analyses the callee under the argument a. If the callee returns b without issuing a call itself, the search continues recursively on r b. Otherwise, the first call is found and the search terminates.
Note that  operates in the spmf monad. So, it can be defined using the fixpoint operator on spmf (Sect. 2.3). Conversely,
operates in the spmf monad. So, it can be defined using the fixpoint operator on spmf (Sect. 2.3). Conversely,  operates in the gpv monad. So, corecursion is the appropriate definition principle. Accordingly, we prove properties about
operates in the gpv monad. So, corecursion is the appropriate definition principle. Accordingly, we prove properties about  by fixpoint induction and about
by fixpoint induction and about  by coinduction. For example, we show that
by coinduction. For example, we show that  is a monad homomorphism. It is also associative (we omit reassociations of tuples for clarity;
is a monad homomorphism. It is also associative (we omit reassociations of tuples for clarity;  denotes
denotes  :
:


If the callee is an oracle  , i.e., an spmf rather than a gpv, it cannot issue further calls. Thus,
, i.e., an spmf rather than a gpv, it cannot issue further calls. Thus,  always returns a result of the form
always returns a result of the form  , i.e., the corecursion in
, i.e., the corecursion in  is not needed. Therefore, we define the execution of a gpv v with
is not needed. Therefore, we define the execution of a gpv v with  as follows (where
as follows (where  is the left inverse to
is the left inverse to  ).
).


When  ’s final state does not matter, we use
’s final state does not matter, we use  .
.
Reductions are the primary use case for composition. They transform the adversary  for one game into an adversary for another game. In general, the oracles of the two games differ. So, the reduction emulates the original oracle
for one game into an adversary for another game. In general, the oracles of the two games differ. So, the reduction emulates the original oracle  using an oracle transformation T, which has access to the new oracle
using an oracle transformation T, which has access to the new oracle  . In this view, the new adversary is built from the composition
. In this view, the new adversary is built from the composition  and the cryptographic assumption executes it with access to
and the cryptographic assumption executes it with access to  . By associativity of composition (see Fig. 7), this is equivalent to executing the original adversary
. By associativity of composition (see Fig. 7), this is equivalent to executing the original adversary  with access to the emulated oracle
with access to the emulated oracle  . Thus, it suffices to establish that the emulation
. Thus, it suffices to establish that the emulation  of
of  is good enough.
is good enough.
3.3 Parametricity and Bisimulation
Our framework provides a set of rules (a logic) for reasoning about the relation between games with oracles. This logic complements the equational theory derived from the shallow embedding. Like for spmf, parametricity guides us in choosing the rules and proving them sound. As the first step, we therefore define a relator  for gpvs. As gpvs form a codatatype, the canonical definition is as a coinductive relation, namely the one specified by (5).Footnote 5
for gpvs. As gpvs form a codatatype, the canonical definition is as a coinductive relation, namely the one specified by (5).Footnote 5


Canonicity ensures parametricity of the coiterator  , the constructor
, the constructor  , and the selector
, and the selector  . For
. For  , e.g., we obtain that for all S, A, and C,
, e.g., we obtain that for all S, A, and C,


Consequently, all the primitive operations in Fig. 5 are parametric, too. As the fixpoint operator preserves parametricity (Theorem 1),  is also parametric. And so are
is also parametric. And so are  and
and  and
and  . Thus, parametricity links
. Thus, parametricity links  with all the gpv operations.
with all the gpv operations.
Similar to spmfs (Sect. 2.4), this link leads to rules for reasoning about game transformations. We do not go into the details here. Instead, we consider the example of replacing an oracle with a bisimilar one as formalised by (6). This rule follows from the parametricity of  by unfolding the definitions.Footnote 6 The premises express that S is a bisimulation relation between the oracles
by unfolding the definitions.Footnote 6 The premises express that S is a bisimulation relation between the oracles  and
and  and relates their initial states. Bisimulation means that whenever two states
and relates their initial states. Bisimulation means that whenever two states  and
and  are related and the oracles are called with c, then they return the same value and the states are related again. The “then” part is expressed by the relation
are related and the oracles are called with c, then they return the same value and the states are related again. The “then” part is expressed by the relation  which
which  lifts to subprobability distributions. The second premise states that S relates the initial states. In the conclusion, we get that running a gpv v (e.g., the adversary) with two bisimilar oracles produces the same outcomes.
lifts to subprobability distributions. The second premise states that S relates the initial states. In the conclusion, we get that running a gpv v (e.g., the adversary) with two bisimilar oracles produces the same outcomes.


In fact, the derivation may be seen as an instance of representation independence [40, 44]. By design, the gpv has only black-box access to the oracle, i.e., they interface only via calls and returns. Thus, the first premise expresses exactly the requirement of representation independence: a relation S that is preserved by all operations of the interface. In Isabelle [31], so-called transfer rules express preservation in point-free style; here,  . The HEG example exploits this idea in two game transformations (Sect. 3.4).
. The HEG example exploits this idea in two game transformations (Sect. 3.4).
There are also limits to what we can derive from parametricity. For example, consider the case where only one of the oracles enters an error state, say because the adversary has guessed a secret. Then, the adversary can distinguish between the oracles and behave differently, i.e., it is not related by  any more. Therefore, we would need a notion of bisimulation up to error, but relational parametricity cannot express this. Thus, we prove the Lemma 3 directly.
any more. Therefore, we would need a notion of bisimulation up to error, but relational parametricity cannot express this. Thus, we prove the Lemma 3 directly.
Lemma 3
(Oracle bisimulation up to error states). Let S be a relation between the states of two oracles  and
and  and let
and let  and
and  be the sets of error states. Define the relation R by
be the sets of error states. Define the relation R by  iff
iff  and if
and if  then x = y and
then x = y and  . Then
. Then  if
if
-
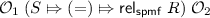 , and
, and -
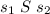 and
and  , and
, and -
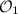 and
and 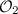 are lossless in error states and error states are never left, and
are lossless in error states and error states are never left, and -
v issues finitely many calls and never fails, i.e., all spmfs in v are lossless.
3.4 Security of Hashed Elgamal Encryption
Now, we illustrate how our framework supports proofs about games with oracles by reducing the IND-CPA security of Hashed Elgamal encryption to the computational Diffie-Hellman (CDH) assumption. The CDH assumption states that it is hard to compute  given
given  and
and  . For comparison with the existing proofs in Certicrypt [14] and EasyCrypt [13] (Sect. 4), we reduce the security to the set version LCDH of CDH, where the adversary may return a finite set of candidates for
. For comparison with the existing proofs in Certicrypt [14] and EasyCrypt [13] (Sect. 4), we reduce the security to the set version LCDH of CDH, where the adversary may return a finite set of candidates for  . The reduction from LCDH to CDH is straightforward.
. The reduction from LCDH to CDH is straightforward.
LCDH is formalised as follows. The LCDH adversary  is a probabilistic function from two group elements to a set of group elements. Its advantage
is a probabilistic function from two group elements to a set of group elements. Its advantage  is the probability of
is the probability of  in the security game
in the security game  shown in Fig. 8.
shown in Fig. 8.
In the random oracle model [15], hash functions are idealised as random functions. The random oracle  shown in Fig. 9 implements such a random function. Its state
shown in Fig. 9 implements such a random function. Its state  is a map from group elements (inputs) to bitstrings (outputs), which associates previous queries with the outputs. Upon each call, the oracle looks up the input x in the map
is a map from group elements (inputs) to bitstrings (outputs), which associates previous queries with the outputs. Upon each call, the oracle looks up the input x in the map  and returns the corresponding output if found. If not, it returns a fresh bitstring bs of length n and updates the map
and returns the corresponding output if found. If not, it returns a fresh bitstring bs of length n and updates the map  to associate x with bs.
to associate x with bs.
The security of HEG is shown by a sequence of game transformations. They closely follow [13], so we do not present them in detail here. Instead, we focus on some steps to highlight the use of parametricity, equational reasoning, and the program logic. In the following, we assume a fixed IND-CPA adversary  which makes only finitely many calls and does not fail. This technical restriction is necessary to apply Lemma 3.
which makes only finitely many calls and does not fail. This technical restriction is necessary to apply Lemma 3.
The first step changes the game such that it records the adversary’s queries to the hash oracle using the oracle transformation  from Fig. 4b. So the first game
from Fig. 4b. So the first game  is the same as
is the same as  from Fig. 4c except that the calls to the adversary are replaced by
from Fig. 4c except that the calls to the adversary are replaced by  and
and  . The equality
. The equality  follows from parametricity and bisimilarity of
follows from parametricity and bisimilarity of  and the identity oracle transformation
and the identity oracle transformation  due to representation independence, and the fact that
due to representation independence, and the fact that  is the identity for gpv composition. The bisimulation relation
is the identity for gpv composition. The bisimulation relation  identifies all states. The equality is proven automatically by Isabelle’s prover for representation independence [31] using the transfer rules
identifies all states. The equality is proven automatically by Isabelle’s prover for representation independence [31] using the transfer rules  and
and  and equational rewriting. In fact, the latter rule is another instance of representation independence, as the two oracle transformations differ only in the update of the local state. The transfer rule
and equational rewriting. In fact, the latter rule is another instance of representation independence, as the two oracle transformations differ only in the update of the local state. The transfer rule  formalises the connection. The parametricity prover derives the transfer rule for the oracles from this.
formalises the connection. The parametricity prover derives the transfer rule for the oracles from this.
In the second step, we push the oracle transformation into the oracle exploiting associativity (cf. Fig. 7) and distribute the outermost  to the calls of the adversary. This changes the monad from gpv to spmf, in which
to the calls of the adversary. This changes the monad from gpv to spmf, in which  commutes (1). Additionally, the new game
commutes (1). Additionally, the new game  returns a second boolean to flag whether the adversary caused a call to the hash oracle with the group element
returns a second boolean to flag whether the adversary caused a call to the hash oracle with the group element  . By equational reasoning only, we prove that
. By equational reasoning only, we prove that  where the hash oracle starts in the initial state
where the hash oracle starts in the initial state  .
.
The third transformation replaces the hash for the challenge ciphertext with a random bitstring which is not recorded in the hash oracle’s map. By the fundamental lemma, the difference in the success probabilities is bounded by the error event, which is in this case the flag introduced in  . The assumption of the fundamental lemma is proven using the rules of the program logic. In particular, we apply Lemma 3 on the call to
. The assumption of the fundamental lemma is proven using the rules of the program logic. In particular, we apply Lemma 3 on the call to  , as the oracles are not bisimilar if any of the remaining queries calls the hash function on
, as the oracles are not bisimilar if any of the remaining queries calls the hash function on  .
.
We do not go into the details of the remainder of the proof, as it applies the same techniques as before. The one time pad lemma is used to make the challenge ciphertext independent of the challenge bit b similar to optimistic sampling in Sect. 2.5. As the set of queries now is just the domain of the map of the hash oracle, we replace  with
with  using representation independence. Finally, we show by equational reasoning that the first boolean of the game is just a coin flip and the second corresponds to the LCDH game for the transformed adversary
using representation independence. Finally, we show by equational reasoning that the first boolean of the game is just a coin flip and the second corresponds to the LCDH game for the transformed adversary  (see Fig. 10).Footnote 7 In summary, we obtain
(see Fig. 10).Footnote 7 In summary, we obtain


4 Comparison with Existing Frameworks
In this section, we compare our framework with the existing tools CertiCrypt [14], EasyCrypt [13], FCF [42], and Verypto [8] in four respects: readability, expressiveness, the trusted codebase, and the formalisation effort.
Readability is important for two reasons. First, security definitions should resemble those in the cryptographic literature such that cryptographers are able to understand and evaluate them. Second, intuitive syntax supports the users during the formalisation, as they can focus on formalising the arguments rather than trying to understand hardly readable programs. All frameworks achieve good readability, but in different ways. CertiCrypt and EasyCrypt embed an imperative procedural language in their logics. They closely model Bellare’s and Rogaway’s idea of a stateful language with oracles as procedures [16]. Verypto deeply embeds a higher order language with mutable references based on de Bruijn indices in HOL. Readability is regained by reflecting the syntax in HOL’s term language using parsing and pretty-printing tricks. In contrast, FCF and our framework shallowly embed a functional language with monadic sequencing in Coq and Isabelle/HOL, respectively. Like in Shoup’s treatment [48], the state of the adversary and the oracles must be passed explicitly. This improves clarity as it makes explicit which party can access which parts of the state. Conversely, it can also be a source for errors, as it is the user who must ensure that the states be used linearly.
Expressiveness has two dimensions. First, the syntax and the semantic domain determine the expressiveness of the language. CertiCrypt and EasyCrypt support discrete subprobability distributions and a procedural while language, but no fixpoint operator, although fixpoints could be defined in CertiCrypt’s semantic domain similar to our work (Sect. 2.3 and Theorem 1). Fixpoints do not increase the expressiveness over a while combinator, but lead to more natural formulations of programs. EasyCrypt additionally provides a module system to support abstraction and reuse. Verypto is the most general framework, as it builds on measure theory and therefore supports continuous distributions and higher order functions—at the price of incurring measurability proof obligations. FCF’s semantics allows only probability distributions with finite support, so no fixpoint operator can be defined. The syntax further restricts probabilistic effects to random sampling of bitstrings and conditional probabilities. For programs with oracle access, FCF provides equivalents to our operations  , and
, and  . Further effectful operators (such as
. Further effectful operators (such as  cannot be added by the user, but require changes to the language formalisation itself. Conversely, FCF’s deterministic pure sublanguage includes all functions and types from the library of the proof assistant thanks to the shallow embedding. Abstraction and reuse come from Coq’s module system. Like FCF, our framework is integrated with the libraries and facilities of the proof assistant. It extends this advantage to probabilistic programs with oracle access, as we define also these languages directly in the semantic domain. Thus, users can define new control structures on the spot, if needed. It supports discrete subprobabilities similar to CertiCrypt and EasyCrypt and in addition features a fixpoint operator.
cannot be added by the user, but require changes to the language formalisation itself. Conversely, FCF’s deterministic pure sublanguage includes all functions and types from the library of the proof assistant thanks to the shallow embedding. Abstraction and reuse come from Coq’s module system. Like FCF, our framework is integrated with the libraries and facilities of the proof assistant. It extends this advantage to probabilistic programs with oracle access, as we define also these languages directly in the semantic domain. Thus, users can define new control structures on the spot, if needed. It supports discrete subprobabilities similar to CertiCrypt and EasyCrypt and in addition features a fixpoint operator.
Second, the embedding and the logic determine what kind of security properties can be formalised. All frameworks support concrete security proofs. Thanks to the deep embedding, CertiCrypt and Verypto also support statements about efficiency and thus asymptotic security statements, which is impossible in EasyCrypt and ours, because HOL functions are extensional. FCF comes with an axiomatic cost model for efficiency, which is not formally connected to an operational model. This is possible despite the shallow embedding as long as extensionality is not assumed. In these three frameworks, asymptotic bounds are derived from concrete bounds. So no work is saved by reasoning asymptotically.
The trusted code base influences the trustworthiness of a mechanised proof and should be as small as possible. Proof assistants like Coq and Isabelle consist of a small kernel and can additionally produce proof terms or proof objects that an independent checker can certify. Consequently, CertiCrypt, FCF, and our framework achieve high ranks there. Verypto falls behind because its measure theory is only axiomatized rather than constructed definitionally. EasyCrypt does not have a small kernel, so the whole implementation in OCaml and the external SMT solvers must be trusted.
The formalisation effort determines the usability of a framework. For this comparison, we estimate the effort by the proof length measured in line counts. Clearly, proof styles affect line counts, so the numbers must be taken with a grain of salt. Nevertheless, they roughly indicate the effort required to produce such proofs. Table 1 lists the length (in lines) of the security statement for different cryptographic algorithms and frameworks. The line count includes the statement of the concrete security theorem, its proof, and all intermediate games. It does not cover the cryptographic algorithm itself nor the security definition. We obtained the numbers by inspecting the proof scripts distributed with the frameworks. Unfortunately, there are no line counts for Verypto because we could not get access to the sources.
As Petcher and Morrisett have already observed [43], shallow embeddings (FCF, ours) have an advantage over deep ones (CertiCrypt, Verypto), as all the reasoning infrastructure and libraries of the proof assistant can be reused directly; a deep embedding would need to encode the libraries in the syntax of the language. Despite being more general, our framework leads to shorter proofs than FCF. We see two reasons for this gap. First, our language works directly in the semantic domain, even for effectful programs. This gives a richer equational theory and all conversions between syntax and semantics become superfluous. For example, their rule for loop fission holds only in the relational logic, but it is a HOL equality in our model. Second, Isabelle’s built-in proof automation, in particularly conditional rewriting, provides a reasonable level of automation, especially for the equational proofs mentioned above. So far, we have not yet implemented any problem-specific proof tactics. Such tactics could automate the proofs even more, especially the manual reasoning with commutativity of sequencing. In comparison to EasyCrypt, the state of the art in proof automation, we achieve a similar degree of automation.
5 Further Related Work
In Sect. 4, we have already compared our framework with the existing ones for mechanising game playing proofs. In this section, we review further related work.
The tool CryptoVerif by Blanchet [20] can prove secrecy and correspondence properties such as authentication of security protocols. As it can even discover intermediate games itself, the tool achieves a much higher degree of automation than any of the frameworks including ours. The language—a process calculus inspired by the \(\pi \) calculus—distinguishes between a unique output process and possibly many input processes, which communicate via channels. Our gpvs also distinguish between inputs and outputs, but composition works differently. In CryptoVerif, several input processes may be able to receive an output and the semantics picks one uniformly randomly. In our setting, the callee represents all input processes and receives all calls. In principle, one could embed Blanchet’s calculus in our semantic domain of gpvs using a different composition operator. Then, CryptoVerif’s abstractions could be proven sound in our framework.
The functional programming language F\(^*\) [17, 49] has been used to verify implementations of cryptographic algorithms and protocols [12]. Security properties are formulated as type safety of an annotated, dependently-typed program and the type checker ensures type safety. While this approach scales to larger applications [18], the security properties cannot be stated concisely as the typing assertions are scattered over the whole implementation.
Affeldt et al. [2] formalise pmfs in Coq and apply this to coding theory.
Audebaud and Paulin-Mohring [5] formalised the spmf monad in Coq. They also define the approximation order  on spmfs and show that it forms an \(\omega \)-complete partial order, i.e., countable chains have least upper bounds. Using Kleene’s fixpoint theorem, they obtain a fixpoint operator for continuous functions. We generalise their result in that arbitrary spmf chains have least upper bounds. Thus, monotonicity (rather than continuity) suffices for the fixpoints.
on spmfs and show that it forms an \(\omega \)-complete partial order, i.e., countable chains have least upper bounds. Using Kleene’s fixpoint theorem, they obtain a fixpoint operator for continuous functions. We generalise their result in that arbitrary spmf chains have least upper bounds. Thus, monotonicity (rather than continuity) suffices for the fixpoints.
CertiCrypt [14] uses their monad as the semantic domain for programs and adds the lifting operator  . Zanella Béguelin proves a special case of Theorem 1, where the functions f and g are projections of a joint continuous function [51].
. Zanella Béguelin proves a special case of Theorem 1, where the functions f and g are projections of a joint continuous function [51].
Cock [24] develops a shallow embedding of a probabilistic guarded command language in HOL. Programs are interpreted as monotone transformers of bounded expectations, which form a complete lattice. So, recursive functions can be defined using fixpoints. He focuses on proving functional correctness properties using non-relational Hoare triples and verification conditions.
Our framework reuses the existing infrastructure for relational parametricity in Isabelle/HOL, but in new ways. The Lifting package [31] exploits representation independence to transfer theorems between raw types and their quotients or subtypes. Lammich’s tool AutoRef [35] uses transfer rules to refine abstract datatypes and algorithms to executable code. Blanchette et al. [23] use parametricity to express well-formedness conditions for operators under which corecursion may appear in corecursive functions. In contrast, we derive a relational logic for reasoning about shallowly embedded programs from parametricity and apply representation independence to replace oracles in games by bisimilar ones.
6 Conclusion and Future Work
In this paper, we have integrated a language for monadic probabilistic functions with black-box access to oracles in higher order logic. Several examples demonstrate that cryptographic algorithms and security definitions can be expressed in this language. A rich equational theory and a relational logic support the formalisation of cryptographic arguments. The definitions and proofs have been mechanised using the proof assistant Isabelle/HOL.
Although our logic is similar to those in FCF and EasyCrypt, our approach is different: we derive the rules in a principled way from parametricity of the operators. This approach can help in finding the appropriate rules when new operations are introduced, and in proving them sound. Petcher and Morrisett, e.g., add a monadic map operation to FCF’s language and an appropriate reasoning rule to their logic [43]. They show soundness for the rule by induction, which takes 22 proof steps. In our approach, their rule is an instance of parametricity of the map operator, which Isabelle’s parametricity prover can establish automatically.
This work is motivated by the goal of formalising computational soundness results. Whether our framework scales to such large applications is still an open question. In our cryptographic examples, it compares favourably to the state of the art. Indeed, our initial attempts in formalising the CoSP framework [9] are encouraging that our approach will work. Therefore, the next steps will focus on formalising these results and improving proof automation.
Our framework cannot express efficiency notions such as polynomial runtime yet. Hence, asymptotic reasoning, which dominates in CS proofs, can be used only in limited ways. This is the flipside of the shallow embedding: As HOL functions are extensional, we cannot exploit HOL syntax in the reasoning. It seems possible to adapt Petcher’s and Morrisett’s axiomatic cost model [42], but the benefits are not yet clear. A less axiomatic alternative is to formalise a small programming language, connect it to HOL’s functions and derive the bounds in terms of the operational semantics. Verypto [8] and the higher-order complexity analysis for Coq by Jouannaud and Xu [33] might be good starting points.
Beyond cryptographic arguments and computational soundness, our semantic domain of generative probabilistic values could be applied in different contexts. In previous work [38], we used a (less abstract) precursor to model interactive programs in HOL. The domain could also serve as a basis for formalising and verifying CryptoVerif or as a backend for the new EasyCrypt, as EasyCrypt’s logic and module system resemble Isabelle’s.
In this direction, it would be interesting to investigate whether gpvs admit a ccpo structure in which where the basic operations are monotone. Currently, corecursion and coinduction are available. The ccpo structure would allow us to additionally define functions recursively and use induction as proof principle. The problem is that limits must preserve discreteness of the subprobability distributions. It is not easy to move to arbitrary measure-theoretic distributions, as codatatypes in HOL require a cardinality bound on the functor through which they recurse; otherwise, they cannot be defined in HOL [28].
Notes
- 1.
In the formalisation, we construct the type
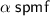 by combining the existing monad for probability mass functions [30] with an exception monad. This way, most of our primitive operations can be defined in terms of the primitive operations of the two monads. Hence, we can derive many of their properties, in particular parametricity (Sect. 2.4), from the latter’s.
by combining the existing monad for probability mass functions [30] with an exception monad. This way, most of our primitive operations can be defined in terms of the primitive operations of the two monads. Hence, we can derive many of their properties, in particular parametricity (Sect. 2.4), from the latter’s. - 2.
As our embedding is shallow, we cannot define a deduction system in the logic. Rather, we derive the rules directly from the semantics, i.e., show soundness. Completeness is therefore achieved dynamically: new rules can be derived if necessary, in particular when a new operation is introduced.
- 3.
Wadler showed that if all types are \(\omega \)-ccpos, all functions are continuous and all relations are admissible and strict, then the fixpoint operator (defined by countable iteration) is parametric [50]. We do not consider the fixpoint operator as part of the language itself, but as a definition principle for recursive user-specified functions. That is, we assume that
 is always applied to a (monotone) function. Consequently, preservation of parametricity suffices and we do not need Wadler’s restrictions of the semantic domains. Instead, monotonicity (instead of continuity, see the discussion in Sect. 2.3) is expressed as a precondition on the given functions.
is always applied to a (monotone) function. Consequently, preservation of parametricity suffices and we do not need Wadler’s restrictions of the semantic domains. Instead, monotonicity (instead of continuity, see the discussion in Sect. 2.3) is expressed as a precondition on the given functions. - 4.
- 5.
The type constructor
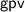 takes three type arguments, so we should expect
takes three type arguments, so we should expect  to take three relations, too. However, the third argument occurs in a negative position in the codatatype definition. Therefore, the relator does not enjoy useful properties such as monotonicity and distributivity over relation composition. Consequently, Isabelle’s infrastructure for parametricity treats these arguments as fixed (dead in the terminology of [22]). So,
to take three relations, too. However, the third argument occurs in a negative position in the codatatype definition. Therefore, the relator does not enjoy useful properties such as monotonicity and distributivity over relation composition. Consequently, Isabelle’s infrastructure for parametricity treats these arguments as fixed (dead in the terminology of [22]). So,  takes only relations for the first two arguments and fixes the third to the identity relation
takes only relations for the first two arguments and fixes the third to the identity relation  as can be seen in (5). In practice, we have not found this specialisation to be restrictive.
as can be seen in (5). In practice, we have not found this specialisation to be restrictive. - 6.
- 7.
The oracle transformation in this reduction is degenerate, as
 emulates the oracle without access to further oracles. Thus, we use
emulates the oracle without access to further oracles. Thus, we use  directly instead of
directly instead of  .
.
References
Abadi, M., Rogaway, P.: Reconciling two views of cryptography (The computational soundness of formal encryption). J. Cryptology 15(2), 103–127 (2002)
Affeldt, R., Hagiwara, M., Sénizergues, J.: Formalization of Shannon’s theorems. J. Automat. Reason. 53(1), 63–103 (2014)
Aharoni, R., Berger, E., Georgakopoulos, A., Perlstein, A., Sprüssel, P.: The max-flow min-cut theorem for countable networks. J. Combin. Theory Ser. B 101, 1–17 (2011)
Armando, A., et al.: The AVANTSSAR platform for the automated validation of trust and security of service-oriented architectures. In: Flanagan, C., König, B. (eds.) TACAS 2012. LNCS, vol. 7214, pp. 267–282. Springer, Heidelberg (2012)
Audebaud, P., Paulin-Mohring, C.: Proofs of randomized algorithms in Coq. Sci. Comput. Program. 74(8), 568–589 (2009)
Bacelar Almeida, J., Barbosa, M., Bangerter, E., Barthe, G., Krenn, S., Zanella Béguelin, S.: Full proof cryptography: verifiable compilation of efficient zero-knowledge protocols. In: CCS 2012, pp. 488–500. ACM (2012)
Backes, M., Barthe, G., Berg, M., Grégoire, B., Kunz, C., Skoruppa, M., Zanella Béguelin, S.: Verified security of Merkle-Damgård. In: CSF 2012, pp. 354–368 (2012)
Backes, M., Berg, M., Unruh, D.: A formal language for cryptographic pseudocode. In: Cervesato, I., Veith, H., Voronkov, A. (eds.) LPAR 2008. LNCS (LNAI), vol. 5330, pp. 353–376. Springer, Heidelberg (2008)
Backes, M., Hofheinz, D., Unruh, D.: CoSP: a general framework for computational soundness proofs. In: CCS 2009, pp. 66–78. ACM (2009)
Backes, M., Malik, A., Unruh, D.: Computational soundness without protocol restrictions. In: CCS 2012, pp. 699–711. ACM (2012)
Ballarin, C.: Locales: A module system for mathematical theories. J. Automat. Reason. 52(2), 123–153 (2014)
Barthe, G., Fournet, C., Grégoire, B., Strub, P.Y., Swamy, N., Zanella Béguelin, S.: Probabilistic relational verification for cryptographic implementations. In: POPL 2014, pp. 193–205. ACM (2014)
Barthe, G., Grégoire, B., Heraud, S., Béguelin, S.Z.: Computer-aided security proofs for the working cryptographer. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 71–90. Springer, Heidelberg (2011)
Barthe, G., Grégoire, B., Zanella Béguelin, S.: Formal certification of code-based cryptographic proofs. In: POPL 2009, pp. 90–101. ACM (2009)
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: CCS 1993, pp. 62–73. ACM (1993)
Bellare, M., Rogaway, P.: The security of triple encryption and a framework for code-based game-playing proofs. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 409–426. Springer, Heidelberg (2006)
Bengtson, J., Bhargavan, K., Fournet, C., Gordon, A.D., Maffeis, S.: Refinement types for secure implementations. ACM Trans. Program. Lang. Syst. 33(2), 8:1–8:45 (2011)
Bhargavan, K., Fournet, C., Kohlweiss, M., Pironti, A., Strub, P.Y.: Implementing TLS with verified cryptographic security. In: S&P 2013, pp. 445–459. IEEE (2013)
Blanchet, B.: An efficient cryptographic protocol verifier based on Prolog rules. In: CSFW 2001, pp. 82–96. IEEE (2001)
Blanchet, B.: A computationally sound mechanized prover for security protocols. IEEE Trans. Dependable Secure Comput. 5(4), 193–207 (2008)
Blanchet, B., Jaggard, A.D., Rao, J., Scedrov, A., Tsay, J.K.: Refining computationally sound mechanized proofs for Kerberos. In: FCC 2009 (2009)
Blanchette, J.C., Hölzl, J., Lochbihler, A., Panny, L., Popescu, A., Traytel, D.: Truly modular (Co)datatypes for Isabelle/HOL. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 93–110. Springer, Heidelberg (2014)
Blanchette, J.C., Popescu, A., Traytel, D.: Foundational extensible corecursion: A proof assistant perspective. In: ICFP 2015, pp. 192–204. ACM (2015)
Cock, D.: Verifying probabilistic correctness in Isabelle with pGCL. In: SSV 2012. EPTCS, vol. 102, pp. 1–10 (2012)
Cortier, V., Kremer, S., Warinschi, B.: A survey of symbolic methods in computational analysis of cryptographic systems. J. Automat. Reason. 46, 225–259 (2011)
Desharnais, J.: Labelled Markov Processes. Ph.D. thesis, McGill University (1999)
Elgamal, T.: A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theory 31(4), 469–472 (1985)
Gunter, E.L.: Why we can’t have SML-style datatype declarations in HOL. In: Claesen, L.J.M., Gordon, M.J.C. (eds.) TPHOLs 1992, pp. 561–568. Elsevier, North-Holland (1993)
Halevi, S.: A plausible approach to computer-aided cryptographic proofs. Cryptology ePrint Archive, Report 2005/181 (2005)
Hölzl, J., Lochbihler, A., Traytel, D.: A formalized hierarchy of probabilistic system types. In: Urban, C., Zhang, X. (eds.) ITP 2015. LNCS, vol. 9236, pp. 203–220. Springer, Heidelberg (2015)
Huffman, B., Kunčar, O.: Lifting and Transfer: a modular design for quotients in Isabelle/HOL. In: Gonthier, G., Norrish, M. (eds.) CPP 2013. LNCS, vol. 8307, pp. 131–146. Springer, Heidelberg (2013)
Hurd, J.: A formal approach to probabilistic termination. In: Carreño, V.A., Muñoz, C.A., Tahar, S. (eds.) TPHOLs 2002. LNCS, vol. 2410, pp. 230–245. Springer, Heidelberg (2002)
Jouannaud, J.P., Xu, W.: Automatic complexity analysis for programs extracted from Coq proof. In: CLASE 2005. ENTCS, vol. 153(1), pp. 35–53 (2006)
Krauss, A.: Recursive definitions of monadic functions. In: PAR 2010. EPTCS, vol. 43, pp. 1–13 (2010)
Lammich, P.: Automatic data refinement. In: Blazy, S., Paulin-Mohring, C., Pichardie, D. (eds.) ITP 2013. LNCS, vol. 7998, pp. 84–99. Springer, Heidelberg (2013)
Larsen, K.G., Skou, A.: Bisimulation through probabilistic testing. Inf. Comp. 94(1), 1–28 (1991)
Lochbihler, A.: Formalisation accompanying this paper. http://www.infsec.ethz.ch/research/projects/FCSPI/ESOP2016.html
Lochbihler, A., Züst, M.: Programming TLS in Isabelle/HOL. Isabelle Workshop 2014 (2014)
Meier, S., Cremers, C.J.F., Basin, D.: Efficient construction of machine-checked symbolic protocol security proofs. J. Comput. Secur. 21(1), 41–87 (2013)
Mitchell, J.C.: Representation independence and data abstraction. In: POPL 1986, pp. 263–276. ACM (1986)
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL – A Proof Assistant for Higher-Order Logic. LNCS, vol. 2283. Springer, Heidelberg (2002)
Petcher, A., Morrisett, G.: The foundational cryptography framework. In: Focardi, R., Myers, A. (eds.) POST 2015. LNCS, vol. 9036, pp. 53–72. Springer, Heidelberg (2015)
Petcher, A., Morrisett, G.: A mechanized proof of security for searchable symmetric encryption. In: CSF 2015, pp. 481–494. IEEE (2015)
Reynolds, J.C.: Types, abstraction and parametric polymorphism. In: IFIP 1983. Information Processing, vol. 83, pp. 513–523. North-Holland/IFIP (1983)
Rutten, J.J.M.M.: Relators and metric bisimulations. Electr. Notes Theor. Comput. Sci. 11, 252–258 (1998)
Sack, J., Zhang, L.: A general framework for probabilistic characterizing formulae. In: Kuncak, V., Rybalchenko, A. (eds.) VMCAI 2012. LNCS, vol. 7148, pp. 396–411. Springer, Heidelberg (2012)
Schmidt, B., Meier, S., Cremers, C.J.F., Basin, D.A.: Automated analysis of Diffie-Hellman protocols and advanced security properties. In: CSF 2012, pp. 78–94. IEEE (2012)
Shoup, V.: Sequences of games: A tool for taming complexity in security proofs. Cryptology ePrint Archive, Report 2004/332 (2004)
Swamy, N., Chen, J., Fournet, C., Strub, P.Y., Bhargavan, K., Yang, J.: Secure distributed programming with value-dependent types. J. Funct. Program. 23(4), 402–451 (2013)
Wadler, P.: Theorems for free! In: FPCA 1989, pp. 347–359. ACM (1989)
Zanella Béguelin, S.: Formal Certification of Game-Based Cryptographic Proofs. Ph.D. thesis, École Nationale Supérieure des Mines de Paris (2010)
Acknowledgements
Johannes Hölzl helped us with formalising spmfs on top of his probability formalisation and with the proof of countable support of spmf chains. Christoph Sprenger and Dmitriy Traytel and the anonymous reviewers suggested improvements of the presentation and the examples. This work was supported by SNSF grant 153217 “Formalising Computational Soundness for Protocol Implementations”.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Lochbihler, A. (2016). Probabilistic Functions and Cryptographic Oracles in Higher Order Logic. In: Thiemann, P. (eds) Programming Languages and Systems. ESOP 2016. Lecture Notes in Computer Science(), vol 9632. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49498-1_20
Download citation
DOI: https://doi.org/10.1007/978-3-662-49498-1_20
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49497-4
Online ISBN: 978-3-662-49498-1
eBook Packages: Computer ScienceComputer Science (R0)







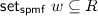 and
and 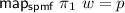 and
and  for some w
for some w
 for all A and
for all A and 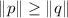










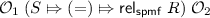 , and
, and and
and  , and
, and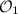 and
and 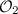 are lossless in error states and error states are never left, and
are lossless in error states and error states are never left, and





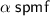 by combining the existing monad for probability mass functions [
by combining the existing monad for probability mass functions [ is always applied to a (monotone) function. Consequently, preservation of parametricity suffices and we do not need Wadler’s restrictions of the semantic domains. Instead, monotonicity (instead of continuity, see the discussion in Sect.
is always applied to a (monotone) function. Consequently, preservation of parametricity suffices and we do not need Wadler’s restrictions of the semantic domains. Instead, monotonicity (instead of continuity, see the discussion in Sect.  is not the greatest fixpoint of a polynomial functor, as the recursion goes through the non-polynomial functor
is not the greatest fixpoint of a polynomial functor, as the recursion goes through the non-polynomial functor  . Still, the type is well-defined, as
. Still, the type is well-defined, as  is a bounded natural functor [
is a bounded natural functor [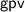 takes three type arguments, so we should expect
takes three type arguments, so we should expect  to take three relations, too. However, the third argument occurs in a negative position in the codatatype definition. Therefore, the relator does not enjoy useful properties such as monotonicity and distributivity over relation composition. Consequently, Isabelle’s infrastructure for parametricity treats these arguments as fixed (dead in the terminology of [
to take three relations, too. However, the third argument occurs in a negative position in the codatatype definition. Therefore, the relator does not enjoy useful properties such as monotonicity and distributivity over relation composition. Consequently, Isabelle’s infrastructure for parametricity treats these arguments as fixed (dead in the terminology of [ takes only relations for the first two arguments and fixes the third to the identity relation
takes only relations for the first two arguments and fixes the third to the identity relation  as can be seen in (
as can be seen in ( and the premises of (
and the premises of ( .
. emulates the oracle without access to further oracles. Thus, we use
emulates the oracle without access to further oracles. Thus, we use  directly instead of
directly instead of  .
.