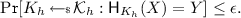Encrypt or Decrypt? To Make a Single-Key Beyond Birthday Secure Nonce-Based MAC

Abstract

At CRYPTO 2016, Cogliati and Seurin have proposed a highly secure nonce-based MAC called Encrypted Wegman-Carter with Davies-Meyer ($\textsf {EWCDM}$) construction, as $\textsf {E}_{K_2}\bigl (\textsf {E}_{K_1}(N)\oplus N\oplus \textsf {H}_{K_h}(M)\bigr )$ for a nonce N and a message M. This construction achieves roughly $2^{2n/3}$ bit MAC security with the assumption that $\textsf {E}$ is a PRP secure n-bit block cipher and $\textsf {H}$ is an almost xor universal n-bit hash function. In this paper we propose Decrypted Wegman-Carter with Davies-Meyer ($\textsf {DWCDM}$) construction, which is structurally very similar to its predecessor $\textsf {EWCDM}$ except that the outer encryption call is replaced by decryption. The biggest advantage of $\textsf {DWCDM}$ is that we can make a truly single key MAC: the two block cipher calls can use the same block cipher key $K=K_1=K_2$. Moreover, we can derive the hash key as $K_h=\textsf {E}_K(1)$, as long as $|K_h|=n$. Whether we use encryption or decryption in the outer layer makes a huge difference; using the decryption instead enables us to apply an extended version of the mirror theory by Patarin to the security analysis of the construction. $\textsf {DWCDM}$ is secure beyond the birthday bound, roughly up to $2^{2n/3}$ MAC queries and $2^n$ verification queries against nonce-respecting adversaries. $\textsf {DWCDM}$ remains secure up to $2^{n/2}$ MAC queries and $2^n$ verification queries against nonce-misusing adversaries.

1 Introduction

Pseudo-Random Functions or in short PRF is an important tool for studying almost all symmetric-key cryptographic systems that use secret keys, including encryption, authentication and authenticated-encryption. But unfortunately, very few PRFs are actually available in practice, and it is not easy to construct a sufficiently secure PRF. As a result, Pseudo-Random Permutations or in short PRPs or block ciphers, which are available in plenty [9, 10, 15, 20], replace the PRF and are deployed as building blocks for almost every cryptographic systems.

Although various available block ciphers [9, 10, 15, 20] can be assumed to be PRFs, but such an assumption comes at the cost of quadratic security degradation due to the PRF-PRP switch [5], which is often called the “birthday bound security degradation”. This loss of security is sometimes acceptable in practice if the block size of the cipher is large enough (e.g. AES-128). But with lightweight block ciphers with relatively small block sizes (e.g. 64-bit), whose number has grown tremendously in recent years (e.g. [1, 2, 9, 10, 20]), this security loss severely limits their applicability, and as a result it seems to be challenging to use these small ciphers in modern-day lightweight cryptography (e.g. Smart Card, RFID etc.).

In order to save these ciphers from obsolescence, various PRP-to-PRF constructions have been proposed in recent years that guarantee higher security than the usual birthday bound security. Such constructions are often called BBB (Beyond Birthday Bound)—i.e., security against more than $2^{n/2}$ queries where n is the block size of the underlying cipher. A popular BBB construction is the XOR of permutations [3, 6, 23, 28].

XOR of Permutations. Bellare et al. [6] suggested a way to construct a PRF from PRPs by taking the xor (more generally sum) of two independent PRPs,

$$\mathsf {XOR}_{\textsf {E}_{K_1}, \textsf {E}_{K_2}}(x) = \textsf {E}_{K_1}(x) \oplus \textsf {E}_{K_2}(x).$$

This construction was later analyzed by Lucks [23] who proved its security up to $2^{2n/3}$ queries. Bellare and Impagliazzo have shown a BBB security $O(nq/2^n)$ of single-keyed variant of this construction [3]. However, their proof was sketchy and hard to verify. Subsequently, a lot of efforts have been invested towards improving the bound of XOR construction and its single-keyed variant (even proving up to n-bit security) by Patarin [28, 31, 32], but the proof contains serious gaps. Later Cogliati et al. generalized this result to the xor of three or more independent PRPs [12]. Recently, Dai et al. [16] have provided a verifiable n-bit security proof of the XOR construction using the chi-squared method. Although, the original proof contained a glitch, as pointed out by Bhattacharya and Nandi [8], it was later fixed in the full version of [16].

The XOR construction provides a solution for encryption by combining itself with the counter (CTR) mode of encryption, resulting in a BBB secure nonce-based encryption mode, called CENC, proposed by Iwata [21], who showed its security upto $O(2^{2n/3})$ queries against all nonce-respecting adversaries. Later, Iwata et al. [22] provided its optimal security bound based on the mirror theory technique [32]. Recently, Bhattacharya and Nandi [8] have given its optimal security bound by analysing the PRF security of variable output length xor of permutations using chi-squared method.

Though useful for encryption, the XOR construction does not seem to be directly usable for authentication as we have to extend the domain size, so that the construction can authenticate long messages. This can be done by hashing the message, but with the XOR construction it seems that we need some subtle combination with a double-block hash function, as employed in PMAC_Plus [33], 1K-PMAC_Plus [17] and LightMAC_Plus [26].

Encrypted Davies-Meyer. The above problem with the XOR construction in authentication was solved by Cogliati and Seurin [13], who proposed a PRP-to-PRF conversion method, called Encrypted Davies-Meyer (EDM). The EDM construction is defined as follows:

$$\mathsf {EDM}_{\textsf {E}_{K_1}, \textsf {E}_{K_2}}(x) = \textsf {E}_{K_2}(\textsf {E}_{K_1}(x) \oplus x).$$

EDM uses two independent block-cipher keys and achieves $O(q^{3}/2^{2n})$ security [13]. Soon after, Dai et al. [16] improved its bound to $O(q^4/2^{3n})$ by applying chi-squared method. Concurrently, Mennink and Neves [24] proved its almost optimal security, i.e. $O(2^n/67n)$, using mirror theory technique. Recently, Cogliati and Seurin have proved a BBB security $O(q/2^{2n/3})$ of single-keyed EDM [14], as originally conjectured by themselves [13].

Encrypted Wegman-Carter with Davies-Meyer. Following the construction of EDM, Cogliati and Seurin extended the idea to construct EWCDM, a nonce-based BBB secure MAC, which is defined as follows:

$$\mathsf {EWCDM}_{\textsf {E}_{K_1}, \textsf {E}_{K_2}, \textsf {H}_{K_h}}(N, M) = \textsf {E}_{K_2} \bigl (\textsf {E}_{K_1}(N) \oplus N \oplus \textsf {H}_K(M) \bigr ),$$

where N is the nonce and M is the message to be authenticated. Note that, EWCDM uses two independent block-cipher keys, $K_1$ and $K_2$, and also another independent hash-key $K_h$ for the AXU hash function.¹ In this way, EDM obviated the necessity of using double-block hash function that existed with the XOR construction. It has been proved that EWCDM is secure against all nonce-respecting MAC adversaries² that make at most $2^{2n/3}$ MAC queries and $2^{n}$ verification queries. Cogliati and Seurin also proved $O(2^{n/2})$ security of the construction against nonce-misusing adversaries. Later, Mennink and Neves [24] proved its n-bit PRF security using mirror theory in the nonce respecting setting and mentioned that the analysis straightforwardly generalizes to the analysis for unforgeability or for the nonce-misusing setting of the construction. The trick involved in proving the optimal security of EWCDM is by replacing the last block cipher call with its inverse. This subtle change does not make any difference in the output distribution and as a bonus, it trivially allows one to express the output of the construction as a sum of two random permutations (or in general a bi-variate affine equation³). It is only this feature which is captured by the mirror theory to derive the security bound of the construction.

Motivation behind This Work. As evident from the definition of the construction, EWCDM requires three keys; two block cipher keys $K_1$ and $K_2$ and one hash key $K_h$. Constructions with multiple keys necessarily demand larger storage space for storing the secret keys, which is sometimes infeasible for lightweight crypto devices. All popular MACs, including CMAC [27] and HMAC [4], require only a single secret key. But most of the time reducing the number of keys without compromising the security is not a trivial task.

Cogliati and Seurin [13] believed that BBB security should hold for single-keyed EWCDM (with $K_1 = K_2$) but be likely cumbersome to prove. As mentioned earlier, Cogliati and Seurin recently proved that single-keyed EDM (not EWCDM) is BBB secure, but the proof is highly complicated. Moreover, it is not clear at all how to build on this result to prove the MAC security of EWCDM construction with $K_1 = K_2$. In fact, Cogliati and Seurin, in their proof of single-keyed EDM [14], state that

“For now, we have been unable to extend the current (already cumbersome) counting used for the proof of the single-permutation EDM construction to the more complicated case of single-key EWCDM.”

Thus, we expect that proving the MAC security of single-keyed EWCDM should be a notably hard task and very likely require heavy mathematical tools like Sum Capture Lemma as already used for single-keyed EDM. This motivates us to design an another single-keyed, nonce-based MAC built from block ciphers (and a hash function) with BBB security that can be proven by a simpler approach.

Our Contribution. Our contribution in this paper is fourfold which we outline as follows:

• DWCDM: New Nonce-Based MAC. We propose Decrypted Wegman-Carter with Davies-Meyer, in short DWCDM, a nonce-based BBB secure MAC. The design philosophy of DWCDM is inspired from the trick used in [24] while proving the optimal security of EWCDM. Recall that, in [24], authors replace the last block cipher call with its inverse so that the output of EWCDM can be expressed as a sum of two independent PRPs. But the same trick does not work at the time of using the same block cipher key in the construction. This phenomenon triggers us to design a nonce based MAC, very similar to EWCDM, in which instead of using the encryption algorithm in the last block-cipher call, we use its decryption algorithm so that the output of the construction can be expressed as a sum of two identical PRPs and hence the name Decrypted Wegman-Carter with Davies-Meyer. The construction is single-keyed in the sense that the same block cipher key is used for the two cipher calls. Schematic diagram of DWCDM is shown in Fig. 1 where the last $n \slash 3$ bits of the nonce N is zero, i.e. $N=N^*\Vert 0^{n/3}$. We would like to mention here that one cannot use the full n-bit nonce in DWCDM as that would end up with a birthday bound MAC attack which is described in Sect. 4.1. We show that DWCDM is secure up to $2^{2n/3}$ MAC queries and $2^n$ verification queries against nonce-respecting adversaries. We also show that DWCDM is secure up to $2^{n/2}$ MAC queries and $2^n$ verification queries in the nonce-misuse setting, where the bound is tight. As a concrete example of DWCDM, we present an instantiation of DWCDM with the AXU hash function being realized via PolyHash [25]. We show that nPolyMAC achieves $2^{2n/3}$-bit MAC security in the nonce-respecting setting.

• Extended Mirror Theory. Since, our study of interest is the MAC security of the construction, we require to analyze the number of solutions of a system of affine bi-variate equations along with affine uni-variate and bi-variate non-equations⁴. Such a general treatment of analysing system of affine equations with non-equations was only mentioned in [32] without giving any formal analysis. To the best of our knowledge, this is the first time we analyse such a generic system of equations with non-equations, which we regard to as extended mirror theory and our MAC security proofs of DWCDM and 1K-DWCDM are crucially based on this new result.

• 1K-DWCDM: “Pure” Single-Keyed Variant of DWCDM. Moreover, we exhibit a truly single-keyed nonce-based MAC construction, 1K-DWCDM. Under the condition that the length of the hash key is equal to the block size as $|K_h|=n$, we can even derive the hash key as $K_h = \textsf {E}_K(0^{n-1} \Vert 1)$, which results in the construction 1K-DWCDM. We prove that 1K-DWCDM is essentially as secure as DWCDM.

• Potentiality of Achieving Higher Security. Finally, we show how one can boost the security for DWCDM type constructions using extended generalized version of Mirror Theory.

Proof Approach. Our MAC security proof of DWCDM and 1K-DWCDM is fundamentally relied on Patarin’s H-coefficient technique [29]. Similar to the technique of [13, 19], we cast the unforgeability game of MAC to an equivalent indistinguishability game, with some suitable choice of ideal world, that allows us to apply the H-coefficient technique for bounding the distinguishing advantage of the construction of our concern.

As mentioned earlier that one can express the output of DWCDM as a sum of two identical permutations. Thus, q many such evaluations of DWCDM gives us a system of q many affine bi-variate equations

$$ {\left\{ \begin{array}{ll} \textsf {E}_K(N_1) \oplus \textsf {E}_K(T_1) = N_1 \oplus H_{K_h}(M_1) \\ \textsf {E}_K(N_2) \oplus \textsf {E}_K(T_2) = N_2 \oplus H_{K_h}(M_2) \\ ~~~~~~~~~~~~~~~~~~~~~~~~\vdots \\ \textsf {E}_K(N_q) \oplus \textsf {E}_K(T_q) = N_q \oplus H_{K_h}(M_q) \end{array}\right. } $$

Along with this, we also need to ensure that the verification attempt of the adversary should fail (as a part of the good transcript), i.e. for a verification query $(N', M', T'$), chosen by the adversary, we should always have

$$\textsf {E}^{-1}_K(\textsf {E}_{K}(N') \oplus N' \oplus H_{K_h}(M')) \ne T'.$$

Hence, it tells us that we also need to incorporate affine non-equations along with the system of bi-variate affine equations. This leads us to extend the mirror theory technique (extension as in incorporating affine non-equations along with affine bi-variate equations). We require the result of extended mirror theory while lower bounding the real interpolation probability for a good transcript.

Remark 1

We would like to point out that a possible alternative approach is to use the chi-square method, a recently discovered technique which has been reported in [7, 8, 16]. It is interesting to observe that in some settings chi-square outperforms H-coefficient technique in terms of guaranteeing security with quadratic improvement on the number of queries that adversary can make [16]. However, it is difficult to apply this technique in our construction. The reason behind this is the lack of sufficient entropy of the conditional distribution when we condition on the hash key. The same holds true for the analysis of EWCDM as well. In fact, this negative phenomenon motivates us to consider DWCDM so that we can represent the construction as a sum of permutations and eventually apply extended mirror theory.

2 Preliminaries

Symbols and Notations. For a set $\mathcal {X}$, denotes that X is sampled uniformly at random from $\mathcal {X}$ and independent to all random variables defined so far. $\{0,1\}^n$ denotes the set of all binary strings of length n. The set of all functions from $\mathcal {X}$ to $\mathcal {Y}$ is denoted as $\textsf {Func}(\mathcal {X}, \mathcal {Y})$ and the set of all permutations over $\mathcal {X}$ is denoted as $\textsf {Perm}(\mathcal {X})$. $\textsf {Func}_{\mathcal {X}}$ denotes the set of all functions from $\mathcal {X}$ to $\{0,1\}^n$ and $\textsf {Perm}$ denotes the set of all permutations over $\{0,1\}^n$. We often write $\textsf {Func}$ instead of $\textsf {Func}_{\mathcal {X}}$ when the domain of the functions is understood from the context. We write [q] to refer to the set $\{1, \ldots , q\}$.

For any binary string x, |x| denotes the length i.e. the number of bits in x. For $x, y \in \{0,1\}^n$, we write $z = x \oplus y$ to denote the modulo 2 addition of x and y. We write $\mathbf 0$ to denote the zero element of the field $\{0,1\}^n$ (i.e. $0^n$) and $\mathbf 1$ to denote $0^{n-1} \Vert 1$. For integers $1 \le b \le a$, we write $(a)_{b}$ to denote $a(a-1) \ldots (a-b+1)$, where $(a)_0 = 1$ by convention.

2.1 Security Definitions

PRF and PRP and SPRP. A keyed function with key space $\mathcal {K}$, domain $\mathcal {X}$ and range $\mathcal {Y}$ is a function $\textsf {F} : \mathcal {K} \times \mathcal {X} \rightarrow \mathcal {Y}$ and we denote $\textsf {F}(K, X)$ by $\textsf {F}_{K}(X)$. Similarly, a keyed permutation with key space $\mathcal {K}$ and domain $\mathcal {X}$ is a mapping $\textsf {E} : \mathcal {K} \times \mathcal {X} \rightarrow \mathcal {X}$ such that for all key $K \in \mathcal {K}$, $X \mapsto \textsf {E}(K, X)$ is a permutation over $\mathcal {X}$ and we denote $\textsf {E}_{K}(X)$ for $\textsf {E}(K, X)$.

PRF. Given an oracle algorithm $\mathsf {A}$ with oracle access to a function from $\mathcal {X}$ to $\mathcal {Y}$, making at most q queries, running time is at most t and outputting a single bit. We define the prf-advantage of $\mathsf {A}$ against the family of keyed functions $\textsf {F}$ as

We say that $\textsf {F}$ is a $(q, t, \epsilon )$ secure PRF, if $\mathbf {Adv}^{\mathrm {PRF}}_{\textsf {F}}(q, t) := \max \limits _{\textsf {A}} \mathbf {Adv}^{\mathrm {PRF}}_{\textsf {F}}(\textsf {A}) \le \epsilon$, where the maximum is taken over all adversaries A that makes q many queries and running time is at most t.

PRP. Given an oracle algorithm $\mathsf {A}$ with oracle access to a permutation of $\mathcal {X}$, making at most q queries, running time is at most t and outputting a single bit. We define the prp-advantage of $\mathsf {A}$ against the family of keyed permutations $\textsf {E}$ as

We say that $\textsf {E}$ is a $(q, t, \epsilon )$ secure PRP, if $\mathbf {Adv}^{\mathrm {PRP}}_{\textsf {E}}(q, t) := \max \limits _{\textsf {A}} \mathbf {Adv}^{\mathrm {PRP}}_{\textsf {E}}(\textsf {A}) \le \epsilon$, where the maximum is taken over all adversaries A that makes q many queries and running time is at most t.

SPRP. Given an oracle algorithm $\mathsf {A}$ with oracle access to a permutation and its inverse over $\mathcal {X}$, making at most $q^{+}$ queries to permutation and $q^{-}$ queries to inverse permutation, running time is at most t and outputting a single bit. We define the sprp-advantage of $\mathsf {A}$ against the family of keyed permutations $\textsf {E}$ as

We say that $\textsf {E}$ is a $(q, t, \epsilon )$ secure SPRP, if $\mathbf {Adv}^{\mathrm {SPRP}}_{\textsf {E}}(q, t) := \max \limits _{\textsf {A}} \mathbf {Adv}^{\mathrm {SPRP}}_{\textsf {E}}(\textsf {A}) \le \epsilon$, where the maximum is taken over all adversaries A that makes q many encryption and decryption queries altogether and running time is at most t.

MACs. Given four non-empty finite sets $\mathcal {K}, \mathcal {N}, \mathcal {M}$ and $\mathcal {T}$, a nonce based keyed function with key space $\mathcal {K}$, nonce space $\mathcal {N}$, message space $\mathcal {M}$ and range $\mathcal {T}$ is a keyed function whose domain is $\mathcal {N} \times \mathcal {M}$ and range is $\mathcal {T}$ and we write $\textsf {F}(K, N, M)$ as $\textsf {F}_K(N,M)$.

Definition 1

(Nonce Based MAC). Let $\mathcal {K}, \mathcal {N}, \mathcal {M}$ and $\mathcal {T}$ be four non-empty finite sets and $\mathsf {F} : \mathcal {K} \times \mathcal {N} \times \mathcal {M} \rightarrow \mathcal {T}$ be a nonce based keyed function. For $K \in \mathcal {K}$, let $\mathsf {Ver}_K$ be the verification oracle that takes as input $(N, M, T) \in \mathcal {N} \times \mathcal {M} \times \mathcal {T}$ and outputs 1 if $\mathsf {F}_K(N,M) = T$, otherwise outputs 0. A $(q_m, q_v, t)$ adversary against the MAC security of $\mathsf {F}$ is an adversary $\mathsf {A}$ with access to two oracles $\mathsf {F}_K$ and $\mathsf {Ver}_K$ for $K \in \mathcal {K}$ such that it makes at most $q_m$ many MAC queries to first oracle and $q_v$ many verification queries to second oracle. We say that $\mathsf {A}$ forges $\mathsf {F}$ if any of its queries to $\mathsf {Ver}_K$ returns 1. The advantage of $\mathsf {A}$ against the MAC security of $\mathsf {F}$ is defined as

where the probability is taken over the randomness of the underlying key and the random coin of adversary $\mathsf {A}$ (if any). We assume that $\mathsf {A}$ does not make any verification query (N, M, T) to $\mathsf {Ver}_K$ if T is obtained in previous MAC query with input (N, M) and it does not repeat any query. We call such an adversary as “non-trivial” adversary. The adversary is said to be “nonce respecting” if it does not repeat nonces in its queries to the MAC oracle⁵.

Regular And AXU Hash Function. Let $\mathcal {K}_h, \mathcal {X}, \mathcal {Y}$ be three non-empty finite sets and $\mathsf {H}$ be a keyed function $\mathsf {H} : \mathcal {K}_h \times \mathcal {X} \rightarrow \mathcal {Y}$. Then,

• (1) $\mathsf {H}$ is said to be an $\epsilon$ regular hash function, if for any $X \in \mathcal {X}$ and any $Y \in \mathcal {Y}$,

  

  (1)

• (2) $\mathsf {H}$ is said to be an $\epsilon$ almost xor universal (AXU) hash function if for any distinct $X, X' \in \mathcal {X}$ and for any $Y \in \mathcal {Y}$,

  

  (2)

• (3) $\mathsf {H}$ is said to be an $\epsilon$ 3-way regular hash function if for any distinct $X_1, X_2, ,X_3 \in \mathcal {X}$ and for any non-zero $Y \in \mathcal {Y}$,

  

  (3)

In the following, we state that PolyHash [25] is one of the examples of algebraic hash function which is $\ell /2^n$ regular, AXU as well as 3-way regular hash function.

Proposition 1

Let $\mathsf {Poly} : \{0,1\}^n \times (\{0,1\}^n)^* \rightarrow \{0,1\}^n$ be a hash function defined as follows: For a fixed key $K_h \in \{0,1\}^n$ and for a fixed message M, we first apply an injective padding such as $10^*$ i.e., pad 1 followed by minimum number of zeros so that the total number of bits in the padded message becomes multiple of n. Let the padded message be $M^* = M_1 \Vert M_2 \Vert \ldots \Vert M_l$ where for each i, $|M_i| = n$. Then we define

$$\begin{aligned} {\mathsf {Poly}_{K_h}(M) = M_l \cdot K_h \oplus M_{l-1} \cdot K^2_h \oplus \ldots \oplus M_1 \cdot K^{l}_{h},} \end{aligned}$$

(4)

where l is the number of n-bit blocks. Then, $\mathsf {Poly}$ is $\ell /2^n$ regular, AXU and 3-way regular hash function, where $\ell$ denotes the maximum number of message blocks of size n-bits.

The proof of the result lies around in finding the number of roots of a non-zero polynomial over the hash key $K_h$ with message blocks being the coefficients of the polynomial. The details of the proof of can be found in [18].

3 Patarin’s Mirror Theory

Mirror theory, as defined in [32] is the theory of evaluating the number of solutions of affine system of equalities and non-equalities in a finite group. Patarin, who coined this theory, has given a lower bound on the number of solutions of a finite system of affine bi-variate equations using an inductive proof when the variables in the equations are wor samples [30]. The proof is tractable upto the order of $2^{2n/3}$ security bound, but the proof becomes highly complex and too difficult to verify in the case of deriving the optimal security bound. In specific, once the first-order recursion is considered, one needs to consider a second-order recursion, and so on, until the n-th recursion. For the i-th order recursion, there are $O(2^i)$ many cases and Patarin’s proof only addresses the first (and perhaps the second) order recursion by a tedious analysis, but the cases of the higher-order ones are quite different, and it’s not at all clear how to bridge the gap, given an exponential number of cases that one has to consider. Moreover, to the best of our knowledge, the proof did not consider any affine non-equation as well.

In this section we extend the Mirror theory in the context of our MAC security to incorporate the affine non-equations (that includes uni-variate and bi-variate non-equations) along with a system of affine bi-variate equations. In the following, we prove that when the number of affine bi-variate equations is $q \le 2^{2n/3}$ and the number of non-equations is $v \le 2^n$ (v is the total number of affine uni-variate and bi-variate non equations), then the number of solutions becomes at least $(2^n)_{3q/2} / 2^{nq}$. For the sake of presentation and interoperability with the results in the remainder of the paper, we use different parameterization and naming convention.

3.1 General Setting of Mirror Theory

Given a bi-variate affine equation $P \oplus Q = \lambda$ over $\mathrm {GF}(2^n)$, the associated linear equation of this affine equation is $P \oplus Q = \mathbf {0}$. Now, given $\lambda _1, \ldots , \lambda _q \in \mathrm {GF}(2^n) \setminus \mathbf 0$ which we write as $\mathrm {\Lambda } = (\lambda _1, \ldots , \lambda _q)$, let us consider a system of q many bi-variate affine equations over $\mathrm {GF}(2^n)$:

$$\mathcal {E}_{\mathrm {\Lambda }} = \{P_{n_1} \oplus P_{t_1} = \lambda _1, P_{n_2} \oplus P_{t_2} = \lambda _2, \ldots , P_{n_q} \oplus P_{t_q} = \lambda _q\}.$$

Given a function $\phi : \{n_1, t_1, \ldots , n_q, t_q\} \rightarrow \mathcal {I}$, called index mapping function, we associate another system of bi-variate affine equations:

$$\mathcal {E}_{\mathrm {\Lambda },\phi } = \{P_{\phi (n_1)} \oplus P_{\phi (t_1)} = \lambda _1, P_{\phi (n_2)} \oplus P_{\phi (t_2)} = \lambda _2, \ldots , P_{\phi (n_q)} \oplus P_{\phi (t_q)} = \lambda _q\}.$$

Let $\alpha$ denotes the cardinality of the image set of $\phi$. Then, $\mathcal {E}_{\mathrm {\Lambda }, \phi }$ is a system of bi-variate affine equations over $\alpha$ variables. In our paper, a specific choice of $\mathcal {I}$ would be $\{0,1\}^n$.

Example. Consider a system of equations:

$$\{P_{1} \oplus P_2 = \lambda _1, P_1 \oplus P_3 = \lambda _2, P_2 \oplus P_4 = \lambda _3\}.$$

Then, the index mapping function for the above system of equations is $\phi (n_1) = 1, \phi (t_1) = 2, \phi (n_2) = 1, \phi (t_2) = 3, \phi (n_3) = 2, \phi (t_3) = 4$. For this system of equations $\alpha = 4$.

Equation-Dependent Graph. For index mapping function $\phi : \{n_1, t_1, \ldots , n_q, t_q\} \rightarrow \mathcal {I}$, we associate a undirected graph $G_{\phi } = ([q], \mathcal {S})$ where $\{i, j\} \in \mathcal {S}$ if

$$~|\{\phi (n_i), \phi (t_i)\} \cap \{\phi (n_j), \phi (t_j)\}~| \ge 1$$

or if $i =j$ and $\phi (n_i) = \phi (t_i)$. We call such an edge a self-loop. In other words, we introduce an edge between two equations (node represents the equation number) in the equation-dependent graph if the corresponding equations have at least one common unknown variable. Note that the set $\{\phi (n_i), \phi (t_i)\}$ can be a multi-set.

For a subset $\{i_1, \ldots , i_c\} \subseteq [q]$, let

$$\{P_{\phi (n_{i_1})} \oplus P_{\phi (t_{i_1})} = \mathbf {0}, P_{\phi (n_{i_2})} \oplus P_{\phi (t_{i_2})} = \mathbf {0}, \ldots , P_{\phi (n_{i_c})} \oplus P_{\phi (t_{i_c})} = \mathbf {0}\}$$

be the sub-system of associated linear equations. We say this sub-system of associated linear equations is linearly dependent if $\{i_1, \ldots , i_c\}$ is the minimal set and all variables $P_x$, which appeared in the above sub-system, appears exactly twice. Depending on the value of c (for the minimal linearly dependent sub-system), we have the following three cases;

• (i) $c =1$: Self-loop. If there exists i such that $\phi (n_i) = \phi (t_i)$.

• (ii) $c =2$: Parallel-edge. If there exists $i \ne j$ such that either:

  $$(a)~ \phi (n_i) = \phi (n_j) \text{ and } \phi (t_i) =\phi (t_j) \text{ or } (b)~ \phi (n_i) = \phi (t_j) \text{ and } \phi (t_i) = \phi (n_j).$$

• (iii) $c \ge 3$: Alternating-cycle. If there exists distinct $i_1, i_2, \ldots , i_c$ such that for every $j \in [c]$ either

  • $\phi (n_{i_j}) \in \{\phi (n_{i_{j+1}}), \phi (t_{i_{j+1}})\}$ and $\phi (t_{i_j}) \in \{\phi (n_{i_{j-1}}), \phi (t_{i_{j-1}})\}$ or

  • $\phi (t_{i_j}) \in \{\phi (n_{i_{j+1}}), \phi (t_{i_{j+1}})\}$ and $\phi (n_{i_j}) \in \{\phi (n_{i_{j-1}}), \phi (t_{i_{j-1}})\}$.

When $i=1$, $i-1$ is considered as c and when $i = c$, $i+1$ is considered as 1. We say that $\phi$ is dependent if any one of the above condition holds. Otherwise, we call it independent. Given an independent $\phi$, the graph $G_{\phi }$ becomes a simple graph and $\mathcal {E}_{\mathrm {\Lambda },\phi }$ becomes linearly independent. In this case, the number of variables present in a connected component $C = \{i_1, \ldots , i_c\}$ of $G_{\phi }$ (i.e., the size of the set $\{\phi (n_{i_1}), \phi (t_{i_1}), \ldots ,\phi (n_{i_c}), \phi (t_{i_c}) \}$) is exactly $c+1$. We call the set $\{\phi (n_{i_1}), \phi (t_{i_1}), \ldots ,\phi (n_{i_c}), \phi (t_{i_c}) \}$ a block. The block maximality, denoted by $\xi _{\max }$, of an independent $\phi$ is defined as $\zeta _{\max }+1$ where $\zeta _{\max }$ is the size of the maximum connected components of $G_{\phi }$ (Note that, a block with p many elements introduces $p-1$ many affine equations.).

3.2 Extended Mirror Theory

In this section, we introduce the extended Mirror theory technique by incorporating two types of non-equations with a finite number of bi-variate affine equations. We consider (i) uni-variate affine non-equation of the form $X_i \ne c$ and (ii) bi-variate affine non-equation of the form $X_i \oplus Y_i \ne c$, where c is a non-zero constant. In particular, we lower bound the number of solutions of a finite number of affine equations⁶ and uni(bi-) variate affine non-equations. To begin with, let us investigate what happens when we introduce a single uni(bi-) variate affine non-equation with a finite number of affine equations.

Let $\mathcal {E}^{=}$ be a system of q many affine equations of the form

$$\begin{aligned} \mathcal {E}^{=} = \{P_{n_1} \oplus P_{t_1} = \lambda _1, \ldots , P_{n_q} \oplus P_{t_q} = \lambda _q\}. \end{aligned}$$

(5)

Let $\phi$ be an index mapping function that maps from $\{n_1, t_1, \ldots , n_q, t_q\} \rightarrow \mathcal {I}$. Let $\mathrm {\Lambda }_{=} = (\lambda _1, \lambda _2, \ldots , \lambda _q)$, where each $\lambda _i \in \mathrm {GF}(2^n) \setminus \mathbf 0$. Now, for an independent choice of $\phi$, $\mathcal {E}^{=}_{\phi , \mathrm {\Lambda }_{=}}$ is a linearly independent set of q many affine equations. Let $\mathcal {E}^{\ne }$ be a system of r many bi-variate affine non-equations and $v-r$ many uni-variate affine non-equations of the form

$$\begin{aligned}&\mathcal {E}^{\ne } =\quad \{P_{n_{q+1}} \oplus P_{t_{q+1}} \ne \lambda '_{1}, \ldots , P_{n_{(q + r)}} \oplus P_{t_{(q + r)}} \ne \lambda '_{r}\} \\&\quad \quad \bigcup \{P_{n_{q+r+1}} \ne \lambda '_{r+1}, \ldots , P_{n_{(q + v)}} \ne \lambda '_{v}\}. \end{aligned}$$

We denote $\mathrm {\Lambda }_{\ne } = (\lambda '_{1}, \lambda '_{2}, \ldots , \lambda '_{v})$, where each $\lambda '_i \in \mathrm {GF}(2^n) \setminus \mathbf 0$, and $\mathrm {\Lambda '} = (\lambda _1, \lambda _2, \ldots , \lambda _q, \lambda '_{1}, \lambda '_{2}, \ldots , \lambda '_{v})$. Now, for the system of affine equations and non-equations $\mathcal {E} := \mathcal {E}^{=} \cup \mathcal {E}^{\ne }$, we consider the index mapping function

$$\phi ' : \{n_1, t_1, \ldots , n_q, t_q, n_{q+1}, t_{q+1}, \ldots , n_{q+v}, t_{q+v}\} \rightarrow \mathcal {I}.$$

Moreover, we denote $\phi := \phi '_{|q}$ to be the index mapping function that maps $\{n_1, t_1, \ldots , n_q, t_q\} \rightarrow \mathcal {I}$ and $\mathrm {\Lambda }_{=} := \mathrm {\Lambda '}_{|q}$ to be $(\lambda _1, \lambda _2, \ldots , \lambda _q)$.

Characterizing Good $(\phi ', \mathrm {\Lambda '})$. We say that a pair $(\phi ', \mathrm {\Lambda '})$ is good if

• ($\textsf {C1}$) $\phi$ is independent and for all $x \ne y$, $P_{\phi (x)} = P_{\phi (y)}$ cannot be generated from the system of equations $\mathcal {E}^{=}_{\phi , \mathrm {\Lambda }_{=}}$.

• ($\textsf {C2}$) for all $j \in [v]$ and $i_1, \ldots , i_c \in [q]$, $c \ge 0$, such that $\{i_1, \ldots , i_c, q+j\}$ is dependent system then $\lambda _{i_1} \oplus \cdots \oplus \lambda _{i_c} \oplus \lambda '_{j} \ne \mathbf 0$.

In words, a good $(\phi ', \mathrm {\Lambda '})$ says that: (i) the system of equation $\mathcal {E}_{\phi , \mathrm {\Lambda }_{=}}$ is linearly independent system of equations and one cannot generate an equation of the form $P_{\phi (x)} = P_{\phi (y)}$ by linearly combining the equation of $\mathcal {E}_{\phi , \mathrm {\Lambda }_{=}}$. Moreover, (ii) by linearly combining the equation of $\mathcal {E}_{\phi , \mathrm {\Lambda }_{=}}$, one cannot generate an equation of the form $P_{x} \oplus P_{y} = \lambda _{x,y}$ such that $P_{x} \oplus P_{y} \ne \lambda _{x,y}$ already exist in $\mathcal {E}^{\ne }_{\phi ', \mathrm {\Lambda '}}$.

Summarizing above, we state and prove the following main theorem, which we call as Extended Mirror Theorem for $\xi _{\max } = 3$. For the notational simplicity we assume the index set $\mathcal {I} = [\alpha ]$.

Theorem 1

Let $(\mathcal {E}^{=} \cup \mathcal {E}^{\ne }, \phi ', \mathrm {\Lambda '})$ be a system of q many affine equations and v many uni(bi-) variate affine non-equations associated with index mapping function $\phi '$ over $\mathrm {GF}(2^n)$ which are of the form

$$\begin{aligned}&(a) P_{\phi (n_i)} \oplus P_{\phi (t_i)} = \lambda _i (\ne \mathbf {0}), ~\forall i \in [q] \\&(b) P_{\phi (n_j)} \oplus P_{\phi (t_j)} \ne \lambda '_j (\ne \mathbf {0}), ~\forall j \in [q+1, q+r]\\&(c) P_{\phi (n_j)} \ne \lambda ''_j (\ne \mathbf {0}), ~\forall j \in [q+r+1, q+v] \end{aligned}$$

over the set of $\alpha$ many unknown variables $\mathcal {P} = \{P_1, \ldots , P_\alpha \}$ such that $P_{a}$ may be equals to some $P_{\phi (n_i)}$ or $P_{\phi (t_i)}$, where $a \in \{\phi (n_{j}), \phi (t_{j})\}, j \in [q+1, q+v]$. Now, if

• (i)  $(\phi ', \mathrm {\Lambda '})$ is good and

• (ii)  $\xi _{\max } = 3$

then the number of solutions for $\mathcal {P}$, denoted by $h_{\frac{3q}{2}}$ such that $P_i \ne P_j$ for all distinct $i, j \in \{1, \ldots , \alpha \}$ is

$$\begin{aligned} h_{\frac{3q}{2}} \ge \frac{(2^n)_{\frac{3q}{2}}}{2^{nq}} \bigg (1 - \frac{5q^3}{2^{2n}} - \frac{v}{2^n} \bigg ). \end{aligned}$$

(6)

Proof

As mentioned, our proof is an inductive proof based on the number of blocks u. Our first observation is that as $(\phi ', \mathrm {\Lambda '})$ is good, $\phi$ is independent and thus $\xi _{\max } = \zeta _{\max } + 1$ and hence, the maximum number of variables $P_i$ that can reside in the same block is 3. For the simplicity of the proof, assume that we have exactly 3 variables at each blocks. Now, it is easy to see that Eq. (6) holds when $u = 1$.

As the next step of the proof, let $h_{3u}$ be the solutions for first 2u many affine equations, which we denote as $\mathcal {E}_{2u}^{=}$. Now as soon as we add the $(u+1)^{th}$ block, we consider the following bi-variate affine equations $P_{3u+1} \oplus P_{3u+2} = \lambda _{2u + 1}, P_{3u+1} \oplus P_{3u+3} = \lambda _{2u + 2}$ and those bi-variate affine non-equations which are of the form $P_{\sigma _i} \oplus P_{\delta _i} \ne \lambda '_i, ~\text{ where }~\sigma _i \in \{ 1,\ldots ,3u+3 \}, \delta _i \in \{3u+1, 3u+2, 3u+3\}$ and also those uni-variate affine non-equations of the form $P_{\delta _i} \ne \lambda ''_i, ~\text{ where }~ \delta _i \in \{3u+1, 3u+2, 3u+3 \}$. Let $v'$ and $v''$ be the number of such bi-variate and uni-variate affine non-equations. Now, note that each such bi-variate affine non-equation of the form $P_{\sigma _i} \oplus P_{\delta _i} \ne \lambda '_i$ where $\sigma _i \in \{ 1, \ldots , 3u+3\}, \delta _i \in \{3u+1, 3u+2, 3u+3\}$ can be written as $P_{3u+1} \ne P_{\sigma _i} \oplus \lambda ^{\star }_{i}$, where $\sigma _i \in \{ 1, \ldots , 3u+3\}$ and $\lambda ^{\star }_{i} \in \{\lambda '_i, \lambda '_i \oplus \lambda _{2u+1}, \lambda '_i \oplus \lambda _{2u+2}\}$. Moreover, each such uni-variate affine non-equation of the form $P_{\delta _i} \ne \lambda ''_i$ where $\delta _i \in \{3u+1, 3u+2, 3u+3 \}$ can be written as $P_{3u+1} \ne \lambda ^{\star \star }_{i}$, where $\lambda ^{\star \star }_i \in \{\lambda ''_i, \lambda ''_i \oplus \lambda _{2u+1}, \lambda ''_i \oplus \lambda _{2u+2}\}$.

Now $h_{3u+3}$ counts for the number of solutions to $\{P_1, \ldots , P_{3u}, P_{3u+1}, P_{3u+2}, P_{3u+3}\}$ such that

• $\{P_1, \ldots , P_{3u}\}$ is a valid solution of $\mathcal {E}_{2u}^{=}$.

• $P_{3u+1} \oplus P_{3u+2} = \lambda _{2u + 1}, P_{3u+1} \oplus P_{3u+3} = \lambda _{2u + 2}$.

• $P_{3u+1} \notin \{P_1, \ldots , P_{3u}, P_1 \oplus \lambda _{2u+1}, \ldots , P_{3u} \oplus \lambda _{2u+1}, P_1 \oplus \lambda _{2u+2}, \ldots , P_{3u} \oplus \lambda _{2u+2}\}$.

• $P_{3u+1} \notin \{ P_{\sigma _1} \oplus \lambda ^{\star }_{1}, \ldots , P_{\sigma _{v'}} \oplus \lambda ^{\star }_{v'} \}$.

• $P_{3u+1} \notin \{ \lambda ^{\star \star }_{1}, \ldots , \lambda ^{\star \star }_{v''} \}$.

Let $V_1 = \{P_1, \ldots , P_{3u}\}, V_2 = \{P_1 \oplus \lambda _{2u+1}, \ldots , P_{3u} \oplus \lambda _{2u+1}\}$, $V_3 = \{P_1 \oplus \lambda _{2u+2}, \ldots , P_{3u} \oplus \lambda _{2u+2}\}$, $V_4 = \{P_{\sigma _1} \oplus \lambda ^{\star }_{1}, \ldots , P_{\sigma _{v'}} \oplus \lambda ^{\star }_{v'} \}$ and $V_5= \{ \lambda ^{\star \star }_{1}, \ldots , \lambda ^{\star \star }_{v''}\}$. Note that, $|V_i| = 3u, i = 1, 2, 3$ and $|V_4|=v'$, $|V_5|=v''$. Therefore, we can write

$$\begin{aligned} h_{3u+3}= & {} h_{3u}(2^n-|V_1 \cup V_2 \cup V_3 \cup V_4 \cup V_5|) \ge h_{3u}(2^n-|V_1| - |V_2| - |V_3| - |V_4| - |V_5|) \\&\ge h_{3u}(2^n-9u-v'-v''). \end{aligned}$$

By applying repeated induction, we obtain

$$h_{\frac{3q}{2}} \ge \bigg (2^n - 9(\frac{q}{2} - 1) - v' - v''\bigg )h_{3(\frac{q}{2}-1)} \ge \ldots \ge \prod _{u=0}^{q/2-1} (2^n - 9u - v' - v'')$$

for which we have,

$$\begin{aligned}&\frac{h_{\frac{3q}{2}}2^{nq}}{(2^n)_{\frac{3q}{2}}} \ge \prod _{u=0}^{q/2-1} \frac{2^{2n}(2^n - 9u - v' -v'')}{(2^n - 3u)(2^n - 3u - 1)(2^n - 3u - 2)} \\&\qquad \quad \ge \prod _{u=0}^{q/2-1} \frac{2^{2n}(2^n-9u-v'-v'')}{2^{3n}-(9u+3)2^{2n}+(27u^2+18u+2)2^{n}} \\&\qquad \quad {\mathop {\ge }\limits ^{[1]}} \prod _{u=0}^{q/2-1} \Bigg (1+ \frac{3}{2^n} - \frac{27u^2+18u+2}{2^{2n}} - \frac{v'+v''}{2^n}\Bigg ) \\&\qquad \quad {\mathop {\ge }\limits ^{[2]}} \prod _{u=0}^{q/2-1} \Bigg (1 - \frac{27u^2}{2^{2n}} - \frac{9u^2}{2^{2n}} - \frac{v'+v''}{2^n} \Bigg ) \ge \prod \limits _{u=0}^{q/2-1} \Bigg (1 - \frac{36u^2}{2^{2n}} - \frac{v'+v''}{2^n}\Bigg ) \\&\qquad \quad \ge \Bigg (1 - \sum \limits _{u=0}^{q/2-1} \frac{36u^2}{2^{2n}} - \sum \limits _{u=0}^{q/2-1} \frac{v'+v''}{2^n}\Bigg ) {\mathop {\ge }\limits ^{[3]}} \Bigg (1 - \frac{5q^3}{2^{2n}} - \frac{v}{2^n}\Bigg ) \end{aligned}$$

where [1] follows from the assumptions $u \le 2^n/9$, [2] follows as $\frac{9u^2}{2^{2n}} \ge \frac{(18u+3)}{2^{2n}}-\frac{3}{2^n}$ and [3] follows as $\sum \limits _{u=0}^{q/2-1} (v'+v'') \le v$.    $\square$

4 DWCDM and Its Security Result

In this section, we discuss our proposed construction DWCDM and state its security in nonce respecting and nonce misuse setting. Let us recall the DWCDM construction $\textsf {DWCDM}[\textsf {E}, \textsf {E}^{-1}, \textsf {H}](N, M) := \textsf {E}^{-1}_K(\textsf {E}_K(N) \oplus N \oplus \textsf {H}_{K_h}(M))$ where $N = N^* \Vert 0^{n/3}$. $\textsf {E}_K$ is a n-bit block cipher and $\textsf {H}_{K_h}$ is an $\epsilon _{1}$-regular, $\epsilon _{2}$-AXU and $\epsilon _{3}$-3-way regular n-bit keyed hash function. A schematic diagram of DWCDM is shown in Fig. 1. Note that, DWCDM is structurally similar to EWCDM, but unlike EWCDM, our construction uses the same block cipher key and the last block cipher call of EWCDM is replaced by its decryption function. Moreover, DWCDM cannot exploit the full nonce space like EWCDM, otherwise its beyond birthday security will be compromised as explained below.

Fig. 1.

Decrypted Wegman-Carter with Davies-Meyer construction.

4.1 Why DWCDM Cannot Accommodate Full n-bit Nonce

As mentioned above, for DWCDM we need to reduce the nonce space to $2n \slash 3$-bits. If it uses the full nonce space then using a nonce respecting adversary $\textsf {A}$ who set the tags as nonce repeatedly, can mount a birthday bound forging attack on DWCDM as follows:

Suppose, an adversary starts with query (N, M) and then makes a chain of queries of the form $(T_{i-1},M)$ where $(T_{i-1}, M)$ is the i-th query and $T_{i-1}$ is the response of the previous $(i-1)$-th query, until the first time collision occurs (i.e. a response matches with one of the previous responses). If the adversary makes upto $q \approx 2^{n/2}$ queries, it gets a collision $T_i=T_j$ with high probability. Interestingly, if $(j-i)$⁷ is even (which holds with probability $1 \slash 2$), then

$$T_j=T_i \text{ iff } (T_i+T_{i+1}+\cdots +T_{j-1} = \mathbf {0}).$$

Now, this property can be easily used A to predict $T_i=T_j$ if it finds $T_i+T_{i+1}+\cdots +T_{j-1} = \mathbf {0}$ for some i, j such that $(j-i) \text{ is } \text{ even }$.

However, if we restrict the nonce space to $2n \slash 3$ bits, then this attack doesn’t work because now using the tag as a valid nonce is a probabilistic event. Probability that a tag is a valid nonce is $2^{-n/3}$. This restricts the adversary from forming a chain as used in the attack. In fact, if adversary makes $2^{2n/3}$ many MAC queries then the expected number of tags whose last $n\slash 3$ bits are all zeros is $2^{n/3}$. Now, if adversary uses these $2^{n/3}$ tags as the nonces, then the expected number of tags whose last $n \slash 3$ bits are zeros is 1 and then adversary cannot proceed further. This phenomenon effectively invalidates the above attack to happen.

4.2 Nonce Respecting Security of DWCDM

In this section, we state that DWCDM is secure up to $2^{2n/3}$ MAC queries and $2^n$ verification queries against nonce respecting adversaries. Formally, the following result bounds the MAC advantage of DWCDM against nonce respecting adversaries.

Theorem 2

Let $\mathcal {M}, \mathcal {K}$ and $\mathcal {K}_{h}$ be finite and non-empty sets. Let $\mathsf {E} : \mathcal {K} \times \{0,1\}^n \rightarrow \{0,1\}^n$ be a block cipher and $\mathsf {H} : \mathcal {K}_h \times \mathcal {M} \rightarrow \{0,1\}^n$ be an $\epsilon _{1}$ regular, $\epsilon _{2}$ AXU and $\epsilon _{3}$ 3-way regular hash function. Then, the MAC advantage for any $(q_m,q_v,t)$ nonce respecting adversary against $\mathsf {DWCDM}[\mathsf {E}, \mathsf {E}^{-1}, \mathsf {H}]$ is given by,

$$\begin{aligned} \mathbf {Adv}^{\mathrm {MAC}}_{\mathsf {DWCDM}[\mathsf {E}, \mathsf {E}^{-1}, \mathsf {H}]}(q_m,q_v,t)\le & {} \mathbf {Adv}^{\mathrm {SPRP}}_{\mathsf {E}}(q_m+q_v,t') + \frac{2q_m}{2^{2n/3}} + q_m \epsilon _1 + \frac{2q_m \epsilon _2}{2^{n/3}} \\+ & {} \max \{ q_v\epsilon _{1}, 2q_v\epsilon _{2}, 2q_v\epsilon _{3}, \frac{q_m}{2^{2n/3}} \} + \frac{(q_m + q_v)}{2^n} + \frac{5q_m^3}{2^{2n}}, \end{aligned}$$

where $t'=O(t+(q_m + q_v)t_H)$, $t_H$ be the time for computing the hash function. By assuming $\epsilon _{1}, \epsilon _2, \epsilon _3 \approx 2^{-n}$ and $q_m \le 2^{2n/3}$, $\mathsf {DWCDM}$ is secured up to roughly $q_m \approx 2^{2n/3}$ MAC queries and $q_v \approx 2^{n}$ verification queries.

4.3 Nonce Misuse Security of DWCDM

Similar to EWCDM [13], one can prove that $\textsf {DWCDM}[\textsf {E}, \textsf {E}^{-1}, \textsf {H}]$ is birthday bound secure MAC against nonce misuse adversaries. In particular, DWCDM is secure up to $2^{n/2}$ MAC queries and $2^n$ verification queries against nonce misuse adversaries and that the security bound is essentially tight. More formally, we have the following MAC security result of DWCDM in nonce misuse setting.

Theorem 3

Let $\mathcal {M}, \mathcal {K}$ and $\mathcal {K}_{h}$ be finite and non-empty sets, $\mathsf {E} : \mathcal {K} \times \{0,1\}^n \rightarrow \{0,1\}^n$ be a block cipher and $\mathsf {H} : \mathcal {K}_h \times \mathcal {M} \rightarrow \{0,1\}^n$ be an $\epsilon _{1}$ regular and $\epsilon _{2}$ AXU hash function. Then, the MAC security of $\mathsf {DWCDM}[\mathsf {E}, \mathsf {E}^{-1}, \mathsf {H}]$ in nonce misuse setting is given by

$$\mathbf {Adv}^{\mathrm {MAC}}_{\mathsf {DWCDM}}(q_m,q_v,t) \le \mathbf {Adv}^{\mathrm {SPRP}}_{\mathsf {E}}(q_m+q_v,t') + q_m^2 \epsilon _{2} + \frac{4q_m^2}{2^n} + q_m \epsilon _{1} + \frac{(q_m + q_v)}{2^n},$$

where $t' = O(t + q(q_m + q_v)t_H), t_H$ be the time for computing hash function.

By assuming $\epsilon _{1} \approx 2^{-n}$ and $\epsilon _{2} \approx 2^{-n}$, DWCDM is secure up to roughly $q_m \approx 2^{n/2}$ MAC queries and $q_v \approx 2^{n}$ verification queries. The proof of this theorem can be found in the full version [18].

Tightness of the Bound

We show that the above bound of DWCDM is tight by demonstrating a forging attack which shows thats roughly $2^{n/2}$ MAC queries are enough to break the MAC security of DWCDM when an adversary is allowed to repeat nonce only for once. The attack is as follows:

• 1. Adversary $\textsf {A}$ makes q many MAC queries $(N_i, M_i)$ with distinct nonces where a collision in the response, i.e. $T_i = T_j$ for some $i < j$ occurs.

• 2. Make a MAC query $(N_j, M_i)$. Let $T_{q+1}$ be the response.

• 3. Forge with $(N_{i}, M_j, T_{q+1})$.

As $\mathsf {\Pi }(T_{q+1}) = \mathsf {\Pi }(N_i) \oplus N_i \oplus \textsf {H}_{K_h}(M_j)$, $(N_i,M_j,T_{q+1})$ is a valid forgery. If we make $q=2^{n/2}$ many queries, with very high probability, we will get a collision in step 1, and mount the attack. Note that, the attack does not exploit any specific properties of the hash function and a single time repetition of nonce makes the construction vulnerable above birthday bound security.

4.4 nPolyMAC: An Instantiation of DWCDM

In this section, we propose nPolyMAC, an algebraic hash function based instantiation of DWCDM, as defined in Eq. (4), as the underlying hash function of DWCDM construction.

PolyHash [25] is one of the popular examples of algebraic hash function. For a hash key $K_h$ and a for a fixed message M, we first apply an injective padding such as $10^*$ i.e., pad 1 followed by minimum number of zeros so that the total number of bits in the padded message becomes multiple of n. Let the padded message be $M^* = M_1 \Vert M_2 \Vert \ldots \Vert M_l$ where for each i, $|M_i| = n$. Then we define

$$\textsf {Poly}_{K_h}(M) = M_l \cdot K_h \oplus M_{l-1} \cdot K_h^2 \oplus \ldots \oplus M_{1} \cdot K^{l}_h.$$

It has already been shown in Proposition 1 that Poly is a $\ell /2^n$ regular, AXU and 3-way regular hash function. Following these results, we show in the following that $\textsf {nPolyMAC}[\textsf {Poly}, \textsf {E}, \textsf {E}^{-1}]$ is secure up to $2^{2n/3}$ MAC and $2^n$ verification queries against nonce respecting adversaries.

Theorem 4

Let $\mathcal {K}, \mathcal {K}_h$ and $\mathcal {M}$ be three non-empty finite sets. Let $\mathsf {E}: \mathcal {K} \times \{0,1\}^n \rightarrow \{0,1\}^n$ be a block cipher. Then, the MAC security of $\mathsf {nPolyMAC}$ in nonce respecting setting is given by

$$\mathbf {Adv}^{\mathrm {MAC}}_{\mathsf {nPolyMAC}}(q_m, q_v, t) \le \mathbf {Adv}^{\mathrm {SPRP}}_{\mathsf {E}}(q_m + q_v, t') + \frac{11q_m \ell }{2^{2n/3}} + \frac{3q_v \ell }{2^n},$$

where $t' = O(t+(q_m + q_v)\ell )$, $\ell$ be the maximum number of message blocks among all q queries.

The proof of the theorem directly follows from Proposition 1 and Theorem 2 with the assumption $q_m \le 2^{2n/3}$.

5 Proof of Theorem 2

In this section, we prove Theorem 2. We would like to note that we will often refer to the construction $\textsf {DWCDM}[\textsf {E}, \textsf {E}^{-1}, \textsf {H}]$ as simply $\textsf {DWCDM}$ where the underlying primitives are assumed to be understood.

The first step of the proof is the standard switch from the computational setting to the information theoretic one by replacing $\textsf {E}_K$ and $\textsf {E}^{-1}_{K}$ with an n-bit uniform random permutation $\mathsf {\Pi }$ and $\mathsf {\Pi }^{-1}$ at the cost of $\mathbf {Adv}^{\mathrm {SPRP}}_{\textsf {E}}(q_m + q_v, t')$ and denote the construction as $\textsf {DWCDM}^*[\mathsf {\Pi }, \mathsf {\Pi }^{-1}, \textsf {H}]$. Hence,

$$\begin{aligned} \mathbf {Adv}^{\mathrm {MAC}}_{\mathsf {DWCDM}}(q_m,q_v,t) \le \mathbf {Adv}^{\mathrm {SPRP}}_{\mathsf {E}}(q_m + q_v,t') + \underbrace{\mathbf {Adv}^{\mathrm {MAC}}_{\mathsf {DWCDM}^*}(q_m,q_v,t)}_{\delta ^*}. \end{aligned}$$

(7)

To upper bound $\delta ^*$, we consider that $\textsf {Rand}$ be a perfect random oracle that on input (N, M) returns T, sampled uniformly at random from $\{0,1\}^n$, whereas $\textsf {Rej}$ be an oracle with inputs (N, M, T), returns always $\bot$ (i.e. rejects). Now, due to [13, 19] we write

$$\delta ^* {:=} \max \limits _{\mathsf {D}} \Pr [\mathsf {D}^{\textsf {TG}[\mathsf {\Pi }, \mathsf {\Pi }^{-1}, \mathsf {H}_{K_h}], \textsf {VF}[\mathsf {\Pi }, \mathsf {\Pi }^{-1}, \mathsf {H}_{K_h}]} = 1] - \Pr [\mathsf {D}^{\textsf {Rand}, \textsf {Rej}} = 1],$$

where the maximum is taken over all non-trivial distinguishers D. This formulation allows us to apply the H-Coefficient Technique [29], as we explain in more detail below, to prove

$$\begin{aligned} \delta ^* \le \frac{2q_m}{2^{2n/3}} + q_m \epsilon _1 + \frac{2q_m \epsilon _2}{2^{n/3}} + \max \{ q_v\epsilon _{1}, 2q_v\epsilon _{2}, 2q_v\epsilon _{3}, \frac{q_m}{2^{2n/3}} \} + \frac{(q_m + q_v)}{2^n} + \frac{5q_m^3}{2^{2n}}. \end{aligned}$$

(8)

H-Coefficient Technique. From now on, we fix a non-trivial distinguisher $\mathsf {D}$ that interacts with either (1) the real oracle $(\textsf {TG}[\mathsf {\Pi }, \mathsf {\Pi }^{-1}, \textsf {H}_{K_h}], \textsf {VF}[\mathsf {\Pi }, \mathsf {\Pi }^{-1}, \textsf {H}_{K_h}])$ for a random permutation $\mathsf {\Pi }$, its inverse $\mathsf {\Pi }^{-1}$ and a random hashing key $K_h$ or (2) the ideal oracle $(\textsf {Rand}, \textsf {Rej})$ making at most $q_m$ queries to its left (MAC) oracle and at most $q_v$ queries to its right (verification) oracle, and outputting a single bit. We let

$$\mathbf {Adv}(\mathsf {D}) = \Pr [\mathsf {D}^{\textsf {TG}[\mathsf {\Pi }, \mathsf {\Pi }^{-1}, \mathsf {H}_{K_h}], \textsf {VF}[\mathsf {\Pi }, \mathsf {\Pi }^{-1}, \mathsf {H}_{K_h}]} = 1] - \Pr [\mathsf {D}^{\textsf {Rand}, \textsf {Rej}} = 1].$$

We assume that $\mathsf {D}$ is computationally unbounded and hence wlog deterministic and that it never repeats a query. Let

$$\tau _m := \{(N_1, M_1, T_1), (N_2, M_2, T_2), \ldots , (N_{q_m}, M_{q_m}, T_{q_m})\}$$

be the list of MAC queries of $\mathsf {D}$ and its corresponding responses. Note that, as D is nonce respecting, there cannot be any repetition of triplet in $\tau _m$. Let also

$$\tau _v := \{(N'_1, M'_1, T'_1, b'_1), (N'_2, M'_2, T'_2, b'_2), \ldots , (N'_{q_v}, M'_{q_v}, T'_{q_v}, b'_{q_v})\}$$

be the list of verification queries of $\mathsf {D}$ and its corresponding responses, where for all j, $b'_j \in \{\top ,\bot \}$ denotes the accept $(b'_j = \top )$ or reject $(b'_j = \bot )$. The pair $(\tau _m, \tau _v)$ constitutes the query transcript of the attack. For convenience, we slightly modify the experiment where we reveal to the distinguisher (after it made all its queries and obtains corresponding responses but before it output its decision) the hashing key $K_h$, if we are in the real world, or a uniformly random dummy key $K_h$ if we are in the ideal world. All in all, the transcript of the attack is $\tau = (\tau _m, \tau _v, K_h)$ where $\tau _m$ and $\tau _v$ is the tuple of MAC and verification queries respectively. We will often simply name a tuple $(N, M, T) \in \tau _m$ a MAC query, and a tuple $(N', M', T', b) \in \tau _v$ a verification query.

A transcript $\tau$ is said to be an attainable (with respect to $\mathsf {D}$) transcript if the probability to realize this transcript in ideal world is non-zero. For an attainable transcript $\tau = (\tau _m, \tau _v, K_h)$, any verification query $(N'_i, M'_i, T'_i, b'_i) \in \tau _v$ is such that $b'_i = \bot$. We denote $\varTheta$ to be the set of all attainable transcripts and $X_{\mathrm {re}}$ and $X_{\mathrm {id}}$ denotes the probability distribution of transcript $\tau$ induced by the real world and ideal world respectively. In the following we state the main lemma of the H-coefficient technique (see e.g. [11] for the proof).

Lemma 1

Let $\mathsf {D}$ be a fixed deterministic distinguisher and $\varTheta = \varTheta _{\mathrm {g}} \sqcup \varTheta _{\mathrm {b}}$ (disjoint union) be some partition of the set of all attainable transcripts. Suppose there exists $\epsilon _{\mathrm {ratio}} \ge 0$ such that for any $\tau \in \varTheta _{\mathrm {g}}$,

$$\frac{\Pr [X_{\mathrm {re}} = \tau ]}{\Pr [X_{\mathrm {id}} = \tau ]} \ge 1 - \epsilon _{\mathrm {ratio}},$$

and there exists $\epsilon _{\mathrm {bad}} \ge 0$ such that $\Pr [X_{\mathrm {id}} \in \varTheta _{\mathrm {b}}] \le \epsilon _{\mathrm {bad}}$. Then, $\mathbf {Adv}(\mathsf {D}) \le \epsilon _{\mathrm {ratio}} + \epsilon _{\mathrm {bad}}$.

The remaining of the proof of Theorem 2 is structured as follows: in Sect. 5.1 we define the transcript graph; in Sect. 5.2 we define bad transcripts and upper bound their probability in the ideal world; in Sect. 5.3, we analyze good transcripts and prove that they are almost as likely in the real and the ideal world. Theorem 2 follows easily by combining Lemma 1, Eqs. (7) and (8) above, and Lemmas 3 and 4 proven below.

5.1 Transcript Graph

Given a transcript $\tau = (\tau _m, \tau _v, K_h)$, we define the following two types of graphs: (a) MAC Graph and (b) Verification Graph.

MAC Graph. Given a transcript $\tau = (\tau _m, \tau _v, K_h)$, we define the MAC graph, denoted as $G^\mathtt{{m}}_{\tau }$ as follows:

$$G^\mathtt{{m}}_{\tau } = ([q_m], E^\mathtt{{m}}) \text{ where } E^\mathtt{{m}} = \{(i,j) \in [q_m] \times [q_m] : N_i = T_j \vee N_j = T_i \vee T_i = T_j\}.$$

For the sake of convenience, we denote the edge (i, j) as a dotted line when $T_i = T_j$, else we denote it as a continuous line. Thus, the edge set of $G^\mathtt{{m}}_{\tau }$ consists of two different types of edges as depicted in Fig. 2(a) and (b). Note that, for a MAC graph we cannot have edges of type (c).

Fig. 2.

Different types of edges of MAC and Verification Graphs. $(a): N_i = T_j / T_i = N_j$, $(b): T_i = T_j$, $(c): N_i=N_j$.

Given such a MAC graph, we can partition the set of vertices in the following way: if vertex i and j are connected by an edge then they belong to the same partition. Each partition is called a component of the graph and the number of vertices in the component is called its size, which we denote as $\zeta$.

Verification Graph. Given a MAC graph $G^\mathtt{{m}}_{\tau }$, we define Verification graph, denoted as $G_{\tau }^\mathtt{{v}}$, by extending $G^\mathtt{{m}}_{\tau }$ with adding one more vertex and at most two edges for incorporating a verification query as follows: For convenience, we reorder the set of MAC queries and verification queries so that all verification queries appears after all MAC queries. Therefore, after such a reordering, j-th verification query becomes $(q_m + j)$-th verification query. Let $(q_m + j)$-th verification query be $(N'_{q_m + j}, M'_{q_m + j}, T'_{q_m + j}, b'_{q_m + j}) \in \tau _v$ and $G^\mathtt{{m}}_{\tau }$ be the MAC graph corresponding to $\tau = (\tau _m, \tau _v, K_h)$. Then we define $G^\mathtt{{v}}_{\tau } = ([q_m] \cup \{q_m + j\}, E^\mathtt{{v}})$ where $E^\mathtt{{v}}$ is defined as follows:

$$E^\mathtt{{v}} = E^\mathtt{{m}} ~\cup ~ \{(q_m + j, r), (q_m + j, s) : r \ne s \in [q_m] \text { such that either of (1)}{-}\text {(4) holds}\}.$$

$${\left\{ \begin{array}{ll} (1)~ N'_{q_m + j} = N_r \wedge T'_{q_m + j} = N_s \\ (2)~ N'_{q_m + j} = N_r \wedge T'_{q_m + j} = T_s \\ (3)~ N'_{q_m + j} = T_r \wedge T'_{q_m + j} = N_s \\ (4)~ N'_{q_m + j} = T_r \wedge T'_{q_m + j} = T_s \end{array}\right. } $$

Definition 2

(Valid Cycle). A cycle $C = (i_1, i_2, \ldots , i_p)$ of length p in the MAC graph $G^\mathtt{{m}}_{\tau }$ is said to be valid if the imposed equality pattern of (N, T), generated out of C, derives

$$\mathbf {0} = \bigoplus \limits _{i \in C} \bigg (N_{i} \oplus \mathsf {H}_{K_h}(M_i)\bigg )$$

equation from the given system of equations.

Similar to the definition of valid cycle of MAC graph, one can define the valid cycle for the Verification graph also. Note that, the definition of valid cycle in MAC graph or verification graph actually resembles to the alternating cycle as stated in Sect. 3.1. Now, we make an important observations about the MAC queries (in ideal oracle) as follows:

Lemma 2

For two MAC queries i, j, we have

$$(a) \text{ if } i<j,~\Pr [T_j=N_i]=\frac{1}{2^n};~~~(b) \text{ if } i>j,~\Pr [T_j=N_i]=\frac{1}{2^{n/3}}.$$

Proof

Proof of the first result holds due to the randomness of $T_j$, i.e. a randomly sampled value $T_j$ is equal to a fixed nonce value $N_i$ holds with probability $2^{-n}$. For the later one, condition $i>j$ ensures that one can set the nonce value $N_i$ to a previously sampled tag value $T_j$. But this would be valid only when the last $n \slash 3$ bits of $T_i$ are all zero, probability of which is $2^{-n/3}$.    $\square$

5.2 Definition and Probability of Bad Transcripts

In this section, we define and bound the probability of bad transcript in ideal world. But, before that we first briefly justify the reason about our identified bad events and there after we define the bad transcript accordingly.

Let $\tau = (\tau _m, \tau _v, K_h)$ be an attainable transcript. Then, for all MAC queries $(N_i, M_i, T_i)$ in real oracle, we have

$$i \in \{1, \ldots , q_m\}, \mathsf {\Pi }(N_i) \oplus \mathsf {\Pi }(T_i) = N_i \oplus \textsf {H}_{K_h}(M_i).$$

Moreover, for all verification queries $(N'_a, M'_a, T'_a, b_a)$ in real oracle, we have

$$a \in \{1, \ldots , q_v\}, \mathsf {\Pi }(N'_a) \oplus \mathsf {\Pi }(T'_a) \ne N'_a \oplus \textsf {H}_{K_h}(M'_a).$$

We refer to the system of equations as “MAC Equations” which involve only the MAC queries. Similarly, we refer to the system of non-equations as “Verification non-equations” which involve only the verification queries.

Therefore, from a given attainable transcript $\tau$, one can write exactly $q_m$ many affine equations and $q_v$ many non-equations. Now, as one needs to lower bound the number of solutions of this system of equations and non-equations (for analyzing the real interpolation probability), it essentially leads us to the model of extended Mirror theory where the equivalence of two set up is established as follows:

$$ {\left\{ \begin{array}{ll} \phi '(n_i) = N_i, ~ \phi '(t_i) = T_i, ~ \lambda _i = N_i \oplus \mathsf {H}_{K_h}(M_i), ~ i \in \{1, \ldots , q_m\} \\ \phi '(n_a) = N'_a, ~ \phi '(t_a) = T'_a, ~\lambda '_a = N'_a \oplus \mathsf {H}_{K_h}(M'_a), ~ a \in \{1, \ldots , q_v\} \end{array}\right. } $$

Recall that, $(\phi ', \mathrm {\Lambda '})$ where $\mathrm {\Lambda '} = (\lambda _1, \ldots , \lambda _{q_m}, \lambda '_1, \ldots , \lambda '_{q_v})$, was characterized to be bad if either of the following holds:

(i):

$\phi (n_i) = \phi (t_i)$.

(ii):

-:

$\phi (n_i) = \phi (n_j) \text{ and } \phi (t_i) =\phi (t_j)$

-:

$\phi (n_i) = \phi (t_j) \text{ and } \phi (t_i) = \phi (n_j)$ for $i \ne j \in [q_m]$.

(iii):

there is an alternating cycle.

(iv):

for all $j \in [q_v]$ and $i_1, \ldots , i_c \in [q_m]$, $c \ge 0$, such that $\{i_1, \ldots , i_c, q_m+j\}$ is dependent system then $\lambda _{i_1} \oplus \cdots \oplus \lambda _{i_c} \oplus \lambda '_{j} = \mathbf {0}$.

where $\phi = \phi '_{|q_m}$. Therefore, with the help of equivalence of two set up as established above, we justify our identified bad events:

• $(i) \Rightarrow N_i = T_i$

• $(ii) \Rightarrow$ existence of a valid cycle in the MAC graph $G_{\tau }^\mathtt{{m}}$.

• $(iii) \Rightarrow N_i \oplus \mathsf {H}_{K_h}(M_i) = N_j \oplus \mathsf {H}_{K_h}(M_j), T_i = T_j$ or $N_i = T_j, N_i \oplus \mathsf {H}_{K_h}(M_i) = N_j \oplus \mathsf {H}_{K_h}(M_j)$ such that $i \ne j \in [q_m]$.

Moreover, recall that while considering the non-equation then we considered that any of $q_v$ non-equations can be determined from a subset of $q_m$ many affine equations with their corresponding sum of $\lambda$ constant becomes zero, which is to say that

• the verification graph $G_{\tau }^\mathtt{{v}}$ contains any valid cycle.

Summarizing above, we now define the bad transcript.

Definition 3

A transcript $\tau = (\tau _m, \tau _v, K_h)$ is said to be $\mathsf {bad}$ if the associated MAC graph $G^\mathtt{{m}}_{\tau }$ and the Verification graph $G_{\tau }^\mathtt{{v}}$ satisfies the either of the following properties:

• $\mathsf {B0}:$ $\exists i \in [q_m]$ such that $T_i = \mathbf {0}$.

• $\mathsf {B1}:$ $G^\mathtt{{m}}_{\tau }$ has a component of size 3 or more.

• $\mathsf {B2}:$ $G^\mathtt{{m}}_{\tau }$ contains a valid cycle of any arbitrary length that also includes the self loop (that implicitly takes care of the condition $N_i = T_i$).

• $\mathsf {B3}:$ $G_{\tau }^\mathtt{{v}}$ contains a valid cycle of any arbitrary length that involves the verification query.

Moreover, $\tau$ is also said to be bad if

• $\mathsf {B4}:$ $\exists i \ne j \in [q_m] \text{ such } \text{ that } N_i \oplus \mathsf {H}_{K_h}(M_i) = N_j \oplus \mathsf {H}_{K_h}(M_j), T_i = T_j$.

• $\mathsf {B5}$: $\exists i \ne j \in [q_m] \text{ such } \text{ that } N_i = T_j, N_i \oplus \mathsf {H}_{K_h}(M_i) = N_j \oplus \mathsf {H}_{K_h}(M_j)$.

• $\mathsf {B6}:$ $\exists i \in [q_m] \text{ such } \text{ that } \mathsf {H}_{K_h}(M_i) = N_i$.

Condition $\textsf {B1}$ actually imposes a restriction on the block maximality as we do not allow to have a larger component size for a good transcript. Condition B6 ensures that for a good transcript, all the elements of the tuple $\big (N_1 \oplus \textsf {H}_{K_h}(M_1), \ldots , N_{q_m} \oplus \textsf {H}_{K_h}(M_{q_m}) \big )$ are non-zero. Note that, if we do not consider the condition B6, then for a good attainable transcript the real interpolation probability would become zero.

We denote $\varTheta _b \subseteq \varTheta$ be the set of all attainable bad transcripts and the event B denotes $\textsf {B} := \textsf {B0} \vee \textsf {B1} \vee \textsf {B2} \vee \textsf {B3} \vee \textsf {B4} \vee \textsf {B5} \vee \textsf {B6}$. We bound the probability of event B in the following lemma, proof of which is deffered to Sect. 5.4.

Lemma 3

Let $X_{\mathrm {id}}$ and $\varTheta _b$ be defined as above. If $q_m \le 2^{2n/3}$ and $q_v \le 2^n$, then

$$\Pr [X_{\mathrm {id}} \in \varTheta _b] \le \epsilon _{\mathsf {bad}} = \frac{2q_m}{2^{2n/3}} + \frac{q_m}{2^n} + q_m \epsilon _1 + \frac{2q_m \epsilon _2}{2^{n/3}} + \max \big \{ q_v\epsilon _{1}, 2q_v \epsilon _{2}, 2q_v\epsilon _{3}, \frac{q_m}{2^{2n/3}} \big \}.$$

5.3 Analysis of Good Transcripts

In this section, we show that for a good transcript $\tau$, realizing $\tau$ is almost as likely in the real world as in the ideal world. Formally, we prove the following lemma.

Lemma 4

Let $\tau = (\tau _m, \tau _v, K_h)$ be a good transcript. Then

$$\frac{\mathsf {p}_{\mathrm {re}}(\tau )}{\mathsf {p}_{\mathrm {id}}(\tau )} := \frac{\Pr [X_{\mathrm {re}} = \tau ]}{\Pr [X_{\mathrm {id}} = \tau ]} \ge (1 - \epsilon _{\mathrm {ratio}}) = \bigg (1 - \frac{5q_m^3}{2^{2n}} - \frac{q_v}{2^n} \bigg ).$$

Proof

Consider the good transcript $\tau = (\tau _m, \tau _v, K_h)$. Since in the ideal world the MAC oracle is perfectly random and the verification always rejects, one simply has

$$\begin{aligned} \mathsf {p}_{\mathrm {id}} := \Pr [X_{\mathrm {id}} = \tau ] = \frac{1}{|\mathcal {K}_h|} \cdot \frac{1}{2^{nq_m}}. \end{aligned}$$

(9)

We must now lower bound the probability of getting $\tau$ in real world. We say that a permutation $\mathsf {\Pi }$ is compatible with $\tau _m$ if $\forall i \in [q_m]$, (i) happens and $\mathsf {\Pi }$ is compatible with $\tau _v$ if $\forall a \in [q_v]$, (ii) happens

$$(i)~ \mathsf {\Pi }(N_i) \oplus \mathsf {\Pi }(T_i) = \underbrace{N_i \oplus \mathsf {H}_{K_h}(M_i)}_{\lambda _i}, ~~ (ii)~ \mathsf {\Pi }(N'_a) \oplus \mathsf {\Pi }(T'_a) \ne \underbrace{N'_a \oplus \mathsf {H}_{K_h}(M'_a)}_{\lambda '_a}.$$

We simply say that $\mathsf {\Pi }$ is compatible with $\tau$ if it is compatible with $\tau _m$ and $\tau _v$. We denote $\textsf {Comp}(\tau )$ the set of permutations that are compatible with $\tau$. Therefore,

Lower Bounding $\textsf {P}_{mv}$: Observe that lower bounding $\textsf {P}_{mv}$ implies lower bounding the probability of the number of solutions to the following system of $q_m$ many equations of the form $\mathsf {\Pi }(N_i) \oplus \mathsf {\Pi }(T_i) = \lambda _i$ and $q_v$ many non-equations of the form $\mathsf {\Pi }(N'_a) \oplus \mathsf {\Pi }(T'_a) \ne \lambda '_a$.

Let us assume the distinct number of random variables in the above set of equations is $\alpha$. As the transcript $\tau$ is good, we have the following properties:

• (i) all $\lambda _i$ values are non-zero (otherwise condition B6 is satisfied).

• (ii) $(\phi ', \mathrm {\Lambda '})$ is good.

• (iii) Finally, block maximality $\xi _{\max }$ is 3.

Above properties enable us directly to apply Theorem 1 to lower bound $\textsf {P}_{mv}$ as follows:

$$\begin{aligned} \mathsf {P}_{mv} \ge \frac{1}{2^{nq_m}} \bigg (1 - \frac{5q_m^3}{2^{2n}} - \frac{q_v}{2^n} \bigg ). \end{aligned}$$

(10)

Therefore, from Eq. (10), we have

$$\begin{aligned} \mathsf {p}_{\mathrm {re}}(\tau ) \ge \frac{1}{|\mathcal {K}_h|} \cdot \frac{1}{2^{nq_m}} \cdot \bigg (1 - \frac{5q_m^3}{2^{2n}} - \frac{q_v}{2^n} \bigg ). \end{aligned}$$

(11)

Finally, taking the ratio of Eqs. (11) to (9), the result follows.    $\square$

5.4 Proof of Lemma 3

In this section, we prove Lemma 3. A more detailed version of this proof can be found in the full version of this paper [18]. In order to bound $\Pr [X_{\mathrm {id}} \in \varTheta _b]$, it is enough to bound $\Pr [\textsf {B}]$. Therefore, we write

$$\begin{aligned} \Pr [\textsf {B}] \le \sum \limits _{\textsf {v} \in \{0,1,4,5,6\}} \Pr [\textsf {Bv}] + \Pr [\textsf {B2}~ | ~\overline{\textsf {B1}}] + \Pr [\textsf {B3}~ | ~\overline{\textsf {B0}} \wedge \overline{\textsf {B1}} \wedge \overline{\textsf {B2}}]. \end{aligned}$$

(12)

In the following, we bound the probabilities of all the bad events individually.

Bounding B0. As the responses are sampled uniformly and independently to all other sampled random variables, $\Pr [\textsf {B0}] \le \frac{q_m}{2^n}$.

Bounding B1. Event B1 occurs if there exists a component of size at least 3 in $G^\mathtt{{m}}_{\tau }$, i.e. there exist a chain of two edges. Depending on whether the edges are dotted (Dot) or continuous (Con), there are three possible choices of components: (Dot-Dot), (Dot-Con) and (Con-Con), as depicted in Fig. 3.

Fig. 3.

Different components of size of three. $(a)~T_i = T_j = T_k$, $(b)~T_i = T_j = N_k$ or $T_i = T_j, N_j = T_k$ and $(c)~N_i = T_j, N_j = T_k$ or $T_i = N_j, T_j = N_k$.

Using Lemma 2 and the fact that each $T_i$ is sampled uniformly at random from $\{0,1\}^n$, one can show that having any such component has a probability of $\frac{q_m}{2^{2n/3}}$ and therefore, we have $\Pr [\textsf {B1}] \le \frac{q_m}{2^{2n/3}}$.

Bounding ${{\mathbf {\mathsf{{B2}}}}}~ | \overline{{\mathbf {\mathsf{{B1}}}}}$. Here we bound the existence of a cycle of length one (self loop) and two (parallel edges), as depicted in Fig. 4(a) and (b). Again using Lemma 2 and the fact that each $T_i$ is sampled uniformly at random from $\{0,1\}^n$, one can show that the probability of having a self loop or parallel edges can be bounded by $\frac{q_m}{2^{2n/3}}$ and therefore $\Pr [\textsf {B2} ~|~ \overline{\textsf {B1}}] \le \frac{q_m}{2^{2n/3}}$.

Fig. 4.

(a) Self Loop in $G^\mathtt{{m}}_{\tau }$: when $N_i = T_i$, (b) Parallel Edges in $G^\mathtt{{m}}_{\tau }$: $N_i = T_j, N_j = T_i$, (c) Self Loop in $G^\mathtt{{v}}_{\tau }$: when $N'_a = T_a$, (d) Parallel Edges in $G^\mathtt{{v}}_{\tau }$: (d.1) $N'_a = N_i, T'_a = T_i$, (d.2) $N'_a=T_i,T'_a=N_i$. Node with concentric circle denotes the verification query node.

Bounding ${\mathbf {\mathsf{{B3}}}} ~|~ \overline{{\mathbf {\mathsf{{B0}}}}} \wedge \overline{{\mathbf {\mathsf{{B1}}}}} \wedge \overline{{\mathbf {\mathsf{{B2}}}}}$. Recall that event B3 holds if there exists any cycle in $G^\mathtt{{v}}_{\tau }$ and the sum of the corresponding $N \oplus \textsf {H}_{K_h}(M)$ is zero. But, as we conditioned on $\overline{\textsf {B0}} \wedge \overline{\textsf {B1}} \wedge \overline{\textsf {B2}}$, it is enough to bound the existence of a cycle of length one (self loop), two (parallel edges) and three (closed triangle).

Self Loop. As the hash function is $\epsilon _{1}$ regular, the probability of having a self loop can be bounded by $q_v \epsilon _{1}$.

Parallel Edges. A parallel edge or cycle of length 2 in $G^\mathtt{{v}}_{\tau }$ implies that the edges would be (i) one dotted and one dashed (Dot-Dash) or (ii) both continuous (Con-Con), as depicted in Fig. 4(d.1) and (d.2). Using Lemma 2 and the fact that the hash function is $\epsilon _2$ AXU, one can show that the probability of having parallel edges can be bounded by $2q_v \epsilon _{2}$.

Closed Triangle. A closed triangle or cycle of length 3 in $G^\mathtt{{v}}_{\tau }$ essentially implies that the triangle must have been form having edges of the form (Con-Dash-Dot), (Con-Con-Con) and (Dot-Dash-Con), as depicted in Fig. 5. Again using Lemma 2 and the fact that the hash function is $\epsilon _3$ 3-way-regular, one can show that the probability of having edges of the above form in $G^\mathtt{{v}}_{\tau }$ is $\max \{2q_v \epsilon _{3}, \frac{q_m}{2^{2n/3}} \}$. Therefore, combining everything together, $\Pr [\textsf {B3} ~|~ \overline{\textsf {B0}} \wedge \overline{\textsf {B1}} \wedge \overline{\textsf {B2}}] \le \max \{2q_v \epsilon _{3}, 2q_v \epsilon _{2}, q_v \epsilon _{1}, \frac{q_m}{2^{2n/3}} \}$.

Fig. 5.

Cycles of length 3 including the verification query which is denoted by the concentric circle node.

Bounding B4: Since, in the ideal oracle the hash key is sampled independent to all previously sampled MAC responses $T_i$, we have $\Pr [\textsf {B4}] \le \frac{q_m^2.\epsilon _{2}}{2^n}$.

Bounding B5: It is easy to see that for fixed i and j, $N_i \oplus \textsf {H}_{K_h}(M_i) = N_j \oplus \textsf {H}_{K_h}(M_j)$ holds with probability $\epsilon _{2}$. Now summing over all possible choices of i and j, using Lemma 2 and assuming $q_m \le 2^{2n/3}$, we obtain $\Pr [\textsf {B5}] \le \frac{q_m \epsilon _2}{2^{n/3}}$.

Bounding B6: For any fixed i the event $N_i = \textsf {H}_{K_h}(M_i)$ occurs with probability $\epsilon _{1}$, due to the regular property of the hash function. Summing over all choices of i, we have $\Pr [\textsf {B6}] \le q_m \epsilon _{1}$.

Finally, by assuming $q_m \le 2^{2n/3}$, Lemma 3 follows from all the above bounds.

6 1K-DWCDM: A Single Keyed DWCDM

Recall that, our proposed construction DWCDM is instantiated with a hash function and a block cipher where the hash key is independent to block cipher keys, leading to have a two-keyed (counting hash key separately from block cipher keys) nonce based MAC. In this section, we transform the DWCDM construction to a purely single keyed construction by setting the underlying hash key $K_h$ to the encryption of $\mathbf 1$ (i.e. $K_h:=\textsf {E}_{K}(\mathbf 1 )$) and argue that the modified construction (that we call as 1K-DWCDM) is secure.

Now, we state and prove that 1K-DWCDM is secure up to $2^{2n/3}$ MAC queries and $2^n$ verification queries against all nonce respecting adversaries. We mainly focus on the nonce respecting security of the construction, as its nonce misuse security is very similar to that of DWCDM and hence we skip it.

Theorem 5

Let $\mathcal {M}$ and $\mathcal {K}$ be finite and non-empty sets. Let $\mathsf {E} : \mathcal {K} \times \{0,1\}^n \rightarrow \{0,1\}^n$ be a block cipher and $\mathsf {H} : \mathsf {E}_{K}(\mathbf {1}) \times \mathcal {M} \rightarrow \{0,1\}^n$ be an $\epsilon _{1}$ regular, $\epsilon _{2}$ AXU and $\epsilon _{3}$ 3-way regular hash function. Then, the MAC advantage of $\mathsf {1K}\text{- }\mathsf {DWCDM}$ is given by:

$$\begin{aligned} \mathbf {Adv}^{\mathrm {MAC}}_{\mathsf {1K}\text{- }\mathsf {DWCDM}[\mathsf {E}, \mathsf {E}^{-1}, \mathsf {H}]}(q_m,q_v,t)\le & {} \mathbf {Adv}^{\mathrm {SPRP}}_{\mathsf {E}}(q_m+q_v,t') + \frac{3q_m}{2^{2n/3}} + \frac{q_m^2 \epsilon _{2}}{2^n} + \frac{q_v}{2^n-1} \\+ & {} \max \{q_v \epsilon _{1}, 2q_v \epsilon _{2}, 2q_v \epsilon _{3}, \frac{q_m}{2^{2n/3}} \} + q_v \epsilon _{1} + \frac{q_m}{2^n} + \frac{5q_m^3}{2^{2n}}, \end{aligned}$$

where $t' = O(t+(q_m+q_v)t_H)$, $t_{H}$ being the time for computing hash function. Assuming $\epsilon _1, \epsilon _2$ and $\epsilon _3 \approx 2^{-n}$ and $q_m \le 2^{2n/3}$, $\mathsf {1K}\text{- }\mathsf {DWCDM}[\mathsf {E}, \mathsf {E}^{-1}, \mathsf {H}]$ construction is secured up to roughly $2^{2n/3}$ MAC and $2^n$ verification queries.

Proof

The proof approach is similar to the one used in Theorem 2. Using standard argument, we can replace $\textsf {E}_K$ and $\textsf {E}^{-1}_K$ with an n-bit uniform random permutation $\mathsf {\Pi }$ and its inverse $\mathsf {\Pi }^{-1}$, denote the construction as $\textsf {1K-DWCDM}^*[\mathsf {\Pi }, \mathsf {E}^{-1}, \textsf {H}]$ and bound $\mathbf {Adv}^{\mathrm {MAC}}_{\mathsf {1K}\text{- }\mathsf {DWCDM}^*[\mathsf {\Pi }, \mathsf {\Pi }^{-1}, \mathsf {H}]}(\mathsf {A})$:

For this, we first define the ideal oracle which works as follows: for each MAC query (N, M), it samples the response T from $\{0,1\}^n$ uniformly at random and returns it to the distinguisher and for each verification query it returns $\bot$. As before, we reveal the hashing key $K_h$ to the distinguisher after it made all it’s queries and before the final decision. Note that, the hash key is $\textsf {E}_{K}(\mathbf 1 )$ in the real world and a uniformly random dummy key $K_h$, sampled uniformly at random from $\{0,1\}^n$ in the ideal world. Let the transcript of the attack is $\tau = (\tau _m, \tau _v, K_h)$ where $\tau _m$ and $\tau _v$ is the tuple of MAC and verification queries respectively.

Bad Transcript. The definition of bad transcript is similar to that of defined in Sect. 5.2 and therefore, we have the following result:

Let $X_{\mathrm {id}}$ and $\varTheta _b$ be defined as above. If $q_m \le 2^{2n/3}$ and $q_v \le 2^n$, then

$$\begin{aligned} \Pr [X_{\mathrm {id}} \in \varTheta _b] \le \frac{3q_m}{2^{2n/3}} + \frac{q_m^2 \epsilon _{2}}{2^n} + \max \big \{q_v \epsilon _{1}, 2q_v \epsilon _{2}, 2q_v \epsilon _{3}, \frac{q_m}{2^{2n/3}} \big \} + q_v \epsilon _{1} + \frac{q_m}{2^n}. \end{aligned}$$

(13)

Analysis of Good Transcripts. Similar to Lemma 4, we prove that for any good transcript $\tau$, realizing $\tau$ is almost as likely as real and in the ideal world. As the transcript $\tau$ is good, each sampled $T_i$ value is non-zero. Since, in the ideal world the MAC oracle is perfectly random and the verification always rejects, one simply has

$$\begin{aligned} \mathsf {p}_{\mathrm {id}} := \Pr [X_{\mathrm {id}} = \tau ] = \frac{1}{2^n} \cdot \frac{1}{(2^{n}-1)^{q_m}}. \end{aligned}$$

(14)

Now, for the real interpolation probability, we have

$$\Pr [\mathsf {\Pi }(N_i) \oplus \mathsf {\Pi }(T_i) = \lambda _i, \forall i \in [q_m] \text{ and } \mathsf {\Pi }(N'_a) \oplus \mathsf {\Pi }(T'_a) \ne \lambda '_a, \forall a \in [q_v]].$$

Additionally, if the adversary makes any verification query $(N'_a, M'_a, T'_a)$ with tag $T'_a$ set to $\mathbf 1$, then we need to ensure that

$$\begin{aligned} \mathsf {\Pi }(N'_a) \ne \underbrace{\mathsf {\Pi }(\mathbf {1}) \oplus N'_a \oplus \mathsf {H}_{\mathsf {\Pi }(\mathbf {1})}(M'_a)}_{\lambda ''_a}, \forall a \in [q_v]]. \end{aligned}$$

(15)

Since, the hash key, i.e., $\mathsf {\Pi }(\mathbf 1 )$, is revealed to the adversary after the interaction is over, the right hand side of the non-Eq. (15) becomes a constant, which makes it a uni-variate affine non-equation and then it is satisfied by condition (c) of Theorem 1. Therefore, we have

$$\begin{aligned} \mathsf {p}_{\mathrm {re}}(\tau )= & {} \frac{1}{2^n} \cdot \Pr [\mathsf {\Pi }(N_i) \oplus \mathsf {\Pi }(T_i) = \lambda _i, \forall i \in [q_m], \mathsf {\Pi }(N'_a) \oplus \mathsf {\Pi }(T'_a) \ne \lambda '_a, \nonumber \\&~~~~~~~~~~~~~ \mathsf {\Pi }(N'_a) \ne \lambda ''_a, \forall a \in [q_v]] \nonumber \\\ge & {} \frac{1}{2^n} \cdot \frac{1}{(2^{n}-1)^{q_m}} \cdot \bigg (1 - \frac{5q_m^3}{2^{2n}} - \frac{q_v}{2^n-1} \bigg ). \end{aligned}$$

(16)

The last inequality follows using similar to the proof of Lemma 4 and Eq. (10). Finally, from Eqs. (14) and (16), we compute the ratio as follows:

$$\begin{aligned} \frac{\mathsf {p}_{\mathrm {re}}(\tau )}{\mathsf {p}_{\mathrm {id}}(\tau )} \ge \bigg (1 - \frac{5q_m^3}{2^{2n}} - \frac{q_v}{2^n-1} \bigg ). \end{aligned}$$

(17)

Finally, Theorem 5 follows from Eqs. (13) and (17).    $\square$

7 Towards Higher Security of DWCDM

In this section, we briefly describe how to boost the security of DWCDM upto $(k-1)/k$-bit for a general k. The underlying construction remains as it is, however the nonce space is increased to $(k-1)n/k$-bits i.e., $\textsf {DWCDM\_k}[\textsf {E}, \textsf {H}](N, M) := \textsf {E}^{-1}_K(\textsf {E}_K(N) \oplus N \oplus \textsf {H}_{K_h}(M))$ but here we consider $N = N^* \Vert 0^{n/k}$ where $N^*$ is a $(k-1)n/k$ bit nonce. For this, we first state the following conjecture on Mirror theory, which is a generalized version of extended Mirror theorem as introduced in Sect. 3.2.

Conjecture 1

(Extended Mirror Theorem for $\xi _{\max } = k$). Let $(\mathcal {E}^{=} \cup \mathcal {E}^{\ne }, \phi ', \mathrm {\Lambda '})$ be a system of q many affine equations and v many affine non-equations associated with index mapping function $\phi '$ over $\mathrm {GF}(2^n)$ which are of the form $P_{\phi (n_i)} \oplus P_{\phi (t_i)} = \lambda _i$ for $i \in [q]$ and $P_{\phi (n_j)} \oplus P_{\phi (t_j)} \ne \lambda '_j (\ne \mathbf {0})$ for $j \in [q+1, q+v]$ over the set of $\alpha$ many unknown variables $\mathcal {P} = \{P_1, \ldots , P_\alpha \}$ such that $P_{a}$ may be equals to some $P_{\phi (n_i)}$ or $P_{\phi (b_j)}$, where $a \in \{\phi (n_{j}), \phi (t_{j})\}, j \in [q, q+v]$. Now, if

• (i)  $(\phi ', \mathrm {\Lambda '})$ is good and

• (ii)  $\xi _{\max } = k$

then the number of solutions for $\mathcal {P}$, denoted by $h_{\beta }$ (where $\beta =\frac{kq}{k-1}$) such that $P_i \ne P_j$ for all distinct $i, j \in \{1, \ldots , \alpha \}$ is

$$\begin{aligned} h_{\beta } \ge \frac{(2^n)_{\beta }}{2^{nq}} \bigg (1 - O\bigg (\frac{q^k}{2^{(k-1)n}} + \frac{v}{2^n}\bigg ) \bigg ). \end{aligned}$$

(18)

Assuming this conjecture holds, we have the following result on the MAC advantage of DWCDM_k:

Theorem 6

Let $\mathsf {E}$ be a block cipher and $\mathsf {H}$ be an $\epsilon _1$ regular, $\epsilon _2$ AXU and $\epsilon _j$ j-way regular hash function,⁸ for all $3 \le j \le k$ (e.g., $\mathrm {PolyHash}$). Then, the MAC advantage for any $(q_m,q_v,t)$ nonce-respecting adversary against $\mathsf {DWCDM\_k}$ is given by,

$$\begin{aligned} \mathbf {Adv}^{\mathrm {MAC}}_{\mathsf {DWCDM\_k}}(q_m,q_v,t)\le & {} \mathbf {Adv}^{\mathrm {SPRP}}_{\mathsf {E}}(q_m+q_v,t') + O(q_m^k/2^{n(k-1)}+q_v.\epsilon ), \end{aligned}$$

where $q_v = \max \{\epsilon _1, \epsilon _2, \epsilon _j\}$ and $t'=O(t+(q_m + q_v)t_H)$.

The proof will be similar to the proof of Theorem 2. We first define the transcript, associated MAC and the verification graph as before.

Now, we call a transcript $\tau = (\tau _m, \tau _v, K_h)$ to be $\mathsf {bad}$ if the associated MAC graph $G^\mathtt{{m}}_{\tau }$ and the Verification graph $G_{\tau }^\mathtt{{v}}$ satisfies the either of the following properties:

• $\mathsf {B1'}:$ $G^\mathtt{{m}}_{\tau }$ has a component of size k or more.

• $\mathsf {B2'}:$ $G^\mathtt{{m}}_{\tau }$ contains a valid cycle of length less than k.

• $\mathsf {B3'}:$ $G_{\tau }^\mathtt{{v}}$ contains a valid cycle of length less than or equals to k that involves the verification query.

Moreover, $\tau$ is also said to be bad if it satisfies $\mathsf {B0},\mathsf {B4},\mathsf {B5},\mathsf {B6}$ (as defined in Definition 3).

Here we will mainly consider bounding $\textsf {B1'}$, $\textsf {B2'}$ and $\textsf {B3'}$, as the remaining ones are already done. Here we provide a sketch for bounding each of this event:

Bounding B1’. Event B1’ occurs if there exists a component of size at least k in $G^\mathtt{{m}}_{\tau }$. This essentially implies there is a chain of $(k-1)$ edges. Let there are $c_1$ number of edges are of the form $T_i=N_j$ with $i < j$. Here we claim that

$$\Pr [\textsf {B1'}] \le q_m. \bigg (\frac{q_m}{2^n}\bigg )^{k-c_1}. \bigg (\frac{1}{2^{k/n}}\bigg )^{c_1}.$$

As $k \ge 4$, the above bound is $O(q_m^k/2^{n(k-1)})$.

Bounding B2’. Event B2’ occurs if there exists a cycle of size less than k in $G^\mathtt{{m}}_{\tau }$. Let us bound a cycle of length $c < (k-1)$. Again, assume there are $c_1$ number of edges of the form $T_i=N_j$ with $i < j$. Using similar argument as above,

$$\Pr [\textsf {B2'}] \le \bigg (\frac{q_m}{2^n}\bigg )^{c-c_1}. \bigg (\frac{1}{2^{k/n}}\bigg )^{c_1}.$$

It is easy to see that for any c, the above bound is $O(q_m/2^n)$.

Bounding B3’. Event B3’ occurs if there exists a cycle of size less than or equals to k in $G^\mathtt{{v}}_{\tau }$. Extending similar arguments used in Lemma 3 to bound the event B3, one can show that if H is $\epsilon$ j-way regular for all $j \le k$ then

$$\Pr [\textsf {B3'}] \approx O\bigg (\frac{q_v.\epsilon .q_m^c}{2^{nc}}\bigg ), c \ge 0.$$

Combining everything together, we have

$$\Pr [\textsf {B}] \approx O(q_m^k/2^{n(k-1)}+q_v.\epsilon ).$$

Next, we fix a good transcript $\tau$. Now, to obtain the lower bound of the probability of getting $\tau$ in real world, we need a lower bound on the probability of the number of solutions to a system of $q_m$ many equations and $q_v$ many non-equations. Again, we can do that using an extended Mirror theory result with maximal block size $\xi _{\max } = k$. From Conjecture 1, we have

$$\begin{aligned} \mathsf {p}_{\mathrm {re}}(\tau ) \ge \frac{1}{|\mathcal {K}_h|} \cdot \frac{1}{2^{nq_m}} \cdot \bigg (1 - O\bigg (\frac{q_m^k}{2^{(k-1)n}} + \frac{q_v}{2^n}\bigg ) \bigg ). \end{aligned}$$

(19)

The theorem follows by applying Patarin’s H-Coefficient Technique.    $\square$

Remark 2

We would like to clarify that increasing the nonce space does not have any relation with the increase in security. We have restricted the nonce space of DWCDM to $2n \slash 3$-bit (note that this is minimum as we must allow $2^{2n/3}$ many MAC queries with distinct nonces) purely because of the simplicity of the extended mirror theory analysis. One can of course increase the nonce space to $(k-1)n/k$-bit for any $k \le n$, but that increases the block maximality $(\xi _{\max })$ to k and hence the analysis of the extended mirror theory would become tedious and involved.

8 Conclusion

In this paper we have proposed DWCDM, a single keyed nonce based MAC, which is structurally identical to $\textsf {EWCDM}$ except that the outer encryption call is replaced by the decryption call and same key is used for both the block cipher calls. Using an extended mirror theory results, we have shown that $\textsf {DWCDM}$ is secure roughly up to $2n \slash 3$-bit against nonce-respecting adversaries and $n \slash 2$-bit against nonce-misuse adversaries. We have also provided an intuition on how to boost the nonce-respecting security of DWCDM upto $(k-1)/k$-bit for a general k.