Abstract
We consider the following basic question: to what extent are standard secret sharing schemes and protocols for secure multiparty computation that build on them resilient to leakage? We focus on a simple local leakage model, where the adversary can apply an arbitrary function of a bounded output length to the secret state of each party, but cannot otherwise learn joint information about the states.
We show that additive secret sharing schemes and high-threshold instances of Shamir’s secret sharing scheme are secure under local leakage attacks when the underlying field is of a large prime order and the number of parties is sufficiently large. This should be contrasted with the fact that any linear secret sharing scheme over a small characteristic field is clearly insecure under local leakage attacks, regardless of the number of parties. Our results are obtained via tools from Fourier analysis and additive combinatorics.
We present two types of applications of the above results and techniques. As a positive application, we show that the “GMW protocol” for honest-but-curious parties, when implemented using shared products of random field elements (so-called “Beaver Triples”), is resilient in the local leakage model for sufficiently many parties and over certain fields. This holds even when the adversary has full access to a constant fraction of the views. As a negative application, we rule out multi-party variants of the share conversion scheme used in the 2-party homomorphic secret sharing scheme of Boyle et al. (Crypto 2016).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Linear Secret Sharing Scheme
- Leak Location
- Leakage Resilience
- Share Conversion
- Small Characteristic Fields
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
The recent attacks of Meltdown and Spectre [38, 41] have brought back to the forefront the question of side-channel leakage and its effects. Starting with the early works of Kocher et al. [39, 40], side-channel attacks have demonstrated vulnerabilities in cryptographic primitives. Moreover, there are often inherent tradeoffs between efficiency and leakage resilience, where optimizations increase the susceptibility to side-channel attacks.
A large body of work on the theory of leakage resilient cryptography (cf. [1, 21, 42]) studies the possibility of constructing cryptographic schemes that remain secure in the presence of partial leakage of the internal state. One prominent direction of investigation has been designing leakage resilient cryptographic protocols for general computations [19, 22, 26, 31, 35].
The starting point for most of these works is the observation that some standard cryptographic schemes are vulnerable to very simple types of leakage. Moreover, analyzing the leakage resilience of others seems difficult. This motivates the design of new cryptographic schemes that deliver strong provable leakage resilience guarantees.
In this work, we forgo designing special-purpose leakage resilient schemes and focus on studying the properties of existing common designs. We want to understand:
To what extent are standard cryptographic schemes leakage resilient?
We restrict our attention to linear secret sharing schemes and secure multiparty computation (MPC) protocols that build on them. In particular, we would like to understand the leakage resilience properties of the most commonly used secret sharing schemes, like additive secret sharing and Shamir’s scheme, as well as simple MPC protocols that rely on them.
Analyzing existing schemes has a big advantage, as it can potentially allow us to enjoy their design benefits while at the same time enjoying a strong leakage-resilience guarantee. Indeed, classical secret sharing schemes and MPC protocols have useful properties which the specially designed leakage-resilient schemes are not known to achieve. For instance, linear secret sharing schemes can be manipulated via additive (and sometimes multiplicative) homomorphism, and standard MPC protocols can offer resilience to faults and a large number of fully corrupted parties. Finally, classical schemes are typically more efficient than special-purpose leakage-resilient schemes.
Local Leakage. We study leakage resilience under a simple and natural model of local leakage attacks. The local leakage model has the following three properties: (1) The attacker can leak information about each server’s state locally, independently of the other servers; this is justified by physical separation. (2) Only a few bits of information can be leaked about the internal state of each server; this is justified by the limited precision of measurements of physical quantities such as time or power. (3) The leakage is adversarial, in the sense that the adversary can decide what function of the secret state to leak. This is due to the fact that the adversary may have permission to legally execute programs on the server or have other forms of influence that can somewhat control the environment.
The local leakage model we consider is closely related to other models that were considered in the literature under the names “only computation leaks” (OCL) [7, 15, 26, 42], “intrusion resilience” [20], or “bounded communication leakage” [31]. These alternative models are typically more general in that they allow the leakage to be adaptive, or computable by an interactive protocol, whereas the leakage model we consider is non-adaptive.
Despite its apparent simplicity, our local leakage model can be quite powerful and enable very damaging attacks. In particular, in any linear secret sharing scheme over a field  of characteristic 2, an adversary can learn a bit of the secret by leaking just one bit from each share. Surprisingly, in the case of Shamir’s scheme, full recovery of a multi-bit secret is possible by leaking only one bit from each share [34]. Some of the most efficient implementations of MPC protocols (such as the ones in [2, 16, 36]) are based on secret sharing schemes over
of characteristic 2, an adversary can learn a bit of the secret by leaking just one bit from each share. Surprisingly, in the case of Shamir’s scheme, full recovery of a multi-bit secret is possible by leaking only one bit from each share [34]. Some of the most efficient implementations of MPC protocols (such as the ones in [2, 16, 36]) are based on secret sharing schemes over  and are thus susceptible to such an attack.
and are thus susceptible to such an attack.
As mentioned earlier, most prior works on leakage-resilient cryptography (see Sect. 1.2 below) design special-purpose leakage-resilient schemes. These works have left open the question of analyzing (variants of) standard schemes and protocols. Such an analysis is motivated by the hope to obtain better efficiency and additional security features.
1.1 Our Results
We obtain three kinds of results. First, we analyze the local leakage resilience of linear secret sharing schemes. Then, we apply these results to prove the leakage resilience of some natural MPC protocols. Finally, we present a somewhat unexpected application of these techniques to rule out the existence of certain local share conversion schemes. Our results are based on Fourier analytic techniques developed in the context of additive combinatorics. See Sect. 1.2 for details. We now give a more detailed overview of these results.
Leakage resilience of linear secret sharing schemes. In a linear secret sharing scheme over a finite field  , the secret is an element
, the secret is an element  and the share obtained by each party consists of one or more linear combinations of s and \(\ell \) random field elements. We consider a scenario where n parties hold a linear secret sharing of either \( s_0 \) or \( s_1 \) specified by the adversary \( \mathcal {A}\). (Due to linearity, we can assume without loss of generality that \(s_0=0\) and \(s_1=1\).) The adversary can also specify arbitrary leakage functions
and the share obtained by each party consists of one or more linear combinations of s and \(\ell \) random field elements. We consider a scenario where n parties hold a linear secret sharing of either \( s_0 \) or \( s_1 \) specified by the adversary \( \mathcal {A}\). (Due to linearity, we can assume without loss of generality that \(s_0=0\) and \(s_1=1\).) The adversary can also specify arbitrary leakage functions  such that each function
such that each function  outputs m bits of leakage from the share held by the j-th party. The adversary’s goal is to determine if the shared secret is \( s_0 \) or \( s_1 \). In this setting we provide the following theorems.
outputs m bits of leakage from the share held by the j-th party. The adversary’s goal is to determine if the shared secret is \( s_0 \) or \( s_1 \). In this setting we provide the following theorems.
Theorem 1.1
(Informally, Additive Secret Sharing). Let p be a prime. There exists a constant \( c_p < 1 \) such that, for sufficiently large n, the additive secret sharing scheme over \( \mathbb {F}_p\) is local leakage resilient when \(\left\lfloor (\log p)/4 \right\rfloor \) bits are leaked from every share.
In more detail, for any \(\left\lfloor (\log p)/4 \right\rfloor \)-bit output leakage functions  and any two secrets \( s_0, s_1 \), the statistical distance between the leakage distributions \(\varvec{\tau } (\mathbf {x}) \) and \(\varvec{\tau } (\mathbf {y}) \) is at most \( p c_p^{n} \), where
and any two secrets \( s_0, s_1 \), the statistical distance between the leakage distributions \(\varvec{\tau } (\mathbf {x}) \) and \(\varvec{\tau } (\mathbf {y}) \) is at most \( p c_p^{n} \), where  is obtained by applying the leakage functions to a random share
is obtained by applying the leakage functions to a random share  of \( s_0 \) and, similarly, \( \varvec{\tau } (\mathbf {y}) \) is obtained by leaking from random shares of \( s_1 \).
of \( s_0 \) and, similarly, \( \varvec{\tau } (\mathbf {y}) \) is obtained by leaking from random shares of \( s_1 \).
For a more precise statement see Corollaries 4.6 and 4.7.
In contrast to the theorem above, if the additive secret sharing were over  , the adversary could distinguish between the two secrets by just leaking the least significant bit of each share and adding those up to reveal the least significant bit of the secret. We show the following result for Shamir’s secret sharing.
, the adversary could distinguish between the two secrets by just leaking the least significant bit of each share and adding those up to reveal the least significant bit of the secret. We show the following result for Shamir’s secret sharing.
Theorem 1.2
(Informally, Shamir Secret Sharing). For large enough n, for primes \(p \approx n\), the (n, t)-Shamir secret sharingFootnote 1 over \( \mathbb {F}_p\) is local leakage resilient for \( t = n - o(\log n) \) when \( (\log p)/4 \) bits are leaked from every share.
Shamir’s secret sharing is typically used with threshold \(t=cn\) for some constant \(c>0\), in which case the above result is not applicable. While we cannot prove local leakage resilience, we do not know of attacks in this parameter regime. We conjecture the following:
Conjecture 1.3
(Shamir Secret Sharing). Let \( c > 0 \) be a constant. For large enough n, \( (n, t=cn)\)-Shamir Secret Sharing is 1-bit local leakage resilient. That is, for any family of functions  with 1-bit output,
with 1-bit output,
where  where \( \mathbf {x}\leftarrow \mathsf {ShaSh}_{n,cn}(0) \) and
where \( \mathbf {x}\leftarrow \mathsf {ShaSh}_{n,cn}(0) \) and  .
.
Classical MPC protocols like the BGW protocol use Shamir secret sharing with \( c= 1/3 \) or 1 / 2. Observe that proving the conjecture for a specific constant c immediately implies the conjecture for any constant \( c' > c \). This follows from the fact that (n, cn) -Shamir Shares can be locally converted to random \( (n,c'n) \)-Shamir Shares for \( c' > c \).Footnote 2
Application to leakage-resilient MPC. We use the leakage resilience of linear secret sharing schemes to show that the honest-but-curious variant of the GMW [25] protocol with a “Beaver Triples” setup [3] (that we call GMW with shared product preprocessing) is local leakage resilient.
For the MPC setting, we modify the leakage model as follows to allow for a stronger adversary. The adversary \( \mathcal {A}\) is allowed to corrupt a fraction of the parties, see their shares and views of the entire protocol execution. In addition, \(\mathcal {A}\) specifies local leakage functions for the non-corrupted parties and receives the corresponding leakage on their individual views.
The honest-but-curious GMW protocol with shared product preprocessing works as follows. The parties wish to evaluate an arithmetic circuit C on an input x. The parties receive random shares of the input x under a linear secret sharing scheme and random shares of Beaver triples under the same scheme.Footnote 3 The protocol proceeds gate by gate where the parties maintain a secret sharing of the value at each gate. For input, addition and inverse (\( -1 \)) gates, parties locally manipulate their existing shares to generate the shares for these gates. For multiplication gate, where we multiply \( z_1 \) and \( z_2 \) to get z, the parties first construct \( z_1 - a \) and \( z_2 - b \) by subtracting the shares of the inputs and Beaver triples (a, b, ab) and broadcasting these values. Then the parties can locally construct a secret sharing of \( z = z_1 \cdot z_2 \) by using the following relation:
We show that when the underlying protocol is local leakage resilient, this protocol can also tolerate local leakage. We can prove leakage resilience in a simulation-based definition. See Sect. 5 for details. Informally, when the additive secret sharing scheme is used, we show the following.
Theorem 1.4
(Informally, Leakage Resilience of GMW). For large enough n, for any prime p, the GMW protocol with shared product preprocessing and additive secret sharing over \(\mathbb {F}_p\) is local leakage resilient where the adversary can corrupt n / 2 parties, learn their entire state and, then locally leak \( (\log p)/4 \) bits each from all the uncorrupted parties.
On the impossibility of local share conversion. In the problem of local share conversion [4, 14], n parties hold a share of a secret s under a secret sharing scheme \( \mathcal {L}\). Their goal is to locally, without interaction, convert their shares to shares of a related secret \( s' \) under a different secret sharing scheme \( \mathcal {L}' \) such that \( (s, s') \) satisfy a pre-specified relation R. We assume R is not trivial in the sense that it is permissible to map shares of every secret s to shares of a fixed constant. Local share conversion has been used to design protocols for Private Information Retrieval [4]. More recently, different kinds of local share conversion were used to construct Homomorphic Secret Sharing (HSS) schemes [11, 17, 23]. Using techniques similar to the ones for leakage resilience, we rule out certain nontrivial instances of local share conversion. We first state our results and then discuss their relevance to constructions of HSS schemes.
Theorem 1.5
(Informally, Impossibility of Local Share Conversion). Three-party additive secret sharing over \( \mathbb {F}_p\), for any prime \( p > 2 \), cannot be converted to additive secret sharing over  , with constant success probability (\( > 5/6 \)), for any non-trivial relation R on the secrets.
, with constant success probability (\( > 5/6 \)), for any non-trivial relation R on the secrets.
The proof of this result uses a Fourier analytic technique similar to the analysis of the Blum-Luby-Rubinfeld linearity test [9]. We also show a similar impossibility result for Shamir secret sharing. See the full version for the precise general statement. This result relies crucially on a technique of Green and Tao [33]. We elaborate more in Sect. 2.
Relevance to HSS Schemes. At the heart of the DDH-based 2-party HSS scheme of Boyle et al. [11] and its Paillier-based variant of Fazio et al. [23] is an efficient local share conversion algorithm of the following special form. The two parties hold shares \( g^{x} \) and \( g^{y} \) respectively of \(b\in \{0,1\}\), such that \( g^b = g^x \cdot g^y \). The conversion algorithm enables them to locally compute additive shares of the bit b over the integers \(\mathbb {Z}_{}\), with small (inverse polynomial) failure probability. Note that this implies similar conversion to additive sharing over \( \mathbb {Z}_{2} \). One approach to constructing 3-party HSS schemes would be to generalize this local share conversion scheme to 3 parties, i.e., servers holding random \( g^x \), \( g^y \) and \( g^z \) respectively, such that \( g^b = g^x \cdot g^y \cdot g^z \), can locally convert these shares to additive shares of the bit b over integers. We rule out this approach by showing that even when given the exponents x, y and z in the clear (i.e. \( x + y + z = b \) over \( \mathbb {Z}_{p} \)), locally computing additive shares of b over \(\mathbb {Z}_{2}\) (or the integers) is impossible. A similar share conversion from (noisy) additive sharing over \(\mathbb {Z}_{p}\) to additive sharing over \(\mathbb {Z}_{2}\) was used by Dodis et al. [17] to obtain an LWE-based construction of 2-party HSS and spooky encryption. However, in this case there is an alternative route of reducing the multi-party case to the 2-party case that avoids our impossibility result.
1.2 Related Work
Our work was inspired by the surprising result of Guruswami and Wootters [34] mentioned above. This work turned attention to the fact that some natural linear secret sharing schemes miserably fail to offer local leakage resilience over fields of characteristic 2, in that leaking only one bit from each share is sufficient to fully recover a multi-bit secret.
The traditional “leakage” model considered in multi-party cryptography allows the adversary to fully corrupt up to t parties and learn their entire secret state. This t-bounded leakage model motivated secret sharing schemes designed to protect information [8, 43] and secure multiparty computation (MPC) protocols designed to protect computation [6, 13, 25, 45]. The same leakage model was also considered at the hardware level, where parties are replaced by atomic gates [35]. The t-bounded leakage considered in all these works is quite different from the local leakage model we consider: we allow partial leakage from every secret state, whereas the t-bounded model allows full leakage from up to t secret states. While resilience to t-bounded leakage was shown to imply resilience to certain kinds of “noisy leakage” [18, 22] or “low-complexity leakage” [10], it clearly does not imply local leakage resilience in general. Indeed, additive secret sharing over  is highly secure in the t-bounded model and yet is totally insecure in the local leakage model.
is highly secure in the t-bounded model and yet is totally insecure in the local leakage model.
The literature on leakage resilient cryptography is extensive, thus we discuss a few of the most relevant works. A closely related work by Dziembowski and Pietrzak [21] is one of those works that design new constructions to withstand leakage. Their secret sharing scheme uses artificially long shares that are hard to retrieve in full, as the model bounds the amount of bits that can be leaked. The length of the shares of course impacts the performance of the protocol. The reconstruction of the secret is an interactive process.
Boyle et al. [12] consider the problem of leakage-resilient coin-tossing and reduce it to a certain kind of leakage-resilient verifiable secret sharing. Here too, a new construction of (nonlinear) secret sharing is developed in order to achieve these results.
Goldwasser and Rothblum [26] give a general transformation that takes any algorithm and creates a related algorithm that computes the same function and can tolerate leakage. This approach can be viewed as a special-purpose MPC protocol for a constant number of parties that offers local leakage resilience (and beyond) [7]. However, this construction is quite involved and offers poor concrete leakage resilience and efficiency overhead.
Most relevant to our MPC-related results is the recent work of Goyal et al. [31] on leakage resilient secure two-party computation (see also [24]). This work analyzes the resilience of a GMW-style protocol under a similar (in fact, more general) type of leakage to the local leakage model we consider. One key difference is that the protocol from [31] modifies the underlying circuit (incurring a considerable overhead) whereas we apply the GMW protocol to the original circuit. Also, our approach applies to a large number of parties of which a large fraction can be entirely corrupted, whereas the construction in [31] is restricted to the two-party setting.
Our results use techniques developed in the context of additive combinatorics. See Tao and Vu [44] for an exposition on Fourier analytic methods used in additive combinatorics. The works most relevant to ours are works by Green and Tao [33] and follow-ups by Gowers and Wolf [28,29,30]. The relation of these works and their techniques to ours is discussed in Sect. 2.4.
2 Overview of the Techniques
2.1 Leakage Resilience of Secret Sharing Schemes
Very simple local leakage attacks exist for linear secret sharing schemes over small characteristic fields. These attacks stem from the abundance of additive subgroups in these fields. This gives rise to the hope that linear schemes over fields of prime order, that lack such subgroups, are leakage resilient. We start by considering the simpler case of additive secret sharing.
Additive secret sharing. We define \(\mathsf {AddSh}(s)\) to be a function that outputs random shares  such that
such that  Let
Let  be some leakage functions. We want to show that for all secrets
be some leakage functions. We want to show that for all secrets  , the leakage distributions are statistically close. That is,
, the leakage distributions are statistically close. That is,

where  is the total leakage the adversary sees on the shares
is the total leakage the adversary sees on the shares  .
.
We know that there is a local leakage attack on  : simply leak the least significant bit (\( \mathsf {lsb}\)) from all the parties and add the outputs to reconstruct the \(\mathsf {lsb}\) of the secret. What enables the attack on
: simply leak the least significant bit (\( \mathsf {lsb}\)) from all the parties and add the outputs to reconstruct the \(\mathsf {lsb}\) of the secret. What enables the attack on  while \( \mathbb {F}_p\) is unaffected?
while \( \mathbb {F}_p\) is unaffected?
To understand this difference, it is instructive to start with an example. Let us consider additive secret sharing over  for 3 parties. We know that,
for 3 parties. We know that,

This attack works because  has many subgroups that are closed under addition. Let \( A_0 = \mathsf {lsb}^{-1}(0) \) and \( A_1 = \mathsf {lsb}^{-1}(1) \). The set \( A_0 \) is an additive subgroup of
has many subgroups that are closed under addition. Let \( A_0 = \mathsf {lsb}^{-1}(0) \) and \( A_1 = \mathsf {lsb}^{-1}(1) \). The set \( A_0 \) is an additive subgroup of  and \( A_1 \) is a coset of \( A_0 \). Furthermore, the \( \mathsf {lsb}\) function is a homomorphism from
and \( A_1 \) is a coset of \( A_0 \). Furthermore, the \( \mathsf {lsb}\) function is a homomorphism from  to the quotient groupFootnote 4
to the quotient groupFootnote 4  . The \( \mathsf {lsb}\) leakage tells us which coset each share
. The \( \mathsf {lsb}\) leakage tells us which coset each share  is in. Then by adding these leakages, we can infer if \( x\in A_0 \) or \( x \in A_1 \) (i.e., to which coset it belongs).
is in. Then by adding these leakages, we can infer if \( x\in A_0 \) or \( x \in A_1 \) (i.e., to which coset it belongs).
Let us consider the analogous situation over \( \mathbb {F}_p\) for a prime p. The group \( \mathbb {F}_p\) does not have any subgroups. In fact, it has an opposite kind of expansion property: that adding any two sets results in a larger set.
Theorem 2.1
(Cauchy-Davenport Inequality). Let \( A, B\subset \mathbb {F}_p\). Let  . Then,
. Then,
So, if we secret shared a random secret over \( \mathbb {F}_p\) and got back leakage output indicating that  ,
,  , and
, and  , we can infer that \( x \in B_1 + B_2 + B_3 \). But because of this expansion property, the set \( B_1 + B_2 + B_3 \) is a lot larger than the sets \( B_i \)’s individually. This is in contrast to the
, we can infer that \( x \in B_1 + B_2 + B_3 \). But because of this expansion property, the set \( B_1 + B_2 + B_3 \) is a lot larger than the sets \( B_i \)’s individually. This is in contrast to the  case where e.g. \( A_0 + A_1 \) was the same size as \( A_0 \).
case where e.g. \( A_0 + A_1 \) was the same size as \( A_0 \).
This gives an idea of why the \( \mathsf {lsb}\) attack does not work. Some information is lost because of expansion. This is not sufficient for us though. What we need to show is stronger. We want to show that even given the leakage, the secret is almost completely hidden. This is a more “distributional” statement.
We model it as follows: Let us say that we have n parties where party j holds the share  . The adversary \( \mathcal {A}\) has specified leakage functions
. The adversary \( \mathcal {A}\) has specified leakage functions  and received back the leakage \(\varvec{\ell } = \ell _{1}, \ell _{2}, \dots , \ell _{n} \) where
and received back the leakage \(\varvec{\ell } = \ell _{1}, \ell _{2}, \dots , \ell _{n} \) where  : the leakage on the j-th share. We want to show that even conditioned on this leakage, the probability that the secret was \( s_0 \) vs \( s_1 \) is close to a half. That is, we want to show the following:
: the leakage on the j-th share. We want to show that even conditioned on this leakage, the probability that the secret was \( s_0 \) vs \( s_1 \) is close to a half. That is, we want to show the following:

Below, we will sketch an argument showing that leaking from the additive shares of 0 is statistically close to leaking from a uniformly random element

From Eq. (2), Eq. (1) follows by a simple hybrid argument as shares of any other secret s are simply shares of 0 with the secret s added to the first party’s share. That is, let \( \mathbf {e}_1 = (1, 0, 0, \dots , 0)\),

To understand this probability better, let us consider the following operator:

By picking the functions \( f_j \)’s appropriately, we can model the probability. Define  as follows: \( 1_{\ell _{j}} (x) = 1\) if the output of the leakage function
as follows: \( 1_{\ell _{j}} (x) = 1\) if the output of the leakage function  on input x is \( \ell _{j} \), i.e.,
on input x is \( \ell _{j} \), i.e.,  and, 0 otherwise. Notice that we can write the probability of leakage output being \( \varvec{\ell } \) in terms of the operator \( \varLambda \) as follows,
and, 0 otherwise. Notice that we can write the probability of leakage output being \( \varvec{\ell } \) in terms of the operator \( \varLambda \) as follows,

The probability of the leakage being \( \varvec{\ell } \) on the uniform distribution is simply a product of the expectations:

where  . So, we want to show:
. So, we want to show:

The tool we use to bound the difference  is Fourier analysis. At the heart of this is a nice property of the \( \varLambda \) operator: the Fourier spectrum of \( \varLambda \) is very similar to the standard form as follows. For \( \varLambda \) defined over a linear code C:
is Fourier analysis. At the heart of this is a nice property of the \( \varLambda \) operator: the Fourier spectrum of \( \varLambda \) is very similar to the standard form as follows. For \( \varLambda \) defined over a linear code C:

\( \varLambda \) can be equivalently represented on the dual code \( C^\perp \) (see Lemma 4.9),
with the ‘Fourier coefficients’  where \( \omega = \exp (2\pi i / p) \) is a root of unity. Observe that as
where \( \omega = \exp (2\pi i / p) \) is a root of unity. Observe that as  . So,
. So,  , the term corresponding to the all-zeros codeword in the dual code. Hence, the error term we have to bound is the following:
, the term corresponding to the all-zeros codeword in the dual code. Hence, the error term we have to bound is the following:

Note that, at this point, it is interesting to observe how the presence of subgroups (over  ) and the lack thereof (over \( \mathbb {F}_p\)) manifests itself. Over
) and the lack thereof (over \( \mathbb {F}_p\)) manifests itself. Over  because of the non-trivial subgroups, these non-zero Fourier coefficients can be large and hence the error term is not small. On the other hand, over \( \mathbb {F}_p\), we can show that each non-zero Fourier coefficient is strictly smaller than the zero-th coefficient and measurably so. This lets us bound the error term. First we elaborate on the large Fourier coefficient over
because of the non-trivial subgroups, these non-zero Fourier coefficients can be large and hence the error term is not small. On the other hand, over \( \mathbb {F}_p\), we can show that each non-zero Fourier coefficient is strictly smaller than the zero-th coefficient and measurably so. This lets us bound the error term. First we elaborate on the large Fourier coefficient over  and then we state results for \( \mathbb {F}_p\).
and then we state results for \( \mathbb {F}_p\).
Large coefficients over  . Each Fourier basis function over
. Each Fourier basis function over  is indexed by a vector
is indexed by a vector  and the Fourier coefficient for
and the Fourier coefficient for  is given by
is given by  . Over
. Over  , non-zero Fourier coefficients can be as large as the zero-th coefficient, which is always the largest for binary valued functions.
, non-zero Fourier coefficients can be as large as the zero-th coefficient, which is always the largest for binary valued functions.
To use the running example, in the case of the \( \mathsf {lsb}\) function, let  and consider the \( 1_{\mathsf {lsb}= 1} \) to be the function which returns 1 if the lsb is 1 and 0 otherwise. So, \( 1_{\mathsf {lsb}= 1} \) is 1 on the set \( A_1 \) and 0 on \( A_0 \). The non-zero Fourier coefficient indexed by
and consider the \( 1_{\mathsf {lsb}= 1} \) to be the function which returns 1 if the lsb is 1 and 0 otherwise. So, \( 1_{\mathsf {lsb}= 1} \) is 1 on the set \( A_1 \) and 0 on \( A_0 \). The non-zero Fourier coefficient indexed by  is as large as the zero-th Fourier coefficient since:
is as large as the zero-th Fourier coefficient since:  as half of the inputs satisfy \( \mathsf {lsb}= 1 \), and also,
as half of the inputs satisfy \( \mathsf {lsb}= 1 \), and also,  because when \( 1_{\mathsf {lsb}=1}(x) = 1 \), then \( x_k = 1 \) and \( 1_{\mathsf {lsb}= 1}(\vec x) \cdot (-1)^{x_k} = -1 \). So, these two Fourier coefficients are equally large in magnitude. Hence the error term can be quite large.
because when \( 1_{\mathsf {lsb}=1}(x) = 1 \), then \( x_k = 1 \) and \( 1_{\mathsf {lsb}= 1}(\vec x) \cdot (-1)^{x_k} = -1 \). So, these two Fourier coefficients are equally large in magnitude. Hence the error term can be quite large.
Bounds on \( \mathbb {F}_p\). Bounding \(\widehat{1_{\ell _{j}}}(\alpha )\) for non-zero \(\alpha \in \mathbb {F}_p\), we prove prove the following result:
where \( \text {SD}\) denotes the statistical distance between the two distributions,  ,
,  (with U being the uniform distribution over \(\mathbb {F}_p^n\)), and t is the minimum distance of the dual code \( C^\perp \). We prove this formally in Sect. 4.3. When applied to the code \( C = \mathsf {AddSh}(0) \), we have \(|C^\perp | = p\) and this implies that additive secret sharing is leakage resilient, proving Theorem 1.1. We strengthen the result in Corollary 4.7 to avoid this dependence on \(|C^\perp | = p\).
(with U being the uniform distribution over \(\mathbb {F}_p^n\)), and t is the minimum distance of the dual code \( C^\perp \). We prove this formally in Sect. 4.3. When applied to the code \( C = \mathsf {AddSh}(0) \), we have \(|C^\perp | = p\) and this implies that additive secret sharing is leakage resilient, proving Theorem 1.1. We strengthen the result in Corollary 4.7 to avoid this dependence on \(|C^\perp | = p\).
Applying the result to Reed-Solomon Codes, the codes underlying (t, n)-Shamir Secret Sharing, gives us Theorem 1.2. Also note that in the case of Shamir secret sharing, \( |C^\perp | = p^{n-t}\) and hence this proof works only when \( n-t \) is small.
2.2 Application to Leakage Resilience of MPC Protocols
Given the leakage resilience of additive secret sharing over \( \mathbb {F}_p\), we can show that the following honest-but-curious variant of the GMW protocol [25] (GMW with shared product preprocessing) using Beaver Triples [3] is leakage resilient. The protocol is described in Fig. 1. Recall that in our leakage model, the adversary \( \mathcal {A}\) is allowed to corrupt a fraction of the parties, see their views of the entire protocol execution and then specify leakage functions  for the non-corrupted parties and receive this leakage on their individual views.
for the non-corrupted parties and receive this leakage on their individual views.
We consider two settings, the first being with private outputs where the adversary does not see the output of the non-corrupted parties and the second with public outputs where the parties broadcast their output shares at the end to reconstruct the final output and the adversary sees them.
In both models, we show that the adversary’s view (i.e., the views of the corrupted parties and the leakage on all the uncorrupted parties’ views) can be simulated by a simulator which gets nothing (in the private-outputs setting) and gets all the shares of the output (in the public-outputs setting).
To prove the result, we need two ingredients: (a) the leakage resilience of additive secret sharing over \( \mathbb {F}_p\) and, (b) a lemma formalizing the following intuition: In the GMW protocol, each party learns a share of a secret sharing of the value at each gate in the circuit and nothing more. The first ingredient we have shown above, and we now describe the second. In Lemmas 5.8 and 5.9, we formally state and prove this intuition in both the private-outputs and public-outputs setting and here we provide an informal statement.
Lemma 2.2
(Informal). On an input \( \vec x \), let \( {(z_g)}_{g \in G_{\times }} \) denote the value at multiplication gate g. The joint view of any subset \( \varTheta \) of the parties,  , can be simulated given their shares of the inputs and of the values at each multiplication gate.
, can be simulated given their shares of the inputs and of the values at each multiplication gate.

Given the lemma, proving local leakage resilience in the private-outputs setting is a hybrid argument. Because of the lemma, the adversary can leak from party j a function of  and
and  . The simulator \( \mathsf {LeakSim}\), not knowing the input \( \vec x \), picks random values \( \vec x{'}, {(z_g{'})}_{g \in G_{\times }} \) instead, secret shares them and then leaks from these values according to the leakage functions
. The simulator \( \mathsf {LeakSim}\), not knowing the input \( \vec x \), picks random values \( \vec x{'}, {(z_g{'})}_{g \in G_{\times }} \) instead, secret shares them and then leaks from these values according to the leakage functions  specified by \( \mathcal {A}\).
specified by \( \mathcal {A}\).
Then via a hybrid, we show that these two distributions are close to each other. If the local leakage can distinguish between the two distributions, then we can use them to construct leakage functions that violate the local leakage resilience of a single instance of the underlying secret sharing scheme.
The proof in the public-outputs setting has a subtlety that the adversary sees not only the local leakage from the uncorrupted parties, but also their final outputs. In this case, we first observe that the final output is a fixed linear function of the circuit values \( z_g \) of the multiplication gates and of the input values \(x_i\). Using this observation, the simulator picks the shares of the multiplication gates conditioned on the output values seen. And we can show a similar reduction to the local leakage resilience of the underlying secret sharing scheme. This proves Theorem 1.4.
2.3 On Local Share Conversion
In this section, we sketch the techniques used to show Theorem 1.5: that three-party additive secret sharing over \( \mathbb {F}_p\), for any prime \( p > 2 \), cannot be converted to additive secret sharing over \( \mathbb {Z}_{2} \), even with a small error, for any non-trival relation R on the secrets.
Our results on impossibility of local share conversion are derived by viewing the output of the share conversion schemes as leakage on the original shares and that the adversary instead of being able to do arbitrary computation, can only add the leakage outputs over \( \mathbb {Z}_{2} \).
Impossibility of Share Conversion of Additive Secret Sharing from \( \mathbb {F}_p\) to \( \mathbb {Z}_{2} \). We start with the impossibility of local share conversion of additive secret sharings from \( \mathbb {F}_p\) to \( \mathbb {Z}_{2} \) for any non-trivial relation R on the secrets.Footnote 5 The analysis is inspired by Fourier analytic reinterpretations of linearity testing [9] and group homomorphism testing [5].
Assume that \( g_1,g_2, g_3 :\mathbb {F}_p\rightarrow \mathbb {Z}_{2} \) form a 3-party local share conversion scheme for additive secret sharing for some relation R where shares of 0 in \( \mathbb {F}_p\) have to be mapped to shares of 0 in \( \mathbb {Z}_{2} \) and shares of 1 in \( \mathbb {F}_p\) have to be mapped to shares of 1 in \( \mathbb {Z}_{2} \) (with high probability, say 99%).Footnote 6 That is, if \( x_1 + x_2 + x_3 = b \), then \( g_1(x_1) + g_2(x_2) + g_3(x_3) = b\) for  . It is convenient for us to define the real-valued analogues \( G_i(x) = (-1)^{g_i(x)} \). At the heart of this proof is the following operator:
. It is convenient for us to define the real-valued analogues \( G_i(x) = (-1)^{g_i(x)} \). At the heart of this proof is the following operator:

The first observation is that if shares of 0 over \( \mathbb {F}_p\) are mapped to shares of 0 over \( \mathbb {Z}_{2} \) with high probability (say \( 99\% \)), then the value of this operator is quite high as,

The crux of the argument is an ‘inverse theorem’ style lemma which characterizes functions \( G_1 \)’s that result in a large value for \( \varLambda \). This lemma shows that if \( \varLambda (G_1, G_2, G_3) \) is high, then each of the functions \( G_1, G_2 \) and \( G_3 \) are ‘almost’ constant functions, i.e., for most x’s, \( G_i(x) \) is the same fixed value. Given this lemma, the impossibility result follows. Because the functions \( G_i \)’s (and hence \( g_i \)’s) are almost always constant, even given secret shares of 1 as input, they would still output shares of 0 as output.
To complete the proof, we need to argue that \( G_1 \) is an almost constant function. This proof has two parts: the first part which is generic to any field  is to show that if \( \varLambda \) is large, then \( G_1 \) has a large Fourier coefficient. In the second part, we show that if \( G_1 \) has a large Fourier coefficient, then \( G_1 \) is an almost constant function. This part is specific to \( \mathbb {F}_p\).
is to show that if \( \varLambda \) is large, then \( G_1 \) has a large Fourier coefficient. In the second part, we show that if \( G_1 \) has a large Fourier coefficient, then \( G_1 \) is an almost constant function. This part is specific to \( \mathbb {F}_p\).
To show the first part, we rewrite \( \varLambda (G_1, G_2, G_3) \) over the Fourier basis (using Lemma 4.9) to get
this follows from Lemma 4.9 as the dual code of additive shares of 0 is the code generated by the all-ones vector. We can now use Cauchy-Schwarz inequality with the fact that \( \sum _{a} |\widehat{G}_i(a)|^2 = 1 \) to get that,
This implies that \( |\widehat{G}_1|_{\infty } \) is large. Now we show the second part, which is specific to \( \mathbb {F}_p\). We need to show that \( g_1 \) is almost constant function. We want to show that if some Fourier coefficient of \( G_1 \) is large (larger than \(\frac{2}{3}\)), then it has to be the zero-th coefficient. The zero-th coefficient measures the bias of \( G_1 \): if the coefficient is small, then \( G_1 \) is close to balanced, and if this coefficient is large, then \( G_1 \) is an almost constant function. Although proving this for all primes is somewhat tedious, the intuition is easy to grasp. Let \( p = 3 \) and \( \omega = \exp (2\pi i / 3)\) be a root of unity. A non-zero Fourier coefficient of \( G_1 \) takes the following form:  for \(a \ne 0 \). Because \( G_1 \) takes values in
for \(a \ne 0 \). Because \( G_1 \) takes values in  and \( \omega ^{ax} \) takes all values
and \( \omega ^{ax} \) takes all values  , these two functions cannot be too correlated. And hence the Fourier coefficient cannot be too large: \(| \widehat{G}_1(a) | \le 2/3\). This completes the proof.
, these two functions cannot be too correlated. And hence the Fourier coefficient cannot be too large: \(| \widehat{G}_1(a) | \le 2/3\). This completes the proof.
The Impossibility of Share Conversion from Shamir Secret Sharing from \( \mathbb {F}_p\) to Additive Sharing on  . We now briefly discuss the techniques used to prove the result on local conversion of (n, t)-Shamir secret sharing over \( \mathbb {F}_p\), for \(n = 2t-1\). Again consider a relation R where Shamir shares of 0 over \( \mathbb {F}_p\) have to be mapped to additive shares of 0 over
. We now briefly discuss the techniques used to prove the result on local conversion of (n, t)-Shamir secret sharing over \( \mathbb {F}_p\), for \(n = 2t-1\). Again consider a relation R where Shamir shares of 0 over \( \mathbb {F}_p\) have to be mapped to additive shares of 0 over  and Shamir shares of 1 have to be mapped to additive shares of 1 over
and Shamir shares of 1 have to be mapped to additive shares of 1 over  . Let \( g_1, g_2, \dots , g_5\) be the local share conversion functions used. We want to follow a similar strategy: first show that the corresponding function \(G_i = (-1)^{g_i}\) has a large Fourier coefficient. Then, similar to the additive secret sharing proof, show that if \( G_i \) has a large Fourier coefficient, then \( G_i \) is ‘almost constant’ and hence derive a contradiction.
. Let \( g_1, g_2, \dots , g_5\) be the local share conversion functions used. We want to follow a similar strategy: first show that the corresponding function \(G_i = (-1)^{g_i}\) has a large Fourier coefficient. Then, similar to the additive secret sharing proof, show that if \( G_i \) has a large Fourier coefficient, then \( G_i \) is ‘almost constant’ and hence derive a contradiction.
In the first part, we want to use the fact that Shamir shares of 0 over \( \mathbb {F}_p\) are converted to additive shares of 0 over  to infer that \( G_1 \) (say) has a large Fourier coefficient. The proof is a specialized case of the work of Green and Tao [33]. In the proof, the value of an appropriately defined operator \( \varLambda \):
to infer that \( G_1 \) (say) has a large Fourier coefficient. The proof is a specialized case of the work of Green and Tao [33]. In the proof, the value of an appropriately defined operator \( \varLambda \):

is bound by the “Gowers’ Uniformity Norm” (the \( U^2 \) norm) of the function \( G_1 \). Then using a connection between the \( U^2 \) norm and Fourier bias, we can derive that \( G_1 \) has a large Fourier coefficient. For details see the full version.
2.4 Additive Combinatorics Context
We provide some context for these techniques. Such \( \varLambda \) style operators have been studied quite a bit in number theory. They can be used to represent many fascinating questions about the distribution of prime numbers. To give some examples, What is the density of three-term arithmetic progressions in primes? is a question about the operator  where \( 1_P \) is 1 if x is a prime and 0 otherwise. Also, the twin primes conjecture can be framed in terms of the operator
where \( 1_P \) is 1 if x is a prime and 0 otherwise. Also, the twin primes conjecture can be framed in terms of the operator  . Green and Tao [33] and subsequent works by Wolf and Gowers [28,29,30] tried to understand the following question: let \( L_1, L_2, \dots , L_m \) be linear equations from
. Green and Tao [33] and subsequent works by Wolf and Gowers [28,29,30] tried to understand the following question: let \( L_1, L_2, \dots , L_m \) be linear equations from  to
to  . Can we bound the following expectation:
. Can we bound the following expectation:

This is a very general question. And roughly speaking, they give the following answer. These works define two measures of complexity (termed as Cauchy-Shwarz Complexity and True Complexity respectively) and show that if a system of linear equations has complexity k, then,Footnote 7

where  is the k-th order Gowers’ Uniformity Norm [27]. This method of bounding \( \varLambda \) by the Gowers’ norm has been very influential in number theory. This method is what we use to prove the results on Shamir secret sharing. We first bound an appropriately defined operator \( \varLambda \) by the Gowers’ \( U^2 \) norm and then exploit a connection between the \( U^2 \) and Fourier analysis. Such a technique does not suffice to give desired results in the case of leakage resilience of \((n,t=cn)\)-Shamir secret sharing for two reasons (for some constant \(c > 0\)). The first reason is that constant C derived from this method is often extremely large and has an exponential dependence on the number of equations m. Also the second reason is that in our setting, the functions \( f_i \)’s are chosen by the adversary. So, showing that
is the k-th order Gowers’ Uniformity Norm [27]. This method of bounding \( \varLambda \) by the Gowers’ norm has been very influential in number theory. This method is what we use to prove the results on Shamir secret sharing. We first bound an appropriately defined operator \( \varLambda \) by the Gowers’ \( U^2 \) norm and then exploit a connection between the \( U^2 \) and Fourier analysis. Such a technique does not suffice to give desired results in the case of leakage resilience of \((n,t=cn)\)-Shamir secret sharing for two reasons (for some constant \(c > 0\)). The first reason is that constant C derived from this method is often extremely large and has an exponential dependence on the number of equations m. Also the second reason is that in our setting, the functions \( f_i \)’s are chosen by the adversary. So, showing that  is small is either very challenging or just not true for some adversarially chosen functions \( f_i \)’s. On the other hand, we do not know how to translate this in to an local leakage attack on Shamir secret sharing either and hence a strong win-win result eludes us.
is small is either very challenging or just not true for some adversarially chosen functions \( f_i \)’s. On the other hand, we do not know how to translate this in to an local leakage attack on Shamir secret sharing either and hence a strong win-win result eludes us.
3 Preliminaries
We denote by \(\mathbb {C}\) the field of complex numbers, by \(\text {SD}\) the statistical distance (or total variation distance), and by \(\equiv \) the equality of distributions.
3.1 Linear Codes
Secret sharing schemes are closely related to linear codes, that we define next.
Definition 3.1
(Linear Code). A subset  is an [n, k, d] -linear code over field
is an [n, k, d] -linear code over field  if C is a subspace of
if C is a subspace of  of dimension k such that: for all \( \vec x \in C \setminus \{\vec 0 \} \), \( \mathsf {HammingDistance}(\vec x) \ge d \) (i.e., the minimum distance between two elements of the code is at least d). A code is called Maximum Distance Separable (MDS) if \( n - k + 1 = d \). The dual code of the code C is defined as
of dimension k such that: for all \( \vec x \in C \setminus \{\vec 0 \} \), \( \mathsf {HammingDistance}(\vec x) \ge d \) (i.e., the minimum distance between two elements of the code is at least d). A code is called Maximum Distance Separable (MDS) if \( n - k + 1 = d \). The dual code of the code C is defined as  .
.
Proposition 3.2
The dual code \( C^\perp \) of an [n, k, d] MDS code C is itself an MDS code with parameters \( [n, n - k, k+1] \).
Example 3.3
(Reed-Solomon Code). The \( [n, k, n-k+1] \)-Reed-Solomon code over  such that
such that  interprets a message
interprets a message  as \( p(x) = m_1 + m_2 x + \dots + m_{k} x^{k-1} \) and encodes it as \( (p(\alpha _1), p(\alpha _2), \dots , p(\alpha _n) )\) where
as \( p(x) = m_1 + m_2 x + \dots + m_{k} x^{k-1} \) and encodes it as \( (p(\alpha _1), p(\alpha _2), \dots , p(\alpha _n) )\) where  is a fixed set of evaluation points. Reed-Solomon code is an MDS code.
is a fixed set of evaluation points. Reed-Solomon code is an MDS code.
3.2 Linear Secret Sharing Schemes
We recall the definition of (threshold) secret sharing schemes.
Definition 3.4
(Secret Sharing Scheme). An (n, t) -secret sharing scheme over field  is defined by a pair \( ({\mathsf {Share}}, {\mathsf {Rec}}) \) where \( {\mathsf {Share}}\) is a randomized mapping of an input
is defined by a pair \( ({\mathsf {Share}}, {\mathsf {Rec}}) \) where \( {\mathsf {Share}}\) is a randomized mapping of an input  to shares for each party
to shares for each party  and the reconstruction algorithm \( {\mathsf {Rec}}\) is a function mapping a set A and the corresponding shares
and the reconstruction algorithm \( {\mathsf {Rec}}\) is a function mapping a set A and the corresponding shares  to a secret
to a secret  , such that the following properties hold:
, such that the following properties hold:
-
1.
Reconstruction.
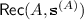 outputs the secret s for all A where \( \left| A \right| > t \).
outputs the secret s for all A where \( \left| A \right| > t \). -
2.
Security. For any set A such that \( \left| A \right| \le t \), the joint distribution of shares received by the subset of parties A,
 where \(\mathbf {s} \leftarrow {\mathsf {Share}}(s)\), is independent of the secret s.
where \(\mathbf {s} \leftarrow {\mathsf {Share}}(s)\), is independent of the secret s.
When we use these schemes to encode vectors, it should be interpreted as sharing each element of the vector under the underlying scheme.
An important particular case of secret sharing scheme are linear secret sharing schemes. Actually all the schemes we consider in this paper are linear.
Definition 3.5
An (n, t) -SSS \(({\mathsf {Share}}, {\mathsf {Rec}})\) over  is linear if
is linear if
-
1.
the codomain of \({\mathsf {Share}}\) is the vector space
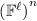 , for some positive integer \(\ell \) (i.e., each share is a vector of \(\ell \) field elements),
, for some positive integer \(\ell \) (i.e., each share is a vector of \(\ell \) field elements), -
2.
for any
 , \({\mathsf {Share}}(s)\) is uniformly distributed over an affine subspace of
, \({\mathsf {Share}}(s)\) is uniformly distributed over an affine subspace of  ,
, -
3.
for any
 :
: 
Let us now recall the two classical linear secret sharing schemes we are using.
Example 3.6
(Additive Secret Sharing \((\mathsf {AddSh}_n,\mathsf {AddRec}_n)\)). The additive secret sharing scheme \((\mathsf {AddSh}_n,\mathsf {AddRec}_n)\) for n parties over a field  is a linear \((n,n-1)\)-secret sharing scheme defined as follows. Shares \(\mathsf {AddSh}_n(s) = \mathbf {s}\) of a secret
is a linear \((n,n-1)\)-secret sharing scheme defined as follows. Shares \(\mathsf {AddSh}_n(s) = \mathbf {s}\) of a secret  are generated as follows:
are generated as follows:  , and
, and  . The reconstruction of s from \(\mathbf {s}\) is done as follows:
. The reconstruction of s from \(\mathbf {s}\) is done as follows:  .
.
Example 3.7
(Shamir Secret Sharing \((\mathsf {ShaSh}_{n,t},\mathsf {ShaRec}_{n,t})\)). The Shamir secret sharing scheme \((\mathsf {ShaSh}_{n,t},\mathsf {ShaRec}_{n,t})\) of degree t for n parties over a field  (with
(with  ) is a linear (n, t)-secret sharing scheme defined as follows. Let
) is a linear (n, t)-secret sharing scheme defined as follows. Let  be n distinct arbitrary non-zero field elements. Shares \(\mathsf {ShaSh}_{n,t}(s) = \mathbf {s}\) of a secret
be n distinct arbitrary non-zero field elements. Shares \(\mathsf {ShaSh}_{n,t}(s) = \mathbf {s}\) of a secret  are generated as follows: generate a uniformly random polynomial P of degree at most t over
are generated as follows: generate a uniformly random polynomial P of degree at most t over  with constant coefficient s (i.e., \(P(0) = s\)), the share
with constant coefficient s (i.e., \(P(0) = s\)), the share  is
is  . Given shares
. Given shares  with \(A \subseteq [n]\) and \(\left| A \right| > t\), the reconstruction works as follows: it computes the Lagrange coefficients \(\lambda _j = \prod _{i \in A \setminus \{j\}} (\alpha _{i} / (\alpha _{i} - \alpha _{j}))\) and output
with \(A \subseteq [n]\) and \(\left| A \right| > t\), the reconstruction works as follows: it computes the Lagrange coefficients \(\lambda _j = \prod _{i \in A \setminus \{j\}} (\alpha _{i} / (\alpha _{i} - \alpha _{j}))\) and output  .
.
3.3 Fourier Analysis
In this section, we present the notion of Fourier coefficients of a function and some of its properties. Most of the calculations needed about Fourier coefficients are deferred to the corresponding sections for the ease of readability. For an excellent survey on how Fourier Analytic methods are used in Additive Combinatorics, see [32].
Let \( \mathbb {G}\) be any finite abelian group. A character is a homomorphism \( \chi :\mathbb {G}\rightarrow \mathbb {C}\) from the group \( \mathbb {G}\) to \( \mathbb {C}\), i.e., \( \chi (a+b) = \chi (a) \cdot \chi (b) \) for all \( a,b\in \mathbb {G}\). For any finite abelian group \( \mathbb {G}\), the set of characters \( \widehat{\mathbb {G}}\) is a group (under the operation point-wise product) isomorphic to \( \mathbb {G}\). We will use \( \widehat{F}\left( \alpha \right) \) to denote the Fourier coefficient corresponding to \( \chi _\alpha \). The reader should note that while we define Fourier coefficients in generality, we would be primarily use Fourier analysis on the groups  for some prime p.
for some prime p.
Definition 3.8
(Fourier Coefficients). For functions \( f : \mathbb {G}\rightarrow \mathbb {C}\), the Fourier basis is composed of the group \(\widehat{\mathbb {G}}\) of characters \( \chi : \mathbb {G}\rightarrow \mathbb {C}\). We define the Fourier coefficient \( \widehat{f}\left( \chi \right) \) corresponding to a character \( \chi \) as

As we would use Fourier analysis on the additive group  . We describe the Fourier characters over
. We describe the Fourier characters over  . Let \( \omega = \exp (2\pi i /p) \) be a primitive p-th root of unity. Then, the characters for \( \mathbb {F}_p\) are given by \( \chi _\alpha (x) = \omega ^{\alpha \cdot x} \) where \( \alpha \in \mathbb {F}_p\). We sometimes abuse notation and write \(\widehat{f}(\alpha )\) instead of \(\hat{f}(\chi _\alpha )\).
. Let \( \omega = \exp (2\pi i /p) \) be a primitive p-th root of unity. Then, the characters for \( \mathbb {F}_p\) are given by \( \chi _\alpha (x) = \omega ^{\alpha \cdot x} \) where \( \alpha \in \mathbb {F}_p\). We sometimes abuse notation and write \(\widehat{f}(\alpha )\) instead of \(\hat{f}(\chi _\alpha )\).
We follow the “standard” notation in additive combinatorics. In this notation, when working on the group \( \mathbb {G}\), the Haar measure is used which assigns the weight \( \left| \mathbb {G} \right| ^{-1} \) to every \( x\in \mathbb {G}\) and when working on \( \widehat{\mathbb {G}}\), the counting measure is used which assigns the weight 1 to every \( \alpha \in \widehat{\mathbb {G}}\). Using these measures generally eliminates the need for normalization. So, when we talk about norms, these will always be taken with respect to the underlying measure. That is,

We note that the Fourier Transform has the following properties. These follow easily from the orthogonality relation on the characters: \( \sum _{x \in \mathbb {F}_p} \omega ^{a\cdot x} \) is p when \( a =0 \) and 0 otherwise.
Theorem 3.9
Let \( f,g : \mathbb {G}\rightarrow \mathbb {C}\) be two functions. Let \( \widehat{\mathbb {G}}\) denote the group of characters of \( \mathbb {G}\). The following hold:
- (a):
-
(Parseval’s identity) We have,
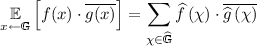
In particular, \( \Vert {f}\Vert _2 = \Vert \widehat{f} \Vert _2 \) where
 and \( \Vert {\widehat{f}}\Vert _2 = \sum _{\chi \in \widehat{\mathbb {G}}} \widehat{f}\left( \chi \right) ^2 \).
and \( \Vert {\widehat{f}}\Vert _2 = \sum _{\chi \in \widehat{\mathbb {G}}} \widehat{f}\left( \chi \right) ^2 \). - (b):
-
(Fourier Inversion Formula) For any \( x \in \mathbb {G}\), \( f(x) = \sum _{\chi \in \widehat{\mathbb {G}}} \widehat{f}\left( \chi \right) \cdot \overline{\chi (x)} \).
Finally, we introduce the notion of bias. A function is biased if it is highly correlated with some Fourier character.
Definition 3.10
(Bias). For a function \( f: \mathbb {G}\rightarrow \mathbb {C}\), the bias of f is defined as,
We need a calculation on certain sums of roots of unity. Let A be a subset of \( \mathbb {Z}_{k} \). And let \( \gamma = e^{i\cdot 2\pi /k} \). We want to bound sums of the form \( \varvec{\gamma }^A = \sum _{x\in A }\gamma ^x \). We state and prove the Lemma below. We will use the lemma to show that non-trivial Fourier coefficients of certain functions have to be smaller than the trivial one.
Lemma 3.11
Let k be a positive integer. Let \( \zeta _k: [0,k] \rightarrow \mathbb {R}_{\ge 0} \) be defined as \( \zeta _k(x) = \frac{\sin (x\pi /k)}{\sin (\pi /k)}\) with \( \zeta (0) = 0\). Let  . Then
. Then
We will show that the sum is maximized when A is an interval. The proof of the claim is an extremal argument. If an element does not lie in the direction of the sum, we can remove it and add something in the direction to increase the norm.
Proof
Pick the A that maximizes this sum. If possible, let A not be an interval. Let \( \zeta =\sum _{a\in A} \omega ^a \). If \( \left| \zeta \right| = 0 \), then the lemma holds as the sum over an interval of the same size would be higher. Hence, let \(\left| \zeta \right| > 0 \), consider the subset \( A' \) of size t consisting of all the roots of unity most ‘aligned’ with \( \zeta \). That is, for all \( a \in A' \) and  , \( \omega ^a \circ \zeta \ge \omega ^b \circ \zeta \) where \( \circ \) is the complex dot product.Footnote 8 If \( A = A' \), then we are done.
, \( \omega ^a \circ \zeta \ge \omega ^b \circ \zeta \) where \( \circ \) is the complex dot product.Footnote 8 If \( A = A' \), then we are done.
Otherwise, pick \( a \in A'\setminus A \) and \( b \in A \setminus A' \). Consider the set  . We claim that it has a bigger sum. That is, \( |\varvec{\gamma }^{A''} | \ge |\varvec{\gamma }^{A}| = \left| \zeta \right| \). Observe that
. We claim that it has a bigger sum. That is, \( |\varvec{\gamma }^{A''} | \ge |\varvec{\gamma }^{A}| = \left| \zeta \right| \). Observe that  . And as \( \zeta \circ a \ge \zeta \circ b \), \( \zeta \circ (a - b) \ge 0 \). Hence, \( \cos \theta \ge 0 \) where \( \theta \) is the angle between \( \zeta \) and \( (a-b) \). This implies that \( \theta \in [-\pi /2, \pi /2] \) and hence \( |\zeta - b + a| = |\zeta + (a-b)| \ge |\zeta | \). This yields a contradiction if A is not an interval.
. And as \( \zeta \circ a \ge \zeta \circ b \), \( \zeta \circ (a - b) \ge 0 \). Hence, \( \cos \theta \ge 0 \) where \( \theta \) is the angle between \( \zeta \) and \( (a-b) \). This implies that \( \theta \in [-\pi /2, \pi /2] \) and hence \( |\zeta - b + a| = |\zeta + (a-b)| \ge |\zeta | \). This yields a contradiction if A is not an interval.
The fact that \( \varvec{\gamma }^{A^\star } = \zeta _k(t)\) is derived using a basic trigonometry calculation:
where the last equality follows from the fact that the angle between \( \gamma ^t \) and \( -1 \) is \(( \pi - 2t\pi /k )\) and hence, \( \left| \gamma ^t -1 \right| = 2\cos ( (\pi - 2t\pi /k)/2 ) = 2\sin (\pi t/k)\). And the result follows. \(\square \)
4 On Leakage Resilience of Secret Sharing Schemes
4.1 Definitions and Basic Properties
We consider a model of leakage where the adversary can first choose a subset of \(\varTheta \subseteq [n]\) parties and get their full shares and then leak m bits each from all the shares of all the (other) parties. Formally, what is learned by the adversary on a sharing \(\mathbf {s}\) is the following:

where  is a family of n leakage functions that output m bits and
is a family of n leakage functions that output m bits and  are the complete shares of the parties corrupted. The adversary can choose the functions \( \vec \tau \) arbitrarily.
are the complete shares of the parties corrupted. The adversary can choose the functions \( \vec \tau \) arbitrarily.
Definition 4.1
(Local Leakage Resilient). Let \(\varTheta \) be a subset of [n]. A secret sharing scheme \( ({\mathsf {Share}}, {\mathsf {Rec}}) \) is said to be \( (\varTheta , m, \varepsilon ) \)-local leakage resilient (or \((\varTheta ,m,\varepsilon )\)-LL resilient for short) if for every leakage function family  where
where  has an m-bit output, and for every pair of secrets \( s_0, s_1 \),
has an m-bit output, and for every pair of secrets \( s_0, s_1 \),

A secret sharing scheme \(({\mathsf {Share}},{\mathsf {Rec}})\) is said to be \((\theta ,m,\varepsilon )\)-LL resilient if it is \((\varTheta ,m,\varepsilon )\)-LL resilient for any subset \(\varTheta \subseteq [n]\) of size at most \(\theta \).
Remark 4.2
We remark that we can consider an equivalent definition where for each distribution  of leakage function family
of leakage function family  :
:

Observe that an standard notion of (n, t)-secret sharing scheme corresponds to (t, 0, 0)-Local Leakage resilient: that is, complete access to the shares of t parties and no information about the others.
Note that in the leakage model, the adversary is not allowed to adaptively choose the leakage functions. As discussed in the introduction, this is a very meaningful and well-motivated leakage model. Next, demonstrate some attacks in this model. We formalize the observation that linear secret sharing schemes over small characteristic fields are not local leakage resilient.
Example 4.3
(Attack on Schemes Over Small Characteristic Fields). Over fields of small characteristic like  that have many additive subgroups, secret sharing schemes with linear reconstruction are not local leakage resilient. We give some examples of such attacks. They are not hard to generalize. Let
that have many additive subgroups, secret sharing schemes with linear reconstruction are not local leakage resilient. We give some examples of such attacks. They are not hard to generalize. Let  be the secret that is shared among n-parties as shares
be the secret that is shared among n-parties as shares  . Consider the following attacks:
. Consider the following attacks:
-
Additive Secret Sharing. The adversary can locally leak the least significant bit of each share
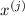 . Adding them up, the adversary can reconstruct the least significant bit of x.
. Adding them up, the adversary can reconstruct the least significant bit of x. -
Shamir Secret Sharing. For a similar attack, observe that
 where \( \lambda _j \)’s are fixed Lagrange coefficients. So to attack the scheme, the adversary locally multiplies the share
where \( \lambda _j \)’s are fixed Lagrange coefficients. So to attack the scheme, the adversary locally multiplies the share  with \( \lambda _j \) and leaks the least significant bit. This again reveals the least significant bit of x. The recent work of Guruswami and Wootters [34] shows how such leakage can be used to even completely reconstruct x.
with \( \lambda _j \) and leaks the least significant bit. This again reveals the least significant bit of x. The recent work of Guruswami and Wootters [34] shows how such leakage can be used to even completely reconstruct x.
Example 4.4
(Attack on Few Parties). If the number of parties n is a constant, then the additive secret sharing over \(\mathbb {F}_p\) is not LL-resilient. The adversary can distinguish between secrets \( < p/2 \) and \( > p/2\) by local leakage. The adversary locally leaks  if the share
if the share  (seeing the share as integer in \(\{0,\dots ,p-1\}\)). If all the leakages output 1, the adversary can conclude that the secret
(seeing the share as integer in \(\{0,\dots ,p-1\}\)). If all the leakages output 1, the adversary can conclude that the secret  . On the other hand, if the secret is larger than p / 2, then all the leakage outputs will never be 1 simultaneously. In the \( < p/2 \) case, the probability of all the secrets being \( < p/2n \) is about \( (1/2n)^n \), a constant. Similar attacks can also be performed on Shamir secret sharing. We stress that this is not the most effective attack, but it is an attack nonetheless. This attack is similar to the one in [37, Footnote 8].
. On the other hand, if the secret is larger than p / 2, then all the leakage outputs will never be 1 simultaneously. In the \( < p/2 \) case, the probability of all the secrets being \( < p/2n \) is about \( (1/2n)^n \), a constant. Similar attacks can also be performed on Shamir secret sharing. We stress that this is not the most effective attack, but it is an attack nonetheless. This attack is similar to the one in [37, Footnote 8].
4.2 Leakage Resilience of Additive and Shamir Secret Sharings
We are now in a position to state the main technical result of this section. That, if no family of local leakage functions can distinguish between shares picked uniformly at random and shares picked from a ‘good’ linear code. We will then prove a slightly better parameters in the case of additive-secret sharing.
Theorem 4.5
Let \( C \subset \mathbb {F}_p^n\) be any linear \( [n, t, n-t] \) code. Let  be any family of leakage functions where
be any family of leakage functions where  . Let \( c_m = \frac{2^m \sin (\pi /2^m)}{p \sin (\pi /p)} < 1\) (when \(2^m < p\)). Then,
. Let \( c_m = \frac{2^m \sin (\pi /2^m)}{p \sin (\pi /p)} < 1\) (when \(2^m < p\)). Then,
where \( U_n \) is the uniform distribution on \( \mathbb {F}_p^n \) and:

We observe that Theorem 4.5 yields the following two corollaries for additive secret sharing and Shamir secret sharing. We can strengthen the result slightly for additive secret sharing. We state it in Corollary 4.7. We first prove the corollaries assuming Theorem 4.5 and then prove Theorem 4.5.
Corollary 4.6
(Leakage Resilience of Additive Secret Sharing). The additive secret sharing \(\mathsf {AddSh}_n\) for n parties is \((\theta ,m,\varepsilon )\)-LL resilient where:
Proof
This corollary follows from the following claim after remarking that, when \(\theta \) parties reveal their share, an additive secret sharing with n parties becomes an additive secret sharing with \(n-\theta \) parties.
Claim 4.6.1
Let  be any family of m-bit output leakage functions. Let \( c_m = \frac{2^m \sin (\pi /2^m)}{p \sin (\pi /p)} < 1 \) (when \(2^m < p\)). Then for all secrets \( s_0,s_1 \in \mathbb {F}_p\),
be any family of m-bit output leakage functions. Let \( c_m = \frac{2^m \sin (\pi /2^m)}{p \sin (\pi /p)} < 1 \) (when \(2^m < p\)). Then for all secrets \( s_0,s_1 \in \mathbb {F}_p\),
Proof
Let C be the support of \( \mathsf {AddSh}(0) \). Note that C is an \( [n, n-1, 1] \) linear code and \( \mathsf {AddSh}(0) \) is uniformly distributed on C. Also note that the distribution \( \mathsf {AddSh}(s) \) is a coset of \( \mathsf {AddSh}(0) \), i.e., \( \mathsf {AddSh}(s) \) can be obtained by first sampling \( \mathbf {x} \leftarrow \mathsf {AddSh}(0) \) and then adding a fixed vector \( s \cdot \mathbf {e} = (s, 0, 0, \dots 0) \) to \( \mathbf {x} \). So, for any secret s,
where  and
and  for \(j > 1\).
for \(j > 1\).
Using triangle inequality, we can complete the proof:
\(\square \)
\(\square \)
In the case of additive secret sharing, we can strength the result slightly to show the following:
Corollary 4.7
(Leakage Resilience of Additive Secret Sharing). The additive secret sharing \(\mathsf {AddSh}_n\) for n parties is \((\theta ,m,\varepsilon )\)-LL resilient where:
Note that the difference between Corollary 4.6 and Corollary 4.7 is that in the stronger claim, the bound on the adversary’s advantage does not degrade as the prime increases. Corollary 4.7 is proved in Sect. 4.3. In the case of Shamir secret sharing, we can prove the following result.
Corollary 4.8
(Leakage Resilience of Shamir Secret Sharing). The Shamir secret sharing \(\mathsf {ShaSh}_n\) for n parties is \((\theta ,m,\varepsilon )\)-LL resilient where:
We defer the proofs of both corollaries to the full version.
4.3 Proof of Theorem 4.5
In this section, we prove Theorem 4.5. The proof is divided into three parts. In Lemma 4.9, we show that the operator \( \varLambda \) has a good representation in the Fourier Basis. In Lemma 4.10, we show bounds on the Fourier coefficients and then prove Theorem 4.5 using these two lemmas. Due to the lack of space, we prove Lemmas 4.9 and 4.10 in the full version.
On Fourier Expansion of \( \varLambda \). First, we show that expectation of product of functions over a code can be represented as a sum of products over the dual code.
Lemma 4.9
(Poisson Summation Formula). Let \( p > 2\) be a prime and \( \omega = \exp (\frac{2\pi i}{p})\). Let \( C \subset \mathbb {F}_p^n\) be a linear code with dual code is \( C^\perp \). Let \( f_1, f_2 \dots f_n :\mathbb {F}_p\rightarrow \mathbb {C}\) be functions. Let \( \varLambda \) be defined as follows:

where \( \vec x= (x_1, x_2, \dots , x_n) \). Then, the following holds:

where  .
.
Bounds on Fourier Coefficients. We want to bound terms of the form \( \widehat{1_{A}}\left( \alpha \right) \) for sets A. We now show bounds on such terms over \( \mathbb {F}_p\). We state the lemma required in the proof of Theorem 4.5 for such bounds.
Lemma 4.10
Let \( \omega = e^{i \cdot 2\pi /p} \). For any set A, let \( \varvec{\omega }^{A} = \sum _{x \in A} \omega ^x \). For any partition \( A_1, A_2 \dots A_{2^m}\) of \( \mathbb {F}_p\), let \( c_m = \frac{2^m \sin (\pi /2^m)}{p \sin (\pi /p)} \). Then,
Completing the Proof. At this point, given Lemmas 4.9 and 4.10 we can complete the proof of Theorem 4.5.
Proof
(Proof of Theorem 4.5). For the sake of simplicity, we abuse notation and define \( 1_{\ell _{j}}(x) =1 \) if  and 0 otherwise. We can express the statistical distance as follows:
and 0 otherwise. We can express the statistical distance as follows:

where the second equality follows from Lemma 4.9, the third equality follows from the fact that  . The first inequality follows from triangle inequality. To complete the proof, we bound each individual term. Before that, we need the following claim:
. The first inequality follows from triangle inequality. To complete the proof, we bound each individual term. Before that, we need the following claim:
Claim 4.10.1
For any \( \alpha \ne 0\) and a leakage function  , let \(1_{\ell _{}}(x) = 1 \) if and only if \( \tau (x) = \ell _{} \). Then,
, let \(1_{\ell _{}}(x) = 1 \) if and only if \( \tau (x) = \ell _{} \). Then,  .
.
Proof
Observe that  . As \( \alpha \ne 0 \), as the sets \( {( \tau ^{-1}(\ell _{}) )}_{\ell _{}} \) partition \(\mathbb {F}_p\), so do the sets \( {( A_{\ell _{}} = \alpha \tau ^{-1}(\ell _{}) )}_{\ell _{}} \). Thus, using Lemma 4.10, we get that,
. As \( \alpha \ne 0 \), as the sets \( {( \tau ^{-1}(\ell _{}) )}_{\ell _{}} \) partition \(\mathbb {F}_p\), so do the sets \( {( A_{\ell _{}} = \alpha \tau ^{-1}(\ell _{}) )}_{\ell _{}} \). Thus, using Lemma 4.10, we get that,

This completes the proof. \(\square \)

We observe that  . If
. If  . On the other hand, if \( \alpha _j \ne 0 \), as the sets \( {( \tau _j^{-1}(\ell _{j}) )}_{\ell _{j}} \) partition \(\mathbb {F}_p\), so do the sets \( {( A_{\ell _{j}} = \alpha _j\tau _j^{-1}(\ell _{j}) )}_{\ell _{j}} \). Thus, if \(\alpha _j \ne 0\), using Lemma 4.10, we get that,
. On the other hand, if \( \alpha _j \ne 0 \), as the sets \( {( \tau _j^{-1}(\ell _{j}) )}_{\ell _{j}} \) partition \(\mathbb {F}_p\), so do the sets \( {( A_{\ell _{j}} = \alpha _j\tau _j^{-1}(\ell _{j}) )}_{\ell _{j}} \). Thus, if \(\alpha _j \ne 0\), using Lemma 4.10, we get that,  . Hence, we get that,
. Hence, we get that,

where \( \mathsf {HW} (\cdot )\) denotes the Hamming weight. The last inequality follows from the fact that the dual code \(C^\perp \) has minimum distance t, as C is a \( [n, t, n-t] \) MDS linear code. \(\square \)
Now we add up the contributions from each  to complete the proof.
to complete the proof.
5 Leakage Resilience of GMW with Preprocessing
In this section, we describe an application of the results on leakage resilience of secret sharing to MPC protocols. We show that a variant of the GMW protocol with preprocessing is leakage resilient.
We consider arithmetic circuits over a field  over a basis
over a basis  where the \( -1 \) gate negates the input. For convenience, we have input gates that read a field element from the input. The following definition of an MPC protocol is adapted from [31] (Definition 3).
where the \( -1 \) gate negates the input. For convenience, we have input gates that read a field element from the input. The following definition of an MPC protocol is adapted from [31] (Definition 3).
Definition 5.1
(n-party protocol with encoded input and output). An n-party protocol for  is defined by \( \varPi = (I, \mathbf {R}, \mathbf {M}, O) \), where:
is defined by \( \varPi = (I, \mathbf {R}, \mathbf {M}, O) \), where:
-
Input Encoder.
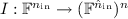 is a randomized input encoder circuit, which maps an input \( \vec x \) for f to a tuple of protocol inputs
is a randomized input encoder circuit, which maps an input \( \vec x \) for f to a tuple of protocol inputs  one for each party.
one for each party. -
Randomness.
 are distributions over
are distributions over  that capture the random inputs of the parties. They are assumed to be correlated due to preprocessing.
that capture the random inputs of the parties. They are assumed to be correlated due to preprocessing. -
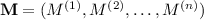 are deterministic next message functions where
are deterministic next message functions where 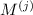 determines the next message sent by party j as a function of its input
determines the next message sent by party j as a function of its input 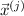 , random input
, random input  , and the sequence of messages received in the previous rounds. Messages are sent in rounds where each party sends a message to possibly every other party. After a predetermined number of rounds, the function
, and the sequence of messages received in the previous rounds. Messages are sent in rounds where each party sends a message to possibly every other party. After a predetermined number of rounds, the function  returns a local output
returns a local output  for party j.
for party j. -
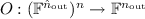 is a deterministic output decoder circuit, which maps a tuple of protocol outputs
is a deterministic output decoder circuit, which maps a tuple of protocol outputs 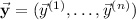 to an output \( \vec y \) of f.
to an output \( \vec y \) of f.
For  , we denote by \( \varPi (\vec x) \) the output of \( \varPi \) on input \(\vec x \), namely the result of applying the input encoder I to \(\vec x \), interacting as specified by \( \mathbf {R}, \mathbf {M} \), and applying the output decoder O to the vector of protocol outputs. We say that \( \varPi \) is correctly computes
, we denote by \( \varPi (\vec x) \) the output of \( \varPi \) on input \(\vec x \), namely the result of applying the input encoder I to \(\vec x \), interacting as specified by \( \mathbf {R}, \mathbf {M} \), and applying the output decoder O to the vector of protocol outputs. We say that \( \varPi \) is correctly computes  if for every input
if for every input  , we have
, we have  .
.
We denote by \( {\mathbf {view}}(\vec x) \) the joint distribution  obtained by running \( \varPi \) on input \( \vec x \), where
obtained by running \( \varPi \) on input \( \vec x \), where  includes the encoded input
includes the encoded input  , the random input
, the random input  (sampled from
(sampled from  ), and the sequence of messages received by party j. (The messages sent by party j as well as its output
), and the sequence of messages received by party j. (The messages sent by party j as well as its output  are uniquely determined by
are uniquely determined by  .)
.)
We denote by \({\mathbf {out}}(\vec x)\) the joint distribution of the outputs \(\vec {\mathbf {y}}\).
5.1 Security Definitions
The definition we consider uses the simulation paradigm. We only consider an honest-but-curious definition, albeit one where the adversary can leak information from the views of the uncorrupted parties. We consider two security notions: private-output local leakage resilience and public-outputs local leakage resilience.
In the private-output case, the adversary does not learn the local outputs  of non-corrupted parties nor the output \(\vec y = \varPi (\vec x)\). This would model the setting where a client wants to delegate some computation \(f(\vec x)\) to some leaky servers: the client secret shares \(\vec x\) into \(\vec {\mathbf {x}}\), sends each share
of non-corrupted parties nor the output \(\vec y = \varPi (\vec x)\). This would model the setting where a client wants to delegate some computation \(f(\vec x)\) to some leaky servers: the client secret shares \(\vec x\) into \(\vec {\mathbf {x}}\), sends each share  to the server i, the servers run the protocol \(\varPi \), and each server i sends back its output share
to the server i, the servers run the protocol \(\varPi \), and each server i sends back its output share  to the client.
to the client.
In the public-outputs case, the adversary learns all the local outputs \(\vec {\mathbf {y}}\) of all the parties (and in particular learns the output \(\vec y = O(\vec {\mathbf {y}}) = \varPi (\vec x)\)). This models a setting where at the end of the computation, the parties would broadcast their local outputs  to jointly reconstruct the output \(\vec y\).
to jointly reconstruct the output \(\vec y\).
Definition 5.2
(Private-Output Local Leakage Resilient Protocol). We say that \( \varPi \) is \( (\varTheta , m, \varepsilon ) \)-private-output local leakage resilient for f (or \( (\varTheta , m, \varepsilon ) \)-priv-LL-resilient for short) if \( \varPi \) correctly computes f, and the following security requirement holds. For any family of local leakage functions  where
where  is a function that outputs m bits, there exists a simulator \(\mathsf {LeakSim}_{\varTheta ,\vec {\varvec{\tau }}}\) such that, and for any input
is a function that outputs m bits, there exists a simulator \(\mathsf {LeakSim}_{\varTheta ,\vec {\varvec{\tau }}}\) such that, and for any input  , we have
, we have
We say that \(\varPi \) is \((\theta ,m,\varepsilon )\)-priv-LL-resilient if \(\varPi \) is \((\varTheta ,m,\varepsilon )\)-LL-resilient for all subsets \(\varTheta \subseteq [n]\) of at most size \(\theta \).
Definition 5.3
(Public-Outputs Local Leakage Resilient Protocol). We say that \( \varPi \) is \( (\varTheta , m, \varepsilon ) \)-public-outputs local leakage resilient for f (or \( (\varTheta , m, \varepsilon ) \)-pub-LL-resilient for short) if \( \varPi \) correctly computes f, and the following security requirement holds. For any family of local leakage functions  where
where  is a function that outputs m bits, there exists a simulator \(\mathsf {LeakSim}_{\varTheta ,\vec {\varvec{\tau }}}\) such that, and for any input
is a function that outputs m bits, there exists a simulator \(\mathsf {LeakSim}_{\varTheta ,\vec {\varvec{\tau }}}\) such that, and for any input  , we have
, we have
We say that \(\varPi \) is \((\theta ,m,\varepsilon )\)-pub-LL-resilient if \(\varPi \) is \((\varTheta ,m,\varepsilon )\)-pub-LL-resilient for all subsets \(\varTheta \subseteq [n]\) of at most size \(\theta \).
Both definitions model a protocol executed in the presence of a real-world adversary \(\mathcal {A}\) that may corrupt a subset \(\varTheta \) of the parties. The adversary learns the entire view of corrupted parties (and in the second case, also the output of all parties). The adversary also leaks independently m bits from each party. As we consider semi-honest corruptions, the adversary can only observe their views but does not modify the messages they send.
Note that the classical notion of security against semi-honest adversaries corrupting \(\theta \) parties is equivalent to \((\theta ,0,\varepsilon )\)-priv-LL-resilient.
5.2 GMW with Shared Product Preprocessing
Notation. Let f be a function computed by a given circuit C. Let G be the set of all gates in C and \( G_{\times }\) be the set of multiplication gates in C. For any input \(\vec x \), let \( z_g \) denote the value at gate \( g\in G\) in the circuit C when the input is \(\vec x \).
In Fig. 2, we describe a variant of the GMW [25] protocol based on the ideas of Beaver triples [3] that we call GMW with shared product preprocessing. The protocol works with any linear secret sharing. We show that if the underlying linear secret sharing is local leakage resilient, then the protocol is pub-LL-resilient and priv-LL-resilient.
Let us first prove correctness.
Proposition 5.4
(Correctness). The protocol \(\varPi \) in Fig. 2 on any input \( \vec x \) correctly computes \( f(\vec x)\).
Proof
To prove correctness, we show that at every gate g, the parties maintain a linear secret sharing of the value \( z_g \). This is easy to verify for the addition, \( -1 \) and input gates. We will only do the verification for the multiplication case.
Consider any multiplication gate g with input gates \( g_1, g_2 \). Assume that the parties have a valid secret sharing \( \mathbf {z}_{g_1} \) and \( \mathbf {z}_{g_2} \) of values \( z_{g_1} \) and \( z_{g_2} \) respectively. Pick any valid Beaver triple \( (\mathbf {a}_g, \mathbf {b}_g, \mathbf {(ab)}_g )\). We need to show that \( \mathbf {z}_g \) as computed is a valid secret sharing of \( z_g = z_{g_1} z_{g_2} \). We remark that:
By linearity \(\mathbf {z}_g\) is a secret sharing of:
This concludes the proof. \(\square \)
We have the following security theorems.
Theorem 5.5
If the linear secret sharing scheme \(({\mathsf {Share}},{\mathsf {Rec}})\) is \((\varTheta ,m,\varepsilon )\)-LL-resilient then the protocol \(\varPi \) in Fig. 2 is \((\varTheta ,m, \varepsilon )\)-priv-LL-resilient.
Theorem 5.6
If the linear secret sharing scheme \(({\mathsf {Share}},{\mathsf {Rec}})\) is \((\varTheta ,m,\varepsilon )\)-LL-resilient then the protocol \(\varPi \) in Fig. 2 is \((\varTheta ,m, \varepsilon )\)-pub-LL-resilient.
Since an (n, t)-secret sharing scheme is (t, 0, 0)-LL-resilient, when instantiated with an (n, t)-secret sharing scheme, the protocol is (t, 0, 0)-priv-LL resilient and thus secure against a semi-honest adversaries corrupting up to t parties.
Before we prove Theorems 5.5 and 5.6, let us state the following lemma that is proven in the full version.
Lemma 5.7
(Parallel Composition of LL-Resilience). If \(({\mathsf {Share}},{\mathsf {Rec}})\) is a \((\varTheta ,m,\varepsilon )\)-LL-resilient linear secret sharing scheme, then for any leakage function family  where
where  has an m-bit output, and for any
has an m-bit output, and for any  :
:

Note that the bound on statistical distance does not degrade with the size of the vectors.
5.3 Proof of Private-Output Local Leakage Resilience (Theorem 5.5)
To prove the private-output local leakage resilience (Theorem 5.5), we first start with a lemma that characterizes what information the parties see, both individually and jointly. Informally, we show that, when the protocol evaluates the circuit C on input \( \vec x \), the view of each party (or any subset of parties) can be simulated given a set of common random values and additive shares given to the party (or parties) of the value in each gate. Then, the leakage resilience of the secret sharing scheme allows us to replace the secret sharings used by the simulator by secret sharings of any arbitrary value.
Lemma 5.8
There exists simulator \( {\mathsf {S}}\) such that for every input \( \vec x \), the following two distributions are identical.

Assuming Lemma 5.8, the proof of Theorem 5.5 (private-output-LL-resilience of \( \varPi \)) is immediate. Formal proofs are provided in the full version.
5.4 Proof of Public-Outputs Local Leakage Resilience (Theorem 5.6)
To prove the public-outputs local leakage resilience (Theorem 5.6), we extend Lemma 5.8 to take into account the output shares.
Lemma 5.9
There exists a simulator \( {\mathsf {S}}' \) such that for every input \( \vec x \), the following two distributions are identical.

Assuming Lemma 5.9, the proof of Theorem 5.5 (pub-LL-resilience of \( \varPi \)) is immediate. Formal proofs are provided in the full version.
Notes
- 1.
In the whole paper, a (n, t)-Shamir secret sharing scheme or Shamir secret sharing scheme with thereshold t uses polynomials of degree t, so that the secret cannot be recovered from a collusion of up to t parties. The secret can be recovered from \(t+1\) parties.
- 2.
This can be done by locally adding shares of a random \( (n,c'n) \)-Shamir share of 0 to the given (n, cn) - Shamir shares.
- 3.
A Beaver triple consists of (a, b, ab) where a, b are randomly chosen field elements.
- 4.
To recall, in the quotient group
 , the elements are the cosets \( A_0, A_1 \). The sum of two cosets is the coset formed by the sum of elements of the first cosets with elements of the second coset. Because of the structure, \( A_0 + A_0 = A_0 \), \( A_0 + A_1 = A_1 \) and so on.
, the elements are the cosets \( A_0, A_1 \). The sum of two cosets is the coset formed by the sum of elements of the first cosets with elements of the second coset. Because of the structure, \( A_0 + A_0 = A_0 \), \( A_0 + A_1 = A_1 \) and so on. - 5.
A relation is trivial if no matter what secret is shared, a constant output by the conversion scheme would satisfy correctness. Or put another way, in a non-trivial relation R, there exist \( s_0 \) and \( s_1 \) such that \( s_0 \) has to be mapped to 0 and \( s_1 \) has to be mapped to 1 in the relation R.
- 6.
We consider more general case in the full version which also tolerates a higher error probability of 1 / 6.
- 7.
Both complexity measures do not assign complexity to all possible linear forms. To give an example, the linear form \(( L_1(x) = x, L_2(x) = x+2 )\), which corresponds to the twin primes conjecture, is not assigned a complexity value and the twin primes conjecture is still open.
- 8.
\( z_1 \circ z_2 = x_1x_2 + y_1y_2 \) where \( z_b = x_b + i\cdot y_b \) is the dot product of \( z_1 \) and \( z_2 \). Equivalently, \( z_1 \circ z_2 = |z_1| |z_2| \cos \theta \) where \( \theta \) is the angle between \( z_1 \) and \( z_2 \).
References
Akavia, A., Goldwasser, S., Vaikuntanathan, V.: Simultaneous hardcore bits and cryptography against memory attacks. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 474–495. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_28
Araki, T., Furukawa, J., Lindell, Y., Nof, A., Ohara, K.: High-throughput semi-honest secure three-party computation with an honest majority. In: CCS (2016)
Beaver, D.: Efficient multiparty protocols using circuit randomization. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 420–432. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_34
Beimel, A., Ishai, Y., Kushilevitz, E., Orlov, I.: Share conversion and private information retrieval. In: CCC (2012)
Ben-Or, M., Coppersmith, D., Luby, M., Rubinfeld, R.: Non-abelian homomorphism testing, and distributions close to their self-convolutions. Random Struct. Algorithms (2008)
Ben-Or, M., Goldwasser, S., Wigderson, A.: Completeness theorems for non-cryptographic fault-tolerant distributed computation (extended abstract). In: STOC (1988)
Bitansky, N., Dachman-Soled, D., Lin, H.: Leakage-tolerant computation with input-independent preprocessing. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 146–163. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_9
Blakley, G.: Safeguarding cryptographic keys. In: AFIPS National Computer Conference (1979)
Blum, M., Luby, M., Rubinfeld, R.: Self-testing/correcting with applications to numerical problems. J. Comput. Syst. Sci. 47, 549–595 (1993)
Bogdanov, A., Ishai, Y., Viola, E., Williamson, C.: Bounded indistinguishability and the complexity of recovering secrets. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part III. LNCS, vol. 9816, pp. 593–618. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_21
Boyle, E., Gilboa, N., Ishai, Y.: Breaking the circuit size barrier for secure computation under DDH. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 509–539. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_19
Boyle, E., Goldwasser, S., Kalai, Y.T.: Leakage-resilient coin tossing. In: Peleg, D. (ed.) DISC 2011. LNCS, vol. 6950, pp. 181–196. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-24100-0_16
Chaum, D., Crépeau, C., Damgård, I.: Multiparty unconditionally secure protocols (extended abstract). In: Pomerance, C. (ed.) CRYPTO 1987. LNCS, vol. 293, pp. 462–462. Springer, Heidelberg (1988). https://doi.org/10.1007/3-540-48184-2_43
Cramer, R., Damgård, I., Ishai, Y.: Share conversion, pseudorandom secret-sharing and applications to secure computation. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 342–362. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30576-7_19
Dachman-Soled, D., Liu, F., Zhou, H.: Leakage-resilient circuits revisited – optimal number of computing components without leak-free hardware. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 131–158. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_5
Damgård, I., Pastro, V., Smart, N.P., Zakarias, S.: Multiparty computation from somewhat homomorphic encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 643–662. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_38
Dodis, Y., Halevi, S., Rothblum, R.D., Wichs, D.: Spooky encryption and its applications. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part III. LNCS, vol. 9816, pp. 93–122. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_4
Duc, A., Dziembowski, S., Faust, S.: Unifying leakage models: from probing attacks to noisy leakage. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 423–440. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_24
Dziembowski, S., Faust, S.: Leakage-resilient circuits without computational assumptions. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 230–247. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_13
Dziembowski, S., Pietrzak, K.: Intrusion-resilient secret sharing. In: FOCS (2007)
Dziembowski, S., Pietrzak, K.: Leakage-resilient cryptography. In: FOCS (2008)
Faust, S., Rabin, T., Reyzin, L., Tromer, E., Vaikuntanathan, V.: Protecting circuits from leakage: the computationally-bounded and noisy cases. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 135–156. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_7
Fazio, N., Gennaro, R., Jafarikhah, T., Skeith III, W.E.: Homomorphic secret sharing from paillier encryption. In: Okamoto, T., Yu, Y., Au, M.H., Li, Y. (eds.) ProvSec 2017. LNCS, vol. 10592, pp. 381–399. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-68637-0_23
Genkin, D., Ishai, Y., Weiss, M.: How to construct a leakage-resilient (stateless) trusted party. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10678, pp. 209–244. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70503-3_7
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game or a completeness theorem for protocols with honest majority. In: STOC 1987 (1987)
Goldwasser, S., Rothblum, G.N.: How to compute in the presence of leakage. SICOMP (2015). https://doi.org/10.1137/130931461
Gowers, W.T.: A new proof of Szemerédi’s theorem. Geom. Funct. Anal. 11, 465–588 (2001)
Gowers, W.T., Wolf, J.: The true complexity of a system of linear equations. Proc. London Math. Soc. 100, 155–176 (2010)
Gowers, W.T., Wolf, J.: Linear forms and higher-degree uniformity for functions on \( \mathbb{F}_n^p \). Geom. Funct. Anal. 21, 36–39 (2011)
Gowers, W.T., Wolf, J.: Linear forms and quadratic uniformity for functions on \( \mathbb{F}_n^p \). Mathematika 57, 215–237 (2011)
Goyal, V., Ishai, Y., Maji, H.K., Sahai, A., Sherstov, A.A.: Bounded-communication leakage resilience via parity-resilient circuits. In: FOCS (2016)
Green, B.: Montréal notes on quadratic Fourier analysis. Add. Comb. 43, 69–102 (2007)
Green, B., Tao, T.: Linear equations in primes. Ann. Math. 171, 1753–1850 (2010)
Guruswami, V., Wootters, M.: Repairing reed-solomon codes. IEEE Trans. Inf. Theory 63, 5684–5698 (2017)
Ishai, Y., Sahai, A., Wagner, D.A.: Private circuits: securing hardware against probing attacks. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 463–481. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_27
Keller, M., Orsini, E., Scholl, P.: MASCOT: faster malicious arithmetic secure computation with oblivious transfer. In: CCS (2016)
Kiltz, E., Pietrzak, K.: Leakage resilient elgamal encryption. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 595–612. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_34
Kocher, P., Genkin, D., Gruss, D., Haas, W., Hamburg, M., Lipp, M., Mangard, S., Prescher, T., Schwarz, M., Yarom, Y.: Spectre attacks: exploiting speculative execution. ArXiv e-prints, January 2018
Kocher, P.C.: Timing attacks on implementations of Diffie-Hellman, RSA, DSS, and other systems. In: Koblitz, N. (ed.) CRYPTO 1996. LNCS, vol. 1109, pp. 104–113. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68697-5_9
Kocher, P., Jaffe, J., Jun, B.: Differential power analysis. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 388–397. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_25
Lipp, M., Schwarz, M., Gruss, D., Prescher, T., Haas, W., Mangard, S., Kocher, P., Genkin, D., Yarom, Y., Hamburg, M.: Meltdown. ArXiv e-prints
Micali, S., Reyzin, L.: Physically observable cryptography. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 278–296. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_16
Shamir, A.: How to share a secret. Commun. ACM 22, 612–613 (1979)
Tao, T., Vu, V.H.: Additive Combinatorics. Cambridge University Press, Cambridge (2006)
Yao, A.C.: How to generate and exchange secrets (extended abstract). In: FOCS (1986)
Acknowledgements
We thank the Crypto reviewers for helpful comments.
The first and fourth authors were supported by the Defense Advanced Research Projects Agency (DARPA) and U.S. Army Research Office (ARO) under Contract No. W911NF-15-C-0236. The second author did some of the work when he was a summer intern at IBM Research. He was supported in part by NSF Grants CNS-1413920 and CNS-1350619, and by the Defense Advanced Research Projects Agency (DARPA) and the U.S. Army Research Office (ARO) under contracts W911NF-15-C-0226 and W911NF-15-C-0236. The third author was supported in part by ERC grant 742754, ISF grant 1709/14, NSF-BSF grant 2015782, and a grant from the Ministry of Science and Technology, Israel and Department of Science and Technology, Government of India.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Benhamouda, F., Degwekar, A., Ishai, Y., Rabin, T. (2018). On the Local Leakage Resilience of Linear Secret Sharing Schemes. In: Shacham, H., Boldyreva, A. (eds) Advances in Cryptology – CRYPTO 2018. CRYPTO 2018. Lecture Notes in Computer Science(), vol 10991. Springer, Cham. https://doi.org/10.1007/978-3-319-96884-1_18
Download citation
DOI: https://doi.org/10.1007/978-3-319-96884-1_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96883-4
Online ISBN: 978-3-319-96884-1
eBook Packages: Computer ScienceComputer Science (R0)


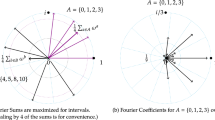



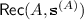 outputs the secret s for all A where
outputs the secret s for all A where  where
where 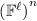 , for some positive integer
, for some positive integer  ,
,  ,
,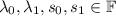 :
: 
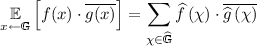
 and
and 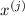 . Adding them up, the adversary can reconstruct the least significant bit of x.
. Adding them up, the adversary can reconstruct the least significant bit of x. where
where  with
with 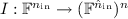 is a randomized
is a randomized  one for each party.
one for each party. are distributions over
are distributions over  that capture the random inputs of the parties. They are assumed to be correlated due to preprocessing.
that capture the random inputs of the parties. They are assumed to be correlated due to preprocessing.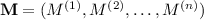 are deterministic
are deterministic 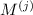 determines the next message sent by party j as a function of its input
determines the next message sent by party j as a function of its input 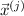 , random input
, random input  , and the sequence of messages received in the previous rounds. Messages are sent in rounds where each party sends a message to possibly every other party. After a predetermined number of rounds, the function
, and the sequence of messages received in the previous rounds. Messages are sent in rounds where each party sends a message to possibly every other party. After a predetermined number of rounds, the function  returns a local output
returns a local output  for party j.
for party j.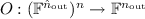 is a deterministic
is a deterministic 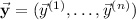 to an output
to an output 
 , the elements are the cosets
, the elements are the cosets 