Abstract
Since its inception, public-key encryption (\(\mathsf {PKE}\)) has been one of the main cornerstones of cryptography. A central goal in cryptographic research is to understand the foundations of public-key encryption and in particular, base its existence on a natural and generic complexity-theoretic assumption. An intriguing candidate for such an assumption is the existence of a cryptographically hard language  .
.
In this work we prove that public-key encryption can be based on the foregoing assumption, as long as the (honest) prover in the zero-knowledge protocol is efficient and laconic. That is, messages that the prover sends should be efficiently computable (given the  witness) and short (i.e., of sufficiently sub-logarithmic length). Actually, our result is stronger and only requires the protocol to be zero-knowledge for an honest-verifier and sound against computationally bounded cheating provers.
witness) and short (i.e., of sufficiently sub-logarithmic length). Actually, our result is stronger and only requires the protocol to be zero-knowledge for an honest-verifier and sound against computationally bounded cheating provers.
Languages in  with such laconic zero-knowledge protocols are known from a variety of computational assumptions (e.g., Quadratic Residuocity, Decisional Diffie-Hellman, Learning with Errors, etc.). Thus, our main result can also be viewed as giving a unifying framework for constructing \(\mathsf {PKE}\) which, in particular, captures many of the assumptions that were already known to yield \(\mathsf {PKE}\).
with such laconic zero-knowledge protocols are known from a variety of computational assumptions (e.g., Quadratic Residuocity, Decisional Diffie-Hellman, Learning with Errors, etc.). Thus, our main result can also be viewed as giving a unifying framework for constructing \(\mathsf {PKE}\) which, in particular, captures many of the assumptions that were already known to yield \(\mathsf {PKE}\).
We also show several extensions of our result. First, that a certain weakening of our assumption on laconic zero-knowledge is actually equivalent to \(\mathsf {PKE}\), thereby giving a complexity-theoretic characterization of \(\mathsf {PKE}\). Second, a mild strengthening of our assumption also yields a (2-message) oblivious transfer protocol.
Full version available at: https://eccc.weizmann.ac.il/report/2017/172.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Oblivious Transfer
- Complexity-theoretic Characterization
- Hash Proof System
- Pseudoentropy
- Deterministic Provers
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Underlying symmetric key encryption is a centuries-old idea: shared secrets enable secure communication. This idea takes many forms: the Caeser cipher, the unconditionally secure one-time pads, fast heuristic constructions like AES, and a multitude of candidates based on the hardness of a variety of problems. The discovery of public-key encryption, by Diffie and Hellman [DH76] and Rivest, Shamir and Adleman [RSA78], was revolutionary as it gave us the ability to communicate securely without any shared secrets. Needless to say, this capability is one of the cornerstones of secure communication in today’s online world.
As is typically the case in cryptography, we are currently very far from establishing the security of public-key cryptography unconditionally. Rather, to establish security, we rely on certain computational intractability assumptions. Despite four decades of extensive research, we currently only know constructions of public-key encryption from a handful of assumptions, most notably assumptions related to the hardness of factoring, finding discrete logarithms and computational problems related to lattices (as well as a few more exotic assumptions).
One of the central open problems in cryptography is to place public-key encryption on firmer complexity-theoretic grounding, ideally by constructing public-key encryption from the minimal assumption that one-way functions exist. Such a result seems well beyond current techniques, and by the celebrated result of Impagliazzo and Rudich [IR89] requires a non-blackbox approach. Given that, a basic question that we would like to resolve is the following:

Our motivation for asking this question is twofold. First, we seek to understand: Why is it the case that so few assumptions give us public-key encryption? What kind of “structured hardness” is required? Secondly, we hope that this understanding can guide the search for new concrete problems that yield public-key encryption.
1.1 Our Results
Our main result is a construction of a public-key encryption scheme from a general complexity-theoretic assumption: namely, the existence of a cryptographically hard language  that has a laconic (honest-verifier) statistical zero-knowledge argument-system. We first discuss the notions mentioned above, and then proceed to state the main result more precisely (yet still informally).
that has a laconic (honest-verifier) statistical zero-knowledge argument-system. We first discuss the notions mentioned above, and then proceed to state the main result more precisely (yet still informally).
By a cryptographically hard language we mean an  language that is average-case hard to decide with a solved instance generator. Namely, that there are two distributions \( \textsf {Y} _{}\) and \( \textsf {N} _{}\), over YES and NO instances of the language respectively, such that (1) \( \textsf {Y} _{}\) and \( \textsf {N} _{}\) are computationally indistinguishable; and (2) there exists an efficient solved instance generator for the YES distribution.Footnote 1 A proof-system is laconic [GH98, GVW02] if the number of bits sent from the prover to the verifier is very small.Footnote 2 An argument-system is similar to an interactive proof, except that soundness is only required to hold against computationally bounded (i.e., polynomial time) cheating provers. Honest verifier zero-knowledge means that the honest verifier learns no more in the interaction than the fact that
language that is average-case hard to decide with a solved instance generator. Namely, that there are two distributions \( \textsf {Y} _{}\) and \( \textsf {N} _{}\), over YES and NO instances of the language respectively, such that (1) \( \textsf {Y} _{}\) and \( \textsf {N} _{}\) are computationally indistinguishable; and (2) there exists an efficient solved instance generator for the YES distribution.Footnote 1 A proof-system is laconic [GH98, GVW02] if the number of bits sent from the prover to the verifier is very small.Footnote 2 An argument-system is similar to an interactive proof, except that soundness is only required to hold against computationally bounded (i.e., polynomial time) cheating provers. Honest verifier zero-knowledge means that the honest verifier learns no more in the interaction than the fact that  (i.e., the verifier can simulate the honest interaction by itself). Thus, our main result can be stated as follows:
(i.e., the verifier can simulate the honest interaction by itself). Thus, our main result can be stated as follows:
Theorem 1.1
(Informally Stated, see Theorem 2.6). Assume that there exists a cryptographically hard language  with an r-round statistical honest-verifier zero-knowledge argument-system, with constant soundness, that satisfies the following two requirements:
with an r-round statistical honest-verifier zero-knowledge argument-system, with constant soundness, that satisfies the following two requirements:
-
Efficient Prover: The strategy of the honest prover can be implemented in polynomial-time, given the
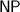 witness.Footnote 3
witness.Footnote 3
-
Laconic Prover: The prover sends at most q bits in each of the r rounds, such that \(r^2 \cdot q^3 = O(\log {n})\), where n is the input length.
Then, there exists a public-key encryption (\(\mathsf {PKE}\)) scheme.
We emphasize that requiring only honest-verifier zero-knowledge (as opposed to full-fledged zero-knowledge) and computational soundness (i.e., an argument-system) weakens our assumption, and therefore only strengthens our main result. We also comment that we can handle provers that are less laconic (i.e., send longer messages) by assuming that the language  is sub-exponentially hard. Lastly, we remark the assumption in Theorem 1.1 may be viewed as a generalization of the notion of hash proof systems [CS02].Footnote 4 We discuss this point in more detail in Sect. 1.2.
is sub-exponentially hard. Lastly, we remark the assumption in Theorem 1.1 may be viewed as a generalization of the notion of hash proof systems [CS02].Footnote 4 We discuss this point in more detail in Sect. 1.2.
1.1.1 Instantiations
Many concrete assumptions (which are already known to yield public-key encryption schemes) imply the conditions of Theorem 1.1. First, number-theoretic assumptions such as Quadratic Residuosity (\(\mathsf {QR}\)) and Decisional Diffie-Hellman (\(\mathsf {DDH}\)) can be shown to imply the existence of a cryptographically hard  language with a laconic and efficient
language with a laconic and efficient  argument-system and therefore satisfy the conditions of Theorem 1.1 (these and the other implications mentioned below are proven in the full version of this paper).
argument-system and therefore satisfy the conditions of Theorem 1.1 (these and the other implications mentioned below are proven in the full version of this paper).
We can also capture assumptions related to lattices and random linear codes by slightly relaxing the conditions of Theorem 1.1. Specifically, Theorem 1.1 holds even if we relax the completeness, soundness and zero-knowledge conditions of the argument-system to hold only for most (but not necessarily all) of the instances (chosen from the average-case hard distribution). We call arguments with these weaker properties average-case  arguments.
arguments.
It is not hard to see that lossy encryption [PVW08, BHY09] yields such an average-case laconic and efficient zero-knowledge argument-system. Recall that a \(\mathsf {PKE}\) scheme is lossy if its public-keys are indistinguishable from so-called “lossy keys” such that a ciphertext generated using such a lossy key does not contain information about the underlying plaintext. Consider the following proof-system for the language consisting of all valid public-keys: given an allegedly valid public-key, the verifier sends to the prover an encryption of a random bit b and expects to get in response the value b. It is not hard to see that this protocol is a laconic and efficient average-case  argument-system.
argument-system.
Several concrete assumptions yield cryptographically hard languages with average-case laconic and efficient  arguments (whether via lossy encryption or directly). Most notably, Learning With Errors (\(\mathsf {LWE}\)) [Reg05], Learning Parity with Noise (\(\mathsf {LPN}\)) with small errors [Ale03] and most of the assumptions used by Applebaum et al. [ABW10] to construct \(\mathsf {PKE}\), all imply the existence of such languages.
arguments (whether via lossy encryption or directly). Most notably, Learning With Errors (\(\mathsf {LWE}\)) [Reg05], Learning Parity with Noise (\(\mathsf {LPN}\)) with small errors [Ale03] and most of the assumptions used by Applebaum et al. [ABW10] to construct \(\mathsf {PKE}\), all imply the existence of such languages.
Thus, Theorem 1.1 gives a common framework for constructing public-key encryption based on a variety of different intractability assumptions (all of which were already known to yield public-key encryption via a variety of somewhat ad hoc techniques), see also Fig. 1.
One notable hardness assumption that we do not know to imply our assumption (even the average-case variant) is integer factorization (and the related RSA assumption). We consider a further weakening of our assumption that captures also the factoring and RSA assumptions. As a matter of fact, we show that this further relaxed assumption is actually equivalent to the existence of a public-key encryption scheme. We discuss this in more detail in Sect. 1.1.3.
1.1.2 Perspective — From  -Hardness to Public-Key Encryption
-Hardness to Public-Key Encryption
As noted above, one of the central goals in cryptography is to base public-key encryption on a general notion of structured hardness. A natural candidate for such structure is the class  of statistical zero-knowledge proofs, since many of the assumptions that are known to yield public-key encryption have
of statistical zero-knowledge proofs, since many of the assumptions that are known to yield public-key encryption have  proof-systems. Indeed, it is enticing to believe that the following dream version of Theorem 1.1 holds:
proof-systems. Indeed, it is enticing to believe that the following dream version of Theorem 1.1 holds:
Open Problem 1.1
Assume that there exists a cryptographically-hard language  . Then, there exists a public-key encryption scheme.
. Then, there exists a public-key encryption scheme.
(Here by  we refer to the class of languages having statistical zero-knowledge proof-systems rather than argument-systems as in Theorem 1.1. Assuming this additional structure only makes the statement of Open Problem 1.1 weaker and therefore easier to prove.)
we refer to the class of languages having statistical zero-knowledge proof-systems rather than argument-systems as in Theorem 1.1. Assuming this additional structure only makes the statement of Open Problem 1.1 weaker and therefore easier to prove.)
Instantiations of our assumption. Dashed arrows means that we only obtain average-case completeness, soundness and zero-knowledge. The (*) sign means that most, but not all, assumptions from [ABW10] imply our assumption.
Solving Open Problem 1.1 would be an outstanding breakthrough in cryptography. For instance, it would allow us to base public-key cryptography on the intractability of the discrete logarithm (\(\mathsf {DLOG}\)) problem,Footnote 5 since (a decision problem equivalent to) \(\mathsf {DLOG}\) has a perfect zero-knowledge proof-systemFootnote 6 [GK93], or under the plausible quasi-polynomial average-caseFootnote 7 hardness of the graph isomorphism problem (via the perfect zero-knowledge protocol of [GMW87]).
We view Theorem 1.1 as an initial step toward solving Open Problem 1.1. At first glance, it seems that Theorem 1.1 must be strengthened in two ways in order to solve Open Problem 1.1. Namely, we need to get rid of the requirements that the (honest) prover is (1) efficient and (2) laconic. However, it turns out that it suffices to remove only one of these restrictions, no matter which one, in order to solve Open Problem 1.1. We discuss this next.
Handling Inefficient Provers. Sahai and Vadhan [SV03] showed a problem, called statistical distance, which is both (1) complete for  , and (2) has an extremely laconic honest-verifier statistical zero-knowledge proof in which the prover only sends a single bit (with constant soundness error). The immediate implication is that any
, and (2) has an extremely laconic honest-verifier statistical zero-knowledge proof in which the prover only sends a single bit (with constant soundness error). The immediate implication is that any  protocol can be compressed to one in which the prover sends only a single bit.
protocol can be compressed to one in which the prover sends only a single bit.
Unfortunately, the foregoing transformation does not seem to maintain the computational efficiency of the prover. Thus, removing the requirement that the prover is efficient from Theorem 1.1 (while maintaining the laconism requirement) would solve Open Problem 1.1.
Handling Non-Laconic Provers. Suppose that we managed to remove the laconism requirement from Theorem 1.1 and only required the prover to be efficient. It turns out that the latter would actually imply an even stronger result than that stated in Open Problem 1.1. Specifically, assuming only the existence of one-way functions, Haitner et al. [HNO+09] construct (non-laconic) statistical zero-knowledge arguments for any  language, with an efficient prover. Thus, removing the laconism requirement from Theorem 1.1 would yield public-key encryption based merely on the existence of one-way functions.
language, with an efficient prover. Thus, removing the laconism requirement from Theorem 1.1 would yield public-key encryption based merely on the existence of one-way functions.
In fact, even a weaker result would solve Open Problem 1.1. Suppose we could remove the laconism requirement from Theorem 1.1 while insisting that the proof-system has statistical soundness (rather than computational). Such a result would solve Open Problem 1.1 since Nguyen and Vadhan [NV06] showed that every language in  has an
has an  protocol in which the prover is efficient (given the
protocol in which the prover is efficient (given the  witness).
witness).
To summarize, removing the laconism requirement from Theorem 1.1, while still considering an argument-system, would yield public-key encryption from one-way functions (via [HNO+09]). On the other hand, removing the laconism requirement while insisting on statistical soundness would solve Open Problem 1.1 (via [NV06]). (Note that neither the [NV06] nor [HNO+09] proof-systems are laconic, so they too cannot be used directly together with Theorem 1.1 to solve Open Problem 1.1.)
1.1.3 Extensions
We also explore the effect of strengthening and weakening our assumption. A natural strengthening gives us oblivious transfer, and as mentioned above, a certain weakening yields a complete complexity-theoretic characterization of public-key encryption.
A Complexity-Theoretic Characterization. The assumption from which we construct public-key encryption (see Theorem 1.1) requires some underlying hard decision problem. In many cryptographic settings, however, it seems more natural to consider hardness of search problems (e.g., integer factorization). Thus, we wish to explore the setting of laconic  arguments when only assuming the hardness of computing a witness for an instance sampled from a solved instance generator. Namely, an
arguments when only assuming the hardness of computing a witness for an instance sampled from a solved instance generator. Namely, an  relation for which it is hard, given a random instance, to find a corresponding witness.
relation for which it is hard, given a random instance, to find a corresponding witness.
We introduce a notion of (computationally sound) proof-systems for such  search problems, which we call arguments of weak knowledge (\(\mathsf {AoWK}\)). Loosely speaking, this argument-system convinces the verifier that the prover with which it is interacting has at least some partial knowledge of some witness. Or in other words, no efficient cheating prover can convince the verifier to accept given only the input. We further say that an \(\mathsf {AoWK}\) is zero-knowledge if the verifier learns nothing beyond the fact that the prover has the witness.
search problems, which we call arguments of weak knowledge (\(\mathsf {AoWK}\)). Loosely speaking, this argument-system convinces the verifier that the prover with which it is interacting has at least some partial knowledge of some witness. Or in other words, no efficient cheating prover can convince the verifier to accept given only the input. We further say that an \(\mathsf {AoWK}\) is zero-knowledge if the verifier learns nothing beyond the fact that the prover has the witness.
We show that Theorem 1.1 still holds under the weaker assumption that there is an efficient and laconic  -\(\mathsf {AoWK}\) (with respect to some hard solved instance generator). Namely, the latter assumption implies the existence of \(\mathsf {PKE}\). Furthermore, we also show that the same assumption is also implied by any \(\mathsf {PKE}\) scheme, thus establishing an equivalence between the two notions which also yields a certain complexity-theoretic characterization of public-key encryption.
-\(\mathsf {AoWK}\) (with respect to some hard solved instance generator). Namely, the latter assumption implies the existence of \(\mathsf {PKE}\). Furthermore, we also show that the same assumption is also implied by any \(\mathsf {PKE}\) scheme, thus establishing an equivalence between the two notions which also yields a certain complexity-theoretic characterization of public-key encryption.
Oblivious Transfer. Oblivious Transfer (\(\mathsf {OT}\)) is a fundamental cryptographic primitive, which is complete for the construction of general secure multiparty computation ( ) protocols [GMW87, Kil88]. We show that by making a slightly stronger assumption, Theorem 1.1 can extended to yield a (two-message) semi-honest \(\mathsf {OT}\) protocol.
) protocols [GMW87, Kil88]. We show that by making a slightly stronger assumption, Theorem 1.1 can extended to yield a (two-message) semi-honest \(\mathsf {OT}\) protocol.
For our \(\mathsf {OT}\) protocol, in addition to the conditions of Theorem 1.1, we need to further assume that there is a way to sample instances x such that it is hard to tell whether  or
or  even given the coins of the sampling algorithm.Footnote 8 We refer to this property as enhanced cryptographic hardness in analogy to the notion of enhanced trapdoor permutations.
even given the coins of the sampling algorithm.Footnote 8 We refer to this property as enhanced cryptographic hardness in analogy to the notion of enhanced trapdoor permutations.
1.2 Related Works
Cryptography and Hardness of  . Ostrovsky [Ost91] showed that the existence of a language in
. Ostrovsky [Ost91] showed that the existence of a language in  with average-case hardness implies the existence of one-way functions. Our result can be interpreted as an extension of Ostrovsky’s result: By assuming additional structure on the underlying
with average-case hardness implies the existence of one-way functions. Our result can be interpreted as an extension of Ostrovsky’s result: By assuming additional structure on the underlying  protocol, we construct a public-key encryption scheme. In fact, some of the ideas underlying our construction are inspired by Ostrovsky’s one-way function.
protocol, we construct a public-key encryption scheme. In fact, some of the ideas underlying our construction are inspired by Ostrovsky’s one-way function.
Average-case  hardness also implies constant-round statistically hiding commitments [OV08], a primitive not implied by one-way functions in a black-box way [HHRS15]. Assuming the existence of an average-case hard language in a subclass of
hardness also implies constant-round statistically hiding commitments [OV08], a primitive not implied by one-way functions in a black-box way [HHRS15]. Assuming the existence of an average-case hard language in a subclass of  (i.e., of languages having perfect randomized encodings), Applebaum and Raykov [AR16] construct Collision Resistant Hash functions.
(i.e., of languages having perfect randomized encodings), Applebaum and Raykov [AR16] construct Collision Resistant Hash functions.
In the other direction, some cryptographic primitives like homomorphic encryption [BL13], lossy encryption, witness encryption and indistinguishability obfuscators [KMN+14, PPS15], and \(\mathsf {PIR}\) (computational private information retrieval) [LV16] imply the existence of average-case hard problems in  .Footnote 9 We also mention that many other primitives, such as one-way functions, public-key encryption and oblivious transfer do not imply the existence of average-case hard problems in
.Footnote 9 We also mention that many other primitives, such as one-way functions, public-key encryption and oblivious transfer do not imply the existence of average-case hard problems in  (under black-box reductions) [BDV16].
(under black-box reductions) [BDV16].
Hash Proof-Systems. Hash Proof-Systems, introduced by Cramer and Shoup [CS02], are a cryptographic primitive which, in a nutshell, can be described as a cryptographically hard language in  with a one-round
with a one-round  protocol in which the honest prover is efficient given the
protocol in which the honest prover is efficient given the  witness and deterministic (and without loss of generality sends only a single bit). This is precisely what we assume for our main result except that we can handle randomized provers that send more bits of information (and the protocol can be multi-round). This special case of deterministic provers is significantly simpler to handle (and will serve as a warmup when describing our techniques). Our main technical contribution is handling arbitrary randomized provers.
witness and deterministic (and without loss of generality sends only a single bit). This is precisely what we assume for our main result except that we can handle randomized provers that send more bits of information (and the protocol can be multi-round). This special case of deterministic provers is significantly simpler to handle (and will serve as a warmup when describing our techniques). Our main technical contribution is handling arbitrary randomized provers.
Public-key encryption schemes have been shown to imply the existence of certain weak hash proof-systems [HLWW16]. Hash proof-systems were also shown in [GOVW12] to yield resettable statistical zero-knowledge proof-systems.
Laconic Provers. A study of interactive proofs in which the prover is laconic (i.e., transmits few bits to the verifier) was initiated by Goldreich and Håstad [GH98] and was further explored by Goldreich, Vadhan and Wigderson [GVW02]. These focus in these works is on general interactive proofs (that are not necessarily zero-knowledge) and their main results are that laconic interactive proofs are much weaker than general (i.e., non-laconic) interactive proofs.
1.3 Techniques
To illustrate the techniques used, we sketch the proof of a slightly simplified version of Theorem 1.1. Specifically, we construct a \(\mathsf {PKE}\) given a cryptographically hard language  with a single-round efficient-prover and laconic
with a single-round efficient-prover and laconic  argument-system (we shall briefly mention the effect of more rounds where it is most relevant). For simplicity, we also assume that the
argument-system (we shall briefly mention the effect of more rounds where it is most relevant). For simplicity, we also assume that the  protocol has perfect completeness and zero-knowledge. In the actual construction, given in the technical sections, we handle constant completeness error, negligible simulation error, and more rounds of interaction. Lastly, since we find the presentation more appealing, rather than presenting a public-key scheme, we construct a single-round key-agreement protocol.Footnote 10 Any such protocol can be easily transformed into a public-key encryption scheme.
protocol has perfect completeness and zero-knowledge. In the actual construction, given in the technical sections, we handle constant completeness error, negligible simulation error, and more rounds of interaction. Lastly, since we find the presentation more appealing, rather than presenting a public-key scheme, we construct a single-round key-agreement protocol.Footnote 10 Any such protocol can be easily transformed into a public-key encryption scheme.
Let  be a cryptographically hard language with an
be a cryptographically hard language with an  argument-system with prover \(\mathbf {P}\), verifier \(\mathbf {V}\) and simulator \(\mathbf {S}\). We assume that the argument-system has perfect completeness, no simulation error and soundness error s, for some \(s>0\). Let
argument-system with prover \(\mathbf {P}\), verifier \(\mathbf {V}\) and simulator \(\mathbf {S}\). We assume that the argument-system has perfect completeness, no simulation error and soundness error s, for some \(s>0\). Let  be a solved-instance generator for
be a solved-instance generator for  producing samples of the form (x, w), where
producing samples of the form (x, w), where  and w is a valid witness for x. The fact that
and w is a valid witness for x. The fact that  is cryptographically hard means that there exists a sampler
is cryptographically hard means that there exists a sampler  that generates NO instances for
that generates NO instances for  that are computationally indistinguishable from the YES instances generated by
that are computationally indistinguishable from the YES instances generated by  .
.
Deterministic Prover. As a warmup, we assume first that the honest prover in the  argument-system is deterministic. As will be shown below, this case is significantly easier to handle than the general case, but it is a useful step toward our eventual protocol.
argument-system is deterministic. As will be shown below, this case is significantly easier to handle than the general case, but it is a useful step toward our eventual protocol.
We construct a key-agreement protocol between Alice and Bob as follows. First Alice generates a solved instance-witness pair  . Alice then sends \( x\) across to Bob. Bob runs the simulator \(\mathbf {S}(x)\) to generate a transcript \( (a', b', r') \), where \(a'\) corresponds to the verifier’s message, \(b'\) corresponds to the prover’s message and \(r'\) correspond to the simulated random string for the verifier.Footnote 11 Bob sends the first message \( a' \) across to Alice. Bob then outputs the simulated second message \( b' \). Alice uses the witness \(w\) to generate the prover’s response \(b\) (i.e., the prover \(\mathbf {P}\)’s actual response given the message \(a'\) from the verifier) and outputs \(b\). The protocol is also depicted in Fig. 2.
. Alice then sends \( x\) across to Bob. Bob runs the simulator \(\mathbf {S}(x)\) to generate a transcript \( (a', b', r') \), where \(a'\) corresponds to the verifier’s message, \(b'\) corresponds to the prover’s message and \(r'\) correspond to the simulated random string for the verifier.Footnote 11 Bob sends the first message \( a' \) across to Alice. Bob then outputs the simulated second message \( b' \). Alice uses the witness \(w\) to generate the prover’s response \(b\) (i.e., the prover \(\mathbf {P}\)’s actual response given the message \(a'\) from the verifier) and outputs \(b\). The protocol is also depicted in Fig. 2.
To argue that Fig. 2 constitutes a key-agreement protocol, we need to show that Alice and Bob output the same value, and that no efficient eavesdropper Eve (who only sees their messages) can predict this output with good probability.
That they agree on the same value follows from the fact that the prover is deterministic and the simulation is perfect. More specifically, since the simulation is perfect, the distribution of the simulated verifier’s message \(a'\) is the same as that of the actual verifier’s message; and now since the prover is deterministic, given \( (x,w,a') \), the prover’s response \( b\), which is also Alice’s output, is fixed. Since the simulation is perfect and  , if the simulator outputs \((a',b',r')\), then \(b'\), which is Bob’s output, is necessarily equal to \(b\).
, if the simulator outputs \((a',b',r')\), then \(b'\), which is Bob’s output, is necessarily equal to \(b\).
Next, we show that any eavesdropper Eve who is able to guess Bob’s output in the protocol can be used to break the cryptographic hardness of  . Suppose Eve is able to guess Bob’s output in the protocol with probability p. This means that given only x and \(a'\), where \((a',b',r')\) is produced by the simulator \(\mathbf {S}(x)\), Eve is able to find the message \(b'\):
. Suppose Eve is able to guess Bob’s output in the protocol with probability p. This means that given only x and \(a'\), where \((a',b',r')\) is produced by the simulator \(\mathbf {S}(x)\), Eve is able to find the message \(b'\):

As the  argument has perfect completeness, and the simulation is also perfect, the transcripts produced by the simulator (on YES instances) are always accepted by the verifier. As Eve is able to produce the same prover messages as the simulator, her messages will also be accepted by the verifier. Namely,
argument has perfect completeness, and the simulation is also perfect, the transcripts produced by the simulator (on YES instances) are always accepted by the verifier. As Eve is able to produce the same prover messages as the simulator, her messages will also be accepted by the verifier. Namely,

Again using the fact that the simulation is perfect, we can replace the simulated message \(a'\) and simulated coin tosses \(r'\) with a verifier message \(a\) and coins r generated by a real execution of the protocol:

Recall that  samples no-instances that are computationally indistinguishable from the YES instances generated by
samples no-instances that are computationally indistinguishable from the YES instances generated by  . If x had been a NO instance sampled using
. If x had been a NO instance sampled using  , then the (computational) soundness of the
, then the (computational) soundness of the  argument implies that the verifier would reject with probability \(1-s\):
argument implies that the verifier would reject with probability \(1-s\):

where s is the soundness error. If p is larger than s by a non-negligible amount, then we have a distinguisher, contradicting the cryptographic hardness of  . So, no efficient eavesdropper can recover the agreed output value with probability noticeably more than s, the soundness error of the
. So, no efficient eavesdropper can recover the agreed output value with probability noticeably more than s, the soundness error of the  argument.
argument.
Notice that so far we have only guaranteed that the probability of success of the eavesdropper is s, which may be as large as a constant (rather than negligible).Footnote 12 Nevertheless, using standard amplification techniques (specifically those of Holenstein and Renner [HR05]) we can compile the latter to a full-fledged key-agreement protocol.
Randomized Prover. So far we have handled deterministic provers. But what happens if the prover were randomized? Agreement is now in jeopardy as the prover’s message \(b\) is no longer completely determined by the instance x and the verifier’s message a. Specifically, after Alice receives the simulated verifier message \(a'\) from Bob, she still does not know the value of \(b'\) that Bob obtained from the simulator – if she ran \(\mathbf {P}(x,w,a')\), she could get one of several possible b’s, any of which could be the correct \(b'\). Roughly speaking, Alice only has access to the distribution from which \(b'\) was sampled (but not to the specific value that was sampled).
Eve, however, has even less to work with than Alice; we can show, by an approach similar to (but more complex than) the one we used to show that no polynomial-time eavesdropper can guess \(b'\) in the deterministic prover case, that no polynomial-time algorithm can sample from any distribution that is close to the true distribution of \(b'\) for most x’s and \(a'\)’s.
We make use of this asymmetry between Alice and Eve in the knowledge of the distribution of \(b'\) (given x and a) to perform key agreement. We do so by going through an intermediate useful technical abstraction, which we call a Trapdoor Pseudoentropy Generator, that captures this asymmetry. We first construct such a generator, and then show how to use any such generator to do key agreement.
Trapdoor Pseudoentropy Generator. A distribution is said to possess pseudoentropy [HILL99] if it is computationally indistinguishable from another distribution that has higher entropyFootnote 13. We will later claim that in the protocol in Fig. 2 (when used with a randomized prover), the distribution of \(b'\) has some pseudoentropy for the eavesdropper who sees only x and \(a'\). In contrast, Alice, who knows the witness w, can sample from the distribution that \(b'\) was drawn from. This set of properties is what is captured by our notion of a trapdoor pseudoentropy generator.
A trapdoor pseudoentropy generator consists of three algorithms. The key generation algorithm \(\mathsf {KeyGen}\) outputs a public and secret key pair \((\mathsf {pk},\mathsf {sk})\). The encoding, given a public key \(\mathsf {pk}\), outputs a pair of strings (u, v), where we call u the public message and v the private message.Footnote 14 The decoding algorithm \(\mathsf {Dec}\), given as input the corresponding secret key and the public message u, outputs a value \(v'\). These algorithms are required to satisfy the following properties (simplified here for convenience):
-
Correctness: The distributions of v and \(v'\) are identical, given \(\mathsf {pk}\), \(\mathsf {sk}\), and u.
-
Pseudoentropy: The distribution of v has some pseudoentropy given \(\mathsf {pk}\) and u.
Correctness here only means that the secret key can be used to sample from the distribution of the private message v corresponding to the given public message u. This captures the weaker notion of agreement observed in the protocol earlier when Alice had sampling access to the distribution of Bob’s output.
The pseudoentropy requirement says that without knowledge of the secret key, the private message v seems to have more entropy – it looks “more random” than it actually is. This is meant to capture the asymmetry of knowledge between Alice and Eve mentioned earlier.
Constructing a Trapdoor Pseudoentropy Generator. Our construction of a trapdoor pseudoentropy generator is described in Fig. 3. It is an adaptation of the earlier key exchange protocol for deterministic provers (from Fig. 2). The public key is an instance x in the language \(\mathcal {L}\) and the corresponding secret key is a witness w for x – these are sampled using the solved-instance generator. To encode with public key x, the simulator from the  argument for \(\mathcal {L}\) is run on x and the simulated verifier message \(a'\) is set to be the public message, while the simulated prover message \(b'\) is the private message. To decode given x, w and \(a'\), the actual prover is run with this instance, witness and verifier message, and the response it generates is output.
argument for \(\mathcal {L}\) is run on x and the simulated verifier message \(a'\) is set to be the public message, while the simulated prover message \(b'\) is the private message. To decode given x, w and \(a'\), the actual prover is run with this instance, witness and verifier message, and the response it generates is output.
Now we argue that this is a valid pseudoentropy generator. Since we will need to be somewhat precise, for the rest of this section, we introduce the jointly-distributed random variables X, A and B, where X represents the instance (sampled from  ), A represents the verifier’s message (with respect to X), and B represents the prover’s response (with respect to X and A). Note that since the simulation in the
), A represents the verifier’s message (with respect to X), and B represents the prover’s response (with respect to X and A). Note that since the simulation in the  argument is perfect, A and B represent the distributions of the messages output by the simulator as well.
argument is perfect, A and B represent the distributions of the messages output by the simulator as well.
The correctness of our construction follows from the perfect zero knowledge of the underlying  argument – the private message v produced by \(\mathsf {Enc}\) here is the simulated prover’s message \(b'\), while the output of \(\mathsf {Dec}\) is the actual prover’s response b with the same instance and verifier’s message. Both of these have the same distribution, which corresponds to that of B conditioned on \(X = x\) and \(A~=~a'\).
argument – the private message v produced by \(\mathsf {Enc}\) here is the simulated prover’s message \(b'\), while the output of \(\mathsf {Dec}\) is the actual prover’s response b with the same instance and verifier’s message. Both of these have the same distribution, which corresponds to that of B conditioned on \(X = x\) and \(A~=~a'\).
In order to satisfy the pseudoentropy condition, the variable B needs to have some pseudoentropy given X and A. What we know, as mentioned earlier, is that B is unpredictable given X and A – that no polynomial-time algorithm, given x and \(a'\), can sample from a distribution close to that of the corresponding prover’s message b. Towards this end, we will use a result of Vadhan and Zheng [VZ12], who give a tight equivalence between unpredictability and pseudoentropy. Applied to our case, their results say what we want – that the variable B has additional pseudoentropy \(\log (1/s)\) given X and A, where s is the soundness error from the  argument. More precisely, there exists a variable C such that:
argument. More precisely, there exists a variable C such that:
where the above expressions refer to Shannon entropy. The result of Vadhan and Zheng applies only when the variable B has a polynomial-sized domain, which holds since the proof-system is laconic (this is the first out of several places in which we use the laconism of the proof-system). The above shows that the construction in Fig. 3 is indeed a trapdoor pseudoentropy generator. Finally, and this will be crucial ahead, note that the private message produced by \(\mathsf {Enc}\) is short (i.e., the same length as the prover’s message in the  argument we started with).
argument we started with).
In the case of an  protocol with r rounds, the above construction would be modified as follows. The encoder \(\mathsf {Enc}\) samples a transcript from \(\mathbf {S}(x)\), picks \(i \in [r]\) at random, sets the public message u to be all the messages in the transcript upto the verifier’s message in the \(i^{\text {th}}\) round, and the private message v to be the prover’s message in the \(i^{\text {th}}\) of the transcript. The decoder \(\mathsf {Dec}\) samples \(v'\) by running the prover on the partial transcript u to get the actual prover’s response in the \(i^{\text {th}}\) round.Footnote 15 Zero knowledge ensures that \(v'\) and v are distributed identically, and unpredictability arguments similar to the ones above tell us that \(v'\) has pseudoentropy at least \(\log (1/s)/r\).
protocol with r rounds, the above construction would be modified as follows. The encoder \(\mathsf {Enc}\) samples a transcript from \(\mathbf {S}(x)\), picks \(i \in [r]\) at random, sets the public message u to be all the messages in the transcript upto the verifier’s message in the \(i^{\text {th}}\) round, and the private message v to be the prover’s message in the \(i^{\text {th}}\) of the transcript. The decoder \(\mathsf {Dec}\) samples \(v'\) by running the prover on the partial transcript u to get the actual prover’s response in the \(i^{\text {th}}\) round.Footnote 15 Zero knowledge ensures that \(v'\) and v are distributed identically, and unpredictability arguments similar to the ones above tell us that \(v'\) has pseudoentropy at least \(\log (1/s)/r\).
From Laconic Trapdoor Pseudoentropy Generator to Key Agreement. Next, given a trapdoor pseudoentropy generator, such as the one in Fig. 3, we show how to construct a single-round key agreement protocol. We start with a pseudoentropy generator in which the public key is \(\mathsf {pk}\), the private key is \(\mathsf {sk}\), the public message is u, the private message is v, and the output of \(\mathsf {Dec}\) is \(v'\). The random variables corresponding to these are the same symbols in upper case. v and \(v'\) come from the distribution \(V_{\mathsf {pk},u}\) (V conditioned on \(PK=\mathsf {pk}\) and \(U=u\)), and V has additional pseudo-Shannon-entropy \(\eta \) given PK and U, where \(\eta \) can be thought of as a constant (\(\eta \) was \(\log (1/s)\) in the foregoing construction).
In the key agreement protocol, first Alice samples a key pair \((\mathsf {pk},\mathsf {sk})\) for the pseudoentropy generator and sends the public key \(\mathsf {pk}\) to Bob. Bob runs \((u,v) \leftarrow \mathsf {Enc}(\mathsf {pk})\), keeps the private message v and sends the public message u to Alice. We would like for Alice and Bob to agree on the string v. In order for this to be possible, Bob needs to send more information to Alice so as to specify the specific v that was sampled from \(V_{\mathsf {pk},u}\). A natural idea is for Bob to send, along with the message u, a hash h(v) of v, where h is a sampled from a pairwise independent hash function family \(\mathcal {H}\).
Alice, on receiving the hash function \( h\) and the hash value \( h(v) \), uses rejection sampling to find v. She can sample freely from the distribution \(V_{\mathsf {pk},u}\) by running \(\mathsf {Dec}(\mathsf {sk},u)\) because she knows the secret key \(\mathsf {sk}\) of the pseudoentropy generator and the public message u. She keeps drawing samples \( v' \) from \(V_{\mathsf {pk},u}\), until she finds one that hashes to \( h(v) \). Note that this brute force search is only feasible if the number of strings in the support of V is small, which is the case if the number of bits in v is small – considering the big picture, this is one of the reasons we want the prover from the  argument to be laconic.
argument to be laconic.
The main question now is how to set the length of the hash function. On the one hand, having a long hash helps agreement, as more information is revealed to Alice about v. On the other hand, security demands a short hash that does not leak “too much” information about v.
For agreement, roughly speaking, if the hash length were more than the max-entropyFootnote 16 of V given PK and U, which we denote by \( \text {H}_{\max }(V | PK, U) \), then the set of possible prover responses is being hashed to a set of comparable size, so with good probability, the hash value h(v) will have a unique pre-image, which Alice can identify.
For security we would like to argue, using the Leftover Hash Lemma, that to any eavesdropper h(v) looks uniformly random given \((\mathsf {pk}, u, h)\). This would be true if the hash length were less than the min-entropyFootnote 17 of V given PK and U, which we denote by \( \text {H}_{\min }(V| PK, U) \). Unfortunately, both of the above conditions cannot hold simultaneously because the min-entropy is upper-bounded by the max-entropy.
At this point we use the fact that Eve is computationally bounded. Hence, a computational analogue of high min-entropy, which we will call pseudo-min-entropy, would suffice for security. Concretely, consider a random variable C such that (PK, U, C) is computationally indistinguishable from (PK, U, V). Furthermore, suppose that the min-entropy of C given PK and U is considerably larger than the hash length. We can then use the Leftover Hash Lemma to argue that h(V) looks uniform to efficient eavesdroppers:
where R is the uniform distribution over the range of \(h\).
The benefit of this observation is that, since C is only required to be computationally close and not statistically close to V, the min-entropy of C given PK and U could be much larger than that of V given PK and U. And if we can find a C such that \(\text {H}_{\min }(C | PK, U)\) is sufficiently larger than \(\text {H}_{\max }(V | PK, U)\), then we will indeed be able to choose a hash length that is both large enough for agreement and small enough for security.
Also notice that for the agreement to work, it is not necessary for the hash length to be larger than the max-entropy of V (given PK and U) itself – instead, if there was another variable D such that (PK, U, D) is statistically close to (PK, U, V), and also Alice is somehow able to sample from D given \(PK = \mathsf {pk}\) and \(U = u\), then it is sufficient for the hash to be longer than \(\text {H}_{\max }(D | PK, U)\). Given such a variable, Bob will operate as he did earlier, but Alice can assume that he is actually sampling from \(D_{\mathsf {pk},u}\) instead of \(V_{\mathsf {pk},u}\), and since these two distributions are close most of the time, the probability of Alice’s subsequent computation going wrong is small. This helps us because now we might be able to find such a D that has lower max-entropy given PK and U than V, and then \(\text {H}_{\min }(C | PK, U)\) would only have to be larger than this.
Following these observations, we set ourselves the following objective: find variables C and D such that:
What we do know about V is that it has some pseudo-Shannon-entropy given PK and U. That is, there is a variable C such that:
The rest of our construction deals with using this pseudo-Shannon-entropy to achieve the objectives above. This we do using a technique from Information Theory dating back to Shannon [Sha48] which is often referred to in the cryptography literature as flattening of distributions, which we describe next. We note that this technique has found use in cryptography before [HILL99, GV99, SV03].
Flattening and Typical Sets. The central idea here is that repetition essentially reduces the general case to the case where the distribution is “almost flat”. Namely, if we start with a distribution that has Shannon entropy \( \xi \) and repeat it k times, then the new distribution is close to being uniform on a set whose size is roughly \( 2^{k \xi } \). This set is called the typical set; it consists of all elements whose probability is close to \( 2^{-k\xi } \).
In our case, consider the distribution \(( PK^k,U^k,V^k)\), which is the k-fold product repetition of (PK, U, V). Roughly speaking, we define the typical set of \( V^k \) conditioned on any \((\mathbf {pk},\mathbf {u})\) in the supportFootnote 18 of \( (PK^k,U^k) \) as followsFootnote 19:

Considering the typical set is useful for several reasons. On the one hand, the typical set is quite small (roughly \( 2^{k\text {H}(V|PK,U)} \)) in size, which means that any distribution supported within it has somewhat low max-entropy. On the other hand, there is an upper bound on the probability of any element that occurs in it, which could be useful in lower bounding min-entropy, which is what we want to do.
The most important property of the typical set it that it contains most of the probability mass of the conditional repeated distribution. That is, for most \((\mathbf {pk},\mathbf {u},\mathbf {v})\) sampled from \((PK^k,U^k,V^k)\), it holds that \(\mathbf {v}\) lies in the typical set conditioned on \((\mathbf {pk},\mathbf {u})\); quantitatively, Holenstein and Renner [HR11] show the following:

where q is the number of bits in each sample from V. Recall that in our earlier construction of the trapdoor pseudoentropy generator, this corresponds to the length of the prover’s message in the  argument we started with. We want the above quantity to be quite small, which requires that \(k \gg q^2\). This is one of the considerations in our ultimate choice of parameters, and is another reason we want the prover’s messages to not be too long.
argument we started with. We want the above quantity to be quite small, which requires that \(k \gg q^2\). This is one of the considerations in our ultimate choice of parameters, and is another reason we want the prover’s messages to not be too long.
Back to \(\mathsf {PKE}\) Construction. We shall use the above facts to now show that \(V^k\) has pseudo-min-entropy given \(PK^k\) and \(U^k\). Let C be the random variable from the expression (3) above that we used to show that V has pseudo-Shannon-entropy. After repetition, we have that:

Next, consider the variable \(C'\) that is obtained by restricting, for each \(\mathbf {pk}\) and \(\mathbf {u}\), the variable \(C^k\) to its typical set conditioned on \((\mathbf {pk},\mathbf {u})\). By applying the bound of Holenstein and Renner (4) with an appropriate choice of k, we infer that:
Further, the upper bound on the probabilities of elements in the typical set tells us that \(C'\) has high min-entropyFootnote 20 given \(PK^k\) and \(U^k\):
Putting the above few expressions together tells us that \(V^k\) has some pseudo-min-entropy given \(PK^k\) and \(U^k\), which is in fact somewhat more than its Shannon entropy:
This satisfies our objective of getting a variable – \(V^k\) here – that has high pseudo-min-entropy (given \(PK^k\) and \(U^k\)). Our goal is now to find another variable that is statistically close to \(V^k\) given \(PK^k\) and \(U^k\), and also has small max-entropy given \(PK^k\) and \(U^k\). We do this using the same approach as above. Consider the variable \(V'\) that is constructed from \(V^k\) in the same way \(C'\) was from \(C^k\) – for each \((\mathbf {pk},\mathbf {u})\), restrict \(V^k\) to its typical set conditioned on \((\mathbf {pk},\mathbf {u})\). Again, bound (4) tells us that the new distribution is close to the old one. And also, because of the upper bound on the size of the typical set, we have an upper bound on the max-entropyFootnote 21 of \(V'\) given \(PK^k\) and \(U^k\).
Putting together expressions (5) and (6), we find that the relationship we want between these entropies of \(C'\) and \(V'\) is indeed satisfied:
To summarize, we manage to meet the conditions of expression (2) with respect to \((PK^k,U^k,V^k)\) (instead of (PK, U, V)) with \({C}'\) taking the role of C and \(V'\) taking the role of D. We can now finally fix the length of our hash – call it \(\ell \) – to be between \(\text {H}_{\max }(V'|PK^k,U^k)\) and \(\text {H}_{\min }(C' | PK^k,U^k)\), which can be done by setting it to a value between \(\text {H}(V^k|PK^k,U^k)\) and \(\text {H}(V^k|PK^k,U^k) + k\eta \) for an appropriate k, and emulate the earlier protocol. We will be able to use the Leftover Hash Lemma as desired to argue security and use the low max-entropy of \(V'\) to argue agreement.
The final key agreement protocol from a trapdoor pseudoentropy generator is presented in Fig. 4.
How Laconic? To examine how long the prover’s message can be, lets recall the restrictions of our construction. First, we need both parties to be efficient. While Bob is clearly efficient, Alice performs an exhaustive search over the domain of possible prover messages. The size of this domain is \(2^{q\cdot k}\) because the parties repeat the underlying protocol k times and the length of each prover’s message is q bits. For Alice to be efficient, this domain has to be polynomial-sized, requiring that \(q\cdot k = O(\log {n})\), where n is the input length. Second, we need that the concentration bound for the typical set (Eq. (4)) to be meaningful; that is, we need \(k/q^2\) to be at least a constant. Together, these imply that \(q^3\) needs to be \(O(\log {n})\). Lastly, this setting of parameters also suffices for the [VZ12] result that we used in Eq. (1).
2 The Assumption and Main Theorem
In this section, we specify our assumption on the existence of laconic zero-knowledge proof-systems, and state our main theorem regarding its implication for public-key encryption. Due to space limitations, the formal descriptions of our constructions and the proof of our theorem are deferred to the full version of this paper.
We first introduce some necessary definitions and notations. Throughout this section, we use  to denote an
to denote an  language with witness relation
language with witness relation  . We use
. We use  and
and  to denote probabilistic polynomial-time algorithms that are to be seen as sampling algorithms for YES and NO instances of
to denote probabilistic polynomial-time algorithms that are to be seen as sampling algorithms for YES and NO instances of  . More specifically, the sampler
. More specifically, the sampler  outputs samples of the form (x, w) such that with all but negligible probability (in \(\lambda \)), it holds that
outputs samples of the form (x, w) such that with all but negligible probability (in \(\lambda \)), it holds that  . We call
. We call  a solved instance generator. On the other hand,
a solved instance generator. On the other hand,  outputs samples x such that with all but negligible probability,
outputs samples x such that with all but negligible probability,  . We shall not rely on the fact that the NO sampler
. We shall not rely on the fact that the NO sampler  is an efficient algorithm. Still we find it easier to present it as such for symmetry with
is an efficient algorithm. Still we find it easier to present it as such for symmetry with  (which must be efficient).
(which must be efficient).
We shall be concerned with properties of the tuple  – the language
– the language  equipped with (efficiently sampleable) distributions over its YES and NO instances (where YES instances come with corresponding witnesses). Since the choice of YES and NO distributions is always clear from the context, we often simply refer to the above tuple as the language (although we actually mean the language
equipped with (efficiently sampleable) distributions over its YES and NO instances (where YES instances come with corresponding witnesses). Since the choice of YES and NO distributions is always clear from the context, we often simply refer to the above tuple as the language (although we actually mean the language  with these specific distributions over its instances). We start by defining what we mean when we say that such a language is cryptographically hard.
with these specific distributions over its instances). We start by defining what we mean when we say that such a language is cryptographically hard.
Definition 2.1
(Cryptographic Hardness). Let  and \(\varepsilon = \varepsilon (\lambda ) \in [0,1]\). The language
and \(\varepsilon = \varepsilon (\lambda ) \in [0,1]\). The language  is \((t,\varepsilon )\) -cryptographically hard if
is \((t,\varepsilon )\) -cryptographically hard if  is a solved instance generator, and for every probabilistic algorithm \( \textsf {A} \) that on input \((1^\lambda ,x)\) runs in time \(t(\lambda )\) and for all sufficiently large
is a solved instance generator, and for every probabilistic algorithm \( \textsf {A} \) that on input \((1^\lambda ,x)\) runs in time \(t(\lambda )\) and for all sufficiently large  it holds that:
it holds that:

where the above probabilities are also over the random coins of \( \textsf {A} \). We say that  is cryptographically hard if it is \((\lambda ^c,1/\lambda ^c)\)-hard for every constant \(c>0\).
is cryptographically hard if it is \((\lambda ^c,1/\lambda ^c)\)-hard for every constant \(c>0\).
Being cryptographically hard is a stronger requirement than the usual notion of average-case hardness (the latter means that it is hard to distinguish a random YES instance from a random NO instance). Specifically, cryptographic hardness requires both (1) average-case hardness and (2) the existence of a solved instance generator (wrt the average-case hard distribution). In particular, the existence of a cryptographically hard language is equivalent to the existence of one-way functions.Footnote 22 As noted above, when we say that the language  is cryptographically hard we are actually implicitly referring to the sampling algorithms
is cryptographically hard we are actually implicitly referring to the sampling algorithms  and
and  .
.
Next we define honest-verifier statistical zero-knowledge ( ) arguments, which are similar to statistical honest-verifier zero-knowledge proofs but the soundness condition is only required to hold against malicious provers that run in polynomial-time. We remark that since we will be using the existence of
) arguments, which are similar to statistical honest-verifier zero-knowledge proofs but the soundness condition is only required to hold against malicious provers that run in polynomial-time. We remark that since we will be using the existence of  arguments to construct other objects, both the relaxations that we employ (namely requiring only computational soundness and honest verifier zero knowledge) only strengthen our results.
arguments to construct other objects, both the relaxations that we employ (namely requiring only computational soundness and honest verifier zero knowledge) only strengthen our results.
Below, we use \((\mathbf {P},\mathbf {V})(1^\lambda ,x)\) to refer to the transcript of an execution of an interactive protocol with prover \(\mathbf {P}\) and verifier \(\mathbf {V}\) on input \((1^\lambda ,x)\). We also use \((\mathbf {P}(w),\mathbf {V})(1^\lambda ,x)\) to denote a similar execution where the prover is additionally given a witness w as an auxiliary input. In both cases, we sometimes also use the same notation to refer to the result (i.e., verifier’s output) of such an execution – the appropriate interpretation will be clear from context.
Definition 2.2
(  Arguments). Let \(c=c(\lambda ) \in [0,1]\) and \(s=s(\lambda ) \in [0,1]\). An interactive protocol \((\mathbf {P}, \mathbf {V})\) is an Honest Verifier
Arguments). Let \(c=c(\lambda ) \in [0,1]\) and \(s=s(\lambda ) \in [0,1]\). An interactive protocol \((\mathbf {P}, \mathbf {V})\) is an Honest Verifier  Argument with completeness error c and soundness error s for a language
Argument with completeness error c and soundness error s for a language  , with witness relation
, with witness relation  , if the following properties hold:
, if the following properties hold:
-
Efficiency: Both \(\mathbf {P}\) and \(\mathbf {V}\) are probabilistic polynomial-time algorithms.
-
Completeness: For any
 , and all large enough
, and all large enough  :
: 
where the parameter c is called the completeness error.
-
Soundness: For any probabilistic polynomial-time cheating prover \(\mathbf {P}^\star \), any
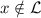 , and large enough
, and large enough  :
: 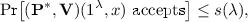
where the parameter s is called the soundness error.
-
Honest Verifier Statistical Zero Knowledge: There is a probabilistic polynomial-time algorithm \(\mathbf {S}\) (called the simulator) that when given any
 simulates the transcript of the interactive proof on input x. That is, for any
simulates the transcript of the interactive proof on input x. That is, for any  and for all sufficiently large
and for all sufficiently large  :
: 
Note that our definition only deals with  languages and requires that the prover is efficient. Typically, when defining an
languages and requires that the prover is efficient. Typically, when defining an  proof (rather than argument) this is not done, and the honest prover is allowed to be computationally unbounded. However, this is the natural choice since we focus on argument systems (where the soundness requirement is only against malicious provers that are also efficient).
proof (rather than argument) this is not done, and the honest prover is allowed to be computationally unbounded. However, this is the natural choice since we focus on argument systems (where the soundness requirement is only against malicious provers that are also efficient).
Remark 2.3
(Restricted-view Simulation). For our main result, it suffices that the simulator only simulates the transcript of the interactive proof and not the random-coins of the verifier. The standard definition of simulation is stronger – it also requires that the simulator output random-coins for the verifier that are consistent with the transcript. Ostrovsky [Ost91] called the weaker notion restricted-view simulation, and showed that average-case hard languages with honest-verifier  proofs with restricted-view simulation (without efficient provers) imply the existence of one-way functions.
proofs with restricted-view simulation (without efficient provers) imply the existence of one-way functions.
We will be dealing with  arguments that have additional properties captured by the next definition. Recall that a round in an interactive proof is a pair of messages, the first one (possibly empty) from \(\mathbf {V}\) to \(\mathbf {P}\), and the next the other way.
arguments that have additional properties captured by the next definition. Recall that a round in an interactive proof is a pair of messages, the first one (possibly empty) from \(\mathbf {V}\) to \(\mathbf {P}\), and the next the other way.
Definition 2.4
(Laconism). Let  and
and  . An interactive protocol \((\mathbf {P}, \mathbf {V})\) is said to be r-round and q-laconic if it has at most \(r(\lambda )\) rounds, and each message from \(\mathbf {P}\) to \(\mathbf {V}\) is at most \(q(\lambda )\) bits long when run on any input \((1^\lambda ,x)\), for large enough \(\lambda \).
. An interactive protocol \((\mathbf {P}, \mathbf {V})\) is said to be r-round and q-laconic if it has at most \(r(\lambda )\) rounds, and each message from \(\mathbf {P}\) to \(\mathbf {V}\) is at most \(q(\lambda )\) bits long when run on any input \((1^\lambda ,x)\), for large enough \(\lambda \).
We can now state our main assumption as follows.
Assumption 2.5
There exists a cryptographically hard language  for which there is an r-round and q-laconic honest-verifier
for which there is an r-round and q-laconic honest-verifier  argument with completeness error c and soundness error s such that:
argument with completeness error c and soundness error s such that:
-
There is a constant \(\beta > 0\) such that \(1 - c(\lambda ) > s(\lambda ) + \beta \), for large enough
 .
. -
q and r are such that \(r^2 \cdot q^3 = O(\log (\lambda ))\).
Our main result is given in the next theorem.
Theorem 2.6
(\(\mathsf {PKE}\) from Laconic  ). If Assumption 2.5 holds, then there exists a public-key encryption scheme.
). If Assumption 2.5 holds, then there exists a public-key encryption scheme.
The construction of our public-key encryption scheme from Assumption 2.5, and the proof of Theorem 2.6, are presented in the full version of this paper. There, in addition, we consider two relaxations of Assumption 2.5, each of which still suffices for our construction. We also present a comparison of our assumptions to concrete assumptions that have been used in the past to construct public-key encryption.
Notes
- 1.
Loosely speaking, a solved-instance generator for the YES distribution \( \textsf {Y} _{}\) of an average-case hard language
 is an algorithm that generates samples
is an algorithm that generates samples  (where
(where 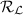 is the
is the  relation) and where x is distributed according to \( \textsf {Y} _{}\).
relation) and where x is distributed according to \( \textsf {Y} _{}\). - 2.
Laconic proof-systems with constant soundness and very short communication (e.g., just a single bit) are indeed known. As a matter of fact, many of the known hard problems that are known to yield public-key encryption schemes have such laconic
 proof-systems (see Sect. 1.1.1).
proof-systems (see Sect. 1.1.1). - 3.
In the context of argument-systems (in contrast to general interactive proofs), the assumption that the honest prover is efficient goes without saying. Nevertheless, we wish to emphasize this point here.
- 4.
As a matter of fact, hash proof systems can be viewed as a special case of our assumption in which the (honest) prover is deterministic or, equivalently, sends only a single bit. In contrast, we handle arbitrary randomized provers (that are sufficiently laconic) and indeed most of the technical difficulty arises from handling this more general setting. See additional details in Sect. 1.2.
- 5.
Public-key schemes based on assumptions related to discrete log such as the decisional (or even computational) Diffie Hellman assumption are known to exist. Nevertheless, basing public-key encryption solely on the hardness of discrete log has been open since the original work of Diffie and Hellman [DH76].
- 6.
That proof-system is actually laconic but it is unclear how to implement the prover efficiently.
- 7.
Graph isomorphism is in fact known to be solvable in polynomial-time for many natural distributions, and the recent breakthrough result of Babai [Bab16] gives a quasi-polynomial worst-case algorithm. Nevertheless, it is still conceivable that Graph Isomorphism is average-case quasi-polynomially hard (for some efficiently samplable distribution).
- 8.
In particular, the sampling algorithm that tosses a coin \(b \in \{0,1\}\) and outputs
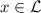 if \(b=0\) and
if \(b=0\) and  otherwise does not satisfy the requirement (since the value of b reveals whether
otherwise does not satisfy the requirement (since the value of b reveals whether  ).
). - 9.
- 10.
Loosely speaking, a key agreement protocol allows Alice and Bob to agree on a common key that is unpredictable to an external observer that has wire tapped their communication lines.
- 11.
Throughout this paper, we use the convention that primed symbols are for objects associated with a simulated (rather than real) execution of the protocol.
- 12.
This error can be made negligible by parallel repetition [BIN97] (recall that parallel repetition preserves honest-verifier zero-knowledge). Doing so however makes the prover’s messages longer. While this is not an issue when dealing with deterministic provers, it will prove to be problematic in the general case of a randomized prover.
- 13.
By default, the measure of entropy employed is that of Shannon entropy. The Shannon entropy of a variable X given Y is defined as:
 .
. - 14.
We refer to this procedure as an encoding algorithm because we think of the public message as an encoding of the private message.
- 15.
For simplicity, assume that the prover is stateless so it can be run on a partial transcript. In the actual proof we handle stateful provers as well.
- 16.
The max entropy corresponds to the logarithm of the support size. The conditional max entropy of a random variable X given Y is defined as: \(\text {H}_{\max }(X|Y) = \max _y\log \left( |Supp(X|Y=y)| \right) \).
- 17.
The min-entropy of a variable X given Y is defined as:
 .
. - 18.
The support of \((PK^k,U^k)\) consists of vectors with k elements. We represent vectors by bold symbols, e.g., \(\mathbf {v}\).
- 19.
The actual definition quantifies how different from \(2^{-kH}\) the probability is allowed to be.
- 20.
\(\text {H}_{\min }(C'|PK^k,U^k)\) could actually be slightly less than the approximate lower bound presented here because there is some slack allowed in the definition of the typical set – it can contain elements whose probabilities are slightly larger than \(2^{-k\text {H}(C|PK,U)}\). We need to pick this slack carefully – if it is too large, \(C'\) loses its min-entropy, and if it is too small the typical set also becomes too small and the bound in (4), which actually depends on this slack, becomes meaningless. This is another constraint on our choice of parameters.
- 21.
The same caveats as in Footnote 20 regarding the min-entropy of \(C'\) apply here as well.
- 22.
That YES instances are indistinguishable from NO instances implies that it is hard to compute a witness for a YES instance. Given this, a function that takes coins for
 and outputs the instance (but not the witness) generated by
and outputs the instance (but not the witness) generated by 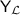 is one-way (c.f., [Gol08, Proposition 7.2]). For the other direction, assuming that one-way functions exist implies the existence of a linear-stretch pseudorandom generators (PRG) G [HILL99]. The language that is cryptographically hard contains those strings that are in the range of G. The solved instance generator samples a random string r and outputs G(r) as the input and r as the witness. The corresponding NO distribution is that of a random string in the range of the PRG.
is one-way (c.f., [Gol08, Proposition 7.2]). For the other direction, assuming that one-way functions exist implies the existence of a linear-stretch pseudorandom generators (PRG) G [HILL99]. The language that is cryptographically hard contains those strings that are in the range of G. The solved instance generator samples a random string r and outputs G(r) as the input and r as the witness. The corresponding NO distribution is that of a random string in the range of the PRG.
References
Applebaum, B., Barak, B., Wigderson, A.: Public-key cryptography from different assumptions. In: Proceedings of the 42nd ACM Symposium on Theory of Computing, STOC 2010, Cambridge, Massachusetts, USA, 5–8 June 2010, pp. 171–180 (2010)
Alekhnovich, M.: More on average case vs approximation complexity. In: Proceedings of the 44th Symposium on Foundations of Computer Science (FOCS 2003), Cambridge, MA, USA, 11–14 October 2003, pp. 298–307. IEEE Computer Society (2003)
Applebaum, B., Raykov, P.: On the relationship between statistical zero-knowledge and statistical randomized encodings. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 449–477. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_16
Babai, L.: Graph isomorphism in quasipolynomial time [extended abstract]. In Proceedings of the 48th Annual ACM SIGACT Symposium on Theory of Computing, STOC 2016, Cambridge, MA, USA, 18–21 June 2016, pp. 684–697 (2016)
Bitansky, N., Degwekar, A., Vaikuntanathan, V.: Structure vs hardness through the obfuscation lens. IACR Cryptology ePrint Archive 2016:574 (2016)
Bellare, M., Hofheinz, D., Yilek, S.: Possibility and impossibility results for encryption and commitment secure under selective opening. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 1–35. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01001-9_1
Bellare, M., Impagliazzo, R., Naor, M.: Does parallel repetition lower the error in computationally sound protocols? In: 38th Annual Symposium on Foundations of Computer Science, FOCS 1997, Miami Beach, Florida, USA, 19–22 October 1997, pp. 374–383 (1997)
Bogdanov, A., Lee, C.H.: Limits of Provable Security for Homomorphic Encryption. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 111–128. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_7
Cramer, R., Shoup, V.: Universal hash proofs and a paradigm for adaptive chosen ciphertext secure public-key encryption. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 45–64. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_4
Diffie, W., Hellman, M.E.: New directions in cryptography. IEEE Trans. Inf. Theory 22(6), 644–654 (1976)
Goldreich, O., Håstad, J.: On the complexity of interactive proofs with bounded communication. Inf. Process. Lett. 67(4), 205–214 (1998)
Goldreich, O., Kushilevitz, E.: A perfect zero-knowledge proof system for a problem equivalent to the discrete logarithm. J. Cryptol. 6(2), 97–116 (1993)
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game or a completeness theorem for protocols with honest majority. In: Proceedings of the 19th Annual ACM Symposium on Theory of Computing, New York, New York, USA, pp. 218–229 (1987)
Goldreich, O.: Computational Complexity - A Conceptual Perspective. Cambridge University Press, Cambridge (2008)
Garg, S., Ostrovsky, R., Visconti, I., Wadia, A.: Resettable statistical zero knowledge. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 494–511. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_28
Goldreich, O., Vadhan, S.P.: Comparing entropies in statistical zero knowledge with applications to the structure of SZK. In: Proceedings of the 14th Annual IEEE Conference on Computational Complexity, Atlanta, Georgia, USA, 4–6 May 1999, p. 54 (1999)
Goldreich, O., Vadhan, S., Wigderson, A.: On interactive proofs with a laconic prover. Comput. Complex. 11(1–2), 1–53 (2002)
Haitner, I., Hoch, J.J., Reingold, O., Segev, G.: Finding collisions in interactive protocols–tight lower bounds on the round and communication complexities of statistically hiding commitments. SIAM J. Comput. 44(1), 193–242 (2015)
Håstad, J., Impagliazzo, R., Levin, L.A., Luby, M.: A pseudorandom generator from any one-way function. SIAM J. Comput. 28(4), 1364–1396 (1999)
Hazay, C., López-Alt, A., Wee, H., Wichs, D.: Leakage-resilient cryptography from minimal assumptions. J. Cryptol. 29(3), 514–551 (2016)
Haitner, I., Nguyen, M.-H., Ong, S.H., Reingold, O., Vadhan, S.P.: Statistically hiding commitments and statistical zero-knowledge arguments from any one-way function. SIAM J. Comput. 39(3), 1153–1218 (2009)
Holenstein, T., Renner, R.: One-way secret-key agreement and applications to circuit polarization and immunization of public-key encryption. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 478–493. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_29
Holenstein, T., Renner, R.: On the randomness of independent experiments. IEEE Trans. Inf. Theory 57(4), 1865–1871 (2011)
Impagliazzo, R., Rudich, S.: Limits on the provable consequences of one-way permutations. In: Proceedings of the Twenty-First Annual ACM Symposium on Theory of Computing, pp. 44–61. ACM (1989)
Kilian, J.: Founding crytpography on oblivious transfer. In: Proceedings of the Twentieth Annual ACM Symposium on Theory of Computing, pp. 20–31. ACM (1988)
Komargodski, I., Moran, T., Naor, M., Pass, R., Rosen, A., Yogev, E.: One-way functions and (im)perfect obfuscation. In: 55th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2014, Philadelphia, PA, USA, 18–21 October 2014, pp. 374–383. IEEE Computer Society (2014)
Liu, T., Vaikuntanathan, V.: On basing private information retrieval on NP-hardness. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016, Part I. LNCS, vol. 9562, pp. 372–386. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_16
Nguyen, M.-H., Vadhan, S.P.: Zero knowledge with efficient provers. In: Proceedings of the 38th Annual ACM Symposium on Theory of Computing, Seattle, WA, USA, 21–23 May 2006, pp. 287–295 (2006)
Ostrovsky, R.: One-way functions, hard on average problems, and statistical zero-knowledge proofs. In: Proceedings of the Sixth Annual Structure in Complexity Theory Conference, Chicago, Illinois, USA, 30 June - 3 July 1991, pp. 133–138 (1991)
Ong, S.J., Vadhan, S.: An equivalence between zero knowledge and commitments. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 482–500. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_27
Pandey, O., Prabhakaran, M., Sahai, A.: Obfuscation-based non-black-box simulation and four message concurrent zero knowledge for NP. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 638–667. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_25
Peikert, C., Vaikuntanathan, V., Waters, B.: A framework for efficient and composable oblivious transfer. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 554–571. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_31
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Gabow, H.N., Fagin, R. (eds.) Proceedings of the 37th Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, 22–24 May 2005, pp. 84–93. ACM (2005)
Rothblum, R.: Homomorphic encryption: from private-key to public-key. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 219–234. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_14
Rivest, R.L., Shamir, A., Adleman, L.M.: A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 21(2), 120–126 (1978)
Shannon, C.E.: A mathematical theory of communication. Bell Syst. Tech. J. 27(3), 379–423 (1948)
Sahai, A., Vadhan, S.: A complete problem for statistical zero knowledge. J. ACM (JACM) 50(2), 196–249 (2003)
Vadhan, S., Zheng, C.J.: Characterizing pseudoentropy and simplifying pseudorandom generator constructions. In: Proceedings of the Forty-Fourth Annual ACM Symposium on Theory of Computing, pp. 817–836. ACM (2012)
Acknowledgments
We thank Vinod Vaikuntanathan for his encouragement and for helpful discussions. We thank the anonymous reviewers for very useful comments and in particular for suggesting the abstraction of trapdoor pseudoentropy generator.
Research supported in part by NSF Grants CNS-1413920 and CNS-1350619, and by the Defense Advanced Research Projects Agency (DARPA) and the U.S. Army Research Office under contracts W911NF-15-C-0226 and W911NF-15-C-0236. The third author was also supported by the SIMONS Investigator award agreement dated 6-5-12 and the Cybersecurity and Privacy Institute at Northeastern University.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Berman, I., Degwekar, A., Rothblum, R.D., Vasudevan, P.N. (2018). From Laconic Zero-Knowledge to Public-Key Cryptography. In: Shacham, H., Boldyreva, A. (eds) Advances in Cryptology – CRYPTO 2018. CRYPTO 2018. Lecture Notes in Computer Science(), vol 10993. Springer, Cham. https://doi.org/10.1007/978-3-319-96878-0_23
Download citation
DOI: https://doi.org/10.1007/978-3-319-96878-0_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96877-3
Online ISBN: 978-3-319-96878-0
eBook Packages: Computer ScienceComputer Science (R0)





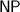 witness.
witness. -Hardness to Public-Key Encryption
-Hardness to Public-Key Encryption



 , and all large enough
, and all large enough  :
: 
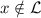 , and large enough
, and large enough  :
: 
 simulates the transcript of the interactive proof on input x. That is, for any
simulates the transcript of the interactive proof on input x. That is, for any  and for all sufficiently large
and for all sufficiently large  :
: 
 .
. is an algorithm that generates samples
is an algorithm that generates samples  (where
(where  is the
is the  relation) and where x is distributed according to
relation) and where x is distributed according to  proof-systems (see Sect.
proof-systems (see Sect.  if
if  otherwise does not satisfy the requirement (since the value of b reveals whether
otherwise does not satisfy the requirement (since the value of b reveals whether  ).
). .
. .
. and outputs the instance (but not the witness) generated by
and outputs the instance (but not the witness) generated by 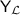 is one-way (c.f., [
is one-way (c.f., [