Abstract
The paper is concerned with the fine boundary between expressive power and reducibility of semantic and intensional notions in the context of arithmetical theories. I will consider three notions of reduction of a theory characterizing a semantic or a modal notion to the underlying arithmetical base theory – relative interpretability, speed up, conservativeness – and highlight a series of cases where moving between equally satisfactory base theories and keeping the semantic or modal principles fixed yields incompatible results. I then consider the impact of the non-uniform behaviour of these reducibility relations on the philosophical significance we usually attribute to them.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
- 2.
Note on terminology: In what follows, we employ the adjective ‘intensional’ and ‘modal’ in an inclusive sense, familiar to medieval authors such as Ockham, which comprehend also truth and propositional attitudes.
- 3.
- 4.
For details on the subexponential theories \(\mathsf {S}^1_2\), I Δ 0 + Ω 1 the standard reference is still (Hájek and Pudlák 1993, §V).
- 5.
It should be noticed that Halbach’s (1999) contains a cut-elimination argument that was later shown to contain a gap. The problem there was exactly this absence of a suitable machinery to control the complexity of boxed formulas in proofs of \(\mathbb {L}_B\)-formulas.
- 6.
For the reader not familiar with subsystems of first-order arithmetic, it may be useful to know that it’s easy to find theories that are proper sub-theories of E A but still sequential. One example is Buss’ theory \(\mathsf {S}^1_2\) mentioned above.
- 7.
The argument is folklore, see for instance Halbach (2014, §8).
- 8.
For a formally precise definition, see for instance (Visser 2013).
- 9.
Here’s a proof: Let’s assume that U is locally interpretable in V . In V , either C o n(U) or ¬C o n(U). If the former, an interpretation can be found via the Henkin-Feferman arithmetized completeness theorem. If the latter, then there is a finite V 0 ⊆ V such that V ⊢C o n(V 0) →C o n(U 0) for all finite U 0 ⊂ U. Therefore V proves C o n(U 0). But then, by the well-known argument due to Feferman (1960), one can find an intensional consistency statement C o n ∗(U) such that V ⊢C o n ∗(U). We can then employ the Henkin-Feferman construction again.
- 10.
Personal communication.
- 11.
For a full argument, see Nicolai (2016a).
- 12.
Notice for instance, that a form of full commutation with negation is needed even for the principle
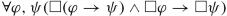 (K)
(K)that is required to close provability under
 .
. - 13.
Where \(2^x_0=x\) and \(2^x_{y+1}=2^{2^x_y}\).
- 14.
See Fischer (2014, 4.11) for a proof in the case of PA. The method can however be generalized to all B.
- 15.
This desideratum was clearly emphasized in Halbach’s influential monograph:
…a base theory must contain at least a theory about the objects to which truth can be ascribed. […] The axioms of the truth theory can serve their purpose only if the base theory allows one to express certain facts about syntactic operations; […] it should be provable in the base theory that a conjunction is different from its conjuncts and different from any disjunction.[…] The decisive advantage of using Peano Arithmetic is that I do not have to develop a formal theory that can be used as base theory…(Halbach 2014, §2)
- 16.
A suggestion along these lines has been recently made by Fujimoto in Deflationism beyond arithmetic. Unpublished manuscript.
References
Cantini, A. 1989. Notes on formal theories of truth. Zeitschrift für Logik un Grundlagen der Mathematik 35: 97–130.
Feferman, S. 1960. Arithmetization of metamathematics in a general setting. Fundamenta Mathematicae 49(1): 35–92.
Field, H. 1999. Deflating the conservativeness argument. Journal of Philosophy 96(10): 533–540.
Fischer, M. 2014. Truth and speed-up. Review of Symbolic Logic 7(2): 319–340.
Fischer, M., and L. Horsten. 2015. The expressive power of truth. Review of Symbolic Logic 8(2): 345–369.
Fujimoto, K. 2017. Deflationism beyond arithmetic. Synthese 1–25. Online-first version.
Halbach, V. 1999. Conservative theories of classical truth. Studia Logica 62(3): 353–370.
Halbach, V. 2014. Axiomatic theories of truth, Revised ed. Cambridge: Cambridge University Press.
Horsten, L. 2012. The Tarskian turn. Oxford: MIT University Press.
Horwich, P. 1998. Truth. Oxford: Clarendon Press.
Hájek, P., and P. Pudlák. 1993. Metamathematics of first-order arithmetic. Perspectives in mathematical logic. Berlin, New York: Springer.
Jech, T. 2008. Set theory, The 3rd millennium ed. Berlin: Springer.
Ketland, J. 1999. Deflationism and Tarski’s paradise. Mind 108(429): 69–94.
Leigh, G. 2015. Conservativity for theories of compositional truth via cut elimination. The Journal of Symbolic Logic 80(3): 845-865
McGee, V. 1991. Truth, vagueness, and paradox. Indianapolis/Cambridge: Hackett.
Nicolai, C. 2015. Deflationary truth and the ontology of expressions. Synthese 192(12): 4031–4055.
Nicolai, C. 2016a. A note on typed truth and consistency assertions. Journal of Philosophical Logic 45(1): 89–119.
Nicolai, C. 2016b. More on systems of truth and predicative comprehension. In Objectivity, realism, and proof. FilMat studies in the philosophy of mathematics, ed. F. Boccuni, and A. Sereni. Cham: Springer.
Nicolai, C., and V. Halbach. 2017. On the costs of nonclassical logic. Journal of Philosophical Logic, Online First: https:doi.org/10.1007/s10992-017-9424-3.
Pudlák, P. 1983. Some prime elements in the lattice of interpretability types. Transactions of the American Mathematical Society 280: 255–275.
Pudlák, P. 1985. Cuts, consistency statements, and interpretations. Journal of Symbolic Logic 50: 423–441.
Pudlák, P. 1998. The lengths of proofs. In Handbook of proof theory, vol. 137 of Studies in logic and the foundations of mathematics, ed. Samuel R. Buss, 547–637. Amsterdam/Lausanne/New York: Elsevier.
Shapiro, S. 1998. Proof and truth: Through thick and thin. Journal of Philosophy 95(10): 493–521.
Simpson, S.G. 2009. Subsystems of second order arithmetic. Perspectives in logic. New York: Association for symbolic logic.
Stern, J. 2016. Towards predicate approaches to modality. New York: Springer.
Tarski, A. 1956. Der Wahrhetisbegriff in den formalisierten Sprachen. In Logic, semantics, metamathematics, 152–278. Oxford: Clarendon Press.
Visser, A. 2013. What is the right notion of sequentiality. In New studies in weak arithmetics, CSLI lecture notes, vol. 211, ed. C. Charampolas, P. Cegielski, and C. Dimitracopoulos, 229–272. Stanford: Publications and Presses Universitaires du Pole de Recherche et d’Enseingement Superieur Paris-est.
Acknowledgements
This research has been supported by the European Commission, grant no. 658285 FOREMOTIONS. I would like to thank Martin Fischer, Albert Visser, and an anonymous referee for useful comments and insights.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Nicolai, C. (2018). On Expressive Power Over Arithmetic. In: Piazza, M., Pulcini, G. (eds) Truth, Existence and Explanation. Boston Studies in the Philosophy and History of Science, vol 334. Springer, Cham. https://doi.org/10.1007/978-3-319-93342-9_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-93342-9_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-93341-2
Online ISBN: 978-3-319-93342-9
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


 .
.