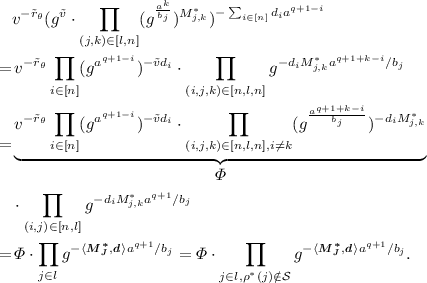Practical Large Universe Attribute-Set Based Encryption in the Standard Model

Abstract

Attribute-set based encryption is a promising branch of attribute-based encryption which deals with the case when many attributes are only meaningful in groups or in sets and helps to avoid the exponential growth of attributes. We propose a feasible and efficient attribute-set based encryption scheme which is large universe, unbounded and supports composite attributes, using linear secret sharing schemes as the underlying tool. Additionally, our construction has been proved to be selectively secure in the standard model while previous ones could only be proved to be secure in the generic group model.

1 Introduction

In cloud computing system, the cloud service providers may be honest but curious about the customer data for the analysis of user behavior or advertising. A feasible solution is that owners encrypt sensitive data before uploading them. Compared with the traditional one-to-one encryption, Attribute-Based Encryption (ABE), as an excellent cryptographic access control mechanism, is quite preferable for data encryption and sharing based on the recipients’ ability to satisfy a policy. ABE is an excellent cryptographic access control mechanism achieving the sharing of encrypted data. However, in many scenarios, separate attributes cannot give a good satisfaction for the various requirements, they are only meaningful when they are organized as the groups or sets.

There are mainly two types of ABE schemes: Ciphertext-Policy ABE (CP-ABE), where ciphertexts are associated with access policies and keys are associated with sets of attributes, and Key-Policy ABE (KP-ABE), where keys are associated with access policies and ciphertexts are associated with sets of attributes. In this work, we focus on the challenge how to organize attributes efficiently.

• 1. Attributes are often related with each other. Many attributes are only meaningful in groups or in sets.

• 2. Separate attributes cannot give a great satisfaction for various requirements in practice, which will lead to the consequence of a large number of repeated attributes in the access policy.

The concept of Attribute-set based encryption (ASBE) was first proposed by Bobba, et al. [5] in 2009. However, their construction is based on the access tree and proved secure in generic group model. The scheme [18] is constructed based on the [5] and also could only be proved secure in the generic model. In this work, we propose a new scheme which is more practical. Compared with the scheme of Bobba et al. [5], our scheme can achieve the properties of large universe and unbounded, and is constructed based on the Linear Secret Sharing Schemes (LSSS). Using the prime order groups and partition techniques [16], it is efficient and selectively secure in the standard model. In order to achieve the collusion attacks resistant ability, we use a different randomness to mask each component for each individual attribute and composite attribute set.

1.1 Related Work

Sahai and Waters first proposed the concept of Attribute-based Encryption [17] in 2005, as a generalization of Fuzzy Identity-based Encryption by using threshold gates as the access structure. Then ABE comes into two flavors, Key-Policy ABE (KP-ABE) and Ciphertext-Policy ABE (CP-ABE). Goyal et al. proposed the first KP-ABE scheme [7], which supports monotonic Boolean encryption policies. The first construction of CP-ABE was given by Bethencourt et al. [4], whose security proof was based on the generic group model. Okamoto et al. first gave a bounded fully secure construction in the standard model [9]. Until now many works have been presented to achieve the unbounded or large universe properties in ABE [8, 13]. But most of them were somewhat limited such as restricting the expressiveness of policies or using random oracle model. In 2013, Rouselakis and Waters proposed a large universe and unbounded ABE scheme [16] and proved it to be selectively secure using the partitioning style techniques. Later in 2014, Wang and Feng proposed a large universe ABE scheme for lattices [20]. In 2016, Li et al. proposed a practical construction for large universe hierarchical ABE scheme [10] and Zhang et al. proposed an accountable large universe ABE scheme supporting monotone access structures [21].

There are many other schemes focus on the problem of how to organize attributes in ABE to make it practical and efficient. One study is hierarchical ABE (HABE) [6, 11, 12, 19]. Another is ASBE. Note that ASBE is quite different from many existing HABE schemes in organizing attributes. Attributes in former is composite such as {University A, Master}, while in the latter they are hierarchical, that is, there is a relation between the superior and the subordinate. ASBE was first proposed by Bobba et al. [5] in 2009. In ASBE, attributes are organized into a recursive family of sets. In Bobba’s work, access policy was based on binary access tree. A hierarchical attribute-set based encryption construction was proposed in 2012 [18]. Then in the following years between 2013 and 2015, many applications based on ASBE were proposed [1, 2, 14, 15].

1.2 Our Contribution

We propose a practical Attribute-set based encryption scheme which is large universe, unbounded and supports composite attributes, we also prove our scheme to be selectively secure in the standard model.

We overcame the following difficulties to construct the CP-ASBE scheme.

• We used a different randomness to mask each component for each individual attribute and composite attribute set to achieve the collusion attacks resistant ability.

• To achieve an efficient ASBE construction, we improved the linear secret sharing schemes to support the composite attributes.

• We defined the formal security model, then by borrowing the idea of partition technique, we overcame the challenges appeared in security proof process and proved our scheme to be selective security in the standard model.

1.3 Organization

The remainder of the paper is organized as follows. Section 2 gives necessary background on bilinear maps, access structure, linear secret sharing schemes, algorithms and complexity assumptions. Then we formalize our CP-ASBE scheme and define its security model. We propose a construction of CP-ASBE with a formal security proof in Sects. 3 and 4. We give a belief conclusion in Sect. 5.

2 Preliminaries

Bilinear maps. Let $\mathbb {G}_0$ and $\mathbb {G}_1$ be two multiplicative cyclic groups of prime order p. Let g be a generator of $\mathbb {G}_0$ and e be a bilinear map, $e:\mathbb {G}_0\times \mathbb {G}_0 \rightarrow \mathbb {G}_1$. The bilinear map e has the following properties:

• 1. Bilinearity: For all $u,v\in \mathbb {G}_0$ and $a,b \in \mathbb {Z}_p$, we have $e(u^a,v^b)=e(u,v)^{ab}$.

• 2. Non-degeneracy: $e(g,g) \ne 1$.

Linear Secret Sharing Schemes (LSSS) [3]. Some modifications will be made in LSSS to support composite attribute sets. First, a secret sharing scheme II over a set of parties $\mathcal {P}$ realizing access structure is linear over $\mathbb {Z}_p$ if

• 1. The share of a secret $s \in \mathbb {Z}_p$ for each attribute form a vector over $\mathbb {Z}_p$.

• 2. For each access structure $\mathbb {A}$ on U which is the attribute universe, there exists a matrix $M \in Z_p^{l\times n}$ with l rows and n columns, which is called the share-generating matrix and a function $\rho$, which is defined as the mapping from rows of M to attributes in U, i.e. $\rho :[l]\rightarrow \mathcal {U}$. For all $i = 1, \cdots , l$, the $i^{th}$ row of M is associated with an attribute $\rho (i)$. Let the function $\rho$ define the party labeling row i as $\rho (i)$. To share the secret $s \in \mathbb {Z}_p$, we first consider the column vector $\mathbf {y}=(s,y_2,\cdots , y_n)^T$, where s is the secret to be shared, and $y_2, \cdots , y_n \in \mathbb {Z}_p$ are randomly chosen. Then $M\mathbf {y}$ is the vector of l shares of the secret s according to II. The share $(M\mathbf {y})_i$ belongs to party $\rho (i)$, that is, the attribute of $\rho (i)$.

According to [6], every LSSS enjoys the linear reconstruction property. Suppose II is an LSSS for the access structure $\mathbb {A}$. Let $\mathcal {S}$ be any authorized set if $\mathbb {A}(\mathcal {S})=1$, and let $I \subset \{1,2,\cdots ,l\}$ be defined as $I=\{i:\rho (i)\in \mathcal {S}\}$. Then there exist constants $\{d_i \in Z_p\}_{i \in I}$ such that, if $\{\lambda _i\}(i \in I)$ are valid shares of any secret s according to II, then $\sum _{i \in I}d_i\cdot \lambda _i=s$.

Furthermore, to support composite attribute sets, that is only attributes in the same set can be used to satisfy the access policy, one natural idea is to re-share the shares obtained from the outer set. Take the depth of key structure being 2, that is, $d=2$ as an example, we will first generate a share $d_i(1\le i \le k)$ of the secret for each attribute subset: $A_0,A_1,A_2,\cdots , A_k$. And then for each attribute subset $A_i$, it takes the share $d_i$ as a new secret to share with the attributes $(a_{i1}, \cdots ,a_{in_i})$ in it where $n_i$ is the number of attributes in set $A_i$. When the depth of key structure is greater than d, iterate the process discussed above several times until there is no composite attribute subsets.

Algorithms. Our LU-CP-ASBE scheme consists of the following five algorithms:

• Setup $(1^\lambda ) \rightarrow (PK, MK)$: This is a randomized algorithm that takes a security parameter $\lambda \in N$ encoded in unary, it generates the public parameters PK and master key MK.

• KeyGen $(PK,MK,\mathcal {S}) \rightarrow SK$: The private key generation algorithm is a randomized algorithm that takes as input the public parameters PK, the master key MK, and attribute set $\mathcal {S}$. It outputs a user’s secret key SK.

• Encrypt $(PK,M,\mathbb {A}) \rightarrow CT$: This is a randomized algorithm that takes as input the public parameters PK, a plaintext message M, and an access structure $\mathbb {A}$. It outputs ciphertext CT.

• Decrypt $(PK,SK,CT) \rightarrow M$: The decryption algorithm takes as input the public parameters PK, a secret key SK of a user with a set of attributes $\mathcal {S}$, and a ciphertext CT that was encrypted under access structure $\mathbb {A}$. It outputs the message M if $\mathcal {S}$ satisfies $\mathbb {A}$. Otherwise, it outputs a symbol of $\perp$.

Assumption. Initially the challenger calls the groups generation algorithm with the security parameter as input and then picks a random group element $g \in \mathbb {G}_0$, $q+2$ random exponents $a, s, b_1, b_2, \cdots , b_q \in \mathbb {Z}_p$. Then he sends to the adversary the group description $(p,\mathbb {G}_0, \mathbb {G}_1, e)$ and all of the following terms:

$$\begin{aligned} \begin{aligned}&g, g^s\\&g^{a^i},g^{b^j},g^{sb_j},g^{a^ib_j},g^{a^ib_j^2}&\forall (i,j) \in [q,q]\\&g^{a^ib_j/b_{j^\prime }^2}&\forall (i,j,j^{\prime }) \in [2q,q,q]\ with\ j \ne j^{\prime }\\&g^{a^i/b_j}&\forall (i,j) \in [2q,q]\ with\ i \ne q + 1\\&g^{sa^ib_j/b_{j^{\prime }}},g^{sa^ib_j/b_{j^{\prime }}^2}&\forall (i,j,j^{\prime }) \in [q,q,q]\ with\ j \ne j^{\prime } \end{aligned} \end{aligned}$$

It is hard for the adversary to distinguish $e(g,g)^{sa^{q+1}} \in \mathbb {G}_1$ from an element which is randomly chosen from $\mathbb {G}_1$.

We say that the q-type assumption holds if no PPT adversary has a non-negligible advantage in solving the q-type problem.

Selective security model. We give the definition of the security model for our large universe CP-ASBE (LU-CP-ASBE) scheme. In our LU-CP-ASBE model, attributes are divided into simple attributes and composite attributes. Note that once some component in composite attribute sets satisfies the access structure, the associated user is said to be authorized. We described the security model by a game between an adversary $\mathcal {A}$ and a challenger $\mathcal {B}$ and is parameterized by the security parameter $\lambda \in \mathbb {N}$. The phases of the game are as follows:

• Init: The adversary $\mathcal {A}$ declares the access structure $\mathbb {A}^*$ which he wants to attack, and then sends it to the challenger $\mathcal {B}$.

• Setup: The challenger $\mathcal {B}$ runs the Setup$(1^\lambda )$ algorithm and gives the public parameters PK to the adversary $\mathcal {A}$.

• Phase 1: The adversary $\mathcal {A}$ is allowed to issue queries for secret keys for users with sets of attributes $(\mathcal {S}_1), (\mathcal {S}_2), \cdots , (\mathcal {S}_{Q_1})$. For each $(\mathcal {S}_i)$, the challenger $\mathcal {B}$ calls KeyGen$(PK,MK,\mathcal {S}_i) \rightarrow SK_i$ and sends $SK_i$ to $\mathcal {A}$. The only restriction is that $\mathcal {S}_i$ does not satisfy $\mathbb {A}^*$.

• Challenge: The adversary $\mathcal {A}$ submits two equal length messages $M_0$ and $M_1$. The challenger $\mathcal {B}$ flips a random coin $b \in \{0,1\}$, and encrypts $M_b$ with $\mathbb {A}^*$. The ciphertext is passed to $\mathcal {A}$.

• Phase 2: Phase 1 is repeated.

• Guess: The adversary $\mathcal {A}$ outputs a guess $b^\prime$ of b.

The advantage of an adversary $\mathcal {A}$ in this game is defined as $|Pr[b^\prime =b]-1/2|$.

A CP-ASBE scheme is selectively secure if all probabilistic polynomial time (PPT) adversaries have negligible advantage in $\lambda$ in the security game above.

3 Our Construction

In this section, we present the construction of LU-CP-ASBE scheme where the attributes are assumed to be divided into simple attributes and composite attributes. Composite attributes are expressed in the form of attribute sets. To prevent users from making the collusion attack, we use a unique random number to bind the attribute with the attribute set it belongs to. The public parameters consist of seven group elements (g, u, h, w, v, X, Y) where $X = w^{\beta }, Y=e(g,g)^{\alpha }$. These parameters are utilized in two layers, attribute layer (the u, h terms) and the secret sharing layer (the w term). Attribute layer provides a hash function to map arbitrary attributes as group elements. And the secret sharing layer is the main part to be modified for transforming CP-ABE into CP-ASBE. w term, the secret sharing layer, holds the secret randomness r associated with a user and the secret randomness $r_{ij}$ associated with each attribute during key generation.

Let $\mathbb {G}_0$ be a bilinear group of prime order p, and let g be a generator of $\mathbb {G}_0$. In addition, let $e:\mathbb {G}_0 \times \mathbb {G}_0 \rightarrow \mathbb {G}_1$ denote the bilinear map. A security parameter $\lambda$ will determine the size of the groups. We assume that users’ attributes are elements in $\mathbb {Z}_p^*$, however, attributes can be any meaningful unique strings using a collision resistant hash function $H:\{0,1\}^* \rightarrow \mathbb {Z}_p^*$.

Our construction follows.

• Setup $(1^\lambda , d=2) \rightarrow (PK,MK)$. The input parameter d is the depth of key structures, which is decided at setup phase and restricted to be less than d. For convenience, here we show a scheme with the key structure depth of 2, although it can be easily extended to arbitrary depth.

  The algorithm calls the group generation algorithm $\mathcal {G}(1^{\lambda })$ and gets the descriptions of the groups and the bilinear mapping $D=(p,\mathbb {G}_0, \mathbb {G}_1, e)$. Then it picks the random terms $g, u, h, w, v \in \mathbb {G}_0$ and $\alpha , \beta \in \mathbb {Z}_p$. The setup algorithm issues the public parameters PK as: (D, g, u, h, w, v, X, Y) and keeps the master key $MK(\alpha , \beta )$ as secret.

• KeyGen $(PK, MK, \mathcal {S}=\{A_0, \cdots , A_k\} \subseteq \mathbb {Z}_p) \rightarrow SK$. As what has been explained in Sect. 2, $A_0$ is the set of simple attributes in the outer set, and $A_i(i \in [1, k])$ are composite attribute sets in depth 1. Let $A_i=\{a_{i,1}, a_{i,2}, \cdots , a_{i,n_i}\}$, where $a_{i,j}$ denotes the $j^{th}$ attribute appearing in set $A_i$. The KeyGen algorithm first picks $k+1$ random exponents $r, r_1, r_2, \cdots , r_k \in \mathbb {Z}_p$, r for the user u and $r_0, r_1, r_2, \cdots , r_k$ for each composite attribute set $A_i \in \mathcal {S}, 0 \le i \le k$. It also picks random exponent $r_{i,j}$ for each attribute in $\mathcal {S}$. Then calculate $K_0=g^{\alpha }w^r$ and for each $\theta \in [0, k]$ calculate: $K_1^{\{\theta \}}=g^{r_\theta }, L^{\{\theta \}}=g^{\frac{r+r_{\theta }}{\beta }}, K_{i, 2}^{\{\theta \}}=g^{r_{\theta , i}}, K_{i,3}^{\{\theta \}}=(u^{a_{\theta , i}}h)^{r_{\theta ,i}}v^{-r_{\theta }}$.

  It outputs the secret key SK as: $(\mathcal {S}, K_0, \{ K_1^{\{\theta \}},L^{\{\theta \}}, K_{i,2}^{\{\theta \}},K_{i,3}^{\{\theta \}}\}_{\theta \in [0,k],i \in [n_i]})$.

  Note that the operations on exponents are module the order p of the group, which is prime.

• Encrypt $(m,(M,\rho ))\rightarrow CT$. The encryption algorithm takes the plaintext message m and the access policy encoded by LSSS as input, where $M\in \mathbb {Z}_p^{l \times q}$ and $\rho$ is a function mapping the row number to the corresponding attribute. The encryption algorithm then randomly picks $\mathbf {y}=(s,y_2,\cdots , y_q) \in \mathbb {Z}_p^{q\times 1}$ and s is the random secret to be shared. The vector of shares is denoted as $\mathbf {\lambda }=(\lambda _1, \cdots , \lambda _l)=(\lambda _{01}, \cdots , \lambda _{0n_0}, \cdots , \lambda _{\gamma 1}, \cdots , \lambda _{\gamma n_\gamma })^T=M\cdot \mathbf {y}$.

  It then chooses $\theta \cdot \tau$ random values $t_{\theta \tau } \in \mathbb {Z}_p$ and for every $\theta \in [0, \gamma ], \tau \in [n_{\theta }]$ computes

  $$\begin{aligned}&C=me(g,g)^{\alpha s}, D_0=g^s,\\&C_{\tau , 1}^{\{\theta \}}=w^{\lambda _{\mathcal {X}}}v^{t_{\mathcal {X}}}, C_{\tau , 2}^{\{\theta \}}=(u^{\rho (\mathcal {X})}h)^{-t_{\mathcal {X}}},C_{\tau , 3}^{\{\theta \}}=g^{t_{\mathcal {X}}},\hat{C}_{\tau }^{\{\theta \}}=X^{\lambda _{\mathcal {X}}} \end{aligned}$$

  Then publishes the ciphertext CT as:

  $$(C, (M, \rho ), D_0, \{C_{\tau , 1}^{\{\theta \}}, C_{\tau , 2}^{\{\theta \}}, C_{\tau , 3}^{\{\theta \}}, \hat{C}_{\tau }^{\{\theta \}}\}_{\theta \in [0, \gamma ], \tau \in [n_\theta ]}).$$

  $\mathcal {X} \in [l]$ is the row number of each attribute where $\mathcal {X}=\sum _{i \in [0,\theta )}n_{\theta }+\tau$.

• Decrypt $(SK,CT) \rightarrow m$. The decryption algorithm first finds the set I of the attributes, $I=\{i:\rho (i)\in A\}$. Then if set I exists, there exists constant coefficient $\{d_i \in \mathbb {Z}_p\}_{i \in I}$ such that $\sum _{i \in I}d_i\cdot \mathbf {M_l}=(1,0,\cdots ,0)$, where $\mathbf {M_l}$ is the $i^{th}$ row of matrix M. Then we have $\sum _{i\in I}d_i \lambda _i=s$.

  Function $\psi (i)$ defines subset $\dot{A}$ that $\rho (i)$ belongs to and function $\varPhi (i)$ defines the position of $\rho (i)$ in $\dot{A}_{\psi (i)}$. Denote the set $\{i:i\in I \cap \psi (i)\}$ as $I_{\theta }$. Now the decryption algorithm calculates

  $$F=\prod _{\theta \in \psi (i)}\frac{\prod _{i \in I_{\theta }}e((\hat{C}_{\varPhi (i)}^{\{\theta \}})^{d_i},L^{\{\theta \}})}{\prod _{i \in I_{\theta }}(e(K_1^{\{\theta \}},C_{\varPhi (i),1}^{\{\theta \}})e(K_{\tau ,2}^{\{\theta \}},C_{\varPhi (i),2}^{\{\theta \}})e(K_{\tau ,3}^{\{\theta \}},C_{\varPhi (i),3}^{\{\theta \}}))^{d_i}}.$$

  where $\tau$ is the index of the attribute $\rho (i)$ in subset $A_{\theta }$. The algorithm outputs plaintext m as $C\cdot F / (D_0,K_0)$.

• Correctness.

  $$\begin{aligned} F_{\theta }\!=\!\prod _{i \in I_{\theta }}(e(K_1^{\{\theta \}},C_{\varPhi (i),1}^{\{\theta \}})e(K_{\tau ,2}^{\{\theta \}},C_{\varPhi (i),2}^{\{\theta \}})e(K_{\tau ,3}^{\{\theta \}},C_{\varPhi (i),3}^{\{\theta \}}))^{d_i}\!=\!\prod _{i\in I_{\theta }}e(g,w)^{r_{\theta }d_i \lambda _i} \end{aligned}$$

  Translate $F_{\theta }$ to $F_{\theta ^{\prime }}$ by the following way.

  $$F_{\theta ^{\prime }}=\frac{e(\prod _{i \in I_{\theta }}(\hat{C}_{\varPhi (i)}^{\{\theta \}})^{d_i},L^{\{\theta \}})}{F_{\theta }}=\frac{e(\prod _{i\in I_{\theta }}X^{d_i \lambda _i},g^{\frac{r+r_{\theta }}{\beta }})}{\prod _{i \in I_{\theta }}e(g,w)^{r_{\theta }d_i\lambda _i}}=e(g,w)^{r\sum _{i \in I_{\theta }}d_i \lambda _i}$$

  Then we have $F=\prod _{\theta \in \psi (i)}F_{\theta ^{\prime }}=e(g,w)^{r\sum _{i \in I}d_i \lambda _i}=e(g,w)^{rs}$ and $m=C\cdot F/(D_0,K_0)=me(g,g)^{\alpha s}e(g,w)^{rs}/e(g^s,g^{\alpha }w^r)$.

4 Selective Security Proof

In this section, we will give the concrete security proof of our LU-CP-ASBE scheme.

• Theorem 1. If the $q-1$ assumption is selectively secure in polynomial time, then all PPT adversaries with a challenge matrix of size $l \times n$, where $l, n \le q$, have a negligible advantage in selectively breaking our scheme.

• Proof. To prove the theorem, we will suppose that there exists a PPT adversary $\mathcal {A}$ with a challenge matrix that satisfies the restriction, which has a non-negligible advantage $Adv_{\mathcal {A}}$ in selectively breaking our scheme. Using the attacker, we will build a PPT simulator $\mathcal {B}$ that can challenge the $q-1$ assumption with a non-negligible advantage.

• Init. The adversary $\mathcal {A}$ declares a challenge access policy $\mathbb {A}=(M_*,\rho _*)$ which he wants to attack, and then sends it to the challenger $\mathcal {B}$. Each row of $M_*$ will be labeled by an attribute and $\rho (i)$ denotes the label of $i^{th}$ row $\mathbf {M_*}$.

• Setup. $\mathcal {B}$ is supposed to generate the public parameters of system. It implicitly sets the master key to be $\alpha =a^{q+1}+\tilde{\alpha },\beta =\tilde{\beta }/s$ where a, s and q are set in the assumption and $\tilde{\alpha }, \tilde{\beta }$ are random exponents known to $\mathcal {B}$. Notice that in this way $\alpha$ and $\beta$ is correctly distributed and a is information-theoretically hidden from $\mathcal {A}$. Also $\mathcal {B}$ chooses $\tilde{v}, \tilde{u}, \tilde{h} \in \mathbb {Z}_p$ randomly, and gives the following public parameters PK to $\mathcal {A}$.

  $$\begin{aligned}&g=g,\ w=g^a,u=g^{\tilde{u}}\cdot \prod _{(j,k)\in [l,n]}(g^{a^k/b_j^2})^{M_{j,k}^*},\\&h=g^{\tilde{h}}\cdot \prod _{(j,k)\in [l,n]}(g^{a^k/b_j^2})^{-\rho ^*(j)M_{j,k}^*},v=g^{\tilde{v}}\cdot \prod _{(j,k)\in [l,n]}(g^{a^k/b_j})^{M_{j,k}^*},\\&e(g,g)^{\alpha }=e(g^a,g^{a^q})\cdot e(g,g)^{\tilde{\alpha }},X=w^{\beta }=g^{a\tilde{\beta }/s}. \end{aligned}$$

• Phase 1. Now challenger $\mathcal {B}$ has to produce secret keys for tuples which consists of non-authorized attribute sets $\mathcal {S}=\{A_0,A_1,A_2,\cdots ,A_k\}$, where $A_i=\{a_{i1},a_{i2},\cdots ,a_{in_i}\}$. The only restriction is that $\mathcal {S}$ does not satisfy $\mathbb {A}^*$. Consequently, there exists a vector $\mathbf {d}=(d_1,d_2,\cdots ,d_n)^T\in \mathbb {Z}_p^n$ such that $d_1=-1$ and $\langle \mathbf {M_l^*},\mathbf {d}\rangle =0$ for all $i \in I=\{i|i\in [l] \cap \rho ^*(i) \in \mathcal {S}\}$. $\mathcal {B}$ computes $\mathbf {d}$ using linear algebra. Then $\mathcal {B}$ picks $\tilde{r}$ for the user and $\tilde{r}_\theta (\theta \in [k])$ for each attribute subset randomly from $\mathbb {Z}_p$, and for simplicity we let $\tilde{r}_0=\tilde{r}$. Then $\mathcal {B}$ implicitly have

  $$\begin{aligned} r&=\tilde{r}_{\theta }-d_1a^q-\cdots -d_na^{q+1-n}=\tilde{r}_{\theta }-\sum _{i\in [n]}d_ia^{q+1-i} \ (\theta \in [0,k]),\\ r_{\theta }&=\tilde{r}_{\theta } + d_1a^q + \cdots + d_na^{q+1-n}=\tilde{r}_{\theta }+\sum _{i\in [n]}d_i a^{q+1-i} \ (\theta \in [0,k]). \end{aligned}$$

  Each $r_{\theta }$ is properly distributed due to $\tilde{r}_{\theta }$. Then using the suitable terms from the assumption, $\mathcal {B}$ calculates:

  $$\begin{aligned} K_0^{\{\theta \}}&=g^{\alpha }w^{r_{\theta }}=g^{\tilde{\alpha }}(g^a)^{\tilde{r}_{\theta }}\prod _{i=2}^n(g^{a^{q+2-i}})^{d_i}, K_1^{\{\theta \}}&=g^{r_{\theta }}=g^{\tilde{r}_{\theta }}\prod _{i\in [n]}(g^{a^{q+1-i}})^{d_i},\\ L^{\{\theta \}}&=g^{(r+r_{\theta })/\beta }=g^{(\tilde{r}_0+\tilde{r}_{\theta })s/\tilde{\beta })}. \end{aligned}$$

  Additionally, for each attribute $a_{\theta \tau }$ in attribute subset $A_{\theta }$, $\mathcal {B}$ compute the terms $K_{i,2}^{\{\theta \}}=g^{r_{\theta ,i}}$ and $K_{i,3}^{\{\theta \}}=(u^{a_{\theta ,i}}h)^{r_{\theta ,i}}v^{-r_{\theta }}$. The part $v^{-r_{\theta }}$ is

  

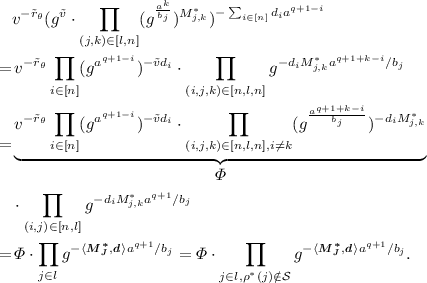
  The $\varPhi$ part can be calculated by the simulator using the assumption, while the second part cannot. Simulator $\mathcal {B}$ implicitly sets

  $$\begin{aligned} r_{\theta , \tau }&=\tilde{r}_{\theta , \tau }+r_{\theta }\cdot \sum _{i^{\prime } \in [l],\rho ^*(i^{\prime }) \notin \mathcal {S}} \frac{b_{i^{\prime }}}{a_{\theta \tau }-\rho ^*(i^{\prime })}\\&=\tilde{r}_{\theta , \tau } + \tilde{r}_{\theta } \cdot \sum _{i^{\prime } \in [l],\rho ^*(i^{\prime }) \notin \mathcal {S}}\frac{b_{i^{\prime }}}{a_{\theta \tau }-\rho ^*(i^{\prime })}+\sum _{\{i,i^{\prime }\} \in [n,l],\rho ^*(i^{\prime })\notin \mathcal {S}} \frac{d_ib_{i^{\prime }}a^{q+1-i}}{a_{\theta \tau }-\rho ^*(i^{\prime })}. \end{aligned}$$

  where $r_{\theta , \tau }$ is properly distributed. Notice that $r_{\theta , \tau }$ is well defined only for attributes that has nothing to do with the policy, therefore, the denominators $a_{\theta \tau }-\rho ^*(i^{\prime })$ are non-zero. The $(u^{a_{\theta ,i}}h)^{r_{\theta ,i}}$ part in $K_{i,3}^{\{\theta \}}$ is computed as

  $$\begin{aligned}&(u^{a_{\theta ,i}}h)^{\tilde{r}_{\theta ,l}}\cdot (K_{i,2}^{\{\theta \}}/g^{\tilde{r}_{\theta , l}})^{\tilde{u}a_{\theta ,i}+\tilde{h}}\cdot \prod _{(i^{\prime },j,k)\in [l,l,n],\rho ^*(i^{\prime })\notin \mathcal {S}}g^{\frac{\tilde{r}_{\theta }M_{j,k}^*b_{i^{\prime }}a^k(a_{\theta ,i}-\rho ^*(j))}{b_j^2(a_{\theta \tau }-\rho ^*(i^{\prime }))}}\\&\cdot \prod _{(i,i^{\prime },j,k)\in [n,l,l,n],\rho ^*(i^{\prime })\notin \mathcal {S}}g^{\frac{M_{j,k}^*d_ib_{i^{\prime }}a^{q+k+1-i}(a_{\theta ,i}-\rho ^*(j))}{b_j^2(a_{\theta \tau }-\rho ^*(i^{\prime }))}}\\&=\varPsi \cdot \prod _{(i,j)\in [n,l],\rho ^*(j)\notin \mathcal {S}}g^{\frac{M_{j,i}^*d_ib_ja^{q+1}(a_{\theta ,i}-\rho ^*(j))}{b_j^2(a_{\theta \tau }-\rho ^*(j))}}=\varPsi \cdot \prod _{j\in [l],\rho ^*(j)\notin \mathcal {S}}g^{\frac{\langle \mathbf {M_j^*},\mathbf {d}\rangle a^{q+1}}{b_j}}. \end{aligned}$$

  where $\varPsi$ and $K_{i,2}^{\{\theta \}}$ can be calculated using the terms in our assumption. The non-computable parts of $(u^{a_{\theta ,i}}h)^{r_{\theta ,i}}$ and $v^{-r_{\theta }}$ term can cancel with each other. In this way simulator $\mathcal {B}$ can calculate $K_{i,2}^{\{\theta \}}$ and $K_{i,3}^{\{\theta \}}$ and send the decryption key $SK=(\mathcal {S},\{K_0^{\{\theta \}},K_1^{\{\theta \}},L^{\{\theta \}},K_{i,2}^{\{\theta \}},K_{i,3}^{\{\theta \}}\}_{\theta \in [0,k],i \in [n_{\theta }]})$ to $\mathcal {A}$.

• Challenge. The adversary $\mathcal {A}$ submits two equal length message $m_0$ and $m_1$. Then $\mathcal {B}$ flips a random coin $b\xleftarrow {\$}\{0,1\}$ and constructs $C=m_bTe(g,g)^{\tilde{\alpha }s}$ and $D_0=g^s$ where T is the challenge term. Then $\mathcal {B}$ is supposed to generate the other components in ciphertext and it sets implicitly $\mathbf {y}=(s,sa+\tilde{y}_2,sa^2+\tilde{y}_3,\cdots ,sa^{n-1}+\tilde{y}_n)$ where $\tilde{y}_2,\tilde{y}_3,\cdots ,\tilde{y}_n \xleftarrow {\$}Z_p$. Since $\mathbf {\lambda }=M^*\mathbf {y}$, we have that $\lambda _{\mathcal {X}}=\sum _{i\in [n]}M_{\mathcal {X},i}^*sa^{i-1}+\sum _{i=2}^nM_{\mathcal {X},i}^*\tilde{y}_l=\sum _{i\in [n]}M_{\mathcal {X},i}^*sa^{i-1}+\tilde{\lambda }_{\mathcal {X}}$ for each row $\mathcal {X}\in [l]$. And for each now $\mathcal {B}$ sets implicitly $t_{\mathcal {X}}=-sb_{\mathcal {X}}$ which is properly distributed. Using this, $\mathcal {B}$ calculates

  $$\begin{aligned}&C_{\tau ,1}^{\{\theta \}}=w^{\lambda _{\mathcal {X}}}v^{t_{\mathcal {X}}}\\&=w^{\tilde{\lambda }_{\mathcal {X}}}\cdot \prod _{i \in [n]}g^{M_{\mathcal {X},i}^*sa^i}\cdot g^{-sb_{\mathcal {X}}\tilde{v}}\cdot \prod _{(j,k)\in [l,n]}g^{-\frac{sa^kb_{\mathcal {X}}M_{j,k}^*}{b_j}}\\&=w^{\tilde{\lambda }_{\mathcal {X}}}\cdot \prod _{i \in [n]}g^{M_{\mathcal {X},i}^*sa^i}\cdot g^{-sb_{\mathcal {X}}\tilde{v}}\cdot \prod _{k\in [n]}g^{-sa^kM_{\mathcal {X},k}^*}\cdot \prod _{(j,k)\in [l,n],j \ne \mathcal {X}}g^{-\frac{sa^kb_{\mathcal {X}}M_{j,k}^*}{b_j}}\\&=w^{\tilde{\lambda }_{\mathcal {X}}}\cdot (g^{sb_{\mathcal {X}}})^{-\tilde{v}}\cdot \prod _{(j,k)\in [l,n],j \ne \mathcal {X}}(g^{\frac{sa^kb_{\mathcal {X}}}{b_j}})^{-M_{j,k}^*},\\&C_{\tau ,2}^{\{\theta \}}=(u^{\rho ^*(\mathcal {X})}h)^{-t_{\mathcal {X}}}\\&=(g^{sb_{\mathcal {X}}})^{-(\tilde{u}\rho ^*(\mathcal {X})+\tilde{h})}\cdot (\prod _{(j,k)\in [l,n]}g^{(\rho ^*(\mathcal {X})-\rho ^*(j))M_{j,k}^*a^k/b_j^2})^{-sb_{\mathcal {X}}}\\&=(g^{sb_{\mathcal {X}}})^{-(\tilde{u}\rho ^*(\mathcal {X})+\tilde{h})} \cdot (\prod _{(j,k)\in [l,n],j \ne \mathcal {X}}g^{sb_{\mathcal {X}}a^k/b_j^2})^{-(\rho ^*(\mathcal {X})-\rho ^*(j))M_{j,k}^*},\\&C_{\tau ,3}^{\{\theta \}}=(g^{sb_{\mathcal {X}}})^{-1},\\&\hat{C}_{\theta }=X^{\lambda _{\mathcal {X}}}=X^{\tilde{\lambda }_{\mathcal {X}}} \cdot \prod _{i \in [n]}g^{M_{\mathcal {X},i}^*s\tilde{\beta }/sa^i}=X^{\tilde{\lambda }_{\mathcal {X}}}\cdot \prod _{i\in [n]}(g^{a^i})^{M_{\mathcal {X},i}^*\tilde{\beta }}. \end{aligned}$$

  where $\mathcal {X}=\sum _{i=0}^{\theta }n_{\theta }+\tau$.

  By using $t_{\mathcal {X}}=-sb_{\mathcal {X}}$, term v can cancel with the unknown powers of $w^{\lambda _{\mathcal {X}}}$ and similarly by using $\beta =\tilde{\beta }/s$, the unknown powers in $\hat{C}_{\theta }$ can also be canceled. Now there is nothing non-computable for $\mathcal {B}$ in terms $C_{i,2}^{\{\theta \}},C_{i,3}^{\{\theta \}}$ and $\hat{C}_{\theta }$.

  So far, $\mathcal {B}$ successfully generates the correct ciphertext under the access structure $(M,\rho )$ using the suitable terms in our assumption and public parameters PK. Finally, $\mathcal {B}$ sends the challenged ciphertext CT

  $$(C,(M,\rho ),D_0,\{C_{\tau ,1}^{\{\theta \}},C_{\tau ,2}^{\{\theta \}},C_{\tau ,3}^{\{\theta \}}\}_{\theta \in [0,m],\tau \in [n_{\theta }]},\{\hat{C}_\theta \}_{\theta \in [m]})$$

  to the attacker $\mathcal {A}$.

• Phase 2. Phase 1 is repeated.

• Guess. The adversary $\mathcal {A}$ is supposed to output a guess $b^{\prime }$ of b to $\mathcal {B}$. If $b^{\prime }=b$, $\mathcal {B}$ outputs 0 and claim the challenge term is $T=e(g,g)^{a^{q+1}s}$, otherwise, it outputs 1 and the challenge term T is random.

  Since the probability of $T=e(g,g)^{a^{q+1}s}$ equals 1 / 2, $\mathcal {B}$ has an advantage of $Adv_{\mathcal {A}}/2$ to break the q-type security assumption.

5 Conclusion

In this paper, we proposed a feasible and efficient attribute-set based encryption scheme, which can be applied in the scenario where many attributes are only meaningful in groups or in sets as they describe users. Our scheme is large universe, unbounded and powerful in expressing complex access policies. Additionally, it is proved to be selectively secure under the q-type assumption.