Logics for Bisimulation and Divergence

Abstract

The study of modal logics and various bisimulation equivalences so far shows the following progression: 1. weak bisimilarity is characterized by Hennessy-Milner logic (HML), a simple propositional modal logic with a weak possibility modality, and 2. extending HML by refining the weak possibility modality one obtains a logic which characterizes branching bisimilarity, a refinement of weak bisimilarity, and 3. further extending the logic with a divergence modality one obtains a logic which characterizes branching bisimilarity with explicit divergence, a refinement of branching bisimilarity. In this paper, we explore the development by exchanging the above 2 and 3, i.e. by first extending HML with a divergence modality and then refining the weak possibility modality in the extended logic. We have the following findings: A. extending HML with a new divergence modality one obtains a new logic which characterizes complete weak bisimilarity, an equivalence relation with distinguishing power in between weak bisimilarity and branching bisimilarity with explicit divergence; B. further extending the obtained logic by refining the weak possibility modality in it one obtains another logic which characterizes branching bisimilarity with explicit divergence. As main results of the paper, the logic in A. provides a modal characterization for complete weak bisimilarity, and moreover the two new logics in A. and B. are both sub-logics of the known logic obtained in above 3.

Supported by the CAS-INRIA major project No. GJHZ1844.

1 Introduction

Weak bisimilarity is a popular equivalence relation introduced by Milner [9]. It is defined through the notion of weak bisimulation which was proposed by Milner [9] based on an idea independently discovered by van Benthem [4] and Park [8]. The importance of weak bisimulation is that it not only defines an equivalence relation but also provides a verification technique for the equality. A well-known theoretical result for weak bisimilarity is that the equivalence is characterized by a modal logic which is known as Hennessy-Milner logic (HML) [2] in the following sense: two processes are equivalent with respect to weak bisimilarity if and only if they satisfy exactly the same set of HML formulas.

Because weak bisimilarity does not preserve divergence, i.e. it is possible for two equivalent processes that one of them is capable of endless internal computations while the other is not, various divergence preserving versions of weak bisimulation equivalences and pre-orders are studied later [1, 3, 5, 13]. Complete weak bisimilarity is a newly proposed divergence preserving weak bisimulation equivalence [10]. Like weak bisimilarity, complete weak bisimilarity is supported by a bisimulation verification technique called inductive weak bisimulation, which can be very helpful in practical verification that concerns divergence. One of the main aims of this paper is to find a modal logic which characterizes complete weak bisimilarity just as HML characterizes weak bisimilarity.

We will put our study into a more general context. The study of modal logics and various bisimulation equivalences so far shows the following progression which reveals the co-related increase for the expressive power of the logics and the distinguishing power of the equivalences:

• 1. Weak bisimilarity is characterized by HML which is a simple propositional modal logic with a weak possibility modality [2];

• 2. Extending HML by refining the weak possibility modality one obtains a logic which characterizes branching bisimilarity [5, 6], a refinement of weak bisimilarity proposed in [12],

• 3. Further extending the logic with a divergence modality one obtains a logic which characterizes branching bisimilarity with explicit divergence [13], a refinement of branching bisimilarity proposed in [12].

In this paper, we explore the development by exchanging the order of 2 and 3, i.e. by first extending HML with a divergence modality and then refining the weak possibility modality in the extended logic. We have the following findings:

• A. Extending HML with a new divergence modality one obtains a logic which characterizes complete weak bisimilarity, an equivalence relation with distinguishing power in between weak bisimilarity and branching bisimilarity with explicit divergence;

• B. Further extending the obtained logic by refining the weak possibility modality in it one obtains another logic which characterizes branching bisimilarity with explicit divergence.

To summarize the results of the paper:

• The above A. is the wanted result of modal characterization of complete weak bisimilarity.

• The two new logics in A. and B. are both sub-logics of the known logic mentioned in above 3, hence showing a clear picture of the sub-logic relationships of the corresponding characterization results.

• For finite-state systems, we also use the modal characterization to show a reduction from the problem of checking equality of complete weak bisimilarity to the problem of checking equality of ordinary weak bisimilarity, thus provide a decision procedure for the problem of checking equality of finite-state systems with respect to complete weak bisimilarity.

The rest of the paper is organized as follows. Section 2 presents the definitions of the equalities, i.e. weak bisimilarity, complete weak bisimilarity, branching bisimilarity, and branching bisimilarity with explicit divergence. Section 3 studies the relationships of the modal logic characterizations of the equalities. Section 4 studies reductions for decision problems concerning finite-state processes. Section 5 concludes.

2 Bisimulations and Divergence

In this section, after settling some necessary preliminaries, we introduce the main equivalence relation, i.e. complete weak bisimilarity, together with some related equivalences like branching bisimilarity and branching bisimilarity with explicit divergence.

Definition 1

(Labeled transition systems). A labeled transition system (or LTS) is a triple $\mathcal{A}=\langle S,A,{\mathop {\longrightarrow }\limits ^{}}\rangle$ where:

• S is a set of states, A is a set of actions, ${\mathop {\longrightarrow }\limits ^{}}\subseteq S\times (A\cup \{\tau \})\times S$ is the transition relation. $\tau$ is the silent action which is assumed not in A. An element $(s,\alpha ,t)$ of ${\mathop {\longrightarrow }\limits ^{}}$, usually written as $s{\mathop {\longrightarrow }\limits ^{\alpha }}t$, is called a transition;

• A finite run of $\mathcal{A}$ is a finite, nonempty alternating sequence of states and actions: $\rho =s_0\alpha _0s_1\alpha _1\ldots s_{n-1}\alpha _{n-1}s_n$ which begins with a state and ends with a state, such that for $0\le i< n$, $s_{i}{\mathop {\longrightarrow }\limits ^{\alpha _{i}}}s_{i+1}$. We also say that $\rho$ is a finite run from $s_0$ to $s_n$;

• For $\rho =s_0\alpha _0s_1\alpha _1\ldots s_{n-1}\alpha _{n-1}s_n$, define $\mathrm{Act}(\rho )=\alpha _0\alpha _1\ldots \alpha _{n-1},$ and $\mathrm{length}(\rho )=n;$

• An infinite run of $\mathcal{A}$ is an infinite, alternating sequence of states and actions: $\rho =s_0\alpha _0s_1\alpha _1\ldots$ which begins with a state, such that for all for $i=0,1,\ldots$, $s_{i}{\mathop {\longrightarrow }\limits ^{\alpha _{i}}}s_{i+1}$. We also say that $\rho$ is an infinite run from $s_0$;

• A (finite or infinite) $\tau$-run of $\mathcal{A}$ is a (finite or infinite) run of $\mathcal{A}$ in which all actions are $\tau$’s.

For a finite sequence of actions $l\in (A\cup \{\tau \})^*$, let $\widehat{l}\in A^*$ be the sequence obtained by deleting all $\tau$’s from l.

We use standard notations for multi-step $\tau$ transitions, and the so-called double-arrow transitions: write $s{\mathop {\Longrightarrow }\limits ^{}}s'$ if there is a finite $\tau$-run from s to $s'$; write $s{\mathop {\Longrightarrow }\limits ^{\alpha }}s'$ if there exist $t,t'$ such that $s{\mathop {\Longrightarrow }\limits ^{}}t,t{\mathop {\longrightarrow }\limits ^{\alpha }}t', t'{\mathop {\Longrightarrow }\limits ^{}}s'$. Note the important difference between $s{\mathop {\Longrightarrow }\limits ^{}}s'$ and $s{\mathop {\Longrightarrow }\limits ^{\tau }}s'$: the former means that from s to $s'$ there is a finite $\tau$-run (could be a $\tau$-run with zero length), while the latter means that from s to $s'$ there is a finite $\tau$-run with non-zero length. Thus $s{\mathop {\Longrightarrow }\limits ^{}}s$ holds for all $s\in S$, while $s{\mathop {\Longrightarrow }\limits ^{\tau }}s$ holds only when s is on a $\tau$-loop consisting of one or more $\tau$-transitions. Also for $l\in (A\cup \{\tau \})^*$ we will write $s{\mathop {\Longrightarrow }\limits ^{\widehat{l}}}s'$ if there is a finite run $\rho$ from s to $s'$ with $Act(\rho )=l$. Note that $s{\mathop {\Longrightarrow }\limits ^{\epsilon }}s'$ means exactly $s{\mathop {\Longrightarrow }\limits ^{}}s'$, where $\epsilon$ is the empty string.

Next, we review the well-known notions of weak bisimulation, weak bisimilarity [9], and branching bisimulation, branching bisimilarity [12].

Definition 2

(Weak and branching bisimulations). Let $\mathcal{A}=\langle S,A,{\mathop {\longrightarrow }\limits ^{}}\rangle$ be an LTS. A binary relation $R\subseteq S\times S$ is a weak bisimulation if it is symmetric and moreover for all $(s,t)\in R$ the following holds:

whenever $s{\mathop {\longrightarrow }\limits ^{\alpha }}s'$, then there exists $t'$ such that $t{\mathop {\Longrightarrow }\limits ^{\hat{\alpha }}}t'$ and $(s',t')\in R$.

A binary relation $R\subseteq S\times S$ is a branching bisimulation if it is symmetric and moreover for all $(s,t)\in R$ the following holds:

whenever $s{\mathop {\longrightarrow }\limits ^{\alpha }}s'$, then either $\alpha =\tau$, and there exists $t'$ such that $t{\mathop {\Longrightarrow }\limits ^{}}t'$ and $(s,t'), (s',t')\in R$, or there exist $t',t''$ such that $t{\mathop {\Longrightarrow }\limits ^{}}t',t'{\mathop {\longrightarrow }\limits ^{\alpha }}t''$ and $(s,t'),(s',t'')\in R$.

Now define two relations $\approx , \approx _b$ as follows:

$$\begin{aligned} \begin{array}{ccl} \approx &{}=&{}\bigcup \{ R \, | \, R \,\,{ is\,\, a \,\,weak\,\, bisimulation} \},\\ \approx _b&{}=&{}\bigcup \{ R \, | \, R\,\,{ is\,\, a\,\, branching \,\,bisimulation} \}. \end{array} \end{aligned}$$

The notions of weak and branching bisimulations enjoy some nice properties as stated in the following Lemmas 1 and 2, which then lead to the important Theorem 1 that justifies Definition 2.

Lemma 1

If $\{ R_i \, | \, i\in I \}$ is a set of weak bisimulations, then $\bigcup \{ R_i \, | \, i\in I \}$ is a weak bisimulation. If $\{ R_i \, | \, i\in I \}$ is a set of branching bisimulations, then $\bigcup \{ R_i \, | \, i\in I \}$ is a branching bisimulation.

For two binary relations $R_1,R_2$, we write $R_1\cdot R_2$ for the composition of $R_1$ and $R_2$, i.e. $R_1\cdot R_2=\{ (s,t) \, | \, \exists u.(s,u)\in R_1,(u,t)\in R_2 \}$.

Lemma 2

If $R_1,R_2$ are weak bisimulations, then $R_1\cdot R_2\cup R_2\cdot R_1$ is also a weak bisimulation. If $R_1,R_2$ are branching bisimulations, then $R_1\cdot R_2\cup R_2\cdot R_1$ is also a branching bisimulation.

The proofs of the above two lemmas directly follow from Definition 2 (Note that we modified the conditions for branching bisimulation as in [11]). With the above two lemmas, it is routine to prove the following theorem, which justifies the definitions of $\approx$ and $\approx _b$.

Theorem 1

$\approx$ is an equivalence relation, and it is the largest weak bisimulation. $\approx _b$ is an equivalence relation, and it is the largest branching bisimulation.

With Theorem 1, $\approx$ and $\approx _b$ are usually called weak bisimilarity and branching bisimilarity respectively.

It is well-known that neither $\approx$ nor $\approx _b$ preserves divergence, i.e. it is possible for two states s and t such that $s\approx t$ while there is an infinite $\tau$-run from s but no infinite $\tau$-run from t.

In order to obtain divergence preserving relations, we can adopt the approach used in [12] by introducing the following definition.

Definition 3

(Weak and branching bisimulation with explicit divergence). Let $\mathcal{A}=\langle { S,A,{\mathop {\longrightarrow }\limits ^{}}}\rangle$ be an LTS. A state $s\in S$ is said divergent with respect to an equivalence relation $\equiv$, written $s\Uparrow _\equiv$, if from s there is an infinite $\tau$-run $\rho$ such that all the states on $\rho$ are $\equiv$-equivalent to s.

An equivalence relation $\equiv$ on S is called a weak bisimulation with explicit divergence if $\equiv$ is a weak bisimulation and moreover whenever $s\equiv t$ it holds that $s\Uparrow _\equiv$ if and only if $t\Uparrow _\equiv$.

An equivalence relation $\equiv$ on S is called a branching bisimulation with explicit divergence if $\equiv$ is a branching bisimulation and moreover whenever $s\equiv t$ it holds that $s\Uparrow _\equiv$ if and only if $t\Uparrow _\equiv$.

Now define two relations $\approx ^\triangle , \approx _b^\triangle$ as follows:

$$\begin{aligned} \begin{array}{ccl} \approx ^\triangle &{}=&{}\bigcup \{ \equiv \, | \, \equiv \,\,{ is\,\, a\,\, weak \,\,bisimulation\,\, with \,\,explicit \,\,divergence} \},\\ \approx _b^\triangle &{}=&{}\bigcup \{ \equiv \, | \, \equiv \,\,{ is\,\, a\,\, branching\,\, bisimulation \,\,with \,\,explicit \,\,divergence} \}. \end{array} \end{aligned}$$

$\approx ^\triangle$ and $\approx _b^\triangle$ are called weak bisimilarity with explicit divergence and branching bisimilarity with explicit divergence respectively.

At this point, let us see a non-trivial example of branching bisimulation with explicit divergence. Define $\equiv _{sc}$, the strongly connected relation, such that $s\equiv _{sc}t$ if and only if $s{\mathop {\Longrightarrow }\limits ^{}}t$ and $t{\mathop {\Longrightarrow }\limits ^{}}s$. That is $s\equiv _{sc}t$ just in case s and t can reach each other by performing $\tau$ actions. It only takes a second to check that $\equiv _{sc}$ is an equivalence relation. Moreover we have:

Proposition 1

$\equiv _{sc}$ is a branching bisimulation with explicit divergence.

The following lemma is easy to prove.

Lemma 3

If $\equiv$ is a weak bisimulation with explicit divergence, then $\equiv$ preserves divergence, i.e. whenever $s\equiv t$ then there is an infinite $\tau$-run from s if and only if there is one from t.

With this lemma, we can show that $\approx ^\triangle$ preserves divergence as follows. If $\rho$ is an infinite $\tau$-run from s and $s\approx ^\triangle t$, then there is a weak bisimulation with explicit divergence $\equiv$ such that $s\equiv t$, then by Lemma 3 there is an infinite $\tau$-run from t, thus $\approx ^\triangle$ preserves divergence. One is tempting to say that with Lemma 3, $\approx ^\triangle$ obviously preserves divergence, since $\approx ^\triangle$ is a weak bisimulation with explicit divergence. However, to apply Lemma 3 in this way, we first have to prove that $\approx ^\triangle$ is a weak bisimulation with explicit divergence, and at least for the moment we do not know if this is indeed the case.

Thus, as the definitions of $\approx$ and $\approx _b$ are justified by Theorem 1, the definitions of $\approx ^\triangle$ and $\approx ^\triangle _b$ also need justification. That is to say we need to confirm that $\approx ^\triangle$ as defined is indeed the largest weak bisimulation with explicit divergence and, $\approx ^\triangle _b$ the largest branching bisimulation with explicit divergence (as it is stated in the definition we even do not know whether $\approx ^\triangle$ and $\approx ^\triangle _b$ are equivalence relations!). But this time the task is not as easy, since we no longer have the corresponding lemmas available as Lemmas 1 and 2 for Theorem 1. As a matter of fact this implies that we do not know whether the notion of weak bisimulation with explicit divergence is a fixed-point of some monotonic functions on the complete lattice of equivalence relations, and hence the Knaster-Tarski fixed-point theorem is not applicable in this case. Thus we need to find a different way to justify Definition 3. For the time being we have the following obvious lemma, which clarifies the justification task.

Lemma 4

$\approx ^\triangle$ ($\approx ^\triangle _b$) is the largest weak (branching) bisimulation with explicit divergence if and only if the largest weak (branching) bisimulation with explicit divergence exists.

Justification of the definition of $\approx _b^\triangle$ can be found in [13, 14], while not in [12] where it was introduced the first time. While a justification for $\approx ^\triangle _b$ might be taken as granted, a justification for $\approx ^\triangle$ may seem to be more necessary. This is because in a weak bisimulation equivalence relation, unlike branching bisimulation, an infinite $\tau$-run from a process may be matched by an infinite $\tau$-run from a related process in a way that the sequences of equivalence classes passed through by the two runs may not be the same. So one needs to be more careful in dealing with $\approx ^\triangle$. According to Lemma 4, in order to prove that $\approx ^\triangle$ is a weak bisimulation with explicit divergence we only need to show that the largest weak bisimulation with explicit divergence exists. This approach was taken in [10], where two relations called complete weak bisimilarity and complete branching bisimilarity were constructed and proved to be the largest weak bisimulation with explicit divergence and largest branching bisimulation with explicit divergence respectively. In this paper, for self containment we will present a justification of the definition of $\approx ^\triangle$ in the next section, by using the logical characterization result. For the convenience of names, in the paper we will freely use the name of complete weak (branching) bisimilarity as synonym for weak (branching) bisimilarity with explicit divergence.

3 Modal Characterization

The main aims of this section is to look for a modal logic characterization of complete weak bisimilarity $\approx ^\triangle$, and study its relationship with logic characterizations of other bisimulation equivalences. For that, we first review some of the existing logic characterization results.

In [2] a modal logic, later known as Hennessy-Milner logic (HML), was introduced and proved that two given processes are equivalent under weak bisimularity $\approx$ if and only if they satisfy the same set of HML formulas. This is the so-called Hennessy-Milner theorem. The key constructor in HML is the weak possibility modality $\langle \!\langle u\rangle \!\rangle F$, which asserts that after the observation of u some state with property F is reached. In [6], the weak possibility modality was refined to an until modality in the form of $F_1\langle \alpha \rangle F_2$, meaning that there is a finite $\tau$-run such that all the states on it satisfy $F_1$, and the last state can perform an $\alpha$ action and arrives at a state satisfying $F_2$, and it was proved that the refined logic characterizes branching bisimilarity $\approx _b$, just as HML characterizes weak bisimilarity. In [5] the weak possibility modality was refined to a just-before modality in the form of $F_1\{\alpha \}F_2$, meaning that there is a finite $\tau$-run such that the last state satisfies $F_1$ and can perform an $\alpha$ action and arrives at a state satisfying $F_2$, and it was proved that the refined logic, named $\varPhi _{jb}$, also characterizes branching bisimilarity $\approx _b$. In [13], $\varPhi _{jb}$ was further extended to the logic $\varPhi _{jb}^\triangle$ with a divergence modality in the form of $\varDelta F$, meaning that there is an infinite $\tau$-run on which eventually all the states satisfy F, and it was proved that $\varPhi _{jb}^\triangle$ characterizes branching bisimilarity with explicit divergence $\approx _b^\triangle$.

As the starting point of the work of this paper, we describe a modal logic HMLb$\varDelta$ which is basically $\varPhi _{jb}^\triangle$ with a derived operator $\langle \!\langle u\rangle \!\rangle$. The set of formulas of HMLb$\varDelta$ is defined by the following syntax of BNF rules:

where I is an index set which could be infinite, $\{u\}$ (with $u\in A\cup \{\epsilon \}$) is the just-before modality introduced in [5], $\langle \!\langle u\rangle \!\rangle$ is the usual weak possibility modality as in [9], and $\varDelta$ is the divergence modality introduced in [13].

Definition 4

Let $\mathcal{A}=\langle S,A,{\mathop {\longrightarrow }\limits ^{}}\rangle$ be an LTS. The satisfaction relation $\models$ between states and formulas of HMLb$\varDelta$ is defined by induction on the structure of formulas as follows:

• 1. $s\models \bigwedge _{i\in I}F_i$ if, for all $i\in I$, $s\models F_i$;

• 2. $s\models \lnot F$ if $s\models F$ does not hold;

• 3. $s\models F_1\{u\}F_2$ if there exist $t,t'\in S$ such that $t\models F_1,t'\models F_2$, $s{\mathop {\Longrightarrow }\limits ^{}}t$ and ($t{\mathop {\longrightarrow }\limits ^{u}}t'$ (when $u\in A$) or $t{\mathop {\longrightarrow }\limits ^{\tau }}t'$ (when $u=\epsilon$)) or there is $t\in S$ such that $t\models F_1, t\models F_2$, $s{\mathop {\Longrightarrow }\limits ^{}}t$ and $u=\epsilon$;

• 4. $s\models \langle \!\langle u\rangle \!\rangle F$ if there is $t\in S$ such that $s{\mathop {\Longrightarrow }\limits ^{u}}t$ and $t\models F$;

• 5. $s\models \varDelta F$ if there is an infinite $\tau$-run $\sigma$ from s such that $\sigma =s\tau s_1\tau s_2\ldots s_i\tau \ldots$ and there is $n>0$ such that $s_i\models F$ for all $i\ge n$ (in other words, there are only finitely many positions on $\sigma$ where F does not hold).

First note that this logic can express some interesting properties of infinite behaviours of processes. For example, $\varDelta \mathbf{true}$ asserts the existence of an infinite $\tau$-run, where $\mathbf{true}$ is a short hand for $\bigwedge _{i\in \emptyset }F_i$ (which is the first formula of HMLb$\varDelta$ according to the BNF rules). The logic is basic, however it might be more expressive than one expect due to the use of infinite conjunction with the construction $\bigwedge _{i\in I}F_i$ when I is an infinite set.

As usual we will write binary conjunction $F_1\wedge F_2$ for $\bigwedge _{i\in \{1,2\}}F_i$, and binary disjunction $F_1\vee F_2$ for $\lnot \bigwedge _{i\in \{1,2\}}\lnot F_i$. For two HMLb$\varDelta$ formulas $F_1,F_2$, we say that $F_1$ and $F_2$ are equivalent logic formulas, written $F_1\Leftrightarrow F_2$, if for any process s of any LTS it holds that $s\models F_1$ if and only if $s\models F_2$.

The following proposition shows that $\langle \!\langle u\rangle \!\rangle$ is a derived operator in the sense that it can be defined in terms of the just-before operator $\{u\}$.

Proposition 2

For any HMLb$\varDelta$ formula F and $a\not =\tau$, the following equivalences hold:

• 1. $\langle \!\langle \epsilon \rangle \!\rangle F\Leftrightarrow \mathbf{true}\{\epsilon \}F$;

• 2. $\langle \!\langle a\rangle \!\rangle F\Leftrightarrow \mathbf{true}\{a\}(\mathbf{true}\{\epsilon \}F)$.

Proof

Immediately follows from Definition 4.    $\square$

We write HMLb for the sub-logic of HMLb$\varDelta$ which consists of formulas constructed without the divergence modality $\varDelta$. Then HML, the normal Hennessy-Milner logic, is a sub-logic of HMLb consisting of formulas constructed without the just-before modality $\{u\}$. With the result in Proposition 2 that $\langle \!\langle u\rangle \!\rangle$ is a derived operator of $\{u\}$, then the following is a theorem which immediately follows from the characterization result for $\varPhi ^\triangle _{jb}$ in [13].

Theorem 2

(HMLb$\varDelta$ characterization of $\approx _b^\triangle$). Let s, t be two states. Then $s\approx _b^\triangle t$ if and only if s and t satisfy the same set of HMLb$\varDelta$ formulas.

Likewise, the following is a theorem immediately follows from the characterization result for $\varPhi _{jb}$ in [5].

Theorem 3

(HMLb characterization of $\approx _b$). Let s, t be two states. Then $s\approx _bt$ if and only if s and t satisfy the same set of HMLb formulas.

The following is the famous Hennessy-Milner theorem, which can be found in Chap. 10 of [9].

Theorem 4

(HML characterization of $\approx$). Let s, t be two states. Then $s\approx t$ if and only if s and t satisfy the same set of HML formulas.

The last three theorems give modal logic characterizations for $\approx ^\triangle _b, \approx _b$ and $\approx$ respectively, still missing is a modal logic characterization for $\approx ^\triangle$. Considering that HMLb is the extension of HML by the just-before modality and that HMLb$\varDelta$ is the extension of HML by the just-before and the divergence modality, an obvious attempt is to extend HML with the divergence modality and hopefully that will give us a logic which characterizes $\approx ^\triangle$. However it turns out that the divergence construction $\varDelta F$ is not preserved by $\approx ^\triangle$, as the following example shows.

Example 1

The drawing shows an LTS $\mathcal{P}=\langle S,A,{\mathop {\longrightarrow }\limits ^{}}\rangle$ where $A=\{ a_i \, | \, i\ge 0 \}$, $S=\{ s_i \, | \, i\ge 0 \}\cup \{ t_i \, | \, i\ge 0 \}$, and the transition relation is as follows:

• for each $i\ge 0$, if i is even then there are exactly three transitions out of $s_i$:

  $s_i{\mathop {\longrightarrow }\limits ^{a_i}}s_{i}, s_i{\mathop {\longrightarrow }\limits ^{\tau }}s_{i+1}, s_i{\mathop {\longrightarrow }\limits ^{\tau }}s_{i+2}$;

  if i is odd then there are exactly two transitions out of $s_i$:

  $s_i{\mathop {\longrightarrow }\limits ^{a_i}}s_{i}, s_i{\mathop {\longrightarrow }\limits ^{\tau }}s_{i+1}$.

• for each $i\ge 0$, there are exactly two transitions out of $t_i$:

  $t_i{\mathop {\longrightarrow }\limits ^{a_i}}t_i, t_i{\mathop {\longrightarrow }\limits ^{\tau }}t_{i+1}$.

Now define $\equiv$ to be the following relation:

$$\{ (s_i,s_i) \, | \, i\ge 0 \}\cup \{ (t_i,t_i) \, | \, i\ge 0 \}\cup \{ (s_i,t_i) \, | \, i\ge 0 \} \cup \{ (t_i,s_i) \, | \, i\ge 0 \}.$$

The following facts about $\equiv$ are easy to verify:

• 1. $\equiv$ is an equivalence relation;

• 2. $\equiv$ is a weak bisimulation;

• 3. for every $s\in S$, whenever $s{\mathop {\longrightarrow }\limits ^{\tau }}t$ then $s\not \equiv t$. Hence whenever $s\equiv t$ then $s\Uparrow _\equiv$ if and only if $t\Uparrow _\equiv$.

Thus $\equiv$ is a weak bisimulation with explicit divergence, and $s_0\approx ^\triangle t_0$. In the following we show that there is an HML formula F such that $\varDelta F$ is satisfied by $s_0$ and not by $t_0$.

Let $F_k$ be the following formula:

$$\begin{aligned} (\langle \!\langle a_{2k}\rangle \!\rangle \mathbf{true}\wedge \langle \!\langle a_{2k+1}\rangle \!\rangle \mathbf{true}) \vee (\lnot \langle \!\langle a_{2k}\rangle \!\rangle \mathbf{true}\wedge \lnot \langle \!\langle a_{2k+1}\rangle \!\rangle \mathbf{true}). \end{aligned}$$

That is, $F_{k}$ asserts that the pair of actions $a_{2k}$ and $a_{2k+1}$ are either both enabled or both disabled. It is clear that $F_k$ holds for every state of S except $s_{2k+1}$ and $t_{2k+1}$. Thus $\bigwedge \{ F_k \, | \, k\ge 0 \}$ holds on every even numbered position (i.e. $s_0,t_0,s_2,t_2,\ldots$) while does not hold on every odd numbered position (i.e. $s_1,t_1,s_3,t_3,\ldots$).

Now $\varDelta \bigwedge \{ F_k \, | \, k\ge 0 \}$ is satisfied by $s_0$ but not by $t_0$. To see that, note that from $s_0$ there is an infinite $\tau$-run $\sigma =s_0\tau s_2\tau \ldots s_{2k}\tau \ldots$ and every state on $\sigma$ satisfies $\bigwedge \{ F_k \, | \, k\ge 0 \}$, while the only infinite $\tau$-run from $t_0$ is $t_0\tau t_1\tau \ldots$, on which there are infinitely many states that do not satisfy $\bigwedge \{ F_k \, | \, k\ge 0 \}$.    $\square$

Thus, we need to find a different divergence modality. For that we introduce the weak divergence modality $\varDelta _\epsilon$ into HMLb$\varDelta$, by extending the BNF rules as follows:

$$ F{::}=\ldots |\ \varDelta _\epsilon F. $$

And then add the following interpretation into Definition 4.

• 6. $s\models \varDelta _\epsilon F$ if there is an infinite $\tau$-run $\sigma$ from s such that for every state $s'$ on $\sigma$ it holds that $s'{\mathop {\Longrightarrow }\limits ^{}}t$ for some $t\models F$.

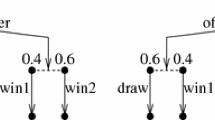
The following is a depiction of the condition for $s\models \varDelta _\epsilon F$.

Proposition 3

For any HMLb$\varDelta$ formula F, the following equivalence holds:

$$\varDelta _\epsilon F\Leftrightarrow \varDelta \langle \!\langle \epsilon \rangle \!\rangle F.$$

Proof

Immediately follows from Definition 4 together with the above interpretation for $\varDelta _\epsilon F$.    $\square$

This proposition shows that $\varDelta _\epsilon$ is a derived operator of $\varDelta$ and $\langle \!\langle \epsilon \rangle \!\rangle$, and that with $\varDelta _\epsilon$ added into HMLb$\varDelta$ the expressiveness of the extended logic does not increase. So we still call the logic HMLb$\varDelta$ after extending with $\varDelta _\epsilon$, and we write HML$\varDelta _\epsilon$ for the sub-logic where the only modalities allowed are the weak possibility modality $\langle \!\langle u\rangle \!\rangle$ and the weak divergence modality $\varDelta _\epsilon$. With the new divergence modality we can obtain another sub-logic HMLb$\varDelta _\epsilon$ in which $\varDelta _\epsilon$ is allowed but not $\varDelta$.

Given a sub-logic L of HMLb$\varDelta$, it induces an equivalence relation $\equiv _L$ on states such that $s\equiv _Lt$ if and only if s and t satisfy the same set of formulas in the sub-logic. We call $\equiv _L$ the equivalence induced by L. The following is a summary of the sub-logics of HMLb$\varDelta$ that we concerned about and the corresponding induced equivalences:

• 1. Let $\equiv _b^\triangle$ be the equivalence induced by HMLb$\varDelta$;

• 2. Let $\equiv _b$ be the equivalence induced by HMLb;

• 3. Let $\equiv _w$ be the equivalence induced by HML;

• 4. Let $\equiv _w^{\triangle _\epsilon }$ be the equivalence induced by HML$\varDelta _\epsilon$;

• 5. Let $\equiv _b^{\triangle _\epsilon }$ be the equivalence induced by HMLb$\varDelta _\epsilon$.

In the rest of this section we will show that HML$\varDelta _\epsilon$ characterizes $\approx ^\triangle$, i.e. $\approx ^\triangle$ coincides with $\equiv ^{\triangle _\epsilon }_w$. To prove $\approx ^\triangle \subseteq \equiv ^{\triangle _\epsilon }_w$, we show that for every weak bisimulation with explicit divergence $\equiv$ it holds that $\equiv \subseteq \equiv ^{\triangle _\epsilon }_w$ (Lemma 5). To prove $\equiv ^{\triangle _\epsilon }_w\subseteq \approx ^\triangle$, we show that $\equiv ^{\triangle _\epsilon }_w$ is a weak bisimulation with explicit divergence (Lemma 8).

Example 1 shows what $\varDelta F$ is not preserved by $\approx ^\triangle$, while the following lemma guarantees that $\varDelta _\epsilon F$ is preserved by $\approx ^{\triangle }$. Here we omit the proof.

Lemma 5

Let $\equiv$ be a weak bisimulation with explicit divergence, F be an HML$\varDelta _\epsilon$ formula. If $s\equiv t$ and $s\models F$, then $t\models F$. Thus if $\equiv$ is a weak bisimulation with explicit divergence then $\equiv \subseteq \equiv ^{\triangle _\epsilon }_w$.

Lemma 6

Let $s{\mathop {\Longrightarrow }\limits ^{}}t$. Then

• 1. whenever $t\models F_1\{u\}F_2$ then $s\models F_1\{u\} F_2$;

• 2. whenever $t\models \langle \!\langle u\rangle \!\rangle F$ then $s\models \langle \!\langle u\rangle \!\rangle F$;

• 3. whenever $t\models \varDelta _\epsilon F$ then $s\models \varDelta _\epsilon F$.

Proof

We only prove 3. With the similar idea we can prove 1 and 2.

Suppose $t\models \varDelta _\epsilon F$. Thus from t there is an infinite $\tau$-run $\rho$ such that for each state $t'$ on $\rho$ there exists $t''$ with $t'{\mathop {\Longrightarrow }\limits ^{}}t''$ and $t''\models F$. Now since $s{\mathop {\Longrightarrow }\limits ^{}}t$, by adding a prefix to $\rho$ we can easily obtain an infinite run $\rho '$ with starting state s such that for each state $t'$ on $\rho '$ there exists $t''$ with $t'{\mathop {\Longrightarrow }\limits ^{}}t''$ and $t''\models F$, hence $s\models \varDelta _\epsilon F$.    $\square$

The following is the so-called stuttering lemma for $\equiv ^{\triangle _\epsilon }_w$.

Lemma 7

If $s{\mathop {\Longrightarrow }\limits ^{}}s',s'{\mathop {\Longrightarrow }\limits ^{}}t,$ and $s\equiv ^{\triangle _\epsilon }_wt$ then $s\equiv ^{\triangle _\epsilon }_ws'$.

Proof

In this case we only need to prove the following: for any HML$\varDelta _\epsilon$ formula F, it holds that $s\models F$ if and only if $s'\models F$. We carry out the proof by induction on the structure of F.

For $\bigwedge _{i\in I}F_i$, we have the following sequence of equivalences: $s\models \bigwedge _{i\in I}F_i$ iff $s\models F_i\hbox { for every }i\in I$ (by definition of $\models$) iff $s'\models F_i\hbox { for every }i\in I$ (by induction hypothesis) iff $s'\models \bigwedge _{i\in I}F_i$ (by definition of $\models$). In the same way we can prove it for the case $\lnot F$.

For $\langle \!\langle u\rangle \!\rangle F$, suppose $s\models \langle \!\langle u\rangle \!\rangle F$. Then $t\models \langle \!\langle u\rangle \!\rangle F$ by $s\equiv _w^{\triangle _\epsilon }t$, then it immediately follows that $s'\models \langle \!\langle u\rangle \!\rangle F$ by $s'{\mathop {\Longrightarrow }\limits ^{}}t$ and Lemma 6. On the other hand, suppose $s'\models \langle \!\langle u\rangle \!\rangle F$, then $s\models \langle \!\langle u\rangle \!\rangle F$ immediately follows by $s{\mathop {\Longrightarrow }\limits ^{}}s'$ and Lemma 6. In the same way we can prove it for the case $\varDelta _\epsilon F$.    $\square$

Lemma 8

$\equiv ^{\triangle _\epsilon }_w$ is a weak bisimulation with explicit divergence.

Proof

To prove that $\equiv ^{\triangle _\epsilon }_w$ is a weak bisimulation with explicit divergence, we need to establish the following:

• 1. $\equiv ^{\triangle _\epsilon }_w$ is an equivalence relation;

• 2. $\equiv ^{\triangle _\epsilon }_w$ is a weak bisimulation;

• 3. if $s\equiv ^{\triangle _\epsilon }_w t$, then $s\Uparrow _{\equiv ^{\triangle _\epsilon }_w}$ iff $t\Uparrow _{\equiv ^{\triangle _\epsilon }_w}$.

It is obvious that $\equiv ^{\triangle _\epsilon }_w$ is an equivalence relation. The way to prove that $\equiv ^{\triangle _\epsilon }_w$ is a weak bisimulation is exactly the same as the way to prove that $\equiv _w$ is a weak bisimulation [9]. We prove 3. in the following.

First, let us note that for a pair of states s, t with $s\not \equiv ^{\triangle _\epsilon }_w t$, by the definition of $\equiv ^{\triangle _\epsilon }_w$ there exists an HML$\varDelta _\epsilon$ formula $F^s_t$, which is often called a distinguishing formula of s and t, such that $s\models F^s_t$ and .

Suppose $s\equiv ^{\triangle _\epsilon }_w t$, and $s\Uparrow _{\equiv ^{\triangle _\epsilon }_w}$, then there is an infinite $\tau$-run $\rho$ from s with all the states on it $\equiv ^{\triangle _\epsilon }_w$-equivalent to s. We construct the following formula $F^s$

$$\begin{aligned} \bigwedge \{ F^{s}_u \, | \, t{\mathop {\Longrightarrow }\limits ^{\tau }}u,u\not \equiv ^{\triangle _\epsilon }_ws \}. \end{aligned}$$

Clearly $s\models F^s$. Moreover $s\models \varDelta _\epsilon F^s$, since for any state $s'$ on $\rho$, there is $s''$ such that $s'{\mathop {\Longrightarrow }\limits ^{}}s''$ and $s''\models F^s$ (just take $s''$ to be $s'$, thus $s'{\mathop {\Longrightarrow }\limits ^{}}s'$, and $s'\models F^s$ by $s'\equiv ^{\triangle _\epsilon }_ws$). Now because $t\equiv ^{\triangle _\epsilon }_w s$, thus $t\models \varDelta _\epsilon F^s$. In the following we will show that $t\models \varDelta _\epsilon F^s$ implies $t\Uparrow _{\equiv ^{\triangle _\epsilon }_w}$.

Since $t\models \varDelta _\epsilon F^s$, there is an infinite $\tau$-run $\sigma$ from t such that for any state $t'$ on $\sigma$ there exists $t''$ with $t'{\mathop {\Longrightarrow }\limits ^{}}t''$ and $t''\models F^s$. Now we will show that if $t'$ is a state on $\rho$ then $t'\equiv ^{\triangle _\epsilon }_w t$.

Note that the construction of $F^s$ guarantees the following property:

if $t{\mathop {\Longrightarrow }\limits ^{}}t'$ and $t'\models F^{s}$ then $t'\equiv ^{\triangle _\epsilon }_wt$.

To see that, let $t{\mathop {\Longrightarrow }\limits ^{\tau }}t'$. Suppose $t'\not \equiv ^{\triangle _\epsilon }_w t$, then , which implies because in this case $F^{s}_{t'}$, which is a distinguishing formula of s and $t'$, is one of the conjuncts of $F^{s}$, and .

Now for any state $t'$ on $\sigma$, since $t{\mathop {\Longrightarrow }\limits ^{}}t'$ and $t'{\mathop {\Longrightarrow }\limits ^{}}t''$ for some $t''$ with $t''\models F^s$, and by the above property of $F^s$ we know that $t''\equiv ^{\triangle _\epsilon }_w t$, then by Lemma 7 $t'\equiv ^{\triangle _\epsilon }_w t$, thus $\sigma$ is the infinite $\tau$-run that we are looking for.    $\square$

At last, we can state the modal characterization theorem for $\approx ^\triangle$.

Theorem 5

(HML$\varDelta _\epsilon$ characterization of $\approx ^\triangle$) $\equiv ^{\triangle _\epsilon }_w$coincides with $\approx ^\triangle$, that is for any pair of states s and t, $s\approx ^\triangle t$ if and only if s and t satisfy the same set of HML$\varDelta _\epsilon$ formulas.

Proof

By Lemma 5, $\approx ^\triangle \subseteq \equiv ^{\triangle _\epsilon }_w$, and by Lemma 8 $\equiv ^{\triangle _\epsilon }_w$ is a weak bisimulation with explicit divergence, hence $\equiv ^{\triangle _\epsilon }_w\subseteq \approx ^\triangle$.    $\square$

And at the same time we obtain the following theorem which justifies the definition of $\approx ^\triangle$.

Theorem 6

$\approx ^\triangle$ is a weak bisimulation with explicit divergence, and it is the largest weak bisimulation with explicit divergence.

Proof

By Lemmas 5 and 8, $\equiv ^{\triangle _\epsilon }_w$ is the largest weak bisimulation with explicit divergence. By Theorem 5 $\approx ^\triangle$ is the same as $\equiv ^{\triangle _\epsilon }_w$, hence $\approx ^\triangle$ is the largest weak bisimulation with explicit divergence.    $\square$

Perhaps a little surprise is the following new modal characterization result for branching bisimilarity with explicit divergence $\approx ^\triangle _b$.

Theorem 7

(HMLb$\varDelta _\epsilon$ characterization of $\approx _b^\triangle$). Let s, t be two states. Then $s\approx _b^\triangle t$ if and only if s and t satisfy the same set of HMLb$\varDelta _\epsilon$ formulas.

Proof

Here we give the following sketch.

Suppose $s\approx _b^{\triangle }t$ and $s\models F$ for some HMLb$\varDelta _\epsilon$ formula F, just note that by Proposition 3 there is an HMLb$\varDelta$ formula $F'$ with $F'\Leftrightarrow F$, then $s\models F'$ and by Theorem 2 $t\models F'$ thus $t\models F$.

For the other direction, we prove that $\equiv ^{\triangle _\epsilon }_b$ is a branching bisimulation with explicit divergence. We can prove that $\equiv ^{\triangle _\epsilon }_b$ is a branching bisimulation in the same way to prove that $\equiv _b$ is a branching bisimulation as the proof of Theorem 3 in [5]. Suppose $s\equiv ^{\triangle _\epsilon }_bt$ and there is an infinite $\tau$-run from s with all the states on the run in the same $\equiv ^{\triangle _\epsilon }_b$-equivalence class of s, we can prove that there is an infinite $\tau$-run from t with all the states on the run in the same $\equiv ^{\triangle _\epsilon }_b$-equivalence class of t as we prove it for $\equiv ^{\triangle _\epsilon }_w$ in Lemma 8, with the help of a lemma similar to Lemma 7 with $\equiv ^{\triangle _\epsilon }_b$ in place of $\equiv ^{\triangle _\epsilon }_w$.    $\square$

By Theorems 2 and 7, HMLb$\varDelta$ and HMLb$\varDelta _\epsilon$ both characterize $\approx _b^\triangle$. Now the results about the relationships of various bisimulation equivalence relations and the logics can be summarized as the above lattice shaped diagrams, where on the left the equality on the higher end of an edge is included in the equality on the lower end of the edge, and on the right the logic on the lower end of an edge is a sub-logic of the one on the higher end of the edge, and the dotted lines represent the logic characterization results.

4 Divergence in Finite State Systems

The motivating problem of this section is the problem of checking complete weak bisimilarity for finite-state processes:

given an LTS $\langle S,A,{\mathop {\longrightarrow }\limits ^{}}\rangle$ and two states $s,t\in S$, where S and A are finite sets, decide whether $s\approx ^\triangle t$.

We will show that this problem can be solved by reducing it to the problem of checking weak bisimilarity for finite-state processes which can be solved by a well-known partition algorithm [7]:

given an LTS $\langle S,A,{\mathop {\longrightarrow }\limits ^{}}\rangle$ and two states $s,t\in S$, where S and A are finite sets, decide whether $s\approx t$.

The reduction is as follows. Let $\mathcal{P}=\langle S,A,{\mathop {\longrightarrow }\limits ^{}}\rangle$ be a finite-state labeled transition system, i.e. both S and A are finite sets, $\delta$ be an action not in A. Then we can construct a new finite-state LTS $\mathcal{P}_\delta =\langle \widehat{S}, \widehat{A},{\mathop {\longrightarrow }\limits ^{}}'\rangle$ where $\widehat{S}=\{ \hat{s} \, | \, s\in S \}$, $\widehat{A}=A\cup \{\delta \}$, ${\mathop {\longrightarrow }\limits ^{}}'=\{ (\hat{s},\alpha ,\hat{s}') \, | \, s{\mathop {\longrightarrow }\limits ^{\alpha }}s' \}\cup \{ (\hat{s},\delta ,\hat{s}) \, | \, s{\mathop {\Longrightarrow }\limits ^{\tau }}s \}$.

The idea of the reduction is pretty straightforward: in a finite-state system, the existence of an infinite $\tau$-run from a state s is equivalent to the existence of a so-called looping state $s'$ such that $s{\mathop {\Longrightarrow }\limits ^{}}s'$ and $s'{\mathop {\Longrightarrow }\limits ^{\tau }}s'$, and then the looping states can be marked by a particular new action $\delta$. Thus the transitions of the constructed system $\mathcal{P}_\delta$ is like the original system $\mathcal{P}$ except that every looping state s is indicated by a new transition $\hat{s}{\mathop {\longrightarrow }\limits ^{\delta }}{}'\hat{s}$. In the following when there will cause no confusion we will simply write $\hat{s}{\mathop {\longrightarrow }\limits ^{\alpha }}\hat{t}$ instead of $\hat{s}{\mathop {\longrightarrow }\limits ^{\alpha }}{}'\hat{t}$ for $s,t\in S$.

Now to complete the reduction, we will show that for any $s,t\in S$, it holds that $s\approx ^\triangle t$ if and only if $\hat{s}\approx \hat{t}$. Then in order to check whether $s\approx ^\triangle t$ we only need to check whether $\hat{s}\approx \hat{t}$. For any $s,t\in S$, in order to show that $s\approx ^\triangle t$ if and only if $\hat{s}\approx \hat{t}$, we can show that $\equiv \subseteq S\times S$ is a weak bisimulation with explicit divergence if and only if $\widehat{\equiv }=\{ (\hat{s},\hat{t}) \, | \, s\equiv t \}$ is a weak bisimulation. However, with the logic characterization results of the last section, here we will take a different approach which reveals essential properties of the reduction construction as stated in the following Theorems 8 and 9 and allows us to obtain more general results as stated in the following Theorem 10.

We define a translation function $^{\overline{\ \ }}$ which maps every HMLb$\varDelta$ formula F to another HMLb$\varDelta$ formula $\overline{F}$. The function is inductively defined on the structure of the formula as follows:

Theorem 8

If F is an HMLb$\varDelta$ formula, then $\overline{F}$ is an HMLb formula. Moreover if F is an HML$\varDelta _\epsilon$ formula, then $\overline{F}$ is an HML formula.

For a finite-state LTS $\mathcal{P}=\langle S,A,{\mathop {\longrightarrow }\limits ^{}}\rangle$, let $\mathcal{P}_\delta =\langle \widehat{S}, A,{\mathop {\longrightarrow }\limits ^{}}'\rangle$ be the finite-state LTS constructed above, $s\in S$. Then for any HMLb$\varDelta$ formula F, it holds that $s\models F$ if and only if $\hat{s}\models \overline{F}$.

The proof, which is omitted here, is a routine induction on the structure of the formulas. Here we just explain the idea behind the translation function $^{\overline{\ \ }}$ from which one can see the rationale behind Theorem 8. The key is to understand why $F_1\{\delta \}F_2$ is translated to $\lnot \mathbf{true}$. As we have pointed out above, $\delta$ is an action which is not in A and which is used in the reduction to mark divergence. That implies that any process s from $\mathcal{P}$ is not capable of an $\delta$ action, hence the property $F_1\{\delta \}F_2$ will never be satisfied by any process from $\mathcal{P}$. That is why $F_1\{\delta \}F_2$ is translated to $\lnot \mathbf{true}$. For the same reason $\langle \!\langle \delta \rangle \!\rangle F$ is also translated to $\lnot \mathbf{true}$.

Also, we can define a translation function $\underline{\ \ }$ which maps every HMLb formula F to an HMLb$\varDelta$ formula $\underline{F}$. The function is inductively defined on the structure of the formula as follows:

Theorem 9

If F is an HMLb formula, then $\underline{F}$ is an HMLb$\varDelta$ formula. Moreover if F is an HML formula, then $\underline{F}$ is an HML$\varDelta _\epsilon$ formula.

For a finite-state LTS $\mathcal{P}=\langle S,A,{\mathop {\longrightarrow }\limits ^{}}\rangle$, let $\mathcal{P}_\delta =\langle \widehat{S}, A,{\mathop {\longrightarrow }\limits ^{}}'\rangle$ be the finite-state LTS constructed above, $s\in S$. Then for any HMLb formula F, it holds that $s\models \underline{F}$ if and only if $\hat{s}\models F$.

Now we obtain the following theorem which guarantees the correctness of our reduction.

Theorem 10

For a finite-state LTS $\mathcal{P}=\langle S,A{\mathop {\longrightarrow }\limits ^{}}\rangle$, let $\mathcal{P}_\delta =\langle \widehat{S}, A,{\mathop {\longrightarrow }\limits ^{}}'\rangle$ be the finite-state LTS constructed above. Then for $s,t\in S$:

• 1. $s\approx ^\triangle t$ if and only if $\hat{s}\approx \hat{t}$;

• 2. $s\approx ^\triangle _b t$ if and only if $\hat{s}\approx _b\hat{t}$.

Proof

Here we only prove 1. The way to prove 2. is the same. Since $\approx ^\triangle$ coincides with $\equiv ^{\triangle _\epsilon }_w$ and $\approx$ coincides with $\equiv _w$, to prove 1. we only need to prove that $s\equiv ^{\triangle _\epsilon }_wt$ if and only if $\hat{s}\equiv _w\hat{t}$.

Suppose $s\equiv ^{\triangle _\epsilon }_wt$. If $\hat{s}\models F$ for some HML formula F, then by Theorem 9, $\underline{F}$ is an HML$\varDelta _\epsilon$ formula and $s\models \underline{F}$. Then by the condition that $s\equiv ^{\triangle _\epsilon }_wt$, we have $t\models \underline{F}$, and again by Theorem 9, $\hat{t}\models F$. Thus $\hat{s}\equiv _w\hat{t}$.

Suppose $\hat{s}\equiv _w\hat{t}$. If $s\models F$ for some HML$\varDelta _\epsilon$ formula F, then by Theorem 8, $\overline{F}$ is an HML formula and $\hat{s}\models F$. Then by the condition that $\hat{s}\equiv \hat{t}$, we have $\hat{t}\models \overline{F}$, and again by Theorem 8, $t\models F$. Thus $s\equiv ^{\triangle _\epsilon }_wt$.    $\square$

Theorem 8 also suggests a simple solution to the model checking problem for HMLb$\varDelta$ (which can have many solutions). The model checking problem here is to ask, for any given state s of a fnite-state LTS $\mathcal{P}$ and any given finite HMLb$\varDelta$ formula F (finite in the sense that only finite conjunctions are allowed in F), how to decide whether $s\models F$ holds or not. By Theorem 8, this problem can be reduced to the problem of deciding if $\hat{s}\models \overline{F}$ holds or not, which comes with simple decision procedures because here $\hat{s}$ is a state in the finite-state LTS $\mathcal{P}_\delta$ and $\overline{F}$ is a finite HMLb formula.

5 Conclusion

To summarize, by introducing a new divergence modality, the weak divergence modality $\varDelta _\epsilon$, we obtain logic characterization results for two divergence sensitive bisimulation equivalence relations. One is the first modal logic characterization for complete weak bisimilarity $\approx ^\triangle$, and the other is a new modal logic characterization for branching bisimilarity with explicit divergence $\approx _b^{\triangle }$. With these new characterization results we showed a clear picture of the sub-logic relationships of various logic characterization results. By using these new characterization results, we provide reductions from the divergence sensitive equality checking problems and model checking problems to the divergence blind equality checking problems and model checking problems respectively for finite-state systems.

Complete weak bisimilarity $\approx ^\triangle$ was first defined in [10], which is a refinement of weak bisimilarity $\approx$ [9] by taking divergence behavior into account. Since this is a relatively new equivalence relation, the logic characterization problem and equality checking problem for finite-state systems have not been treated before this paper. The relation $\approx _b^{\triangle }$ was defined in [12] which is a refinement of branching bisimilarity $\approx _b$ [12]. In [15], the equality checking problem of stutter equivalence on Kripke structures is solved by a reduction to the equality checking problem of divergence blind stutter equivalence problem. Stutter equivalence and divergence blind stutter equivalence are the Kripke structure versions of branching bisimilarity with explicit divergence and branching bisimilarity. The reduction presented in Sect. 4 is inspired by the reduction in [15].

The study of modal logic characterization of bisimulation equivalence relations was initiated by Hennessy and Milner in [2]. For branching bisimilarity, modal characterization results were studied in [5, 6], where different modalities for branching structures were used. In [6], besides the extension of Hennessy-Milner logic with the until operator mentioned earlier in the paper, two other logics were proposed to characterize branching bisimilarity. One is another extension of Hennessy-Milner logic which exploits the power of backward modalities. The other is CTL$^*$ without the next-time operator interpreted over all paths, not just over maximal ones. In [13] a modal logic was proposed to characterize branching bisimilarity with explicit divergence by combining modalities for branching bisimilarity in [5] and a divergence modality $\varDelta$. In [14], an extension of CTL$^*$ without the next operator is proposed which also characterizes branching bisimilarity with explicit divergence.