Abstract
An updatable encryption scheme allows to periodically rotate the encryption key and move already existing ciphertexts from the old to the new key. These ciphertext updates are done with the help of a so-called update token and can be performed by an untrusted party, as the update never decrypts the data. Updatable encryption is particularly useful in settings where encrypted data is outsourced, e.g., stored on a cloud server. The data owner can produce an update token, and the cloud server can update the ciphertexts.
We provide a comprehensive treatment of ciphertext-independent schemes, where a single token is used to update all ciphertexts. We show that the existing ciphertext-independent schemes and models by Boneh et al. (CRYPTO’13) and Everspaugh et al. (CRYPTO’17) do not guarantee the post-compromise security one would intuitively expect from key rotation. In fact, the simple scheme recently proposed by Everspaugh et al. allows to recover the current key upon corruption of a single old key. Surprisingly, none of the models so far reflects the timely aspect of key rotation which makes it hard to grasp when an adversary is allowed to corrupt keys. We propose strong security models that clearly capture post-compromise and forward security under adaptive attacks. We then analyze various existing schemes and show that none of them is secure in this strong model, but we formulate the additional constraints that suffice to prove their security in a relaxed version of our model. Finally, we propose a new updatable encryption scheme that achieves our strong notions while being (at least) as efficient as the existing solutions.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
In data storage, key rotation refers to the process of (periodically) exchanging the cryptographic key material that is used to protect the data. Key rotation is considered good practice as it hedges against the impact of cryptographic keys being compromised over time. For instance, the Payment Card Industry Data Security Standard (PCI DSS) [24], which specifies how credit card data must be stored in encrypted form mandates key rotation, meaning that encrypted data must regularly be moved from an old to a fresh key. Many cloud storage providers that implement data-at-rest encryption, such as Google and Amazon, employ a similar feature [15]. The trivial approach to update an existing ciphertext towards a new key is to decrypt the ciphertext and re-encrypt the underlying plaintext from scratch using the fresh key. Implementing this approach for secure cloud storage applications where the data owner outsources his data in encrypted form to a potentially untrusted host is not trivial, though: Either the owner has to download, re-encrypt and upload all ciphertexts, which makes outsourcing impractical, or the encryption keys have to be sent to the host, violating security.
Updatable Encryption. A better solution for updating ciphertexts has been proposed by Boneh et al. [10]: in what they call an updatable encryption scheme, the data owner can produce a short update token that allows the host to re-encrypt the data himself, while preserving the security of the encryption, i.e., the token allows to migrate ciphertexts from an old to a new key, but does not give the host an advantage in breaking the confidentiality of the protected data. Boneh et al. also proposed a construction (\(\mathsf {BLMR}\)) based on key-homomorphic PRFs, which essentially is a symmetric proxy re-encryption scheme (PRE) where one sequentially re-encrypts data from one epoch to the next.
While being somewhat similar in spirit, PRE and updatable encryption do have different security requirements: PRE schemes often keep parts of the ciphertexts static throughout re-encryption, as there is no need to make a re-encrypted ciphertexts independent from the original ciphertext it was derived from. In updatable encryption, however, the goal should be that an updated ciphertext is as secure as a fresh encryption; in particular, it should look like an independently computed ciphertext even given previous ones. Thus, any scheme that produces linkable ciphertexts, such as the original \(\mathsf {BLMR}\) construction, cannot guarantee such a security notion capturing post-compromise security of updated ciphertexts.
Ciphertext-Independence vs. Ciphertext-Dependence. In the full version of their paper, Boneh et al. [9] provide security notions for updatable encryption, which aim to cover the desired indistinguishability of updated ciphertexts. To satisfy that notion, they have to remove the linkability from the \(\mathsf {BLMR} \) scheme, which they achieve by moving to the setting of ciphertext-dependent updates. In ciphertext-dependent schemes, the owner no longer produces a single token that can update all ciphertexts, but produces a dedicated token for each ciphertext. Therefore, the owner has to download all outsourced ciphertexts, compute a specific token for every ciphertext, and send all tokens back to the host.
Clearly, ciphertext-dependent schemes are much less efficient and more cumbersome for the data owner than ciphertext-independent ones. They also increase the complexity of the update procedure for the host, who has to ensure that it applies the correct token for each ciphertext—any mistake renders the updated ciphertexts useless. Another, more subtle disadvantage of ciphertext-dependent schemes is that they require the old and new keys to be present together for a longer time, as the owner needs both keys to derive the individual tokens for all of his ciphertexts. Deleting the old key too early might risk losing the ability of decrypting ciphertexts that have not been upgraded yet, whereas keeping the old key too long makes an attack at that time more lucrative—the adversary obtains two keys at the same time. In a ciphertext-independent scheme, the old key can and should be deleted immediately after the token has been derived.
In a recent work [15], Everspaugh et al. provide a systematic treatment for such ciphertext-dependent schemes and observe that computing the token often does not require access to the full ciphertext, but only to a short ciphertext header, which allows to moderately improve the efficiency of this approach. Everspaugh et al. also show that the security notions from [9] do not cover the desired property of post-compromise security of updated ciphertexts. They provide two new security notions and propose schemes that can provably satisfy them. As a side-result, they also propose a security definition for ciphertext-independent schemes and suggest a simple xor-based scheme ( ) for this setting.
) for this setting.
Ambiguity of Security Models. Interestingly, both previous works phrase the algorithms and security models for updatable encryption in the flavor of normal proxy re-encryption. That leads to a mismatch of how the scheme is used and modeled—in practice, an updatable encryption scheme is used in a clear sequential setting, updating ciphertexts as the key progresses. The security model offers more and unrealistic flexibility, though: it allows to rotate keys and ciphertexts across arbitrary epochs, jumping back in forth in time. This flexibility gives the adversary more power than he has in reality and, most importantly, makes the security that is captured by the model hard to grasp, as it is not clear when the adversary is allowed to corrupt keys.
Non-intuitive security definitions increase the risk that proofs are flawed or that schemes are unintentionally used outside the security model. And in fact, the way that Everspaugh et al. [15] define security for (ciphertext-independent) schemes is ambiguous, and only the weaker interpretation of their model allows their scheme  to be proven secure. However, this weaker interpretation does not guarantee any confidentiality after a secret key got compromised, as it allows key corruption only after the challenge epoch. Thus, an updatable scheme that is secure only in such a weak model does not provide the intuitive security one would expect from key rotation: namely that after migrating to the new key, the old one becomes useless and no longer of value to the adversary. To the contrary, all previous keys still require strong protection or secure deletion.
to be proven secure. However, this weaker interpretation does not guarantee any confidentiality after a secret key got compromised, as it allows key corruption only after the challenge epoch. Thus, an updatable scheme that is secure only in such a weak model does not provide the intuitive security one would expect from key rotation: namely that after migrating to the new key, the old one becomes useless and no longer of value to the adversary. To the contrary, all previous keys still require strong protection or secure deletion.
Importance of Post-Compromise Security. Realizing secure deletion in practice is virtually impossible, as keys may be copied or moved across the RAM, swap partitions, and SSD memory blocks, and thus we consider post-compromise security an essential property of updatable schemes. Avoiding the assumption of securely deleted keys and re-gaining security after a temporary corruption has recently inspired numerous works on how to achieve post-compromise security in other encryption settings [6, 13, 14, 16]. Note that an updatable encryption scheme that is not post-compromise secure can even reduce the security compared with a scheme where keys are never rotated: as one expects old keys to be useless after rotation, practitioners can be misled to reduce the safety measures for “expired” keys, which in turn makes key compromises more likely. For the example of Everspaugh et al. simple  scheme [15], a compromised old key allows to fully recover the fresh key.
scheme [15], a compromised old key allows to fully recover the fresh key.
This leaves open the important question how to design a ciphertext-independent scheme that achieves post-compromise security, capturing the full spirit of updatable encryption and key rotation.
Our Contributions. In this work we provide a comprehensive treatment for ciphertext-independent updatable encryption schemes that have clear advantages in efficiency and ease-of-deployment over the ciphertext-dependent solutions. We model updatable encryption and its security in the natural sequential manner that is inherent in key rotation, avoiding the ambiguity of previous works, and clearly capturing all desired security properties. We also analyze the (in)security of a number of existing schemes and finally propose a construction that provably satisfies our strong security notions.
Strong Security Models. We define updatable encryption in its natural form where keys and ciphertexts sequentially evolve over time epochs. To capture security, we allow the adversary to adaptively corrupt secret keys, update tokens and ciphertexts in any combination of epochs as long as this does not allow him to trivially decrypt a challenge ciphertext. In our first notion, indistiguishability of encryptions ( ), such a challenge ciphertext will be a fresh encryption \(C_d\) of one of two messages \(m_0, m_1\) under the current epoch key, and the task of the adversary is to guess the bit d. This is the standard CPA game adapted to the updatable encryption and adaptive corruption setting. Our second notion, indistiguishability of updates (
), such a challenge ciphertext will be a fresh encryption \(C_d\) of one of two messages \(m_0, m_1\) under the current epoch key, and the task of the adversary is to guess the bit d. This is the standard CPA game adapted to the updatable encryption and adaptive corruption setting. Our second notion, indistiguishability of updates ( ), returns as a challenge the re-encryption \(C'_d\) of a ciphertext either \(C_0\) or \(C_1\), and an adversary again has to guess the bit d.
), returns as a challenge the re-encryption \(C'_d\) of a ciphertext either \(C_0\) or \(C_1\), and an adversary again has to guess the bit d.
We stress that this second property is essential for the security of updatable encryption schemes, as it captures confidentiality of updated encryptions, whereas  only guarantees security for ciphertexts that originate from a fresh encryption. While
only guarantees security for ciphertexts that originate from a fresh encryption. While  is similar to the security of symmetric proxy re-encryption schemes,
is similar to the security of symmetric proxy re-encryption schemes,  is a property that is special to the context of key rotation. And thus, contrary to a common belief, a symmetric PRE scheme cannot directly be used for secure updatable encryption [10, 15, 22]!
is a property that is special to the context of key rotation. And thus, contrary to a common belief, a symmetric PRE scheme cannot directly be used for secure updatable encryption [10, 15, 22]!
In the ciphertext-independent setting, capturing the information that the adversary can infer from a certain amount of corrupted tokens, keys and ciphertexts is a delicate matter, as, e.g., an update token allows the adversary to move any ciphertext from one epoch to the next. We observe that all existing constructions leak more information than necessary. Instead of hard-coding the behavior of the known schemes into the security model, we propose a set of leakage profiles, and define both the optimal and currently achievable leakage.
We then compare our model to the existing definition for encryption indistinguishability by Everspaugh et al. [15]. We argue that their definition can be interpreted in two ways: the weaker interpretation rules out post-compromise security, but allows the  construction to be secure, whereas the stronger interpretation is closer to our
construction to be secure, whereas the stronger interpretation is closer to our  model. However, in their stronger version, as well as in our
model. However, in their stronger version, as well as in our  notion, we show that
notion, we show that  cannot be secure by describing a simple attack that allows to recover the challenge secret key after compromising one old key. We further show that
cannot be secure by describing a simple attack that allows to recover the challenge secret key after compromising one old key. We further show that  is strictly stronger than the weak interpretation of [15], but incomparable to the stronger one, due to the way both models handle adversarial ciphertexts.
is strictly stronger than the weak interpretation of [15], but incomparable to the stronger one, due to the way both models handle adversarial ciphertexts.
Provably Secure Constructions. We further analyze several schemes according to the new definitions (Sect. 5), the results are summarized in Table 1. First, we consider a simple construction (called \(\mathsf {2ENC} \)) that is purely based on symmetric primitives. Unfortunately, the scheme cannot satisfy our strong security notions. Yet, instead of simply labeling this real-world solution as insecure, we formulate the additional constraints on the adversarial behavior that suffice to prove its security in relaxed versions of our  and
and  models.
models.
 and
and  definitions. The symbol (✓) denotes that a schemes requires additional constraints on the tokens that can be corrupted to achieve the security notion.)
definitions. The symbol (✓) denotes that a schemes requires additional constraints on the tokens that can be corrupted to achieve the security notion.)We then turn our attention to less efficient but more secure schemes, starting with the \(\mathsf {BLMR} \) construction by Boneh et al. [10] that uses key-homomorphic PRFs. We show that the original \(\mathsf {BLMR}\) scheme does satisfy our  notion but not
notion but not  , and also propose a slight modification \(\mathsf {BLMR+}\) that improves the latter and achieves a weak form of update indistinguishability. While \(\mathsf {BLMR} \) seems to be a purely symmetric solution on the first glance, any instantiation of the underlying key-homomorphic PRFs so far requires modular exponentiations or is built from lattices. The same holds for the recent ciphertext-dependent construction by Everspaugh et al. [15] that also relies on key-homomorphic PRFs and suggests a discrete-logarithm based instantiation.
, and also propose a slight modification \(\mathsf {BLMR+}\) that improves the latter and achieves a weak form of update indistinguishability. While \(\mathsf {BLMR} \) seems to be a purely symmetric solution on the first glance, any instantiation of the underlying key-homomorphic PRFs so far requires modular exponentiations or is built from lattices. The same holds for the recent ciphertext-dependent construction by Everspaugh et al. [15] that also relies on key-homomorphic PRFs and suggests a discrete-logarithm based instantiation.
Acknowledging that secure updatable encryption schemes seem to inherently require techniques from the public-key world, we then build a scheme that omits the intermediate abstraction of using key-homomorphic PRFs which allows us to take full advantage of the underlying group operations. Our construction (\(\mathsf {RISE} \), for Re-randomizable ciphertext-Independent Symmetric Elgamal) can be seen as the classic ElGamal-based proxy re-encryption scheme combined with a fresh re-randomization upon each re-encryption. We prove that this scheme fully achieves both of our strong security definitions.
We compare the schemes in terms of efficiency in Table 2. The costs for encryption and updates of our most secure \(\mathsf {RISE} \) scheme are—on the owner side—even lower than the costs in the less secure \(\mathsf {BLMR} \) scheme and the recent ciphertext-dependent scheme \(\mathsf {ReCrypt}\) by Everspaugh et al. [15]. The solution by Everspaugh et al. shifts significantly many expensive update operations to the data owner, who has to compute two exponentiation for each ciphertext (block) that shall be updated, whereas our scheme requires the owner to compute only a single exponentiation for the update of all ciphertexts.
In Appendix A, we additionally analyze a “hybrid-encryption” scheme  that is widely used in practical data-at-rest protection, where the encrypted plaintext is stored together with the encryption key wrapped under an epoch key. The scheme provides rather weak guarantees when viewed as an updatable encryption scheme, but may still be useful in certain scenarios due to the efficient key update.
that is widely used in practical data-at-rest protection, where the encrypted plaintext is stored together with the encryption key wrapped under an epoch key. The scheme provides rather weak guarantees when viewed as an updatable encryption scheme, but may still be useful in certain scenarios due to the efficient key update.
 and \(\mathsf {2ENC} \) are omitted here as they are purely symmetric solutions.)
and \(\mathsf {2ENC} \) are omitted here as they are purely symmetric solutions.)Other Related Work. Beyond the previous work on updatable encryption [9, 10, 15] that we already discussed above, the most closely related line of work is on (symmetric) proxy re-encryption (PRE) [2, 3, 7, 8, 12, 17, 20,21,22]. Notably, the recent work of Berners-Lee [7] builds on the work of Everspaugh et al. [15] and views the concept of ciphertext-dependent updates as a desirable security feature of PRE in general, as it reduces the freedom of a possibly untrusted proxy. The recent work of Myers and Shull [22] studies hybrid PRE schemes aiming at efficient solutions for key rotation and access revocation. As stressed before, however, while being similar in the sense that PRE allows a proxy to move ciphertexts from one key to another, the desired security guarantees have subtle differences and the security property of  that is crucial for updatable encryption is neither covered nor needed by PRE.
that is crucial for updatable encryption is neither covered nor needed by PRE.
While this means that a secure PRE does not automatically yield a secure updatable encryption scheme, it does not prevent PREs from being secure in the updatable encryption sense as well—but this has to be proven from scratch. In fact, our schemes are strongly inspired by proxy re-encryption: For the simple double-encryption scheme discussed by Ivan and Dodis [18], we show that a weak form of security can be proven, and our most secure scheme \(\mathsf {RISE} \) combines the ElGamal-based PRE with re-randomization of ciphertexts. We also observe similar challenges in designing schemes that limit the “power” of the token, which is related to the long-standing problem of constructing efficient PRE’s that are uni-directional, multi-hop and collusion-resistant.
In the context of tokenization, which is the process of consistently replacing sensitive elements, such as credit card numbers, with non-sensitive surrogate values, the feature of key rotation has recently been studied by Cachin et al. [11]. Their schemes are inherently deterministic, and thus their results are not applicable to the problem of probabilistic encryption, but we follow their formalization of modeling key rotation in a strictly sequential manner.
Finally, a recent paper of Ananth et al. [1] provides a broader perspective on updatable cryptography, but targets generic and rather complex schemes with techniques such as randomized encodings. The definitions in their work have linkability hardcoded, as randomness has to remain the same across updates, which is in contrast to our goal of achieving efficient unlinkable schemes for the specific case of updatable encryption.
2 Preliminaries
Symmetric Encryption. A symmetric encryption scheme \(\mathsf {SE}\) consists of a key space \(\mathcal {K}\) and three polynomial-time algorithms \(\mathsf {SE.kgen}\), \(\mathsf {SE.enc}\), \(\mathsf {SE.dec}\) satisfying the following conditions:
-
\(\mathsf {SE.kgen}\) : The probabilistic key generation algorithm takes as input a security parameter and produces an encryption key \(k\in \mathcal {K}\). That is, \(k{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE.kgen}(\lambda )\).
-
\(\mathsf {SE.enc}\) : The probabilistic encryption algorithm takes a key \(k\in \mathcal {K}\) and a message \(m\in \mathcal {M}\) and returns a ciphertext C, written as \(C{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE.enc}({k},{m})\).
-
\(\mathsf {SE.dec}\) : The deterministic decryption algorithm \(\mathsf {SE.dec}\) takes a key \(k\in \mathcal {K}\) and a ciphertext C to return a message \((\mathcal {M}\cup \{\bot \}) \ni m \leftarrow \mathsf {SE.dec}({k},{C})\)
For correctness we require that for any key \(k\in \mathcal {K}\), any message \(m\in \mathcal {M}\) and any ciphertext \(C{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE.enc}({k},{m})\), we have \(m\leftarrow \mathsf {SE.dec}({k},{C})\).
Chosen-Plaintext Security. The  security of a symmetric encryption scheme \(\mathsf {SE}\) is defined through the following game
security of a symmetric encryption scheme \(\mathsf {SE}\) is defined through the following game  with adversary \(\mathcal {A}\). Initially, choose \(b {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\{0,1\}\) and \({k}_{} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE.kgen}(\lambda )\). Run adversary \(\mathcal {A}\) with oracle \(\mathcal {O}_\mathsf {enc}(m)\), which computes \(C {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE.enc}({k}_{}, m)\) and returns C. When \(\mathcal {A}\) outputs two messages \(m_0,m_1\) with \(|m_0|=|m_1|\) and a state \( state \), compute \(\tilde{C}{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE.enc}({k}_{}, m_b)\) and run \(\mathcal {A}(\tilde{C}, state )\), again with access to oracle \(\mathcal {O}_\mathsf {enc}\). When \(\mathcal {A}\) outputs a bit \(\tilde{b}\), the game is won if \(b=\tilde{b}\). The
with adversary \(\mathcal {A}\). Initially, choose \(b {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\{0,1\}\) and \({k}_{} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE.kgen}(\lambda )\). Run adversary \(\mathcal {A}\) with oracle \(\mathcal {O}_\mathsf {enc}(m)\), which computes \(C {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE.enc}({k}_{}, m)\) and returns C. When \(\mathcal {A}\) outputs two messages \(m_0,m_1\) with \(|m_0|=|m_1|\) and a state \( state \), compute \(\tilde{C}{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE.enc}({k}_{}, m_b)\) and run \(\mathcal {A}(\tilde{C}, state )\), again with access to oracle \(\mathcal {O}_\mathsf {enc}\). When \(\mathcal {A}\) outputs a bit \(\tilde{b}\), the game is won if \(b=\tilde{b}\). The  advantage of \(\mathcal {A}\) is defined as
advantage of \(\mathcal {A}\) is defined as  , and \(\mathsf {SE}\) is called
, and \(\mathsf {SE}\) is called  -secure if for all efficient adversaries \(\mathcal {A}\) the advantage is negligible in \(\lambda \).
-secure if for all efficient adversaries \(\mathcal {A}\) the advantage is negligible in \(\lambda \).
Decisional Diffie-Hellman Assumption. Our final construction requires a group \((\mathbb {G},g,p)\) as input where \(\mathbb {G}\) denotes a cyclic group \(\mathbb {G}= \langle g \rangle \) of order p in which the Decisional Diffie-Hellman (DDH) problem is hard w.r.t. \(\lambda \), i.e., p is a \(\lambda \)-bit prime. More precisely, a group (\(\mathbb {G},g,p)\) satisfies the DDH assumption if for any efficient adversary \(\mathcal {A}\) the probability \(\left| \Pr [\mathcal {A}(\mathbb {G},p,g,g^a, g^b,g^{ab})]-\Pr [\mathcal {A}(\mathbb {G},p,g,g^a, g^b,g^c)]\right| \) is negligible in \(\lambda \), where the probability is over the random choice of p, g, the random choices of \(a,b,c \in \mathbb {Z}_p\), and \(\mathcal {A}\)’s coin tosses.
3 Formalizing Updatable Encryption
We now present our formalization of updatable encryption and its desired security features, and discuss how our security model captures these properties.
An updatable encryption scheme contains algorithms for a data owner and a host. The owner encrypts data using the \(\mathsf {UE}_{}.\mathsf {enc}\) algorithm, and then outsources the ciphertexts to the host. To this end, the data owner initially runs an algorithm \(\mathsf {UE}_{}.\mathsf {setup}\) to create an encryption key. The encryption key evolves with epochs, and the data is encrypted with respect to a specific epoch e, starting with \(e=0\). When moving from epoch e to epoch \(e+1\), the owner invokes an algorithm \(\mathsf {UE}_{}.\mathsf {next}\) to generate the key material \({k}_{e+1}\) for the new epoch and an update token \({\varDelta }_{e+1}\). The owner then sends \({\varDelta }_{e+1}\) to the host, deletes \({k}_{e}\) and \({\varDelta }_{e+1}\) immediately, and uses \({k}_{e+1}\) for encryption from now on. After receiving \({\varDelta }_{e+1}\), the host first deletes \({\varDelta }_{e}\) and then uses an algorithm \(\mathsf {UE}_{}.\mathsf {upd}\) to update all previously received ciphertexts from epoch e to \(e+1\), using \({\varDelta }_{e+1}\). Hence, during some epoch e, the update token from \(e-1\) to e is available at the host, but update tokens from earlier epochs have been deleted. (The host could already delete the token when all ciphertexts are updated, but as this is hard to model in the security game, we assume the token to be available throughout the full epoch.)
Definition 1
(Updatable Encryption). An updatable encryption scheme \({\mathsf {UE}_{}}\) for message space \(\mathcal {M}\) consists of a set of polynomial-time algorithms \(\mathsf {UE}_{}.\mathsf {setup}\), \(\mathsf {UE}_{}.\mathsf {next}\), \(\mathsf {UE}_{}.\mathsf {enc}, \mathsf {UE}_{}.\mathsf {dec}\), and \(\mathsf {UE}_{}.\mathsf {upd}\) satisfying the following conditions:
-
\(\mathsf {UE}_{}.\mathsf {setup}\) : The algorithm \(\mathsf {UE}_{}.\mathsf {setup}\) is a probabilistic algorithm run by the owner. On input a security parameter \(\lambda \), it returns a secret key \({k}_{0}{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UE}_{}.\mathsf {setup}(\lambda ).\)
-
\(\mathsf {UE}_{}.\mathsf {next}\) : This probabilistic algorithm is also run by the owner. On input a secret key \({k}_{e}\) for epoch e, it outputs a new secret key \({k}_{e+1}\) and an update token \(\varDelta _{e+1}\) for epoch \(e+1\). That is, \(({k}_{e+1}, \varDelta _{e+1}) {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UE}_{}.\mathsf {next}( {k}_{e}).\)
-
\(\mathsf {UE}_{}.\mathsf {enc}\) : This probabilistic algorithm is run by the owner, on input a message \(m \in \mathcal {M}\) and key \({k}_{e}\) of some epoch e returns a ciphertext \( C_e {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UE}_{}.\mathsf {enc}({k}_{e}, m).\)
-
\(\mathsf {UE}_{}.\mathsf {dec}\) : This deterministic algorithm is run by the owner, on input a ciphertext \(C_e\) and key \({k}_{e}\) of some epoch e returns \( \{m' / \bot \} \leftarrow \mathsf {UE}_{}.\mathsf {dec}({k}_{e}, C_e).\)
-
\(\mathsf {UE}_{}.\mathsf {upd}\) : This either probabilistic or deterministic algorithm is run by the host. On input a ciphertext \(C_e\) from epoch e and the update token \(\varDelta _{e+1}\), it returns the updated ciphertext \( C_{e+1} \leftarrow \mathsf {UE}_{}.\mathsf {upd}(\varDelta _{e+1}, C_e).\)
Correctness. The correctness condition of an updatable encryption scheme ensures that an update of a valid ciphertext \(C_e\) from epoch e to \(e+1\) leads again to a valid ciphertext \(C_{e+1}\) that can be decrypted under the new epoch key \({k}_{e+1}\). More precisely, we require that for any \(m\in \mathcal {M}\), for any \({k}_{0}{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UE}_{}.\mathsf {setup}(\lambda )\), for any sequence of key/update token pairs \(({k}_{1},{\varDelta }_{1}), \dots , ({k}_{e},{\varDelta }_{e})\) generated as \(({k}_{j+1},{\varDelta }_{j+1}){\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UE}_{}.\mathsf {next}({k}_{j})\) for \(j=0,\dots ,e-1\) through repeated applications of the key-evolution algorithm, and for any \(C_{0}{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UE}_{}.\mathsf {enc}({k}_{0},m)\), it holds that \(m = \mathsf {UE}_{}.\mathsf {dec}({k}_{e},C_e)\) where \(C_e\) is recursively obtained through \(C_{j+1} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UE}_{}.\mathsf {upd}({k}_{j+1},C_j)\).
3.1 Security Properties
The main goal of updatable encryption is twofold: First, it should enable efficient updates by a potentially corrupt host, i.e., the update procedure and compromise of the update tokens must not reduce the standard security of the encryption. Second, the core purpose of key rotation is to reduce the risk and impact of key exposures, i.e., confidentiality should be preserved or even re-gained in the presence of temporary key compromises, which can be split into forward and post-compromise security. Furthermore, we aim for security against adaptive and retroactive corruptions, modeling that any key or token from a current or previous epoch can become compromised.
-
Token Security: The feature of updating ciphertexts should not harm the standard IND-CPA security of the encryption scheme. That is, seeing updated ciphertexts or even the exposure of all tokens does not increase an adversary’s advantage in breaking the encryption scheme.
-
Forward Security: An adversary compromising a secret key in some epoch \(e^*\) does not gain any advantage in decrypting ciphertexts he obtained in epochs \(e < e^*\) before that compromise.
-
Post-Compromise Security: An adversary compromising a secret key in some epoch \(e^*\) does not gain any advantage in decrypting ciphertexts he obtained in epochs \(e > e^*\) after that compromise.
-
Adaptive Security: An adversary can adaptively corrupt keys and tokens of the current epoch and all previous ones.
Given that updatable encryption schemes can produce ciphertexts in two ways—either via a direct encryption or an update of a previous ciphertext—we require that the above properties must hold for both settings. This inspires our split into two indistinguishability-based security notions, one capturing security of direct encryptions ( ) and one ruling out attacks against updated ciphertexts (
) and one ruling out attacks against updated ciphertexts ( ). Both security notions are defined through experiments run between a challenger and an adversary \(\mathcal {A}\). Depending on the notion, the adversary may issue queries to different oracles, defined in the next section. At a high level, \(\mathcal {A}\) is allowed to adaptively corrupt arbitrary choices of secret keys and update tokens, as long as they do not allow him to trivially decrypt the challenge ciphertext.
). Both security notions are defined through experiments run between a challenger and an adversary \(\mathcal {A}\). Depending on the notion, the adversary may issue queries to different oracles, defined in the next section. At a high level, \(\mathcal {A}\) is allowed to adaptively corrupt arbitrary choices of secret keys and update tokens, as long as they do not allow him to trivially decrypt the challenge ciphertext.
The Importance of Post-Compromise Security. We have formalized updatable encryption in the strict sequential setting it will be used in, and in particular modeled key derivation of a new key \({k}_{e+1}\) as a sequential update \((k_{e+1}, \varDelta _{e+1}) {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UE}_{}.\mathsf {next}(k_e)\) of the old key \({k}_{e}\). Previous works [10, 15] instead model key rotation by generating fresh keys via a dedicated \(k_{e+1}{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UE}_{}.\mathsf {kgen}(\lambda )\) algorithm at each epoch and deriving the token as \(\varDelta _{e+1} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UE}_{}.\mathsf {next}(k_e, k_{e+1})\).
One impact of our sequential model is that post-compromise security becomes much more essential, as this property intuitively ensures that new keys are independent of the old ones (which is directly ensured in the previous formalization where keys where generated independently). Without requiring post-compromise security, \(\mathsf {UE}_{}.\mathsf {next}(k_e)\) could generate the new key by hashing the old one: \(k_{e+1} \leftarrow \mathsf {H}(k_e)\). If \(\mathsf {H}\) is modeled as a random oracle, this has no impact for standard or forward security, but any scheme with such a key update loses all security in the post-compromise setting. An adversary compromising a single secret key \({k}_{e}\) can derive all future keys himself.
What we do not Model. The focus of this work is to obtain security against arbitrary key compromises, i.e., an adversary can steal secret keys, update tokens, and outsourced ciphertexts at any epoch. We do not consider attacks where an adversary fully takes over the owner or host and starts manipulating ciphertexts, e.g., providing adversarially generated ciphertexts to the host, or tampering with the update procedure. Thus, we model passive CPA attacks but not active CCA ones, and assume that all ciphertexts and updates are honestly generated. We believe this still captures the main threat in the context of updatable encryption, namely smash-and-grab attacks aiming at compromising the key material.
In fact, this restriction to passive attacks allows us to be more generous when it comes to legitimate queries towards corrupted epochs, as we can distinguish challenge from non-challenge ciphertexts and only prohibit the ones that allow trivial wins. Interestingly, Everspaugh et al. [15] use a similar approach in their stronger CCA-like security notion for ciphertext-dependent schemes where they are able to recognize whether a ciphertext is derived from the challenge and prevent these from being updated towards a corrupt key. They are able to recognize challenge ciphertexts as all keys are generated honestly, i.e., they are known to the challenger, and updates are required to be deterministic. The latter allows the challenger to trivially keep track of the challenge ciphertext, but it also makes misuse of the schemes more likely: if a scheme is implemented with probabilistic updates—which intuitively seems to only increase security—then one steps outside of the model and loses all security guarantees. In our model, we allow updates to be probabilistic, and in fact, the security of our strongest construction crucially relies on the re-randomization of updated ciphertexts.
3.2 Definition of Oracles
During the interaction with the challenger in the security definitions, the adversary may access oracles for encryption, for moving the key to the next epoch, for corrupting the token or secret key, and for updating ciphertexts into the current epoch. In the following description, the oracles may access the state of the challenger during the experiment. The challenger initializes a \({\mathsf {UE}_{}}\) scheme with global state \(({k}_{e}, \varDelta _{e}, \mathbf {S}, e)\) where \( {k}_{0}\leftarrow \mathsf {UE}_{}.\mathsf {setup}(\lambda )\), \({\varDelta }_{0}\leftarrow \bot \), and \(e\leftarrow 0\), and \(\mathbf {S}\) consists of initially empty sets \(\mathcal {L}, \tilde{\mathcal {L}}, \mathcal {C}, \mathcal {K}\) and \(\mathcal {T}\). Furthermore, let \(\tilde{e}\) denote the challenge epoch, and \(e_{\mathsf {end}}\) denote the final epoch in the game.
The sets \(\mathcal {L}, \tilde{\mathcal {L}}, \mathcal {C}, \mathcal {K}\) and \(\mathcal {T}\) are used to keep track of the generated and updated ciphertexts, and the epochs in which \(\mathcal {A}\) corrupted a secret key or token, or learned a challenge-ciphertext (Fig. 1):
-
\(\mathcal {O}_\mathsf {enc}(m)\) : On input a message \(m\in \mathcal {M}\), compute \(C{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UE}_{}.\mathsf {enc}({k}_{e},m)\) where \({k}_{e}\) is the secret key of the current epoch e. Add C to the list of ciphertexts \(\mathcal {L}\leftarrow \mathcal {L}\cup \{(C, e)\}\) and return the ciphertext to the adversary.
-
 : When triggered, this oracle updates the secret key, produces a new update value as \(({k}_{e+1}, \varDelta _{e+1}) {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UE}_{}.\mathsf {next}({k}_{e})\), and updates the global state to \(({k}_{e+1}, \varDelta _{e+1}, \mathbf {S}, e+1)\). If the challenge query was already made, this call will also update the challenge ciphertext into the new epoch, i.e., it runs \(\tilde{C}_{e+1} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UE}_{}.\mathsf {upd}(\varDelta _{e+1}, \tilde{C}_{e})\) for \((\tilde{C}_{e}, {e}) \in \tilde{\mathcal {L}}\) and sets \(\tilde{\mathcal {L}}\cup \{(\tilde{C}_{e+1}, {e+1})\}\).
: When triggered, this oracle updates the secret key, produces a new update value as \(({k}_{e+1}, \varDelta _{e+1}) {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UE}_{}.\mathsf {next}({k}_{e})\), and updates the global state to \(({k}_{e+1}, \varDelta _{e+1}, \mathbf {S}, e+1)\). If the challenge query was already made, this call will also update the challenge ciphertext into the new epoch, i.e., it runs \(\tilde{C}_{e+1} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UE}_{}.\mathsf {upd}(\varDelta _{e+1}, \tilde{C}_{e})\) for \((\tilde{C}_{e}, {e}) \in \tilde{\mathcal {L}}\) and sets \(\tilde{\mathcal {L}}\cup \{(\tilde{C}_{e+1}, {e+1})\}\). -
\(\mathcal {O}_\mathsf {upd} (C_{e-1})\) : On input a ciphertext \(C_{e-1}\), check that \((C_{e-1}, {e-1}) \in \mathcal {L}\) (i.e., it is an honestly generated ciphertext of the previous epoch \(e-1\)), compute \(C_{e} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {UE}_{}.\mathsf {upd}(\varDelta _{e}, C_{e-1})\), add \((C_e,e)\) to the list \(\mathcal {L}\) and output \(C_{e}\) to \(\mathcal {A}\).
-
\(\mathcal {O}_\mathsf {corrupt}(\{\mathsf {token}, \mathsf {key}\}, e^*)\) : This oracle models adaptive corruption of the host and owner keys, respectively. The adversary can request a key or update token from the current or any of the previous epochs.
-
Upon input \(\mathsf {token}\), \(e^* \le e\), the oracle returns \(\varDelta _{e^*}\), i.e., the update token is leaked. Calling the oracle in this mode sets \(\mathcal {T} \leftarrow \mathcal {T} \cup \{e^*\}\).
-
Upon input \(\mathsf {key}\), \(e^* \le e\), the oracle returns \({k}_{e^*}\), i.e., the secret key is leaked. Calling the oracle in this mode sets \(\mathcal {K} \leftarrow \mathcal {K} \cup \{ e^* \}\).
-
-
\(\mathcal {O}_\mathsf {upd\tilde{C}} \) : Returns the current challenge ciphertext \(\tilde{C}_{e}\) from \(\tilde{\mathcal {L}}\). Note that the challenge ciphertext gets updated to the new epoch by the
 oracle, whenever a new key gets generated. Calling this oracle sets \(\mathcal {C} \leftarrow \mathcal {C} \cup \{ e \}\).
oracle, whenever a new key gets generated. Calling this oracle sets \(\mathcal {C} \leftarrow \mathcal {C} \cup \{ e \}\).
Fine-grained corruption modeling. Note that in the case of key-corruption in an epoch \(e^*\), the oracle \(\mathcal {O}_\mathsf {corrupt}(\mathsf {key}, e^*)\) only reveals the secret key \({k}_{e^*}\), but not the update token of the epoch. This assumes erasure of the token as an ephemeral value on the owner side. If the adversary also wants to learn the token, he can make a dedicated query for token-corruption in the same epoch. This allows to capture more fine-grained corruption settings.
Moreover, we have chosen to give the adversary a dedicated challenge-update oracle \(\mathcal {O}_\mathsf {upd\tilde{C}} \) that simply returns the updated challenge ciphertext of the current epoch, i.e., it does not require knowledge of the challenge ciphertext from the previous epoch. This gives the adversary more power compared with the definition in earlier models [10, 15]: Therein, an adversary wanting to know an updated version of the challenge ciphertext for some epoch \(e' > \tilde{e}\) (with \(\tilde{e}\) denoting the challenge epoch) had to make update queries in all epochs from \(\tilde{e}\) to \(e'\), which in turn is only allowed if \(\mathcal {A}\) has not corrupted any secret key between \(\tilde{e}\) and \(e'\). Consequently, \(\mathcal {A}\) could not receive an updated challenge ciphertext after a single key corruption, which we consider too restrictive. Therefore, we internally update the challenge ciphertext with every key rotation and allow the adversary to selectively receive an updated version at every epoch of his choice. Thus, in every epoch after \(\tilde{e}\), the adversary \(\mathcal {A}\) can choose whether he wants to learn the secret key or an updated version of the challenge ciphertext.
3.3 “Leakage” Profiles
The main benefit of ciphertext-independent updatable encryption schemes is that a single token can be used to update all ciphertexts from one epoch to the next. However, the generality of the token also imposes a number of challenges when modeling the knowledge of the adversary after he has corrupted a number of keys, tokens and updated challenge ciphertexts. For instance, if the adversary knows a challenge ciphertext \(\tilde{C}\) from epoch \(\tilde{e}\) and an update token for epoch \(\tilde{e}+1\), he can derive an updated version of \(\tilde{C}\) himself, which is not captured in the set \(\mathcal {C}\) that only reflects the challenge ciphertexts that \(\mathcal {A}\) has directly received from the challenger. This inference of updated ciphertexts via an update token is clearly inherent in ciphertext-independent schemes.
Practical schemes often enable the adversary to derive even more information, e.g., a token might allow not only to update but also to “downgrade” a ciphertext into the previous epoch, i.e., the updates are bi-directional, or even allow to update and downgrade a secret key via a token. While these features are present in all current solutions, we do not see a reason why they should be inherent in updatable encryption in general. Thus, we model different inference options outside of the game by defining extended sets \(\mathcal {T}^*\), \(\mathcal {C}^*\) and \(\mathcal {K}^*\) that capture the information an adversary can infer from the directly learned tokens, ciphertexts or keys. In the security games defined in the next section, we will require the intersection of the extended sets of known challenge ciphertexts \(\mathcal {C}^*\) and known secret keys \(\mathcal {K}^*\) to be empty, i.e., there must not exist a single epoch where the adversary knows both the secret key and the (updated) challenge. We give an example of such direct and inferable information in Fig. 2.
Note that such inference is less an issue for ciphertext-dependent schemes where the owner has to a derive a dedicated token for each ciphertext. This naturally limits the power of the token to the ciphertext it was derived for, and prevents the adversary from using the token outside of its original purpose.
Example of direct and indirect knowledge of an adversary. The boxed values denote \(\mathcal {A}\)’s directly received information as captured in \(\mathcal {K}, \mathcal {T}\) and \(\mathcal {C}\), whereas the circled ones denote the inferable values for a scheme with token-inference and bi-directional updates of ciphertexts and keys.
Capturing Key Updates. In many schemes (in fact all the ones we will consider), an update token does not only allow to update ciphertexts, but also the secret key itself. That is, if an adversary has learned a key \({k}_{e}\) of epoch e and the update token \(\varDelta _{e+1}\) of the following epoch, then he can also derive the new key \({k}_{e+1}\). If that is the only possible derivation, we call this an uni-directional key update. If in addition also key downgrades are possible, i.e., a key \({k}_{e}\) can be derived from \({k}_{e+1}\) and \(\varDelta _{e+1}\), we call this bi-directional key updates.
In the context of proxy re-encryption, a similar property is known as “collusion-resistance”. So far only uni-directional and single-hop schemes satisfy this property, though [2, 3, 12, 17, 20, 21], indicating that preventing keys to be updatable in a more flexible setting is a challenging property.
For defining uni- and bi-directional key updates we use the information contained in \(\mathcal {K}\) and \(\mathcal {T}\) to derive the inferable information. Recall that \(\mathcal {K}\) denotes the set of epochs in which the adversary has obtained the secret key. The sets \(\mathcal {K}_\mathsf {uni}^*\) and \(\mathcal {K}_\mathsf {bi}^*\) are then defined via the recursive predicate  as follows:
as follows:


Capturing Token Inference from Subsequent Secret Keys. The second indirect knowledge we model is the derivation of an update token from two subsequent secret keys. This is possible in all existing schemes where a token \(\varDelta _{e+1}\) is deterministically derived from the keys \({k}_{e}\) and \({k}_{e+1}\). In fact, all previous definitions explicitly model the token computation as an algorithm that receives both keys as input, instead of using an algorithm that updates the key and produces an update token at the same time. While the former is clearly a necessary design choice for proxy re-encryption, it is less so for updatable encryption where keys are generated in a strictly sequential order. Yet, if such token inference is possible, we define an extended set \(\mathcal {T}^*\) that contains all update tokens that the adversary has either obtained directly or derived himself from corrupted keys.
More, precisely, for schemes with token-inference, the adversary can derive from any two subsequent keys \({k}_{e}\) and \({k}_{e+1}\) the update token \(\varDelta _{e+1}\) from epoch e to \(e+1\). We capture this by defining \(\mathcal {T}^*\) via the sets \(\mathcal {T}\) of corrupted token epochs and \(\mathcal {K}^*\) denoting the extended set of corrupted key epochs as defined above.

On a first glance it might look like we could run into a definitional loop between inferred tokens and keys, as the extended set \(\mathcal {T}^*\) based on \(\mathcal {K}^*\) could now also impact the definition of \(\mathcal {K}^*\) (which we build from \(\mathcal {T}\)). This is not the case though: the additional epochs e that will be contained in \(\mathcal {T}^*\) are epochs where the adversary already knew \({k}_{e}\) and \({k}_{e-1}\). Thus the additional tokens \(\varDelta _e\) where \(e \in \mathcal {T}^* \backslash \mathcal {T}\) would have no impact on a (re-definition) of \(\mathcal {K}^*\) as all inferable keys from \(\varDelta _e\) are already in \(\mathcal {K}^*\).
Capturing Challenge Ciphertext Updates. For capturing all the epochs in which the adversary knows a version of the challenge ciphertext, we define the set \(\mathcal {C}^*\) containing all challenge-equal epochs. Informally, a challenge-equal epoch is every epoch in which the adversary knows a current version of the challenge ciphertext. This can be either obtained via a direct call to the challenge-ciphertext oracle \(\mathcal {O}_\mathsf {upd\tilde{C}} \), or by the adversary computing it himself via a (sequence of) updates. We have to distinguish between two cases, depending on whether the updates are uni- or bi-directional. In schemes with uni-directional updates, an update token \(\varDelta _e\) can only move ciphertexts from epoch \(e-1\) into epoch e, but not vice versa. Note that uni-directional updates are by definition possible in all ciphertext-independent schemes. A scheme where a token \(\varDelta _e\) also allows to downgrade ciphertexts from epoch e to \(e-1\), is called bi-directional.
Clearly, for security, uni-directional schemes are desirable, as the bi-directional property does not provide additional useful features but only allows the adversary to trivially derive more information. However, bi-directional schemes are easier to build, as this is related to the problem of designing uni-directional and multi-hop proxy re-encryption schemes, for which a first (compact) lattice-based solution was proposed only recently [25].
In both cases, we define \(\mathcal {C}_\mathsf {uni}^*\) and \(\mathcal {C}_\mathsf {bi}^*\) by using the information contained in \(\mathcal {C}\), \(\mathcal {T}^*\) and \(\tilde{e}\) to derive the inferable information. Recall that \(\tilde{e}\) denotes the challenge epoch, \(\mathcal {C}\) denotes the set of epochs in which the adversary has obtained an updated version of the ciphertext (via \(\mathcal {O}_\mathsf {upd\tilde{C}} \)), and \(\mathcal {T}^*\) is the augmented set of tokens known to the adversary. The sets \(\mathcal {C}^*_\mathsf {uni}\) and \(\mathcal {C}^*_\mathsf {bi}\) of all challenge-equal ciphertexts are then defined via the recursive predicate  as follows:
as follows:


Optimal Leakage. The optimal leakage, capturing only the inference minimally necessary to perform ciphertext-independent updates would be \(\mathcal {T}^* = \mathcal {T}\), \(\mathcal {K}^* = \mathcal {K}\) and \(\mathcal {C}^* = \mathcal {C}^*_\mathsf {uni}\). That is, there is no token inference, keys cannot be updated via a token and ciphertext updates are only uni-directional. All our schemes have leakage \((\mathcal {T}^*, \mathcal {C}^*_\mathsf {bi}, \mathcal {\mathcal {K}}^*_\mathsf {bi})\), and we leave it as an interesting open problem whether efficient schemes with less leakage exist. Interestingly, the extended set of corrupted tokens \(\mathcal {T}^*\) does not give the adversary more power in our  and
and  definitions, compared with definitions that are based only on \(\mathcal {T}\).
definitions, compared with definitions that are based only on \(\mathcal {T}\).
3.4 Security Notions for Updatable Encryption
We are now ready to formally define the security notions for updatable encryption schemes in the remainder of this section. We propose two indistinguishability-based notions—the first capturing the security of fresh encryptions in the presence of key evolutions and adaptive corruptions, and the second defining the same security for updated ciphertexts.
Adaptive Encryption Indistinguishability (IND-ENC). Our  notion ensures that ciphertexts obtained from the \(\mathsf {UE}_{}.\mathsf {enc}\) algorithm do not reveal any information about the underlying plaintexts even when \(\mathcal {A}\) adaptively compromises a number of keys and tokens before and after the challenge epoch. Thus this definition captures forward and post-compromise security.
notion ensures that ciphertexts obtained from the \(\mathsf {UE}_{}.\mathsf {enc}\) algorithm do not reveal any information about the underlying plaintexts even when \(\mathcal {A}\) adaptively compromises a number of keys and tokens before and after the challenge epoch. Thus this definition captures forward and post-compromise security.
Definition 2
( ). An updatable encryption scheme \({\mathsf {UE}_{}}\) is said to be
). An updatable encryption scheme \({\mathsf {UE}_{}}\) is said to be  -secure if for all probabilistic polynomial-time adversaries \(\mathcal {A}\) it holds that
-secure if for all probabilistic polynomial-time adversaries \(\mathcal {A}\) it holds that  for some negligible function \(\epsilon \).
for some negligible function \(\epsilon \).

This experiment follows the typical IND-CPA definition, but additionally grants the adversary access to the  , \(\mathcal {O}_{\mathsf {upd}}\), \(\mathcal {O}_\mathsf {corrupt}\) and \(\mathcal {O}_\mathsf {upd\tilde{C}} \) oracles defined in Sect. 3.2. To exclude trivial wins, we require that \(\mathcal {A}\) has not learned the secret key in any challenge-equal epoch. Recall that a “challenge-equal” epoch is every epoch in which the adversary knows a current version of the challenge ciphertext. This can be either obtained via a direct call to the challenge-ciphertext oracle or by the adversary computing it himself via a (sequence of) updates. The exact set of challenge-equal epochs (\(\mathcal {C}^*\)) and secret keys that are known to the adversary (\(\mathcal {K}^*\)) depends on the leakage profile, which has to specified when proving
, \(\mathcal {O}_{\mathsf {upd}}\), \(\mathcal {O}_\mathsf {corrupt}\) and \(\mathcal {O}_\mathsf {upd\tilde{C}} \) oracles defined in Sect. 3.2. To exclude trivial wins, we require that \(\mathcal {A}\) has not learned the secret key in any challenge-equal epoch. Recall that a “challenge-equal” epoch is every epoch in which the adversary knows a current version of the challenge ciphertext. This can be either obtained via a direct call to the challenge-ciphertext oracle or by the adversary computing it himself via a (sequence of) updates. The exact set of challenge-equal epochs (\(\mathcal {C}^*\)) and secret keys that are known to the adversary (\(\mathcal {K}^*\)) depends on the leakage profile, which has to specified when proving  security. For all schemes proven secure in this work, the leakage profile is the one defined in Sect. 3.3.
security. For all schemes proven secure in this work, the leakage profile is the one defined in Sect. 3.3.
Insufficiency of  for Full Post-Compromise Security. It is often claimed that symmetric proxy re-encryption (PRE) can be used for updatable encryption, indicating that security of symmetric PRE is sufficient for the security of key-evolving schemes [10, 15, 22]. In fact, the security definition for ciphertext-independent schemes given by Boneh et al. [10] and Everspaugh et al. [15] coincides with the security of symmetric PRE. Our
for Full Post-Compromise Security. It is often claimed that symmetric proxy re-encryption (PRE) can be used for updatable encryption, indicating that security of symmetric PRE is sufficient for the security of key-evolving schemes [10, 15, 22]. In fact, the security definition for ciphertext-independent schemes given by Boneh et al. [10] and Everspaugh et al. [15] coincides with the security of symmetric PRE. Our  definition can be seen as a strengthened version (as it allows adaptive corruptions) of such PRE security adapted to the sequential setting of an updatable encryption scheme. However, an updatable scheme only satisfying
definition can be seen as a strengthened version (as it allows adaptive corruptions) of such PRE security adapted to the sequential setting of an updatable encryption scheme. However, an updatable scheme only satisfying  would not necessarily provide the security properties one expects. Note that in the
would not necessarily provide the security properties one expects. Note that in the  definition above, the challenge is a fresh encryption of one of the two challenge messages \(m_0,m_1\), but not an updated ciphertext. Thus,
definition above, the challenge is a fresh encryption of one of the two challenge messages \(m_0,m_1\), but not an updated ciphertext. Thus,  security cannot guarantee anything about the security of updates. In fact, a scheme where the update algorithm \(\mathsf {UE}_{}.\mathsf {upd}\) includes all the old ciphertexts \(C_0, \dots C_e\) in the updated ciphertext \(C_{e+1}\) could be considered
security cannot guarantee anything about the security of updates. In fact, a scheme where the update algorithm \(\mathsf {UE}_{}.\mathsf {upd}\) includes all the old ciphertexts \(C_0, \dots C_e\) in the updated ciphertext \(C_{e+1}\) could be considered  secure, but clearly lose all security if a single old key gets compromised.
secure, but clearly lose all security if a single old key gets compromised.
We therefore also propose a second definition that requires indistinguishability of updates, and in combination with  guarantees the security properties one expects from updatable encryption.
guarantees the security properties one expects from updatable encryption.
Adaptive Update Indistinguishability (IND-UPD). The  notion ensures that an updated ciphertext obtained from the \(\mathsf {UE}_{}.\mathsf {upd}\) algorithm does not reveal any information about the previous ciphertext, even when \(\mathcal {A}\) adaptively compromises a number of keys and tokens before and after the challenge epoch. Thus this definition again captures forward and post-compromise security in an adaptive manner. We will informally refer to this notion also as unlinkability.
notion ensures that an updated ciphertext obtained from the \(\mathsf {UE}_{}.\mathsf {upd}\) algorithm does not reveal any information about the previous ciphertext, even when \(\mathcal {A}\) adaptively compromises a number of keys and tokens before and after the challenge epoch. Thus this definition again captures forward and post-compromise security in an adaptive manner. We will informally refer to this notion also as unlinkability.
Definition 3
( ). An updatable encryption scheme \({\mathsf {UE}_{}}\) is said to be
). An updatable encryption scheme \({\mathsf {UE}_{}}\) is said to be  -secure if for all probabilistic polynomial-time adversaries \(\mathcal {A}\) it holds that
-secure if for all probabilistic polynomial-time adversaries \(\mathcal {A}\) it holds that  for some negligible function \(\epsilon \).
for some negligible function \(\epsilon \).

This experiment is similar to  , but instead of requiring a fresh encryption to be indistinguishable, we let the adversary provide two ciphertexts \(C_0\) and \(C_1\) and return the update \(\tilde{C}\) of one of them. The task of the adversary is to guess which ciphertext got updated. Note that the adversary is allowed to corrupt the secret key \({k}_{\tilde{e}-1}\), i.e., from right before the challenge epoch. Similar as in
, but instead of requiring a fresh encryption to be indistinguishable, we let the adversary provide two ciphertexts \(C_0\) and \(C_1\) and return the update \(\tilde{C}\) of one of them. The task of the adversary is to guess which ciphertext got updated. Note that the adversary is allowed to corrupt the secret key \({k}_{\tilde{e}-1}\), i.e., from right before the challenge epoch. Similar as in  we exclude trivial wins where the adversary learned the secret key of a challenge-equal epoch. Moreover, if the update algorithm is deterministic, \(\mathcal {A}\) is also not allowed to update any of the two challenge ciphertexts into the challenge epoch himself.
we exclude trivial wins where the adversary learned the secret key of a challenge-equal epoch. Moreover, if the update algorithm is deterministic, \(\mathcal {A}\) is also not allowed to update any of the two challenge ciphertexts into the challenge epoch himself.
4 Comparison with Existing Models
We now compare our security notion with the definition proposed by Everspaugh et al. [15], which in turn builds upon the work by Boneh et al. [9]. We also discuss the  scheme that was claimed to be a secure ciphertext-independent scheme [15]. Note that, for ciphertext-independent schemes, only the property of encryption indistinguishability (UP-IND-BI in [15]) was previously defined but not the additional update indistinguishability, and thus our comparison focuses on
scheme that was claimed to be a secure ciphertext-independent scheme [15]. Note that, for ciphertext-independent schemes, only the property of encryption indistinguishability (UP-IND-BI in [15]) was previously defined but not the additional update indistinguishability, and thus our comparison focuses on  .
.
The UP-IND-BI definition by Everspaugh et al. [15] is ambiguous, and we show that one can either interpret the model such that it excludes any key compromises before the challenge (i.e., it does not cover post-compromise security), or it is closer to our model and allows a restricted form of key corruptions before the challenge. We refer to the former as  and to the latter as
and to the latter as  model. We stress that neither
model. We stress that neither  nor
nor  used in our comparison is the verbatim definition presented in [15]. Both are adaptions of the UP-IND-BI model to the sequential setting that we use in our work and in which updatable schemes are naturally used. This adaptation revealed an ambiguity in the UP-IND-BI model w.r.t. whether it allows key corruptions before the challenge.
used in our comparison is the verbatim definition presented in [15]. Both are adaptions of the UP-IND-BI model to the sequential setting that we use in our work and in which updatable schemes are naturally used. This adaptation revealed an ambiguity in the UP-IND-BI model w.r.t. whether it allows key corruptions before the challenge.
One reason for the ambiguity is that the  scheme, which is claimed secure, is secure only in the
scheme, which is claimed secure, is secure only in the  model, but not in
model, but not in  : we show that it loses all security if the adversary can corrupt an old key, which is allowed in the stronger model, as well as in our
: we show that it loses all security if the adversary can corrupt an old key, which is allowed in the stronger model, as well as in our  game.
game.
Overall we show the following:
Theorem 1
 .
.
4.1  vs.
vs. 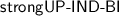
The key reason for the ambiguity of the security definition by Everspaugh et al. [15] is that the security game does not convey the notion of epochs and thus it is not clear when the adversary is allowed to corrupt secret keys. The definition considers static corruptions, and assumes a known threshold t that separates honest from corrupted keys. That is, all keys \({k}_{1}, \dots , {k}_{t}\) are assumed to be uncorrupted, whereas the keys \({k}_{{t+1}}, \dots , {k}_{\kappa }\) are considered corrupted and are given to the adversary. Jumping ahead, the security notion then allows challenge queries for all keys \({k}_{i}\) where \(i \le t\) and disallows any update or token corruption queries towards a corrupt key \({k}_{j}\), i.e., where \(j > t\).
One interpretation is that the threshold t strictly separates honest from corrupt epochs, i.e., the uncorrupted keys \({k}_{1}, \dots , {k}_{t}\) belong to the first t epochs in which the adversary can request the challenge. We call this the  model, as all corrupted keys \({k}_{{t+1}}, \dots , {k}_{\kappa }\) must occur after the challenge epoch(s).
model, as all corrupted keys \({k}_{{t+1}}, \dots , {k}_{\kappa }\) must occur after the challenge epoch(s).
The second interpretation is that \({k}_{1}, \dots , {k}_{t}\) merely refer to some t honest keys, but not necessarily to the first t epochs. That is, the corrupt keys could belong to arbitrary epochs, and key compromises before the challenge epoch(s) would be allowed. We call this the  model.
model.
Honest vs. Adversarial Ciphertexts. The  and
and  definitions do not distinguish between challenge and non-challenge ciphertexts in the responses to the update oracle, and allow \(\mathcal {O}_\mathsf {upd} \) to be called with arbitrary ciphertexts. Thus, in contrast to our definition that only allows updates of honestly generated ciphertexts, the oracle \(\mathcal {O}_\mathsf {upd} (C_e)\) omits the check whether \((C_e,e) \in \mathcal {L}\) and simply returns the updated ciphertext for any input. Consequently, the adversary is not allowed to make any update query towards a corrupted epoch, as the query could be the challenge ciphertext. We show that for
definitions do not distinguish between challenge and non-challenge ciphertexts in the responses to the update oracle, and allow \(\mathcal {O}_\mathsf {upd} \) to be called with arbitrary ciphertexts. Thus, in contrast to our definition that only allows updates of honestly generated ciphertexts, the oracle \(\mathcal {O}_\mathsf {upd} (C_e)\) omits the check whether \((C_e,e) \in \mathcal {L}\) and simply returns the updated ciphertext for any input. Consequently, the adversary is not allowed to make any update query towards a corrupted epoch, as the query could be the challenge ciphertext. We show that for  security, this difference of updating also adversarially crafted ciphertexts prevents our
security, this difference of updating also adversarially crafted ciphertexts prevents our  notion to be strictly stronger than
notion to be strictly stronger than  . For
. For  this does not give the adversary any additional advantage though.
this does not give the adversary any additional advantage though.
The weakUP-IND-BI Model. We follow the original definition by Everspaugh et al. [15] (in its weaker sense) and adopt it to our notation. As our scheme is strictly sequential, we cannot give the adversary all corrupted keys \({k}_{{t+1}}, \dots , {k}_{\kappa }\) already at the beginning of the game, but rather let \(\mathcal {A}\) corrupt them via the \(\mathcal {O}_\mathsf {corrupt}(\mathsf {key}, \cdot )\) oracle. Further, we consider a single challenge query in some epoch \(\tilde{e}\le t\), whereas [15] granted the adversary a dedicated left-or-right oracle for all keys before t.

The winning condition requires that \(\mathcal {A}\) does not learn the update token towards the first corrupted epoch \(e_{t+1}\), nor makes any update query in \(e_{t+1}\), as both would enable the adversary to update the challenge ciphertext into a corrupted epoch.
This weaker interpretation does not guarantee any confidentiality after a secret key got compromised, as it allows key corruption only after the challenge epoch. Thus, an updatable scheme that is secure only in the  model does not provide the intuitive security one would expect from key rotation: namely that after migrating to the new key, the old one becomes useless and no longer of value to the adversary. To the contrary, all previous keys still require strong protection or secure deletion.
model does not provide the intuitive security one would expect from key rotation: namely that after migrating to the new key, the old one becomes useless and no longer of value to the adversary. To the contrary, all previous keys still require strong protection or secure deletion.
The strongUP-IND-BI Model. In the stronger interpretation, \(\mathcal {A}\) can corrupt a set of arbitrary epochs, i.e., also before he makes the challenge query, but has to commit to them upfront. Whereas Everspaugh et al. [15] hand the adversary all keys already at the beginning, we let \(\mathcal {A}\) retrieve them sequentially via the \(\mathcal {O}_\mathsf {corrupt}(\mathsf {key}, \cdot )\) oracle in all epochs that he announced as corrupted in the beginning of the game.

The second winning condition forbids the adversary to receive any token that is connected to an epoch where \(\mathcal {A}\) knows the secret key. This can be seen as the bi-directionality of key updates hard-coded in the experiment, which is captured in our  definition via the definition of \(\mathcal {K}^*_\mathsf {bi}\). The third condition forbids any ciphertext updates towards a corrupted epoch.
definition via the definition of \(\mathcal {K}^*_\mathsf {bi}\). The third condition forbids any ciphertext updates towards a corrupted epoch.
4.2 Insecurity of  in the
in the  and
and  Model
Model
Everspaugh et al. [15] proposed a simple construction, termed  , as a secure ciphertext-independent updatable encryption scheme. We now show that this scheme is neither secure in the stronger interpretation of their model nor in our
, as a secure ciphertext-independent updatable encryption scheme. We now show that this scheme is neither secure in the stronger interpretation of their model nor in our  definition.
definition.
The  scheme relies on a standard symmetric encryption scheme \(\mathsf {SE}\) which it uses in a simple hybrid construction. Therein, every message gets encrypted under a fresh key x and x gets xor’d under the epoch key \(k_e\). For updating a ciphertext, only the part depending on \(k_e\) gets updated via the token \(\varDelta _{e+1} \leftarrow (k_{e} \oplus k_{e+1})\).
scheme relies on a standard symmetric encryption scheme \(\mathsf {SE}\) which it uses in a simple hybrid construction. Therein, every message gets encrypted under a fresh key x and x gets xor’d under the epoch key \(k_e\). For updating a ciphertext, only the part depending on \(k_e\) gets updated via the token \(\varDelta _{e+1} \leftarrow (k_{e} \oplus k_{e+1})\).
-
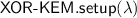 : return \(k_0 {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\)
: return \(k_0 {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\) -
 : \(k_{e+1} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\), \(\varDelta _{e+1} \leftarrow (k_{e} \oplus k_{e+1})\), return \(({k}_{e+1}, \varDelta _{e+1})\)
: \(k_{e+1} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\), \(\varDelta _{e+1} \leftarrow (k_{e} \oplus k_{e+1})\), return \(({k}_{e+1}, \varDelta _{e+1})\) -
 : \(x {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\), return \(C_e \leftarrow ((k_e \oplus x), \mathsf {SE}.\mathsf {enc}(x, m))\)
: \(x {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\), return \(C_e \leftarrow ((k_e \oplus x), \mathsf {SE}.\mathsf {enc}(x, m))\) -
 : parse \(C_e = (C^1,C^2)\), return \(C_{e+1} \leftarrow (( C^1 \oplus \varDelta _{e+1}),C^2)\)
: parse \(C_e = (C^1,C^2)\), return \(C_{e+1} \leftarrow (( C^1 \oplus \varDelta _{e+1}),C^2)\) -
 : parse \(C_e = (C^1,C^2)\), return \(\mathsf {SE}.\mathsf {dec} (k_e \oplus C^1, C^2)\)
: parse \(C_e = (C^1,C^2)\), return \(\mathsf {SE}.\mathsf {dec} (k_e \oplus C^1, C^2)\)
Attack against  . We now present a simple attack against the
. We now present a simple attack against the  scheme, for which we only require the adversary to learn one key in some epoch before the challenge epoch. Let this epoch be \(e < \tilde{e}\), to which \(\mathcal {A}\) commits before the game starts. In epoch e, \(\mathcal {A}\) requests the secret key \(k_e\) via \(\mathcal {O}_{\mathsf {corrupt}}(\mathsf {key}, e)\). and also makes a standard encryption query \(\mathcal {O}_{\mathsf {enc}}(m)\) receiving a ciphertext \(C_e =((k_e \oplus x), \mathsf {SE}.\mathsf {enc}(x, m))\). The adversary then computes \(x \leftarrow C^1_e \oplus k_e\), where \(C^1_e\) denotes the first part \((k_e \oplus x)\) of the ciphertext. Then, in all epochs from e to \(\tilde{e}\), the adversary requests an updated version of \({C}_e\) via \(\mathcal {O}_{\mathsf {upd}}(\cdot )\). Note that
scheme, for which we only require the adversary to learn one key in some epoch before the challenge epoch. Let this epoch be \(e < \tilde{e}\), to which \(\mathcal {A}\) commits before the game starts. In epoch e, \(\mathcal {A}\) requests the secret key \(k_e\) via \(\mathcal {O}_{\mathsf {corrupt}}(\mathsf {key}, e)\). and also makes a standard encryption query \(\mathcal {O}_{\mathsf {enc}}(m)\) receiving a ciphertext \(C_e =((k_e \oplus x), \mathsf {SE}.\mathsf {enc}(x, m))\). The adversary then computes \(x \leftarrow C^1_e \oplus k_e\), where \(C^1_e\) denotes the first part \((k_e \oplus x)\) of the ciphertext. Then, in all epochs from e to \(\tilde{e}\), the adversary requests an updated version of \({C}_e\) via \(\mathcal {O}_{\mathsf {upd}}(\cdot )\). Note that  forbids updates only towards but not from a corrupt key, and thus these queries are legitimate. Finally, in the challenge epoch \(\tilde{e}\), \(\mathcal {A}\) uses the updated (non-challenge) ciphertext \({C}_{\tilde{e}} = ((k_{\tilde{e}} \oplus x), \mathsf {SE}.\mathsf {enc}(x, m))\) and its previously computed x to derive the secret key \(k_{\tilde{e}}\) of the challenge epoch. Clearly, he can now trivially win the
forbids updates only towards but not from a corrupt key, and thus these queries are legitimate. Finally, in the challenge epoch \(\tilde{e}\), \(\mathcal {A}\) uses the updated (non-challenge) ciphertext \({C}_{\tilde{e}} = ((k_{\tilde{e}} \oplus x), \mathsf {SE}.\mathsf {enc}(x, m))\) and its previously computed x to derive the secret key \(k_{\tilde{e}}\) of the challenge epoch. Clearly, he can now trivially win the  game, and did not violate any of the winning restrictions. The same attack applies in our
game, and did not violate any of the winning restrictions. The same attack applies in our  game.
game.
In the  game, however, this attack is not possible, as \(\mathcal {A}\) does not see a secret key before the challenge epoch, and is also not allowed to update any ciphertext into a corrupt epoch (i.e., he cannot perform the same attack by updating a non-challenge ciphertext into a corrupt epoch after \(\tilde{e}\)).
game, however, this attack is not possible, as \(\mathcal {A}\) does not see a secret key before the challenge epoch, and is also not allowed to update any ciphertext into a corrupt epoch (i.e., he cannot perform the same attack by updating a non-challenge ciphertext into a corrupt epoch after \(\tilde{e}\)).
Weakening the  Model. A tempting easy “fix” would be to forbid any updates from a corrupted epoch into an honest epoch in the
Model. A tempting easy “fix” would be to forbid any updates from a corrupted epoch into an honest epoch in the  model. This would allow the
model. This would allow the  scheme to be proven secure, and at the same time preserve \(\mathcal {A}\)’s capability of corrupting keys before the challenge epoch.
scheme to be proven secure, and at the same time preserve \(\mathcal {A}\)’s capability of corrupting keys before the challenge epoch.
However, this “fix” would significantly weaken the guaranteed security, as it essentially disallows the adversary to see any updated ciphertexts after an attack. For instance, the following attack would be excluded by the model: Assume the adversary at some epoch e corrupts the secret key \(k_e\) and one ciphertext \(C_e\) from a large set of outsourced ciphertexts. Then, the key gets rotated into \(k_{e+1}\) and all ciphertexts get re-encrypted to the new key. In that new epoch \(e+1\), the adversary learns neither \(k_{e+1}\) nor the update token, but steals all ciphertexts from the database. Intuitively, confidentiality of these updated ciphertexts should be guaranteed, as the adversary never compromised the key and all ciphertexts in the same epoch. This attack would not be covered by the model though, and the  scheme becomes entirely insecure if such an attack happens, as it allows the adversary to decrypt all re-encrypted ciphertexts even though he never corrupted \(k_{e+1}\).
scheme becomes entirely insecure if such an attack happens, as it allows the adversary to decrypt all re-encrypted ciphertexts even though he never corrupted \(k_{e+1}\).
4.3  vs.
vs. 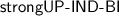 (and
(and  )
)
 serves as a separating example between the
serves as a separating example between the  and the two stronger
and the two stronger  ,
,  models, and both models are in fact strictly stronger than
models, and both models are in fact strictly stronger than  . Such a strict relation does not exist between
. Such a strict relation does not exist between  and
and  though: we show that both models are incomparable. Below we give the high-level ideas for the two separating examples, and refer to the full version [19] for their detailed descriptions as well as for the argumentation why
though: we show that both models are incomparable. Below we give the high-level ideas for the two separating examples, and refer to the full version [19] for their detailed descriptions as well as for the argumentation why  implies
implies  .
.
Separating Example I (strongUP-IND-BI  IND-ENC). The first separating example exploits the fact that in
IND-ENC). The first separating example exploits the fact that in  , the adversary is not allowed to update any ciphertext into a corrupt epoch, whereas
, the adversary is not allowed to update any ciphertext into a corrupt epoch, whereas  allows such updates for non-challenge ciphertexts. We derive a scheme \({\mathsf {UE}_{}}'\) from a secure \({\mathsf {UE}_{}}\) where we let the token \(\varDelta _{e+1}\) also contain an encryption \({C}_{ key }\) of the old key \(k_{e}\) under the new key \(k_{e+1}\). Further, when updating, \({\mathsf {UE}_{}}'\) appends \({C}_{key}\) to the updated ciphertext.
allows such updates for non-challenge ciphertexts. We derive a scheme \({\mathsf {UE}_{}}'\) from a secure \({\mathsf {UE}_{}}\) where we let the token \(\varDelta _{e+1}\) also contain an encryption \({C}_{ key }\) of the old key \(k_{e}\) under the new key \(k_{e+1}\). Further, when updating, \({\mathsf {UE}_{}}'\) appends \({C}_{key}\) to the updated ciphertext.
In the  game, this change cannot increase \(\mathcal {A}\)’s advantage as he is not allowed to see any token towards a corrupt epoch \(e^*\), nor make any updates towards \(e^*\). In all other epochs, \(C_{ key }\) is an encryption under a key unknown to the adversary. However, in the
game, this change cannot increase \(\mathcal {A}\)’s advantage as he is not allowed to see any token towards a corrupt epoch \(e^*\), nor make any updates towards \(e^*\). In all other epochs, \(C_{ key }\) is an encryption under a key unknown to the adversary. However, in the  game, \(\mathcal {A}\) can corrupt the secret key \(k_{\tilde{e}+1}\) in the epoch after he makes the challenge query, and update an arbitrary non-challenge ciphertext from \(\tilde{e}\) to \(\tilde{e}+1\) using the \(\mathcal {O}_\mathsf {upd} \) oracle. From there he extracts \({C}_{ key }\), decrypts \(k_{\tilde{e}}\) and can now trivially win the
game, \(\mathcal {A}\) can corrupt the secret key \(k_{\tilde{e}+1}\) in the epoch after he makes the challenge query, and update an arbitrary non-challenge ciphertext from \(\tilde{e}\) to \(\tilde{e}+1\) using the \(\mathcal {O}_\mathsf {upd} \) oracle. From there he extracts \({C}_{ key }\), decrypts \(k_{\tilde{e}}\) and can now trivially win the  game as he knows the secret key of the challenge epoch.
game as he knows the secret key of the challenge epoch.
Separating Example II (IND-ENC  strongUP-IND-BI). Our model is not strictly stronger than
strongUP-IND-BI). Our model is not strictly stronger than  , due to fact that we are more restrictive for ciphertexts that can be updated. Whereas we only allow honestly generated ciphertexts \(C_e\) to be updated (which is enforced by \(\mathcal {O}_\mathsf {upd} \) checking whether \(C_e \in \mathcal {L}\)),
, due to fact that we are more restrictive for ciphertexts that can be updated. Whereas we only allow honestly generated ciphertexts \(C_e\) to be updated (which is enforced by \(\mathcal {O}_\mathsf {upd} \) checking whether \(C_e \in \mathcal {L}\)),  is more generous and returns the update of any ciphertext (as they aim for authenticated encryption). This can be exploited to turn a secure scheme \({\mathsf {UE}_{}}\) into \({\mathsf {UE}_{}}''\) that is secure in our
is more generous and returns the update of any ciphertext (as they aim for authenticated encryption). This can be exploited to turn a secure scheme \({\mathsf {UE}_{}}\) into \({\mathsf {UE}_{}}''\) that is secure in our  model, but insecure according to
model, but insecure according to  . The idea is to modify the update algorithm, such that it returns the update token when it gets invoked with a special ciphertext, that would never occur for an honest encryption.
. The idea is to modify the update algorithm, such that it returns the update token when it gets invoked with a special ciphertext, that would never occur for an honest encryption.
In the  game, the update oracle then enables the adversary to obtain tokens in epochs where he would not be allowed to learn a token directly, leading to trivial wins without violating the winning condition. An adversary in our
game, the update oracle then enables the adversary to obtain tokens in epochs where he would not be allowed to learn a token directly, leading to trivial wins without violating the winning condition. An adversary in our  game cannot benefit from this modification, as it cannot poke the update oracle on the adversarially crafted ciphertext. We explain in the full version of this paper why the same idea does not apply for the
game cannot benefit from this modification, as it cannot poke the update oracle on the adversarially crafted ciphertext. We explain in the full version of this paper why the same idea does not apply for the  model, which is in fact strictly weaker than
model, which is in fact strictly weaker than  .
.
4.4 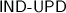 vs.
vs. 
Our  definition is similar in spirit to the re-encryption indistinguishability notion
definition is similar in spirit to the re-encryption indistinguishability notion  by Everspaugh et al. [15], which captures post-compromise security of updates as well. However, the
by Everspaugh et al. [15], which captures post-compromise security of updates as well. However, the  notion was only proposed for ciphertext-dependent schemes. Note that the difference between ciphertext-dependent and independent schemes has a significant impact on the achievable security: a single update token in the ciphertext-independent setting has much more functionality than in ciphertext-dependent schemes, which in turn gives the adversary more power when he compromises such tokens. Thus, no ciphertext-independent scheme can satisfy the
notion was only proposed for ciphertext-dependent schemes. Note that the difference between ciphertext-dependent and independent schemes has a significant impact on the achievable security: a single update token in the ciphertext-independent setting has much more functionality than in ciphertext-dependent schemes, which in turn gives the adversary more power when he compromises such tokens. Thus, no ciphertext-independent scheme can satisfy the  definition. Our
definition. Our  definition formalizes this extra power in ciphertext-independent schemes in a way that carefully excludes trivial wins but still captures strong post-compromise guarantees. The aspect that
definition formalizes this extra power in ciphertext-independent schemes in a way that carefully excludes trivial wins but still captures strong post-compromise guarantees. The aspect that  allows adaptive corruptions, whereas
allows adaptive corruptions, whereas  only considers static ones, makes both definitions incomparable.
only considers static ones, makes both definitions incomparable.
Interestingly, in the ciphertext-dependent setting, this property has a somewhat “esoteric” flavor as it got motivated by an exfiltration attack where the adversary fully breaks into both the host and owner, compromising all ciphertexts and keys but is only able to extract a small amount of information at that time. The re-encryption indistinguishability should then guarantee that when the key gets rotated and the adversary compromises all the updated ciphertexts again (but not the new key), the previously extracted information becomes useless. This seems to be a somewhat contrived attack scenario, and might lead to the impression that such update indistinguishability is rather an optional feature. This is not the case for ciphertext-independent schemes: without the dedicated  property an updatable encryption scheme does not guarantee any security of the updated ciphertexts when an old key gets compromised!
property an updatable encryption scheme does not guarantee any security of the updated ciphertexts when an old key gets compromised!
5 Constructions
We analyze several constructions of updatable encryption with respect to our security notions of indistinguishability of encryptions ( ) and updates (
) and updates ( ). First, we analyze the simple double-encryption construction that is purely based on symmetric primitives (Sect. 5.1). Unfortunately, the scheme cannot satisfy our strong security notions. We formulate the additional constraints on the adversarial behavior that suffices to prove its security in relaxed versions of our
). First, we analyze the simple double-encryption construction that is purely based on symmetric primitives (Sect. 5.1). Unfortunately, the scheme cannot satisfy our strong security notions. We formulate the additional constraints on the adversarial behavior that suffices to prove its security in relaxed versions of our  and
and  models.
models.
We then proceed to less efficient but more secure schemes, starting with the \(\mathsf {BLMR} \) construction by Boneh et al. [10] based on key-homomorphic PRFs (Sect. 5.2). We show that the original \(\mathsf {BLMR} \) scheme satisfies  but not
but not  , and also propose a slight modification \(\mathsf {BLMR+}\) that improves the latter and achieves a weak form of update indistinguishability.
, and also propose a slight modification \(\mathsf {BLMR+}\) that improves the latter and achieves a weak form of update indistinguishability.
In Sect. 5.3, we introduce a new ElGamal-based scheme \(\mathsf {RISE}\) and show that it fully achieves both of our strong security definitions. While proposing a “public-key solution” for a symmetric key primitive might appear counter-intuitive at first, we stress that the efficiency is roughly comparable to that of \(\mathsf {BLMR}\) under known instantiations for the key-homomorphic PRF (same number of exponentiations). Also, taking advantage of the underlying group operations allows us to get full  security.
security.
All of our schemes allow to infer token from two subsequent keys and bi-directional updates of the ciphertexts and keys. Thus, all theorems are with respect to the leakage profile \((\mathcal {T}^*, \mathcal {K}_\mathsf {bi}^*, \mathcal {C}^*_\mathsf {bi})\) as defined in Sect. 3.3.
In the Appendix A, we additionally describe and analyze a symmetric KEM construction  , which is widely used in practice since it does not require an (expensive) re-encryption of the payload data upon key rotation. This scheme is, however, better suited for deployment within the cloud infrastructure, because it requires the encryption keys to be sent to the host performing the re-encryption. Furthermore, the fact that the data is not re-encrypted makes ciphertexts fully linkable. We therefore show only basic encryption security and under a weak adversary model.
, which is widely used in practice since it does not require an (expensive) re-encryption of the payload data upon key rotation. This scheme is, however, better suited for deployment within the cloud infrastructure, because it requires the encryption keys to be sent to the host performing the re-encryption. Furthermore, the fact that the data is not re-encrypted makes ciphertexts fully linkable. We therefore show only basic encryption security and under a weak adversary model.
5.1 Double Encryption (\(\mathsf {2ENC} \))
An approach that is based only on symmetric encryption is to first encrypt the plaintext under an “inner key,” and subsequently encrypt the resulting ciphertext under a second, “outer key.” In each epoch, the outer key is changed, and the ciphertext is updated by decrypting the outer encryption and re-encrypting under the new key. This scheme has been proposed by Ivan and Dodis [18] as symmetric uni-directional proxy re-encryption.Footnote 1 It has also appeared in other contexts, such as so-called “over-encryption” for access revocation in cloud storage systems [4]. More formally, this scheme can be phrased as an updatable encryption scheme \(\mathsf {2ENC} \) as follows.
-
\(\mathsf {2ENC}.\mathsf {setup} (\lambda )\) : \({k}_{0}^o{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\), \({k}_{}^i {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\), return \({k}_{0} \leftarrow ({k}_{0}^o, k^i)\)
-
 : parse \({k}_{e} = ({k}_{e}^o, {k}_{}^i)\), create \({k}_{e+1}^o {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\),
: parse \({k}_{e} = ({k}_{e}^o, {k}_{}^i)\), create \({k}_{e+1}^o {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\),\(\varDelta _{e+1} \leftarrow ({k}_{e}^o, {k}_{e+1}^o)\), \({k}_{e+1} \leftarrow ({k}_{e+1}^o, {k}_{}^i)\),
return \(({k}_{e+1}, \varDelta _{e+1})\)
-
\(\mathsf {2ENC}.\mathsf {enc}({k}_{e},m)\) : parse \({k}_{e} = ({k}_{e}^o, {k}_{}^i) \leftarrow {k}_{e}\),
return \(C_e \leftarrow \mathsf {SE.enc}({k}_{e}^o, \mathsf {SE.enc}({k}_{}^i, m))\)
-
\(\mathsf {2ENC}.\mathsf {upd} (\varDelta _{e+1},C_e)\) : parse \(\varDelta _{e+1} = ({k}_{e}^o, {k}_{e+1}^o)\),
return \(C_{e+1} \leftarrow \mathsf {SE.enc}({k}_{e+1}^o,\mathsf {SE.dec}({k}_{e}^o, C_e))\)
-
\(\mathsf {2ENC}.\mathsf {dec} ({k}_{e},C_e)\) : parse \({k}_{e} = ({k}_{e}^o, {k}_{}^i) \), return \(\mathsf {SE.dec}({k}_{e}^o, \mathsf {SE.dec}({k}_{}^i, C))\)
Clearly this scheme does not achieve our desired  security: A ciphertext can be decrypted if an adversary sees the secret key of some epoch and one of the tokens relating to the epoch where he learned the ciphertext. However, we show that this is the only additional attack, i.e., if the adversary never sees such a combination of tokens and keys, then the scheme is secure, which is formalized by the following theorem.
security: A ciphertext can be decrypted if an adversary sees the secret key of some epoch and one of the tokens relating to the epoch where he learned the ciphertext. However, we show that this is the only additional attack, i.e., if the adversary never sees such a combination of tokens and keys, then the scheme is secure, which is formalized by the following theorem.
Theorem 2
(\(\mathsf {2ENC} \) is weakly  secure). Let \(\mathsf {SE}\) be an
secure). Let \(\mathsf {SE}\) be an  -secure encryption scheme, then \(\mathsf {2ENC} \) is (weakly)
-secure encryption scheme, then \(\mathsf {2ENC} \) is (weakly)  -secure if the following additional condition holds: If \(\mathcal {A}\) makes any query to \(\mathcal {O}_\mathsf {corrupt}(\mathsf {key}, \cdot )\), then, for any challenge-equal epoch \(e \in \mathcal {C}^*\), \(\mathcal {A} \) must not call \(\mathcal {O}_\mathsf {corrupt}(\mathsf {token}, \cdot )\) for epochs e or \(e+1\).
-secure if the following additional condition holds: If \(\mathcal {A}\) makes any query to \(\mathcal {O}_\mathsf {corrupt}(\mathsf {key}, \cdot )\), then, for any challenge-equal epoch \(e \in \mathcal {C}^*\), \(\mathcal {A} \) must not call \(\mathcal {O}_\mathsf {corrupt}(\mathsf {token}, \cdot )\) for epochs e or \(e+1\).
The proof of this theorem turns out to be surprisingly subtle and is provided in the full version [19]. As intuitively expected, it consists of two reductions to the  security of \(\mathsf {SE}\), but the reduction for the outer encryption part is complicated by the fact that \(\mathcal {A} \) may call either \(\mathcal {O}_\mathsf {corrupt}\) or \(\mathcal {O}_\mathsf {upd\tilde{C}} \) adaptively and in multiple epochs. Instead of guessing all epochs, which would lead to a large loss in tightness, we devise a specific hybrid argument and formalize the intuition that only epochs with a query to \(\mathcal {O}_\mathsf {upd\tilde{C}} \) can help \(\mathcal {A} \) in gaining advantage.
security of \(\mathsf {SE}\), but the reduction for the outer encryption part is complicated by the fact that \(\mathcal {A} \) may call either \(\mathcal {O}_\mathsf {corrupt}\) or \(\mathcal {O}_\mathsf {upd\tilde{C}} \) adaptively and in multiple epochs. Instead of guessing all epochs, which would lead to a large loss in tightness, we devise a specific hybrid argument and formalize the intuition that only epochs with a query to \(\mathcal {O}_\mathsf {upd\tilde{C}} \) can help \(\mathcal {A} \) in gaining advantage.
It is also easy to see that the double encryption scheme is not  secure: The inner ciphertext remains static and an adversary seeing tokens that allow him to unwrap the outer encryption can trivially link ciphertexts across epochs. But we again show that this is the only attack, i.e., \(\mathsf {2ENC} \) achieves a weak form of
secure: The inner ciphertext remains static and an adversary seeing tokens that allow him to unwrap the outer encryption can trivially link ciphertexts across epochs. But we again show that this is the only attack, i.e., \(\mathsf {2ENC} \) achieves a weak form of  security if the adversary is restricted to learn at most one update token \({\varDelta }_{e}\) for an epoch e for which he also obtained the challenge ciphertext in epochs e or \(e-1\).
security if the adversary is restricted to learn at most one update token \({\varDelta }_{e}\) for an epoch e for which he also obtained the challenge ciphertext in epochs e or \(e-1\).
Theorem 3
(\(\mathsf {2ENC} \) is weakly  secure). Let \(\mathsf {SE}\) be an
secure). Let \(\mathsf {SE}\) be an  -secure encryption scheme, then \(\mathsf {2ENC} \) is (weakly)
-secure encryption scheme, then \(\mathsf {2ENC} \) is (weakly)  -secure if the following additional condition holds: For any challenge-equal epoch \(e \in \mathcal {C}^*\), \(\mathcal {A} \) must not call \(\mathcal {O}_\mathsf {corrupt}(\mathsf {token}, \cdot )\) for epochs e or \(e+1\).
-secure if the following additional condition holds: For any challenge-equal epoch \(e \in \mathcal {C}^*\), \(\mathcal {A} \) must not call \(\mathcal {O}_\mathsf {corrupt}(\mathsf {token}, \cdot )\) for epochs e or \(e+1\).
The proof follows along the lines of that for Theorem 2, with the main difference that we have to distinguish between the cases where the single special query \(\mathcal {O}_\mathsf {corrupt}(\mathsf {token}, e)\) occurs before or after the challenge epoch \({\tilde{e}}\). The proof is given in the full version of this paper [19].
5.2 Schemes from Key-Homomorphic PRFs (\(\mathsf {BLMR} \) and \(\mathsf {BLMR+} \))
Boneh et al. [10] proposed an updatable encryption scheme based on key-homomorphic pseudorandom functions, to which we will refer to as \(\mathsf {BLMR}\)-scheme. We first recall the notion of key-homomorphic PRFs and then present the \(\mathsf {BLMR} \) and our improved \(\mathsf {BLMR+} \) scheme.
Definition 4
(Key-homomorphic PRF [9]). Consider an efficiently computable function \(\mathsf {F}: \mathcal {K}\times \mathcal {X}\rightarrow \mathcal {Y}\) such that \((\mathcal {K}, \oplus )\) and \((\mathcal {Y},\otimes )\) are both groups. We say that \(\mathsf {F}\) is a key-homomorphic PRF if the following properties hold:
-
1.
\(\mathsf {F}\) is a secure pseudorandom function.
-
2.
For every \(k_1,k_2 \in \mathcal {K}\), and every \(x \in \mathcal {X}\): \(\mathsf {F}(k_1, x) \otimes \mathsf {F}(k_2,x) = \mathsf {F}((k_1 \oplus k_2),x)\)
A simple example of a secure key-homomorphic PRF is the function \(\mathsf {F}(k, x) =\mathsf {H}(x)^k\) where \(\mathcal {Y}= \mathbb {G}\) is an additive group in which the DDH assumption holds, and \(\mathsf {H}\) is a random oracle [23].
Based on such a key-homomorphic PRF \(\mathsf {F}\), the \(\mathsf {BLMR} \) construction is described as the following scheme:
-
\(\mathsf {BLMR}.\mathsf {setup} (\lambda )\) : compute \({k}_{0} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {F}.\mathsf {kgen}(\lambda )\), return \({k}_{0}\)
-
 : \({k}_{e+1} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {F}.\mathsf {kgen}(\lambda )\), return \(({k}_{e+1}, ({k}_{e} \oplus {k}_{e+1}))\)
: \({k}_{e+1} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {F}.\mathsf {kgen}(\lambda )\), return \(({k}_{e+1}, ({k}_{e} \oplus {k}_{e+1}))\) -
\(\mathsf {BLMR}.\mathsf {enc}({k}_{e},m)\) : \(N {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathcal {X}\), return \(((\mathsf {F}({k}_{e}, N) \otimes m), N)\)
-
\(\mathsf {BLMR}.\mathsf {dec} ({k}_{e},C_e)\) : parse \(C_e = (C_1, N)\), return \(m \leftarrow C_1 \otimes \mathsf {F}({k}_{e},N)\).
-
\(\mathsf {BLMR}.\mathsf {upd} ({\varDelta }_{e+1}, C_e)\) : parse \(C_e = (C_1, N)\), return \(((C_1 \otimes \mathsf {F}({\varDelta }_{e+1},N)), N)\)
Indeed, the subsequent theorem shows that \(\mathsf {BLMR}\) is  -secure.
-secure.
Theorem 4
(\(\mathsf {BLMR} \) is  -secure). Let \(\mathsf {F}\) be a key-homomorphic PRF where \(\mathsf {F}.\mathsf {kgen}(\lambda )\) returns uniformly random elements from \(\mathcal {K}\), then \(\mathsf {BLMR} \) is
-secure). Let \(\mathsf {F}\) be a key-homomorphic PRF where \(\mathsf {F}.\mathsf {kgen}(\lambda )\) returns uniformly random elements from \(\mathcal {K}\), then \(\mathsf {BLMR} \) is  -secure.
-secure.
The proof uses an alternative characterization of PRF (as in the original proof in [10]) together with the techniques already used in the proofs of the \(\mathsf {2ENC}\) scheme. The proof is given in the full paper [19]. The \(\mathsf {BLMR} \) scheme does not achieve the notion  of update-indistinguishability though, as the second part of the ciphertext remains static throughout the updates. This might have inspired the change to the ciphertext-dependent setting in the full version of Boneh et al.’s paper [9]. Ciphertext-dependent updates, however, have the disadvantage that the key owner must produce one update token for each ciphertext to be updated. We show that a mild form of
of update-indistinguishability though, as the second part of the ciphertext remains static throughout the updates. This might have inspired the change to the ciphertext-dependent setting in the full version of Boneh et al.’s paper [9]. Ciphertext-dependent updates, however, have the disadvantage that the key owner must produce one update token for each ciphertext to be updated. We show that a mild form of  security can be achieved in the ciphertext-independent setting via a simple modification to the \(\mathsf {BLMR} \) scheme.
security can be achieved in the ciphertext-independent setting via a simple modification to the \(\mathsf {BLMR} \) scheme.
The \(\mathsf {BLMR+} \) scheme. The \(\mathsf {BLMR+} \) scheme follows the basic structure of \(\mathsf {BLMR}\), but additionally encrypts the nonce. In more detail, in every epoch the owner also generates a second key \(k'_e {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\) of a symmetric encryption scheme and encrypts the nonce-part N of each ciphertext under that key. In \(\mathsf {BLMR+}\), we simply include the old and new symmetric key into the update token and let the host re-encrypt the nonce.
The choice to simply reveal both keys might seem odd, but (in certain attack scenarios) it does not reveal more information to a corrupt host than what every updatable encryption scheme leaks anyway. Looking at two consecutive epochs, a corrupt host knows which updated and old ciphertext belong together – as he generated them – and thus letting him re-encrypt a static nonce does not reveal any additional information. The main advantage of \(\mathsf {BLMR+} \) over \(\mathsf {BLMR} \) is that an adversary seeing only (updated) ciphertexts of different epochs cannot tell anymore which of them belong together. Clearly, this unlinkability is limited, though, as an adversary can still link ciphertexts whenever he also learned a related token which allows him to decrypt the static nonce.
In more detail, this modification results in the following scheme \(\mathsf {BLMR+} \):
-
\(\mathsf {BLMR+}.\mathsf {setup} (\lambda )\) : \(k^1_0 {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {F}.\mathsf {kgen}(\lambda )\), \(k^2_0 {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\), return \({k}_{0} \leftarrow (k^1_0, k^2_0)\)
-
 : parse \({k}_{e} = (k^1_e, k^2_e)\),
: parse \({k}_{e} = (k^1_e, k^2_e)\),create \(k^1_{e+1} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {F}.\mathsf {kgen}(\lambda )\), \(k^2_{e+1} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\),
\({k}_{e+1} \leftarrow (k^1_{e+1}, k^2_{e+1})\), \({\varDelta }_{e+1} \leftarrow (k^1_{e} \oplus k^1_{e+1}, (k^2_{e}, k^2_{e+1}))\),
return \(({k}_{e+1}, {\varDelta }_{e+1})\)
-
\(\mathsf {BLMR+}.\mathsf {enc}({k}_{e},m)\) : parse \({k}_{e} = (k^1_e, k^2_e)\), draw \(N {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathcal {X}\),
\(C^1 \leftarrow \mathsf {F}(k^1_e, N) \otimes m\), \(C^2 {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {enc}(k^2_e, N)\), return \(C_e \leftarrow (C^1,C^2)\)
-
\(\mathsf {BLMR+}.\mathsf {dec} ({k}_{e},C_e)\) : parse \({k}_{e} = (k^1_e, k^2_e)\) and \(C_e = (C^1,C^2)\),
\(N \leftarrow \mathsf {SE}.\mathsf {dec} (k^2_e, C^2)\), return \(m \leftarrow C^1 \otimes \mathsf {F}(k^1_e,N)\)
-
\(\mathsf {BLMR+}.\mathsf {upd} ({\varDelta }_{e+1}, C_e)\) : parse \({\varDelta }_{e+1} = (\varDelta '_{e+1}, (k^2_{e}, k^2_{e+1}))\) and \(C_e = (C^1_e,C^2_e)\),
\(N \leftarrow \mathsf {SE}.\mathsf {dec} (k^2_e, C^2)\), \(C^1_{e+1} \leftarrow C^1_e \otimes \mathsf {F}(\varDelta '_{e+1},N)\), \(C^2_{e+1} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {enc}(k^2_{e+1}, N)\),
return \(C_{e+1} \leftarrow (C^1_{e+1},C^2_{e+1})\)
We first state the following corollary as an easy extension of Theorem 4 on \(\mathsf {BLMR} \). The encryption of the nonce can be easily simulated in the reduction.
Corollary 1
The \(\mathsf {BLMR+} \) scheme is  secure.
secure.
We then prove that the modified \(\mathsf {BLMR+}\) scheme described above indeed achieves a weak form of  security. The intuition behind the level of security specified in the following theorem is that knowing either a token or the key of the ciphertexts later used in the challenge in a round before the challenge allows the adversary to decrypt the nonce. Also, obtaining the challenge ciphertext and a related token after the challenge query allows the adversary to decrypt the nonce. To obtain unlinkability, we cannot allow the adversary to access the nonce both before and after the challenge query in epoch \(\tilde{e}\). The theorem formalizes that we have security unless the adversary gains this access.
security. The intuition behind the level of security specified in the following theorem is that knowing either a token or the key of the ciphertexts later used in the challenge in a round before the challenge allows the adversary to decrypt the nonce. Also, obtaining the challenge ciphertext and a related token after the challenge query allows the adversary to decrypt the nonce. To obtain unlinkability, we cannot allow the adversary to access the nonce both before and after the challenge query in epoch \(\tilde{e}\). The theorem formalizes that we have security unless the adversary gains this access.
Theorem 5
(\(\mathsf {BLMR+} \) is weakly  secure). Let \(\mathsf {F}\) be a key-homomorphic PRF, and assume that all elements of \(\mathcal {X}\) are encoded as strings of the same length. Let \(\mathsf {SE}\) be a
secure). Let \(\mathsf {F}\) be a key-homomorphic PRF, and assume that all elements of \(\mathcal {X}\) are encoded as strings of the same length. Let \(\mathsf {SE}\) be a  -secure symmetric encryption scheme. Then, the scheme \(\mathsf {BLMR+} \) is (weakly)
-secure symmetric encryption scheme. Then, the scheme \(\mathsf {BLMR+} \) is (weakly)  -secure if the following additional condition holds: Let \(e_\mathsf {first}\) denote the epoch in which the first ciphertext that is later used as challenge \(C_0\) or \(C_1\) was encrypted. If there exist some \(e^* \in \{e_\mathsf {first}, \dots , {\tilde{e}}-1\}\) where \(e^* \in \mathcal {K}^* \cup \mathcal {T}^*\), i.e., \(\mathcal {A}\) knows the secret key \({k}_{e^*}\) or token \(\varDelta _{e^*}\), then for any challenge-equal epoch \(e \in \mathcal {C}^*\), \(\mathcal {A} \) must not call \(\mathcal {O}_\mathsf {corrupt}(\mathsf {token}, \cdot )\) for epochs e or \(e+1\).
-secure if the following additional condition holds: Let \(e_\mathsf {first}\) denote the epoch in which the first ciphertext that is later used as challenge \(C_0\) or \(C_1\) was encrypted. If there exist some \(e^* \in \{e_\mathsf {first}, \dots , {\tilde{e}}-1\}\) where \(e^* \in \mathcal {K}^* \cup \mathcal {T}^*\), i.e., \(\mathcal {A}\) knows the secret key \({k}_{e^*}\) or token \(\varDelta _{e^*}\), then for any challenge-equal epoch \(e \in \mathcal {C}^*\), \(\mathcal {A} \) must not call \(\mathcal {O}_\mathsf {corrupt}(\mathsf {token}, \cdot )\) for epochs e or \(e+1\).
The proof of this theorem is essentially a combination of the techniques used in the proofs of Theorems 3 and 4. It is provided in the full version [19].
5.3 Updatable Encryption Based on ElGamal (\(\mathsf {RISE} \))
We finally present a scheme that achieves both strong notions of indistinguishability of encryptions ( ) and updates (
) and updates ( ). This scheme uses the classical proxy re-encryption idea based on ElGamal that was originally proposed by Blaze et al. [8], but uses it in the secret-key setting. This alone would not be secure though, as parts of the ciphertext would remain static. What we additionally exploit is that ElGamal ciphertexts can be re-randomized by knowing only the public key. Thus, we add the “public-key” element of the epoch to the token and perform a re-randomization whenever a ciphertext gets updated. This makes it the first of the considered schemes where the update algorithm is probabilistic. Interestingly, probabilistic updates are not allowed in the work by Everspaugh et al. [15] which require updates to be deterministic such that the challenger in the security game can keep track of the challenge ciphertexts. Further, in the security proof we also rely on the key anonymity property [5] of ElGamal, which guarantees that ciphertexts do not leak information about the public key under which they are encrypted.
). This scheme uses the classical proxy re-encryption idea based on ElGamal that was originally proposed by Blaze et al. [8], but uses it in the secret-key setting. This alone would not be secure though, as parts of the ciphertext would remain static. What we additionally exploit is that ElGamal ciphertexts can be re-randomized by knowing only the public key. Thus, we add the “public-key” element of the epoch to the token and perform a re-randomization whenever a ciphertext gets updated. This makes it the first of the considered schemes where the update algorithm is probabilistic. Interestingly, probabilistic updates are not allowed in the work by Everspaugh et al. [15] which require updates to be deterministic such that the challenger in the security game can keep track of the challenge ciphertexts. Further, in the security proof we also rely on the key anonymity property [5] of ElGamal, which guarantees that ciphertexts do not leak information about the public key under which they are encrypted.
The use of public-key techniques for secret-key updatable encryption may appear unnecessary. We emphasize, however, that previous constructions are based on key-homomorphic PRFs, all instantiations of which are based on such techniques as well. By contrast, the direct use of the group structure without the intermediate abstraction allows us to implement the re-randomization and thereby achieve full  security.
security.
In fact, in terms of exponentiations, an encryption in our \(\mathsf {RISE} \) scheme is as efficient as in \(\mathsf {BLMR} \) and in Everspaugh et al.’s. ReCrypt scheme [15], whereas the computations of update tokens and ciphertext updates are even more efficient than in [15] due to the ciphertext-independent setting of our work.
Let \((\mathbb {G}, g, q)\) be system parameters available as CRS such that the DDH problem is hard w.r.t. \(\lambda \), i.e., q is a \(\lambda \)-bit prime. The scheme \(\mathsf {RISE} \) is described as follows.
-
\(\mathsf {RISE}.\mathsf {setup} (\lambda )\) : \(x {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathbb {Z}_ q ^*\), set \({k}_{0} \leftarrow (x, g^{x})\), return \({k}_{0}\)
-
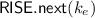 : parse \({k}_{e} = (x, y)\), draw \(x' {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathbb {Z}_ q ^*\),
: parse \({k}_{e} = (x, y)\), draw \(x' {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathbb {Z}_ q ^*\),\({k}_{e+1}\leftarrow (x', g^{x'})\), \({\varDelta }_{e+1} \leftarrow (x'/x, g^{x'})\) return \(({k}_{e+1}, {\varDelta }_{e+1})\)
-
\(\mathsf {RISE}.\mathsf {enc}({k}_{e},m)\) : parse \({k}_{e} = (x,y)\), \(r{\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathbb {Z}_ q \), return \(C_e \leftarrow ({y}^r, g^r m )\)
-
\(\mathsf {RISE}.\mathsf {dec} ({k}_{e},C_e)\) : parse \({k}_{e} = (x,y)\) and \(C_e = (C_{1} ,C_{2})\), return \(m' \leftarrow C_{2} \cdot C_{1}^{-1/{x}}\)
-
\(\mathsf {RISE}.\mathsf {upd} ({\varDelta }_{e+1}, C_e)\) : parse \({\varDelta }_{e+1} = (\varDelta , y')\) and \(C_e = (C_1,C_2)\),
\(r' {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathbb {Z}_ q \), \(C'_1 \leftarrow C_1^{\varDelta } \cdot {y'}^{r'}\), \(C'_2 \leftarrow C_2 \cdot {g}^{r'}\), return \(C_{e+1} \leftarrow (C'_1,C'_2)\)
The keys x for the encryption scheme are chosen from \(\mathbb {Z}_ q ^*\) instead of \(\mathbb {Z}_ q \) as usual. The reason is that the update is multiplicative, and this restriction makes sure that each key is uniformly random in \(\mathbb {Z}_ q ^*\). As this changes the distribution only negligibly, the standard Diffie-Hellman argument still applies. (However, the adaptation simplifies the security proof.)
The detailed proofs of the following theorems are provided in the full version of this paper [19].
Theorem 6
(\(\mathsf {RISE} \) is  secure). The updatable encryption scheme \(\mathsf {RISE} \) is
secure). The updatable encryption scheme \(\mathsf {RISE} \) is  secure under the DDH assumption.
secure under the DDH assumption.
On a high-level, the proof exploits two properties of ElGamal encryption. First, a re-randomized ciphertext has the same distribution as a fresh encryption of the same plaintext. Second, as ElGamal encryption is key-anonymous [5], i.e., encryptions under two different public keys are indistinguishable, the adversary cannot distinguish between encryptions under the actual round key and encryptions under an independent, random key. These observations are used in game hops to make the challenge ciphertext independent from the information that the adversary learns by querying the other oracles. The remainder is a reduction to the DDH assumption, which underlies the security of ElGamal.
We also show that the scheme \(\mathsf {RISE} \) is unlinkable. This property is mainly achieved by the re-randomization of the updates, but also leverages the key anonymity of ElGamal ciphertexts.
Theorem 7
(\(\mathsf {RISE} \) is  secure). The updatable encryption scheme \(\mathsf {RISE} \) is
secure). The updatable encryption scheme \(\mathsf {RISE} \) is  secure under the DDH assumption.
secure under the DDH assumption.
The proof follows roughly along the same lines as that of Theorem 6. It is complicated a bit by the fact that, in contrast to  , non-updated versions of the challenge-ciphertexts exist in the game even prior to the actual challenge epoch, which means that in the reduction we have to guess certain parameters, such as the epochs directly preceding the challenge epoch in which the adversary obtains update tokens, to keep the simulation consistent. Nevertheless, we show that, with a proper construction of the hybrid argument, the loss remains polynomial.
, non-updated versions of the challenge-ciphertexts exist in the game even prior to the actual challenge epoch, which means that in the reduction we have to guess certain parameters, such as the epochs directly preceding the challenge epoch in which the adversary obtains update tokens, to keep the simulation consistent. Nevertheless, we show that, with a proper construction of the hybrid argument, the loss remains polynomial.
One might wonder whether one could more generally build a secure updatable encryption scheme from any secure symmetric proxy re-encryption with key-anonymity that additionally allows public re-randomization of ciphertexts. For that analysis one would need a security notion for such a primitive schemes that also allows adaptive corruptions as in our models. However, so far, even for plain (symmetric) proxy re-encryption adaptive corruptions have only been considered for schemes that are uni-directional and single-hop, i.e., where the re-encryption capabilities would not be sufficient for updatable encryption.
6 Conclusion and Open Problems
We have provided a comprehensive model for ciphertext-independent updatable encryption schemes, complementing the recent work of Everspaugh et al. [15] that focuses on ciphertext-dependent schemes. Ciphertext-independent schemes are clearly superior in terms of efficiency and ease-of-use when key rotation is required for large volumes of ciphertexts, whereas ciphertext-dependent solutions give a more fine-grained control over the updatable information.
We formalized updatable encryption and its desired properties in the strict sequential manner it will be used, avoiding the ambiguity of previous security models. Our two notions  and
and  guarantee that fresh encryptions and updated ciphertext are secure even if an adversary can adaptively corrupt several keys and tokens before and after learning the ciphertexts.
guarantee that fresh encryptions and updated ciphertext are secure even if an adversary can adaptively corrupt several keys and tokens before and after learning the ciphertexts.
Somewhat surprisingly, and contradictory to the claim in [15], we have shown that the  scheme is not a secure ciphertext-independent schemes in such a strong sense. For the (existing) schemes \(\mathsf {2ENC}\), \(\mathsf {BLMR}\), \(\mathsf {BLMR+}\), and
scheme is not a secure ciphertext-independent schemes in such a strong sense. For the (existing) schemes \(\mathsf {2ENC}\), \(\mathsf {BLMR}\), \(\mathsf {BLMR+}\), and  , we formalized the security of the schemes by specifying precisely the conditions on the adversary under which a weak form of
, we formalized the security of the schemes by specifying precisely the conditions on the adversary under which a weak form of  and
and  security is achieved. We also specified a scheme that builds on ElGamal encryption. By additionally exploiting the algebraic structure of the underlying groups, instead of using the key-homomorphic PRF abstraction as in previous works, we were able to build a scheme that fully achieves our strong security notions while being at least as efficient as existing schemes that are either weaker or require ciphertext-dependent tokens.
security is achieved. We also specified a scheme that builds on ElGamal encryption. By additionally exploiting the algebraic structure of the underlying groups, instead of using the key-homomorphic PRF abstraction as in previous works, we were able to build a scheme that fully achieves our strong security notions while being at least as efficient as existing schemes that are either weaker or require ciphertext-dependent tokens.
All schemes we analyze allow to infer tokens from keys, and enable bi-directional updates of ciphertexts and keys, whereas an ideal updatable encryption scheme should only allow uni-directional updates of ciphertexts. Building such an ideal scheme is related to the open challenge of building proxy re-encryption schemes that are uni-directional, multi-hop and collusion-resistant. Yet, while most proxy re-encryption work is in the public-key setting, updatable encryption has secret keys, so the construction of schemes with similar properties may be easier and is an interesting and challenging open problem.
Notes
- 1.
It is uni-directional in a proxy re-encryption scheme; the proxy removes the outer layer. As an updatable scheme, which replaces the outer layer, it is bi-directional.
- 2.
In OpenStack Swift, for instance, the “proxy server” nodes have access to the keys, whereas the role of the “object server” nodes is to store the ciphertext.
References
Ananth, P., Cohen, A., Jain, A.: Cryptography with updates. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part II. LNCS, vol. 10211, pp. 445–472. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_15
Ateniese, G., Benson, K., Hohenberger, S.: Key-private proxy re-encryption. In: Fischlin, M. (ed.) CT-RSA 2009. LNCS, vol. 5473, pp. 279–294. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00862-7_19
Ateniese, G., Fu, K., Green, M., Hohenberger, S.: Improved proxy re-encryption schemes with applications to secure distributed storage. ACM Trans. Inf. Syst. Secur. 9(1), 1–30 (2006)
Bacis, E., De Capitani di Vimercati, S., Foresti, S., Paraboschi, S., Rosa, M., Samarati, P.: Access control management for secure cloud storage. In: Deng, R., Weng, J., Ren, K., Yegneswaran, V. (eds.) SecureComm 2016. LNICST, vol. 198, pp. 353–372. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-59608-2_21
Bellare, M., Boldyreva, A., Desai, A., Pointcheval, D.: Key-privacy in public-key encryption. In: Boyd, C. (ed.) ASIACRYPT 2001. LNCS, vol. 2248, pp. 566–582. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45682-1_33
Bellare, M., Singh, A.C., Jaeger, J., Nyayapati, M., Stepanovs, I.: Ratcheted encryption and key exchange: the security of messaging. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part III. LNCS, vol. 10403, pp. 619–650. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_21
Berners-Lee, E.: Improved security notions for proxy re-encryption to enforce access control. Cryptology ePrint Archive, Report 2017/824 (2017). http://eprint.iacr.org/2017/824
Blaze, M., Bleumer, G., Strauss, M.: Divertible protocols and atomic proxy cryptography. In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 127–144. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054122
Boneh, D., Lewi, K., Montgomery, H., Raghunathan, A.: Key homomorphic PRFs and their applications. Cryptology ePrint Archive, Report 2015/220 (2015). http://eprint.iacr.org/2015/220
Boneh, D., Lewi, K., Montgomery, H., Raghunathan, A.: Key homomorphic PRFs and their applications. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 410–428. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_23
Cachin, C., Camenisch, J., Freire-Stoegbuchner, E., Lehmann, A.: Updatable tokenization: Formal definitions and provably secure constructions. Cryptology ePrint Archive, Report 2017/695 (2017). http://eprint.iacr.org/2017/695
Chow, S.S.M., Weng, J., Yang, Y., Deng, R.H.: Efficient unidirectional proxy re-encryption. In: Bernstein, D.J., Lange, T. (eds.) AFRICACRYPT 2010. LNCS, vol. 6055, pp. 316–332. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-12678-9_19
Cohn-Gordon, K., Cremers, C., Dowling, B., Garratt, L., Stebila, D.: A formal security analysis of the signal messaging protocol. In: EuroS&P (2017)
Cohn-Gordon, K., Cremers, C., Garratt, L.: On post-compromise security. Cryptology ePrint Archive, Report 2016/221 (2016). http://eprint.iacr.org/2016/221
Everspaugh, A., Paterson, K., Ristenpart, T., Scott, S.: Key rotation for authenticated encryption. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part III. LNCS, vol. 10403, pp. 98–129. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_4
Günther, F., Mazaheri, S.: A formal treatment of multi-key channels. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10403, pp. 587–618. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_20
Hohenberger, S., Rothblum, G.N., shelat, A., Vaikuntanathan, V.: Securely obfuscating re-encryption. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 233–252. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_13
Ivan, A., Dodis, Y.: Proxy cryptography revisited. In: NDSS 2003. The Internet Society, February 2003
Lehmann, A., Tackmann, B.: Updatable encryption with post-compromise security. Cryptology ePrint Archive, Report 2018/118 (2018). http://eprint.iacr.org/2018/118
Libert, B., Vergnaud, D.: Multi-use unidirectional proxy re-signatures. In: Ning, P., Syverson, P.F., Jha, S. (eds.) ACM CCS 2008, pp. 511–520. ACM Press, October 2008
Libert, B., Vergnaud, D.: Tracing malicious proxies in proxy re-encryption. In: Galbraith, S.D., Paterson, K.G. (eds.) Pairing 2008. LNCS, vol. 5209, pp. 332–353. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85538-5_22
Myers, S., Shull, A.: Efficient hybrid proxy re-encryption for practical revocation and key rotation. Cryptology ePrint Archive, Report 2017/833 (2017). http://eprint.iacr.org/2017/833
Naor, M., Pinkas, B., Reingold, O.: Distributed pseudo-random functions and KDCs. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 327–346. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48910-X_23
PCI Security Standards Council: Requirements and security assessment procedures. PCI DSS v3.2 (2016)
Polyakov, Y., Rohloff, K., Sahu, G., Vaikuntanthan, V.: Fast proxy re-encryption for publish/subscribe systems. Cryptology ePrint Archive, Report 2017/410 (2017). http://eprint.iacr.org/2017/410
Acknowledgments
This work has been supported in part by the European Commission through the Horizon 2020 Framework Programme (H2020-ICT-2014-1) under grant agreements number 644371 WITDOM and 644579 ESCUDO-CLOUD, and through the Seventh Framework Programme under grant agreement number 321310 PERCY, and in part by the Swiss State Secretariat for Education, Research and Innovation (SERI) under contract numbers 15.0098 and 15.0087.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Symmetric Key-Encapsulation ()
A Symmetric Key-Encapsulation ( )
)
We additionally analyze a scheme that can be considered as a symmetric key-encapsulation mechanism (KEM) together with a standard symmetric encryption scheme. The KEM has one key \({k}_{e}\) per epoch e, and for each ciphertext it wraps an “inner” key x under which the actual message is encrypted. During an update, where the token is given by two keys \(({k}_{e}, {k}_{e+1})\) of subsequent epochs, all inner keys are simply un-wrapped using \({k}_{e}\) and re-wrapped under the new key \({k}_{e+1}\).
This scheme is used in practical data-at-rest protection at cloud storage providers. The keys are, however, managed within the cloud storage systems. Not all nodes are equal; there are nodes that have access to the keys, and nodes that store the encrypted data.Footnote 2 In this scenario, it is acceptable to have the proxy nodes perform the updates. We stress that the scheme is not applicable for outsourcing encrypted data, as it fully reveals the secret keys in the update procedure!
We describe the algorithms in a slightly different way to consider  as a ciphertext-independent updatable encryption scheme. The algorithms are described in more detail as the scheme
as a ciphertext-independent updatable encryption scheme. The algorithms are described in more detail as the scheme  as follows.
as follows.
-
 : return \(k_0 {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\)
: return \(k_0 {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\) -
 : \(k_{e+1} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\), \(\varDelta _{e+1} \leftarrow (k_{e}, k_{e+1})\), return \(({k}_{e+1}, \varDelta _{e+1})\)
: \(k_{e+1} {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\), \(\varDelta _{e+1} \leftarrow (k_{e}, k_{e+1})\), return \(({k}_{e+1}, \varDelta _{e+1})\) -
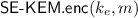 : \(x {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\), return \(C_e \leftarrow (\mathsf {SE}.\mathsf {enc}(k_e, x), \mathsf {SE}.\mathsf {enc}(x, m))\)
: \(x {\mathop {\leftarrow }\limits ^{\scriptscriptstyle \mathrm {r}}}\mathsf {SE}.\mathsf {kgen}(\lambda )\), return \(C_e \leftarrow (\mathsf {SE}.\mathsf {enc}(k_e, x), \mathsf {SE}.\mathsf {enc}(x, m))\) -
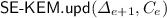 : parse \(C_e = (C^1,C^2)\), and \(\varDelta _{e+1} = (k_{e}, k_{e+1})\), return \(C_{e+1} \leftarrow (\mathsf {SE}.\mathsf {enc}(k_{e+1},\mathsf {SE}.\mathsf {dec} (k_e,C^1)),C^2)\)
: parse \(C_e = (C^1,C^2)\), and \(\varDelta _{e+1} = (k_{e}, k_{e+1})\), return \(C_{e+1} \leftarrow (\mathsf {SE}.\mathsf {enc}(k_{e+1},\mathsf {SE}.\mathsf {dec} (k_e,C^1)),C^2)\) -
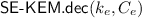 : parse \(C_e = (C^1,C^2)\), return \(\mathsf {SE}.\mathsf {dec} (\mathsf {SE}.\mathsf {dec} (k,C^1), C^2)\)
: parse \(C_e = (C^1,C^2)\), return \(\mathsf {SE}.\mathsf {dec} (\mathsf {SE}.\mathsf {dec} (k,C^1), C^2)\)
While this scheme is very similar to the hybrid AE as described by Everspaugh el al. [15], our description differs in that the token is independent of the ciphertext, and consists of the keys \(({k}_{e}, {k}_{e+1})\) used for encryption in epochs e and \(e+1\). In cloud storage systems where the keys for data-at-rest encryption are managed within the cloud, this is a faithful description of the real behavior.
The security that can be offered by such a solution is necessarily limited. First, if the adversary obtains a challenge in epoch e and also sees one of the tokens in epochs e or \(e+1\), the  security is immediately broken. Furthermore, as the ciphertext update does not re-encrypt the second component, the ciphertexts are linkable through the epochs, i.e.,
security is immediately broken. Furthermore, as the ciphertext update does not re-encrypt the second component, the ciphertexts are linkable through the epochs, i.e.,  cannot achieve any form of
cannot achieve any form of  security. Still, we show that under the described (strict) constraints, the scheme guarantees a mild form of
security. Still, we show that under the described (strict) constraints, the scheme guarantees a mild form of  security.
security.
Theorem 8
( is weakly
is weakly  secure). Let \(\mathsf {SE}\) be an
secure). Let \(\mathsf {SE}\) be an  -secure encryption scheme, then
-secure encryption scheme, then  is (weakly)
is (weakly)  -secure if the following additional condition holds: For any challenge-equal epoch \(e \in \mathcal {C}^*\), \(\mathcal {A} \) must not call \(\mathcal {O}_\mathsf {corrupt}(\mathsf {token}, \cdot )\) for epochs e or \(e+1\).
-secure if the following additional condition holds: For any challenge-equal epoch \(e \in \mathcal {C}^*\), \(\mathcal {A} \) must not call \(\mathcal {O}_\mathsf {corrupt}(\mathsf {token}, \cdot )\) for epochs e or \(e+1\).
The proof is very similar to the one of Theorem 2 and is provided in the full paper [19].
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Lehmann, A., Tackmann, B. (2018). Updatable Encryption with Post-Compromise Security. In: Nielsen, J., Rijmen, V. (eds) Advances in Cryptology – EUROCRYPT 2018 . EUROCRYPT 2018. Lecture Notes in Computer Science(), vol 10822. Springer, Cham. https://doi.org/10.1007/978-3-319-78372-7_22
Download citation
DOI: https://doi.org/10.1007/978-3-319-78372-7_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-78371-0
Online ISBN: 978-3-319-78372-7
eBook Packages: Computer ScienceComputer Science (R0)






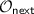 : When triggered, this oracle updates the secret key, produces a new update value as
: When triggered, this oracle updates the secret key, produces a new update value as  oracle, whenever a new key gets generated. Calling this oracle sets
oracle, whenever a new key gets generated. Calling this oracle sets 
 vs.
vs. 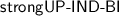
 in the
in the  and
and  Model
Model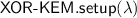 : return
: return  :
:  :
:  : parse
: parse  : parse
: parse  vs.
vs. 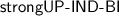 (and
(and  )
)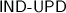 vs.
vs. 
 : parse
: parse  :
:  : parse
: parse 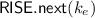 : parse
: parse  )
) : return
: return  :
: 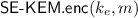 :
: 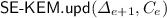 : parse
: parse 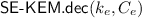 : parse
: parse 