Bloom Filter Encryption and Applications to Efficient Forward-Secret 0-RTT Key Exchange

Abstract

Forward secrecy is considered an essential design goal of modern key establishment (KE) protocols, such as TLS 1.3, for example. Furthermore, efficiency considerations such as zero round-trip time (0-RTT), where a client is able to send cryptographically protected payload data along with the very first KE message, are motivated by the practical demand for secure low-latency communication.

For a long time, it was unclear whether protocols that simultaneously achieve 0-RTT and full forward secrecy exist. Only recently, the first forward-secret 0-RTT protocol was described by Günther et al. (Eurocrypt 2017). It is based on Puncturable Encryption. Forward secrecy is achieved by “puncturing” the secret key after each decryption operation, such that a given ciphertext can only be decrypted once (cf. also Green and Miers, S&P 2015). Unfortunately, their scheme is completely impractical, since one puncturing operation takes between 30 s and several minutes for reasonable security and deployment parameters, such that this solution is only a first feasibility result, but not efficient enough to be deployed in practice.

In this paper, we introduce a new primitive that we term Bloom Filter Encryption (BFE), which is derived from the probabilistic Bloom filter data structure. We describe different constructions of BFE schemes, and show how these yield new puncturable encryption mechanisms with extremely efficient puncturing. Most importantly, a puncturing operation only involves a small number of very efficient computations, plus the deletion of certain parts of the secret key, which outperforms previous constructions by orders of magnitude. This gives rise to the first forward-secret 0-RTT protocols that are efficient enough to be deployed in practice. We believe that BFE will find applications beyond forward-secret 0-RTT protocols.

The full version of this paper is available in the IACR Cryptology ePrint archive.

1 Introduction

One central ingredient to secure today’s Internet are key exchange (KE) protocols with the most prominent and widely deployed instantiations thereof in the Transport Layer Security (TLS) protocol [15]. Using a KE protocol, two parties (e.g., a server and a client) are able to establish a shared secret (session key) which afterwards can be used to cryptographically protect data to be exchanged between those parties. The process of arriving at a shared secret requires the exchange of messages between client and server, which adds latency overhead to the protocol. The time required to establish a key is usually measured in round-trip times (RTTs). A novel design goal, which was introduced by Google’s QUIC protocol and also adopted in the upcoming version of TLS 1.3, aims at developing zero round-trip time (0-RTT) protocols with strong security guarantees. So far, quite some effort was made in the cryptographic literature, e.g. [21, 31], and, indeed, 0-RTT protocols are probably going to be used heavily in the future Internet as TLS version 1.3 [28] is approaching fast. Already today, Google’s QUIC protocol [29] is used on Google webservers and within the Chrome and Opera browsers to support 0-RTT. Unfortunately, none of the above mentioned protocols are enjoying 0-RTT and full forward secrecy at the same time. Only recently, Günther, Hale, Jager, and Lauer (GHJL henceforth) [20] made progress and proposed the first 0-RTT key exchange protocol with full forward secrecy for all transmitted payload messages. However, although their 0-RTT protocol offers the desired features, their construction is not yet practical.

In more detail, GHJL’s forward-secure 0-RTT key-exchange solution is based on puncturable encryption (PE), which they showed can be constructed in a black-box way from any selectively secure hierarchical identity-based encryption (HIBE) scheme. Loosely speaking, PE is a public-key encryption primitive which provides a $\mathsf{Puncture}$ algorithm that, given a secret key and ciphertext, produces an updated secret key that is able to decrypt all ciphertexts except the one it has been punctured on. PE has been introduced by Green and Miers [19] (GM henceforth) who provide an instantiation relying on a binary-tree encryption (BTE) scheme—or selectively secure HIBE—together with a key-policy attribute-based encryption (KP-ABE) [18] scheme for non-monotonic (NM) formulas with specific properties. In particular, the KP-ABE needs to provide a non-standard property to enhance existing secret keys with additional NOT gates, which is satisfied by the NM KP-ABE in [27]. Since then, PE has proved to be a valuable building block to construct public-key watermarking schemes [13], forward-secret proxy re-encryption [14], or for achieving chosen-ciphertext security for fully-homomorphic encryption [11]. However, the mentioned PE instantiations from [11, 13] are based on indistinguishability obfuscation and, thus, do not yield practical schemes at all while [14] uses the same techniques as in GHJL.

When looking at the two most efficient PE schemes available, i.e., GM and GHJL, they still come with severe drawbacks. In particular, puncturing in GHJL is highly inefficient and takes several seconds to minutes on decent hardware for reasonable deployment parameters. In the GM scheme, puncturing is more efficient, but the cost of decryption is very significant and increases with the number of puncturings. More precisely, cost of decryption requires a number of pairing evaluations that depends on the number of puncturings, and can be in the order of $2^{10}$ to $2^{20}$ for realistic deployment parameters. These issues make both of them especially unsuitable for the application in forward-secret 0-RTT key exchange in a practical setting.

Contributions. In this paper, we introduce Bloom filter encryption (BFE), which can be considered as a variant of PE [11, 13, 19, 20]. The main difference to other existing PE constructions is that in case of BFE, we tolerate a non-negligible correctness error.¹ This allows us to construct PE and in particular puncturable key encapsulation (PKEM) schemes with highly efficient puncturing and in particular where puncturing only requires a few very efficient operations, i.e., to delete parts of the secret key, but no further expensive cryptographic operations. Altogether, this makes BFE a very suitable building block to construct practical forward-secret 0-RTT key exchange. In more detail, our contributions are as follows:

• We formalize the notion of BFE by presenting a suitable security model. The intuition behind BFE is to provide a highly efficient decryption and puncturing. Interestingly, puncturing mainly consists of deleting parts of the secret key. This approach is in contrast to existing puncturable encryption schemes, where puncturing and/or decryption is a very expensive operation.

• We propose efficient constructions of BFE. First, we present a direct construction which uses ideas from the Boneh-Franklin identity-based encryption (IBE) scheme [9]. Additionally, we present a black-box construction from a ciphertext-policy attibute-based encryption (CP-ABE) scheme that only needs to be small-universe (i.e., bounded) and support threshold policies, which allows us to achieve compact ciphertexts. To improve efficiency, we finally provide a time-based BFE (TB-BFE) from selectively-secure HIBEs.

• To achieve CCA security, we adopt the Fujisaki-Okamoto (FO) transformation [16] to the BFE setting. This is technically non-trivial, and therefore we consider it as another interesting aspect of this work. In particular, the original FO transformation [16] works only for schemes with perfect correctness. Recently, Hofheinz et al. [23] described a variant which works also for schemes with negligible correctness error. We adopt the FO transformation to BFE and PKEMs with non-negligible correctness error respectively. To this end, we formalize additional properties of the PKEM that are required to apply the FO transform to BFE schemes, and show that our CPA-secure constructions satisfy them. This serves as a template that allows an easy application of the FO transform in a black-box manner to BFE schemes.

• We provide a construction of a forward-secret 0-RTT key exchange protocol (in the sense of GHJL) from TB-BFE. Furthermore, we give a detailed comparison of (TB-)BFE with other PE schemes and discuss the efficiency in the context of the proposed application to forward-secret 0-RTT key exchange. In particular, our construction of forward-secret 0-RTT key-exchange from TB-BFE has none of the drawbacks mentioned in the introduction (at the cost of a somewhat larger secret key, that, however, shrinks with the number of puncturings). Consequently, our forward-secret 0-RTT key exchange can be seen as a significant step forward to construct very practical forward-secret 0-RTT key exchange protocols.

On tolerating a non-negligible correctness error for 0-RTT. The huge efficiency gain of our construction stems partially from the relaxation of allowing a non-negligible correctness error, which, in turn, stems from the potentially non-negligible false-positive probability of a Bloom filter. While this is unusual for classical public-key encryption schemes, we consider it as a reasonable approach to accept a small, but non-negligible correctness error for the 0-RTT mode of a key exchange protocol, in exchange for the huge efficiency gain.

For example, a chance that the key establishment fails allows to use 0-RTT in 9999 out of 10000 cases on average, which is a significant practical efficiency improvement. Furthermore, the communicating parties can implement a fallback mechanism which immediately continues with running a standard 1-RTT key exchange protocol with perfect correctness, if the 0-RTT exchange fails. Thus, the resulting protocol can have the same worst-case efficiency as a 1-RTT protocol, while most of the time 0-RTT is already sufficient to establish a key and full forward secrecy is always achieved.

Compared to other practical 0-RTT solutions, note that both TLS 1.3 [28] and QUIC [29] have similar fallback mechanisms. Furthermore, in order to achieve at least a very weak form of forward secrecy, they define so called tickets [28] or server configuration (SCFG) messages [29], which expire after a certain time. Forward secrecy is only achieved after the ticket/SCFG message has expired and the associated secrets have been erased. Therefore the lifetime should be kept short. If a client connects to a server after the ticket/SCFG message has expired, then the fallback mechanism is invoked and a full 1-RTT handshake is performed. In particular, for settings where a client connects only occasionally to a server, and for reasonably chosen parameters and a moderate life time of the ticket/SCFG message, which at least guarantees some weak form of forward secrecy, this requires a full handshake more often than with our approach.

Finally, note that puncturable encryption with perfect (or negligible) correctness error inherently seems to require secret keys whose size at least grows linearly with the number of puncturings. This is because any such scheme inherently must (implicitly or explicitly) encode information about the list of punctured ciphertexts into the secret key, which lower-bounds the size of the secret key. By tolerating a non-negligible correctness error, we are also able to restrict the growth of the secret key to a limit which seems tolerable in practice.

2 Bloom Filter Encryption

The key idea behind Bloom Filter Encryption (BFE) is that the key pair of such a scheme is associated to a Bloom filter (BF) [7], a probabilistic data structure for the approximate set membership problem with a non-negligible false-positive probability in answering membership queries. The initial secret key $\mathsf {sk}$ output by the key generation algorithm of a BFE scheme corresponds to an empty BF where all bits are set to 0. Encryption takes a message M and the public key $\mathsf {pk}$, samples a random element s (acting as a tag for the ciphertext) corresponding to the universe $\mathcal {U}$ of the BF and encrypts a message using $\mathsf {pk}$ with respect to the k positions set in the BF by s. A ciphertext is then basically identified by s and decryption works as long as at least one index pointed to by s in the BF is still set to 0. Puncturing the secret key with respect to a ciphertext (i.e., the tag s of the ciphertext) corresponds to inserting s in the BF (i.e., updating the corresponding indices to 1 and deleting the corresponding parts of the secret key). This basically means updating $\mathsf {sk}$ such that it no longer can decrypt any position indexed by s.

2.1 Formal Definition of Bloom Filters

A Bloom filter (BF) [7] is a probabilistic data structure for the approximate set membership problem. It allows a succinct representation T of a set $\mathcal {S}$ of elements from a large universe $\mathcal {U}$. For elements $s\in \mathcal {S}$ a query to the BF always answers 1 (“yes”). Ideally, a BF would always return 0 (“no”) for elements $s \not \in \mathcal {S}$, but the succinctness of the BF comes at the cost that for any query to $s \not \in \mathcal {S}$ the answer can be 1, too, but only with small probability (called the false-positive probability).

We will only be interested in the original construction of Bloom filters by Bloom [7], and omit a general abstract definition. Instead we describe the construction from [7] directly. For a general definition refer to [26].

Definition 1

(Bloom Filter). A Bloom filter $\mathsf {B}$ for set $\mathcal {U}$ consists of algorithms $\mathsf {B}= (\mathsf{BFGen}, \mathsf{BFUpdate}, \mathsf{BFCheck})$, which are defined as follows.  

$\mathsf{BFGen}(m,k)$::

This algorithm takes as input two integers $m,k \in \mathbb {N}$. It first samples k universal hash functions $H_1, \ldots , H_k$, where $H_j : \mathcal {U}\rightarrow [m]$, defines $H := (H_j)_{j \in [k]}$ and $T := 0^m$ (that is, T is an m-bit array with all bits set to 0), and outputs (H, T).

$\mathsf{BFUpdate}(H,T,u)$::

Given $H = (H_j)_{j \in [k]}$, $T \in \{0,1\} ^m$, and $u\in \mathcal {U}$, this algorithm defines the updated state $T'$ by first assigning $T' := T$. Then, writing $T'[i]$ to denote the i-th bit of $T'$, it sets $T'[H_j(u)] := 1$ for all $j \in [k]$, and finally returns $T'$.

$\mathsf{BFCheck}(H,T,u)$::

Given $H = (H_j)_{j \in [k]}$, $T \in \{0,1\} ^m$ where we write T[i] to denote the i-th bit of T, and $u\in {\mathcal {U}}$, this algorithm returns a bit $b := \bigwedge _{j\in [k]} T[H_j(u)]$

 

Relevant properties of Bloom filters. Let us summarize the properties of Bloom filters relevant to our work.  

Perfect completeness. :

A Bloom filter always “recognizes” elements that have been added with probability 1. More precisely, let ${\mathcal {S}} = (s_1, \ldots , s_n) \in {\mathcal {U}}^n$ be any vector of n elements of ${\mathcal {U}}$. Let and define

$$ T_i = \mathsf{BFUpdate}(H,T_{i-1},s_i) \text { for } i \in [n]. $$

Then for all $s^* \in {\mathcal {S}}$ and all with $m, k \in \mathbb {N}$, it holds that

$$ \mathsf {Pr}\left[ \mathsf{BFCheck}(H,T_n,s^*) = 1 \right] = 1. $$

Compact representation of $\mathcal {S}$.:

Independent of the size of the set ${\mathcal {S}} \subset {\mathcal {U}}$ and the representation of individual elements of ${\mathcal {U}}$, the size of representation T is a constant number of m bits. A larger size of ${\mathcal {S}}$ increases only the false-positive probability, as discussed below, but not the size of the representation.

Bounded false-positive probability. :

The probability that an element which has not yet been added to the Bloom filter is erroneously “recognized” as being contained in the filter can be made arbitrarily small, by choosing m and k adequately, given (an upper bound on) the size of ${\mathcal {S}}$.

More precisely, let ${\mathcal {S}} = (s_1, \ldots , s_n) \in {\mathcal {U}}^n$ be any vector of n elements of ${\mathcal {U}}$. Then for any $s^* \in {\mathcal {U}} \setminus {\mathcal {S}}$, we have

$$ \mathsf {Pr}\left[ \mathsf{BFCheck}(H,T_n,s^*) = 1 \right] \approx (1-e^{-kn/m})^k, $$

where , $T_i = \mathsf{BFUpdate}(H,T_{i-1},s_i) \text { for } i \in [n]$, and the probability is taken over the random coins of $\mathsf{BFGen}$.

 

Discussion on the choice of parameters. In order to provide a first intuition on the choice of parameters n, m and k for the use of BFs within BFE, we subsequently discuss some reasonable choices. Let us assume that we want to have $n=2^{20}$, which amounts to adding for a full year every day about $2^{12}$ elements to the BF. Then, assuming the optimal number of hash functions k, and tolerating a false-positive probability of $p=10^{-3}$, we obtain a size of the BF given by , as $m \approx 15\,\text {Mb} \approx 2\,\text {MB}$. The optimal number of hash functions k is given by , and we will instantiate Bloom filters with

This yields a correctness error $p \approx (1-e^{-kn/m})^k = (1-e^{-n/m \cdot \left\lceil \frac{m}{n} \right\rceil \ln 2})^k \le 2^{-k}$. For above parameters n, m and p we obtain $k = 10$.

Looking ahead to the BFE construction in Sect. 2.5, at a 120-bit security level (using the pairing-friendly BLS12-381 curve), this choice of parameters would yield ciphertexts of size $<720$ B and public as well as secret keys of size $<100$ B and $\approx 700$ MB respectively. Thereby, we need to emphasize that initially the secret key (representing the empty BF) has its maximum size, but every puncturing (i.e., addition of an element to the BF), reduces the size of the secret key. Moreover, we stress that the false-positive probability represents an upper bound as it assumes that all $n=2^{20}$ elements are already added to the BF, i.e., the secret key has already been punctured with respect to $2^{20}$ ciphertexts. Finally, when we use our time-based BFE approach (TB-BFE) from Sect. 2.7, we can even reduce the secret key size by reducing the maximum number of puncturings at the cost of switching the time intervals more frequently.

2.2 Formal Model of BFE

Subsequently, we introduce the formal model for BFE which essentially is a variant of puncturable encryption (PE) [11, 13, 19, 20] with the only difference that with BFE we tolerate a non-negligible correctness error. Thus, although we are speaking of BFE, we choose to introduce a formal model for PE with a relaxed correctness definition² and treat BFE as an instantiation of PE. Consequently, our Definition 2 below is a variant of the one in [20], with the only difference that we allow the key generation to take the additional parameters m and k (of the BF) as input, which specify the correctness error.

For 0-RTT key establishment, our prime application in this paper, we do not need a full-blown encryption scheme, but only a key-encapsulation mechanisms (KEM) to transport a symmetric encryption key. Consequently, we chose to present our definitions by means of a puncturable KEM (PKEM). We stress that defining PKEM instead of PE does not represent any limitation, as any KEM can generically be converted into a secure full-blown encryption scheme [16]. Conversely, any secure encryption scheme trivially yields a secure KEM. Nonetheless, for completeness, we give stand-alone definitions of PE tolerating a non-negligible correctness error in the full version.

Definition 2

(PKEM). A puncturable key encapsulation (PKEM) scheme with key space $\mathcal {K}$ is a tuple $\mathsf{(KGen,Enc,Punc,Dec)}$ of $\mathsf{PPT}$ algorithms:  

${\mathsf {KGen}}(1^\lambda ,m,k):$ :

Takes as input a security parameter $\lambda$, parameters m and k and outputs a secret and public key $(\mathsf {sk},\mathsf {pk})$ (we assume that $\mathcal {K}$ is implicit in $\mathsf {pk}$).

$\mathsf {Enc}(\mathsf {pk}):$ :

Takes as input a public key $\mathsf {pk}$ and outputs a ciphertext C and a symmetric key $\mathsf {K}$.

$\mathsf {Punc}(\mathsf {sk},C):$ :

Takes as input a secret key $\mathsf {sk}$, a ciphertext C and outputs an updated secret key $\mathsf {sk} '$.

$\mathsf {Dec}(\mathsf {sk},C):$ :

Takes as input a secret key $\mathsf {sk}$, a ciphertext C and outputs a symmetric key $\mathsf {K}$ or $\bot$ if decapsulation fails.

 

Correctness. We start by defining correctness of a PKEM scheme. Basically, here one requires that a ciphertext can always be decapsulated with unpunctured secret keys. However, we allow that if punctured secret keys are used for decapsulation then the probability that the decapsulation fails is bounded by some non-negligible function in the scheme’s parameters m, k.

Definition 3

(Correctness). For all $\lambda , m,k,\in \mathbb {N}$, any and , we have that $\mathsf {Dec}(\mathsf {sk},C)=\mathsf {K}$. Moreover, for any (arbitrary interleaved) sequence $i = 1,\ldots , \ell$ (where $\ell$ is determined by m, k) of invocations of for any $C'\ne C$ it holds that $\mathsf {Pr}\left[ \mathsf {Dec}(\mathsf {sk} ',C)=\bot \right] \le \mu (m,k),$ where $\mu (\cdot )$ is some (possibly non-negligible) bound.

2.3 Additional Properties of a PKEM

In this section, we will define additional properties of a PKEM. One will be necessary for the application to 0-RTT key exchange from [20]. The others are required to construct a CCA-secure PKEM via the Fujisaki-Okamoto (FO) transformation, as described in Sect. 2.6. We will show below that our constructions of CPA-secure PKEMs satisfy these additional properties, and thus are suitable for our variant of the FO transformation, and to construct 0-RTT key exchange.

Extended correctness. Intuitively, we first require an extended variant of correctness which demands that (1) decapsulation yields a failure when attempting to decapsulate under a secret key previously punctured for that ciphertext. This is analogous to [20]. Second, we additionally demand that (2) decapsulating an honest ciphertext with the unpuctured key does always succeed and (3) if decryption does not fail, then the decapsulated value must match the key returned by the $\mathsf {Enc}$ algorithm, for any key $\mathsf {sk} '$ obtained from applying any sequence of puncturing operations to the initial secret key $\mathsf {sk}$.

Definition 4

(Extended Correctness). For all $\lambda ,m,k,\ell \in \mathbb {N}$, any and and any (arbitrary interleaved and possibly empty) sequence $C_1, \ldots , C_\ell$ of invocations of it holds that:

• 1. Impossibility of false-negatives:

  $\mathsf {Dec}(\mathsf {sk} ',C_i)=\bot$ for all $i\in [\ell ]$.

• 2. Perfect correctness of the initial, non-punctured secret key:

  If then $\mathsf {Dec}(\mathsf {sk},C) = \mathsf {K}$, where $\mathsf {sk}$ is the initial, non-punctured secret key.

• 3. Semi-correctness of punctured secret keys:

  If $\mathsf {Dec}(\mathsf {sk} ',C) \ne \bot$ then $\mathsf {Dec}(\mathsf {sk} ',C) = \mathsf {Dec}(\mathsf {sk},C)$.

Separable randomness. We require that the encapsulation algorithm $\mathsf {Enc}$ essentially reads the key directly from its random input tape. Intuitively, this will later enable us to make the randomness r used by the encapsulation algorithm $\mathsf {Enc}$ dependent on the key $\mathsf {K}$ computed by $\mathsf {Enc}$.

Definition 5

(Separable Randomness). Let $\mathsf {PKEM} = ({\mathsf {KGen}},\mathsf {Enc},\mathsf {Punc},\mathsf {Dec})$ be a PKEM. We say that $\mathsf {PKEM}$ has separable randomness, if one can equivalently write the encapsulation algorithm $\mathsf {Enc}$ as

for uniformly random $(r,\mathsf {K}) \in \{0,1\}^{\rho +\lambda }$, where $\mathsf {Enc}(\cdot ;\cdot )$ is a deterministic algorithm whose output is uniquely determined by $\mathsf {pk}$ and the randomness $(r,\mathsf {K}) \in \{0,1\}^{\rho +\lambda }$.

Remark

We note that one can generically construct a separable PKEM from any non-separable PKEM. Given a non-separable PKEM with encapsulation algorithm $\mathsf {Enc}$, a separable PKEM with encryption algorithm $\mathsf {Enc}'$ can be obtained as follows:  

$\mathsf {Enc}'(\mathsf {pk}; (r,\mathsf {K}')):$ :

Run , set $C':= (C,\mathsf {K}\oplus \mathsf {K}')$ return $(C', \mathsf {K}')$.

 

We need separability in order to apply our variant of the FO transformation, which is the reason why we have to make it explicit. Alternatively, we could have started from a non-separable PKEM and applied the above construction. However, this adds an additional component to the ciphertext, while the construction given in Sect. 2.5 will already be separable, such that we can avoid this overhead.

Publicly-checkable puncturing. Finally, we need that it is efficiently checkable whether the decapsulation algorithm outputs $\bot = \mathsf {Dec}(\mathsf {sk},C)$, given not the secret key $\mathsf {sk}$, but only the public key $\mathsf {pk}$, the ciphertext C to be decrypted, and the sequence $C_1, \ldots , C_w$ at which the secret key $\mathsf {sk}$ has been punctured.

Definition 6

(Publicly-Checkable Puncturing). Let $\mathcal {Q} = (C_1, \ldots , C_w)$ be any list of ciphertexts. We say that $\mathsf {PKEM}$ allows publicly-checkable puncturing, if there exists an efficient algorithm $\mathsf {CheckPunct}$ with the following correctness property.

• 1. Run .

• 2. Compute and $\mathsf {sk} = \mathsf {Punc}(\mathsf {sk},C_i)$ for $i \in [w]$.

• 3. Let C be any string. We require that

  

From a high-level perspective, this additional property will be necessary to simulate the decryption oracle properly in the CCA security experiment when our variant of the FO transformation is applied. Together with the second and third property of Definition 4, it replaces the perfect correctness property required in the original FO transformation.

Min-entropy of ciphertexts. Following [23], we require that ciphertexts of a randomness-separable PKEM have sufficient min-entropy, even if $\mathsf {K}$ is fixed:

Definition 7

($\gamma$-Spreadness). Let $\mathsf {PKEM} = ({\mathsf {KGen}},\mathsf {Enc},\mathsf {Punc},\mathsf {Dec})$ be a randomness-separable PKEM with ciphertext space $\mathcal C$. We say that $\mathsf {PKEM}$ is $\gamma$-spread, if for any honestly generated $\mathsf {pk}$, any key $\mathsf {K}$ and any $C \in \mathcal C$

2.4 Security Definitions

We define three notions of security for PKEMs. The two “standard” security notions are indistinguishability under chosen-plaintext ($\mathsf {IND\text {-}CPA}$) and chosen-ciphertext ($\mathsf {IND\text {-}CCA}$) attacks. We also consider one-wayness under chosen-plaintext attacks ($\mathsf {OW\text {-}CPA}$). The latter is the weakest notion among the ones considered in this paper, and implied by both $\mathsf {IND\text {-}CPA}$ and $\mathsf {IND\text {-}CCA}$, but sufficient for our generic construction of $\mathsf {IND\text {-}CCA}$-secure PKEMs.

Indistinguishability-based security. Figure 1 defines the $\mathsf {IND\text {-}CPA}$ and $\mathsf {IND\text {-}CCA}$ experiments for PKEMs. The experiments are similar to the security notions for conventional KEMs, but the adversary can arbitrarily puncture the secret key via the $\mathsf {Punc}$ oracle and retrieve the punctured secret key via the $\mathsf{Corr}$ oracle, once it has been punctured on the challenge ciphertext $C^*$.

Fig. 1.

Indistinguishability-based security for PKEMs.

Definition 8

(Indistinguishability-Based Security of PKEM). For $\mathsf{T \in \{\mathsf {IND\text {-}CPA},\mathsf {IND\text {-}CCA} \}}$, we define the advantage of an adversary $\mathcal {A}$ in the $\mathsf{T}$ experiment $\mathbf{Exp}^{\mathsf {T}}_{\mathcal {A},\mathsf{PKEM}}(\lambda ,m,k)$ as

$$\begin{aligned} \mathbf{Adv}^{\mathsf {T}}_{\mathcal {A},\mathsf{PKEM}}(\lambda ,m,k):= \left| \mathsf {Pr}\left[ \mathbf{Exp}^{\mathsf{T}}_{\mathcal {A},\mathsf{PKEM}}(\lambda ,m,k) =1 \right] - \frac{1}{2} \right| . \end{aligned}$$

A puncturable key-encapsulation scheme $\mathsf{PKEM}$ is $\mathsf{T\in \{\mathsf {IND\text {-}CPA},\mathsf {IND\text {-}CCA} \}}$ secure, if $\mathbf{Adv}^{\mathsf {T}}_{\mathcal {A},\mathsf{PKEM}}(\lambda ,m,k)$ is a negligible function in $\lambda$ for all $m,k>0$ and all PPT adversaries $\mathcal {A}$.

One-wayness under chosen-plaintext attack. Figure 2 defines the $\mathsf {OW\text {-}CPA}$ experiment. The experiment is similar to the $\mathsf {IND\text {-}CPA}$ experiment, except that the goal of the adversary is to recover the encapsulated key, given a random challenge ciphertext.

Fig. 2.

$\mathsf {OW\text {-}CPA}$ security for PKEMs.

Definition 9

(One-Wayness Under Chosen-Plaintext Attack). We define the advantage of an adversary $\mathcal {A}$ in experiment $\mathbf{Exp}^{\mathsf {OW\text {-}CPA}}_{\mathcal {A},\mathsf{PKEM}}(\lambda ,m,k)$ as

$$\begin{aligned} \mathbf{Adv}^{\mathsf {OW\text {-}CPA}}_{\mathcal {A},\mathsf{PKEM}}(\lambda ,m,k):= \mathsf {Pr}\left[ \mathbf{Exp}^{\mathsf {OW\text {-}CPA}}_{\mathcal {A},\mathsf{PKEM}}(\lambda ,m,k) =1 \right] . \end{aligned}$$

A $\mathsf{PKEM}$ is $\mathsf {OW\text {-}CPA}$ secure, if $\mathbf{Adv}^{\mathsf {OW\text {-}CPA}}_{\mathcal {A},\mathsf{PKEM}}(\lambda ,m,k)$ is a negligible function in $\lambda$ for all $m,k>0$ and all PPT adversaries $\mathcal {A}$.

2.5 Basic Bloom Filter Encryption

Bilinear maps and notation. In the sequel, let $\mathsf {BilGen}$ be an algorithm that, on input a security parameter $1^\lambda$, outputs , where $\mathbb {G}_1$, $\mathbb {G}_2$, $\mathbb {G}_T$ are groups of prime order p with bilinear map $e : \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T$ and generators $g_i \in \mathbb {G}_i$ for $i \in \{1,2\}$.

Construction. In the sequel, let , and $g_T = e(g_1,g_2)$. We will always assume that all algorithms described below implicitly receive these parameters as additional input. Let $\mathsf {B}= (\mathsf{BFGen},\mathsf{BFUpdate}, \mathsf{BFCheck})$ be a Bloom filter for set $\mathbb {G}_1$. Furthermore, let $G : \mathbb {N}\rightarrow \mathbb {G}_2$ and $G' : \mathbb {G}_T \rightarrow \{0,1\} ^\lambda$ be cryptographic hash functions (which will be modelled as random oracles [5] in the security proof).

Let $\mathsf {PKEM} = ({\mathsf {KGen}},\mathsf {Enc},\mathsf {Punc},\mathsf {Dec})$ be defined as follows.  

:

This algorithm first generates a Bloom filter instance by running . Then it chooses , and computes and returns

Remark. The reader familiar with the Boneh-Franklin IBE scheme [9] may note that the secret key contains m elements of $\mathbb {G}_2$, each essentially being a secret key of the Boneh-Franklin scheme for “identity” i, $i \in [m]$, with respect to “master public-key” $g^{\alpha } _1$.

 

 

:

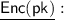This algorithm takes as input a public key $\mathsf {pk}$ of the above form. It samples a uniformly random key and exponent . Then it computes $i_j := H_j(g^{r} _1)$ for $(H_j)_{j \in [k]} := H$, then $y_j = e(g^{\alpha } _1,G(i_j))^r \text { for } j \in [k]$, and finally

$$ C := \left( g^{r} _1, (G'(y_j) \oplus \mathsf {K})_{j \in [k]} \right) . $$

It outputs $(C,\mathsf {K}) \in (\mathbb {G}_1 \times \{0,1\} ^{k\lambda }) \times \{0,1\} ^\lambda$.

Remark. Note that for each $j \in [k]$, the tuple $(g^{r} _1, G'(y_j) \oplus \mathsf {K})$ is essentially a “hashed Boneh-Franklin IBE” ciphertext, encrypting $\mathsf {K}$ for “identity” $i_j = H_j(g^{r} _1)$ and with respect to master public key $g^{\alpha } _1$, where the identity is derived deterministically from a “unique” (with overwhelming probability) ciphertext component $g^{r} _1$. Thus, the ciphertext C essentially consists of k Boneh-Franklin ciphertexts that share the same randomness r, each encrypting the same key $\mathsf {K}$ for an “identity” derived deterministically from $g^{r} _1$.

 

Note also that this construction of $\mathsf {Enc}$ satisfies the requirement of separable randomness from Definition 5. Furthermore, ciphertexts are $\gamma$-spread according to Definition 7 with $\gamma = \log _2 p$, because $g^{r} _1$ is uniformly distributed over $\mathbb {G}_1$.

 

:

Given a ciphertext $C := \left( g^{r} _1, (G'(y_j) \oplus \mathsf {K})_{j \in [k]} \right)$ and secret key $\mathsf {sk} = (T, (\mathsf {sk} [i])_{i \in [m]})$, the puncturing algorithm first computes $T' = \mathsf{BFUpdate}(H,T,g^{r} _1)$. Then, for each $i \in [m]$ it defines

where $T'[i]$ denotes the i-th bit of $T'$. Finally, this algorithm returns

Remark. Note that the above procedure is correct even if the procedure is applied repeatedly with different ciphertexts C, since the $\mathsf{BFUpdate}$ algorithm only changes bits of T from 0 to 1, but never from 1 to 0. So we can delete a secret key element $\mathsf {sk} [i]$ once $T'[i]$ has been set to 1. Furthermore, we have $\mathsf {sk} '[i] = \bot \iff T'[i] = 1$. Intuitively, this will ensure that we can use this key to decrypt a ciphertext $C := \left( g^{r} _1, (G'(y_j) \oplus \mathsf {K})_{j \in [k]} \right)$ if and only if $\mathsf{BFCheck}(H,T,g^{r} _1) = 0$, where (H, T) is the Bloom filter instance contained in the public key. Note also that the puncturing algorithm essentially only evaluates k universal hash functions $H = (H_j)_{j \in [k]}$ and then deletes a few secret keys, which makes this procedure extremely efficient. Finally, observe that the filter state T can be efficiently re-computed given only public information, namely the list of hash functions H contained in $\mathsf {pk}$ and the sequence of ciphertexts $C_1, \ldots , C_w$ on which a secret key has been punctured. This yields the existence of an efficient $\mathsf {CheckPunct}$ according to Definition 6.

 

 

:

Given a secret key $\mathsf {sk} = (T, (\mathsf {sk} [i])_{i \in [m]})$ and a ciphertext $C := \left( C[0],C[i_1], \ldots , C[i_k] \right)$ it first checks whether $\mathsf{BFCheck}(H, T, C[0]) = 1$, and outputs $\bot$ in this case. Otherwise, note that $\mathsf{BFCheck}(H, T, C[0]) = 0$ implies that there exists at least one index $i^*$ with $\mathsf {sk} [i^*] \ne \bot$. It picks the smallest index $i^* \in \{i_1, \ldots , i_k\}$ such that $\mathsf {sk} [i^*] = G(i^*)^\alpha \ne \bot$, computes

$$ y_{i^*} := e(g^{r} _1, G(i^*)^\alpha ), $$

and returns $\mathsf {K}:= C[i^*] \oplus G'(y_{i^*})$.

Remark. If $\mathsf{BFCheck}(H, T_n, C[0]) = 0$, then the decryption algorithm performs a “hashed Boneh-Franklin” decryption with a secret key for one of the identities. Note that $\mathsf {Dec}(\mathsf {sk} _n, C) \ne \bot \iff \mathsf{BFCheck}(H, T, C[0]) = 0$, which guarantees the first extended correctness property required by Definition 4. It is straightforward to verify that the other two extended correctness properties of Definition 4 hold as well.

 

Design choices. We note that we have chosen to base our Bloom filter encryption scheme on hashed Boneh-Franklin IBE instead of standard Boneh-Franklin for two reasons. First, it allows us to keep ciphertexts short and independent of the size of the binary representation of elements of $\mathbb {G}_T$. This is useful, because the recent advances for computing discrete logarithms in finite extension fields [24] apply to the target group of state-of-the-art pairing-friendly elliptic curve groups. Recent assessments of the impact of these advances by Menezes et al. [25] as well as Barbulescu and Duquesne [2] suggest that for currently used efficient curve families such as BN [4] or BLS [3] curves a conservative choice of parameters for the 128 bit security level yields sizes of $\mathbb {G}_T$ elements of $\approx$ 4600–5500 bits. The hash function allows us to “compress” these group elements in the ciphertext to 128 bits. Even if future research enables the construction of bilinear maps where elements of $\mathbb {G}_T$ can be represented by $2\lambda$ bits for $\lambda$-bit security (which is optimal), it is still preferable to hash group elements to $\lambda$ bits to reduce the ciphertext by a factor of about 2. Second, by modelling $G'$ as a random oracle, we can reduce security to a weaker complexity assumption.

Correctness error of this scheme. We will now explain that the correctness error of this scheme is essentially identical to the false-positive probability of the Bloom filter, up to a statistically small distance which corresponds to the probability that two independent ciphertexts share the same randomness r.

For $m,k \in \mathbb {N}$, let , let denote the set of all valid ciphertext with respect to $\mathsf {pk}$. Let ${\mathcal {S}} = (C_1, \ldots , C_n)$ be a list of n ciphertexts, where , and run $\mathsf {sk} _i = \mathsf {Punc}(\mathsf {sk} _{i-1}, C_i)$ for $i \in [n]$ to determine the secret key $\mathsf {sk} _n$ obtained from puncturing $\mathsf {sk} _0$ iteratively on all ciphertexts $C_i \in {\mathcal {S}}$.

Now let us consider the probability

that a newly generated ciphertext $C^* \not \in {\mathcal {S}}$ is not correctly decrypted by $\mathsf {sk} _n$. To this end, let $C^*[0] = g^{r^*} _1$ denote the first component of ciphertext $C^* = (g^{r^*} _1, C_1^*, \ldots , C_k^*)$, and likewise let $C_i[0]$ denote the first component of ciphertext $C_i$ for all $C_i \in {\mathcal {S}}$. Writing $\mathsf {sk} _n = (T_n, (\mathsf {sk} _n[i])_{i \in [m]})$ and $\mathsf {pk} = (g^{\alpha } _1, H)$, one can now verify that we have $\mathsf {Dec}(\mathsf {sk} _n, C^*) \ne \mathsf {K}^* \iff \mathsf{BFCheck}(H, T_n, C^*[0]) = 1$, because $\mathsf{BFCheck}(H, T_n, C^*[0]) = 0$ guarantees that there exists at least one index j such that $\mathsf {sk} _n[H_j(C^*[0])] \ne \bot$, so correctness of decryption follows essentially from correctness of the Boneh-Franklin scheme. Thus, we have to consider the probability that $\mathsf{BFCheck}(H, T_n, C^*[0]) = 1$. We distinguish between two cases:

• 1. There exists an index $i \in [n]$ such that $C^*[0] = C_i[0]$. Note that this implies immediately that $\mathsf{BFCheck}(H, T_n, C^*[0]) = 1$. However, recall that $C^*[0] = g^{r^*} _1$ is a uniformly random element of $\mathbb {G}_1$. Therefore the probability that this happens is upper bounded by n / p, which is negligibly small.

• 2. $C^*[0] \ne C_i[0]$ for all $i \in [n]$. In this case, as explained in Sect. 2.1, the soundness of the Bloom filter guarantees that $\mathsf {Pr}[\mathsf{BFCheck}(H, T_n, C^*[0]) = 1] \approx 2^{-k}$.

In summary, the correctness error of this scheme is approximately $2^{-k} + n/p$. Since n / p is negligibly small, this essentially amounts to the correctness error of the Bloom filter, which in turn depends on the number of ciphertexts n, and the choice of parameters m, k.

Flexible instantiability of this scheme. Our scheme is highly parameterizable in the sense that we can adjust the size of keys and ciphertexts by adjusting the correctness error (determined by the choice of parameters m, k that in turn determine the false-positive probability of the Bloom filter) of our scheme.

Additional properties. As already explained in the remarks after the description of the individual algorithms of $\mathsf {PKEM}$, the scheme satisfies the requirements of Definitions 4, 5, 6, and 7.

$\mathsf {IND\text {-}CPA}$-security. We base $\mathsf {IND\text {-}CPA}$-security on a bilinear computational Diffie-Hellman variant in the bilinear groups generated by $\mathsf {BilGen}$.

Definition 10

(BCDH). We define the advantage of adversary $\mathcal {A}$ in solving the BCDH problem with respect to $\mathsf {BilGen}$ as

where , and .

Theorem 1

From each efficient adversary $\mathcal {B}$ that issues q queries to random oracle $G'$ we can construct an efficient adversary $\mathcal {A}$ with

$$ \mathbf{Adv}^{\mathsf {BCDH}}_{{\mathcal {A}},{\mathsf {BilGen}}}(\lambda ) \ge \frac{\mathbf{Adv}^{\mathsf {IND\text {-}CPA}}_{{\mathcal {B}},{\mathsf {PKEM}}}(\lambda ,m,k)}{kq}. $$

Proof

Algorithm $\mathcal {A}$ receives as input a BCDH-challenge tuple $(g^{r} _1, g^{\alpha } _1, g^{\alpha } _2, h_2)$. It runs adversary $\mathcal {B}$ as a subroutine by simulating the $\mathbf{Exp}^{\mathsf {IND}\text {-}\mathsf {CPA}}_{\mathcal {B},\mathsf {PKEM}}(\lambda ,m,k)$ experiment, including random oracles G and $G'$, as follows.

First, it defines ${\mathcal {Q}} := \emptyset$, runs , and defines the public key as $\mathsf {pk}:= (g^{\alpha } _1, H)$. Note that this public key is identically distributed to a public key output by ${\mathsf {KGen}}(1^\lambda , m, k)$. In order to simulate the challenge ciphertext, the adversary chooses a random key and k uniformly random values , $j \in [k]$, and defines the challenge ciphertext as $C^* := (g_1^r, (Y_j)_{j \in [k]})$. Finally, it outputs $(\mathsf {pk}, C^*, \mathsf {K})$ to $\mathcal {B}$.

Whenever $\mathcal {B}$ queries $\mathsf {Punc}(\mathsf {sk}, \cdot )$ on input $C = (C[0], \ldots )$, then $\mathcal {A}$ updates T by running $T = \mathsf{BFUpdate}(H,T,C[0])$, and ${\mathcal {Q}}\leftarrow {\mathcal {Q}}\cup \{C \}$.

Whenever a random oracle query to $G : \mathbb {N}\rightarrow \mathbb {G}_2$ is made (either by $\mathcal {A}$ or $\mathcal {B}$), with input $\ell \in \mathbb {N}$, then $\mathcal {A}$ responds with $G(\ell )$, if $G(\ell )$ has already been defined. If not, then $\mathcal {A}$ chooses a random integer , and returns $G(\ell )$, where

This definition of G allows $\mathcal {A}$ to simulate the $\mathsf{Corr}$ oracle as follows. When $\mathcal {B}$ queries $\mathsf{Corr}$, then it first checks whether $C^*\in {\mathcal {Q}}$, and returns $\bot$ if this does not hold. Otherwise, note that we must have $\forall j \in [k] : T[H_j(g_1^r)] = 0$, where $H = (H_j)_{j \in [k]}$ and $T[\ell ]$ denotes the $\ell$-th bit of T. Thus, by the simulation of G described above, $\mathcal {A}$ is able to compute and return $G(\ell )^\alpha = (g_2^{r_\ell })^\alpha = (g_2^\alpha )^{r_\ell }$ for all $\ell$ with $\ell \not \in \{H_j(g_1^r) : j \in [k]\}$, and therefore in particular for all $\ell$ with $T[\ell ]=1$. This enables the perfect simulation of $\mathsf{Corr}$.

Finally, whenever $\mathcal {B}$ queries random oracle $G' : \mathbb {G}_T \rightarrow \{0,1\} ^\lambda$ on input y, then $\mathcal {A}$ responds with $G'(y)$, if $G'(y)$ has already been defined. If not, then $\mathcal {A}$ chooses a random string , assigns $G'(y) := Y$, and returns $G'(y)$. Now we have to distinguish between two types of adversaries.

• 1. A Type-1 adversary $\mathcal {B}$ never queries $G'$ on input of a value y, such that there exists $j \in [k]$ such that $y = e(g_1^\alpha , G(H_j(g_1^r)))^r$. Note that in this case the value $Y_j' := G'(e(g_1^\alpha , G(H_j(g_1^r))))$ remains undefined for all $j \in [k]$ throughout the entire experiment. Thus, information-theoretically, a Type-1 adversary receives no information about the key encrypted in the challenge ciphertext $C^*$, and thus can only have advantage $\mathbf{Adv}^{\mathsf {IND\text {-}CPA}}_{{\mathcal {B}},{\mathsf {PKEM}}}(\lambda ,m,k)=0$, in which case the theorem holds trivially.

• 2. A Type-2 adversary queries $G'(y)$ such that there exists $j \in [k]$ with $y = e(g_1^\alpha , G(H_j(g_1^r)))^r$. $\mathcal {A}$ uses a Type-2 adversary to solve the BCDH challenge as follows. At the beginning of the game, it picks two indices uniformly random. When $\mathcal {B}$ outputs y in its $q^*$-th query to $G'$, then $\mathcal {A}$ computes and outputs $W := y \cdot e(g_1^\alpha , g_2^{r})^{-r_\ell }$. Since $\mathcal {B}$ is a Type-2 adversary, we know that at some point it will query $G'(y)$ with $y = e(g_1^\alpha , G(H_j(g_1^r)))^r$ for some $j \in [k]$. If this is the $q^*$-th query and we have $j = j^*$, which happens with probability $1{\slash }(qk)$, then we have

  $$\begin{aligned} W&= y \cdot e(g_1^\alpha , g_2^{r})^{-r_\ell } = e(g_1^\alpha , G(H_j(g_1^r)))^r\cdot e(g_1^\alpha , g_2^{r})^{-r_\ell } \\&= e(g_1^\alpha , h_2 \cdot g_2^{r_\ell })^r \cdot e(g_1^\alpha , g_2^{r})^{-r_\ell } = e(g_1^\alpha , h_2)^r \cdot e(g_1^\alpha , g_2^{r_\ell })^{r}\cdot e(g_1^\alpha , g_2^{r})^{-r_\ell } \end{aligned}$$

  and thus W is a solution to the given BCDH instance.    $\square$

$\mathsf {OW\text {-}CPA}$-Security. The following theorem can either be proven analogous to Theorem 1, or based on the fact that $\mathsf {IND\text {-}CPA}$-security implies $\mathsf {OW\text {-}CPA}$-security. Therefore we give it without proof.

Theorem 2

From each efficient adversary $\mathcal {B}$ that issues q queries to random oracle $G'$ we can construct an efficient adversary $\mathcal {A}$ with

$$ \mathbf{Adv}^{\mathsf {BCDH}}_{{\mathcal {A}},{\mathsf {BilGen}}}(\lambda ) \ge \frac{\mathbf{Adv}^{\mathsf {OW\text {-}CPA}}_{{\mathcal {B}},{\mathsf {PKEM}}}(\lambda ,m,k)}{kq}. $$

Remark 1

The construction presented above allows to switch the roles of $\mathbb {G}_1$ and $\mathbb {G}_2$, i.e., to switch all elements in $\mathbb {G}_1$ to $\mathbb {G}_2$ and vice versa. This might be beneficial regarding the size of the secret key when instantiating our construction using a bilinear group where the representation of elements in $\mathbb {G}_2$ requires more space than the representation of elements in $\mathbb {G}_1$.

2.6 CCA-Security via Fujisaki-Okamoto

We obtain a CCA-secure PKEM by adopting the Fujisaki-Okamoto (FO) transformation [16] to the PKEM setting. Since the FO transformation does not work generically for any KEM, we have to use the additional requirements on the underlying PKEM that have been defined in Sect. 2.3. These additional properties enable us to overcome the difficulty that the original Fujisaki-Okamoto transformation from [16] requires perfect correctness, what no puncturable KEM can provide. We note that Hofheinz et al. [23] give a new, modular analysis of the FO transformation, which also works for public key encryption schemes with negligible correctness error, however, it is not applicable to PKEMs with non-negligible correctness error because the bounds given in [23] provide insufficient security in this case.

Construction. Let $\mathsf {PKEM} = ({\mathsf {KGen}},\mathsf {Enc},\mathsf {Punc},\mathsf {Dec})$ be a PKEM with separable randomness according to Definition 5. Recall that this means that we can write $\mathsf {Enc}$ equivalently as for uniformly random . In the sequel, let R be a hash function (modeled as a random oracle in the security proof), mapping $R : \{0,1\}^* \rightarrow \{0,1\}^{\rho +\lambda }$. We construct a new scheme $\mathsf {PKEM} ' = ({\mathsf {KGen}}',\mathsf {Enc}',\mathsf {Punc}',\mathsf {Dec}')$ as follows.

 

:

This algorithm is identical to ${\mathsf {KGen}}$.

:

Algorithm $\mathsf {Enc}'$ samples . Then it computes $(r,\mathsf {K}') := R(\mathsf {K}) \in \{0,1\} ^{\rho +\lambda }$, runs , and returns $(C,\mathsf {K}')$.

:

This algorithm is identical to $\mathsf {Punc}$.

:

This algorithm first runs , and returns $\bot$ if $\mathsf {K}= \bot$. Otherwise, it computes $(r,\mathsf {K}') = R(\mathsf {K})$, and checks consistency of the ciphertext by verifying that $(C,\mathsf {K}) = \mathsf {Enc}(\mathsf {pk};(r,\mathsf {K}))$. If this does not hold, then it outputs $\bot$. Otherwise it outputs $\mathsf {K}'$.

 

Correctness error and extended correctness. Both the correctness error and the extended correctness according to Definition 4 are not affected by the Fujisaki-Okamoto transform. Therefore these properties are inherited from the underlying scheme. The fact that the first property of Definition 4 is satisfied makes the scheme suitable for the application to 0-RTT key establishment.

$\mathsf {IND\text {-}CCA}$-security. The security proof reduces security of our modified scheme to the $\mathsf {OW\text {-}CPA}$-security of the scheme from Sect. 2.5.

Theorem 3

Let $\mathsf {PKEM} =({\mathsf {KGen}},\mathsf {Enc},\mathsf {Punc},\mathsf {Dec})$ be a BFKEM scheme that satisfies the additional properties of Definitions 4 and 6, and which is $\gamma$-spread according to Definition 7. Let $\mathsf {PKEM} ' = ({\mathsf {KGen}}',\mathsf {Enc}',\mathsf {Punc}',\mathsf {Dec}')$ be the scheme described in Sect. 2.6. From each efficient adversary $\mathcal {A}$ that issues at most $q_\mathcal {O}$ queries to oracle ${\mathcal {O}}$ and $q_R$ queries to random oracle R, we can construct an efficient adversary $\mathcal {B}$ with

$$ \mathbf{Adv}^{\mathsf {OW\text {-}CPA}}_{{\mathcal {B}},{\mathsf {PKEM}}}(\lambda ,m,k) \ge \frac{\mathbf{Adv}^{\mathsf {IND\text {-}CCA}}_{{\mathcal {A}},{\mathsf {PKEM} '}}(\lambda ,m,k) - q_\mathcal {O}/2^\gamma }{q_R}. $$

Proof

We proceed in a sequence of games. In the sequel, ${\mathcal {O}_i}$ is the implementation of the decryption oracle in Game i.

Game 0

This is the original $\mathsf {IND\text {-}CCA}$ security experiment from Definition 8, played with the scheme described above. In particular, the decryption oracle ${\mathcal {O}_0}$ is implemented as follows:

Recall that $\mathsf {K}_0$ denotes the encapsulated key computed by the $\mathsf {IND\text {-}CCA}$ experiment. $\mathsf {K}_0$ is uniquely defined by the challenge ciphertext $C^*$ via $\mathsf {K}_0 := \mathsf {Dec}(\mathsf {sk} _0,C^*)$, where $\mathsf {sk} _0$ is the initial (non-punctured) secret key, since the scheme satisfies extended correctness (Definition 4, second property). Let $Q_0$ denote the event that $\mathcal {A}$ ever queries $\mathsf {K}_0$ to random oracle R. Note that $\mathcal {A}$ has zero advantage in distinguishing $\mathsf {K}'$ from random, until $Q_0$ occurs, because R is a random function. Thus, we have $\mathsf {Pr}[Q_0] \ge \mathbf{Adv}^{\mathsf {IND\text {-}CCA}}_{{\mathcal {A}},{\mathsf {PKEM} '}}(\lambda ,m,k)$. In the sequel, we denote with $Q_i$ the event that $\mathcal {A}$ ever queries $\mathsf {K}_0$ to random oracle R in Game i.

Game 1

This game is identical to Game 0, except that after computing and checking whether $\mathsf {K}\ne \bot$, the experiment additionally checks whether the adversary has ever queried random oracle R on input $\mathsf {K}$, and returns $\bot$ if not. More precisely, the experiment maintains a list

to record all queries $\mathsf {K}$ made by the adversary to random oracle R, along with the corresponding response $(r,\mathsf {K}') = R(\mathsf {K})$. The decryption oracle ${\mathcal {O}_{1}}$ uses this list as follows (boxed statements highlight changes to $\mathcal {O}_{0}$):

Note that Games 0 and 1 are perfectly indistinguishable, unless $\mathcal {A}$ ever outputs a ciphertext C with $\mathcal {O}_{1}(C) = \bot$, but $\mathcal {O}_{0}(C) \ne \bot$. Note that this happens if and only if $\mathcal {A}$ outputs C such that $C = \mathsf {Enc}(\mathsf {pk}; (r,\mathsf {K}))$, where r is the randomness defined by $(r,\mathsf {K}') = R(\mathsf {K})$, but without prior query of $R(\mathsf {K})$.

The random oracle R assigns a uniformly random value $r \in \{0,1\} ^\rho$ to each query, so, by the $\gamma$-spreadness of $\mathsf {PKEM}$, the probability that the ciphertext C output by the adversary “matches” the ciphertext produced by $\mathsf {Enc}(\mathsf {pk}; (r,\mathsf {K}))$ is $2^{-\gamma }$. Since $\mathcal {A}$ issues at most $q_\mathcal {O}$ queries to $\mathcal {O}_{1}$, this yields .

Game 2

We make a minor conceptual modification. Instead of computing $(r,\mathsf {K}') = R(\mathsf {K})$ by evaluating R, $\mathcal {O}_{2}$ reads $(r,\mathsf {K}')$ from list $L_R$. More precisely:

By definition of $L_R$ it always holds that $(r,\mathsf {K}') = R(\mathsf {K})$ for all $(\mathsf {K},(r,\mathsf {K}')) \in L_R$. Indeed $(r,\mathsf {K}')$, is uniquely determined by $\mathsf {K}$, because $(r,\mathsf {K}') = R(\mathsf {K})$ is a function. Since R is only evaluated by $\mathcal {O}_{1}$ if there exists a corresponding tuple $(\mathsf {K},(r,\mathsf {K}')) \in L_R$ anyway, due to the changes introduced in Game 1, oracle $\mathcal {O}_{2}$ is equivalent to $\mathcal {O}_{1}$ and we have $\mathsf {Pr}[Q_{2}] = \mathsf {Pr}[Q_{1}]$.

Game 3

This game is identical to Game 2, except that whenever $\mathcal {A}$ queries a ciphertext C to oracle $\mathcal {O}_{3}$, then $\mathcal {O}_{3}$ first runs the $\mathsf {CheckPunct}$ algorithm associated to $\mathsf {PKEM}$ (cf. Definition 6). If $\mathsf {CheckPunct} (\mathsf {pk},\mathcal {Q},C)=\bot$, then it immediately returns $\bot$. Otherwise, it proceeds exactly like $\mathcal {O}_{2}$. More precisely:

Recall that by public checkability (Definition 6) we have $\bot = \mathsf {Dec}(\mathsf {sk},C) \iff \bot = \mathsf {CheckPunct} (\mathsf {pk},\mathcal {Q}, C)$. Therefore the introduced changes are conceptual, and $\mathsf {Pr}[Q_{3}] = \mathsf {Pr}[Q_{2}]$.

Game 4

We modify the secret key used to decrypt the ciphertext. Let $\mathsf {sk} _0$ denote the initial secret key generated by the experiment (that is, before any puncturing operation was performed). $\mathcal {O}_{4}$ uses $\mathsf {sk} _0$ to compute instead of , where $\mathsf {sk}$ is a possibly punctured secret key. More precisely:

For indistinguishability from Game 3, we show that $\mathcal {O}_{4}(C) = \mathcal {O}_{3}(C)$ for all ciphertexts C. Let us first consider the case $\mathsf {Dec}(\mathsf {sk},C) = \bot$. Then public checkability guarantees that $\mathcal {O}_{4}(C) = \mathcal {O}_{3}(C) = \bot$, due to the fact that $\mathsf {Dec}(\mathsf {sk},C) = \bot \iff \mathsf {CheckPunct} (\mathsf {pk},\mathcal {Q}, C) = \bot$.

Now let us consider the case $\mathsf {Dec}(\mathsf {sk},C) \ne \bot$. In this case, the semi-correctness of punctured keys (3rd requirement of Definition 4) guarantees that $\mathsf {Dec}(\mathsf {sk},C) = \mathsf {Dec}(\mathsf {sk} _0,C) = \mathsf {K}\ne \bot$.

After computing $\mathsf {Dec}(\mathsf {sk} _0,C)$, $\mathcal {O}_{4}$ performs exactly the same operations as $\mathcal {O}_{3}$ after computing $\mathsf {Dec}(\mathsf {sk},C)$. Thus, in this case both oracles are perfectly indistinguishable, too. This yields that the changes introduced in Game 4 are purely conceptual, and we have $\mathsf {Pr}[Q_{4}] = \mathsf {Pr}[Q_{3}]$.

Remark

Due to the fact that we are now using the initial secret key to decrypt C, we have reached a setting where, due to the perfect correctness of the initial secret key $\mathsf {sk} _0$, essentially a perfectly-correct encryption scheme is used – except that the decryption oracle implements a few additional abort conditions. Thus, we can now basically apply the standard Fujisaki-Okamoto transformation, but we must show that we are also able to simulate the additional abort imposed by the additional consistency checks properly. To this end, we first replace these checks with equivalent checks before applying the FO transformation.

Game 5

We replace the consistency checks performed by $\mathcal {O}_{4}$ with an equivalent check. More precisely, $\mathcal {O}_{5}$ works as follows:

This is equivalent, so that we have $\mathsf {Pr}[Q_{5}] = \mathsf {Pr}[Q_{4}]$.

Game 6

Observe that in Game 5 we check whether there exists a tuple $(r,\mathsf {K}')$ with $(\mathsf {K},(r,\mathsf {K}')) \in L_R$ and $(C,\mathsf {K}) = \mathsf {Enc}(\mathsf {pk};(r,\mathsf {K})$, where $\mathsf {K}$ must match the secret key computed by .

In Game 6, we relax this check. We test only whether there exists any tuple $(\tilde{\mathsf {K}},(\tilde{r},\tilde{\mathsf {K}'})) \in L_R$ such that $(C,\tilde{\mathsf {K}}) = \mathsf {Enc}(\mathsf {pk};(\tilde{r},\tilde{\mathsf {K}})$ holds. Thus, it is not explicitly checked whether $\tilde{\mathsf {K}}$ matches the value . Furthermore, the corresponding value $\tilde{\mathsf {K}'}$ is returned. More precisely:

By the perfect correctness of the initial secret key $\mathsf {sk} _0$, we have

$$\begin{aligned} (C,\tilde{\mathsf {K}}) = \mathsf {Enc}(\mathsf {pk};(\tilde{r},\tilde{\mathsf {K}})) \implies \mathsf {Dec}(\mathsf {sk} _0,C) = \tilde{\mathsf {K}}, \end{aligned}$$

so that we must have $\mathsf {K}= \tilde{\mathsf {K}}$. $\mathcal {O}_{6}$ is equivalent to $\mathcal {O}_{5}$, and $\mathsf {Pr}[Q_{6}] = \mathsf {Pr}[Q_{5}]$.

Game 7

This game is identical to Game 6, except that we change the decryption oracle again. Observe that the value $\mathsf {K}$ computed by is never used by $\mathcal {O}_{6}$. Therefore the computation of is obsolete, and we can remove it. More precisely, $\mathcal {O}_{7}$ works as follows.

We have only removed an obsolete instruction, which does not change the output distribution of the decryption oracle. Therefore $\mathcal {O}_{7}$ simulates $\mathcal {O}_{6}$ perfectly, and we have $\mathsf {Pr}[Q_{7}] = \mathsf {Pr}[Q_{6}]$.

Reduction to $\mathsf {OW\text {-}CPA}$-security. Now we are ready to describe the $\mathsf {OW\text {-}CPA}$-adversary $\mathcal {B}$. $\mathcal {B}$ receives $(\mathsf {pk},C^*)$. It samples a uniformly random key and runs the $\mathsf {IND\text {-}CCA}$-adversary $\mathcal {A}$ as a subroutine on input $(\mathsf {pk},C^*,\mathsf {K}')$. Whenever $\mathcal {A}$ issues a $\mathsf {Punc}$- or $\mathsf{Corr}$-query, then $\mathcal {B}$ forwards this query to the $\mathsf {OW\text {-}CPA}$-experiment and returns the response. In order to simulate the decryption oracle $\mathcal {O}$, adversary $\mathcal {B}$ implements the simulated oracle $\mathcal {O}_{7}$ from Game 7 described above. When $\mathcal {A}$ terminates, then $\mathcal {B}$ picks a uniformly random entry , and outputs $\hat{\mathsf {K}}$.

Analysis of the reduction. Let $\hat{Q}$ denote the event that $\mathcal {A}$ ever queries $\mathsf {K}_0$ to random oracle R. Note that $\mathcal {B}$ simulates Game 7 perfectly until $Q_{7}$ occurs, thus we have $\mathsf {Pr}[\hat{Q}] \ge \mathsf {Pr}[Q_{7}]$. Summing up, the probability that the value $\hat{\mathsf {K}}$ output by $\mathcal {B}$ matches the key encapsulated in $C^*$ is therefore at least

   $\square$

Remark on the tightness. Alternatively, we could have based the security of our $\mathsf {IND\text {-}CCA}$-secure scheme on the $\mathsf {IND\text {-}CPA}$ (rather than $\mathsf {OW\text {-}CPA}$) security of $\mathsf {PKEM} '$. In this case, we would have achieved a tighter reduction, as we would have been able to avoid guessing the index , at the cost of requiring stronger security of the underlying scheme.

From $\mathsf {IND\text {-}CCA}$-secure KEMs to $\mathsf {IND\text {-}CCA}$-secure encryption. It is well-known that one can generically transform an $\mathsf {IND\text {-}CCA}$-secure KEM into an $\mathsf {IND\text {-}CCA}$-secure encryption scheme, by combining it with a CCA-secure symmetric encryption scheme [16]. This construction applies to PKEMs as well.

2.7 Time-Based Bloom Filter Encryption

For a standard BFE scheme we have to update the public key after the secret key has been punctured n-times, because otherwise the false-positive probability would exceed an acceptable bound. In this section, we describe a construction of a scheme where the lifetime of the public key is split into time slots. Ciphertexts are associated with time slots, which assumes loosely synchronized clocks between sender and receiver of a ciphertext. The main advantage is that for a given bound on the correctness error, we are able to handle about the same number of puncturings per time slot as the basic scheme during the entire life time of the public key. We call this approach time-based Bloom filter encryption. It is inspired by the time-based approach used to construct puncturable encryption in [19, 20], which in turn is inspired by the construction of forward-secret public-key encryption by Canetti et al. [10].

Note that a time-based BFE scheme can trivially be obtained from any BFE scheme, by assigning an individual public/secret key pair for each time slot. However, if we want to split the life time of the public key into, say, $2^t$ time slots, then this would of course increase the size of keys by a factor $2^t$. Since we want to enable a fine-grained use of time slots, to enable a very large number of puncturings over the entire lifetime of the public key without increasing the false positive probability beyond an unacceptable bound, we want to have $2^t$ as large as possible, but without increasing the size of the public key beyond an acceptable bound. To this end, we give a direct construction which increases the size of secret keys only by an additive amount of additional group elements, which is only logarithmic in the number of time slots. Thus, for $2^t$ time slots we have to add merely about t elements to the secret key, while the size of public keys remains even constant.

Formal definition. Likewise to considering our Bloom filter KEMs as an instantiation of a puncturable KEM with non-negligible correctness error, we can view the time-based approach analogously as an instantiation of a puncturable forward-secret KEM (PFSKEM) [20] with non-negligible correctness error. Consequently, we also chose to stick with the existing formal framework for PFSKEM, which we present subsequently. It is essentially our BFKEM Definition 2, augmented by time slots and an additional algorithm $\mathsf {PuncInt}$ that allows to puncture a secret key not with respect to a given ciphertext in a given time slot, but with respect to an entire time slot.

Definition 11

(PFSKEM [20]). A puncturable forward-secret key encapsulation (PFSKEM) scheme is a tuple of the following $\mathsf{PPT}$ algorithms:  

${\mathsf {KGen}}(1^\lambda ,m,k,t):$ :

Takes as input a security parameter $\lambda$, parameters m and k for the Bloom filter, and a parameter t specifying the number of time slots. It outputs a secret and public key $(\mathsf {sk},\mathsf {pk})$, where we assume that the key-space $\mathcal {K}$ is implicit in $\mathsf {pk}$.

$\mathsf {Enc}(\mathsf {pk},\tau ):$ :

Takes as input a public key $\mathsf {pk}$ and a time slot $\tau$ and outputs a ciphertext C and a symmetric key $\mathsf {K}$.

$\mathsf {PuncCtx}(\mathsf {sk},\tau ,C):$ :

Takes as input a secret key $\mathsf {sk}$, a time slot $\tau$, a ciphertext C and outputs an updated secret key $\mathsf {sk} '$.

$\mathsf {Dec}(\mathsf {sk},\tau ,C):$ :

Takes as input a secret key $\mathsf {sk}$, a time slot $\tau$, a ciphertext C and outputs a symmetric key $\mathsf {K}$ or $\bot$ if decapsulation fails.

$\mathsf {PuncInt}(\mathsf {sk},\tau ):$ :

Takes as input a secret key $\mathsf {sk}$, a time slot $\tau$ and outputs an updated secret key $\mathsf {sk} '$ for the next slot $\tau +1$.

 

Due to the lack of space, we postpone the presentation of correctness, the additional properties (which are rather straightforward adaptions of the ones of a PKEM introduced in Sect. 2.3), as well as the $\mathsf {IND\text {-}CPA}$/$\mathsf {IND\text {-}CCA}$ security notions to the full version.

Hierarchical IB-KEMs. We recall the basic definition of hierarchical identity-based key encapsulation schemes (HIB-KEMs) and their security.

Definition 12

A $(t+1)$-level hierarchical identity-based key encapsulation scheme ($\mathsf {HIB\text {-}KEM}$) with identity space $\mathcal {D} = \mathcal {D} _1 \times \cdots \times \mathcal {D} _{t+1}$, ciphertext space $\mathcal {C}$, and key space $\mathcal {K}$ consists of the following four algorithms:  

$\mathsf {HIBGen} (1^\lambda ):$ :

Takes as input a security parameter and outputs a key pair . We say that is the master public key, and is the level-0 secret key.

:

Takes as input a level-$i-1$ secret key with $i \in [t]$ and an element $d \in \mathcal {D} _i$ and outputs a level-i secret key .

:

Takes as input the master public key and an identity ${{\varvec{d}}} \in \mathcal {D}$ and outputs a ciphertext $C \in \mathcal {C}$ and a key $\mathsf {K}\in \mathcal {K}$.

:

Takes as input a level-t secret key $\mathsf {sk} _t$ and a ciphertext C, and outputs a value $\mathsf {K}\in \mathcal {K} \cup \{\bot \}$, where $\bot$ is a distinguished error symbol.

 

Security definition. We will require only the very weak notion of one-wayness under selective-ID and chosen-plaintext attacks (OW-sID-CPA) where the corresponding experiment is defined in Fig. 3.

Fig. 3.

OW-sID-CPA security for HIB-KEMs.

Definition 13

(OW-sID-CPA Security of HIB-KEM). We define the advantage of an adversary $\mathcal {A}$ in the OW-sID-CPA experiment $\mathbf{Exp}^{\mathsf {OW}\text {-}\mathsf {sID}\text {-}\mathsf {CPA}}_{{\mathcal {A}},\mathsf {HIB}\text {-}\mathsf {KEM}}(\lambda )$ as

$$ \mathbf{Adv}^{\mathsf {OW\text {-}sID\text {-}CPA}}_{{\mathcal {A}},{\mathsf {HIB\text {-}KEM}}}(\lambda ) := \mathsf {Pr}\left[ \mathbf{Exp}^{\mathsf {OW}\text {-}\mathsf {sID}\text {-}\mathsf {CPA}}_{{\mathcal {A}},\mathsf {HIB}\text {-}\mathsf {KEM}}(\lambda )=1\right] . $$

We call a $\mathsf {HIB\text {-}KEM}$ OW-sID-CPA secure, if $\mathbf{Adv}^{\mathsf {OW\text {-}sID\text {-}CPA}}_{{\mathcal {A}},{\mathsf {HIB\text {-}KEM}}}(\lambda )$ is a negligible function in $\lambda$ for all PPT adversaries $\mathcal {A}$.

Time slots. We will construct a Bloom filter encryption scheme that allows to use $2^t$ time slots. We associate the i-th time slot with the string in $\{0,1\} ^t$ that corresponds to the canonical t-bit binary representation of integer i.

Following [10, 19, 20], each time slot forms a leaf of an ordered binary tree of depth t. The root of the tree is associated with the empty string $\epsilon$. We associate the left-hand descendants of the root with bit string 0, and the right-hand descendant with 1. Continuing this way, we associate the left descendant of node 0 with 00 and the right descendant with 01, and so on. We continue this procedure for all nodes, until we have constructed a complete binary tree of depth t. Note that two nodes at level $t'$ of the tree are siblings if and only if their first $t'-1$ bits are equal, and that each bit string in $\{0,1\} ^t$ is associated with a leaf of the tree. Note also that the tree is ordered, in the sense that the leftmost leaf is associated with $0^t$, its right neighbour with $0^{t-1}1$, and so on.

Intuition of the construction. The basic idea behind the construction combines the binary tree approach of [10, 19, 20] with the Bloom filter encryption construction described in Sect. 2.5. We use a HIB-KEM with identity space

$$ \mathcal {D} = \mathcal {D} _1 \times \cdots \times \mathcal {D} _{t+1} = \underbrace{\{0,1\} \times \cdots \times \{0,1\}}_{t \text { times}} \times [m]. $$

Each bit vector $\tau \in \mathcal {D} _1 \times \cdots \times \mathcal {D} _{t} = \{0,1\} ^t$ corresponds to one time slot, and we set $\mathcal {D} _{t+1} = [m]$, where m is the size of the Bloom filter. The hierarchical key delegation property of the HIB-KEM enables the following features:

First, given a HIB-KEM key $\mathsf {sk} _\tau$ for some “identity” (= time slot) $\tau \in \{0,1\} ^t$, we can derive keys for all Bloom filter bits from $\mathsf {sk} _\tau$ by computing

Second, in order to advance from time slot $\tau -1$ to $\tau$, we first compute

As soon as we have computed all Bloom filter keys for time slot $\tau$, we “puncture” the tree “from left to right”, such that we are able to compute all $\mathsf {sk} _{\tau '}$ with $\tau ' > \tau$, but not any $sk_{\tau '}$ with $\tau ' \le \tau$. Here, we proceed exactly as in [10, 19, 20]. That is, in order to puncture at time slot $\tau$, we first compute the HIB-KEM secret keys associated to all right-hand siblings of nodes that lie on the path from node $\tau$ to the root, and then we delete all secret keys associated to nodes that lie on the path from node $\tau$ to the root, including $\mathsf {sk} _\tau$ itself. This yields a new secret key, which contains m level-$(t+1)$ HIB-KEM secret keys plus at most t HIB-KEM secret keys for levels $\le t$, even though we allow for $2^t$ time slots.

Construction. Let $(\mathsf {HIBGen}, \mathsf {HIBDel}, \mathsf {HIBEnc}, \mathsf {HIBDec})$ be a HIB-KEM with key space $\mathcal {K}$ and identity space $\mathcal {D} = \mathcal {D} _1 \times \cdots \times \mathcal {D} _{t+1}$, where $\mathcal {D} _1 = \cdots = \mathcal {D} _t = \{0,1\}$, $\mathcal {D} _{t+1} = [m]$, and m is the size of the Bloom filter. Since we will only need selective security, one can instantiate such a HIB-KEM very efficiently, for example in bilinear groups based on the Boneh-Boyen-Goh [8] scheme, or based on lattices [1]. In the sequel, we will write $\{0,1\} ^t$ shorthand for $\mathcal {D} _1 \times \cdots \times \mathcal {D} _{t}$, but keep in mind that the HIB-KEM supports more fine-grained key delegation. Let $\mathsf {B}= (\mathsf{BFGen}, \mathsf{BFUpdate}, \mathsf{BFCheck})$ be a Bloom filter for set $\{0,1\} ^\lambda$. Furthermore, let $G' : \mathcal {K} \rightarrow \{0,1\} ^\lambda$ be a hash function (which will be modeled as a random oracle [5] in the security proof).

We define $\mathsf {PKEM} = ({\mathsf {KGen}},\mathsf {Enc},\mathsf {PuncCtx},\mathsf {Dec},\mathsf {PuncInt})$ as follows.

This algorithm first runs to generate a Bloom filter, and to generate a key pair. Finally, the algorithm generates the keys for the first time slot. To this end, it first computes the HIB-KEM key for identity $0^t$ by recursively computing

Then it computes the m Bloom filter keys for time slot $0^t$ by computing

and setting $\mathsf {sk} _\mathsf {Bloom}:= (\mathsf {sk} _{0^t|d})_{d \in [m]}$. Finally, it punctures the secret key $\mathsf {sk} _\epsilon$ at position $0^t$, by computing

and setting $\mathsf {sk} _\mathsf {time}:= (\mathsf {sk} _{0^{d-1}|1})_{d \in [t]}$. The algorithm outputs

On input and time slot identifier , this algorithm first samples a random string and a random key . Then it defines k HIB-KEM identities as ${{\varvec{d}}}_j := (\tau ,H_j(c)) \in \mathcal {D} \quad \text {for}\quad j \in [k]$, and generates k HIB-KEM key encapsulations as

Finally, it outputs the ciphertext $C := (c, (C_j, G'(\mathsf {K}_j) \oplus \mathsf {K})_{j \in [k]})$.

Note that the ciphertexts essentially consists of $k+1$ elements of $\{0,1\} ^\lambda$, plus k elements of $\mathcal {C}$, where k is the Bloom filter parameter.

Given a ciphertext $C := (c, (C_j, G'(\mathsf {K}_j) \oplus \mathsf {K})_{j \in [k]})$, and secret key $\mathsf {sk} = (T, \mathsf {sk} _\mathsf {Bloom}, \mathsf {sk} _\mathsf {time})$ where $\mathsf {sk} _\mathsf {Bloom} = (\mathsf {sk} _{\tau |d})_{d \in [m]}$, the puncturing algorithm first computes $T' = \mathsf{BFUpdate}((H_j)_{j \in [k]},T,c)$. Then, for each $i \in [m]$, it defines

where $T'[i]$ denotes the i-th bit of $T'$. Finally, this algorithm sets $\mathsf {sk} _\mathsf {Bloom} ' = (\mathsf {sk} '_{\tau |d})_{d \in [m]}$ and returns $\mathsf {sk} ' = (T', \mathsf {sk} _\mathsf {Bloom} ', \mathsf {sk} _\mathsf {time})$.

Remark

We note again that the above procedure is correct even if the procedure is applied repeatedly, with the same arguments as for the construction from Sect. 2.5. Also, the puncturing algorithm essentially only evaluates k universal hash functions and then deletes a few secret keys, which makes this procedure extremely efficient.

Given $\mathsf {sk} = (T, \mathsf {sk} _\mathsf {Bloom}, \mathsf {sk} _\mathsf {time})$ where $\mathsf {sk} _\mathsf {Bloom} = (\mathsf {sk} _{\tau |d})_{d \in [m]}$ and ciphertext $C := (c, (C_j, G_j)_{j \in [k]})$. If $\mathsf {sk} _{\tau |H_j(c)} = \bot$ for all $j \in [k]$, then it outputs $\bot$. Otherwise, it picks the smallest index j such that $\mathsf {sk} _{\tau |H_j(c)} \ne \bot$, computes

and returns $\mathsf {K}= G_j \oplus G'(\mathsf {K}_j)$.

Remark

Again we have $\mathsf {Dec}(\mathsf {sk}, C) \ne \bot \iff \mathsf{BFCheck}(H, T, c) = 0$, which guarantees extended correctness in the sense of Definition 4.

Given a secret key $\mathsf {sk} = (T, \mathsf {sk} _\mathsf {Bloom}, \mathsf {sk} _\mathsf {time})$ for time interval $\tau ' < \tau$, the time puncturing algorithm proceeds as follows. First, it resets the Bloom filter by setting $T := 0^m$. Then it uses the key delegation algorithm to first compute $\mathsf {sk} _{\tau }$. This key can be computed from the keys contained in $\mathsf {sk} _\mathsf {time}$, because $\mathsf {sk}$ is a key for time interval $\tau ' < \tau$. Then it computes

and redefines $\mathsf {sk} _\mathsf {Bloom}:= (\mathsf {sk} _{\tau |d})_{d \in [m]}$. Finally, it updates $\mathsf {sk} _\mathsf {time}$ by computing the HIB-KEM secret keys associated to all right-hand siblings of nodes that lie on the path from node $\tau$ to the root and adds the corresponding keys to $\mathsf {sk} _\mathsf {time}$. Then it deletes all keys from $\mathsf {sk} _\mathsf {time}$ that lie on the path from $\tau$ to the root.

Remark

Note that puncturing between time intervals may become relatively expensive. Depending on the choice of Bloom filter parameters, in particular on m, this may range between $2^{15}$ and $2^{25}$ HIBE key delegations. However, the main advantage of Bloom filter encryption over previous constructions of puncturable encryption is that these computations must not be performed “online”, during puncturing, but can actually be computed separately (for instance, parallel on a different computer, or when a server has low workload, etc.).

Correctness error of this scheme. With exactly the same arguments as for the scheme from Sect. 2.5, one can verify that the correctness error of this scheme is essentially identical to the false positive probability of the Bloom filter, unless a given ciphertext $C = (c, (C_j, G_j)_{j \in [k]})$ has a value of c which is identical to the value of c of any previous ciphertext. Since c is uniformly random in $\{0,1\} ^\lambda$, this probability is approximately $2^{-k} + n \cdot 2^{-\lambda }$.

Extended correctness. It is straightforward to verify that the scheme satisfies extended correctness in the sense of Definition 4.

CPA Security. Below we state theorem for CPA security of our scheme.

Theorem 4

From each efficient adversary $\mathcal {B}$ that issues q queries to random oracle $G'$ we can construct an efficient adversary $\mathcal {A}$ with

$$ \mathbf{Adv}^{\mathsf {OW\text {-}sID\text {-}CPA}}_{{\mathcal {A}},{\mathsf {HIB\text {-}KEM}}}(\lambda ) \ge \frac{\mathbf{Adv}^{\mathsf {s\text {-}CPA}}_{\mathcal {B},\mathsf{PFSKEM}}(\lambda ,m,k)}{qk}. $$

The proof is almost identical to the proof of Theorem 1 and a straightforward reduction to the security of the underlying HIB-KEM. We sketch it in the full version.

CCA Security. In order to apply the Fujisaki-Okamoto [16] transform in the same way as done in Sect. 2.6 to achieve CCA security, we need to show that the time based variants of the properties presented in Sect. 2.3 are satisfied (for the formal definitions of those properties we refer the reader to the full version). First, using a full-blown HIBE as a starting point yields a separable HIB-KEM as discussed in Sect. 2.3. Hence, the separable randomness is satisfied. Moreover, the publicly-checkable puncturing is given by construction (as in Sect. 2.5). Regarding extended correctness, the impossibility of false-negatives is given by construction, the perfect correctness of the non-punctured secret key is given by the perfect correctness of the HIBE and the semi-correctness of punctured secret keys is given by construction. Finally, $\gamma$-spreadness is also given by construction: the ciphertext component c is chosen uniformly at random from $\{0,1\}^\lambda$. Consequently, all properties are satisfied. We note that one could omit c in the ciphertext if the concretely used HIBE ciphertexts are already sufficiently random. Considering the HIBE of Boneh-Boyen-Goh [8], HIBE ciphertexts are of the form $(g^r,(h_1^{I_1}\cdots h_t^{I_t}\cdot h_0)^r,H(e(g_1,g_2)^r)\oplus \mathsf {K})$, for honestly generated fixed group elements $g,g_1,g_2,h_0,\ldots ,h_t$, universal hash function H, fixed $\mathsf {K}$ and fixed integers $I_1,\ldots ,I_t$. Consequently, we have that the ciphertext has at least min-entropy $\log _2 p$ with p being the order of the groups. We want to mention that also many other HIBE construction satisfy the required properties, including, for example [12, 17, 30].

Remark on CCA Security. Alternatively to applying the FO transform to a PFSKEM satisfying the additional properties of extended correctness, separable randomness, publicly checkable puncturing and $\gamma$-spreadness to obtain CCA security, we can add another HIBE level to obtain IND-CCA security via the CHK transform [10] in the standard model, and thus to avoid random oracles if required.

3 Forward-Secret 0-RTT Key Exchange

In [20], GHJL provide a formal model for forward-secret one-pass key exchange (FSOPKE) by extending the one-pass key exchange [22] by Halevi and Krawczyk. They provide a security model for FSOPKE which requires both forward secrecy and replay protection from the FSOPKE protocol and captures unilateral authentication of the server and mutual authentication simultaneously. We recap the definition of FSOPKE with a slightly adapted correctness notion in the full version.

Construction. The construction in [20] builds on puncturable forward-secret key encapsulation (PFSKEM), and we can now directly plug our construction of time-based BFE (PFSKEM) as defined in Definition 11 into the construction of [20, Definition 12], yielding a forward-secret 0-RTT key exchange protocols with non-negligible correctness error:  

:

Outputs $(\mathsf {pk},\mathsf {sk})$ as follows: if $r=\mathsf {server}$, then obtain $(PK,SK)\leftarrow {\mathsf {KGen}}(1^\lambda ,m,k,t)$ (for suitable choices of m, k and t) and set $\mathsf {pk}:=(PK,\tau _{max})$ and $\mathsf {sk}:=(SK,\tau ,\tau _{max})$, for $\tau :=1$. If $r=\mathsf {client}$, then set $(\mathsf {pk},\mathsf {sk}):=(\bot ,\tau )$, for $\tau :=1$.

:

Outputs $(\mathsf {sk} ',\mathsf {K},M)$ as follows: for $\mathsf {sk} =\tau$ and $\mathsf {pk} =(PK,\tau _{max})$, if $\tau >\tau _{max}$, then set $(\mathsf {sk} ',\mathsf {K},M):=(\mathsf {sk},\bot ,\bot )$, otherwise obtain $(C,\mathsf {K})\leftarrow \mathsf {Enc}(\mathsf {pk},\tau )$ and set $(\mathsf {sk} ',\mathsf {K},M):=(\tau +1,\mathsf {K},C)$.

:

Outputs $(\mathsf {sk} ',\mathsf {K})$ as follows: for $\mathsf {sk} =(SK,\tau ,\tau _{max})$ and $\mathsf {pk} =\bot$, if $SK=\bot$ or $\tau >\tau _{max}$, then set $(\mathsf {sk} ',\mathsf {K}):=(\mathsf {sk},\bot )$ and abort. Obtain $\mathsf {K}\leftarrow \mathsf {Dec}(SK,\tau ,M)$. If $\mathsf {K}=\bot$, then set $(\mathsf {sk} ',\mathsf {K})=(\mathsf {sk},\bot )$, otherwise obtain $SK'\leftarrow \mathsf {PuncCtx}(SK,\tau ,M)$ and set $(\mathsf {sk} ',\mathsf {K})=((SK',\tau ,\tau _{max}),\mathsf {K})$.

:

Outputs $\mathsf {sk} '$ as follows: if $r=\mathsf {server}$, then for $\mathsf {sk} =(SK,\tau ,\tau _{max})$: if $\tau \ge \tau _{max}$, then set $\mathsf {sk} ':=(\bot ,\tau +1,\tau _{max})$ and abort, otherwise obtain $SK'\leftarrow \mathsf {PuncInt}(SK,\tau )$ and set $\mathsf {sk} ':=(SK',\tau +1,\tau _{max})$ and abort. If $r=\mathsf {client}$, then for $sk=\tau$, set $\mathsf {sk} ':=\tau +1$.

 

Correctness of the FSOPKE follows from the (extended) correctness property of the underlying PFSKEM and security guarantees hold due to [20, Theorem 2]. We state the following corollary:

Corollary 1

When instantiated with the PFSKEM from Sect. 2.7, the above FSOPKE construction is a correct and secure FSOPKE protocol (with unilateral authentication).

3.1 Analysis

In Table 1, we provide an overview of all existing practically instantiable approaches to construct forward-secret (time-based) PKEM with the one proposed in this paper.³ We compare all schemes for an arbitrary number $\ell$ of time slots, where for sake of simplicity we assume $\ell =2^w$ for some integer w, (corresponding to our time-based BFE/BFKEM) and only count the expensive cryptographic operations, i.e., such as group exponentiations and pairings.

Table 1. Overview of the existing approaches to PFSKEM. We denote by p the number a secret key is already punctured, and $\ell$ the maximum number of time slots. We consider the GHJL [20] instantiation with the BKP-HIBE of [6], the GM [19] and our instantiations with the BBG-HIBE [8], though other HIBE schemes may lead to different parameters. Finally, note that $p \le 2^{20}$, k and m refer to the parameters in the Bloom filter, where k is some orders of magnitude smaller than $\lambda$, i.e., $k=10$ vs. $\lambda =128$, and $|\mathbb {G}_i|$ denotes the bitlength of an element from $\mathbb {G}_i$.

To quickly summarize the schemes: The most interesting characteristic of our approach compared to previous approaches is that our scheme allows to offload all expensive operation to an offline phase, i.e., to the puncturing of time intervals. Here, in addition to the $O(w^2)$ operations which are common to all existing approaches, we have to generate a number of keys, linear in the size m of the Bloom filter. We believe that accepting this additional overhead in favor of blazing fast online puncturing and decryption operations is a viable tradeoff. For the online phase, our approach has a ciphertext size depending on k (where $k=10$ is a reasonable choice), decryption depends on k, the secret key shrinks with increasing amount of puncturings and one does only require to securely delete secret keys during puncturing (note that all constructions have to implement a secure-delete functionality for secret keys within puncturing anyways). In contrast, decryption and puncturing in GHJL is highly inefficient and takes several seconds to minutes on decent hardware for reasonable deployment parameters as it involves a large amount of $O(\lambda ^2)$ HIBE delegations and consequently expensive group operations. In the GM scheme⁴, puncturing is efficient, but the size of the secret key and thus cost of decryption grows in the number of puncturings p. Hence, it gets impractical very soon. More precisely, cost of decryption requires a number of pairing evaluations that depends on the number of puncturings, and can be in the order of $2^{20}$ for realistic deployment parameters.

4 Conclusion

In this paper we introduced the new notion of Bloom filter encryption (BFE) as a variant of puncturable encryption which tolerates a non-negligible correctness error. We presented various BFKEM constructions. The first one is a simple and very efficient construction which builds upon ideas known from the Boneh-Franklin IBE. The second one, which is presented in the full version, is a generic construction from CP-ABEs which achieves constant size ciphertexts. Furthermore, we extended the notion of BFE to the forward-secrecy setting and also presented a construction of what we call a time-based BFE (TB-BFE). This construction is based on HIBEs and in particular can be instantiated very efficiently using the Boneh-Boyen-Goh Tiny HIBE [8]. Our time-based BFKEM can directly be used to instantiate forward-secret 0-RTT key exchange (fs 0-RTT KE) as in [20].

From a practical viewpoint, our motivation stems from the observation that forward-secret 0-RTT KE requires very efficient decryption and puncturing. Our framework—for the first time—allows to realize practical forward-secret 0-RTT KE, even for larger server loads: while we only require to delete secret keys upon puncturing, puncturing in [20] requires, besides deleting secret-key components, additional computations in the order of seconds to minutes on decent hardware. Likewise, when using [19] in the forward-secret 0-RTT KE protocol given in [20], one requires computations in the order of the current number of puncturings upon decryption, while we achieve decryption to be independent of this number. Finally, we believe that BFE will find applications beyond forward-secret 0-RTT KE protocols.