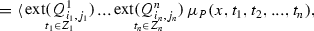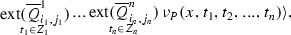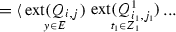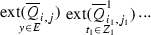1 Short Remarks on Intuitionistic Fuzzy Propositional and Predicate Logics

This paper is an extension of our communication, based on [13].

In classical logic (e.g., [24]), to each proposition (sentence) we juxtapose its truth value: truth—denoted by 1, or falsity—denoted by 0. In the case of fuzzy logic [28], this truth value is a real number in the interval [0, 1] and it is called “truth degree”. In the intuitionistic fuzzy case (see [3, 5, 7, 10]) we add one more value—“falsity degree”—which is again in the interval [0, 1]. Thus, to the proposition p, two real numbers, \(\mu (p)\) and \(\nu (p)\), are assigned with the following constraints:

$$ \mu (p), \nu (p) \in [0, 1] \ \text{ and } \ \mu (p) + \nu (p) \le 1.$$

Here, we define only the operations “disjunction”, “conjunction” and “implication”, originally introduced in [3], which have classical logic analogues, as follows:

$$ V(p \vee q) = \langle \max (\mu (p), \mu (q)), \min (\nu (p), \nu (q))\rangle , $$
$$ V(p \wedge q) = \langle \min (\mu (p), \mu (q)), \max (\nu (p), \nu (q))\rangle , $$
$$ V(p \rightarrow q) = \langle \max (\nu (p), \mu (q)), \min (\mu (p), \nu (q))\rangle . $$

The classical negation is defined by

$$ V(\lnot p) = \langle \nu (p), \mu (p) \rangle . $$

We extend V to all propositional formulas in the usual way.

A formula A is said to be an intuitionistic fuzzy tautology (IFT, for short) if for all evaluations V we have that \(V(A) = \langle a,b\rangle \) implies \(a \ge b\). Two formulas A and B are equivalent, denoted \(A \equiv B\), if \(A \rightarrow B\) and \(B \rightarrow A\) are IFTs.

The idea for evaluation of the propositions was extended for predicates (see [18,19,20,21, 24, 27]) as follows (see, e.g., [5, 7, 12, 22]).

Let x be a variable, obtaining values in a set E and let P(x) be a predicate of the variable x. Let

$$V(P(x)) = \langle \mu (P(x)), \nu (P(x)) \rangle .$$

The IF-interpretations of the quantifiers for all (\(\forall \)) and there exists (\(\exists \)) are introduced in [5, 12, 22] by

$$V(\exists x P(x)) = \langle \sup _{y \in E} \mu (P(y)), \inf _{y \in E} \nu (P(y)) \rangle ,$$
$$V(\forall x P(x)) = \langle \inf _{y \in E} \mu (P(y)), \sup _{y \in E} \nu (P(y)) \rangle .$$

In addition, we assume that E is a finite set, so we can use the following denotations:

$$V(\exists x P(x)) = \langle \max _{y \in E} \mu (P(y)), \min _{y \in E} \nu (P(y)) \rangle ,$$
$$V(\forall x P(x)) = \langle \min _{y \in E} \mu (P(y)), \max _{y \in E} \nu (P(y)) \rangle .$$

The geometrical interpretation of the quantifiers is illustrated in Figs. 1 and 2, where \(x_1,..., x_5\) are the possible values of the variable x and \(V(P(x_1)),...,\) \(V(P(x_5))\) are the corresponding IF-estimations.

Fig. 1
figure 1

Quantifier \(\forall \) in the intuitionistic fuzzy interpretation triangle

Full size image
Fig. 2
figure 2

Quantifier \(\exists \) in the intuitionistic fuzzy interpretation triangle

Full size image

The most important property of the two quantifiers is that each of them juxtaposes to every unary predicate P a point (exactly one for each quantifier) in the IF-interpretational triangle.

In [7] the following assertions are formulated and proved.

Theorem 1

The logical axioms of the theory \(\mathcal K\) (see [24]):

$$ \begin{array}{ll} \text{(a) } &{} \forall x A(x) \rightarrow A(t), \\ &{} \text{ for } \text{ the } \text{ fixed } \text{ variable } t, \\ \text{(b) } &{} \forall x (A \rightarrow B) \rightarrow (A \rightarrow \forall x B), \\ &{} \text{ where } \text{ the } \text{ variable }\, x \text{ is } \text{ not } \text{ free } \text{ in } \text{ A, } \end{array} $$

are IFTs.

Theorem 2

The following formulae (see, e.g. [24]) are IFTs:

$$\begin{array}{ll} \text{(a) }&{}( \forall x A(x) \rightarrow B) \equiv \exists x (A(x) \rightarrow B), \\ &{} \text{ where } \text{ the } \text{ variable }\, x\, \text{ is } \text{ not } \text{ free } \text{ in }\, B, \\ \text{(b) }&{} \exists x A(x) \rightarrow B \equiv \forall x (A(x) \rightarrow B), \\ &{} \text{ where } \text{ the } \text{ variable }\, x\, \text{ is } \text{ not } \text{ free } \text{ in }\,B, \\ \text{(c) }&{}B \rightarrow \forall x A(x) \equiv \forall x (B \rightarrow A(x)), \\ &{} \text{ where } \text{ the } \text{ variable }\, x \text{ is } \text{ not } \text{ free } \text{ in }\, B, \\ \text{(d) }&{}B \rightarrow \exists x A(x) \equiv \exists x (B \rightarrow A(x)), \\ &{} \text{ where } \text{ the } \text{ variable }\, x\, \text{ is } \text{ not } \text{ free } \text{ in }\, B, \\ \text{(e) }&{}( \forall x A \wedge \forall x B) \equiv \forall x (A \wedge B), \\ \text{(f) }&{}( \forall x A \vee \forall x B) \rightarrow \forall x (A \vee B), \\ \text{(g) }&{}\lnot \forall x A \equiv \exists x \lnot A, \\ \text{(h) }&{}\lnot \exists x A \equiv \forall x \lnot A, \\ \text{(i) }&{}\forall x \forall y A \equiv \forall y \forall x A, \\ \text{(j) }&{}\exists x \exists y A \equiv \exists y \exists x A, \\ \text{(k) }&{}\exists x \forall y A \rightarrow \forall y \exists x A, \\ \text{(l) }&{}\forall x (A \rightarrow B) \rightarrow ( \forall x A \rightarrow \forall x B). \end{array} $$

The link between the interpretations of the quantifiers and the topological operators C (closure) and I (interior), defined over IFSs (see [5]), is obvious.

Here, for the first time, we introduce a intuitionistic fuzzy level operator over predicate P. For every \(\alpha , \beta \in [0, 1]\), such that \(\alpha + \beta \le 1\):

$$ N_{\alpha ,\beta }(P) = \{ x | \mu (P(x)) \ge \alpha \ \& \ \nu (P(x)) \le \beta \} \subseteq E.$$

2 Main Results

2.1. Let \(E, Z_1, Z_2,..., Z_n\) be fixed finite linearly ordered sets.

By analogy with intuitionistic fuzzy multi-dimensional sets, introduced in [14,15,16,17], here for the first time, for a predicate P of the variables \(x, z_1, z_2, ..., z_n\), ordered in the present form, we define an intuitionistic fuzzy evaluation function V for P of the form

$$V(P(x,z_1,z_2,...,z_n)) = \langle \mu _P(x,z_1,z_2,...,z_n), \nu _P(x,z_1,z_2,...,z_n)\rangle ,$$

where \(x \in E\) is a (basic) variable, \(z_1 \in Z_1,\) \(z_2 \in Z_2,\) ..., \(z_n \in Z_n\) are additional variables, \(\mu _P(x,z_1,z_2,...,z_n) \in [0, 1],\) \(\nu _P(x,z_1,z_2,...,z_n) \in [0, 1]\) and

$$\mu _P(x,z_1,z_2,...,z_n) + \nu _P(x,z_1,z_2,...,z_n) \le 1.$$

Here, \(\mu _P(x,z_1,z_2,...,z_n)\) and \(\nu _P(x,z_1,z_2,...,z_n)\) are the degrees of validity and non-validity of \(P(x,z_1,z_2,...,z_n)\), respectively.

In the particular case, when \(n = 1\), we obtain the case of temporal IFL (see [4]).

Having in mind the results from [14], we can define the following \((n+1)\)-dimensional quantifiers:

  1. (a)

    (partial) standard quantifier

    $$ V(\exists (x, z_1,z_2,...,z_n) P(x, z_1,z_2,...,z_n))$$
    $$= \langle \max _{y \in E} \mu _P(y, z_1,z_2,..., z_n), \min _{y \in E} \nu _P(y,z_1,z_2,..., z_n) \rangle ,$$
    $$ V(\forall (x, z_1,z_2,...,z_n) P(x, z_1,z_2,...,z_n))$$
    $$= \langle \min _{y \in E} \mu _P(y, z_1,z_2,..., z_n), \max _{y \in E} \nu _P(y, z_1,z_2,..., z_n) \rangle $$
  2. (b)

    (partial) i-quantifiers

    $$ V(\exists ^i (x, z_1,z_2,...,z_n) P(x, z_1,z_2,...,z_n))$$
    $$= \langle \max _{t_i\in Z_i} \mu _P(x,z_1,z_2,...,z_{i-1},t_i, z_{i+1},..., z_n), $$
    $$\min _{t_i\in Z_i} \nu _P(x,z_1,z_2,...,z_{i-1},t_i, z_{i+1},..., z_n) \rangle ,$$
    $$ V(\forall ^i (x, z_1,z_2,...,z_n) P(x, z_1,z_2,...,z_n))$$
    $$= \langle \min _{t_i\in Z_i} \mu _P(x,z_1,z_2,...,z_{i-1},t_i, z_{i+1},..., z_n), $$
    $$\max _{t_i\in Z_i} \nu _P (x,z_1,z_2,...,z_{i-1},t_i, z_{i+1},..., z_n) \rangle $$
  3. (c)

    general additional (shortly, a-) quantifier

    $$ V(\exists ^a (x, z_1,z_2,...,z_n) P(x, z_1,z_2,...,z_n))$$
    $$= \langle \max _{t_1\in Z_1} ... \max _{t_n\in Z_n} \mu _P(x,t_1,t_2,...,t_n), $$
    $$\min _{t_1\in Z_1} ... \min _{t_n\in Z_n} \nu _P(x,t_1,t_2,...,t_n) \rangle ,$$
    $$ V(\forall ^a (x, z_1,z_2,...,z_n) P(x, z_1,z_2,...,z_n)$$
    $$= \langle \min _{t_1\in Z_1} ... \min _{t_n\in Z_n} \mu _P(x,t_1,t_2,...,t_n), $$
    $$\max _{t_1\in Z_1} ... \max _{t_n\in Z_n} \nu _P(x,t_1,t_2,...,t_n) \rangle $$
  4. (d)

    general quantifier

    $$ V(\exists ^g (x, z_1,z_2,...,z_n) P(x, z_1,z_2,...,z_n))$$
    $$= \langle \max _{y \in E}\max _{t_1\in Z_1} ... \max _{t_n\in Z_n} \mu _P(y,t_1,t_2,...,t_n), $$
    $$\min _{y \in E}\min _{t_1\in Z_1} ... \min _{t_n\in Z_n} \nu _P(y,t_1,t_2,...,t_n) \rangle ,$$
    $$ V(\forall ^g (x, z_1,z_2,...,z_n) P(y, z_1,z_2,...,z_n)$$
    $$= \langle \min _{y \in E}\min _{t_1\in Z_1} ... \min _{t_n\in Z_n} \mu _P(y,t_1,t_2,...,t_n), $$
    $$\max _{y \in E}\max _{t_1\in Z_1} ... \max _{t_n\in Z_n} \nu _P(y,t_1,t_2,...,t_n) \rangle $$

Theorem 3

For each of the fifth pairs of quantifiers, the equalities

$$\begin{array}{l} V(\lnot \exists (x, z_1,z_2,...,z_n) \lnot P(x, z_1,z_2,...,z_n)) = \\ = V(\forall (x, z_1,z_2,...,z_n) P(x, z_1,z_2,...,z_n)), \\ V(\lnot \forall (x, z_1,z_2,...,z_n) \lnot P(x, z_1,z_2,...,z_n)) = \\ = V(\exists (x, z_1,z_2,...,z_n) P(x, z_1,z_2,...,z_n)), \\ V(\lnot \exists ^i (x, z_1,z_2,...,z_n) \lnot P(x, z_1,z_2,...,z_n)) = \\ = V(\forall ^i (x, z_1,z_2,...,z_n) P(x, z_1,z_2,...,z_n)), \\ V(\lnot \forall ^i (x, z_1,z_2,...,z_n) \lnot P(x, z_1,z_2,...,z_n)) = \\ = V(\exists ^i (x, z_1,z_2,...,z_n) P(x, z_1,z_2,...,z_n)), \\ V(\lnot \exists ^a (x, z_1,z_2,...,z_n) \lnot P(x, z_1,z_2,...,z_n)) = \\ = V(\forall ^a (x, z_1,z_2,...,z_n) P(x, z_1,z_2,...,z_n), \\ V(\lnot \forall ^a (x, z_1,z_2,...,z_n) \lnot P(x, z_1,z_2,...,z_n)) = \\ = V(\exists ^a (x, z_1,z_2,...,z_n) P(x, z_1,z_2,...,z_n), \\ V(\lnot \exists ^g (x, z_1,z_2,...,z_n) \lnot P(x, z_1,z_2,...,z_n)) = \\ = V(\forall ^g (x, z_1,z_2,...,z_n) P(x, z_1,z_2,...,z_n), \\ V(\lnot \forall ^g (x, z_1,z_2,...,z_n) \lnot P(x, z_1,z_2,...,z_n)) = \\ = V(\exists ^g (x, z_1,z_2,...,z_n) P(x, z_1,z_2,...,z_n) \end{array} $$

hold.

Proof

Let us check the validity of the first equality.

$$ V(\lnot \exists (x, z_1,z_2,...,z_n) \lnot P(x, z_1,z_2,...,z_n))$$
$$= \lnot \exists (x, z_1,z_2,...,z_n) \lnot \langle \mu _P(x,z_1,z_2,...,z_n), $$
$$\nu _P(x,z_1,z_2,...,z_n) \rangle $$
$$= \lnot \exists (x, z_1,z_2,...,z_n) \langle \nu _P(x,z_1,z_2,...,z_n), $$
$$ \mu _P(x,z_1,z_2,...,z_n) \rangle $$
$$= \lnot \langle \max _{y \in E} \nu _P(y, z_1,z_2,..., z_n), \min _{y \in E} \mu _P(y,z_1,z_2,..., z_n) \rangle $$
$$= \langle \min _{y \in E} \mu _P(y,z_1,z_2,..., z_n), \max _{y \in E} \nu _P(y, z_1,z_2,..., z_n) \rangle $$
$$= V(\forall (x, z_1,z_2,...,z_n) P(x, z_1,z_2,...,z_n)).$$

The other equalities are proved in the same manner.

An important Open Problem is: Which other negations from the ones, defined in [11], also satisfy these equalities?

2.2. Here, we extend the defined above intuitionistic fuzzy level operator over predicate P to the following forms:

$$N^{w}_{\alpha ,\beta }(P) = \{ (z_1,z_2,...,z_n) | \max _{y \in E} \mu _P(y, z_1,z_2,..., z_n) \ge \alpha $$
$$ \ \& \ \min _{y \in E} \nu _P(y,z_1,z_2,..., z_n) \le \beta \},$$
$$N^{s}_{\alpha ,\beta }(P) = \{ (z_1,z_2,...,z_n) | \min _{y \in E} \mu _P(y, z_1,z_2,..., z_n) \ge \alpha $$
$$ \ \& \ \max _{y \in E} \nu _P(y,z_1,z_2,..., z_n) \le \beta \},$$
$$N^{w,i}_{\alpha ,\beta }(P) = \{ (x,z_1,z_2,...,z_{i-1},z_{i+1},...,z_n) | $$
$$| \max _{t_i\in Z_i} \mu _P(x,z_1,z_2,...,z_{i-1},t_i, z_{i+1},..., z_n) \ge \alpha $$
$$ \& \ \min _{t_i\in Z_i} \nu _P(x,z_1,z_2,...,z_{i-1},t_i, z_{i+1},..., z_n) \le \beta \},$$
$$N^{s,i}_{\alpha ,\beta }(P) = \{ (x,z_1,z_2,...,z_{i-1},z_{i+1},...,z_n) | $$
$$ | \min _{t_i\in Z_i} \mu _P(x,z_1,z_2,...,z_{i-1},t_i, z_{i+1},..., z_n) \ge \alpha $$
$$ \& \ \max _{t_i\in Z_i} \nu _P(x,z_1,z_2,...,z_{i-1},t_i, z_{i+1},..., z_n) \le \beta \},$$
$$N^{w,a}_{\alpha ,\beta }(P) = \{ x | \max _{t_1\in Z_1} ... \max _{t_n\in Z_n} \mu _P(x,t_1,t_2,...,t_n) \ge \alpha $$
$$ \ \& \ \min _{t_1\in Z_1} ... \min _{t_n\in Z_n} \nu _P(x,t_1,t_2,...,t_n) \le \beta \},$$
$$N^{s,a}_{\alpha ,\beta }(P) = \{ x | \min _{t_1\in Z_1} ... \min _{t_n\in Z_n} \mu _P(x,t_1,t_2,...,t_n) \ge \alpha $$
$$ \ \& \ \max _{t_1\in Z_1} ... \max _{t_n\in Z_n} \nu _P(x,t_1,t_2,...,t_n) \le \beta \}.$$

As for the general quantifier, since its evaluation is just a point in the IF-triangle, the corresponding level operators will be propositions (with value 1 (true) or 0 (false)):

$$ {N}^{w,g}_{\alpha ,\beta }(P) = 1 \Leftrightarrow \max _{y \in E}\max _{t_1\in Z_1} ... \max _{t_n\in Z_n} \mu _{P}(y,t_1,t_2,...,t_n) \ge \alpha $$
$$ \& \ \min _{y \in E}\min _{t_1\in Z_1} ... \min _{t_n\in Z_n} \nu _P(y,t_1,t_2,...,t_n) \le \beta , $$
$$ {N}^{s,g}_{\alpha ,\beta }(P) = 1 \Leftrightarrow \min _{y \in E}\min _{t_1\in Z_1} ... \min _{t_n\in Z_n} \mu _P(y,t_1,t_2,...,t_n) \ge \alpha $$
$$ \& \ \max _{y \in E}\max _{t_1\in Z_1} ... \max _{t_n\in Z_n} \nu _P(y,t_1,t_2,...,t_n) \le \beta . $$

Theorem 4

For every predicate P and for every \(\alpha , \beta \in [0, 1]\), such that \(\alpha + \beta \le 1\), the inclusions:

$$\begin{array}{l} N^{s}_{\alpha ,\beta }(P) \subseteq N^{w}_{\alpha ,\beta }(P), \\ N^{s,i}_{\alpha ,\beta }(P) \subseteq N^{w,i}_{\alpha ,\beta }(P), \\ N^{s,a}_{\alpha ,\beta }(P) \subseteq N^{w,a}_{\alpha ,\beta }(P) \end{array} $$

hold. Moreover,

$$ N^{s,g}_{\alpha ,\beta }(P) = 1 \Longrightarrow N^{w,g}_{\alpha ,\beta }(P) = 1. $$

2.3. It is well known from classical logic that for each predicate P with argument x having a finite of number interpretations \(a_1, a_2, ..., a_n\):

$$V(\forall x P(x)) = V(P(a_1) \wedge P(a_2) \wedge ... \wedge P(a_n)), $$
$$V(\exists x P(x)) = V(P(a_1) \vee P(a_2) \vee ... \vee P(a_n)). $$

Now, having in mind the ideas from [8], we mention that from classical logic, it is well-known that for any two formulas A and B:

$$\begin{aligned} A \vee B&= \lnot A \rightarrow B, \end{aligned}$$
(1)
$$\begin{aligned} A \wedge B&= \lnot (A \rightarrow \lnot B). \end{aligned}$$
(2)

Having the 185 intuitionistic fuzzy implications, described in [8] and the 53 intuitionistic fuzzy negations, generated by them and described in [11], Angelova and Stoenchev constructed in [1] 185 disjunctions and 185 conjunctions, using formulas (1) and (2).

On the other hand, as we can see in [6], the disjunction and the conjunction can have two forms and formulas (1) and (2) can be changed to the following new ones:

$$\begin{aligned} A \vee B&= \lnot A \rightarrow \lnot \lnot B, \end{aligned}$$
(3)
$$\begin{aligned} A \wedge B&= \lnot (\lnot \lnot A \rightarrow \lnot B). \end{aligned}$$
(4)

In [2], Angelova and Stoenchev constructed 185 disjunctions and 185 conjunctions, using the formulas (3) and (4).

Therefore, formulas (1)–(4) must be rewritten to

$$\begin{aligned} A \vee _{i,1} B = \lnot _{\varphi (i)} A \rightarrow _i B, \end{aligned}$$
(5)
$$\begin{aligned} A \wedge _{i,1} B = \lnot _{\varphi (i)} (A \rightarrow _i \lnot _{\varphi (i)} B). \end{aligned}$$
(6)
$$\begin{aligned} A \vee _{i,2} B = \lnot _{\varphi (i)} A \rightarrow _i \lnot _{\varphi (i)} \lnot _{\varphi (i)} B, \end{aligned}$$
(7)
$$\begin{aligned} A \wedge _{i,2} B = \lnot _{\varphi (i)} (\lnot _{\varphi (i)} \lnot _{\varphi (i)} A \rightarrow _i \lnot _{\varphi (i)} B), \end{aligned}$$
(8)

where \(\varphi (i)\) is the subsequent number of the negation that corresponds to the i-th implication (cf. Table 1.3 in [11]).

As it is discussed in [9], we see the possibility for constructing a third group of disjunctions and conjunctions. They will have the forms

$$\begin{aligned} A \vee _{i,3} B = \lnot _{1} A \rightarrow _i B, \end{aligned}$$
(9)
$$\begin{aligned} A \wedge _{i,3} B = \lnot _{1} (A \rightarrow _i \lnot _{1} B). \end{aligned}$$
(10)

The first Open Problem that arises is: Construct all new disjunctions and conjunctions. It is interesting to check whether some disjunctions and conjunctions will coincide. The second Open Problem is to study the behaviour of the new disjunctions and conjunctions. For example, which of them will satisfy De Morgan Laws and in which form of these laws?

Another Open Problem is to study the properties of the disjunctions and conjunctions from (5)–(10). It is very important to check the validity of the separate axioms—of the intuitionistic logic, of Kolmogorov, of Lukasiewicz and Tarski, of Klir and Yuan, and the other ones.

In [9] an idea for lots of new quantifiers was discussed: For each new pair of conjunction and disjunction, we obtain a pair of quantifiers that have the forms

$$V(\forall _{i,j} x P(x)) = V(P(a_1) \wedge _{i,j} P(a_2) \wedge _{i,j} ... \wedge _{i,j} P(a_n)),$$
$$V(\exists _{i,j} x P(x)) = V(P(a_1) \vee _{i,j} P(a_2) \vee _{i,j} ... \vee _{i,j} P(a_n)),$$

where \(i \ (1\le i \le 185)\) and \(j \ (1 \le j \le 3)\) are the indices of the respective pair of conjunction and disjunction that generates the new pair of quantifiers. One important point here is that for the definition to make sense, we need to explicitly define how to iterate the disjunctions and the conjunctions. We use the following left-associative conventions:

$$A_1 \wedge _{i,j} A_2 \wedge _{i,j} ... \wedge _{i,j} A_n \wedge _{i,j} A_{n+1}$$
$$= (A_1 \wedge _{i,j} A_2 \wedge _{i,j} ... \wedge _{i,j} A_n) \wedge _{i,j} A_{n+1}, $$
$$A_1 \vee _{i,j} A_2 \vee _{i,j} ... \vee _{i,j} A_n \vee _{i,j} A_{n+1}$$
$$= (A_1 \vee _{i,j} A_2 \vee _{i,j} ... \vee _{i,j} A_n) \vee _{i,j} A_{n+1}. $$

In the case when \(\wedge _{i,j}\) and \(\vee _{i,j}\) are associative (and commutative), any other grouping (or rearranging) will give the same result.

Obviously, \(\forall _{4,1}\) coincides with the standard quantifier \(\forall \) and \(\exists _{4,1}\) coincides with the standard quantifier \(\exists \).

One special case is the following: using implication \(\rightarrow _{139}\) and negation \(\lnot _1\) we obtain for \(a, b, c, d \in [0, 1]\) and \(a + b, c + d \le 1\):

$$V(\langle a, b \rangle \vee _{139,3} \langle c, d \rangle ) = \left\langle \frac{a + c}{2}, \frac{b + d}{2} \right\rangle = \langle a, b \rangle \wedge _{139,3} \langle c, d \rangle .$$

These operations are commutative, but not associative. If for each i: \(V(P(x_i)) = \langle a_i, b_i \rangle \), then

$$V(\forall _{139,3} x P(x)) = \left\langle \sum \limits _i p_i.a_i, \sum \limits _i p_i.b_i \right\rangle = V(\exists _{139,3} x P(x)),$$

where \(p_1 = \frac{1}{2^{n-1}}\) and \(p_i = \frac{1}{2^{n-i+1}}\) for \(2 \le i \le n\).

Hence, there exists a quantifier’s interpretation for which both quantifiers “\(\forall \)” and “\(\exists \)” coincide. In this case, we check directly, that

$$\lnot _1 \forall _{139,3} x \lnot _1 P(x) = \forall _{139,3} x P(x).$$

It is very interesting that the quantifier \(\forall _{139,3}\) can be regarded as an analogue of the weight center operator W (see, e.g. [6]).

For a finite linearly ordered set X, \(i\in \{1,\ldots ,185\}\), \(j\in \{1,2,3\}\) and \((n+1)\)-dimensional predicate P we define

$$ \min _{x\in X}^{i,j} P(x,y_1,\ldots ,y_n) $$
$$ P(x_1,y_1,\ldots ,y_n) \wedge _{i,j} P(x_2,y_1,\ldots ,y_n) \wedge _{i,j} ... \wedge _{i,j} P(x_m,y_1,\ldots ,y_n), $$
$$ \max _{x\in X}^{i,j} P(x,y_1,\ldots ,y_n)$$
$$= P(x_1,y_1,\ldots ,y_n) \vee _{i,j} P(x_2,y_1,\ldots ,y_n) vee_{i,j} ... \vee _{i,j} P(x_m,y_1,\ldots ,y_n), $$

where \(x_1< x_2< ... < x_m\) are the elements of X, listed in increasing order. Both operations produce a predicate of \(y_1,\ldots ,y_n\).

Let us define

$$ \overline{Q}_{i,j} = \left\{ \begin{array}{ll} \exists _{i,j}, &{} \text { if}\, Q_{i,j}\, \text {is}\, \forall _{i,j} \\ \forall _{i,j}, &{} \text { if}\, Q_{i,j}\, \text {is}\, \exists _{i,j} \end{array}. \right. $$

After these remarks, we continue with definitions of new quantifiers over the \((n+1)\)-dimensional predicate P. Let for \(1 \le i \le 185\) and for \(1 \le j \le 3\): \(Q_{i,j} \in \{ \forall _{i,j}, \exists _{i,j} \}\). Let

Then, for \(i, i_1, ..., i_n \in \{1, 2, ..., 185 \}\) and \(j, j_1, ..., j_n \in \{1, 2, 3\}\), we define:

  1. (e)

    general Q-additional quantifiers

    $$ V((Q^1_{i_1,j_1},Q^2_{i_2,j_2},...,Q^n_{i_n,j_n})(x, z_1,z_2,...,z_n) $$
    $$ P(x, z_1,z_2,...,z_n))$$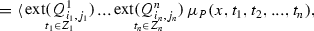
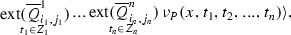
  2. (f)

    general Q-quantifier

    $$ V((Q_{i,j},Q^1_{i_1,j_1},Q^2_{i_2,j_2},...,Q^n_{i_n,j_n})(x, z_1,z_2,...,z_n) $$
    $$P(x, z_1,z_2,...,z_n))$$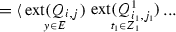

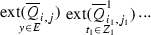
Theorem 5

For each of the third quantifiers, equalities

$$ V(\lnot _1 (Q^1_{i_1,j_1},Q^2_{i_2,j_2},...,Q^n_{i_n,j_n})(x, z_1,z_2,...,z_n) $$
$$\lnot _1 P(x, z_1,z_2,...,z_n))$$
$$ = V((\overline{Q}^1_{i_1,j_1},\overline{Q}^2_{i_2,j_2},...,\overline{Q}^n_{i_n,j_n})(x, z_1,z_2,...,z_n) $$
$$P(x, z_1,z_2,...,z_n))$$
$$ V(\lnot _1 (Q_{i,j},Q^1_{i_1,j_1},Q^2_{i_2,j_2},...,Q^n_{i_n,j_n})(x, z_1,z_2,...,z_n) $$
$$\lnot _1 P(x, z_1,z_2,...,z_n))$$
$$ = V((\overline{Q}_{i,j},\overline{Q}^1_{i_1,j_1},\overline{Q}^2_{i_2,j_2},...,\overline{Q}^n_{i_n,j_n})(x, z_1,z_2,...,z_n) $$
$$P(x, z_1,z_2,...,z_n)).$$

Open Problem: Which of the equalities from Theorems 1 and 2 are valid for the new quantifiers?

3 Conclusion

The so defined multidimensional intuitionistic fuzzy quantifiers can obtain different applications in the area of artificial intelligence. For example, we can use them in procedures for decision making and for intercriteria analysis, in rules of intuitionistic fuzzy expert systems, and others.

All these multidimensional intuitionistic fuzzy quantifiers are first-order. In a next research, we will discuss possibilities for defining second and higher-order multidimensional intuitionistic fuzzy quantifiers. Some properties for standard predicates, discussed in [18,19,20,21, 23,24,25,26,27, 29,30,31] will be studied for the multidimensional intuitionistic fuzzy quantifiers.

In future, we will study the possibility to change the condition “Let \(E, Z_1, Z_2,...,\) \( Z_n\) be fixed finite linearly ordered sets” with which Sect. 2.1 started. When the properties of the new intuitionistic fuzzy conjunctions and disjunctions are studied, probably, we will be able to change this condition with the condition “Let \(E, Z_1, Z_2,..., Z_n\) be fixed finite partially ordered sets”. So, the new constructions will give additional possibilities for application in some areas of the artificial intelligence.