Keywords

1 Introduction

Research in Model Based Testing (MBT) is currently advancing rapidly trying to match the growing demand from industry for more effective and better scalable test development technologies. Since the cost for leaving undetected faults in software grows with its complexity, code and model coverage by tests is often considered insufficient and the guaranteed fault detection becomes the ultimate goal. Accordingly, research in MBT has been addressing fault modeling and fault model driven test generation problems, see, e.g., [2, 38]. Fault models usually refer to test models which formalize reference specifications and/or requirements. State-oriented test models seem to be most popular models among test engineers. Finite state machines (FSM) and input output transition systems (IOTS) are state-oriented models; test generation methods have traditionally been developed separately for these models, even though, as has already been demonstrated, many ideas, especially for fault model based test generation, developed for testing from FSM can successfully be used for testing from IOTS [31].

There exists a significant body of work devoted to the development of methods for test generation from a given FSM to guarantee the complete fault coverage, once a fault model is defined. The pioneering work of Moore [21] and Hennie [13] led to the development of the theory of checking experiments, where faults are modeled by a universe of FSMs with a given number of states, see, e.g., [4, 6, 10, 33]. Checking experiments have already been lifted to FSMs more general than the classical (completely specified and deterministic) Mealy machine, such as partially defined and nondeterministic state machines, see, e.g., [27]. However, practical applications require more extensions to the classical FSM model. These are commonly known as the Extended Finite State Machine (EFSM) models. Various flavors of EFSMs are used in Harel’s statecharts [12], SysML/UML [9], Simulink/Stateflow [32], SDL [11] and other modelling languages. Extensions are often suggested without a formal semantics; this creates a big hurdle for fault-model based test generation. Whenever the semantics of a particular specification language is defined by the tool which supports it, fault models become specific to the tool provider and may not be adequate for implementations coming from other suppliers. General testing approaches usually rely on formally defined extensions of Mealy machine, see, e.g., [26, 36].

Most of the existing work on test generation from EFSM concentrates on the model coverage, see, e.g., [3, 14, 18, 28], which provides no characterization of faults that can be detected by the generated tests. There are some techniques for test generation from EFSM which use certain fault models [26, 36] and limited state/configuration identification sequences [5, 19, 26]. The work of [16] uses checking experiment methods, but requires first to determine input/output equivalence classes from a given specification EFSM and choose concrete inputs. To the best of our knowledge, there is no result in lifting the theory of checking experiments to extended FSMs. This observation is one of the main motivations of this work.

Another motivation comes from research on symbolic automata and transducers, which is driven by several practical problems. The work of [34] mentions applications ranging from modern regex analysis to advanced web security analysis where the so-called sanitizers, string transformation routines are extensively used as the first line of defense against cross site scripting attacks. A large class of sanitizers can be described and analyzed by using symbolic finite state transducers. Symbolic finite automata are introduced as an extension of classical finite state automata that allows transitions to be labeled with predicates. Automata with predicates instead of concrete symbols are also used in [37] and discussed in [23] in the context of natural language processing. The work on learning symbolic automata [20] has also to be mentioned here, since the automata learning shares certain aspects with the testing problem in the following sense. If a black box passes a checking experiment, then under well-defined conditions it is recognized as some automaton. Hence it is important to investigate checking experiments for symbolic automata.

The community focusing on testing from IOTS has also considered extensions to symbolic representation of transition systems which avoid enumerations of its components, see, e.g. [8, 29], but these approaches are not fault model driven, they use one or another test purpose. More references on symbolic approaches in testing could be found, e.g., in [1, 17].

In this paper, we attempt to lift the theory of checking experiments to a special type of EFSM, which extends the deterministic Mealy machine with predicates defined over input variables, considered as its symbolic inputs. We propose a test generation method that produces a symbolic checking experiment, adapting the well-known HSI method [39]. We then investigate under which conditions instances of a symbolic checking experiment can be used for testing black-box implementations, guaranteeing the full fault coverage.

The paper is organized as follows. In Sect. 2, we define the model of FSM with symbolic inputs. In Sect. 3, we study the relations between SIFSMs. Symbolic and concrete checking experiments are introduced in Sect. 4, where we also investigate fault detection capability of concrete tests obtained from symbolic checking experiments. Section 5 summarizes our contributions and presents future work.

2 Definitions and Notations

2.1 Preliminaries

We define an (input) alphabet as a set of guards over variables of well-defined types. Let G denote the universe of guards that are predicates over variables in a fixed set V for which a decision theory, e.g., an SMT solver, exists, excluding the predicates that are always false. G* will denote the universe of input sequences.

Let D V denote the set of all the valuations v of the input variables in the set V, called concrete inputs. A set of concrete inputs is called a symbolic input; both, concrete and symbolic, inputs are represented by guards in G. Henceforth, we use set-theoretical operations on symbolic inputs. In particular, we write v ∈ g, when concrete input v satisfies g. We define some relations between input sequences in G*.

Definition 1.

Given two input sequences α, β ∈ G* of the same length k, α = g 1…g k , β = g’ 1…g’ k , we let α ∩ β = g 1 ∩ g’ 1…g k  ∩ g’ k denote the sequence of intersections of inputs in sequences α and β; α and β are compatible, if for all i = 1, …, k, g i  ∩ g’ i  ≠ ∅. We say that α is a reduction of β, denoted α ⊆ β, if α = α ∩ β. If α is a sequence of concrete inputs as well as a reduction of β then it is called an instance of β; given a finite set of input sequences E ⊆ G*, a set of concrete input sequences I is called an instance of the set E, if I contains at least one instance for each input sequence in E.

2.2 Symbolic Input FSM

We define a model, called a symbolic input finite state machine (SIFSM), which operates in discrete time as a synchronous machine reading values of input variables and setting up the values of output variables. Output variables are assumed to have a finite number of valuations and form a finite output alphabet. On the other hand, there may exist an infinite set of input valuations. SIFSM uses guards on transitions which are executed one at a time.

Definition 2.

A symbolic input finite state machine S (or machine, for short) is a 7-tuple (S, s 0, V, O, F, δ, λ), where

  • S is a finite set of states with the initial state s 0,

  • V is a finite set of input variables over which guards in G are defined,

  • O is a finite set of outputs,

  • F ⊆ S × G is a finite specification domain,

  • δ : F → S is a transition function, and

  • λ : F → O is an output function.

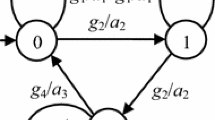
Examples of SIFSM are given in Fig. 1. Examples of realistic systems which can be specified as SIFSM could be found in [15, 28]. In the first work, the Ceiling speed monitoring following the public ETCS system specification [7] is modelled, it has two input and two output variables. In the second work, an HVAC controller specified in Simulink/Stateflow is considered, it has nine input variables, Boolean and naturals, the most complex transition guard comprises 13 terms.

Fig. 1.
figure 1

SIFSMs S, P, and the distinguishing machine S ⊕ P.

Full size image

The semantics of SIFSM is defined by a Mealy state machine with a possibly infinite input set, where the state and output sets remain finite.

Given (s, g) ∈ F, we say that input g is defined in state s ∈ S. Then, G(s) = {g ∈ G | (s, g) ∈ F} contains all inputs defined at s. The machine S is deterministic, if for any (s, g), (s, g’) ∈ F, it holds that g ∩ g’ = ∅. State s of the machine S is input-complete, if for each input valuation v, at least one of its guards evaluates to True, i.e., {v ∈ g | g ∈ G(s)} = D V . The machine S is input-complete, if each state is input-complete. The machine S is normalized, if for all (s, g), (s, g’) ∈ F, δ(s, g) = δ(s, g’) implies that λ(s, g) ≠ λ(s, g’); in other words, the machine has at most one transition with a given output for each ordered pair of states. Any machine that is not normalized can always be converted into a normalized one by merging transitions with the same start and end states as well as the same output and forming the disjunction of their guards. This is a unique compact form of a SIFSM. We will consider only normalized deterministic input-complete specification machines.

An input sequence α ∈ G*, α = g 1…g k , is defined in state s ∈ S, if each input in α is defined in a corresponding state, i.e., if there exist states s 1, …, s k , s k+1, where s 1 = s, such that (s i , g i ) ∈ F and δ(s i , g i ) = s i+1 for each 1 ≤ i ≤ k. Let ΨS(s) denote the set of input sequences defined in state s, and ΨS denote sequences defined in the initial state of S. Moreover, ΩS(s) denotes the set ΨS(s) closed under the reduction relation, called the set of input sequences admissible in state s, i.e., ΩS(s) = {α ∈ G* | β ∈ ΨS(s), α ⊆ β}, and ΩS denotes sequences admissible in the initial state of S. Notice that for an input-complete machine S any concrete input sequence is admissible in every state, i.e., D V * = ΩS(s), for each s ∈ S. We lift the transition and output functions from inputs to admissible input sequences, including the empty sequence ε, as usual: for s ∈ S, δ(s, ε) = s and λ(s, ε) = ε; and for input sequence α ∈ ΩS(s) and input g ∈ ΩS(δ(s, α)), δ(s, αg) = δ(δ(s, α), g’) and λ(s, αg) = λ(s, α)λ(δ(s, α), g’), if g’ ∈ G S((δ(s, α)) and g ⊆ g’.

Considering the input alphabet G, we further extend the transition and output functions to the set of all possible input sequences in G*. The extended transition function describes the set of all possible states which a deterministic machine from a given state can reach in response to input sequence and the extended output reaction function gives the set of all possible corresponding output sequences; these sets are singletons if the input sequence is admissible for the starting state. We define the function Δ : S × G* → 2S as follows. Given s ∈ S and α ∈ G*, we let Δ(s, α) be {δ(s, β) | β ⊆ α, β ∈ ΩS(s)}. Obviously, for any α ∈ ΩS(s), Δ(s, α) = {δ(s, α)}. Similarly, we define the function Λ : S × G* → 2O*. For s ∈ S and α ∈ G*, we define Λ(s, α) = {λ(s, β) | β ⊆ α, β ∈ ΩS(s)}. We call the functions Δ and Λ the extended transition and output functions. For any α ∈ ΩS(s), Λ(s, α) = {λ(s, α)}. Given a set of symbolic input sequences Φ ⊆ G*, the SIFSM S is said to be a Φ-converter if for each α ∈ Φ, |Λ(s 0, α)| = 1.

Given input sequence α, we use pref(α) to denote the set of all prefixes of α. Similar, pref(A) denotes the set of prefixes of sequences in A. The set A is prefix-closed if pref(A) = A.

3 Relations Between SIFSMs

In this section, we extend the classical equivalence and distinguishability relations to SIFSMs and introduce new types of distinguishability which have no counterparts in the classical deterministic Mealy machine. We define a designated symbolic machine which can be used to check the distinguishability of symbolic input finite state machines.

In this paper, we focus our attention on deterministic systems, in which different output sequences produced by two states in response to the same symbolic input sequence indicate that the two states can be distinguished by the input sequence.

Definition 3.

Given states s, s’ ∈ S of S, states s, s’ ∈ S are distinguishable, denoted s ≄ s’, if there exist compatible input sequences α ∈ ΨS(s) and β ∈ ΨS(s’), such that λ(s, (α ∩ β)) ≠ λ(s’, (α ∩ β)); the sequence α ∩ β is called a separating sequence for distinguishable states s and s’.

Since the machine is deterministic, its reacts to a given admissible input sequence as it does to any of its reduction. We have therefore the following corollary.

Corollary 1.

Any instance of a separating sequence is a separating sequence.

The importance of this property of separating sequences becomes evident in the context of testing, as we discussed later.

Given a prefix-closed set of input sequences E ⊆ G*, we let s ≄ E s’ to denote the fact that the set E contains a separating sequence. If E contains no separating sequence then states s and s’ are said to be E-equivalent, denoted s ≃  E s’, and if E = G*, then the states are equivalent, denoted s ≃ s’. The machine is reduced if it has no equivalent states. We further assume that the specification machine S is reduced.

As usual, we define equivalence and distinguishability of machines as the corresponding relation between their initial states.

To decide distinguishability we define a designated machine, where, instead of composing transitions caused by the same input as in the case of FSMs [27], we compose transitions with compatible inputs. The machine has the common behavior of the given machines, as the classical automata product (even lifted to symbolic automata [34]), but in addition it signals when they disagree on output and enters a sink state.

Definition 4.

Given two SIFSMs S = (S, s 0, V, O, F S, δS, λS) and P = (P, p 0, V, O, F P, δP, λP) over the same set of input variables V, a SIFSM C = (C ∪ {∇}, c 0, V, O ∪ {⊥}, F C, δC, λC), where ∇ is a designated sink state, ⊥ is a designated output, is the distinguishing machine for S and P denoted S ⊕ P, if

  • c 0 = (s 0, p 0)

  • F C ⊆ C × G such that for (s, p) ∈ C, g ∩ g’ ∈ G C(s, p), if g ∈ G S(s), g’ ∈ G P(p), and g ∩ g’ ≠ ∅

  • For (s, p) ∈ S × P and g ∩ g’ ∈ G C(s, p), δC((s, p), g ∩ g’) = (δS(s, g), δP(p, g’)) and λC((s, p), g ∩ g’) = λS(δ(s, g)), (δS(s, g), δP(p, g’)) ∈ S × P if λS(s, g) = λP(p, g’) otherwise, i.e., if λS(s, g) ≠ λP(p, g’), then δC((s, p), g ∩ g’) = ∇, and λC((s, p), g ∩ g’) = ⊥.

We further assume that the distinguishing machine is normalized by merging, if needed, transitions with the designated output ⊥ from the same state. By the definition, any input sequence reaching the sink state of the distinguishing machine is a separating sequence for the given machines; the distinguishing machine could be used to decide the equivalence of two distinct machines as well as states in the same machine. To illustrate the above we consider the SIFSMs in Fig. 1, where x is an input variable, a is a constant, 0, 1 and 2 are outputs and T stands for True.

The machines S and P are distinguishable, as the distinguishing machine S ⊕ P shows. The shortest separating sequence is (x ≤ a)(x ≤ a)(x ≤ a). Indeed, in response to it S produces 011, while P produces 010.

In this example, we have that the separating sequence is admissible in both machines, as required; however, it is defined only in one of them, namely, (x ≤ a)(x ≤ a)(x ≤ a) ∈ ΨP, though (x ≤ a)(x ≤ a)(x ≤ a) ∉ ΨS. This sequence is a reduction of the symbolic sequence (x ≤ a)(T)(T) defined in the machine S. Considering the relations between separating and defined sequences we further refine the distinguishability relation.

Definition 5.

Given distinguishable states s, s’ ∈ S of S, s’ is strongly-distinguishable from s if there exists a separating sequence defined in state s, i.e., α ∈ ΨS(s); if state s’ is not strongly-distinguishable from state s, then s’ is said to be weakly-distinguishable from state s.

For two arbitrary states, they could be equivalent, one can be strongly-distinguishable from another, both can be strongly-distinguishable from each other, or both can be weakly-distinguishable from each other. In the last case, they are just distinguishable. Notice that the strongly-distinguishability relationship is not symmetric.

In our example, the machine S is strongly-distinguishable from P, because the separating sequence (x ≤ a)(x ≤ a)(x ≤ a) is defined in P. The machine P, in turn, is weakly-distinguishable from S, since all the separating sequences in the distinguishing machine are not defined in S.

As follows from Corollary 1, if the machines are distinguishable, they are distinguished by any instance of a separating sequence; this is also the case when one machine is strongly-distinguishable from another machine and by the definition the separating sequence is defined in the latter. However, an arbitrary instance of such a sequence may not distinguish a machine that is weakly-distinguishable from another. This difference becomes crucial in conformance testing, when one machine represents a specification and another an implementation under test (IUT). To test the latter, only concrete input sequences would be used, when the IUT is treated as a black box. In the example, assuming that the machine P is the specification and S is the IUT, any instance of the separating sequence (x ≤ a)(x ≤ a)(x ≤ a) can be used to detect non-conformance of the IUT S, as it is not equivalent to P, moreover, S is strongly-distinguishable from P. On the other hand, if the machines swap their roles then since P is weakly-distinguishable from S, then non-conformance of the IUT P cannot be detected by an arbitrary instance of the separating sequence (x ≤ a)(x ≤ a)(x ≤ a).

We formulate a condition under which a SIFSM is either equivalent to or strongly-distinguishable from another SIFSM. It is based on the property of one machine being a converter for all symbolic input sequences defined in another machine. Intuitively, the condition |Λ(m 0, α)| = 1 corresponds to the case when the two machines are equivalent as well as to the case when they produce different output sequences in response to α.

Theorem 1.

Given a (specification) machine S and an (implementation) machine M, if M is a ΨS-converter then M is either equivalent to or strongly-distinguishable from S.

Proof.

Assume that M is a ΨS-converter, i.e., |Λ(m 0, α)| = 1 for each α ∈ ΨS. As S is deterministic, we have that |Λ(s 0, α)| = 1 for each α ∈ ΨS. Assume also that M is not strongly-distinguishable from S. Thus, for each α ∈ ΨS, Λ(m 0, α) ⊇ Λ(s 0, α). It implies that for each α ∈ ΨS, Λ(m 0, α) = Λ(s 0, α), since |Λ(m 0, α)| = |Λ(s 0, α)| = 1. Hence, there is no separating sequence for S and M, i.e., they are equivalent. ♦

Clearly, the sufficient condition is not a necessary one. Consider the machine P in Fig. 1 as an IUT and assume that both transitions from state 4 have the output 0. The modified machine is strongly-distinguishable from S, but it has |Λ(m 0,(x ≤ a)(T))| = 2.

4 Symbolic and Concrete Checking Experiments

In this section, we define symbolic checking experiments following a usual framework for defining complete test suite for a given machine, conformance relation, and fault domain [25]. In this case, we are dealing with specification and implementation SIFSMs in a fault domain containing only normalized deterministic input-complete machines; the conformance relation is the machine equivalence. Complete test suite is considered as checking experiment, which could be symbolic or concrete. In the context of symbolic execution and constraint solving, symbolic experiments are of interest for white box testing, while concrete ones for back box testing, where all test data should be concrete. Another specific feature of testing from SIFSM is that a non-equivalent implementation machine in a fault domain can either be weakly- or strongly-distinguishable, which as we show later has a significant impact on fault detection capability of concrete checking experiments.

Let \( \mathfrak{J} \)(V, m) be the universe of SIFSMs over the input variables V with at most m states. A subset of \( \mathfrak{J} \)(V, m) is called a fault domain for a specification machine S = (S, s 0, V, O, F, δ, λ); it includes SIFSMs which model all possible implementations of S. A set of input sequences E ⊆ ΩS is a checking experiment for S in a fault domain Σ ⊆ \( \mathfrak{J} \)(V, m) iff S ≃  E M implies S ≃ M, for each M ∈ Σ.

We now define main ingredients of symbolic checking experiments, following the classical approach of state identification.

A symbolic state cover C for the machine S is a set which contains the empty sequence and for each state s ∈ S a single defined input sequence α ∈ ΨS, such that δ(s 0, α) = s. A symbolic transition cover T for the machine S is a set {αg | α ∈ C, g ∈ G(δ(s 0, α))}, where C is a symbolic state cover.

Given state s ∈ S of the reduced machine S, a finite set E ⊆ ΩS(s) is a state identifier for s, denoted Id(s), if s ≄ E s’ for each s’ ≠ s. State identifiers in a set H = {Id(s) | s ∈ S} are harmonized if for each pair of distinguishable states s and s’, there exists a separating sequence α ∈ pref(Id(s)) ∩ pref(Id(s’)). A straightforward way of constructing HSIs is to determine a distinguishing machine for each pair of states and include the found sequence in the identifiers of the states in the pair.

Given a symbolic state cover C, a symbolic transition cover T and a set of harmonized state identifiers H = {Id(s) | s ∈ S}, a symbolic HSI experiment is {αγ | α ∈ (C ∪ T), γ ∈ Id(δ(s 0, α))}.

As an example, we construct a symbolic checking experiment for S in Fig. 1. The state cover is {ε, (x ≤ a)}, the transition cover is {(x > a), (x ≤ a), (x ≤ a)(T)}. The symbolic input (x ≤ a) separates states, so Id(1) = Id(2) = (x ≤ a). Then the HSI experiment becomes {(x > a)(x ≤ a), (x ≤ a)(x ≤ a), (x ≤ a)(T)(x ≤ a)}, which could be simplified to {(x > a)(x ≤ a), (x ≤ a)(T)(x ≤ a)}.

Recall that we assume that a specification SIFSM S = (S, s 0, V, O, F, δ, λ) is reduced, normalized, deterministic, and input-complete.

Theorem 2.

Let S be a specification SIFSM, an HSI experiment is a checking experiment for S in the fault domain \( \mathfrak{J} \)(V, n).

Before proving Theorem 2, we demonstrate some auxiliary results.

Lemma 3.

Let S = (S, s 0, V, O, F, δS, λS) be a specification SIFSM, E be an HSI experiment for S and M = (M, m 0, V, O, F M, δM, λM) be a SIFSM from the fault domain \( \mathfrak{J} \)(V, n). If M ≃  E S then M has n states.

Proof.

Let s and s’ be two states of S. There exist α, α‘ ∈ C, such that δS(s 0, α) = s and δS(s 0, α’) = s’. There also exists γ ∈ pref(Id(s)) ∩ pref(Id(s’)), such that αγ, α‘γ ∈ E and Λ(s, γ) ≠ Λ(s’, γ); thus, Λ(Δ(s 0, α), γ) ≠ Λ(Δ(s 0, α‘), γ). As S ≃  E M, we have that Λ(s 0, αγ) = Λ(m 0, αγ) and Λ(s 0, α‘γ) = Λ(m 0, α‘γ). Hence, Λ(Δ(s 0, α), γ) = Λ(Δ(m 0, α), γ) and Λ(Δ(s 0, α‘), γ) = Λ(Δ(m 0, α‘), γ). Thus, Λ(Δ(m 0, α), γ) ≠ Λ(Δ(m 0, α‘), γ) and, therefore, Δ(m 0, α) ≠ Δ(m 0, α‘). We conclude that for each pair of states of S, there exists at least a pair of states of M which are distinct. Therefore, M has at least n states. As M ∈ \( \mathfrak{J} \)(V, n), M has at most n states. Thus, M has n states. ♦

Lemma 4.

Let S = (S, s 0, V, O, F S, δS, λS) be a specification SIFSM, E be an HSI experiment for S and M = (M, m 0, V, O, F M, δM, λM) be a SIFSM from the fault domain \( \mathfrak{J} \)(V, n). If M ≃  E S then there exists a bijection f : S ↔ M, such that for each α ∈ (C ∪ T), f(Δ(s 0, α)) = Δ(m 0, α).

Proof.

C contains n symbolic input sequences, one for each state of S. By Lemma 3, M has n states. Thus, we can define a bijection f : S ↔ M, such that for each α ∈ C, f(Δ(s 0, α)) = Δ(m 0, α). It thus remains to show that for each β ∈ T, we also have that f(Δ(s 0, β)) = Δ(m 0, β). Let β ∈ T and s = Δ(s 0, β). There exists α ∈ C, such that s = Δ(s 0, α). We have that f(s) = Δ(m 0, α). Let α‘ ∈ C, such that s’ = Δ(s 0, α‘) ≠ s. Thus, f(s’) = Δ(m 0, α‘). There also exists γ ∈ pref(Id(s)) ∩ pref(Id(s’)), such that βγ, α‘γ ∈ E and Λ(s, γ) ≠ Λ(s’, γ); thus, Λ(Δ(s 0, β), γ) ≠ Λ(Δ(s 0, α‘), γ). As S ≃  E M, we have that Λ(s 0, βγ) = Λ(m 0, βγ) and Λ(s 0, α‘γ) = Λ(m 0, α‘γ). Hence, Λ(Δ(s 0, β), γ) = Λ(Δ(m 0, β), γ) and Λ(Δ(s 0, α‘), γ) = Λ(Δ(m 0, α‘), γ). Thus, Λ(Δ(m 0, β), γ) ≠ Λ(Δ(m 0, α‘), γ) and, therefore, Δ(m 0, β) ≠ Δ(m 0, α‘) = f(s’) and Δ(m 0, β) ≠ f(s’). It follows that f(s) = Δ(m 0, β) and, thus, f(Δ(s 0, β)) = Δ(m 0, β). ♦

Corollary 2.

If M ≃  E S then for any α, β ∈ ΨS, if Δ(s 0, α) = Δ(s 0, β) then Δ(m 0, α) = Δ(m 0, β).

Proof.

Let M ≃  E S and α, β ∈ ΨS, Δ(s 0, α) = Δ(s 0, β). First, we prove by induction on the prefixes of α that there exists a sequence φ ∈ C, such that Δ(s 0, α) = Δ(s 0, φ) and Δ(m 0, α) = Δ(m 0, φ).

For the base case, we have α = ε. As ε ∈ C, the property holds for φ = α = ε, since obviously Δ(s 0, α) = Δ(s 0, φ) and Δ(m 0, α) = Δ(m 0, φ).

For the inductive case, assume that α = α’g and there exists φ‘ ∈ C, with Δ(s 0, α’) = Δ(s 0, φ‘) and Δ(m 0, α’) = Δ(m 0, φ‘). We have that φ‘g ∈ T. As C is a state cover for S, there exists φ ∈ C, such that Δ(s 0, φ‘g) = Δ(s 0, φ); hence Δ(s 0, α) = Δ(s 0, φ). Thus, due to the properties for the bijection f, it follows that f(Δ(s 0, φ‘g)) = Δ(m 0, φ‘g) and f(Δ(s 0, φ)) = Δ(m 0, φ). It then follows that Δ(m 0, α) = Δ(m 0, φ‘g) = f(Δ(s 0, φ‘g)) = f(Δ(s 0, φ)) = Δ(m 0, φ), hence Δ(m 0, α) = Δ(m 0, φ), concluding the induction proof.

In the same vein, we can prove that there exists a sequence φ‘ ∈ C, such that Δ(s 0, β) = Δ(s 0, φ‘) and Δ(m 0, β) = Δ(m 0, φ‘). As Δ(s 0, α) = Δ(s 0, β) and C contains only one sequence that reaches each state, we have that φ = φ‘. Thus, Δ(m 0, β) = Δ(m 0, φ) = Δ(m 0, φ‘) = Δ(m 0, α), i.e., Δ(m 0, β) = Δ(m 0, α). ♦

Now we are ready to prove Theorem 2.

Proof of Theorem 2.

Let M = (M, m 0, V, O, F M, δM, λM) be a SIFSM from the fault domain \( \mathfrak{J} \)(V, n), such that M ≃  E S. We prove by contradiction that M ≃ S. Assume that M ≄ S. Let β be the shortest symbolic input sequence such that M ≃ {β} S and there exists g ∈ G* such that βg is a separating sequence, i.e., M ≄{βg} S. Thus, Λ(Δ(m 0, β), g) ≠ Λ(Δ(s 0, β), g).

Since E is an HSI experiment {αγ | α ∈ (C ∪ T), γ ∈ Id(δS(s 0, α))}, it contains a sequence φ ∈ C, such that Δ(s 0, φ) = Δ(s 0, β). Then Δ(m 0, φ) = Δ(m 0, β), according to Corollary 2. Since Λ(Δ(m 0, β), g) ≠ Λ(Δ(s 0, β), g), it also holds that Λ(Δ(m 0, φ), g) ≠ Λ(Δ(s 0, φ), g). The HSI experiment contains a transition cover of S then there exists a symbolic input g’, such that (Δ(s 0, φ), g’) ∈ F S, g ⊆ g’, and φg’ ∈ E. M ≃  E S implies that M ≃ {φg’} S. We have that Δ(m 0, φ) = Δ(m 0, β), then Λ(Δ(m 0, β), g’) = Λ(Δ(s 0, β), g’). This contradicts the assumption that Λ(Δ(m 0, β), g) ≠ Λ(Δ(s 0, β), g), as g ⊆ g’.♦

For simplicity, we have considered symbolic experiments for the fault domain \( \mathfrak{J} \)(V, n). Nevertheless, based on the previous results, e.g., [30, 33], the case of a wider fault domain \( \mathfrak{J} \)(V, m), where m > n can also be considered.

Symbolic experiments could be used in the context of white-box testing when symbolic execution of code/model of an implementation SIFSM is possible; however, they cannot be executed against an implementation SIFSM considered as a black box. We further assume that only instances of symbolic experiments can be executed against any implementation SIFSM in a given fault domain.

Consider first the case, when an SIFSM S has a finite number of concrete inputs, in other words, it is a compact representation of a Mealy FSM S’ over the finite input set D V . Then the set of all possible instances of a symbolic checking experiment is finite and is in fact a concrete checking experiment for the SIFSM S. The latter is also a classical checking experiment for the FSM S’.

Theorem 3.

Given a specification machine S with a finite input set D V , let E be a symbolic checking experiment for S in \( \mathfrak{J} \)(V, n). Let also E’ be the set of all possible instances of E and S’ be the FSM obtained by unfolding S. Then, E’ is a concrete checking experiment for S and S’ in \( \mathfrak{J} \)(V, n).

Proof.

As E is a symbolic checking experiment for S in \( \mathfrak{J} \)(V, n), for each M in \( \mathfrak{J} \)(V, n), E contains a separating sequence α distinguishing S and M. Thus, there exists an instance of α which distinguishes S and M and E’ contains this instance; hence E’ distinguishes S and any SIFSM in \( \mathfrak{J} \)(V, n) which is distinguished by E. As E is a symbolic checking experiment for S in \( \mathfrak{J} \)(V, n), it follows that E’ is a checking experiment for S in \( \mathfrak{J} \)(V, n). As S’ is equivalent to S, we have that E’ is also a checking experiment for S’ in \( \mathfrak{J} \)(V, n). ♦

The theorem suggests that checking experiments for SIFSMs with a finite set of concrete inputs can be constructed directly from a given specification machine without first unfolding it into a classical Mealy machine and using one of the existing methods for checking experiment generation. It might also be computationally simpler to first determine all the ingredients of a checking experiment in the symbolic form and then generate all the concrete instances of symbolic sequences one by one.

Next we consider the case when the input variables do not yield a finite set of concrete inputs and we investigate faults detectable by concrete experiments. Since we can execute only a finite number of concrete input sequences, it is interesting to know in which cases the set of single instances of each sequence in a symbolic checking experiment remains a checking experiment for a given fault domain. In the following, we identify several such cases.

Let E be a symbolic checking experiment for S in \( \mathfrak{J} \)(V, n) and let Σ be a subset of \( \mathfrak{J} \)(V, n). We say that E is safely-instantiable for Σ if any instance of E is a concrete checking experiment for S in Σ. We will use \( \mathfrak{J} \)(V, n, ΨS) to denote the subset of \( \mathfrak{J} \)(V, n), which consists of ΨS-converters.

Theorem 4.

Let E be a symbolic checking experiment for S in \( \mathfrak{J} \)(V, n). Then, E is safely-instantiable for \( \mathfrak{J} \)(V, n, ΨS).

Proof.

Let M ∈ \( \mathfrak{J} \)(V, n, ΨS); thus, for each α ∈ ΨS, |Λ(m 0, α)| = 1. According to Theorem 1, the machine M is either equivalent to or strongly-distinguishable from S. Let C be an instance of E. Assume that M is not equivalent to S; thus, M is strongly-distinguishable from S. As E is a symbolic checking experiment for S in \( \mathfrak{J} \)(V, n) and \( \mathfrak{J} \)(V, n, ΨS) ⊆ \( \mathfrak{J} \)(V, n), there exists a symbolic separating sequence α ∈ E, such that M ≄{α} S; by Corollary 1, any instance of the sequence α is also a separating sequence. Thus, the result follows. ♦

Theorem 4 says that any concrete experiment derived from a symbolic checking experiment is also a checking experiment for the machine S in the fault domain \( \mathfrak{J} \)(V, n, ΨS). In other words, a complete concrete test suite can be obtained from a symbolic checking experiment. The question arises as to which structural faults in the implementation machines preserve their property of being ΨS-converters. Addressing this question, we follow the same approach for describing faults as in the classical deterministic Mealy machines, see, e.g., [2, 24]. Implementation faults are usually modeled by mutants of a given machine. Elements of transitions, namely, output and end state, are subjects for mutations, which yield output faults, transfer faults and transition faults combining the first two types of faults.

It is not difficult to see that all possible mutants of the specification SIFSM S with output faults are ΨS-converters, i.e., they are in the fault domain \( \mathfrak{J} \)(V, n, ΨS).

As to transition faults, they should not violate the property of ΨS-converters, namely, a mutant with transition faults should react to any symbolic input sequence defined the specification with a single output sequence. It turns out that mutants with transition faults remain to be ΨS-converters under the following conditions.

Assume that the specification SIFSM S has a fixed set of guards in each and every state, i.e., G(s) = G(s’) = G S for all states s, s’ ∈ S. Let G M denote the set of guards of an implementation SIFSM M with the same property.

Theorem 5.

Given a specification SIFSM S with the set of guards G S then {M ∈ \( \mathfrak{J} \)(V, n) | G M = G S} ⊆ \( \mathfrak{J} \)(V, n, ΨS).

Proof.

Let M ∈ \( \mathfrak{J} \)(V, n), such that G M = G S. Indeed, G M = G S implies ΨM = ΨS. As \( \mathfrak{J} \)(V, n) includes only deterministic machines, we have that |Λ(m 0, α)| = 1 for each α ∈ ΨM; therefore |Λ(m 0, α)| = 1 for each α ∈ ΨS. Thus, M ∈ \( \mathfrak{J} \)(V, n, ΨS). ♦

We identify another sufficient condition considering the case when the set of defined input sequences of each implementation machine in a fault domain is a superset of that of the specification machine. Intuitively, an implementation machine is assumed to preserve in each state guards of the specification or merge some of them.

Theorem 6.

Given a specification SIFSM S, it holds that {M ∈ \( \mathfrak{J} \)(V, n) | ∀α ∈ ΨS, ∀g ∈ G S(δ(s 0, α)), ∃ g’ ∈ G M(δ(m 0, α)), g ⊆ g’} ⊆ \( \mathfrak{J} \)(V, n, ΨS).

Proof.

Let M ∈ \( \mathfrak{J} \)(V, n), such that for each α ∈ ΨS and each g ∈ G S(δ(s 0, α)), there exists g’ ∈ G M(δ(m 0, α)) such that g ⊆ g’. We prove by induction that for each α ∈ ΨS, |Λ(m 0, α)| = 1.

For the basis step, we have that Λ(m 0, ε) = {ε}, i.e., |Λ(m 0, ε)| = 1. For the induction step, assume that α = βg ∈ ΨS and |Λ(m 0, β)| = 1. Let also g ∈ G S(δ(s 0, β)), g’ ∈ G M(δ(m 0, β)), such that g ⊆ g’. We can see that |Λ(δ(m 0, β), g’)| = 1; thus |Λ(δ(m 0, β), g)| = 1. Consequently, |Λ(m 0, βg)| = 1, i.e., |Λ(m 0, α)| = 1; therefore, |Λ(m 0, α)| = 1 for each α ∈ ΨS. Thus, M ∈ \( \mathfrak{J} \)(V, n, ΨS). ♦

This theorem addresses a specific fault model of symbolic implementation machines representing the mutation by merging transitions along with their guards which is not possible in classical FSM, since an implementation FSM should have all the inputs of a specification FSM. In case of SIFSMs, implementation machines have all the input variables of a specification machine, but not necessarily its guards.

Consider SIFSMs in Fig. 1. The machine S can be considered a mutant of the specification machine P, where transitions with guards (x ≤ a) and (x > a) are merged into a transition with the guard T. On the other hand, when the machine S serves as a specification and the machine P is an implementation this mutant has a specific fault of splitting a guard used in the specification SIFSM. To detect such a fault, one has use to use at least two instances of a symbolic input sequence from the checking experiment. Since P is treated as a black box testing, and the way a guard is split is unknown, two concrete tests suffice if they properly “guess” it.

5 Conclusions

We investigated possibilities for lifting the checking experiments theory developed for the classical (Mealy) finite state machine model to its extension, where input alphabet is finite, but consists of predicates defined over input variables with large or even infinite domains. We call it FSM with symbolic inputs, SIFSM. On one hand, this model can be considered as a special type of Extended FSMs (EFSMs) [26], without context variables and operations on variables; on another hand, as symbolic automaton or symbolic transducer [23, 35]. The recent grow of interest towards symbolic models could be explained by advances in constraint solving technology, as SMT solvers become efficient [22].

We lifted the machine equivalence and distinguishability relations to SIFSM and identified new distinguishability relations which have no counterparts in classical deterministic Mealy machines. Then, we defined symbolic checking experiments for deterministic SIFSMs and demonstrated that they could be obtained by mimicking, e.g., a classical HSI method for constructing checking experiments of FSMs (other types of state identification facilities, such as W and Wp, might also be used). Since symbolic experiments could be used for white-box testing, but not for black-box testing, which requires concrete test values, we focused on investigating fault domains for which any concrete instance of a symbolic checking experiment remains a checking experiment.

As expected, in the most general setting, an arbitrary instance of a symbolic checking experiment may not be a checking experiment in the same fault domain. Nevertheless, we found some sufficient conditions for the specification and implementation machines under which any instance of a symbolic checking experiment is also a checking experiment in well-defined fault domains. Under these conditions, non-trivial faults modeled by the identified fault domains are detectable by concrete tests obtained from abstract (symbolic) tests in a symbolic checking experiment. These faults include transition merging, which is only relevant to implementations of SIFSM and not to classical Mealy machines.

The novelty of the results comes from the fact that while FSM checking experiments are known for about 60 years, EFSMs for about 30 years, there are no published results on checking experiments for EFSM which cannot be unfolded into FSM. To the best of our knowledge, it is the first attempt to advance the checking experiment theory to FSMs with a symbolic extension.

While the problem of handling more general EFSMs remains open, we believe that the presented results open a new line of research in checking experiments for symbolic state machines and transition systems.

Our current work concerns, on one hand, relaxing the sufficient conditions of safe-instantiability, and on the other hand, extending the SIFSM model with operations on output variables, thus lifting the checking experiments theory to a wider class of extended finite state machines. We also plan to investigate other fault models for which symbolic checking experiments could be used as efficiently as for the faults satisfying the formulated sufficient conditions.