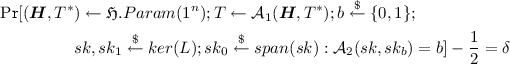Updatable Hash Proof System and Its Applications

Abstract

To tackle with physical attacks to real world cryptosystems, leakage resilient cryptography was developed. In this setting, the adversary is allowed to have access to the internal state of a cryptographic system, thus violates the black-box reduction used in cryptography. Especially when considering continual memory leakage (CML), i.e., there is no predetermined bound on the leakage of the internal information, the task is extremely tough.

In this paper, we solve this problem by introducing a new primitive called updatable hash proof system (UHPS). A UHPS can be viewed as a special Hash proof system (HPS), which served as a fundamental tool in constructing public key encryption (PKE) schemes in both leakage-free and leaky settings. A remarkable property of UHPS is that by simply substituting the HPS component with a UHPS component in a PKE scheme, one obtains a new PKE scheme secure in the CML setting. Moreover, the resulting PKE scheme enjoys the same advantage of the original HPS-based PKE, for instance, still “compatible” with known transforms [8, 20, 24, 32]. We then give instantiations of UHPS from widely-accepted assumptions, including the symmetric external Diffie-Hellman assumption and the d-linear assumption. Interestingly, we notice that when instantiated with concrete assumptions, the resulting chosen-ciphertext secure PKE scheme is by far the most efficient.

R. Yang — This work was mainly done when doing the internship at SKLOIS, IIE, CAS.

1 Introduction

Side-channel attacks are fatal for a real-world cryptosystem. Notably, such attacks can violate the black-box “provable” security of schemes [3, 5, 17, 21, 22, 30, 34]. For instance, the only known working attack for AES is via side-channel attacks [30]. Moreover, it is also possible to launch such an attack remotely, e.g., the timing attacks could break OpenSSL run on a network server [5]. Even worse, via the cold-boot attack, one can read the secret keys stored in the memory directly [17].

As for a countermeasure, engineers are always required to implement the scheme in an environment approximate to the theoretical assumptions, e.g., using extra protection circuits, adding random circles to CPU occupations, or adding metal shields against electromagnetic radiation. But in a word, there is no guarantee whether they have actually realized the design goal.

Leakage Resilient Cryptography. On the other hand, theorists intended to investigate this problem in a more rigorous way, so the leakage resilient cryptography came up. Micali and Reyzin [27] first introduced the notion of physically observable cryptography, where they assumed “computation and only computation leaks information” about the internal state. Many works follows their approach [12, 14, 31]. However, their assumption could not capture the cold-boot attack (memory attack) [17], namely, information leakage of the whole internal state can appear any time during the life span of the scheme.

To cope with memory attacks, Akavia et al. [2] proposed the bounded memory leakage (BML) model, where adversaries can obtain arbitrary function of the whole secret state, as long as the total leakage is limited to a certain amount of bits. But this model is not strong enough since the adversary may launch many attacks and it is not evident to bound the information leakage to a predetermined value.

One way to capture more realistic attackers is to relax the restriction imposed on the leakage function. Dodis et al. [10] proposed the auxiliary input model where the leakage can be arbitrary large and only with the restriction that the secret key is computationally hard to compute given the leakage information.

Another (and maybe a more realistic) way is to consider continual leakage directly. Brakerski et al. [4] and Dodis et al. [9] proposed the continual memory leakage (CML) model. In their models, the entire lifetime of the scheme is partitioned into some periods, and at the end of each period, the internal secret state of the scheme is updated. The adversary is allowed to obtain bounded leakage from the entire internal secret state during each time period, just as in the BML setting, but the total leakage over the lifetime of the scheme is unbounded.

Continual Memory Leakage Model. One may think that it is easy to construct cryptographic schemes in the CML setting. For example, one can construct continual memory leakage resilient (CML) public key encryption (PKE) schemes by generating multiple independent instances of a normal PKE scheme, encrypting messages under all public keys and decrypting with a fresh secret key at each time period. However, this does not satisfy realistic requirements. One reason is that the size of the public key and ciphertexts depend on the number of time periods throughout the lifetime of the scheme. Besides, secret keys not used at present must be stored in some external leak-free storage and key updating can only be executed privately. To exclude such trivial solution, which will not provide actual guidance in practice, the compactness (i.e. all parameters are independent of number of time periods) and the ability of publicly key updating (i.e. secret keys can be updated with only the public parameters) are required for constructions of cryptographic schemes in the CML setting.

In fact, it is rather involved to construct cryptographic schemes in the CML setting. When considering CML-PKE schemes, only a few constructions are known so far [4, 11, 23, 26]. Most of them are based on concrete number-theoretic assumptions directly. Especially, no practical chosen-ciphertext (CCA) secure PKE schme has been presented in this model yet. Therefore, new techniques for constructing CML-PKE schemes are desired.

Hash Proof System. Since first introduced by Cramer and Shoup [8], hash proof system (HPS) gained great success in constructing various cryptographic schemes, such as password-based authenticated key exchange [15], lossy trapdoor functions [19], (leak-free) CCA-secure PKE schemes [8, 24] and PKE schemes in the BML setting [18, 28, 32, 33].

Especially, when constructing PKE schemes in the BML setting, the technique of HPS is essential to obtain leakage resilience. The bottom line is that multiple secret keys are mapped to a single public key in an HPS-based PKE scheme, thus the adversary cannot determine which secret key is in use even bounded leakage is given. Meanwhile, honestly generated ciphertexts are computationally indistinguishable from dishonest ciphertexts, whose decryptings are not determined by the public key but the secret key decrypting it. So the BML adversary cannot decrypt ciphertexts of an HPS-based PKE scheme (actually, they cannot obtain any information from these ciphertexts).

Considering that attacks launched in each time period in the CML setting can just be viewed as bounded memory attacks, one may naturally think that by augmenting HPS with the publicly key updating ability, it can be applied to construct CML-PKE schemes straightforwardly. But this simple idea seems not working: the publicly key updating ability seems incompatible with HPS.

To see this, recall that an HPS is based on a collection of hash functions indexed by a set of secret keys. When evaluating the hash function on an element in the domain, different secret keys may lead to the same result, and we say such secret keys are “equivalent on this element”. All secret keys are mapped to some public keys and those mapped to the same public key will be equivalent on every element in a specific subset of its domain. Also, the subset membership problem (SMP), which demands a PPT algorithm to distinguish a uniform element in this subset from a uniform element in its complement, is hard in HPS, and that leads to the ciphertexts indistinguishability in an HPS-based PKE scheme.

When updating secret keys of HPS in the CML setting, one should generate a new secret key mapped to the same public key. Thus the new key and the old key will be equivalent on every element in the specific subset. But they will not be equivalent on every element in the domain. So an adversary can break the underlying SMP of HPS via the “GUC attack”, namely, generating a secret key, updating it, and checking whether they are equivalent on the challenge element.

Therefore, the following two questions arise naturally: Whether HPS is still effective for building PKEs in the CML setting? If yes, how?

Fig. 1.

Constructing CML-PKE schemes from UHPS and its relation with HPS-based PKE schemes.

1.1 Our Results

In this paper, we investigate these two questions and pose affirmative answers to them. More precisely, we show that in general, an HPS based PKE scheme is in fact secure against continuous memory attacks, as long as the underlying HPS fulfill some additional requirements.

First, we require that secret keys are updated in some pattern, namely, updated keys and old keys are equivalent on elements in a superset of the specific subset. Next, as a substitute of the SMP, we require that elements chosen uniformly from the specific subset and from that superset are computationally indistinguishable. We remark that the GUC attack is not applicable to this indistinguishability. But updating secret keys with certain patterns will cause new problems since the adversary is able to obtain leakage about secret keys continually and thus may learn this pattern (we will discuss how this threatens security of PKE schemes in the proof sketch of Theorem 5). Therefore, we require that all updated keys appear independent and uniform to the adversary, although they are updated with certain patterns.

We call an HPS with these properties “updatable hash proof system” (UHPS), and show how to instantiate it with some widely-accepted assumptions, e.g. the symmetric external Diffie-Hellman (SXDH) assumption and the d-linear assumption in bilinear groups. Interestingly, our instantiations are just extensions of the DDH-based HPS in [8] and one can realize them via modifying existing implementations of DDH-based HPS.

The functionalities of UHPS are summarized in Fig. 1. In particular, by simply substituting the HPS component in an HPS-based PKE with a UHPS component, one obtains a CML-PKE scheme. Interestingly, we show that well-known transforms that upgrade weak (e.g. CPA-secure) PKE schemes into strong (i.e. CCA-secure) PKE schemes are still effective for the resulting CML-PKE schemes. The reason why UHPS is effective in constructing CML-PKE is that honest ciphertexts and dishonest ciphertexts are still indistinguishable when secret keys are updated in some pattern. Also, the key indistinguishability in UHPS can guarantee that real secret keys as well as the pattern are hidden from CML adversaries. So they cannot obtain any information from these ciphertexts just as in the BML setting.

We remark that when instantiated with concrete assumptions, our CCA-secure CML-PKE schemes are much more efficient compared to known results. To show this, we give a brief overview of known constructions of CCA-secure CML-PKE schemes in Sect. 1.2, and give a concrete efficiency comparison between these schemes and our schemes in Sect. 5.2. Besides, we observe that several frameworks for constructing hybrid encryption schemes, including the framework of “constrained CCA (CCCA) secure KEM + authenticated encryption (AE) scheme” [20] and the tag KEM/DEM framework [1], are also robust in the CML setting. Also, it is worth noting that PKE schemes in Wichs’s PhD thesis [36] can be viewed as instantiations of our CPA-secure PKE schemes. In fact, our work provides a modular way to reconsider their schemes and makes the construction of CML-PKE schemes more concise and conceptual simpler.

1.2 Related Work

Now we give a brief overview of approaches applicable to construct CCA-secure CML-PKE schemes. In principle, the Naor-Yung paradigm [29, 35] is robust against continuous memory attacks. That is to say, in the CML setting, one can transform any CPA-secure PKE scheme to be CCA-secure. Alternatively, the CHK transformation [6] can also provide CCA-secure CML-PKE schemes given suitable building blocks, e.g., identity based encryption schemes with continual master key leakage resilience [26]. Recently, a contemporaneous work [23] also shows that one can construct CCA-secure CML-PKE schemes from a variant of lossy trapdoor function. We remark that due to lack of suitable underlying building blocks, the latter two approaches are only applicable to a weaker CML setting where no leakage is allowed during key update.

2 Preliminaries

In this section, we review some useful notations and notions.

Notations. Let S be a finite set, we use $\Vert S \Vert$ and U(S) to denote the size of S and the uniform distribution over S respectively. Also, we write $x \overset{\$}{\leftarrow }S$ to indicate that x is sampled uniformly from S. For a bit string $s \in \{0,1\}^*$, we use $\Vert s \Vert$ to denote the length of s. We use [n] to denote the set $\{1,2,\ldots ,n\}$ for any positive integer n. We write $negl(\cdot )$ to denote a negligible function. Let $\mathcal {X}=\{X_n\}_{n \in \mathbb {N}}$ and $\mathcal {Y}=\{Y_n\}_{n \in \mathbb {N}}$ be two ensembles of random variables. We use $\mathcal {X} \overset{s}{\approx }_{} \mathcal {Y}$ to denote that $\mathcal {X}$ and $\mathcal {Y}$ are statistically indistinguishable and use $\mathcal {X} \overset{c}{\approx }\mathcal {Y}$ to denote that $\mathcal {X}$ and $\mathcal {Y}$ are computationally indistinguishable.

Linear Algebra. Let q be a prime, we introduce some notations of linear algebra over $\mathbb {Z}_q$. We use bold uppercase letters ($\varvec{X}$) to denote matrices and lowercase letters with arrow ($\vec x$) to denote vectors. All vectors used in this paper are column vectors. Let $\vec v_1, \ldots , \vec v_m$ be m vectors in $\mathbb {Z}_q^{n}$, then we denote by $span(\vec v_1, \ldots , \vec v_m)$ the linear space spanned by these vectors. Assuming $\mathcal {V}$ is a subspace of $\mathbb {Z}_q^{n}$ with dimension $d<n$, we denote by $\mathcal {V}^{\perp }$ the orthogonal space of $\mathcal {V}$. We use $Rk_d(\mathbb {Z}_q^{n \times k})$ to denote the set of $n \times k$-matrices with rank d.

Entropy and Extractors. The min-entropy of a discrete random variable X, which measures the worst case predictability of X, is defined as $H_{\infty }(X) =\!\!~-\log (\max _x \Pr [X=x])$. It is often useful to work with the average case of min-entropy that was first defined in [13] as $\mathop {\widetilde{H}_{\infty }}(X \mid Y) = -\log (\mathbb {E}_{y \leftarrow Y}[\max _x \Pr [X=x \mid Y=y]])$. To obtain nearly perfect randomness from sources with high (average case) min-entropy, one can use the (average case) randomness extractor.

Definition 1

([13]). A function $Ext : \mathcal {X} \times \{0,1\}^{t} \rightarrow \mathcal {Y}$ is an (average case) $(k,\,\epsilon )$-strong extractor if for all pairs of random variables $(X,\,I)$ such that X is distributed over $\mathcal {X}$ and $H_{\infty }(X \mid I) \ge k$ ($\mathop {\widetilde{H}_{\infty }}(X \mid I) \ge k$), it holds that $\Delta ((Ext(X,\,R),\,R,\,I),\ (Y,\,R,\,I)) \le \epsilon$ where R is uniform over $\{0,1\}^t$ and Y is uniform over $\mathcal {Y}$.

Such (average case) randomness extractors can be constructed directly from any universal hash family [7] as long as $k \ge \log (\Vert \mathcal {Y} \Vert ) + 2\log {({1}/{\epsilon })}$, and the later primitive can be further constructed directly from natural algebraic operations (e.g. linear combination in $\mathbb {Z}_q$ for a prime q).

3 Updatable Hash Proof System

In this section, we define the notion of UHPS, which is a variant of HPS. Since we intend to use UHPS to construct PKE schemes in the CML setting, publicly key updating ability is demanded and we need properties to support this in UHPS. But as stated in Sect. 1, HPS with publicly key updating ability will suffer from the GUC attack, which breaks the intractability of underlying SMP. Thus we need a substitute of SMP immune to this attack. This is formalized as the subset indistinguishability in UHPS. However, to apply the subset indistinguishability, all secret keys have to be updated in some pattern, which may bring new problems as the adversary may learn this pattern via requesting continual leakage. Therefore, we define some key indistinguishabilities in UHPS here to solve these potential problems. Although several additional properties are defined in UHPS, we observe that they have already been fulfilled by existing instantiations of HPS to some degree and will not take too much extra overhead.

Similar to a normal HPS, a UHPS is based on a collection of hash functions $\mathcal {H}=\{\mathcal {H}_{sk}:\mathcal {C} \rightarrow \mathcal {K}\}_{sk \in \mathcal {SK}}$. Also there exists an efficiently computable projection $\varphi$ from $\mathcal {SK}$ to $\mathcal {PK}$, and a specific set $\mathcal {V} \subset \mathcal {C}$ such that for any $sk_1,sk_2 \in \mathcal {SK}$, $\varphi (sk_1) = \varphi (sk_2)$ if and only if $\forall x \in \mathcal {V},\, \mathcal {H}_{sk_1}(x) = \mathcal {H}_{sk_2}(x)$. Further, for every $x \in \mathcal {V}$, there exists a witness $w \in \mathcal {W}$ proving this. Besides, for any $x \notin \mathcal {V}$, $H_{\infty }(\mathcal {H}_{sk}(x) | \varphi (sk))$ is usually required to be large enough when $sk \overset{\$}{\leftarrow }\mathcal {SK}$, and this is formalized as the universality in UHPS.

Here, we provide the publicly key updating ability via algebraic operations and require that UHPS is key homomorphic, i.e. $\mathcal {SK}$ and $\mathcal {K}$ are finite groups with an efficiently computable operation “+” and $\forall sk_1,sk_2 \in \mathcal {SK}, \forall x \in \mathcal {C}$, we have $\mathcal {H}_{sk_1+sk_2}(x)=\mathcal {H}_{sk_1}(x)+\mathcal {H}_{sk_2}(x)$. Now, we can update a secret key sk by adding it with a specific secret key $sk^*$ s.t. $\forall x \in \mathcal {V}, \mathcal {H}_{sk^*}(x)=0$. Since $\forall x \in \mathcal {V}, \mathcal {H}_{sk+sk^*}(x)=\mathcal {H}_{sk}(x) + \mathcal {H}_{sk^*}(x) = \mathcal {H}_{sk}(x)$, we have $\varphi (sk+sk^*)=\varphi (sk)$, which indicates that the new key and the old key are mapped to the same public key.

For secret keys will be updated continually, fresh updating key is required each time. So we require $span(sk^*)$, which is a specific set such that $\forall sk^{*\prime } \in span(sk^*), \mathcal {H}_{sk^*}(x)=0 \ \rightarrow \ \mathcal {H}_{sk^{*\prime }}(x)=0$, to be efficiently samplable given an initial updating key $sk^*$. To generate the initial updating key, we also demand that $\forall L \subseteq \mathcal {C}$, $ker(L) = \{ sk \mid \forall x \in L, \ \mathcal {H}_{sk}(x) = 0 \}$ is efficiently samplable given a trapdoor $T \in \mathcal {T}$ for L. Besides, due to the requirement for security proofs of PKE schemes, we require that given trapdoors $T_1, T_2 \in \mathcal {T}$ for subsets $L_1, L_2 \subseteq \mathcal {C}$ respectively, it is efficient to generate a trapdoor $T_3 \in \mathcal {T}$ for $L_1 \cup L_2$.

We stress that although we have provided mechanisms to update secret keys in UHPS, we will not fix an updating policy, and one can choose various approaches to performing key update in different scenarios.

Now we present the formal definition.

Definition 2

Let $\lambda$ be a polynomial of the security parameter n, and indicates the bits of challenge information that can be obtained by the distinguisher for “partial key indistinguishability”. A $\lambda$-UHPS $\mathfrak {H}$ consists of five algorithms:

• Instance Generation. $\mathfrak {H}.Param(1^n)$: The instance generation algorithm takes as input the security parameter $1^n$, and outputs an instance $\varvec{H} = (\mathcal {C}, \mathcal {V}, \mathcal {H}, \mathcal {K}, \mathcal {SK}, \mathcal {PK}, \mathcal {T}, \mathcal {W}, \varphi )$ of UHPS with a trapdoor $T^* \in \mathcal {T}$ for $\mathcal {V}$. Here, all sets in $\varvec{H}$ are finite non-empty sets.

• Subset Sampling. $\mathfrak {H}.VSamp(\varvec{H})$: The subset sampling algorithm outputs $x \overset{\$}{\leftarrow }\mathcal {V}$ with a witness $w \in \mathcal {W}$ for $x \in \mathcal {V}$.

• Complement Sampling. $\mathfrak {H}.ISamp(\varvec{H})$: The complement sampling algorithm outputs $x \overset{\$}{\leftarrow }\mathcal {C} \backslash \mathcal {V}$ with a trapdoor $T \in \mathcal {T}$ for $\{x\}$. We remark that we can tolerant a negligible statistical error here, namely, we only require that the sampled elements are statistically indistinguishable from $U(\mathcal {C} \backslash \mathcal {V})$.

• Public Evaluation. $\mathfrak {H}.Pub(\varvec{H}, pk, x, w)$: Given $pk \in \mathcal {PK}$ and $x \in \mathcal {V}$ with its witness $w \in \mathcal {W}$, the public evaluation algorithm outputs $k \in \mathcal {K}$.

• Private Evaluation. $\mathfrak {H}.Priv(\varvec{H}, sk, x)$: Given $sk \in \mathcal {SK}$ and $x \in \mathcal {C}$, the private evaluation algorithm outputs $k = \mathcal {H}_{sk}(x)$.

Moreover, we require that $\mathfrak {H}$ has four basic properties, indicating its correctness and hardness requirements:

• 1. Correctness. For any instance $\varvec{H}$, any (sk, pk) s.t. $pk = \varphi (sk)$, and any $x \in \mathcal {V}$ with its witness w, we have $\mathfrak {H}.Pub(\varvec{H}, pk, x, w) = \mathfrak {H}.Priv(\varvec{H}, sk, x)$.

• 2. Subset Indistinguishability. As a substitute of SMP, this indicates the indistinguishability between elements in $\mathcal {V}$ and not in $\mathcal {V}$, namely, for arbitrary positive integer l, let $(\varvec{H}, T^*) \leftarrow \mathfrak {H}.Param(1^n)$, $x \overset{\$}{\leftarrow }\mathcal {V}$, $sk_1, \ldots , sk_l \overset{\$}{\leftarrow }ker(\mathcal {V})$, $x' \overset{\$}{\leftarrow }\mathcal {C} \backslash \mathcal {V}$, and $sk_1', \ldots , sk_l' \overset{\$}{\leftarrow }ker(\mathcal {V} \cup \{x'\})$, then we have $(\varvec{H}, x, sk_1, \ldots , sk_l) \overset{c}{\approx }(\varvec{H}, x', sk_1', \ldots , sk_l')$.

• 3. Full Key Indistinguishability. For any PPT adversary $\mathcal {A} = (\mathcal {A}_1, \mathcal {A}_2)$, it is hard to distinguish whether two secret keys are “linearly dependent”, i.e. for some function $\delta$ negligible in n, we have

  

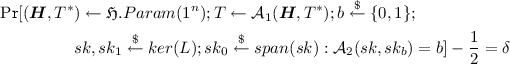
  where L is a subset of $\mathcal {C}$ for which T is a trapdoor.

• 4. Partial Key Indistinguishability. When only partial information is revealed, it is hard to determine whether an updating key is legal. More precisely, for arbitrary function f with range $\{0,1\}^{\lambda }$, let $(\varvec{H}, T^*) \leftarrow \mathfrak {H}.Param(1^n)$, $x \overset{\$}{\leftarrow }\mathcal {C} \backslash \mathcal {V}$, $sk_1, sk_2 \overset{\$}{\leftarrow }ker(\mathcal {V} \cup \{x\})$, $sk_2' \overset{\$}{\leftarrow }ker(\mathcal {V})$, then we have $(\varvec{H}, sk_1, f(\varvec{H}, sk_1, sk_2), x) \overset{s}{\approx }_{} (\varvec{H}, sk_1, f(\varvec{H}, sk_1, sk_2'), x)$. Note that the function f must be independent of x.

In order to indicate how secret keys mapped to the same public key behave in evaluating hash functions on elements not in $\mathcal {V}$, we define the “universality” of UHPS similarly to that of normal HPS with only minimal variance due to the need of keeping some algebra properties of UHPS.

Definition 3

(Universal UHPS ). Let $\tau$ be a function on n. Then a UHPS is $\tau$-universal if for each instance $\varvec{H}$, for any $pk \in \mathcal {PK}$ and any $x \in \mathcal {C} \backslash \mathcal {V}$, we have $H_{\infty }(\mathcal {H}_{SK}(x) \mid \varphi (SK)=pk) \ge \tau$ where SK is a random variable with distribution $U(\mathcal {SK})$.

Definition 4

(Universal$_2$ UHPS). Let $\tau$ be a function on n. Then a UHPS is $\tau$-universal$_2$ if for each instance $\varvec{H}$, we can augment it with an efficiently computable functions $\eta$ from $\mathcal {C} \times \mathcal {K}$ to $\mathcal {Y}$, and for any $pk \in \mathcal {PK}$, any $x, x^* \in \mathcal {C} \backslash \mathcal {V}$ s.t. $x \ne x^*$, any $y \in \mathcal {Y}$, we have $H_{\infty }(\eta (x, \mathcal {H}_{SK}(x)) \mid \varphi (SK)=pk, \eta (x^*, \mathcal {H}_{SK}(x^*)) = y) \ge \tau$, where SK is a random variable with distribution $U(\mathcal {SK})$.

Interestingly, universal$_2$ UHPS can be constructed directly from universal ones by applying the approach in [8] and we give more details about the construction in the full version.

4 Building CML-PKE from UHPS

In this section, we demonstrate the usefulness of UHPS: By substituting a HPS component in the PKE schemes with a UHPS components, some well-established paradigms remain effective in building CML-PKE schemes. As a by-product, the new schemes from UHPS can inherit many interesting features from the corresponding HPS-based schemes. For example, all CCA-secure PKE schemes constructed in this paper can be transformed into tag-KEM/DEM [1], therefore, can be extended to threshold PKE schemes in the CML setting; besides, the scheme from UHPS plus AE can be formalized in the “CCCA KEM + AE” framework. In general, UHPS is applicable to almost all known HPS-based PKE schemes.

Key update is a must for CML-PKE schemes. This is because otherwise the adversary can learn the entire secret state by repeatedly requesting more and more leakage, and no security can be guaranteed then. An adversary considered in this case is further allowed to learn any bounded leakage information (namely, up to $\lambda _M$ bits) in each time period. In some cases, we will consider update phases separately, so we also give another bound $\lambda _U$ on the size of leakage during key updating. We remark that no information can be leaked after the challenge phase, since otherwise the adversary can embed the challenge ciphertext into the leakage query and obtain information about the message. We give the formal definition of PKE schemes in the CML setting as well as its security definition with various security level (namely, the CPA-security and the adaptive CCA-security¹) in the full version.

Two scenarios are mainly considered in the CML setting, namely, the one not allowing leakage during key update (i.e. $\lambda _U=0$) and the one allowing leakage during key update (i.e. $\lambda _U=\lambda _M>0$). The primary difference between constructions of PKE schemes in these two cases is that constructions in the latter case have a more involved key update algorithm. Here, we focus on constructions in the former case and only consider constructions in the latter case in Sect. 4.3. Due to the limit of space, all security proofs and some constructions are omitted and will be given in the full version.

4.1 A CPA-Secure Scheme

We start with a CPA-secure CML-PKE scheme from UHPS, which will help us understand how UHPS functions in constructing CML-PKE schemes. The resulting PKE scheme $\varPi _1$, which is a variant of the HPS-based CPA-secure PKE scheme [8], consists of four algorithms:

• Parameters. Denote n as the security parameter. Let $\mathfrak {H}$ be a $\tau$-universal $\lambda$-UHPS and $(\varvec{H}, \ T^*) \leftarrow \mathfrak {H}.Param(1^n)$ be an instance of $\mathfrak {H}$. Let $Ext:\mathcal {K} \times \{0,1\}^d \rightarrow \{0,1\}^{\iota }$ be an average case $(\tau , \delta )$-strong extractor where $\delta$ is negligible in n and $\tau - \iota \ge 2\log {({1}/{\delta })}$. Sample $sk^* \overset{\$}{\leftarrow }ker(\mathcal {V})$ with $T^*$. The public parameter of $\varPi _1$ is $Params=(\varvec{H},sk^*,Ext)$.

• Key Generation. The key generation algorithm of $\varPi _1$ samples $\overline{sk} \overset{\$}{\leftarrow }\mathcal {SK}$ and evaluates $pk=\varphi (\overline{sk})$. Then it sets $PK=pk$ and $SK=\overline{sk} + sk^{*\prime }$ where $sk^{*\prime } \overset{\$}{\leftarrow }span(sk^*)$.

• Encryption. Given a public key $PK=pk$, to encrypt a message $M \in \{0,1\}^{\iota }$, the encryption algorithm samples $rand \overset{\$}{\leftarrow }\{0,1\}^d$ and runs $\mathfrak {H}.VSamp(\varvec{H})$ to sample $C \overset{\$}{\leftarrow }\mathcal {V}$ with a witness w. Then it evaluates $K=\mathfrak {H}.Pub(\varvec{H}, pk, C, w)$, and $\varPsi =Ext(K,\,rand) \oplus M$, Finally, it outputs $CT=(C,\,\varPsi ,\,rand)$ as ciphertext.

• Decryption. Given a secret key $SK=sk$, to decrypt a ciphertext $CT=(C,\,\varPsi ,\,rand)$, the decryption algorithm computes $K'=\mathfrak {H}.Priv(\varvec{H},\,sk,\,C)$ and outputs $M'=\varPsi \oplus Ext(K',\,rand)$.

• Key Update. Given a secret key $SK=sk$, the update algorithm samples $sk^{*\prime } \overset{\$}{\leftarrow }span(sk^*)$ and outputs a new key $SK'=sk+ sk^{*\prime }$.

Correctness. Let $SK_i = sk^{(i)}$ be the secret key obtained by applying the update algorithm i times to the initial secret key generated by KeyGen and $PK = pk$ be the public key. It is obvious that the correctness holds if for any honestly generated ciphertext $CT=(C,\,\varPsi ,\,rand)$, and for arbitrary natural number i, we have $\mathfrak {H}.Priv(\varvec{H},\,sk^{(i)},\,C) = \mathfrak {H}.Pub(\varvec{H}, pk, C, w)$ where w is the witness for $C \in \mathcal {V}$. This follows directly from the correctness of UHPS because $\varphi (sk^{(i)}) = \varphi (\overline{sk} + sk^{*\prime }) = pk$, where $sk^{*\prime } \in span(sk^*)$.

Security. Security of $\varPi _1$ is guaranteed by Theorem 5 stated as follows.

Theorem 5

$\varPi _1$ is secure against chosen-plaintext attacks in the CML setting with period leakage amount $\lambda _M = \lambda$ and $\lambda _U=0$.

Proof Sketch. Similarly to security proofs of PKE schemes constructed from a normal HPS, we prove Theorem 5 by first altering the way in which the challenge ciphertext is generated, i.e., a challenge ciphertext $CT^*=(C^*,\,\varPsi ^*,\,rand^*)$ s.t. $C^* \notin \mathcal {V}$ is generated instead. This is indistinguishable from an honestly generated ciphertext due to the subset indistinguishability of UHPS. However, we cannot subsequently apply the universal property of UHPS to complete the proof directly. This is because all secret keys throughout lifetime of the scheme will still decrypt $CT^*$ correctly, and the adversary who can obtain leakage about these secret keys continually may learn enough knowledge to break the scheme. Therefore, we should argue that such leakage information will not provide the adversary with practical assistance. It is sufficient to establish the indistinguishability between the real secret keys (i.e. secret keys generated and updated honestly) and the ideal secret keys (i.e. secret keys chosen uniformly over keys mapped to the public key). We do this in two steps. First we apply the full key indistinguishability of UHPS to argue that real secret keys and “semi-ideal” secret keys are indistinguishable. Here we use “semi-ideal” to denote secret keys generated honestly and updated with fresh updating keys chosen uniformly from $ker(\mathcal {V} \cup \{C^*\})$. However, semi-ideal secret keys can still decrypt $CT^*$ correctly. Fortunately, indistinguishability between semi-ideal secret keys and ideal secret keys can be derived from partial key indistinguishability of UHPS since the adversary can only obtain bounded leakage in each time period.

4.2 CCA-Secure Schemes

Then we move on to CCA-secure CML-PKE schemes, which is the main contribution of UHPS. Generally, the bottom line to construct CCA-secure PKE schemes is to prevent the adversary from querying unintended ciphertexts whose decryption will damage the security of the scheme. This is usually performed by applying a suitable authentication.

Three main paradigms are proposed to construct CCA-secure PKE schemes from HPS. In [8], the construction applies a universal$_2$ HPS to provide the authentication and applies a universal HPS to mask the message. Another approach is to employ a single universal$_2$ HPS together with an AE scheme to provide both the authentication and the privacy [24]. Besides, in [32], a new paradigm avoiding the usage of universal$_2$ HPS is given and it applies a universal HPS to mask the message and a one time lossy filter (OT-LF) to provide the authentication. We observe that UHPS is applicable to all these three paradigms. More precisely, by substituting HPS with corresponding UHPS, we can obtain CCA-secure PKE scheme in the CML setting.

We remark that our universal$_2$ UHPS is far less efficient compared to our universal UHPS and it has a much larger secret key, thus the scheme from universal UHPS plus OT-LF can achieve both the best efficiency and the best leakage rate (which will be defined in Sect. 5.2) among all three schemes. So we only present its construction here, and give the other two constructions in Appendix A.

Roughly speaking, an OT-LF is a family of functions indexed by a public key $F_{pk}$ as well as a tag t. Each function will be injective unless the tag comes from some specific set. Moreover, it is hard to generate or even recognize such non-injective tags without a trapdoor $F_{td}$ associated with $F_{pk}$. We refer the reader to [32] for more details about OT-LF. The presented PKE scheme $\varPi _2$ consists of four algorithms:

• Parameters. Denote n as the security parameter. Let $\mathfrak {H}$ be a $\tau$-universal $\lambda$-UHPS and $(\varvec{H}, \ T^*) \leftarrow \mathfrak {H}.Param(1^n)$ be an instance of $\mathfrak {H}$. Let $LF=(LF.Gen, LF.Eval, LF.LTag, LF.DITag)$ be a $(\mathcal {K},\,\ell _{LF})$-OT-LF with the tag space $\mathcal {C} \times \{0,1\}^{l} \times \{0,1\}^{d} \times \mathcal {T}_c$. Let $Ext:\mathcal {K} \times \{0,1\}^d \rightarrow \{0,1\}^{\iota }$ be an average case $(\tau - \ell _{LF}, \delta )$-strong extractor where $\delta$ is negligible in n and $\tau - \ell _{LF} - \iota \ge 2\log {({1}/{\delta })}$. Sample $sk^* \overset{\$}{\leftarrow }ker(\mathcal {V})$ with $T^*$. The public parameter of $\varPi _2$ is $Params=(\varvec{H},sk^*,Ext,LF)$.

• Key Generation. The key generation algorithm of $\varPi _2$ samples $\overline{sk} \overset{\$}{\leftarrow }\mathcal {SK}$, evaluates $pk=\varphi (\overline{sk})$, and runs $LF.Gen(1^n)$ to obtain $F_{pk}$. Then it sets $PK=(pk,F_{pk})$ and $SK=\overline{sk} + sk^{*\prime }$ where $sk^{*\prime } \overset{\$}{\leftarrow }span(sk^*)$.

• Encryption. Given a public key $PK=(pk,F_{pk})$, to encrypt a message $M \in \{0,1\}^{\iota }$, the encryption algorithm samples $rand \overset{\$}{\leftarrow }\{0,1\}^d$, $t_c \overset{\$}{\leftarrow }\mathcal {T}_c$, and runs $\mathfrak {H}.VSamp(\varvec{H})$ to sample $C \overset{\$}{\leftarrow }\mathcal {V}$ with a witness w. Then it evaluates $K=\mathfrak {H}.Pub(\varvec{H}, pk, C, w)$, $\varPsi =Ext(K,\,rand) \oplus M$, and $\varUpsilon =LF_{F_{pk},t}(K)$ where $t=(t_a,t_c)$ and $t_a=(C,\,\varPsi ,\,rand)$. Finally, it outputs $CT=(C,\,\varPsi ,\,rand,\,\varUpsilon ,\,t_c)$ as ciphertext.

• Decryption. Given a secret key $SK\!=\!sk$, to decrypt a ciphertext CT = ($C, \varPsi , rand, \varUpsilon , t_c$), the decryption algorithm computes $K'=\mathfrak {H}.Priv(\varvec{H}, sk, C)$ and checks whether $\varUpsilon =LF_{F_{pk},t}(K')$ where $t=((C, \varPsi , rand), t_c)$. If $\varUpsilon =LF_{F_{pk},t}(K')$, the decryption algorithm outputs $M'=\varPsi \oplus Ext(K', rand)$. Otherwise, it rejects with $\perp$.

• Key Update. Given a secret key $SK=sk$ the update algorithm samples $sk^{*\prime } \overset{\$}{\leftarrow }span(sk^*)$ and outputs a new key $SK'=sk+ sk^{*\prime }$.

Correctness of $\varPi _2$ follows directly from correctness of $\varPi _1$ and security of $\varPi _2$ is guaranteed by Theorem 6 stated as follows.

Theorem 6

$\varPi _2$ is secure against a posteriori chosen-ciphertext attacks in the CML setting with period leakage amount $\lambda _M = \min (\lambda , \tau - (\iota +\ell _{LF}+\omega (\log {n})))$ and $\lambda _U=0$.

Proof Sketch. Proof of Theorem 6 is similar to that of Theorem 5, however, the simulator has to deal with decryption oracle queries here. Fortunately, all decryption oracle queries can be answered by the simulator directly until the “partial key indistinguishability” of UHPS is employed in the proof. As this is a statistical indistinguishability, the simulator can answer decryption oracle queries unless the decryption of the submitted ciphertext is not determined by the public key. This occurs only when a ciphertext $CT=(C,\,\varPsi ,\,rand,\,\varUpsilon ,\,t_c)$ with $C \notin \mathcal {V}$ is queried. But such queries cannot pass the verification in the decryption algorithm with a non-negligible probability. To see this, recall that $\mathop {\widetilde{H}_{\infty }}(\mathcal {H}_{sk}(C))$ is large when $C \notin \mathcal {V}$ since the underlying UHPS is universal and leakage in each time period is bounded, where sk is the current secret key. Also, it is hard for the adversary to sample a non-injective function of OT-LF. Therefore, the adversary can generate the correct $\varUpsilon$ with only a negligible probability. We remark that for privacy, lossy function of OT-LF need to be used when generating the challenge ciphertext and that is why we should use an OT-LF rather than a family of injective one-way functions.

4.3 PKE Schemes with Leakage During Key Update

We stress that, our claim that UHPS is effective in constructing CML-PKE schemes is in fact valid in the setting where leakage during key update is allowable. Compared to PKE schemes in Sects. 4.1 and 4.2, which are only proved secure in the CML setting without leakage during key update, schemes secure in this section have nothing more than a better key updating policy. This is based on the ideas of [11, 25]. More precisely, the secret key of the PKE scheme consists of multiple secret keys of UHPS, and can be updated by computing linear combinations of secret keys of UHPS consist in it.

As more involved algebra operations are introduced here, three additional properties of UHPS are required. First, we require that for each instance $\mathcal {H}$ and any secret key $sk \in \mathcal {SK}$, we have $span(sk) = \{r \circ sk \mid r \in \mathbb {Z}\}$ where $r \circ sk$ is denoted as the key obtained by adding sk r times. Assume the order of $\mathcal {K}$ is q, then for any secret key sk, we can sample $sk' \overset{\$}{\leftarrow }span(sk)$ by just sampling $r \overset{\$}{\leftarrow }\mathbb {Z}_q$ and computing $sk' = r \circ sk$. Next, we require that q is prime. The last requirement is that $ker(\mathcal {V})$ is m-decomposable, namely, $ker(\mathcal {V})$ can be represented by m uniform and independent keys in $ker(\mathcal {V})$. More precisely, for any $l \ge m$, let $sk_i \overset{\$}{\leftarrow }ker(\mathcal {V})$ for $i \in [l]$, then with all but negligible probability, we have “sampling $sk' \overset{\$}{\leftarrow }ker(\mathcal {V})$” is equivalent to “first sampling $sk_1' \overset{\$}{\leftarrow }span(sk_1), \ldots , sk_l' \overset{\$}{\leftarrow }span(sk_l)$ then computing $sk'=sk_1'+ \ldots + sk_l'$”, where the probability is taken over the choices of $sk_i$. Although look unusual, these requirements is satisfied by the construction in Sect. 5.1. We remark that we will use the augmented notion of UHPS with these additional requirements throughout Sect. 4.3.

Now, we are ready to give a formal description of our constructions. Due to the limit of space, we only give a construction with CPA-security here and give CCA-secure ones in the full version. The presented scheme $\varPi _3$ consists of four algorithms:

• Parameters. Denote n as the security parameter. Let $\mathfrak {H}$ be a $\tau$-universal $\lambda$-UHPS and $(\varvec{H}, \ T^*) \leftarrow \mathfrak {H}.Param(1^n)$ be an instance of $\mathfrak {H}$. Assume the order of $\mathcal {K}$ is q and $ker(\mathcal {V})$ is m-decomposable. Let $Ext:\mathcal {K} \times \{0,1\}^d \rightarrow \{0,1\}^{\iota }$ be an average case $(\tau , \delta )$-strong extractor where $\delta$ is negligible in n and $\tau - \iota \ge 2\log {({1}/{\delta })}$. Sample $sk^* \overset{\$}{\leftarrow }ker(\mathcal {V})$ with $T^*$. Let l, a be positive integers. The public parameter of $\varPi _3$ is $Params=(\varvec{H},sk^*,Ext,q,m,l,a)$

• Key Generation. The key generation algorithm of $\varPi _3$ samples $\overline{sk} \overset{\$}{\leftarrow }\mathcal {SK}$ and evaluates $pk=\varphi (\overline{sk})$. Then it sets $PK=pk$ and $SK= \begin{bmatrix} sk_1, \ldots , sk_l \end{bmatrix}^{\intercal }$ where $sk_i = \overline{sk} + r_i \circ sk^*$ and $r_i \overset{\$}{\leftarrow }\mathbb {Z}_q$ for $i \in [l]$.

• Encryption. Given a public key $PK=pk$, to encrypt a message $M \in \{0,1\}^{\iota }$, the encryption algorithm samples $rand \overset{\$}{\leftarrow }\{0,1\}^d$ and runs $\mathfrak {H}.VSamp(\varvec{H})$ to sample $C \overset{\$}{\leftarrow }\mathcal {V}$ with a witness w. Then it evaluates $K=\mathfrak {H}.Pub(\varvec{H}, pk, C, w)$, and $\varPsi =Ext(K,\,rand) \oplus M$, Finally, it outputs $CT=(C,\,\varPsi ,\,rand)$ as ciphertext.

• Decryption. Given a secret key $SK\!=\! \begin{bmatrix} sk_1, \ldots , sk_l \end{bmatrix}^{\intercal }$, to decrypt a ciphertext $CT\!=\!(C, \varPsi , rand)$, the decryption algorithm computes $K'$=$\mathfrak {H}.Priv$ ($\varvec{H}, sk_1, C$) and outputs $M'=\varPsi \oplus Ext(K', rand)$.

• Key Update. Given a secret key $SK= \begin{bmatrix} sk_1, \ldots , sk_l \end{bmatrix}^{\intercal }$, the update algorithm samples $\varvec{A'} \overset{\$}{\leftarrow }Rk_a(\mathbb {Z}_q^{l \times l})$, computes $\varvec{A}$ by setting $\varvec{A}_{i,j} = \varvec{A'}_{i,j} / ( \sum _{k=1}^{l} \varvec{A'}_{i,k} )$, which implies $\varvec{A} \cdot [1, \ldots , 1]^{\intercal } = [1, \ldots , 1]^{\intercal }$, and outputs a new key $SK'= \varvec{A} \circ SK$.

Correctness. Let $SK_i = \begin{bmatrix} sk_1^{(i)}, \ldots , sk_l^{(i)} \end{bmatrix}^{\intercal }$ be the secret key obtained by applying the update algorithm i times to the initial secret key generated by KeyGen and $PK = pk$ be the public key. As shown in the proof of the correctness of $\varPi _1$, to prove the correctness of $\varPi _3$, it is sufficient to prove that for arbitrary natural number i, we have $\varphi (sk_1^{(i)}) = pk$. We first write the initial secret key $SK_0$ as $SK_0 = \begin{bmatrix} sk_1, \ldots , sk_l \end{bmatrix}^{\intercal } = \begin{bmatrix} r_1 \circ sk^* + \overline{sk}, \ldots , r_l \circ sk^* + \overline{sk} \end{bmatrix}^{\intercal } = \begin{bmatrix} r_1, \ldots , r_l \end{bmatrix} ^{\intercal } \circ sk^* + \begin{bmatrix} 1, \ldots , 1 \end{bmatrix}^{\intercal } \circ \overline{sk}$, where $r_1,\ldots ,r_l \in \mathbb {Z}_q$. Assume that for any positive integer j, the jth update matrix is $\varvec{A}_j$, then we have

$$ \begin{aligned} SK_i&= \varvec{A}_i \cdot \varvec{A}_{i-1} \ldots \varvec{A}_1 \circ SK_0 \\&= \varvec{A}_i \cdot \varvec{A}_{i-1} \ldots \varvec{A}_1 \cdot \begin{bmatrix} r_1, \ldots , r_l \end{bmatrix}^{\intercal } \circ sk^* + \varvec{A}_i \cdot \varvec{A}_{i-1} \ldots \varvec{A}_1 \cdot \begin{bmatrix} 1, \ldots , 1 \end{bmatrix}^{\intercal } \circ \overline{sk} \\&= \begin{bmatrix} r_1', \ldots , r_l' \end{bmatrix}^{\intercal } \circ sk^* + \begin{bmatrix} 1, \ldots , 1 \end{bmatrix}^{\intercal } \circ \overline{sk} \end{aligned} $$

Thus, we have $sk_1^{(i)} = r_1' \circ sk^* + \overline{sk}$ for some $r_1' \in \mathbb {Z}_q$ which can lead to the fact that $\varphi (sk_1^{(i)}) = pk$ as we need.

Security. Security of $\varPi _3$ is guaranteed by Theorem 7 stated as follows.

Theorem 7

$\varPi _3$ is secure against chosen-plaintext attacks in the CML setting with period leakage amount $\lambda _M = \min (\lambda /2, (a-2m-3)\log {q} - \omega (\log {n}) )$ and $\lambda _U=\lambda _M$ if $a \le l-m$.

5 Instantiations of Updatable Hash Proof System

In this section, we give instantiations of UHPS from widely-accepted number theoretic assumptions, such as the SXDH assumption and the d-linear assumption. Interestingly, one can in fact implement our instantiations simply via modifying existing implementations of DDH-based HPS in [8], since the former are just extensions of the latter. Here, we extend the original 2-dimensional vector space to a high dimensional one; moreover, as specific secret keys will be made public when constructing PKE schemes, secret keys will be group elements rather than integers; to keep the function of secret keys, we will also base on a bilinear group instead of a normal group. Due to the limit of space, we omit the instantiation from the d-linear assumption here and give it in the full version. Besides instantiations of UHPS, in Sect. 5.2, we also consider parameters of our PKE schemes when built from concrete instantiations of UHPS.

Let $\mathbb {G}_1$, $\mathbb {G}_2$ and $\mathbb {G}_T$ be three groups of prime order q, and g, h be generators of $\mathbb {G}_1$ and $\mathbb {G}_2$ respectively. Let e be a bilinear map $e : \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T$. Our instantiation works on the bilinear group $(\mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, q, g, h, e)$. Let $\varvec{R}=\{r_{i,j}\}_{i \in [m], j \in [n]}$ be a matrix in $\mathbb {Z}_q^{m \times n}$, we denote by $g^{\varvec{R}}$ the matrix $\{g^{r_{i,j}}\}_{i \in [m], j \in [n]} \in \mathbb {G}_1^{m \times n}$. Similar definitions hold in $\mathbb {G}_2$ and $\mathbb {G}_T$ as well. Let $\vec a,\,\vec b$ be two vectors in $\mathbb {Z}_q^{n}$, we define $e(g^{\vec a},h^{\vec b}) = e(g,h)^{{\vec a^{\intercal }} \cdot {\vec b}}$. This can be computed efficiently since $e(g,h)^{{\vec a^{\intercal }} \cdot {\vec b}} = e(g,h)^{\sum _{i=1}^{n} a_i b_i} = \prod _{i=1}^{n} e(g,h)^{a_i b_i} = \prod _{i=1}^{n} e(g^{a_i},h^{b_i})$.

5.1 Instantiation from the SXDH Assumption

The instantiation $\Xi$ is described as follows. Each instance $\varvec{H}$ of $\Xi$ works with a bilinear group $(\mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_{T}, q, g, h, e)$. More precisely, let $\kappa$ be a positive integer, then $\mathcal {C}$, $\mathcal {K}$ and $\mathcal {SK}$ in $\varvec{H}$ are $\mathbb {G}_1^{\kappa }$, $\mathbb {G}_T$ and $\mathbb {G}_2^{\kappa }$ respectively. Also, for any $x = g^{\vec \beta }$ in $\mathcal {C}$ and $sk=h^{\vec s}$ in $\mathcal {SK}$, we have $\mathcal {H}_{sk}(x) = e(g^{\vec \beta }, h^{\vec s})$. Now, let $\vec p$ be a vector in $\mathbb {Z}_q^{\kappa }$. Then we define $\mathcal {V}$ to be $g^{span(\vec p)}$ and for any $x = g^{r \cdot \vec p}$ in $\mathcal {V}$, the witness for $x \in \mathcal {V}$ is $r \in \mathbb {Z}_q$. We also define $\mathcal {PK}$ to be $\mathbb {G}_T$ and $\varphi$ to be the function $\varphi (sk) = \mathcal {H}_{sk}(g^{\vec p})$. Note that for any $sk_1 = h^{\vec s_1}$ and $sk_2 = h^{\vec s_2}$ in $\mathcal {SK}$, we have $\varphi (sk_1) = \varphi (sk_2)$ if and only if $\vec s_1 - \vec s_2 \in span(\vec p)^{\perp }$ if and only if $\forall x \in \mathcal {V}, \mathcal {H}_{sk_1}(x) = \mathcal {H}_{sk_2}(x)$. It is easy to check that $\mathcal {K}$ and $\mathcal {SK}$ are groups as we need. Also, for any $sk_1 = h^{\vec s_1}$ and $sk_2 = h^{\vec s_2}$ in $\mathcal {SK}$, we can evaluate $sk_3 = sk_1 + sk_2$ by setting $sk_3 =h^{\vec s_1 + \vec s_2}$, and $\forall x \in \mathcal {C}$, assuming $x=g^{\vec \beta }$, we have $\mathcal {H}_{sk_3}(x) = e(g^{\vec \beta }, h^{\vec s_1 + \vec s_2}) = e(g^{\vec \beta }, h^{\vec s_1}) \cdot e(g^{\vec \beta }, h^{\vec s_2}) = \mathcal {H}_{sk_1}(x) + \mathcal {H}_{sk_2}(x)$. For any secret key $sk=h^{\vec s}$, we define $span(sk) = \{h^{r \cdot \vec s} \mid r \in \mathbb {Z}_q\}$. It is easy to see that this is in fact the set $\{sk' \mid \forall x \in \mathcal {C}, \mathcal {H}_{sk}(x)=0 \ \rightarrow \ \mathcal {H}_{sk'}(x)=0\}$. For any $L \subseteq \mathcal {C}$, let $\mathcal {L}$ be the vector space spanned by exponents of all elements in L. Obviously, for any $sk = h^{\vec s}$ in $\mathcal {SK}$, $sk \in ker(L)$ if and only if $\vec s \in \mathcal {L}^{\perp }$, so we can set the trapdoor for L to be a basis of $\mathcal {L}$. Also, given trapdoors $T_1, T_2 \in \mathcal {T}$ (i.e. $T_1$ and $T_2$ are basis of vector spaces) for subsets $L_1, L_2 \subseteq \mathcal {C}$ respectively, we can evaluate the trapdoor $T_3$ for $L_1 \cup L_2$ by just evaluating a basis for $span(T_1 \cup T_2)$.

In addition, algorithms of $\Xi$ works as follows:

• Instance Generation. To generate an instance of $\Xi$, the instance generation algorithm first samples a bilinear group $(\mathbb {G}_1,\,\mathbb {G}_2,\,\mathbb {G}_T,q,g,h,e)$ from distributions in an ensemble indexed by n where the SXDH assumption holds. Then it samples $\vec p \overset{\$}{\leftarrow }\mathbb {Z}_q^{\kappa }$ and sets public parameters as described above. The trapdoor $T^*$ for $\mathcal {V}$ is exactly the vector $\vec p$.

• Subset Sampling. The subset sampling algorithm first samples $u \overset{\$}{\leftarrow }\mathbb {Z}_q$, then sets $w=u$ and $x=(g^{\vec p})^{u}$.

• Complement Sampling. The complement sampling algorithm first samples $\vec \beta \overset{\$}{\leftarrow }\mathbb {Z}_q^{\kappa }$ then sets $x=g^{\vec \beta }$ and $T=\vec \beta$. Note that x is statistically indistinguishable from a uniform element in $\mathcal {C} \backslash \mathcal {V}$.

• Public Evaluation. Given a public key $pk = e(g,h)^{\alpha }$ and an element $x \in \mathcal {V}$ with its witness $w=u$, the public evaluation algorithm sets $k=(e(g,h)^{\alpha })^{u}$.

• Private Evaluation. Given a secret key $sk=h^{\vec s}$ and an element $x=g^{\vec \beta }$ in $\mathcal {C}$, the private evaluation algorithm computes $k = \mathcal {H}_{sk}(x) = e(g^{\vec \beta }, h^{\vec s})$.

Theorem 8

Under the SXDH assumption, $\Xi$ is a $\log (q)$-universal $((\kappa -4) \log (q) - \omega (\log (n)))$-UHPS if $\kappa \ge 5$.

Due to the limit of space, we give the proof to Theorem 8 in the full version.

5.2 Parameters

Now we discuss the security level and efficiency of our CML-PKE schemes from the SXDH assumption, namely, in what extent our PKE schemes can resist CML adversaries and how much they will cost when implemented in practice.

Generally, the degree of leakage resilience of a scheme can be measured by the leakage rate, which indicates the ratio of the tolerated leakage amount to the size of the secret state in each time period, i.e. the leakage rate $\rho = \lambda _M / \Vert sk \Vert$. Via simple computation, we can get the leakage rate of each scheme when instantiated with the SXDH assumption, and they are $1-o(1)$, $\frac{1}{5} - o(1)$ and $\frac{1}{442} - o(1)$ for $\varPi _1$, $\varPi _2$ and $\varPi _3$ respectively. We observe that $\varPi _1$ can achieve a better leakage rate compared to $\varPi _2$. This is because to achieve CCA-security, we must ensure that the adversary is not able to get an authentication, which prevent the adversary from querying “bad ciphertexts”, via the leakage. So the allowed leakage amount is smaller in this case. Besides, $\varPi _3$ have a much worse leakage rate compared to $\varPi _1$ and $\varPi _2$ since it has a much larger secret key.

We would also like to give an efficiency comparison between constructions of CCA-secure CML-PKE schemes based on UHPS and other known constructions. For simplicity, we only compare the best efficiency that can be achieved for each approach. Computation and communication overhead caused by operations such as signature and normal hash function are ignored as they are very low. Besides, our comparison is under a security level of 128, which means that breaking these schemes is as hard as breaking a 128-bit block cipher. The comparison is summarized in Table 1. Here, we use “NY” to denote the scheme constructed under the Naor-Yung paradigm, and the building blocks include the PKE scheme in [36], a normal Elgamal PKE scheme, and the Groth-Sahai proof system [16];² we use “CHK” to denote the scheme constructed by applying the CHK transform [6] to the identity-based encryption scheme in [26]; we use “LTDF” to denote the CCA-secure PKE scheme presented in [23]; we use “ours” to denote $\varPi _2$ instantiated from the SXDH assumption. We remark that the construction from CHK transform works in composite-order groups while other three constructions work in prime-order groups, so basic operations will execute slower in this case.

Table 1. Efficiency Comparison.

A Omitted Constructions in Sect. 4.2

In this section, we present the omitted constructions of CCA-secure CML-PKE schemes discussed in Sect. 4.2, namely, the one from twin UHPS, and the one constructed from universal$_2$ UHPS plus AE. We only give the formal description of each schemes here and give their security analysis in the full version.

CCA-secure CML PKE from twin UHPS. The presented PKE scheme $\varPi _4$ consists of four algorithms:

• Parameters. Denote n as the security parameter. Let $\mathfrak {H}$ be a $\tau$-universal $\lambda$-UHPS and $(\varvec{H}, \ T^*) \leftarrow \mathfrak {H}.Param(1^n)$ be an instance of $\mathfrak {H}$. Let $Ext:\mathcal {K} \times \{0,1\}^d \rightarrow \{0,1\}^{\iota }$ be an average case $(\tau , \delta )$-strong extractor where $\delta$ is negligible in n and $\tau - \iota \ge 2\log {({1}/{\delta })}$. Consider a variant of $\mathfrak {H}$ which is identical to $\mathfrak {H}$ except that its hash functions will further take strings in $\{0,1\}^{d}$ and $\{0,1\}^{\iota }$ as input but these extra inputs will be ignored when evaluating hash functions. Let $\mathfrak {H}^{\dag }$ be a $\tau$-universal$_2$ UHPS constructed from this variant via the approach in [8]. Let $\varvec{H}^{\dag }$ be an instance of $\mathfrak {H}^{\dag }$. Recall that $\varvec{H}^{\dag }$ can be generated with $\varvec{H}$ directly and $T^*$ is exactly the trapdoor for $\varvec{H}^{\dag }$. Also for any $L \in \mathcal {C}$, combining multiple secret keys of $\mathfrak {H}$ in ker(L) will lead to a secret key $sk^{\dag }$ of $\mathfrak {H}^{\dag }$ in $ker(L \times \{0,1\}^{d} \times \{0,1\}^{\iota })$. Assume $\mathcal {SK}^{\dag } = \mathcal {SK}^{\kappa }$. Then sample $sk^* \overset{\$}{\leftarrow }ker(\mathcal {V})$ with $T^*$ where $sk^*$ is a secret key of $\mathfrak {H}$. Set $sk^{*\dag } = (sk^{*}, \ldots , sk^{*})$. The public parameter of $\varPi _4$ is $Params=(\varvec{H},sk^*, \varvec{H}^{\dag }, sk^{*\dag }, Ext)$.

• Key Generation. The key generation algorithm of $\varPi _4$ samples $\overline{sk} \overset{\$}{\leftarrow }\mathcal {SK}$, $\overline{sk^{\dag }} \overset{\$}{\leftarrow }\mathcal {SK}^{\dag }$ and evaluates $pk=\varphi (\overline{sk})$, $pk^{\dag }=\varphi ^{\dag }(\overline{sk^{\dag }})$. Then it sets $PK=(pk, pk^{\dag })$ and $SK=(sk,sk^{\dag })$ where $sk = \overline{sk} + sk^{*\prime }$, $sk^{\dag } = \overline{sk^{\dag }} + sk^{*\dag \prime }$, $sk^{*\prime } \overset{\$}{\leftarrow }span(sk^*)$, and $sk^{*\dag \prime } \overset{\$}{\leftarrow }span(sk^{*\dag })$.

• Encryption. Given a public key $PK\!=\!(pk, pk^{\dag })$, to encrypt a message $M \in \{0,1\}^{\iota }$, the encryption algorithm samples $rand \overset{\$}{\leftarrow }\{0,1\}^d$ and runs $\mathfrak {H}.VSamp(\varvec{H})$ to sample $C \overset{\$}{\leftarrow }\mathcal {V}$ with a witness w. Then it evaluates $K=\mathfrak {H}.Pub(\varvec{H}, pk, C, w)$, $\varPsi =Ext(K,\,rand) \oplus M$, and $K^{\dag } = \eta ((C,rand,\varPsi ), \mathfrak {H}^{\dag }.Pub(\varvec{H}^{\dag }, pk^{\dag }, (C, rand, \varPsi ), w))$. Finally, it outputs $CT=(C,\,\varPsi ,\,rand,\,K^{\dag })$ as ciphertext.

• Decryption. Given a secret key $SK=(sk,sk^{\dag })$, to decrypt a ciphertext $CT=(C,\,\varPsi ,\,rand,\,K^{\dag })$, the decryption algorithm computes $K^{\dag \prime } = \eta ((C,rand,\varPsi ), \mathfrak {H}^{\dag }.Priv(\varvec{H}^{\dag },\,sk^{\dag },\,(C, rand, \varPsi )))$ and checks whether $K^{\dag \prime } = K^{\dag }$. If $K^{\dag \prime } = K^{\dag }$, the decryption algorithm computes $K'=\mathfrak {H}.Priv(\varvec{H},\,sk,\,C)$ and outputs $M'=\varPsi \oplus Ext(K',\,rand)$. Otherwise, it rejects with $\perp$.

• Key Update. Given a secret key $SK=(sk,sk^{\dag })$, the update algorithm samples $sk^{*\prime } \overset{\$}{\leftarrow }span(sk^*)$, $sk^{*\dag \prime } \overset{\$}{\leftarrow }span(sk^{*\dag })$, and outputs a new key $SK'=(sk', sk^{\dag \prime })$ where $sk' = sk + sk^{*\prime }$ and $sk^{\dag \prime } = sk^{\dag } + sk^{*\dag \prime }$.

Correctness of $\varPi _4$ can be proved similarly to that of $\varPi _1$ and security of $\varPi _4$ is guaranteed by Theorem 9 stated as follows.

Theorem 9

$\varPi _4$ is secure against a posteriori chosen-ciphertext attacks in the CML setting with period leakage amount $\lambda _M = min(\lambda , \tau -\omega (\log {n}))$ and $\lambda _U=0$.

CCA-secure CML PKE from UHPS plus AE. The presented PKE scheme $\varPi _5$ consists of four algorithms:

• Parameters. Denote n as the security parameter. Let $\mathfrak {H}$ be a $\tau$-universal$_2$ $\lambda$-UHPS and $(\varvec{H}, \ T^*) \leftarrow \mathfrak {H}.Param(1^n)$ be an instance of $\mathfrak {H}$. Assume the range of $\eta$ is $\mathcal {Y}$. We further require that $\tau = \log (\Vert \mathcal {Y} \Vert )$ and this can be fulfilled by our instantiated UHPS. Let $\mathfrak {AE}=(AE.Enc,AE.Dec)$ be an AE scheme. Sample $sk^* \overset{\$}{\leftarrow }ker(\mathcal {V})$ with $T^*$. The public parameter of $\varPi _5$ is $Params=(\varvec{H},sk^*,\mathfrak {AE})$.

• Key Generation. The key generation algorithm of $\varPi _5$ samples $\overline{sk} \overset{\$}{\leftarrow }\mathcal {SK}$ and evaluates $pk=\varphi (\overline{sk})$. Then it sets $PK=pk$ and $SK=\overline{sk} + sk^{*\prime }$ where $sk^{*\prime } \overset{\$}{\leftarrow }span(sk^*)$.

• Encryption. Given a public key $PK=pk$, to encrypt a message M, the encryption algorithm first runs $\mathfrak {H}.VSamp(\varvec{H})$ to sample $C \overset{\$}{\leftarrow }\mathcal {V}$ with a witness w. Then it evaluates $K=\eta (C, \mathfrak {H}.Pub(\varvec{H}, pk, C, w))$, and $\varPsi = AE.Enc(K,M)$. Finally, it outputs $CT=(C,\,\varPsi )$ as ciphertext.

• Decryption. Given a secret key $SK=sk$, to decrypt a ciphertext $CT=(C,\,\varPsi )$, the decryption algorithm computes $K'=\eta (C, \mathfrak {H}.Priv(\varvec{H},\,sk,\,C))$, and outputs $M' = AE.Dec(K',\varPsi )$.

• Key Update. Given a secret key $SK=sk$ the update algorithm samples $sk^{*\prime } \overset{\$}{\leftarrow }span(sk^*)$ and outputs a new key $SK'=sk+ sk^{*\prime }$.

Correctness of $\varPi _5$ follows directly from correctness of $\varPi _1$ and security of $\varPi _5$ is guaranteed by Theorem 10 stated as follows.

Theorem 10

$\varPi _5$ is secure against a posteriori chosen-ciphertext attacks in the CML setting with period leakage amount $\lambda _M = \min (\lambda , \log (1/\epsilon ) - \omega (\log {n}))$ and $\lambda _U=0$ if $\mathfrak {AE}$ is $\epsilon$-secure.