Abstract
The Kappa biochemistry and the MØD organo-chemistry frameworks are amongst the most intensely developed applications of rewriting theoretical methods in the life sciences to date. A typical feature of these types of rewriting theories is the necessity to implement certain structural constraints on the objects to be rewritten (a protein is empirically found to have a certain signature of sites, a carbon atom can form at most four bonds, ...). In this paper, we contribute to the theoretical foundations of these types of rewriting theory a number of conceptual and technical developments that permit to implement a universal theory of continuous-time Markov chains (CTMCs) for stochastic rewriting systems. Our core mathematical concepts are a novel rule algebra construction for the relevant setting of rewriting rules with conditions, both in Double- and in Sesqui-Pushout semantics, augmented by a suitable stochastic mechanics formalism extension that permits to derive dynamical evolution equations for pattern-counting statistics.
An extended version of this paper containing additional technical appendices is available online [9].
You have full access to this open access chapter, Download conference paper PDF
1 Motivation
One of the key applications that rewriting theory may be considered for in the life sciences is the theory of continuous-time Markov chains (CTMCs) modeling complex systems. In fact, since Delbrück’s seminal work on autocatalytic reaction systems in the 1940s [20], the mathematical theory of chemical reaction systems has effectively been formulated as a rewriting theory in disguise, namely via the rule algebra of discrete graph rewriting [11]. In the present paper, we provide the necessary technical constructions in order to consider the CTMCs and analysis methods of relevance for more general types of compositional rewriting theories with conditions, with key examples provided in the form of biochemical graph rewriting in the sense of the Kappa framework (https://kappalanguage.org) [12], and (organo-) chemical graph rewriting in the sense of the MØD framework (https://cheminf.imada.sdu.dk/mod/) [1]. The present paper aims to serve two main purposes: the first consists in providing an extension of the existing category-theoretical rule-algebra frameworks [4, 10, 11] by the rewriting theoretical design feature of incorporating rules with conditions as well as constraints on objects (Sect. 3). Based upon these technical developments, we then investigate to which extent it is possible to utilize the rule-algebraic stochastic mechanics frameworks of the relevant types (Sect. 4) in order to compute evolution equations for the moments of pattern-count observables within the Kappa and MØD frameworks (Sect. 5 and 6).
2 Compositional Rewriting Theories with Conditions
The well-established Double-Pushout (DPO) [21] and Sesqui-Pushout (SqPO) [13] frameworks for rewriting systems over categories with suitable adhesivity properties [23, 24, 26, 30] provide a principled and very general foundation for rewriting theories. In practice, many applications require the rewriting of objects that are not part of an adhesive category themselves, but which may be obtained from a suitable “ambient” category via the notion of conditions on objects. Together with a corresponding notion of constraints on rewriting rules, this yields a versatile extension of rewriting theory. In the DPO setting, this modification had been well-known [21,22,23, 27], while it has been only very recently introduced for the SqPO setting [8]. For the rule algebra constructions presented in the main part of this contribution, we require in addition a certain compositionality property of our rewriting theories (established for the DPO case in [10, 11], for the SqPO case in [4], and for both settings augmented with conditions in [8]).
2.1 Category-Theoretical Prerequisites
Throughout this paper, we will make the following assumptionsFootnote 1:
Assumption 1
 is a finitary
is a finitary  -adhesive category with
-adhesive category with  -initial object,
-initial object,  -effective unions and epi-
-effective unions and epi- -factorization. In the setting of Sesqui-Pushout (SqPO) rewriting, we assume in addition that all final pullback complements (FPCs) along composable pairs of
-factorization. In the setting of Sesqui-Pushout (SqPO) rewriting, we assume in addition that all final pullback complements (FPCs) along composable pairs of  -morphisms exist, and that
-morphisms exist, and that  -morphisms are stable under FPCs.
-morphisms are stable under FPCs.
Both of the main application examples presented within this paper rely upon typed variants of undirected multigraphs.
Definition 1
Let  be the restricted powerset functor (mapping a set S to the set of its subsets \(P\subset S\) with \(1\le |P|\le 2\)). The category \(\mathbf {uGraph}\) [11] of finite undirected multigraphs is defined as the finitary restriction of the comma category
be the restricted powerset functor (mapping a set S to the set of its subsets \(P\subset S\) with \(1\le |P|\le 2\)). The category \(\mathbf {uGraph}\) [11] of finite undirected multigraphs is defined as the finitary restriction of the comma category  . Thus an undirected multigraph is specified as \(G=(E_G,V_G,i_G)\), where \(E_G\) and \(V_G\) are (finite) sets of edges and vertices, respectively, and where
. Thus an undirected multigraph is specified as \(G=(E_G,V_G,i_G)\), where \(E_G\) and \(V_G\) are (finite) sets of edges and vertices, respectively, and where  is the edge-incidence map.
is the edge-incidence map.
Theorem 1
\(\mathbf {uGraph}\) satisfies Assumption 1, both for the DPO- and for the extended SqPO-variant.
Proof
As demonstrated in [11], \(\mathbf {uGraph}\) is indeed a finitary  -adhesive category with
-adhesive category with  -initial object and
-initial object and  -effective unions, for
-effective unions, for  the class of component-wise monic \(\mathbf {uGraph}\)-morphisms. It thus remains to prove the existence of an epi-
the class of component-wise monic \(\mathbf {uGraph}\)-morphisms. It thus remains to prove the existence of an epi- -factorization as well as the properties related to FPCs. To this end, utilizing the fact that the category \(\mathbf {Set}\) upon which the comma category \(\mathbf {uGraph}\) is based possesses an epi-mono-factorization, we may construct the following diagram from a \(\mathbf {uGraph}\)-morphism
-factorization as well as the properties related to FPCs. To this end, utilizing the fact that the category \(\mathbf {Set}\) upon which the comma category \(\mathbf {uGraph}\) is based possesses an epi-mono-factorization, we may construct the following diagram from a \(\mathbf {uGraph}\)-morphism  (for component morphisms \(\varphi _E:E\rightarrow E'\) and \(\varphi _V:V\rightarrow V'\)):
(for component morphisms \(\varphi _E:E\rightarrow E'\) and \(\varphi _V:V\rightarrow V'\)):

The diagram is constructed as follows:
-
1.
Perform the epi-mono-factorizations \(\varphi _E=m_E\circ e_E\) and \(\varphi _V=m_V\circ e_V\), and apply the functor
 in order to obtain the morphisms
in order to obtain the morphisms 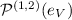 and
and  ; since the functor
; since the functor 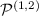 preserves monomorphisms [31],
preserves monomorphisms [31], 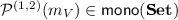 .
. -
2.
Construct the pullback
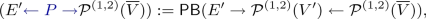
Since monomorphisms are stable under pullback in \(\mathbf {Set}\), having proved that
 implies
implies 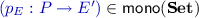 .
. -
3.
By the universal property of pullbacks, there exists a morphism
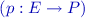 . Let
. Let  be the epi-mono-factorization of this morphism.
be the epi-mono-factorization of this morphism. -
4.
By stability of monomorphisms under composition in \(\mathbf {Set}\), we find that
 , and consequently
, and consequently  yields an alternative epi-mono-factorization of \(\varphi _E\). Then by uniqueness of epi-mono-factorizations up to isomorphism, there must exist an isomorphism
yields an alternative epi-mono-factorization of \(\varphi _E\). Then by uniqueness of epi-mono-factorizations up to isomorphism, there must exist an isomorphism  .
.
We have thus demonstrated that both  and
and  are morphisms in \(\mathbf {uGraph}\). Since morphisms in comma categories are mono-, epi- or iso-morphisms if they are so componentwise [21], we conclude that
are morphisms in \(\mathbf {uGraph}\). Since morphisms in comma categories are mono-, epi- or iso-morphisms if they are so componentwise [21], we conclude that

which finally entails that we have explicitly constructed an epi-mono-factorization of the \(\mathbf {uGraph}\)-morphism  .
.
In order to demonstrate that FPCs along pairs of composable  -morphisms
-morphisms  in \(\mathbf {uGraph}\) exist (for
in \(\mathbf {uGraph}\) exist (for  the class of component-wise monomomophic \(\mathbf {uGraph}\) morphisms), we provide the following explicit construction:
the class of component-wise monomomophic \(\mathbf {uGraph}\) morphisms), we provide the following explicit construction:

2.2 Conditions
Referring to [9, Appendix A.2] for further details and technical definitions, we will utilize as a notational convention the standard shorthand notations
For example, the constraints

express for a given object  that Z contains at least two vertices (if \(Z\vDash \mathsf {c}_{\mathop {\varnothing }}^{(1)}\)), that Z does not contain parallel pairs of directed edges (if \(Z\vDash \mathsf {c}_{\mathop {\varnothing }}^{(2)}\)), and that for every directed edge in Z there also exists a directed edge between the same endpoints with opposite direction (if \(Z\vDash \mathsf {c}_{\mathop {\varnothing }}^{(3)}\)), respectively.
that Z contains at least two vertices (if \(Z\vDash \mathsf {c}_{\mathop {\varnothing }}^{(1)}\)), that Z does not contain parallel pairs of directed edges (if \(Z\vDash \mathsf {c}_{\mathop {\varnothing }}^{(2)}\)), and that for every directed edge in Z there also exists a directed edge between the same endpoints with opposite direction (if \(Z\vDash \mathsf {c}_{\mathop {\varnothing }}^{(3)}\)), respectively.
2.3 Compositional Rewriting with Conditions
Throughout this section, we assume that we are given a type  of rewriting semantics and an
of rewriting semantics and an  -adhesive category
-adhesive category  satisfying the respective variant of Assumption 1. In categorical rewriting theories, the universal constructions utilized such as pushouts, pullbacks, pushout complements and final pullback complements are unique only up to universal isomorphisms. This motivates specifying a suitable notion of equivalence classes of rules with conditions:
satisfying the respective variant of Assumption 1. In categorical rewriting theories, the universal constructions utilized such as pushouts, pullbacks, pushout complements and final pullback complements are unique only up to universal isomorphisms. This motivates specifying a suitable notion of equivalence classes of rules with conditions:
Definition 2
(Rules with conditions). Let  denote the class of (linear) rules with conditions, defined as
denote the class of (linear) rules with conditions, defined as


We define two rules with conditions \(R_j=(r_j,\mathsf {c}_{I_j})\) (\(j=1,2\)) equivalent, denoted \(R_2\sim R_1\), iff \(\mathsf {c}_{I_1}\equiv \mathsf {c}_{I_2}\) and if there exist isomorphisms  such that the diagram on the right commutes. We denote by
such that the diagram on the right commutes. We denote by  the set of equivalence classes under \(\sim \) of rules with conditions.
the set of equivalence classes under \(\sim \) of rules with conditions.
Definition 3
(Direct derivations). Let  and
and  be concrete representatives of some equivalence class
be concrete representatives of some equivalence class  , and let
, and let  be objects. Then a type
be objects. Then a type  direct derivation is defined as a commutative diagram such as below right, where all morphism are in
direct derivation is defined as a commutative diagram such as below right, where all morphism are in  (and with the left representation a shorthand notation)
(and with the left representation a shorthand notation)

with the following pieces of information required relative to the type:
-
1.
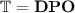 : given
: given 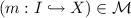 , m is a DPO-admissible match of R into X, denoted
, m is a DPO-admissible match of R into X, denoted  , if \(m\vDash \mathsf {c}_I\) and (A) is constructable as a pushout complement, in which case (B) is constructed as a pushout.
, if \(m\vDash \mathsf {c}_I\) and (A) is constructable as a pushout complement, in which case (B) is constructed as a pushout. -
2.
 : given
: given  , m is a SqPO-admissible match of R into X, denoted
, m is a SqPO-admissible match of R into X, denoted  , if \(m\vDash \mathsf {c}_I\), in which case (A) is constructed as a final pullback complement and (B) as a pushout.
, if \(m\vDash \mathsf {c}_I\), in which case (A) is constructed as a final pullback complement and (B) as a pushout. -
3.
 : given just the “plain rule” r and
: given just the “plain rule” r and  , \(m^{*}\) is a DPO\({}^{\dag }\)-admissible match of r into X, denoted
, \(m^{*}\) is a DPO\({}^{\dag }\)-admissible match of r into X, denoted 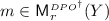 , if (B) is constructable as a pushout complement, in which case (B) is constructed as a pushout.
, if (B) is constructable as a pushout complement, in which case (B) is constructed as a pushout.
For types  , we will sometimes employ the notation \(R_m(X)\) for the object Y.
, we will sometimes employ the notation \(R_m(X)\) for the object Y.
Note that at this point, we have not yet resolved a conceptual issue that arises from the non-uniqueness of a direct derivation given a rule and an admissible match. Concretely, the pushout complement, pushout and FPC constructions are only unique up to isomorphisms. This issue will ultimately be resolved as part of the rule algebraic theory. We next consider a certain composition operation on rules with conditions that is quintessential to our main constructions:
Definition 4
(Rule compositions). Let  be two equivalence classes of rules with conditions, and let
be two equivalence classes of rules with conditions, and let  and \(\mathsf {c}_{I_j}\) be concrete representatives of \(R_j\) (for \(j=1,2\)). For
and \(\mathsf {c}_{I_j}\) be concrete representatives of \(R_j\) (for \(j=1,2\)). For  , an
, an  -span \(\mu =(I_2\hookleftarrow M_{21}\hookrightarrow O_1)\) (i.e. with
-span \(\mu =(I_2\hookleftarrow M_{21}\hookrightarrow O_1)\) (i.e. with  ) is a
) is a  -admissible match of \(R_2\) into \(R_1\) if the diagram below is constructable (with \(N_{21}\) constructed by taking pushout)
-admissible match of \(R_2\) into \(R_1\) if the diagram below is constructable (with \(N_{21}\) constructed by taking pushout)

and if  . Here, the condition \(\mathsf {c}_{I_{21}}\) is computed as
. Here, the condition \(\mathsf {c}_{I_{21}}\) is computed as
In this case, we define the type  composition of \(R_2\) with \(R_1\) along \(\mu \), denoted
composition of \(R_2\) with \(R_1\) along \(\mu \), denoted  , as
, as

where \((O_{21}\leftharpoonup I_{21}):=(O_{21}\leftharpoonup N_{21})\circ (N_{21}\leftharpoonup I_{21})\) (with \(\circ \) the span composition operation).
We refer the interested readers to [9, Appendix A.3] for a summary of the relevant technical results on two variants of concurrency theorems following [8] (where the DPO-type concurrency theorem is of course classical, cf. e.g. [21]).
3 Rule Algebras for Compositional Rewriting with Conditions
The associativity property of rule compositions in both DPO- and SqPO-type semantics for rewriting with conditions as proved in [8] may be fruitfully exploited within rule algebra theory. One possibility to encode the non-determinism in sequential applications of rules to objects is given by lifting each possible configuration  (i.e. isomorphism class of objects) to a basis vector \(\left| X\right\rangle \) of a vector space
(i.e. isomorphism class of objects) to a basis vector \(\left| X\right\rangle \) of a vector space  ; then a rule r is lifted to a linear operator acting on
; then a rule r is lifted to a linear operator acting on  , with the idea that this operator acting upon a basis vector \(\left| X\right\rangle \) should evaluate to the “sum over all possibilities to act with r on X”. We will extend here the general rule algebra framework [4, 6, 10] to the present setting of rewriting rules with conditions.
, with the idea that this operator acting upon a basis vector \(\left| X\right\rangle \) should evaluate to the “sum over all possibilities to act with r on X”. We will extend here the general rule algebra framework [4, 6, 10] to the present setting of rewriting rules with conditions.
We will first lift the notion of rule composition into the setting of a composition operation on a certain abstract vector space over rules, thus realizing the heuristic concept of “summing over all possibilities to compose rules”.
Definition 5
Let  be the rewriting type, and let
be the rewriting type, and let  be a category satisfying the relevant variant of Assumption 1. Let
be a category satisfying the relevant variant of Assumption 1. Let  be an
be an  -vector space, defined via a bijection
-vector space, defined via a bijection  from the set of equivalence classes of linear rules with conditions to the set of basis vectors of
from the set of equivalence classes of linear rules with conditions to the set of basis vectors of  . Let
. Let  denote the type
denote the type  rule algebra product, a binary operation defined via its action on basis elements
rule algebra product, a binary operation defined via its action on basis elements  (for
(for  ) as
) as

We refer to  as the
as the  -type rule algebra over
-type rule algebra over  .
.
Theorem 2
For type  over a category
over a category  satisfying Assumption 1, the rule algebra
satisfying Assumption 1, the rule algebra  is an associative unital algebra, with unit element \(\delta (R_{\mathop {\varnothing }})\), where \(R_{\mathop {\varnothing }}:=(\mathop {\varnothing }\hookleftarrow \mathop {\varnothing }\hookrightarrow \mathop {\varnothing };\mathsf {true})\).
is an associative unital algebra, with unit element \(\delta (R_{\mathop {\varnothing }})\), where \(R_{\mathop {\varnothing }}:=(\mathop {\varnothing }\hookleftarrow \mathop {\varnothing }\hookrightarrow \mathop {\varnothing };\mathsf {true})\).
Proof
Associativity follows from [9, Theorem 7], while unitality, i.e. that

follows directly from an explicit computation of the relevant rule compositions.
As alluded to in the introduction, the prototypical example of rule algebras are those of DPO- or (in this case equivalently) SqPO-type over discrete graphs, giving rise as a special case to the famous Heisenberg-Weyl algebra of key importance in mathematical chemistry, combinatorics and quantum physics (see [11] for further details). We will now illustrate the rule algebra concept in an example involving a more general base category.
Example 1
For the category \(\mathbf {uGraph}\) and DPO-type rewriting semantics, consider as an example the following two rules with conditions:

The first rule is a typical example of a rule with application conditions, i.e. here stating that the rule may only link two vertices if they were previously not already linked to each other. The second rule, owing to DPO semantics, can in effect only be applied to vertices without any incident edges. The utility of the rule-algebraic composition operation then consists in reasoning about sequential compositions of these rules, for example (letting \(*:= \star _{DPO}{}\)):

To provide some intuition: the first computation encodes the causal information that the two rules may either be composed along a trivial overlap, or rule \(R_C\) may overlap on one of the vertices in the output of \(R_V\); in the latter case, any vertex to which first \(R_V\) and then \(R_C\) applies must not have had any incident edges, i.e. in particular no edge violating the constraint of \(R_C\), which is why the composite rule \(R_C'\) does not feature any non-trivial constraint. In the other order of composition, the two vertices in the output of \(R_C\) are linked by an edge, so \(R_V\) cannot be applied to any of these two vertices (leaving just the trivial overlap contribution).
Just as the rule algebra construction encodes the compositional associativity property of rule compositions, the following representation construction encodes in a certain sense the properties described by the concurrency theorem:
Definition 6
Let  be an
be an  -adhesive category satisfying Assumption 1. Let
-adhesive category satisfying Assumption 1. Let  be defined as the
be defined as the  -vector space whose set of basis vectors is isomorphic to the setFootnote 2 of iso-classes of objects of
-vector space whose set of basis vectors is isomorphic to the setFootnote 2 of iso-classes of objects of  via a bijection
via a bijection  . Then the
. Then the  -type canonical representation of the
-type canonical representation of the  -type rule algebra over
-type rule algebra over  , denoted
, denoted  , is defined as the morphism
, is defined as the morphism  specified via
specified via

Theorem 3
 as defined above is an algebra homomorphism (and thus in particular a well defined representation).
as defined above is an algebra homomorphism (and thus in particular a well defined representation).
Proof
The proof that we provide in [9, Appendix B.1] is entirely analogous to the one for the case without application conditions [4, 10].
4 Stochastic Mechanics Formalism
Referring to [6, 7, 11] for further details and derivations, suffice it here to highlight the key role played by the algebraic concept of commutators in stochastic mechanics. Let us first provide the constructions of continuous-time Markov chains (CTMCs) and observables in stochastic rewriting systems.
Definition 7
Let  (referred to as dual projection vector) be defined via its action on basis vectors of
(referred to as dual projection vector) be defined via its action on basis vectors of  as
as  .
.
Theorem 4
Let  be a category satisfying the relevant variant of Assumption 1, and let
be a category satisfying the relevant variant of Assumption 1, and let  be the
be the  -type rule algebra of linear rules with conditions over
-type rule algebra of linear rules with conditions over  . Let
. Let  denote the
denote the  -type canonical representation of
-type canonical representation of  . Then the following results hold:
. Then the following results hold:
-
1.
The basis elements of the space
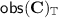 of
of  -type observables, i.e. the diagonal linear operators that arise as (linear combinations of)
-type observables, i.e. the diagonal linear operators that arise as (linear combinations of)  -type canonical representations of rewriting rules with conditions, have the following structure (
-type canonical representations of rewriting rules with conditions, have the following structure (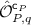 in the DPO case,
in the DPO case,  in the SqPO case):
in the SqPO case):  (14)
(14) -
2.
DPO-type jump closure property: for every linear rule with condition
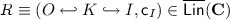 , we find that
, we find that  (15)
(15)where
 is the homomorphism defined via its action on basis elements \(\delta (R)\) for
is the homomorphism defined via its action on basis elements \(\delta (R)\) for  as
as  (16)
(16) -
3.
SqPO-type jump closure property: for every linear rule with condition
 , we find that
, we find that  (17)
(17)whereFootnote 3
 is the homomorphism defined via
is the homomorphism defined via  (18)
(18) -
4.
CTMCs via stochastic rewriting systems: Let
 be the space of (sub-)probability distributions over
be the space of (sub-)probability distributions over  (i.e.
(i.e. 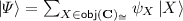 ). Let
). Let 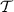 be a collection of N pairs of positive real-valued parameters \(\kappa _j\) (referred to as base rates) and linear rules \(R_j\) with application conditions,
be a collection of N pairs of positive real-valued parameters \(\kappa _j\) (referred to as base rates) and linear rules \(R_j\) with application conditions,  (19)
(19)Then given an initial state
 , the
, the  -type stochastic rewriting system based upon the transitions
-type stochastic rewriting system based upon the transitions  gives rise to the CTMC
gives rise to the CTMC  with time-dependent state
with time-dependent state 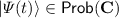 (for \(t\ge 0\)) and evolution equation
(for \(t\ge 0\)) and evolution equation 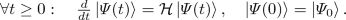 (20)
(20)Here, the infinitesimal generator
 of the CTMC is given by
of the CTMC is given by  (21)
(21)
Proof
See [9, Appendix B.2].
Remark 1
The operation  featuring in the DPO- and SqPO-type jump-closure properties has a very intuitive interpretation: given a linear rule with condition
featuring in the DPO- and SqPO-type jump-closure properties has a very intuitive interpretation: given a linear rule with condition  , the linear operator
, the linear operator  is an observable that evaluates on a basis vector
is an observable that evaluates on a basis vector  as
as  = (# of ways to apply R to X)
= (# of ways to apply R to X) .
.
As for the concrete computational techniques offered by the stochastic mechanics formalism, one of the key advantages of this rule-algebraic framework is the possibility to reason about expectation values (and higher moments) of pattern-count observables in a principled and universal manner. The precise formulation is given by the following generalization of results from [7] to the setting of DPO- and SqPO-type rewriting for rules with conditions:
Theorem 5
Given a CTMC  with time-dependent state
with time-dependent state  (for \(t\ge 0\)), a set of observables
(for \(t\ge 0\)), a set of observables  and n formal variables \(\lambda _1,\dotsc ,\lambda _n\), define the exponential moment-generating function (EMGF) \(M(t;\underline{\lambda })\) as
and n formal variables \(\lambda _1,\dotsc ,\lambda _n\), define the exponential moment-generating function (EMGF) \(M(t;\underline{\lambda })\) as

Then \(M(t;\underline{\lambda })\) satisfies the following formal evolution equation (for \(t\ge 0\)):

Proof
In full analogy to the case of rules without conditions [7], the proof follows from the BCH formula \(e^{\lambda A}Be^{-\lambda A}=e^{ ad_{\lambda A}}(B)\) (for  ). Here, \(ad_A^{\circ 0}(B):=B\), \(ad_A(B):=AB-BA\) (also referred to as the commutator [A, B] of A and B), and \(ad_A^{\circ (q+1)}(B):=ad_A(ad_A^{\circ q}(B))\) for \(q\ge 1\). Finally, the \(q=0\) term in the above expression evaluates identically to 0 due to
). Here, \(ad_A^{\circ 0}(B):=B\), \(ad_A(B):=AB-BA\) (also referred to as the commutator [A, B] of A and B), and \(ad_A^{\circ (q+1)}(B):=ad_A(ad_A^{\circ q}(B))\) for \(q\ge 1\). Finally, the \(q=0\) term in the above expression evaluates identically to 0 due to  .
.
Combining this theorem with the notion of  -type jump-closure, one can in favorable cases express the EMGF evolution equation as a PDE on formal power series in \(\lambda _1,\dotsc ,\lambda _n\) and with t-dependent real-valued coefficients. Referring the interested readers to [7] for further details on this technique, let us provide here a simple non-trivial example of such a calculation.
-type jump-closure, one can in favorable cases express the EMGF evolution equation as a PDE on formal power series in \(\lambda _1,\dotsc ,\lambda _n\) and with t-dependent real-valued coefficients. Referring the interested readers to [7] for further details on this technique, let us provide here a simple non-trivial example of such a calculation.
Example 2
Let us consider a stochastic rewriting system over the category  of finite undirected multigraphs, with objects further constrained by the structure constraint
of finite undirected multigraphs, with objects further constrained by the structure constraint  that prohibits multiedges. Let us consider for type
that prohibits multiedges. Let us consider for type  the four rules with conditions \(R_{E_{\pm }}\) (edge-creation/-deletion) and \(R_{V_{\pm }}\) (vertex creation/deletion), defined as
the four rules with conditions \(R_{E_{\pm }}\) (edge-creation/-deletion) and \(R_{V_{\pm }}\) (vertex creation/deletion), defined as

Here, the prefactors \(\tfrac{1}{2}\) for \(R_{E_{\pm }}\) are chosen purely for convenience. Note that \(R_{E_{+}}\) is the only rule requiring a non-trivial application condition, since linking two vertices with an edge might create a multiedge (precisely when the two vertices were already linked). Introducing base rates  and letting
and letting  , we may assemble the infinitesimal generator
, we may assemble the infinitesimal generator  of a CTMC as
of a CTMC as

One might now ask whether there is any interesting dynamical structure e.g. in the evolution of the moments of the observables that count the number of times each of the transitions of this system is applicable,

The algebraic data necessary in order to formulate EMGF evolution equations are all commutators of the observables with the contributions  to the “off-diagonal part”
to the “off-diagonal part”  of the infinitesimal generator
of the infinitesimal generator  . We will present here for brevity just those commutators necessary in order to compute the evolution equations for the averages of the three observables:
. We will present here for brevity just those commutators necessary in order to compute the evolution equations for the averages of the three observables:
As typical in these types of commutator computations, we find a number of contributions (here \(\hat{A}\), \(\hat{B}\) and \(\hat{C}\)) that were not either observables or based upon rules of the SRS:

Picking for simplicity as an initial state  just the empty graph, and invoking the SqPO-type jump-closure property (cf. Theorem 4) repeatedly in order to evaluate
just the empty graph, and invoking the SqPO-type jump-closure property (cf. Theorem 4) repeatedly in order to evaluate  , the moment EGF evolution equation (23) specializes to the following “Ehrenfest-like” [7] ODE system:
, the moment EGF evolution equation (23) specializes to the following “Ehrenfest-like” [7] ODE system:
This ODE system may be solved exactly (see [9, Appendix C]). We depict in Fig. 1 two exemplary evolutions of the three average pattern counts for different choices of parameters. Since due to SqPO-semantics the vertex deletion and creation transitions are entirely independent of the edge creation and deletion transitions, the vertex counts stabilize on a Poisson distribution of parameter \(\nu _{+}/\nu _{-}\) (where we only present the average vertex count value here). As for the non-linked vertex pair and edge patter counts, the precise average values are sensitive to the parameter choices (i.e. whether or not vertices tend to be linked by an edge or not may be freely tuned in this model via adjusting the parameters).
While the example presented was chosen mainly to illustrate the computational techniques, it highlights the typical feature of the emergence of contributions in the relevant (nested) commutator calculations that may not have been included in the non-diagonal part \(\hat{H}\) of the infinitesimal generator of the CTMC. We refer the interested readers to [7] for an extended discussion of this phenomenon, and for computation strategies for higher-order moment evolution equations.
5 Application Scenario 1: Biochemistry with Kappa
The Kappa platform [18, 19] for rule-based modeling of biochemical reaction systems is based upon the notion of so-called site-graphs that abstract proteins and other complex macro-molecules into agents (with sites representing interaction capacities of the molecules). This open source platform offers a variety of high-performance simulation algorithms (for CTMCs based upon Kappa rewriting rules) as well as several variants of static analysis tools to analyze and verify biochemical models [12]. In view of the present paper, it is interesting to note that since the start of the Kappa development, the simulation-based algorithms have been augmented by differential semantics modules aimed at deriving ODE systems for the evolution of pattern-count observable average values [14, 15, 17, 29]. In this section, we will experiment with a (re-)encoding of Kappa in terms of typed undirected graphs with certain structural constraints that permits to express such moment statistics ODEs via our general rule-algebraic stochastic mechanics formalism. We will then provide an illustrative exemplary computation of ODEs in order to point out certain intrinsic intricacies (notably non-closure properties) typical of such calculations. One of the key theoretical features of Kappa is its foundation upon the notion of rigidity [16]. In practice, the construction involves an ambient category  (which possesses suitable adhesivity properties), a pattern category
(which possesses suitable adhesivity properties), a pattern category  (obtained from
(obtained from  via certain negative constraints) and finally a state category
via certain negative constraints) and finally a state category  (obtained from
(obtained from  via additional positive constraints). We will now present one possible realization of Kappa based upon the
via additional positive constraints). We will now present one possible realization of Kappa based upon the  -adhesive category of typed undirected multigraphs:
-adhesive category of typed undirected multigraphs:
Definition 8
For a Kappa model K, let  be the category of finite undirected multigraphs typed over \(T_K\), where \(T_K\) distinguishes agent vertex types, site vertex types and three forms of edge types: agent-site, site-site and loops on sites. For each agent type vertex \(X\in \{A,B,\ldots \}\), the type graph contains the site type vertices \(x_1:X,\dotsc ,x_{n_X}:X\) (incident to the X-type vertex via an edge, and where \(n_X<\infty \)). \(T_K\) also contains link type edges between sites that encode which sites can be linked, and loops on site type vertices that represent dynamic attributes, such as the phosphorylation state of a site. Indicating the three different edge types by wavy lines (agent-site), solid lines (site-site) and dotted lines (property loops), the agent vertices with filled circles
be the category of finite undirected multigraphs typed over \(T_K\), where \(T_K\) distinguishes agent vertex types, site vertex types and three forms of edge types: agent-site, site-site and loops on sites. For each agent type vertex \(X\in \{A,B,\ldots \}\), the type graph contains the site type vertices \(x_1:X,\dotsc ,x_{n_X}:X\) (incident to the X-type vertex via an edge, and where \(n_X<\infty \)). \(T_K\) also contains link type edges between sites that encode which sites can be linked, and loops on site type vertices that represent dynamic attributes, such as the phosphorylation state of a site. Indicating the three different edge types by wavy lines (agent-site), solid lines (site-site) and dotted lines (property loops), the agent vertices with filled circles  and the site vertices by open circles
and the site vertices by open circles  , and using the placeholder \(\bullet \) for a vertex and a dashed line for an edge of any type, we may introduce the negative constraints defining the pattern category
, and using the placeholder \(\bullet \) for a vertex and a dashed line for an edge of any type, we may introduce the negative constraints defining the pattern category  as
as  , with the set
, with the set  of “forbidden subgraphs” defined as
of “forbidden subgraphs” defined as

Finally, the state category  is obtained from
is obtained from  via imposing a positive constraint
via imposing a positive constraint  that ensures that each agent X is linked to exactly one of each of its site vertices x : X, and if a site x : X can carry a property or alternative variants thereof, it also carries a loop that signifies one of these properties (see the example below for further details). Moreover, a given site x : X must be linked to an agent X (i.e. cannot occur in isolation).
that ensures that each agent X is linked to exactly one of each of its site vertices x : X, and if a site x : X can carry a property or alternative variants thereof, it also carries a loop that signifies one of these properties (see the example below for further details). Moreover, a given site x : X must be linked to an agent X (i.e. cannot occur in isolation).
Example 3
Consider a simple Kappa model with a type graph as below left that introduces two agent types \(\mathsf {K}\) (for “kinase”) and \(\mathsf {P}\) (for “protein”), where \(\mathsf {K}\) has a site \(k:\mathsf {K}\), and where \(\mathsf {P}\) has sites \(p_t,p_l,p_b:\mathsf {P}\). Moreover, the sites \(p_t\) and \(p_b\) can carry properties \(\mathsf {u}\) (“unphosphorylated”) and \(\mathsf {p}\) (“phosphorylated”), depicted as dotted loops in the type graph. Sites \(k:\mathsf {K}\) and \(p_l:\mathsf {P}\) can bind (as indicated by the solid line in the type graph).

As a prototypical example of a Kappa stochastic rewriting system, consider a system based upon the rewriting rules \(k_{\pm }\), \(l_{\pm }\), \(t_{\pm }\) and \(b_{\pm }\). Here, for the rule \(l_{+}\), we have indicated that it must be equipped with an application condition that ensures that the site of the \(\mathsf {K}\)-type agent and the left site of the \(\mathsf {P}\)-type agent must be free before binding. As common practice also in the standard Kappa theory, we otherwise leave in the graphical depictions those application conditions necessary to ensure consistent matches implicit as much as possible. Consider then for a concrete computational example the time-evolution of the average count of the pattern described in the identity rule \(r_{obs_P}\). As typical in Kappa rule specifications \(r_{obs_P}\) as well as several of the other rules depicted only explicitly involve patterns, but not necessarily states, since e.g. in \(r_{obs_P}\) the left site of the \(\mathsf {P}\)-type agent is not mentioned. In complete analogy to the computation presented in Example 2, let us first compute the commutators of the observable \(O_{\mathsf {K}}=\rho (\delta (r_{obs_K};\mathsf {c}_{obs_K}))\) with the operators \(\hat{X}:=\rho (\delta (r_X;\mathsf {c}_X))\):
However, letting \(O^{(\mathsf {x},\mathsf {y})}_{P}\), \(O^{(\mathsf {x},\mathsf {y})}_{link}\) and \(O^{(\mathsf {x},\mathsf {y})}_{free}\) denote the observables for the patterns

one may easily demonstrate that even a comparatively simple observable such as \(O^{(\mathsf {p},\mathsf {p})}_{P}\) already leads to an infinite cascade of contributions to the ODEs for the averages of pattern counts. As typical in these sorts of computations, the discovery of a new pattern observable via applying SqPO-type jump-closure (Theorem 4) to the commutator contributions to \(\tfrac{d}{dt}\langle O^{(\mathsf {p},\mathsf {p})}_{P}\rangle (t)\) leads to the discovery of new pattern observables yet again, such as in

In particular the last observable \(O^{(\mathsf {u},\mathsf {p})}_{free}\) is found to lead to an infinite tower of other observables (i.e. “ODE non-closure”), starting from

This exemplary and preliminary analysis reveals that while the rule-algebraic CTMC implementation is in principle applicable to the formulation and analysis Kappa systems, further algorithmic and theoretical developments will be necessary (including possibly ideas of fragments and refinements as in [14, 15, 29]) in order to obtain a computationally useful alternative rewriting-theoretic implementation of Kappa.
6 Application Scenario 2: Organic Chemistry with MØD
The MØD platform [1] for organo-chemical reaction systems is a prominent example of a DPO-type rewriting theory of high relevance to the life sciences. From a theoretical perspective, MØD has been designed [3] as a rewriting system over so-called chemical graphs, a certain typed and undirected variant of the category \(\mathbf {PLG}\) of partially labelled directed graphs. While the latter category had been introduced in [28] as a key example of an  -
- -adhesive category, with the motivation of permitting label-changes in rewriting rules, it was also demonstrated in loc cit. that \(\mathbf {PLG}\) is not
-adhesive category, with the motivation of permitting label-changes in rewriting rules, it was also demonstrated in loc cit. that \(\mathbf {PLG}\) is not  -adhesive. Since moreover no concrete construction of a tentative variant \(\mathbf {uPLG}\) of \(\mathbf {PLG}\) for undirected graphs, let alone results on the possible adhesivity properties of such a category are known in the literature, we propose here an alternative and equivalent encoding of chemical graphs. We mirror the constructions of [1, 3] in that chemical graphs will be a certain typed variant of undirected graphs, with vertex types representing atom types, edge types ranging over the types \(\{\mathtt {-},\mathtt {=},\mathtt {\#},\mathtt {:}\}\) representing single, double, triple and aromatic bonds, respectively, and with the graphs being required to not contain multiedges. Inspired by the Kappa constructions in the previous section, we opt to represent properties (such as e.g. charges on atoms) as typed loop edges on vertices representing atoms, whence the change of a property (which was the main motivation in [3] for utilizing a variant of \(\mathbf {PLG}\)) may be encoded in a rewriting rule simply via deletion/creation of property-encoding loops. Unfortunately, while the heuristics presented thus far would suggest that chemical graphs in the alternative categorical setting should be just simple typed undirected graphs, the full specification of chemical graphs would also have to include additional, empirical information from the chemistry literature. Concretely, atoms such as e.g. carbon only support a limited variety of bond types and configurations of incident bonds (referred to as valencies), with additional complications such as poly-valencies possible for some types of atoms as illustrated by the following example.
-adhesive. Since moreover no concrete construction of a tentative variant \(\mathbf {uPLG}\) of \(\mathbf {PLG}\) for undirected graphs, let alone results on the possible adhesivity properties of such a category are known in the literature, we propose here an alternative and equivalent encoding of chemical graphs. We mirror the constructions of [1, 3] in that chemical graphs will be a certain typed variant of undirected graphs, with vertex types representing atom types, edge types ranging over the types \(\{\mathtt {-},\mathtt {=},\mathtt {\#},\mathtt {:}\}\) representing single, double, triple and aromatic bonds, respectively, and with the graphs being required to not contain multiedges. Inspired by the Kappa constructions in the previous section, we opt to represent properties (such as e.g. charges on atoms) as typed loop edges on vertices representing atoms, whence the change of a property (which was the main motivation in [3] for utilizing a variant of \(\mathbf {PLG}\)) may be encoded in a rewriting rule simply via deletion/creation of property-encoding loops. Unfortunately, while the heuristics presented thus far would suggest that chemical graphs in the alternative categorical setting should be just simple typed undirected graphs, the full specification of chemical graphs would also have to include additional, empirical information from the chemistry literature. Concretely, atoms such as e.g. carbon only support a limited variety of bond types and configurations of incident bonds (referred to as valencies), with additional complications such as poly-valencies possible for some types of atoms as illustrated by the following example.
Example 4
The Meisenheimer-2-3-rearrangement reaction [32] (cf. also [2]) constitutes an exampleFootnote 4 of a reaction where polyvalence is encountered:

Upon matching this rule into a chemically valid mixture, the N atom on the input of the rule will have valence 5, while on the output it will have valence 3. This type of information is evidently in no way contained in the chemical graphs alone, and must therefore be encoded in terms of suitable additional typing on the graphs and application conditions.
While thus at present no encoding of chemical graphs into a categorical framework with suitable adhesivity properties is available, we posit that it would be highly fruitful in light of the stochastic mechanics framework presented in this paper to develop such an encoding (joint work in progress with J.L. Andersen, W. Fontana and D. Merkle).
7 Conclusion and Outlook
Rewriting theories of DPO- and SqPO-type for rules with conditions over  -adhesive categories are poised to provide a rich theoretical and algorithmic framework for modeling stochastic dynamical systems in the life sciences. The main result of the present paper consists in the introduction of a rule algebra framework that extends the pre-existing constructions [4, 6, 10] precisely via incorporating the notion of conditions. The sophisticated Kappa [12] and MØD [1] bio-/organo-chemistry platforms and related developments have posed one of the main motivations for this work. For both of these platforms, we present a first analysis and stepping stones towards bridging category-theoretical rewriting theories and stochastic mechanics computations. Especially for the organo-chemistry setting, our work motivates the development of a full encoding of (at least a reasonable fragment of) organic chemistry in terms of chemical graphs and rewriting rules thereof, which to date is still unavailable. This encoding will be beneficial also in the development of tracelet-based techniques [5], and is current work in progress.
-adhesive categories are poised to provide a rich theoretical and algorithmic framework for modeling stochastic dynamical systems in the life sciences. The main result of the present paper consists in the introduction of a rule algebra framework that extends the pre-existing constructions [4, 6, 10] precisely via incorporating the notion of conditions. The sophisticated Kappa [12] and MØD [1] bio-/organo-chemistry platforms and related developments have posed one of the main motivations for this work. For both of these platforms, we present a first analysis and stepping stones towards bridging category-theoretical rewriting theories and stochastic mechanics computations. Especially for the organo-chemistry setting, our work motivates the development of a full encoding of (at least a reasonable fragment of) organic chemistry in terms of chemical graphs and rewriting rules thereof, which to date is still unavailable. This encoding will be beneficial also in the development of tracelet-based techniques [5], and is current work in progress.
An intriguing perspective for future developments in categorical rewriting theory consists in developing a robust and versatile methodology for the analysis of ODE systems of pattern-counting observables in stochastic rewriting systems. While the results of this paper permit to formulate dynamical evolution equations for arbitrary higher moments of such observables, in general cases (as illustrated in Sect. 5) the non-closure of the resulting ODE systems remains a fundamental technical challenge. In the Kappa literature, sophisticated conceptual and algorithmic approaches to tackle this problem have been developed such as refinements [14, 16], model reduction techniques [15] and stochastic fragments [25] (see also [7] for an extended discussion). We envision that a detailed understanding of these approaches from within the setting of categorical rewriting and of rule algebra theory could provide a very fruitful enrichment of the methodology of rewriting theory.
Notes
- 1.
We review in Appendix A.1 of [9] (an extended version of the present paper) some of the salient background material on
 -adhesive categories and the relevant notational conventions.
-adhesive categories and the relevant notational conventions. - 2.
We assume here that the isomorphism classes of objects of
 form a set (i.e. not a proper class).
form a set (i.e. not a proper class). - 3.
Since in applications we will always fix the type of rewriting to either DPO or SqPO, we will use the same symbol for the jump-closure operator in both cases.
- 4.
This example reaction was typeset directly via MØD (cf. [9, Appendix D]).
References
Andersen, J.L., Flamm, C., Merkle, D., Stadler, P.F.: A software package for chemically inspired graph transformation. In: Echahed, R., Minas, M. (eds.) ICGT 2016. LNCS, vol. 9761, pp. 73–88. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-40530-8_5
Andersen, J.L., Flamm, C., Merkle, D., Stadler, P.F.: An intermediate level of abstraction for computational systems chemistry. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 375(2109), 20160354 (2017). https://doi.org/10.1098/rsta.2016.0354
Andersen, J.L., Flamm, C., Merkle, D., Stadler, P.F.: Rule composition in graph transformation models of chemical reactions. Match 80(3), 661–704 (2018)
Behr, N.: Sesqui-pushout rewriting: concurrency, associativity and rule algebra framework. In: Echahed, R., Plump, D. (eds.) Proceedings of the Tenth International Workshop on Graph Computation Models (GCM 2019) in Eindhoven, The Netherlands. Electronic Proceedings in Theoretical Computer Science, vol. 309, pp. 23–52. Open Publishing Association (2019). https://doi.org/10.4204/eptcs.309.2
Behr, N.: Tracelets and tracelet analysis of compositional rewriting systems (accepted for ACT2019 in Oxford). arXiv:1904.12829 (2019)
Behr, N., Danos, V., Garnier, I.: Stochastic mechanics of graph rewriting. In: Proceedings of the 31st Annual ACM/IEEE Symposium on Logic in Computer Science - LICS 2016. ACM Press (2016). https://doi.org/10.1145/2933575.2934537
Behr, N., Danos, V., Garnier, I.: Combinatorial conversion and moment bisimulation for stochastic rewriting systems. arXiv:1904.07313 (2019)
Behr, N., Krivine, J.: Compositionality of rewriting rules with conditions. arXiv:1904.09322 (2019)
Behr, N., Krivine, J.: Rewriting theory for the life sciences: a unifying theory of CTMC semantics (extended version). arXiv:2003.09395 (2020)
Behr, N., Sobocinski, P.: Rule algebras for adhesive categories. In: Ghica, D., Jung, A. (eds.) 27th EACSL Annual Conference on Computer Science Logic (CSL 2018). Leibniz International Proceedings in Informatics (LIPIcs), vol. 119, pp. 11:1–11:21. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, Dagstuhl, Germany (2018). https://doi.org/10.4230/LIPIcs.CSL.2018.11
Behr, N., Sobocinski, P.: Rule algebras for adhesive categories (invited extended journal version). arXiv:1807.00785 (2019)
Boutillier, P., et al.: The kappa platform for rule-based modeling. Bioinformatics 34(13), i583–i592 (2018). https://doi.org/10.1093/bioinformatics/bty272
Corradini, A., Heindel, T., Hermann, F., König, B.: Sesqui-pushout rewriting. In: Corradini, A., Ehrig, H., Montanari, U., Ribeiro, L., Rozenberg, G. (eds.) Graph Transformations. Lecture Notes in Computer Science, vol. 4178, pp. 30–45. Springer, Berlin and Heidelberg (2006)
Danos, V., Feret, J., Fontana, W., Harmer, R., Krivine, J.: Rule-based modelling, symmetries, refinements. In: Fisher, J. (ed.) FMSB 2008. LNCS, vol. 5054, pp. 103–122. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-68413-8_8
Danos, V., Feret, J., Fontana, W., Harmer, R., Krivine, J.: Abstracting the differential semantics of rule-based models: exact and automated model reduction. In: 2010 25th Annual IEEE Symposium on Logic in Computer Science. IEEE (2010). https://doi.org/10.1109/lics.2010.44
Danos, V., Heckel, R., Sobocinski, P.: Transformation and refinement of rigid structures. In: Giese, H., König, B. (eds.) ICGT 2014. LNCS, vol. 8571, pp. 146–160. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-09108-2_10
Danos, V., Heindel, T., Honorato-Zimmer, R., Stucki, S.: Moment semantics for reversible rule-based systems. In: Krivine, J., Stefani, J.-B. (eds.) RC 2015. LNCS, vol. 9138, pp. 3–26. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-20860-2_1
Danos, V., Laneve, C.: Formal molecular biology. Theoret. Comput. Sci. 325(1), 69–110 (2004). https://doi.org/10.1016/j.tcs.2004.03.065
Danos, V., Schachter, V. (eds.): CMSB 2004. LNCS, vol. 3082. Springer, Heidelberg (2005). https://doi.org/10.1007/b107287
Delbrück, M.: Statistical fluctuations in autocatalytic reactions. J. Chem. Phys. 8(1), 120–124 (1940). https://doi.org/10.1063/1.1750549
Ehrig, H., Ehrig, K., Prange, U., Taentzer, G.: Fundamentals of Algebraic Graph Transformation. MTCSAES. Springer, Heidelberg (2006). https://doi.org/10.1007/3-540-31188-2
Ehrig, H., Golas, U., Habel, A., Lambers, L., Orejas, F.: \(\cal{M}\)-adhesive transformation systems with nested application conditions. Part 2: embedding, critical pairs and local confluence. Fundamenta Informaticae 118(1–2), 35–63 (2012). https://doi.org/10.3233/FI-2012-705
Ehrig, H., Golas, U., Habel, A., Lambers, L., Orejas, F.: \(\cal{M}\)-adhesive transformation systems with nested application conditions. Part 1: parallelism, concurrency and amalgamation. Math. Struct. Comput. Sci. 24(04) (2014). https://doi.org/10.1017/s0960129512000357
Ehrig, H., Habel, A., Padberg, J., Prange, U.: Adhesive high-level replacement categories and systems. In: Ehrig, H., Engels, G., Parisi-Presicce, F., Rozenberg, G. (eds.) ICGT 2004. LNCS, vol. 3256, pp. 144–160. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30203-2_12
Feret, J., Koeppl, H., Petrov, T.: Stochastic fragments: a framework for the exact reduction of the stochastic semantics of rule-based models. Int. J. Softw. Inf. (IJSI) 7(4), 527–604 (2014)
Gabriel, K., Braatz, B., Ehrig, H., Golas, U.: Finitary \(\cal{M}\)-adhesive categories. Math. Struct. Comput. Sci. 24(04) (2014). https://doi.org/10.1017/S0960129512000321
Habel, A., Pennemann, K.H.: Correctness of high-level transformation systems relative to nested conditions. Math. Struct. Comput. Sci. 19(02), 245 (2009). https://doi.org/10.1017/s0960129508007202
Habel, A., Plump, D.: \(\cal{M}, \cal{N}\)-adhesive transformation systems. In: Ehrig, H., Engels, G., Kreowski, H.-J., Rozenberg, G. (eds.) ICGT 2012. LNCS, vol. 7562, pp. 218–233. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33654-6_15
Harmer, R., Danos, V., Feret, J., Krivine, J., Fontana, W.: Intrinsic information carriers in combinatorial dynamical systems. Chaos: Interdisc. J. Nonlinear Sci. 20(3), 037108 (2010). https://doi.org/10.1063/1.3491100
Lack, S., Sobociński, P.: Adhesive and quasiadhesive categories. RAIRO - Theoret. Inf. Appl. 39(3), 511–545 (2005). https://doi.org/10.1051/ita:2005028
Padberg, J.: Towards M-adhesive categories based on coalgebras and comma categories. arXiv:1702.04650 (2017)
Smith, M.B., March, J.: March’s Advanced Organic Chemistry. Wiley, Hoboken (2006). https://doi.org/10.1002/0470084960
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Behr, N., Krivine, J. (2020). Rewriting Theory for the Life Sciences: A Unifying Theory of CTMC Semantics. In: Gadducci, F., Kehrer, T. (eds) Graph Transformation. ICGT 2020. Lecture Notes in Computer Science(), vol 12150. Springer, Cham. https://doi.org/10.1007/978-3-030-51372-6_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-51372-6_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-51371-9
Online ISBN: 978-3-030-51372-6
eBook Packages: Computer ScienceComputer Science (R0)


 in order to obtain the morphisms
in order to obtain the morphisms 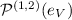 and
and  ; since the functor
; since the functor 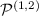 preserves monomorphisms [
preserves monomorphisms [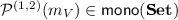 .
.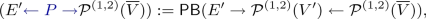
 implies
implies 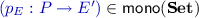 .
.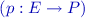 . Let
. Let  be the epi-mono-factorization of this morphism.
be the epi-mono-factorization of this morphism. , and consequently
, and consequently  yields an alternative epi-mono-factorization of
yields an alternative epi-mono-factorization of  .
.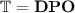 : given
: given 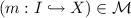 , m is a DPO-admissible match of R into X, denoted
, m is a DPO-admissible match of R into X, denoted  , if
, if  : given
: given  , m is a SqPO-admissible match of R into X, denoted
, m is a SqPO-admissible match of R into X, denoted  , if
, if  : given just the “plain rule” r and
: given just the “plain rule” r and  ,
, 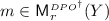 , if (B) is constructable as a pushout complement, in which case (B) is constructed as a pushout.
, if (B) is constructable as a pushout complement, in which case (B) is constructed as a pushout.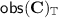 of
of  -type observables, i.e. the diagonal linear operators that arise as (linear combinations of)
-type observables, i.e. the diagonal linear operators that arise as (linear combinations of)  -type canonical representations of rewriting rules with conditions, have the following structure (
-type canonical representations of rewriting rules with conditions, have the following structure (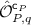 in the DPO case,
in the DPO case,  in the SqPO case):
in the SqPO case): 
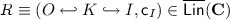 , we find that
, we find that 
 is the homomorphism defined via its action on basis elements
is the homomorphism defined via its action on basis elements  as
as 
 , we find that
, we find that 
 is the homomorphism defined via
is the homomorphism defined via 
 be the space of (sub-)probability distributions over
be the space of (sub-)probability distributions over  (i.e.
(i.e. 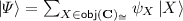 ). Let
). Let 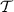 be a collection of N pairs of positive real-valued parameters
be a collection of N pairs of positive real-valued parameters 
 , the
, the  -type stochastic rewriting system based upon the transitions
-type stochastic rewriting system based upon the transitions  gives rise to the CTMC
gives rise to the CTMC  with time-dependent state
with time-dependent state 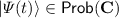 (for
(for 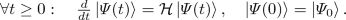
 of the CTMC is given by
of the CTMC is given by 

 -adhesive categories and the relevant notational conventions.
-adhesive categories and the relevant notational conventions. form a set (i.e. not a proper class).
form a set (i.e. not a proper class).