A Family of Tree-Based Generators for Bubbles in Directed Graphs

Abstract

Bubbles are pairs of internally vertex-disjoint (s, t)-paths in a directed graph. In de Bruijn graphs built from reads of RNA and DNA data, bubbles represent interesting biological events, such as alternative splicing (AS) and allelic differences (SNPs and indels). However, the set of all bubbles in a de Bruijn graph built from real data is usually too large to be efficiently enumerated and analysed in practice. In particular, despite significant research done in this area, listing bubbles still remains the main bottleneck for tools that detect AS events in a reference-free context. Recently, in [1] the concept of a bubble generator was introduced as a way for obtaining a compact representation of the bubble space of a graph. Although this generator was quite effective in finding AS events, preliminary experiments showed that it is about 5 times slower than state-of-art methods. In this paper we propose a new family of bubble generators which improve substantially on the previous generator: generators in this new family are about two orders of magnitude faster and are still able to achieve similar precision in identifying AS events. To highlight the practical value of our new generators, we also report some experimental results on a real dataset.

V. Acuña is supported by Fondecyt 1140631, PIA Fellowship AFB170001 and Center for Genome Regulation FONDAP 15090007. G. F. Italiano is partially supported by MIUR, the Italian Ministry for Education, University and Research, under PRIN Project AHeAD (Efficient Algorithms for HArnessing Networked Data). B. Sinaimeri and M.-F. Sagot are partially funded by the French ANR project Aster (2016–2020). Part of this work was done while G. F. Italiano was visiting Université de Lyon and B. Sinaimeri and M.-F. Sagot were visiting LUISS University in Rome.

1 Introduction

The advent of sequencing technologies has revolutionised the study of DNA and RNA data. The information contained in the reads coming from genome or transcriptome sequencing is usually represented by a de Bruijn graph (see e.g., [18, 20]). In this graph bubbles, i.e., pairs of internally vertex-disjoint (s, t)-paths, play an important role in the study of genetic variations, which include Alternative Splicing (AS) in RNA-data [16, 20,21,22] and SNPs (Single Nucleotide Polymorphism), and indels in DNA-data [10, 24, 25]. Since bubbles can be associated to such biologically relevant events, in recent years there have been several theoretical studies on bubbles (see e.g., [3, 4, 19, 21, 23]), and in particular there has been a growing interest in algorithms for listing all bubbles in a directed graph. However, in real data graphs the number of bubbles can be exponential in the size of the graph. As a consequence, in practice current algorithms are able to list only a subset of the bubble space, thus losing the information related to the bubbles that are left unexplored. Furthermore, not every bubble corresponds to a biological event. Indeed, a significant number of these bubbles can be false positives (i.e., they are not biologically relevant events), and are produced as artifacts of the underlying construction of the de Bruijn graph. In this framework, the main question is how to find a subset of bubbles that can be efficiently computed in practice and that correspond to relevant biological events.

To tackle this question, the notion of bubble generator was first introduced in [1]. Intuitively, a bubble generator is a subset of bubbles of polynomial size, from which all the other bubbles in the graph can be obtained through a suitable application of a specific symmetric difference operator. In particular, the generator proposed in [1] contains at most $m \cdot n$ bubbles, where m and n denote respectively the number of edges and vertices in the input graph. Furthermore, the authors of [1] provided an algorithm that, given any bubble B in the graph, is able to find in $O(n^3)$ time the bubbles of the generator that can be combined to produce B through a symmetric difference operator. To test its practical value, the generator was used to find AS events in a real dataset. As reported in [1], this generator was able to achieve about the same precision in identifying AS events as the state-of-art-algorithm KisSplice [16, 20], but unfortunately building the generator was about 5 times slower than finding AS events with KisSplice. Despite its great theoretical value, this poses a serious limitation on the practical application of this generator to large-scale datasets, which are typical of biological applications.

To address this issue, in this paper we present a new family of bubble generators which improves substantially on the generator of [1]. In particular, in the same RNA dataset used in [1], generators in our family are about two orders of magnitude faster in practice than the generator in [1], and improve the precision in identifying AS events from $77.3\%$ to $90\%$. When compared to the state-of-the-art algorithm for identifying AS events, our generators are also much faster than KisSplice [16, 20], have similar precision, and find AS events that KisSplice cannot find. In the experiments, we observed that our new generators also contain many bubbles that correspond to a particular type of AS event, namely intron retention (IR), which is usually considered a hard-to-find event. We believe that our experimental findings make the new generators the method of choice for finding AS events in a reference-free context, especially in large-scale data sets.

From the theoretical viewpoint, our new generators are of minimum size (i.e. size $m-n+1$) for flow graphs, i.e., graphs in which there exists a vertex that can reach all other vertices. In case of general graphs, their size is bounded by $|S| (m-n+1)$, where S is the source set, i.e., a minimum set of vertices that can reach every other vertex in the graph. Although in the worst case this is asymptotically equivalent to the size of the generator in [1], in our experiments the new generators had a much smaller size in practice. Furthermore, the new generators have a much faster decomposition algorithm: given a bubble B it is possible to compute in O(n) time the set of bubbles in the new generators from which B can be composed, while the bubble decomposition algorithm of [1] required as much as $O(n^3)$ time for this task.

To design our new family of generators, we find a way to exploit some connections with cycle bases. We observe that the techniques developed for cycle bases (both in undirected and in directed graphs) cannot be applied directly to bubble generators. Indeed, as reported in [1], the main difference with cycle bases is that in our problem, in order to have biological relevance the following two properties are needed:

($\mathcal{P}_1$):

A bubble generator for a directed graph G must contain only bubbles;

$(\mathcal{P}_2)$:

Each bubble of G should be decomposed into bubbles of the generator, so that only bubbles are generated at each step of this decomposition.

We remark that ensuring properties ($\mathcal{P}_1$) and ($\mathcal{P}_2$) for cycles (in place of bubbles) is already non-trivial. Indeed, Gleiss et al. [8] have shown that it is possible to find a basis composed of directed cycles if the graph is strongly connected. However, this is not known in the case of general directed graphs. On the other side, Property ($\mathcal{P}_2$) is somewhat reminiscent of the notion of cyclically robust cycle bases which allows one to generate all cycles of a given graph by iteratively adding cycles of the basis [11, 15]. Unfortunately, not all graphs have a cyclically robust cycle basis [9] and understanding for which graph classes such a basis can be found is still an important open problem (see e.g., [15]). Despite all these difficulties, we prove that a bubble generator based on spanning trees of the input graph satisfies properties ($\mathcal{P}_1$) and ($\mathcal{P}_2$). Since our bubble generators are identified from a chosen spanning tree, we also investigate the influence of the choice of spanning tree on the resulting generator.

The remainder of this paper is organised as follows. Section 2 presents some definitions that will be used throughout the paper. Section 3 introduces our family of bubble generators for flow graphs and for arbitrary graphs and we prove that it satisfies properties ($\mathcal{P}_1$) and ($\mathcal{P}_2$). Section 4 presents our experimental results: we first provide an empirical analysis of the characteristics of our new bubble generators based on the choice of the spanning tree (Subsect. 4.1) and then we show an application of our new bubble generators in processing and analysing RNA data (Subsect. 4.2). Finally, we conclude with some open problems in Sect. 5.

2 Preliminaries

Throughout the paper, we assume that the reader is familiar with the standard graph terminology, as contained for instance in [6]. A graph is a pair $G = (V,E)$, where V is the set of vertices, and $E\subseteq V\times V$ is the set of edges. For convenience, we may also denote the set of vertices V of G by V(G) and its set of edges E by E(G). We further set $n=|V(G)|$ and $m=|E(G)|$. A graph may be directed or undirected, depending on whether its edges are directed or undirected. In this paper, we deal with graphs that are directed, unweighted, finite and without parallel edges. An edge $e=(u,v)$ is said to be incident to the vertices u and v, and u and v are said to be the endpoints of $e=(u,v)$. For a directed graph, edge $e=(u,v)$ is said to be leaving vertex u and entering vertex v. Alternatively, $e=(u,v)$ is an outgoing edge for u and an incoming edge for v. The in-degree of a vertex v is given by the number of edges entering v, while the out-degree of v is the number of edges leaving v. The degree of v is the sum of its in-degree and out-degree.

We say that a graph $G'=(V',E')$ is a subgraph of a graph $G=(V,E)$ if $V'\subseteq V$ and $E'\subseteq E$. Given a subset of vertices $V'\subseteq V$, the subgraph of G induced by $V'$, denoted by $G_{V'}$, has $V'$ as vertex set and contains all edges of G that have both endpoints in $V'$. Given a subset of edges $E'\subseteq E$, the subgraph of G induced by $E'$, denoted by $G_{E'}$, has $E'$ as edge set and contains all vertices of G that are endpoints of edges in $E'$. Given two subgraphs G and H, their union $G\,\cup \,H$ is the graph F for which $V(F)=V(G)\,\cup \,V(H)$ and $E(F)=E(G)\,\cup \,E(H)$. Their intersection $G\cap H$ is the graph F for which $V(F)=V(G) \cap V(H)$ and $E(F)=E(G)\cap E(H)$.

Let s, t be any two vertices in G. A (directed) path from s to t in G, denoted as , is a sequence of vertices and edges $s=v_1$, $e_1$, $v_2$, $e_2$, $\ldots$, $v_{k-1}$, $e_{k-1}$, $v_k=t$, such that $e_i=(v_i,v_{i+1})$ for $i = 1, 2, \ldots , k-1$. Since there is no danger of ambiguity, in the remainder of the paper we will also denote a path simply as $s=v_1$, $v_2$, $\ldots$, $v_{k-1}$, $v_k=t$ (i.e., as a sequence of vertices). A path is simple if it does not contain repeated vertices, except possibly for the first and the last vertex. Throughout this paper, all the paths considered will be simple and referred to as paths. A path from s to t is also referred to as an (s, t)-path.

A directed graph G is a flow graph if there is one vertex s (referred to as the start vertex) which can reach all other vertices. Given a graph G, a rooted spanning tree T of G is a tree where each leaf is reachable from the root by a directed path. Notice that any flow graph has a spanning tree rooted at the start vertex through a graph visit.

Definition 1

Given a directed graph G and two (not necessarily distinct) vertices $s,t \in V(G)$, an (s, t)-bubble consists of two directed (s, t)-paths that are internally vertex disjoint. Vertex s is the source and t is the target of the bubble. If $s=t$ then exactly one of the paths of the bubble has length 0, and therefore B corresponds to a directed cycle. In this case, we say that B is a degenerate bubble.

Let G be an undirected graph. Two subgraphs $G_1, G_2$ of G can be combined by the operator $\varDelta$ that simply consists in the symmetric difference of the set of edges. More formally, $G_1\,\varDelta \,G_2= (G_1\,\cup \,G_2) \setminus (E(G_1) \cap E(G_2))$ where $E(G_i)$ is the set of edges of $G_i$. If $G_3=G_1\,\varDelta \,G_2$ we say that $G_3$ is generated by $G_1$ and $G_2$. With this operation, it can be shown that the space of all Eulerian subgraphs of G (called the cycle space of G) is a vector space [8, 12, 13, 17].

It is known that a cycle basis for a connected undirected graph G, denoted by $\mathcal {C}(G)$, has dimension $m-n+1$. If the graph G is not connected this is generalised to $m-n+c$, where c is the number of connected components (see, e.g., [8, 12, 13, 17]). For a given graph G and a spanning tree T on it, the insertion of one further edge e of the graph to this tree produces a unique cycle C(T, e). Given a spanning tree T of G, the set $\mathcal {C}(G)=\{C(T,e) | e \in E(G)\setminus E(T)\}$ is called Kirchhoff cycle basis [14].

Let $\mathcal{B}$ be a set of bubbles in G. $\mathcal{B}$ is a bubble generator if each bubble in G can be generated by a subset of bubbles in $\mathcal{B}$. A generator is minimal if it does not contain a proper subset that is also a generator; and a generator is minimum if it has the minimum cardinality. We say that B has a tree decomposition in $\mathcal{B}$, if B can be decomposed in a binary-tree-like-fashion where the leaves correspond to bubbles in $\mathcal {B}$ and the internal nodes are bubbles. Notice that a bubble generator satisfies Property $\mathcal{P}_2$ if every bubble of the graph has a tree-decomposition in $\mathcal{B}$.

3 Defining a Bubble Generator from a Spanning Tree

In this section, we define a bubble generator that satisfies properties ($\mathcal{P}_1$) and ($\mathcal{P}_2$) starting from a spanning tree of the input graph. We consider first flow graphs and then we extend our results to general graphs. Given a flow graph G with start vertex s, we find a rooted spanning tree T of G, by performing any graph visit starting from s. In the experimental results in Sect. 4 we consider different types of visits, such as Depth-First Search, Breadth-First Search and Scan-First Search [5].

Every non-tree edge $e=(u,v)$ encountered during this visit defines a bubble. The source of this bubble is the least common ancestor w of u and v, and its target is v. The two paths of this bubble are the tree path from w to v and the tree path from w to u followed by the edge (u, v). We denote by $B_{T}(G)$ the set of bubbles obtained in this way for the flow graph G.

Theorem 1

Let G be a flow graph with start vertex s, and let $B_{T}(G)$ be the set of bubbles identified by a tree T obtained through a visit starting from s. Then each bubble in G can be generated starting from the bubbles in $B_{T}(G)$ (with a symmetric difference operator), and $|B_{T}(G)| =m-n+1$.

Proof

Let T be a rooted spanning tree of G obtained by a visit starting from s and let $B_{T}(G)$ be the set of bubbles identified by the non-tree edges of T. Consider the undirected graph $G'$ obtained by ignoring the direction of edges in G. We now consider two cases, depending on whether there are parallel edges in $G'$ or not.

Assume first that there are no parallel edges in $G'$. Note that there is a one-to-one mapping between (undirected) cycles in $G'$ and bubbles in G, and that the spanning tree T found in G is trivially a spanning tree for $G'$. It is well-known (see for example [13]) that, given an undirected graph $G'$ without parallel edges, taking the cycles formed by the combination of a path in the spanning tree and a single edge outside the tree yields a cycle basis in $G'$ (with a symmetric difference operator). Consider any bubble B in G and let $B_1, \ldots , B_k$ be the bubbles in $B_{T}(G)$ identified by the non-tree edges of B. If we ignore the directions of the edges, the above property implies that $B\,\varDelta \,B_1 \varDelta \ldots \varDelta B_k$ is empty. Consider now the directed graph G notice that $B\,\varDelta \,B_1 \varDelta \ldots \varDelta B_k$ is again empty as each edge in G appears in exactly one direction. Hence, each bubble in G can be generated starting from the bubbles in $B_{T}(G)$. Since there are $m-(n-1)$ non-tree edges, $|B_{T}(G)| =m-n+1$.

If $G'$ has parallel edges, the previous argument cannot be applied directly. However, in this case a simple reduction will work. Note that in $G'$ there can be at most two parallel edges between any two vertices u and v, corresponding to the two edges (u, v) and (v, u) in the original directed graph G. To deal with this, we transform G into another directed graph $G_o$ as follows: if there are two edges (u, v) and (v, u) in G, we subdivide one of them, say (u, v), by adding a new vertex $x_{uv}$, by removing the edge (u, v) and by adding two new edges $(u,x_{uv}),(x_{uv},v)$. Note that there is a one-to-one mapping between bubbles in G and bubbles in $G_o$: for any vertex $x_{uv}$ in $G_o$, $(u,x_{uv}), (x_{uv},v)$ belong to a bubble $B_o$ in $G_o$ if and only if (u, v) belongs to a corresponding bubble B in G. Furthermore, let $G_{o}'$ be the undirected graph obtained by ignoring the direction of edges in $G_o$. Since $G_o'$ has no parallel edges, each bubble of $G_o$ can be generated starting from the bubbles in $B_{T}(G_o)$. Due to the one-to-one mapping between bubbles of G and bubbles of $G_o$, this implies that each bubble of G can be generated starting from the bubbles in $B_{T}(G_o)$. Let k be the number of new vertices $x_{uv}$ added to $G_o$: note that for each new vertex added to $G_o$, the number of edges of $G_o$ increases by one. This implies that $B_{T}(G)=B_{T}(G_o)=(m+k)-(n+k)+1=m-n+1$ and yields the theorem.   $\blacksquare$

Let G be a flow graph with start vertex s and let T be a spanning tree from s. Since each non-tree edge (u, v) is contained exactly in one bubble of $B_{T}(G)$, Theorem 1 implies that, in order to decompose a generic bubble B into the bubbles of $B_{T}(G)$, one needs to consider all and only the bubbles of $B_{T}(G)$ identified by the non-tree edges of B (with respect to T). Moreover, the set $B_{T}(G)$ can be found efficiently by simply performing a visit from the start vertex s and by returning the non-tree edges.

It is worth mentioning that Theorem 1 can be extended to general graphs as follows. Let G be an arbitrary directed graph G. Let S be a minimum set of vertices from which every vertex of G can be reached. We denoted by S a source set of G. Note that in the worst case, $|S|=O(n)$. For each $s \in S$, let $B_{T}(G,s)$ be the set of bubbles identified by a visit starting from the vertex s of G. Consider the set $B(G,S)=\cup _{s\in S} B_{T}(G,s)$. Observe that the source of any bubble B in G can be reached by at least one vertex s in S. Thus B belongs to a subgraph of G, which is a flow graph rooted in s, and hence can be expressed as a composition of bubbles in $B_{T}(G,s)$. This can be summarised by the following theorem.

Theorem 2

Let G be a directed graph and let S be its source set. Then there is a set of bubbles $\mathcal{B}$, such that each bubble in G can be generated starting from the bubbles in $\mathcal{B}$ (with a symmetric difference operator), and $|\mathcal{B}| \le |S| (m-n+1)$.

Notice that for general graphs, our generator can reach the size of the generator proposed in [1]. However, it will be shown in Sect. 4 that in practice the size of our generator is much smaller. Finally, we show that our generator ensures a tree-like decomposition and thus satisfies Property $\mathcal{P}_2$. In other words, we show that each bubble B in G has a tree decomposition using a subset of bubbles in $\mathcal {B}_T$ and such that in each step we combine only bubbles. To prove this we need first two propositions.

Given a bubble B and two distinct vertices u, v in B (not necessarily distinct from s, t), an (u, v)-chord of B is a directed path from u to v that is internally vertex disjoint with B (i.e. except for u and v, the path has no other vertex in common with B).

Proposition 1

Given a non-degenerate (s, t)-bubble B and an (u, v)-chord of B such that either there is no directed path in B or $\{u,v\} \cap \{s,t\} \ne \emptyset$, then the chord defines two bubbles $B_1$ and $B_2$ such that $B=B_1\,\varDelta \,B_2$.

Proof

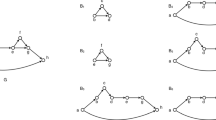
If u and v are on different legs of B, then we define $B_1$ to be the bubble with source u and target t and $B_2$ to be the bubble with source s and target v. Notice that if at least one of u and v coincides with s or t, they can be considered to be in different legs as s and t belong to both legs of B. It is easy to see that $B=B_1\,\varDelta \,B_2$. These cases are depicted in Fig. 1(a)–(d). If u and v are on the same leg of B then we define $B_1$ to be the bubble with source u and target v and $B_2$ to be the bubble with source s and target t. However, if there exists a path from in B (see Fig. 1$(e_2)$) then it is not possible to define the two bubbles $B_1$ and $B_2$. Notice that this is the only case where the (u, v)-chord does not allow to define the two bubbles for which $B=B_1\,\varDelta \,B_2$.    $\blacksquare$

Fig. 1.

All the possible cases considered in Proposition 1. In dotted line we have the edges of the (u, v)-chord, the bubble B is composed by the black and grey edges, the bubble $B_1$ is composed by the black and the dotted line edges and the bubble $B_2$ by the grey and the dotted line edges.

Proposition 2

Given a degenerate bubble B then any (u, v)-chord of B defines two bubbles $B_1$ and $B_2$ such that $B=B_1\,\varDelta \,B_2$.

Proof

The proof follows straightforwardly by observing that every vertex in a directed cycle C has in-degree and out-degree equal to one. After adding the edges of the (u, v)-chord, u has out-degree equal to 2 and v has in-degree 2. Thus the directed cycle C can be written as the sum of $B_1$ that is the non-degenerate bubble with source u and target v and $B_2$ that is the degenerate bubble with source and target u (or v).    $\blacksquare$

Propositions 1 and 2 can be used to prove the following theorem. For lack of space, its proof is deferred to a full version of this paper. Moreover, using the same arguments as for Theorem 2, we can extend it to general graphs.

Theorem 3

Let G be a flow graph with start vertex r, and let $B_{T}(G)$ be the set of bubbles identified by a spanning tree T rooted in r. Then any bubble B in G can be decomposed in O(n) time in bubbles in $B_{T}(G)$ in a tree-like fashion.

4 Experimental Results

To test the usefulness of our family of generators in practice, we applied it to the identification of AS events in RNA data in a reference-free context. In order to compare our generators to both the state-of-art algorithm KisSplice [16, 20] and to the generator defined in [1], we used in our experiments exactly the same dataset as in [1]. This dataset is constructed by selecting the reads corresponding to chromosome 10 from the set of 58 million RNA-seq Illumina paired-end reads extracted from the mouse brain tissue (available in the ENA repository under the following study: PRJEB25574). This leads to a set of 4,932,572 reads. We built the de Bruijn graph from these reads and applied standard sequencing-error-removal procedures by using KisSplice [16, 20]. We recall that KisSplice is a method to find AS events in a reference-free context by enumerating bubbles in a de Bruijn Graph.

For our family, we considered generators coming from three different types of underlying spanning trees, namely Depth-First Search (DFS), Breadth-First Search (BFS) and Scan-First Search (SFS). We recall here that Scan-First Search is the graph search procedure introduced in [5] and which works as follows. As with DFS and BFS, we start from a specified source vertex s and we mark it. At each step, we perform what we call a scan. This selects a marked vertex v and marks all previously unmarked neighbours of v. In other terms, SFS proceeds by scanning a marked and unscanned vertex until all vertices are scanned. Notice that both BFS and DFS can be seen as special cases of SFS. Similarly to BFS and DFS, also SFS can produce a tree as follows. Initially, the tree is empty. Whenever a vertex v is scanned, all the edges between v and its previously unmarked neighbours are added to the tree. In our experiments, we implemented SFS with a random choice of the next vertex to be scanned, and averaged on 1,000 runs with different random seeds.

To compute the source set of the de Bruijn graph, we computed in linear time the DAG of its strongly connected components and chose a vertex from each source. The de Bruijn graph corresponding to our dataset had a total of 83,400 vertices, 99,038 edges and 18,385 source vertices.

Finally, we recall that for general graphs, our new generators are not necessarily minimal. In order to avoid producing duplicates of the same bubble, we discarded a bubble whenever its source was already contained in a tree previously computed from another start vertex. Notice that this does not guarantee the minimality of the generator as there can still be bubbles that can be composed from bubbles that were already present in the generator. For this reason, in general graphs we expect that the size of the generator may vary substantially, depending on the underlying tree chosen.

All our experiments were carried out on a 64-bit machine running Ubuntu 16.04 LTS, equipped with a 2.30 GHz processor Intel(R) Xeon(R) Gold 511, 192 GB of RAM, 16 MB of L3 cache and 1 MB of L2 cache.

4.1 An Empirical Analysis of the Characteristics of the Bubble Generator Based on the Choice of the Spanning Tree

We first explore experimentally some characteristics of bubble generators in our family, depending on the choice of the underlying spanning tree. The parameters we consider are: (i) the size of the generator, (ii) the number of degenerate bubbles (cycles), (iii) the average length of the longest leg, (iv) the average length of the shortest leg, (v) the number of branching bubbles (a branching bubble is a bubble containing more than 5 vertices of in-degree or out-degree greater than 1 [16, 20]).

Table 1 shows the main characteristics of generators in our family. We also include the time required to compute each generator. We do not include in this running time the pre-processing time spent in creating the de Bruijn graph, which is exactly the same for all generators. We refer to a generator in our family simply by the graph search used to generate it and we denote by SP-Gen the generator defined in [1].

Table 1. Characteristics of the generators in our family. The columns represent: the size of the generator, $\#ND_{Bubbles}$ the number of non degenerate bubbles found, $\#D_{Bubbles}$ the number of degenerate bubbles (i.e. cycles), AvgLong and AvgShort the average length of the longest and shortest leg, respectively, and the time the algorithm spent in seconds. Notice that for Scan-First search trees (SFS) we report the mean and the standard deviation of 1000 different runs.

As illustrated in Table 1, the size of all our new generators, independently of the underlying spanning tree, is much smaller than the size of SP-Gen [1]. Furthermore, all our new generators can be computed two orders of magnitude faster than SP-Gen. Furthermore, compared to BFS and SFS, the DFS generator usually has smaller size and its bubbles have longer legs. We also observe that, compared to SP-Gen, the percentage of cycles significantly drops in our new generators: from $12.4\%$ for SP-Gen to $3.1\%$ for DFS, $0.8\%$ for BFS and $0.5\%$ for SFS. This is desirable as cycles are degenerate bubbles that do not correspond to AS events, and thus generators that avoid cycles are preferable.

4.2 Application of the Bubble Generator to the Identification of AS Events in RNA-seq Data

As already mentioned in the introduction, identifying AS events in the absence of a reference genome remains a challenging problem. Local assemblers such as KisSplice [16] are faced with a dramatically large (and often practically unfeasible) running time due to the exponentially large number of bubbles present, most of which are false positives, i.e. they are artificial bubbles not associated with biological events. Indeed, a significantly large number of such artificial bubbles comes from complex subgraphs created by the presence of approximate repeats in the transcriptomic sequence. Thus, tools such as KisSplice use heuristics in order to avoid dealing with large portions of a de Bruijn graph containing such complex subgraphs. Here we show how the set of bubbles belonging to generators in our family can be used to predict AS events. Notice that our method is reference-free; however, in order to evaluate it, we make use of annotated reference genomes to assess if our predictions are correct.

To estimate the precision of our new generators in predicting AS events we proceed as follows. We consider the whole set of bubbles belonging to the generator. We then apply the same filter (based on the length of the legs) as in KisSplice to extract the bubbles that can be considered as putative AS events. To determine the true AS events, we map the putative bubbles to the Mus musculus reference genome and annotations (Ensemble release 94) using STAR [7], which are then analysed by KisSplice2RefGenome [2]. Following [16], a bubble corresponds to a true AS event (or a true positive (TP)) if one leg matches the inclusion isoform and the other the exclusion isoform. Otherwise, the bubble is classified as a false positive. The precision of the method is defined as $TP/(TP+FP)$.

The results for DFS/BFS/SFS and SP-Gen are reported in Table 2. The results show that the number of true AS events found by our generators is comparable to the number of true AS events found by SP-Gen whereas the number of false positives is significantly smaller. Indeed, our generators have a precision between $87.7\%$ and $91.6\%$, compared to $77.3\%$ for the SP-Gen. An interesting aspect of SP-Gen was that it contained many bubbles that were classified as Intron Retention (IR), which is a type of AS event that is generally particularly hard to identify. As shown in Table 2, the number of IR for our generators remains similar to the one found by SP-Gen.

Table 2. Precision of the generators in our family. The columns represent: number of putative AS events, number of true AS events, precision and number of intron retention events.

Since the computation of generators in our family is truly fast in practice, we combined them by taking the union of bubbles coming from different generators and tested whether this would increase the number of AS events found. Notice that the same bubble could be found in two different generators in our family, and thus we eliminated duplicate bubbles in this process. In Table 3 we report the results of different unions of generators in our family (DFS, BFS and 10 randomly chosen runs of SFS), together with the results of SP-Gen and KisSplice. As can be seen, the union of different generators in our family allows us to find more true AS events than both SP-Gen and KisSplice.

Table 3. Combining different generators in our family. The columns represent: number of putative AS events, number of true AS events and precision.

Finally, in [1] it was shown that SP-Gen was able to identify some AS events that will certainly be lost by KisSplice. Indeed, the heuristic used by KisSplice does not generate bubbles containing a number of branching vertices (i.e., vertices with in-degree or out-degree at least 2) higher than some threshold. In KisSplice, the default value for this branching threshold is 5. Increasing the value of this threshold will increase exponentially the running time of the algorithm and thus a large branching threshold is unfeasible in practice. As reported in [1], around 27 true AS events in SP-Gen have a branching number higher than 5, and are lost by KisSplice. For the family of our generators, we have that the number of true AS events that are certainly lost by KisSplice is: (a) 16 for the BFS, (b) 77 for the DFS, and (c) an average of 80 for SFS (averaged over different choices of the random seed).

5 Conclusions and Open Problems

In this paper, we have proposed a new family of bubble generators which improves substantially on the previous generator (SP-Gen [1]): generators in the new family are much faster, i.e., about two orders of magnitude faster than SP-Gen, and they are still able to achieve similar (and sometimes higher) precision in identifying AS events.

Our work raises several new and perhaps intriguing questions. First, we notice that while for flow graphs our family produces minimum generators, for general graphs it is still open to find a minimum bubble generator. Second, the fast computation of our new generators opens the way to the design of algorithms that efficiently combine the bubbles of a generator in order to find more AS events. Third, we believe that the number of false positives could be reduced by adding more biologically motivated constraints. An example of constraint that can be introduced toward this aim is to give a weight to each edge of the de Bruijn graph based on the reads coverage. A true AS event would then correspond to bubbles in which the edges inside a leg must have similar weights (but different legs may have different coverage). Fourth, when constructing a de Bruijn graph from RNA-seq reads, some filters are applied that are meant to eliminate sequencing errors. These filters remove vertices and edges whose coverage by the set of reads is below some given thresholds. Changing those thresholds has a significant impact on the resulting de Bruijn graph, and hence on the set of solutions. Is it possible to compute in a dynamic fashion a bubble generator when this coverage threshold is changing, without having to recompute everything from scratch?