Abstract
We present a history of the Baum–Connes conjecture, the methods involved, the current status, and the mathematics it generated.
To Alain Connes, for providing lifelong inspiration
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
This is important, e.g., for applications to foliations, see Chapter 7.
- 2.
In the case of SL 3(Z), surjectivity of μ r is the open problem; the LHS of the Baum–Connes conjecture was computed in [SG08].
- 3.
Recall that B(d, n) is defined as the quotient of the non-abelian free group F d by the normal subgroup generated by all n’s powers in F d.
- 4.
- 5.
- 6.
We believe that Connes and Moscovici actually had \(C^{\ast }_r(G)\), not C ∗(G), in mind when writing this.
- 7.
As Connes once pointed out: “E Γ is a point on which Γ acts freely!.”
- 8.
Although published only in 1995, the celebrated “ Conspectus” was first circulated in 1981.
- 9.
K-homology is the homology theory dual to topological K-theory. It was shown by Atiyah [Ati70] that an elliptic (pseudo-)differential operator on M defines an element in K 0(M).
- 10.
When B Γ is a general CW-complex we must replace K 0(B Γ) by
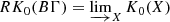 , where X runs along compact subsets of B Γ.
, where X runs along compact subsets of B Γ. - 11.
In terms of Kasparov theory, to be defined in Chapter 3 below, this can be expressed using Kasparov product: \(\beta [D]=[\mathcal {L}_\Gamma ]\otimes _{C(B\Gamma )}[D]\).
- 12.
- 13.
This is actually the same map as the map β from Section 2.5.
- 14.
The fact that it is indeed an equivalence relation does not appear in [BC00].
- 15.
Note that the proof is given there only for discrete groups, but the proof goes over to locally compact group.
- 16.
- 17.
For a nice proof of that result NOT appealing to Atiyah’s L 2-index theorem, see lemma 7.1 in [MV03].
- 18.
Or is a-(T)-menable, according to Gromov.
- 19.
A concrete example of a non-cocompact lattice in Sp(n, 1), is Sp(n, 1)(H(Z)), the group of points of the real algebraic group Sp(n, 1) over the ring H(Z) of integral quaternions. For such a group Conjecture 5 is still open.
- 20.
See the discussion of strong property (T) in 6.3.
- 21.
Until the end of Proposition 7.6, we denote a countable group by Γ∞ rather than Γ, as we view Γ∞ as the limit of its finite quotients Γk.
- 22.
If Γ∞ has property (T), e π is the image in \(C^{\ast }_\pi (\Gamma _\infty )\) of the Kazhdan projection \(e_{\mathcal {G}}\in C^{\ast }_{\mathrm {max}}(\Gamma _\infty )\) from Proposition 5.4.
- 23.
The re-interpretation goes as follows: fix an auxiliary orientation on the edges of E, allowing one to define the coboundary operator d : ℓ 2(V ) → ℓ 2(E) : ϕ↦dϕ, where dϕ(e) = ϕ(e +) − ϕ(e −). Observe that Δ = d ∗d, so that \(\langle \Delta \phi ,\phi \rangle =\|d\phi \|{ }^2=\frac {1}{2}\sum _{x\sim y}|\phi (x)-\phi (y)|{ }^2\). By the Rayleigh quotient, \(\frac {1}{\lambda _1}\) is the smallest constant K > 0 such that ∥ϕ∥2 ≤ K∥dϕ∥2 for every ϕ ⊥ 1. We leave the rest as an exercise.
- 24.
Recall that a group acting properly isometrically on a CAT(0) cube complex, has the Haagerup property, see, e.g., Corollary 1 in [Val18].
- 25.
Amenability (resp. property (T)) can be defined by a fixed point property: existence of a fixed point for affine actions on compact convex sets (resp. affine isometric actions on Hilbert spaces). This makes clear that it is preserved under extensions.
- 26.
Under the assumption that | Γ| coarsely embeds into Hilbert space, the assumption that B Γ is a finite complex was removed by Skandalis et al. [STY02], using their groupoid approach to CBC.
- 27.
Recall from Section 8.2.3 that an entourage is a subset of X × X on which d(., .) is bounded.
- 28.
- 29.
References
P. Antonini, S. Azzali, and G. Skandalis. The Baum-Connes conjecture localized at the unit element of a discrete group. Preprint 2018, arXiv:1807.05892v1, 2018.
F. Astengo, M. Cowling, and B. Di Blasio. The Cayley transform and uniformly bounded representations. J. Funct. Anal., 213(2):241–269, 2004.
G. Arzhantseva and T. Delzant. Examples of random groups. Preprint available on http://irma.math.unistra.fr/~delzant/random.pdf, 2008.
A. Afgoustidis. On the analogy between real reductive groups and Cartan motion groups. iii : A proof of the Connes- Kasparov isomorphism. arXiv :1602.08891, 2016.
G. Arzhantseva, E. Guentner, and J. Špakula. Coarse non-amenability and coarse embeddings. Geom. Funct. Anal., 22(1):22–36, 2012.
C. Anantharaman and J. Renault. Amenable groupoids. In Groupoids in analysis, geometry, and physics (Boulder, CO, 1999), volume 282 of Contemp. Math., pages 35–46. Amer. Math. Soc., Providence, RI, 2001.
M. F. Atiyah and I. M. Singer. The index of elliptic operators. I. Ann. of Math. (2), 87:484–530, 1968.
M. F. Atiyah and W. Schmid. A geometric construction of the discrete series for semisimple Lie groups. Invent. Math., 42:1–62, 1977.
M. F. Atiyah. Global theory of elliptic operators. In Proc. Internat. Conf. on Functional Analysis and Related Topics (Tokyo, 1969), pages 21–30. Univ. of Tokyo Press, Tokyo, 1970.
M. F. Atiyah. Elliptic operators, discrete groups and von Neumann algebras. pages 43–72. Astérisque, No. 32–33, 1976.
C. Akemann and M. Walter. Unbounded negative definite functions. Canad. J. Math., 33(4):862–871, 1981.
D. Bleecker and B. Booß-Bavnbek. Index theory—with applications to mathematics and physics. International Press, Somerville, MA, 2013.
P. Baum and A. Connes. Leafwise homotopy equivalence and rational Pontrjagin classes. In Foliations (Tokyo, 1983), volume 5 of Adv. Stud. Pure Math., pages 1–14. North-Holland, Amsterdam, 1985.
P. Baum and A. Connes. Geometric K-theory for Lie groups and foliations. Enseign. Math. (2), 46(1-2):3–42, 2000.
P. Baum, A. Connes, and N. Higson. Classifying space for proper actions and K-theory of group C ∗-algebras. In C ∗-algebras: 1943–1993 (San Antonio, TX, 1993), volume 167 of Contemp. Math., pages 240–291. Amer. Math. Soc., Providence, RI, 1994.
B. Bekka, P. de la Harpe, and A. Valette. Kazhdan’s property (T), volume 11 of New Mathematical Monographs. Cambridge University Press, Cambridge, 2008.
A. Brown, D. Fisher, and S. Hurtado-Salazar. Zimmer’s conjecture: Subexponential growth, measure rigidity, and strong property (T). Preprint arXiv:1608.04995, 2016.
A. Brown, D. Fisher, and S. Hurtado-Salazar. Zimmer’s conjecture for actions of \(\mathrm {SL}(m,\mathbb {Z})\). Preprint arXiv:1710.02735 , 2017.
R. Beals and P. Greiner. Calculus on Heisenberg manifolds, volume 119 of Annals of Mathematics Studies. Princeton University Press, Princeton, NJ, 1988.
M. Bestvina, C. Horbez, and V. Guirardel. Boundary amenability of Out(F n). Preprint 2017, arXiv:1705.07017, 2017.
P. Baum, N. Higson, and T. Schick. A geometric description of equivariant K-homology for proper actions. In Quanta of maths, volume 11 of Clay Math. Proc., pages 1–22. Amer. Math. Soc., Providence, RI, 2010.
E. Breuillard, M. Kalantar, M. Kennedy, and N. Ozawa. C ∗-simplicity and the unique trace property for discrete groups. Publ. Math. Inst. Hautes Études Sci., 126:35–71, 2017.
H. Bettaieb, M. Matthey, and A. Valette. Unbounded symmetric operators in K-homology and the Baum-Connes conjecture. J. Funct. Anal., 229(1):184–237, 2005.
J.-B. Bost. Principe d’Oka, K-théorie et systèmes dynamiques non commutatifs. Invent. Math., 101:261–333, 1990.
A. Boyer. Harish-Chandra’s Schwartz algebras associated with discrete subgroups of semisimple Lie groups. J. Lie Theory, 27(3):831–844, 2017.
F. Bruhat and J. Tits. Groupes réductifs sur un corps local. Inst. Hautes Études Sci. Publ. Math., (41):5–251, 1972.
P.-A. Cherix, M. Cowling, P. Jolissaint, P. Julg, and A. Valette. Groups with the Haagerup property, volume 197 of Progress in Mathematics. Birkhäuser Verlag, Basel, 2001.
J. Chabert, S. Echterhoff, and R. Meyer. Deux remarques sur l’application de Baum-Connes. C. R. Acad. Sci. Paris Sér. I Math., 332(7):607–610, 2001.
J. Chabert, S. Echterhoff, and R. Nest. The Connes-Kasparov conjecture for almost connected groups and for linear p-adic groups. Publ. Math. Inst. Hautes Études Sci., (97):239–278, 2003.
M. Christ, D. Geller, P. Głowacki, and L. Polin. Pseudodifferential operators on groups with dilations. Duke Math. J., 68(1):31–65, 1992.
M. Cowling and U. Haagerup. Completely bounded multipliers of the Fourier algebra of a simple Lie group of real rank one. Invent. Math., 96(3):507–549, 1989.
I. Chatterji. Property (RD) for cocompact lattices in a finite product of rank one Lie groups with some rank two Lie groups. Geom. Dedicata, 96:161–177, 2003.
Z. Chen. Séries complémentaires des groupes de Lorentz et KK-théorie. J. Funct. Anal., 137(1):76–96, 1996.
A. \(\check {\mathrm {C}}\)ap, C. Harrach, and P. Julg. A Poisson transform adapted to the Rumin complex. Preprint 2019, arXiv:1904.00635, 2019.
A. Connes and H. Moscovici. The L 2-index theorem for homogeneous spaces of Lie groups. Ann. of Math. (2), 115(2):291–330, 1982.
A. Connes and H. Moscovici. Cyclic cohomology, the Novikov conjecture and hyperbolic groups. Topology, 29(3):345–388, 1990.
A. Connes. An analogue of the Thom isomorphism for crossed products of a C ∗-algebra by an action of R. Adv. in Math., 39(1):31–55, 1981.
A. Connes. A survey of foliations and operator algebras. In Operator algebras and applications, Part I (Kingston, Ont., 1980), volume 38 of Proc. Sympos. Pure Math., pages 521–628. Amer. Math. Soc., Providence, R.I., 1982.
M. Cowling. Unitary and uniformly bounded representations of some simple Lie groups. In Harmonic analysis and group representations, pages 49–128. Liguori, Naples, 1982.
I. Chatterji and K. Ruane. Some geometric groups with rapid decay. Geom. Funct. Anal., 15(2):311–339, 2005.
A. \(\check {\mathrm {C}}\)ap and V. Souček. Curved Casimir operators and the BGG machinery. SIGMA Symmetry Integrability Geom. Methods Appl., 3:Paper 111, 17, 2007.
A. \(\check {\mathrm {C}}\)ap, J. Slovák, and V. Souček. Bernstein-Gelfand-Gelfand sequences. Ann. of Math. (2), 154(1):97–113, 2001.
Y. Cornulier, Y. Stalder, and A. Valette. Proper actions of wreath products and generalizations. Trans. Amer. Math. Soc., 364(6):3159–3184, 2012.
Yves Cornulier and Romain Tessera. A characterization of relative Kazhdan property T for semidirect products with abelian groups. Ergodic Theory Dynam. Systems, 31(3):793–805, 2011.
Mathieu Carette, Daniel T. Wise, and Daniel J. Woodhouse. The A-T-menability of some graphs of groups with cyclic edge groups. Math. Proc. Cambridge Philos. Soc., 163(1):145–159, 2017.
S. Dave and S. Haller. Graded hypoellipticity of BGG sequences. arXiv:1705.01659, 2017.
J. Dixmier. LesC ∗-algèbres et leurs représentations. Les Grands Classiques Gauthier-Villars. [Gauthier-Villars Great Classics]. Éditions Jacques Gabay, Paris, 1996. Reprint of the second (1969) edition.
J. Davis and W. Lück. Spaces over a category and assembly maps in isomorphism conjectures in K- and L-theory. K-Theory, 15(3):201–252, 1998.
T. de Laat and M. de la Salle. Strong property (T) for higher-rank simple Lie groups. Proc. Lond. Math. Soc. (3), 111(4):936–966, 2015.
P. de la Harpe. Groupes hyperboliques, algèbres d’opérateurs et un théorème de Jolissaint. C. R. Acad. Sci. Paris Sér. I Math., 307(14):771–774, 1988.
M. de la Salle. A local characterization of Kazhdan projections and applications. to appear in Comment. Math. Helvet.arXiv:1604.01616, 2016.
M. de la Salle. Strong property (T) for higher rank lattices. Preprint arXiv:1711.01900, 2018.
T. de Laat and F. Vigolo. Superexpanders from group actions on compact manifolds. arXiv:1707.01399, 2017.
T. de Laat and F. Vigolo. Superexpanders from group actions on compact manifolds. Preprint 2018, to appear in Geometriae Dedicata arXiv:1707.01399v2, 2018.
C. Druţu and P. Novak. Kazhdan projections, random walks and ergodic theorems. Journal für die reine und angewandte Mathematik, 2017. https://doi.org/10.1515/crelle-2017-0002.
C. Debord and G. Skandalis. Adiabatic groupoid, crossed product by \(\mathbb {R}_+^\ast \) and pseudodifferential calculus. Adv. Math., 257:66–91, 2014.
G. Davidoff, P. Sarnak, and A. Valette. Elementary number theory, group theory, and Ramanujan graphs, volume 55 of London Mathematical Society Student Texts. Cambridge University Press, Cambridge, 2003.
F. Forstnerič and F. Lárusson. Survey of Oka theory. New York J. Math., 17A:11–38, 2011.
D. Fisher, T Nguyen, and W. Van Limbeek. Rigidity of warped cones and coarse geometry of expanders. Preprint, arXiv:1710.03085, 2017.
R. Flores, S. Pooya, and A. Valette. K-homology and K-theory for the lamplighter groups of finite groups. Proc. Lond. Math. Soc. (3), 115(6):1207–1226, 2017.
S. Ferry, A. Ranicki, and J. Rosenberg. A history and survey of the Novikov conjecture. In Novikov conjectures, index theorems and rigidity, Vol. 1 (Oberwolfach, 1993), volume 226 of London Math. Soc. Lecture Note Ser., pages 7–66. Cambridge Univ. Press, Cambridge, 1995.
M. P. Gomez Aparicio. Représentations non unitaires, morphisme de Baum-Connes et complétions inconditionnelles. J. Noncommut. Geom., 3(3):419–446, 2009.
M. P. Gomez-Aparicio. Morphisme de Baum-Connes tordu par une représentation non unitaire. J. K-Theory, 6(1):23–68, 2010.
P.-Y. Gaillard. Transformation de Poisson de formes différentielles. Le cas de l’espace hyperbolique. Comment. Math. Helv., 61(4):581–616, 1986.
E. Guentner, N. Higson, and S. Weinberger. The Novikov conjecture for linear groups. Publ. Math. Inst. Hautes Études Sci., (101):243–268, 2005.
E. Guentner and J. Kaminker. Exactness and the Novikov conjecture. Topology, 41(2):411–418, 2002.
H. Grauert. Selected papers. Vol. I, II. Springer-Verlag, Berlin, 1994. With commentary by Y. T. Siu et al.
M. Gromov. Oka’s principle for holomorphic sections of elliptic bundles. J. Amer. Math. Soc., 2(4):851–897, 1989.
M. Gromov. Random walk in random groups. Geom. Funct. Anal., 13(1):73–146, 2003.
S. Gong, J. Wu, and G. Yu. The Novikov conjecture, the group of volume preserving diffeomorphisms and Hilbert-Hadamard spaces. Preprint 2019, arXiv:1811.02086v2, 2019.
T. Haettel. Virtually cocompactly cubulated artin-tits groups. Preprint 2019, arXiv:1509.08711v4, march 2019.
I. Hambleton and E. K. Pedersen. Identifying assembly maps in K- and L-theory. Math. Ann., 328(1–2):27–57, 2004.
U. Hamenstädt. Geometry of the mapping class groups. I. Boundary amenability. Invent. Math., 175(3):545–609, 2009.
S. Helgason. Differential geometry and symmetric spaces. Pure and Applied Mathematics, Vol. XII. Academic Press, New York-London, 1962.
N. Higson and E. Guentner. Group C ∗-algebras and K-theory. In Noncommutative geometry, volume 1831 of Lecture Notes in Math., pages 137–251. Springer, Berlin, 2004.
N. Higson. Bivariant K-theory and the Novikov conjecture. Geom. Funct. Anal., 10(3):563–581, 2000.
N. Higson and G. G. Kasparov. E-theory and KK-theory for groups which act properly and isometrically on Hilbert space. Invent. Math., 144(1):23–74, 2001.
N. Higson, V. Lafforgue, and G. Skandalis. Counterexamples to the Baum-Connes conjecture. Geom. Funct. Anal., 12(2):330–354, 2002.
N. Higson and J. Roe. On the coarse Baum-Connes conjecture. In Novikov conjectures, index theorems and rigidity, Vol. 2 (Oberwolfach, 1993), volume 227 of London Math. Soc. Lecture Note Ser., pages 227–254. Cambridge Univ. Press, Cambridge, 1995.
N. Higson and J. Roe. Amenable group actions and the Novikov conjecture. J. Reine Angew. Math., 519:143–153, 2000.
J. W. Jenkins. An amenable group with a non-symmetric group algebra. Bull. Amer. Math. Soc., 75:357–360, 1969.
P. Julg and G. G. Kasparov. Operator K-theory for the group SU(n, 1). J. Reine Angew. Math., 463:99–152, 1995.
P. Jolissaint. Rapidly decreasing functions in reduced C ∗-algebras of groups. Trans. Amer. Math. Soc., 317(1):167–196, 1990.
P. Julg. Remarks on the Baum-Connes conjecture and Kazhdan’s property T. In Operator algebras and their applications (Waterloo, ON, 1994/1995), volume 13 of Fields Inst. Commun., pages 145–153. Amer. Math. Soc., Providence, RI, 1997.
P. Julg. Travaux de N. Higson et G. Kasparov sur la conjecture de Baum-Connes. Astérisque, (252):Exp. No. 841, 4, 151–183, 1998. Séminaire Bourbaki. Vol. 1997/98.
P. Julg. La conjecture de Baum-Connes à coefficients pour le groupe Sp(n, 1). C. R. Math. Acad. Sci. Paris, 334(7):533–538, 2002.
P. Julg. How to prove the Baum-Connes conjecture for Sp(n, 1)? Journal of Geometry and Physics, https://doi.org/10.1016/j.geomphys.2019.02.009, 2019.
P. Julg and A. Valette. K-theoretic amenability for SL2(Q p), and the action on the associated tree. J. Funct. Anal., 58(2):194–215, 1984.
P. Julg and A. Valette. Fredholm modules associated to Bruhat-Tits buildings. In Miniconferences on harmonic analysis and operator algebras (Canberra, 1987), volume 16 of Proc. Centre Math. Anal. Austral. Nat. Univ., pages 143–155. Austral. Nat. Univ., Canberra, 1988.
P. Julg and E. van Erp. The geometry of the osculating nilpotent group structures of the Heisenberg calculus. J. Lie Theory, 28(1):107–138, 2018.
M. Karoubi. K-theory. Classics in Mathematics. Springer-Verlag, Berlin, 2008. An introduction, Reprint of the 1978 edition, With a new postface by the author and a list of errata.
G. G. Kasparov. Lorentz groups: K-theory of unitary representations and crossed products. Dokl. Akad. Nauk SSSR, 275(3):541–545, 1984.
G. G. Kasparov. Operator K-theory and its applications. Journal of Soviet Mathematics, 37(6):1373–1396, Jun 1987.
G. G. Kasparov. Equivariant KK-theory and the Novikov conjecture. Invent. Math., 91(1):147–201, 1988.
G. G. Kasparov. K-theory, group C ∗-algebras, and higher signatures (conspectus). In Novikov conjectures, index theorems and rigidity, Vol. 1 (Oberwolfach, 1993), volume 226 of London Math. Soc. Lecture Note Ser., pages 101–146. Cambridge Univ. Press, Cambridge, 1995.
A. Khukhro. Espaces et groupes non exacts admettant un plongement grossier dans un espace de Hilbert, d’après Arzhantseva-Guentner-Špakula, Arzhantseva-Osajda, Osajda, et al. In Séminaire Bourbaki, Vol. 1154, 2018. 2018.
Y. Kida. The mapping class group from the viewpoint of measure equivalence theory. Mem. Amer. Math. Soc., 196(916):viii+190, 2008.
A. W. Knapp. Representation theory of semisimple groups. Princeton Landmarks in Mathematics. Princeton University Press, Princeton, NJ, 2001. An overview based on examples, Reprint of the 1986 original.
G. G. Kasparov and G. Skandalis. Groups acting on buildings, operator K-theory, and Novikov’s conjecture. K-Theory, 4(4):303–337, 1991.
G. G. Kasparov and G. Skandalis. Groups acting properly on “bolic” spaces and the Novikov conjecture. Ann. of Math. (2), 158(1):165–206, 2003.
G. G. Kasparov and G. Yu. The coarse geometric Novikov conjecture and uniform convexity. Adv. Math., 206(1):1–56, 2006.
V. Lafforgue. A proof of property (RD) for cocompact lattices of SL(3, R) and SL(3, C). J. Lie Theory, 10(2):255–267, 2000.
V. Lafforgue. Banach KK-theory and the Baum-Connes conjecture. In Proceedings of the International Congress of Mathematicians, Vol. II (Beijing, 2002), pages 795–812, Beijing, 2002. Higher Ed. Press.
V. Lafforgue. K-théorie bivariante pour les algèbres de Banach et conjecture de Baum-Connes. Invent. Math., 149(1):1–95, 2002.
V. Lafforgue. K-théorie bivariante pour les algèbres de Banach, groupoïdes et conjecture de Baum-Connes. Avec un appendice d’Hervé Oyono-Oyono. J. Inst. Math. Jussieu, 6(3), 2007.
V. Lafforgue. Un renforcement de la propriété (T). Duke Math. J., 143(3):559–602, 2008.
V. Lafforgue. Propriété (T) renforcée banachique et transformation de Fourier rapide. J. Topol. Anal., 1(3):191–206, 2009.
V. Lafforgue. Propriété (T) renforcée et conjecture de Baum-Connes. In Quanta of maths, volume 11 of Clay Math. Proc., pages 323–345. Amer. Math. Soc., Providence, RI, 2010.
V. Lafforgue. La conjecture de Baum-Connes à coefficients pour les groupes hyperboliques. J. Noncommut. Geom., 6(1):1–197, 2012.
M. Land. The analytical assembly map and index theory. J. Noncommut. Geom., 9(2):603–619, 2015.
P.-Y. Le Gall. Théorie de Kasparov équivariante et groupoïdes. C. R. Acad. Sci. Paris Sér. I Math., 324(6):695–698, 1997.
P.-Y. Le Gall. Théorie de Kasparov équivariante et groupoïdes. I. K-Theory, 16(4):361–390, 1999.
B. Liao. Strong Banach property (T) for simple algebraic groups of higher rank. J. Topol. Anal., 6(1):75–105, 2014.
B. Liao. About the obstacle to proving the Baum-Connes conjecture without coefficient for a non-cocompact lattice in Sp 4 in a local field. J. Noncommut. Geom., 10(4):1243–1268, 2016.
R. Lipsman. Group representations. Lecture Notes in Mathematics, Vol. 388. Springer-Verlag, Berlin-New York, 1974. A survey of some current topics.
H. Leptin and D. Poguntke. Symmetry and nonsymmetry for locally compact groups. J. Funct. Anal., 33(2):119–134, 1979.
A. Lubotzky. Discrete groups, expanding graphs and invariant measures. Modern Birkhäuser Classics. Birkhäuser Verlag, Basel, 2010. With an appendix by Jonathan D. Rogawski, Reprint of the 1994 edition.
A. Lubotzky and R.J. Zimmer. Variants of Kazhdan’s property for subgroups of semisimple groups. Israel J. Math., 66(1-3):289–299, 1989.
J. Matoušek. On embedding expanders into l p spaces. Israel J. Math., 102:189–197, 1997.
A. Melin. Lie filtrations and pseudo-differential operators. Preprint, scan available on request from the 2nd author, 1982.
I. Mineyev. Straightening and bounded cohomology of hyperbolic groups. Geom. Funct. Anal., 11(4):807–839, 2001.
A. S. Miscenko. Infinite-dimensional representations of discrete groups, and higher signatures. Izv. Akad. Nauk SSSR Ser. Mat., 38:81–106, 1974.
M. Mendel and A. Naor. Nonlinear spectral calculus and super-expanders. Publ. Math. Inst. Hautes Études Sci., 119:1–95, 2014.
O. Mohsen. On the deformation groupoid of the inhomogeneous pseudo-differential calculus. arXiv:1806.08585, 2018.
G. Mislin and A. Valette. Proper group actions and the Baum-Connes conjecture. Advanced Courses in Mathematics. CRM Barcelona. Birkhäuser Verlag, Basel, 2003.
B. Nica. Relatively spectral morphisms and applications to K-theory. J. Funct. Anal., 255(12):3303–3328, 2008.
S. Nishikawa. Direct splitting method for the Baum-Connes conjecture. Preprint 2019, arXiv:1808.08298v2, 2019.
P. Nowak. Coarsely embeddable metric spaces without Property A. J. Funct. Anal., 252(1):126–136, 2007.
P. W. Nowak and D. Sawicki. Warped cones and spectral gaps. Proc. Amer. Math. Soc., 145(2):817–823, 2017.
H. Oyono-Oyono. Baum-Connes conjecture and group actions on trees. K-Theory, 24(2):115–134, 2001.
D. Osajda. Small cancellation labellings of some infinite graphs and applications. Preprint 2014, arXiv:1406.5015, 2014.
N. Ozawa. Amenable actions and exactness for discrete groups. C. R. Acad. Sci. Paris Sér. I Math., 330(8):691–695, 2000.
N. Ozawa. Local theory and local reflexivity for operator spaces. PhD thesis, Texas A&M University, 2001.
William L. Paschke. K-theory for commutants in the Calkin algebra. Pacific J. Math., 95(2):427–434, 1981.
G. K. Pedersen. C ∗-algebras and their automorphism groups, volume 14 of London Mathematical Society Monographs. Academic Press Inc. [Harcourt Brace Jovanovich Publishers], London, 1979.
M. Pimsner. KK-groups of crossed products by groups acting on trees. Invent. Math., 86(3):603–634, 1986.
R. Ponge. The tangent groupoid of a Heisenberg manifold. Pacific J. Math., 227(1):151–175, 2006.
M. G. Penington and R. J. Plymen. The Dirac operator and the principal series for complex semisimple Lie groups. J. Funct. Anal., 53(3):269–286, 1983.
M. Puschnigg. The Baum-Connes conjecture with coefficients for word-hyperbolic groups (after Vincent Lafforgue). Astérisque, (361):Exp. No. 1062, vii, 115–148, 2014.
M. Pimsner and D. Voiculescu. K-groups of reduced crossed products by free groups. J. Operator Theory, 8(1):131–156, 1982.
J. Roe. Coarse cohomology and index theory on complete Riemannian manifolds. Mem. Amer. Math. Soc., 104(497):x+90, 1993.
J. Roe. Index theory, coarse geometry, and topology of manifolds, volume 90 of CBMS Regional Conference Series in Mathematics. Published for the Conference Board of the Mathematical Sciences, Washington, DC; by the American Mathematical Society, Providence, RI, 1996.
J. Roe. Warped cones and property A. Geom. Topol., 9:163–178, 2005.
J. Ramagge, G. Robertson, and T. Steger. A Haagerup inequality for \(\widetilde A_1\times \widetilde A_1\) and \(\widetilde A_2\) buildings. Geom. Funct. Anal., 8(4):702–731, 1998.
J. Rosenberg and S. Stolz. A “stable” version of the Gromov-Lawson conjecture. In The Čech centennial (Boston, MA, 1993), volume 181 of Contemp. Math., pages 405–418. Amer. Math. Soc., Providence, RI, 1995.
M. Rumin. Differential geometry on C-C spaces and application to the Novikov-Shubin numbers of nilpotent Lie groups. C. R. Acad. Sci. Paris Sér. I Math., 329(11):985–990, 1999.
D. Sawicki. Super-expanders and warped cones. Preprint 2017, arXiv:1704.03865, 2017.
D. Sawicki. Warped cones, (non-)rigidity, and piecewise properties (with a joint appendix with Dawid Kielak). Preprint, arXiv:1707.02960, 2017.
D. Sawicki. Warped cones violate the Baum-Connes conjecture. Preprint available on https://www.impan.pl/~dsawicki/files/counterexamples.pdf, 2017.
T. Schick. Finite group extensions and the Baum-Connes conjecture. Geom. Topol., 11:1767–1775, 2007.
R. Sánchez-García. Bredon homology and equivariant K-homology of \(\mathrm {SL}(3,\mathbb {Z})\). J. Pure Appl. Algebra, 212(5):1046–1059, 2008.
G. Skandalis. Progrès récents sur la conjecture de Baum-Connes. Contribution de Vincent Lafforgue. Astérisque, (276):105–135, 2002. Séminaire Bourbaki, Vol. 1999/2000.
G. Skandalis, J. L. Tu, and G. Yu. The coarse Baum-Connes conjecture and groupoids. Topology, 41(4):807–834, 2002.
R. Swan. Topological examples of projective modules. Trans. Amer. Math. Soc., 230:201–234, 1977.
J. Tits. On buildings and their applications. In Proceedings of the International Congress of Mathematicians (Vancouver, B. C., 1974), Vol. 1, pages 209–220. Canad. Math. Congress, Montreal, Que., 1975.
J.-L. Tu. The Baum-Connes conjecture and discrete group actions on trees. K-Theory, 17(4):303–318, 1999.
J.-L. Tu. La conjecture de Baum-Connes pour les feuilletages moyennables. K-Theory, 17(3):215–264, 1999.
J.-L. Tu. La conjecture de Novikov pour les feuilletages hyperboliques. K-Theory, 16(2):129–184, 1999.
J.-L. Tu. The Baum-Connes conjecture for groupoids. In C ∗-algebras (Münster, 1999), pages 227–242. Springer, Berlin, 2000.
A. Valette. K-theory for the reduced C ∗-algebra of a semisimple Lie group with real rank 1 and finite centre. Quart. J. Math. Oxford Ser. (2), 35(139):341–359, 1984.
A. Valette. Dirac induction for semisimple Lie groups having one conjugacy class of Cartan subgroups. In Operator algebras and their connections with topology and ergodic theory (Buşteni, 1983), volume 1132 of Lecture Notes in Math., pages 526–555. Springer, Berlin, 1985.
A. Valette. Le rôle des fibrés de rang fini en théorie de Kasparov équivariante. Acad. Roy. Belg. Cl. Sci. Mém. Collect.8 o(2), 45(6), 1988.
A. Valette. Introduction to the Baum-Connes conjecture. Lectures in Mathematics ETH Zürich. Birkhäuser Verlag, Basel, 2002. From notes taken by Indira Chatterji, With an appendix by Guido Mislin.
A. Valette. Proper isometric actions on hilbert spaces: a-(T)-menability and Haagerup property. handbook of group actions. Adv. Lect. Math. (ALM), Int. Press, Somerville, MA, IV(41), 2018.
E. van Erp and R. Yuncken. A groupoid approach to pseudodifferential operators. J. Reine Agnew. Math. https://doi.org/10.1515/crelle-2017-0035, 2017.
E. van Erp and R. Yuncken. On the tangent groupoid of a filtered manifold. Bull. Lond. Math. Soc., 49(6):1000–1012, 2017.
F. Vigolo. Measure expanding actions, expanders and warped cones. Trans. Amer. Math. Soc., 371(3):1951–1979, 2019.
D. Vogan, Jr. Representations of real reductive Lie groups, volume 15 of Progress in Mathematics. Birkhäuser, Boston, Mass., 1981.
A. Wassermann. Une démonstration de la conjecture de Connes-Kasparov pour les groupes de Lie linéaires connexes réductifs. C. R. Acad. Sci. Paris Sér. I Math., 304(18):559–562, 1987.
R. Willett. Property A and graphs with large girth. J. Topol. Anal., 3(3):377–384, 2011.
N. E. Wegge-Olsen. K-theory andC ∗-algebras. Oxford Science Publications. The Clarendon Press, Oxford University Press, New York, 1993. A friendly approach.
R. Willett and G. Yu. Higher index theory for certain expanders and Gromov monster groups, I. Adv. Math., 229(3):1380–1416, 2012.
G. Yu. Coarse Baum-Connes conjecture. K-Theory, 9(3):199–221, 1995.
G. Yu. The Novikov conjecture for groups with finite asymptotic dimension. Ann. of Math. (2), 147(2):325–355, 1998.
G. Yu. The coarse Baum-Connes conjecture for spaces which admit a uniform embedding into Hilbert space. Invent. Math., 139(1):201–240, 2000.
R. Yuncken. The Bernstein-Gelfand-Gelfand complex and Kasparov theory for \(\mathrm {SL}(3,\mathbb {C})\). Adv. Math., 226(2):1474–1512, 2011.
R. Zimmer. Ergodic theory and semisimple groups, volume 81 of Monographs in Mathematics. Birkhäuser Verlag, Basel, 1984.
R. Zimmer. Actions of semisimple groups and discrete subgroups. In Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Berkeley, Calif., 1986), pages 1247–1258. Amer. Math. Soc., Providence, RI, 1987.
Acknowledgement
Thanks are due to J.-B. Bost, R. Coulon, N. Higson, V. Lafforgue, P.-Y. Le Gall, H. Oyono-Oyono, N. Ozawa, and M. de la Salle for useful conversations and exchanges.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Aparicio, M.P.G., Julg, P., Valette, A. (2019). The Baum–Connes conjecture: an extended survey. In: Chamseddine, A., Consani, C., Higson, N., Khalkhali, M., Moscovici, H., Yu, G. (eds) Advances in Noncommutative Geometry. Springer, Cham. https://doi.org/10.1007/978-3-030-29597-4_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-29597-4_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-29596-7
Online ISBN: 978-3-030-29597-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


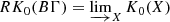 , where X runs along compact subsets of B Γ.
, where X runs along compact subsets of B Γ.