Abstract
We give a survey on higher invariants in noncommutative geometry and their applications to differential geometry and topology.
Dedicated to Alain Connes with great admiration
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
In other words, there is no need to pass to the operator \(\mathcal {F}\) or \(\mathcal {F}(t)\) as in the general case.
- 2.
Note that in this case, all finite order elements in
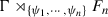 come from Γ.
come from Γ. - 3.
- 4.
Without loss of generality, we can assume N R(Z) is Γ-invariant.
- 5.
A geometric construction of the Siebenmann periodicity map was given by Cappell and Weinberger [CW].
- 6.
Let us review how the homomorphism \(\psi _\ast : K_{1}(C_{L,0}^\ast (\widetilde M)^\Gamma )\to K_{1}(C_{L,0}^\ast (\widetilde M)^\Gamma )\) is defined. The map ψ: M → M lifts to a map \(\widetilde \psi \colon \widetilde M \to \widetilde M\). However, to view \(\widetilde \psi \) as a Γ-equivariant map, we need to use two different actions of Γ on \(\widetilde M\). Let τ be a right action of Γ on \(\widetilde M\) through deck transformations. Then we define a new action τ′ of Γ on \(\widetilde M\) by \(\tau ^{\prime }_g = \tau _{\psi _\ast (g)}\), where ψ ∗: Γ → Γ is the automorphism induced by ψ. It is easy to see that \(\widetilde \psi \colon \widetilde M \to \widetilde M\) is Γ-equivariant, when Γ acts on the first copy of \(\widetilde M\) by τ and the second copy of \(\widetilde M\) by τ′. Let us denote the corresponding C ∗-algebras by \(C_{L,0}^\ast (\widetilde M)_{\tau }^\Gamma \) and \(C_{L,0}^\ast (\widetilde M)_{\tau '}^\Gamma \). Observe that, despite the two different actions of Γ on \(\widetilde M\), the two C ∗-algebras \(C_{L,0}^\ast (\widetilde M)_{\tau }^\Gamma \) and \( C_{L,0}^\ast (\widetilde M)_{\tau '}^\Gamma \) are canonically identical, since an operator is invariant under the action τ if and only if it is invariant under the action τ′.
- 7.
Precisely speaking, φ only defines an outer automorphism of Γ, and one needs to make a specific choice of a representative in Aut( Γ). In any case, any such choice will work for the proof.
- 8.
The C ∗-algebra \(C_{L,0}^\ast (E\Gamma )^\Gamma \) is the inductive limit of \(C_{L,0}^\ast (Y)^\Gamma \), where Y ranges over all Γ-cocompact subspaces of E Γ.
- 9.
Here “invertible” means being invertible on the universal cover of the manifold.
- 10.
- 11.
In fact, even more is true. One can use the same techniques developed in [CWXY] to show that if \(\mathcal A\) is smooth dense subalgebra of \(C_r^\ast (\Gamma )\) for any group Γ (not necessarily hyperbolic) and in addition \(\mathcal A\) is a Fréchet locally m-convex algebra, then there is a well-defined delocalized Connes–Chern character \(Ch_{deloc}\colon K_i(C^*_{L,0}(\widetilde M)^\Gamma )\to \overline {HC}^{deloc}_{\ast }(\mathcal A)\). Of course, in order to pair such a delocalized Connes–Chern character with a cyclic cocycle of \(\mathbb C\Gamma \), the key remaining challenge is to continuously extend this cyclic cocycle of \(\mathbb C\Gamma \) to a cyclic cocycle of \(\mathcal A\).
- 12.
Here the definition of cyclic homology of \(\mathcal B\) takes the topology of \(\mathcal B\) into account, cf. [C2, Section II.5].
References
P. Albin. Stratified surgery and K-theory invariants of the signature operator. https://arxiv.org/abs/1710.00934.
P. Albin, É. Leichtnam, R. Mazzeo, P. Piazza. The signature package on Witt spaces. Ann. Sci. Éc. Norm. Supér. (4) 45 (2012), no. 2, 241–310.
P. Albin, E. Leichtnam, R. Mazzeo, P. Piazza. The Novikov conjecture on Cheeger spaces. J. Noncommut. Geom. 11 (2017), no. 2, 451–506.
G. Arzhantseva, T. Delzant. Examples of random groups. Preprint, 2008.
M. Atiyah. Global theory of elliptic operators. 1970 Proc. Internat. Conf. on Functional Analysis and Related Topics (Tokyo, 1969) pp. 21–30 Univ. of Tokyo Press, Tokyo.
M. Atiyah. Elliptic operators, discrete groups and von Neumann algebras. Colloque “Analyse et Topologie” en l’Honneur de Henri Cartan (Orsay, 1974), pp. 43–72. Astérisque, No. 32–33, Soc. Math. France, Paris, 1976.
M. Atiyah, I. Singer. The index of elliptic operators. I. Ann. of Math. (2) 87 1968 484–530.
P. Antonini, S. Azzali, G. Skandalis. The Baum-Connes conjecture localised at the unit element of a discrete group. arXiv:1807.05892, 2018.
T. AustinRational group ring elements with kernels having irrational dimension. Proc. Lond. Math. Soc. (3), 107(6):1424–1448, 2013.
P. Baum, A. Connes. K-theory for discrete groups Operator algebras and applications, Vol. 1, volume 135 of London Mathematical Society, pages 1–20. Cambridge Univ. Press, Cambridge, 1988.
P. Baum, A. Connes, N. Higson. Classifying space for proper actions and K-theory of groupC ∗-algebras. C∗-algebras: 1943–1993 (San Antonio, TX, 1993), 240–291, Contemp. Math., 167, Amer. Math. Soc., Providence, RI, 1994.
A. Bartels, W. Lück. The Borel Conjecture for hyperbolic and CAT(0)-groups. Ann. of Math. (2) 175 (2012), no. 2, 631–689.
A. Bartels, W. Lück, R. Holger. The K-theoretic Farrell-Jones conjecture for hyperbolic groups. Invent. Math. 172 (2008), no. 1, 29–70.
A. Bartels, D. Rosenthal. On theK-theory of groups with finite asymptotic dimension. J. Reine Angew. Math. 612 (2007), 35–57.
G. Bell, A. Dranishnikov. On asymptotic dimension of groups. Algebr. Geom. Topol. 1 (2001), 57–71 (electronic).
G. Bell, A. Dranishnikov. A Hurewicz-type theorem for asymptotic dimension and applications to geometric group theory. Transactions American Math. Soc. Volume 358, Number 11, 2006, 4749–4764.
M. Bekka, P. Cherix, A. Valette. Proper affine isometric actions of amenable groups. Novikov conjectures, index theorems and rigidity, Vol. 2 (Oberwolfach, 1993), 1–4, London Math. Soc. Lecture Note Ser., 227, Cambridge Univ. Press, Cambridge, 1995.
M. Bestvina, K. Bromberg, K. Fujiwara. Constructing group actions on quasi-trees and applications to mapping class groups. Publ. Math. Inst. Hautes Études Sci. 122 (2015), 1–64.
M. Bestvina, V. Guirardel, C. Horbez. Boundary amenability of Out(F N). arXiv:1705.07017, 2017.
B. Botvinnik , P. B. Gilkey. The eta invariant and metrics of positive scalar curvature. Math. Ann., 302(3):507–517, 1995.
N. Brown, E. Guentner. Uniform embeddings of bounded geometry spaces into reflexive Banach space. Proc. Amer. Math. Soc. 133 (2005), no. 7, 2045–2050.
U. Bunke. A K-theoretic relative index theorem and Callias-type Dirac operators. Math. Ann., 303(2):241–279, 1995.
J. Block, S. Weinberger. Arithmetic manifolds of positive scalar curvature. J. Differential Geom. 52 (1999), no. 2, 375–406.
J. Block, S. Weinberger. Aperiodic tilings, positive scalar curvature and amenability of spaces. J. Amer. Math. Soc. 5 (1992), no. 4, 907–918.
S. Cappell, S. Weinberger. A geometric interpretation of Siebenmann’s periodicity phenomenon. In Geometry and topology (Athens, Ga., 1985), volume 105 of Lecture Notes in Pure and Appl. Math., pages 47–52. Dekker, New York, 1987.
G. Carlsson, B. Goldfarb. The integralK-theoretic Novikov conjecture for groups with finite asymptotic dimension. Invent. Math. 157 (2004), no. 2, 405–418.
G. Carlsson, E. Pedersen. Controlled algebra and the Novikov conjectures forK- andL-theory. Topology 34 (1995), no. 3, 731–758.
S. Chang, S. Ferry, G. Yu. Bounded rigidity of manifolds and asymptotic dimension growth. J. K-Theory 1 (2008), no. 1, 129–144.
S. Chang, S. Weinberger. On invariants of Hirzebruch and Cheeger-Gromov. Geom. Topol. 7 (2003), 311–319.
W. Charlotte. Higher-invariants and the surgery structure set. J. Topol. 6.
X. Chen, J. Wang, Z. Xie, Yu. Delocalized eta invariants, cyclic cohomology and higher rho invariants. arXiv:1901.02378, 2019.
A. Connes. Noncommutative Geometry. Academic Press, 1994.
A. Connes. Cyclic cohomology and the transverse fundamental class of a foliation. Geometric methods in operator algebras (Kyoto, 1983), pages 52–144, volume 123, Pitman Res. Notes Math. Ser., 1986.
A. Connes. Noncommutative differential geometry. Inst. Hautes Études Sci. Publ. Math., (62):257–360, 1985.
A. Connes. On the Chern character ofθsummable Fredholm modules. Comm. Math. Phys. 139 (1991), no. 1, 171–181.
A. Connes, N. Higson. Déformations, morphismes asymptotiques et K-théorie bivariante. (French) [Deformations, asymptotic morphisms and bivariant K-theory] C. R. Acad. Sci. Paris Sér. I Math. 311 (1990), no. 2, 101–106.
A. Connes, H. Moscovici. Cyclic cohomology, the Novikov conjecture and hyperbolic groups. Topology 29 (1990), no. 3, 345–388.
A. Connes, M. Gromov, H. Moscovici. Group cohomology with Lipschitz control and higher signatures. Geom. Funct. Anal. 3 (1993), no. 1, 1–78.
M. Davis. Groups generated by reflections and aspherical manifolds not covered by Euclidean space. Ann. of Math. (2) 117 (1983), no. 2, 293–324.
R. J. Deeley, M. Goffeng. Realizing the analytic surgery group of Higson and Roe geometrically part III: higher invariants. Math. Ann., 366(3-4):1513–1559, 2016.
A. Dranishnikov, S. Ferry, S. Weinberger. An etale approach to the Novikov conjecture. Comm. Pure Appl. Math. 61 (2008), no. 2, 139–155.
A. Dranishnikov, T. Januszkiewicz. Every Coxeter group acts amenably on a compact space. Proceedings of the 1999 Topology and Dynamics Conference (Salt Lake City, UT). Topology Proc. 24 (1999), Spring, 135–141.
F. T. Farrell, W. C. Hsiang. On Novikov’s conjecture for nonpositively curved manifolds. Ann. of Math. (2) 113 (1981), no. 1, 199–209.
T. Farrell, L. Jones. A topological analogue of Mostow’s rigidity theorem. J. Amer. Math. Soc. 2 (1989), no. 2, 257–370.
T. Farrell, L. Jones. Classical aspherical manifolds. CBMS Regional Conference Series in Mathematics, 75. Published for the Conference Board of the Mathematical Sciences, Washington, DC; by the American Mathematical Society, Providence, RI, 1990.
T. Farrell, L. Jones. Topological rigidity for compact non-positively curved manifolds. Differential geometry: Riemannian geometry (Los Angeles, CA, 1990), 229–274, Proc. Sympos. Pure Math., 54, Part 3, Amer. Math. Soc., Providence, RI, 1993.
T. Farrell, L. Jones. Rigidity for aspherical manifolds withπ 1 ⊂GLm(R). Asian J. Math. 2 (1998), no. 2, 215–262.
A. T. Fomenko, A. S. Mishchenko. The index of elliptic operators overC ∗-algebras. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 43 (1979), no. 4, 831–859, 967.
S. Ferry, E. Pedersen. Epsilon surgery theory. Novikov conjectures, index theorems and rigidity, Vol. 2 (Oberwolfach, 1993), 167–226, London Math. Soc. Lecture Note Ser., 227, Cambridge Univ. Press, Cambridge, 1995.
D. Fisher, L. Silberman. Groups not acting on manifolds. Int. Math. Res. Not. IMRN 2008, no. 16, Art. ID rnn060, 11 pp.
S. Ferry, S. Weinberger. Curvature, tangentiality, and controlled topology. Invent. Math. 105 (1991), no. 2, 401–414.
S. Ferry, S. Weinberger. A coarse approach to the Novikov conjecture. Novikov conjectures, index theorems and rigidity, Vol. 1 (Oberwolfach, 1993), 147–163, London Math. Soc. Lecture Note Ser., 226, Cambridge Univ. Press, Cambridge, 1995.
S. Gong, J. Wu, G. Yu. The Novikov conjecture, the group of volume preserving diffeomorphisms and Hilbert-Hadamard spaces. arXiv:1811.02086, 2018.
R. I. Grigorchuk. Degrees of growth of finitely generated groups and the theory of invariant means. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 48 (1984), no. 5, 939–985.
M. Gromov. Hyperbolic groups. In Gersten, Steve M. Essays in group theory. Mathematical Sciences Research Institute Publications. 8. New York: Springer. pp. 75–263.
M. Gromov. Asymptotic invariants of infinite groups. Geometric group theory, Vol. 2 (Sussex, 1991), 1–295, London Math. Soc. Lecture Note Ser., 182, Cambridge Univ. Press, Cambridge, 1993.
M. Gromov. Spaces and questions. GAFA 2000 (Tel Aviv, 1999). Geom. Funct. Anal. 2000, Special Volume, Part I, 118–161.
M. Gromov. Random walks in random groups. Geom. Funct. Anal. 13 (2003), no. 1, 73–146.
M. Gromov, B. Lawson. The classification of simply connected manifolds of positive scalar curvature. Ann. of Math. (2), 111(3):423–434, 1980.
M. Gromov, B. Lawson. Positive scalar curvature and the Dirac operator on complete Riemannian manifolds. Inst. Hautes Études Sci. Publ. Math. No. 58 (1983), 83–196 (1984).
A. Gorokhovsky, H. Moriyoshi , P. Piazza. A note on the higher Atiyah-Patodi-Singer index theorem on Galois coverings. J. Noncommut. Geom., 10(1):265–306, 2016.
E. Guentner, N. Higson, S. Weinberger. The Novikov Conjecture for Linear Groups. Publ. Math. Inst. Hautes Études Sci. No. 101 (2005), 243–268.
E. Guentner, R. Tessera, G. Yu. A notion of geometric complexity and its application to topological rigidity. Invent. Math. 189 (2012), no. 2, 315–357.
E. Guentner, R. Willett, G. Yu. Dynamical complexity and controlled operator K-theory. Groups, Geometry and Dynamics, Vol. 7, 2 (2013) 377–402.
U. Hamenstädt. Geometry of the mapping class groups. I. Boundary amenability. Invent. Math. 175 (2009), no. 3, 545–609.
S. Hanke, T. Schick. The strong Novikov conjecture for low degree cohomology. Geom. Dedicata 135 (2008), 119–127.
N. Higson. Bivariant K-theory and the Novikov conjecture. Geom. Funct. Anal. 10 (2000), no. 3, 563–581.
N. Higson, G. Kasparov. E -theory and KK-theory for groups which act properly and isometrically on Hilbert space. Invent. Math. 144 (2001), no. 1, 23–74.
N. Higson, J. Roe. Mapping surgery to analysis. I. Analytic signatures. K-Theory, 33(4):277–299, 2005.
N. Higson, J. Roe. Mapping surgery to analysis. II. Geometric signatures. K-Theory, 33(4):301–324, 2005.
N. Higson, J. Roe. Mapping surgery to analysis. III. Exact sequences. K-Theory, 33(4):325–346, 2005.
N. Higson, J. Roe. N. Higson and J. Roe. K-homology, assembly and rigidity theorems for relative eta invariants. Pure Appl. Math. Q., 6 (2, Special Issue: In honor of Michael Atiyah and Isadore Singer):555–601, 2010.
N. Higson, V. Lafforgue, G. Skandalis. Counterexamples to the Baum-Connes conjecture. Geom. Funct. Anal. 12 (2002), no. 2, 330–354.
M. Hilsum, G. Skandalis. Georges Invariance par homotopie de la signature à coefficients dans un fibré presque plat. (French) [Homotopy invariance of the signature with coefficients in an almost flat fiber bundle]. J. Reine Angew. Math. 423 (1992), 73–99.
L. Ji. The integral Novikov conjectures for linear groups containing torsion elements. J. Topol. 1 (2008), no. 2, 306–316.
W. B. Johnson, N. L. Randrianarivony. l p (p > 2) does not coarsely embed into a Hilbert space. Proc. Amer. Math. Soc. 134 (2006), 1045–1050 (electronic).
J. Kaminker, J. Miller. Homotopy invariance of the analytic index of signature operators over C ∗-algebras. J. Operator Theory, 14(1):113–127, 1985.
G. Kasparov. Equivariant KK-theory and the Novikov conjecture. Invent. Math. 91 (1988), no. 1, 147–201.
G. Kasparov. K-theory, group C ∗-algebras, and higher signatures (conspectus). In Novikov conjectures, index theorems and rigidity, Vol. 1 (Oberwolfach, 1993), volume 226 of London Math. Soc. Lecture Note Ser., pages 101–146. Cambridge Univ. Press, Cambridge, 1995.
G. Kasparov, G. Skandalis. Groups acting properly on “bolic” spaces and the Novikov conjecture. Ann. of Math. (2) 158 (2003), no. 1, 165–206.
R. C. Kirby, L. C. Siebenmann. Foundational essays on topological manifolds, smoothings, and triangulations. With notes by John Milnor and Michael Atiyah. Annals of Mathematics Studies, No. 88. Princeton University Press, Princeton, N.J.; University of Tokyo Press, Tokyo, 1977. vii+355 pp.
G. Kasparov, G. Yu. The Novikov conjecture and geometry of Banach spaces. Geometry and Topology 16 (2012), no. 3, 1859–1880.
Y. Kida. The mapping class group from the viewpoint of measure equivalence theory. Mem. Amer. Math. Soc. 196 (2008), no. 916.
V. Lafforgue. K-théorie bivariante pour les algèbres de Banach et conjecture de Baum-Connes. (French) [Bivariant K-theory for Banach algebras and the Baum-Connes conjecture] Invent. Math. 149 (2002), no. 1, 1–95.
V. Lafforgue. La conjecture de Baum-Connes à coefficients pour les groupes hyperboliques. (French) [The Baum-Connes conjecture with coefficients for hyperbolic groups] J. Noncommut. Geom. 6 (2012), no. 1, 1–197.
E. Leichtnam, J. Lott, P. Piazza. On the homotopy invariance of higher signatures for manifolds with boundary. J. Differential Geom. 54 (2000), no. 3, 561–633.
E. Leichtnam, P. Piazza. Rho-classes, index theory and Stolz’ positive scalar curvature sequence. J. Topol. 7 (2014), no. 4, 965–1004.
E. Leichtnam, P. Piazza. On higher eta-invariants and metrics of positive scalar curvature. K-Theory, 24(4):341–359, 2001.
E. Leichtnam, P. Piazza. Spectral sections and higher Atiyah-Patodi-Singer index theory on Galois coverings. Geom. Funct. Anal. 8 (1998), no. 1, 17–58.
E. Leichtnam, P. Piazza. Homotopy invariance of twisted higher signatures on manifolds with boundary. Bull. Soc. Math. France, 127(2):307–331, 1999.
J. Lott. Higher eta-invariants. K-Theory, 6(3):191–233, 1992.
J. Lott. DelocalizedL 2-invariants. J. Funct. Anal., 169(1):1–31, 1999.
V. Mathai. The Novikov conjecture for low degree cohomology classes. Geom. Dedicata 99 (2003), 1–15.
I. Mineyev, G. Yu. The Baum-Connes conjecture for hyperbolic groups. Invent. Math. 149 (2002), no. 1, 97–122.
A. S. Mishchenko. Infinite-dimensional representations of discrete groups, and higher signatures. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 38 (1974), 81–106.
M. Manor, A. Naor. Metric cotype. Ann. of Math. (2) 168 (2008), no. 1, 247–298.
A. Nica. Induction theorems for groups of homotopy manifold structures. Mem. Amer. Math. Soc., 39(267):vi+108, 1982.
V. Nistor. Group cohomology and the cyclic cohomology of crossed products. Invent. Math., 99(2):411–424, 1990.
S. P. Novikov. Algebraic construction and properties of Hermitian analogs of k-theory over rings with involution from the point of view of Hamiltonian formalism. Some applications to differential topology and to the theory of characteristic classes. Izv. Akad. Nauk SSSR, v. 34, 1970 I N2, pp. 253–288; II: N3, pp. 475–500.
S. P. Novikov. Topological invariance of rational classes of Pontrjagin. (Russian) Dokl. Akad. Nauk SSSR 163 1965 298–300.
P. Nowak, G. Yu. Large scale geometry. European Mathematical Society Publishing House, 2012.
D. Osajda. Small cancellation labellings of some infinite graphs and applications. arXiv:1406.5015, 2014.
H. Oyono-Oyono, G. Yu. On quantitative operator K-theory. Ann. Inst. Fourier (Grenoble) 65 (2015), no. 2, 605–674.
P. Piazza, T. Schick. Groups with torsion, bordism and rho invariants. Pacific J. Math., 232(2):355–378, 2007.
P. Piazza, T. Schick. Rho-classes, index theory and Stolz’ positive scalar curvature sequence. J. Topol. 7 (2014), no. 4, 965–1004.
P. Piazza, T. Schick. The surgery exact sequence, K-theory and the signature operator. Ann. K-Theory 1 (2016), no. 2.
P. Piazza, V. F. Zenobi. Singular spaces, groupoids and metrics of positive scalar curvature. J. Geom. Phys. 137.
M. Pimsner. KK-groups of crossed products by groups acting on trees. Invent. Math. 86 (1986), no. 3, 603–634.
M. Pimsner, D. Voiculescu. K-groups of reduced crossed products by free groups. J. Operator Theory 8 (1982), no. 1, 131–156.
M. Puschnigg. The Kadison-Kaplansky conjecture for word-hyperbolic groups. Invent. math. 149 (2002), 153–194.
M. Puschnigg. New holomorphically closed subalgebras ofC ∗-algebras of hyperbolic groups. Geom. Funct. Anal. 20 (2010), no. 1, 243–259.
Y. Qiao, J. Roe. On the localization algebra of Guoliang Yu. Forum Math. 22 (2010), no. 4, 657–665.
D. Ramras, R. Tessera, G. Yu. Finite decomposition complexity and the integral Novikov conjecture for higher algebraic K-theory. J. Reine Angew. Math. 694 (2014), 129–178.
J. Roe. Coarse cohomology and index theory on complete Riemannian manifolds. Mem. Amer. Math. Soc. 104 (1993), no. 497.
J. Roe. Index theory, coarse geometry, and topology of manifolds. CBMS Regional Conference Series in Mathematics, 90. Published for the Conference Board of the Mathematical Sciences, Washington, DC; by the American Mathematical Society, Providence, RI, 1996.
J. Roe, Hyperbolic groups have finite asymptotic dimension. Proc. Amer. Math. Soc. 133 (2005), no. 9, 2489–2490.
J. Roe, Positive curvature, partial vanishing theorems, and coarse indices. Proc. Edinb. Math. Soc. (2) 59 (2016), no. 1, 223–233.
J. Rosenberg. C ∗-algebras, positive scalar curvature, and the Novikov conjecture. Inst. Hautes Études Sci. Publ. Math. No. 58 (1983), 197–212 (1984).
J. Rosenberg. Manifolds of positive scalar curvature: a progress report. Surveys in differential geometry. Vol. XI, 259–294, Surv. Differ. Geom., 11, Int. Press, Somerville, MA, 2007.
J. Rosenberg. Analytic Novikov for topologists. Novikov conjectures, index theorems and rigidity, Vol. 1 (Oberwolfach, 1993), 338–372, London Math. Soc. Lecture Note Ser., 226, Cambridge Univ. Press, Cambridge, 1995.
J. Rosenberg, S. Stolz. Metrics of positive scalar curvature and connections with surgery. In Surveys on surgery theory, Vol. 2, volume 149 of Ann. of Math. Stud., pages 353–386. Princeton Univ. Press, Princeton, NJ, 2001.
J. Rosenberg, S. Weinberger. Higher G-indices and applications. Ann. Sci. École Norm. Sup. (4) 21 (1988), no. 4, 479–495.
Z. Sela. Uniform embeddings of hyperbolic groups in Hilbert spaces. Israel J. Math. 80 (1992), no. 1-2, 171–181.
J. -P. Serre. Linear representations of finite groups. Translated from the second French edition by Leonard L. Scott. Graduate Texts in Mathematics, Vol. 42. Springer-Verlag, New York-Heidelberg, 1977.
R. Schoen, S. T. YauOn the structure of manifolds with positive scalar curvature. Manuscripta Math., 28(1-3):159–183, 1979.
G. Skandalis, J. Tu, G. Yu. The coarse Baum-Connes conjecture and groupoids. Topology 41 (2002), no. 4, 807–834.
S. Stolz. Concordance classes of positive scalar curvature metrics. Preprint.
D. Sullivan. Hyperbolic geometry and homeomorphisms. Geometric topology (Proc. Georgia Topology Conf., Athens, Ga., 1977), pp. 543–555, Academic Press, New York-London, 1979.
C. Wahl. The Atiyah-Patodi-Singer index theorem for Dirac operators overC ∗-algebras. Asian J. Math., 17(2):265–319, 2013.
B.-L. Wang, H. Wang. Localized index and L 2-Lefschetz fixed-point formula for orbifolds. J. Differential Geom., 102(2):285–349, 2016.
S. Weinberger. Variations on a theme of Borel. Book draft, available at http://math.uchicago.edu/~shmuel/VTBdraft.pdf.
S. Weinberger. Aspects of the Novikov conjecture. Geometric and topological invariants of elliptic operators (Brunswick, ME, 1988), 281–297, Contemp. Math., 105, Amer. Math. Soc., Providence, RI, 1990.
S. Weinberger, Z. Xie, G. Yu. Additivity of higher rho invariants and nonrigidity of topological manifolds. To appear in Communications on Pure and Applied Mathematics.
S. Weinberger, G. Yu. Finite part of operator K-theory for groups finitely embeddable into Hilbert space and the degree of nonrigidity of manifolds. Geom. Topol. 19 (2015), no. 5, 2767–2799.
R. Willett, G. Yu. Higher index theory. Book draft, available at https://math.hawaii.edu/~rufus/Skeleton.pdf, 2018.
R. Willett, G. Yu. Higher index theory for certain expanders and Gromov monster groups, I. Adv. Math. 229 (2012), no. 3, 1380–1416.
R. Willett, G. Yu. Higher index theory for certain expanders and Gromov monster groups, II. Adv. Math. 229 (2012), no. 3, 1762–1803.
Z. Xie, G. Yu. Positive scalar curvature, higher rho invariants and localization algebras. Adv. Math. 262 (2014), 823–866.
Z. Xie, G. Yu. Higher rho invariants and the moduli space of positive scalar curvature metrics. Adv. Math. 307 (2017), 1046–1069.
Z. Xie, G. Yu. A relative higher index theorem, diffeomorphisms and positive scalar curvature. Adv. Math., 250: 35–73, 2014.
Z. Xie, G. Yu. Delocalized eta invariants, algebraicity, and K-theory of groupC ∗-algebras. arXiv:1805.07617.
Z. Xie, G. Yu, R. Zeidler. On the range of the relative higher index and the higher rho invariant for positive scalar curvature. arXiv:1712.03722.
G. Yu. Localization algebras and the coarse Baum-Connes conjecture. K-Theory 11 (1997), no. 4, 307–318.
G. Yu. The Novikov conjecture for groups with finite asymptotic dimension. Ann. of Math. (2) 147 (1998), no. 2, 325–355.
G. Yu. The coarse Baum-Connes conjecture for spaces which admit a uniform embedding into Hilbert space. Invent. Math. 139 (2000), no. 1, 201–240.
G. Yu. A characterization of the image of the Baum-Connes map. Quanta of maths, 649–657, Clay Math. Proc., 11, Amer. Math. Soc., Providence, RI, 2010.
R. Zeidler. Positive scalar curvature and product formulas for secondary index invariants. J. Topol. 2016.
V. Zenobi. Mapping the surgery exact sequence for topological manifolds to analysis. J. Topol. Anal. 9 (2017), no. 2, 329–361.
V. F. Zenobi. Adiabatic groupoid and secondary invariants in K-theory. Adv. Math. 347.
Acknowledgements
The authors wish to thank Alain Connes for numerous inspiring discussions. The author “Zhizhang Xie” is partially supported by NSF 1500823, NSF 1800737. The author “Guoliang Yu” is partially supported by NSF 1700021, NSF 1564398.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Xie, Z., Yu, G. (2019). Higher invariants in noncommutative geometry. In: Chamseddine, A., Consani, C., Higson, N., Khalkhali, M., Moscovici, H., Yu, G. (eds) Advances in Noncommutative Geometry. Springer, Cham. https://doi.org/10.1007/978-3-030-29597-4_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-29597-4_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-29596-7
Online ISBN: 978-3-030-29597-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


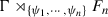 come from Γ.
come from Γ.