Non-Kählerian Compact Complex Surfaces

Abstract

This text follows the lecture series given by the author in the CIME School “Complex non-Kähler geometry” (Cetraro, July 9–13, 2018) and is dedicated to the classification of non-Kählerian surfaces. In the first three sections we present the classical theory:

• The Enriques Kodaira classification for surfaces and the classes of non-Kählerian surfaces,

• Class VII surfaces and their general properties,

• Kato surfaces: construction, classification and moduli.

In Sect. 3.4 we explain the main ideas and techniques used in the proofs of our results on the existence of cycles of curves on class VII surfaces with small b ₂. Section 3.5 deals with criteria for the existence of smooth algebraic deformations of the singular surface obtained by contracting a cycle of rational curves in a minimal class VII surface. We included an Appendix in which we introduce several fundamental objects in non-Kählerian complex geometry (the Picard group of a compact complex manifold, the Gauduchon degree, the Kobayashi-Hitchin correspondence for line bundles, unitary flat line bundles), and we prove basic properties of these objects.

Appendix

3.1.1 The Picard Group and the Gauduchon Degree

Let X be a connected, compact n-dimensional complex manifold. Recall that the Picard group Pic(X) of X is the group of isomorphism classes of holomorphic line bundles on X, and can be identified with $H^1(X,{\mathcal O}^*_X)$. The exponential short exact sequence gives the cohomology exact sequence

where the Neron-Severi group NS(X) is defined by

$$\displaystyle \begin{aligned}\mathrm{NS}(X):= \ker(H^2(X,{\mathbb Z})\to H^2(X,{\mathcal O}_X)). \end{aligned}$$

A class $c\in H^2(X,{\mathbb Z})$ belongs to NS(X) if and only if it can be represented by a closed real 2-form of type (1,1). Denoting by Pic⁰(X) the kernel of the Chern class morphism , we obtain a short exact sequence

(3.8)

and an identification

(3.9)

Remark 1

The image of $2\pi i H^1(X,{\mathbb Z})$ in $H^1(X,{\mathcal O}_X)$ is closed, in particular the quotient ${H^1(X,{\mathcal O}_X)}/{2\pi i H^1(X,{\mathbb Z})}$ has the structure of an Abelian connected complex Lie group.

Proof

The obvious embedding $2\pi i H^1(X,{\mathbb Z})\hookrightarrow H^1(X,{\mathcal O}_X)$ factorizes as

$$\displaystyle \begin{aligned}2\pi i H^1(X,{\mathbb Z})\hookrightarrow H^1(X,i{\mathbb R})\to H^1(X,{\mathcal O}_X). \end{aligned}$$

The coefficients formula shows that $2\pi i H^1(X,{\mathbb Z})$ is a lattice in $H^1(X,i{\mathbb R})$, in particular it is closed in this real vector space. On the other hand, using de Rham and Dolbeault theorems, it is easy to prove that the ${\mathbb R}$-linear morphism $H^1(X,i{\mathbb R})\to H^1(X,{\mathcal O}_X)$ is injective. Therefore $2\pi i H^1(X,{\mathbb Z})$ is closed in an ${\mathbb R}$-linear subspace of $H^1(X,{\mathcal O}_X)$, so it is closed in $H^1(X,{\mathcal O}_X)$. $\blacksquare$

Using (3.8) it follows that

Remark 2

Pic(X) has a natural structure of an Abelian complex Lie group, and Pic⁰(X) is the connected component of its unit element.

For a class c ∈NS(X) we put $\mathrm {Pic}^c(X):= \{[{\mathcal L}]\in \mathrm {Pic}(X)|\ c_1({\mathcal L})=c\}$, and

$$\displaystyle \begin{aligned}\mathrm {Pic}^T(X):= \{[{\mathcal L}]\in \mathrm {Pic}(X)|\ c_1({\mathcal L})\in\mathrm{Tors}\}. \end{aligned}$$

Recall that a Gauduchon metric on X is a Hermitian metric g on X whose Kähler form ω _g satisfies $dd^c \omega _g^{n-1}=0$. An important theorem of Gauduchon states that any conformal class of Hermitian metrics on X contains a Gauduchon metric (which is unique up to constant factor if n⩾2), so there is no obstruction to the existence of Gauduchon metrics.

The degree map associated with a Gauduchon metric g on X is the group morphism

$$\displaystyle \begin{aligned}\mathrm {deg}_g:\mathrm {Pic}(X)\to {\mathbb R} \end{aligned}$$

defined by

$$\displaystyle \begin{aligned} \mathrm {deg}_g({\mathcal L}):= \int_X \frac{i}{2\pi} F_{A_h}\wedge \omega_g^{n-1}, \end{aligned} $$

(3.10)

where h is a Hermitian metric on $\mathcal {L}$, and $F_{A_h}\in iA^{1,1}(X)$ is the curvature of the Chern connection A _h associated with the pair $({\mathcal L},h)$. Changing h will modify the Chern form $c_1({\mathcal L},h):= \frac {i}{2\pi } F_{A_h}$ by a dd ^c-exact form. Since g is Gauduchon, the right hand term of (3.10) is independent of h, so deg_g is well defined.

3.1.2 The Kobayashi-Hitchin Correspondence for Line Bundles

Let (X, g) be a connected, compact complex manifold endowed with a Gauduchon metric. We denote by $\Lambda ^{p,q}_X$ the bundle of (p, q)-forms on X, and by $\Lambda _g:\Lambda ^{p,q}_X\to \Lambda ^{p-1,q-1}_X$ the adjoint of the wedge product operator $\omega _g\wedge \cdot : \Lambda ^{p-1,q-1}_X\to \Lambda ^{p,q}_X$. The same symbol Λ_g will be used for the induced operator A ^{p, q}(X) → A ^{p−1, q−1}(X) between spaces of global forms. Denoting by $\mathrm {vol}_g=\frac {1}{n!}\omega _g^{n}$ the volume form on X, and using the identity Λ_g ω _g = n, we obtain easily the identity

$$\displaystyle \begin{aligned} \alpha\wedge \omega^{n-1}_g=(n-1)!(\Lambda_g \alpha) \mathrm{vol}_g\ \forall \alpha\in A^2(X,{\mathbb C}). \end{aligned} $$

(3.11)

Definition 3

Let ${\mathcal L}$ be a holomorphic line bundle on X. A Hermitian metric h on ${\mathcal L}$ is called Hermitian-Einstein if the real function $i\Lambda _g F_{A_h}$ is constant. If this is the case, this constant is called the Einstein constant of h and is denoted c _h.

Applying (3.11) to $i F_{A_h}=2\pi c_1({\mathcal L},h)$ we obtain the following formula

$$\displaystyle \begin{aligned} c_h=\frac{2\pi}{(n-1)!\mathrm{Vol}_g(X)}\mathrm {deg}_g({\mathcal L}) \end{aligned} $$

(3.12)

for the Einstein constant of a Hermitian-Einstein connection on ${\mathcal L}$. Therefore a Hermitian metric h on ${\mathcal L}$ is Hermitian-Einstein if and only if

$$\displaystyle \begin{aligned}i\Lambda_g F_{A_h}=\frac{2\pi}{(n-1)!\mathrm{Vol}_g(X)}\mathrm {deg}_g({\mathcal L}). \end{aligned}$$

Proposition 4

Let ${\mathcal L}$ be a holomorphic line bundle on X. Then ${\mathcal L}$ admits a Hermitian-Einstein metric h, which is unique up to constant factor.

Proof

Let h ₀ be an arbitrary Hermitian metric on ${\mathcal L}$, and let $u\in {\mathcal C}^\infty (X,{\mathbb R})$. The metric h = e ^u h ₀ is Hermite-Einstein if and only if

$$\displaystyle \begin{aligned}\Lambda_g(i\bar\partial\partial u+ i F_{A_{h_0}})=\frac{2\pi}{(n-1)!\mathrm{Vol}_g(X)}\mathrm {deg}_g({\mathcal L}),\end{aligned}$$

i.e. if and only if u is a solution of the elliptic equation

$$\displaystyle \begin{aligned}i\Lambda_g\bar\partial\partial u=\frac{2\pi}{(n-1)!\mathrm{Vol}_g(X)}\mathrm {deg}_g({\mathcal L})-i \Lambda_gF_{A_{h_0}}. \end{aligned}$$

The definition of $\mathrm {deg}_g({\mathcal L})$ gives

$$\displaystyle \begin{aligned}\int_X \bigg(\frac{2\pi}{(n-1)!\mathrm{Vol}_g(X)}\mathrm {deg}_g({\mathcal L})-i \Lambda_gF_{A_{h_0}}\bigg)\mathrm{vol}_g=0, \end{aligned}$$

so the result follows from Lemma 5 below (see [LT, Corollary 1.2.9]). $\blacksquare$

Lemma 5

Let (X, g) be a connected, compact complex manifold endowed with a Gauduchon metric. Denote by $\underline {{\mathbb R}}$ the line of constant real functions on X. The operator $P=i\Lambda _g\bar \partial \partial : A^0(X,{\mathbb R})\to A^0(X,{\mathbb R})$ has the following properties:

• (1) $\ker (P)= \underline {{\mathbb R}}$.

• (2) $\mathrm {im}(P)= \underline {{\mathbb R}}^{\bot }$ , where the symbol ^⊥ stands for the orthogonal complement with respect to the L ² -inner product.

Proof

• (1) Note first that P is a second order elliptic operator which vanishes on locally defined constant functions (has no 0-order terms in local coordinates). The maximum principle applies and shows that a function $u\in \ker (P)$ is constant around any local maximum. Therefore the non-empty closed subset $u^{-1}(u_{\max })\subset X$ where u attains its global maximum $u_{\max }$ is open in X. Since X is connected, it follows $u^{-1}(u_{\max })=X$, so u is constant.

• (2) Since g is Gauduchon it follows easily that $\underline {{\mathbb R}}\subset \mathrm {im}(P)^\bot$. On the other hand, the symbol of P is self-adjoint, so the index of P vanishes. Taking into account (1) it follows that $\dim (\mathrm {im}(P)^\bot )=1$, so the inclusion $\underline {{\mathbb R}}\subset \mathrm {im}(P)^\bot$ is an equality.

$\blacksquare$

Proposition 4 has an important interpretation in terms of moduli spaces. In order to explain this interpretation, we will change the point of view and we will consider variable unitary connections on a fixed differentiable Hermitian line bundle. Let (L, h) be a differentiable Hermitian line bundle on X, and let ${\mathcal A}(L,h)$ be the set of unitary connection on (L, h). This set is an affine space over the linear space $A^1(X,i{\mathbb R})$ of $i{\mathbb R}$-valued 1-forms on X, so it has a natural Fréchet topology. The gauge real group ${\mathcal C}^\infty (X,\mathrm {S}^1)$ acts on ${\mathcal A}(L,h)$ in the obvious way: denoting by

$$\displaystyle \begin{aligned}d_A:A^0(L)\to A^1(L)\end{aligned}$$

the linear connection associated with A, the gauge action on ${\mathcal A}(L,h)$ satisfies the identity:

$$\displaystyle \begin{aligned}d_{f\cdot A}= f\circ d_A\circ f^{-1}=d_A-df f^{-1}. \end{aligned}$$

The quotient ${\mathcal M}(L,h):= {\mathcal A}(L,h)/{\mathcal C}^\infty (X,\mathrm {S}^1)$, endowed with the quotient topology, is called the moduli space of unitary connections on (L, h). It is an infinite dimensional Hausdorff space [Te4].

Definition 6

Let (L, h) be a differentiable Hermitian line bundle on X with c ₁(L) ∈NS(X). A unitary connection A on (L, h) is called Hermitian-Einstein if the curvature form $F_{A_h}$ has type (1,1) and i Λ_g F _A is constant.

The Hermite-Einstein condition is gauge invariant so, denoting by ${\mathcal A}^{\mathrm {HE}}(L,h)\subset {\mathcal A}(L,h)$ the subspace of Hermitian-Einstein on (L, h), we obtain a closed subspace

$$\displaystyle \begin{aligned}{\mathcal M}^{\mathrm{HE}}(L,h)\to {\mathcal M}(L,h) \end{aligned}$$

called the moduli space of Hermitian-Einstein on (L, h).

Let $\bar \partial _A:A^0(L)\to A^{0,1}(L)$ be the second component of the first order differential operator d _A : A ⁰(L) → A ¹(L) = A ^{1, 0}(L) ⊕ A ^{0, 1}(L). The first condition in Definition 6 means that $\bar \partial _A^2=0$, so $\bar \partial _A$ defines a holomorphic structure ${\mathcal L}_A$ on L; the corresponding sheaf of holomorphic sections is given by

$$\displaystyle \begin{aligned}{\mathcal L}_A(U)=\{s\in \Gamma(U,L)|\ \bar\partial_A s=0\} \end{aligned}$$

for open sets U ⊂ X. The assignment $A\mapsto {\mathcal L}_A$ induces a well defined map

$$\displaystyle \begin{aligned}KH_{g,L,h}:{\mathcal M}^{\mathrm{HE}}(L,h)\to \mathrm {Pic}^{c_1(L)}(X) \end{aligned}$$

called the Kobayashi-Hitchin correspondence associated with (L, h). Proposition 4 can be reformulated as follows:

Corollary 7

Let (L, h) be a differentiable Hermitian line bundle on X with c ₁(L) ∈NS(X). The Kobayashi-Hitchin correspondence

$$\displaystyle \begin{aligned}KH_{g,L,h}:{\mathcal M}^{\mathrm{HE}}(L,h)\to \mathrm {Pic}^{c_1(L)}(X)\end{aligned}$$

is a homeomorphism.

For a class c ∈NS(X) let (L _c, h _c) be a differentiable Hermitian line bundle of Chern class c. The classification theorem for differentiable S¹-bundles shows that (L _c, h _c) is well-defined up to unitary isomorphism.

Remark 8

Corollary 7 gives a homeomorphism

$$\displaystyle \begin{aligned}KH_g:{\mathcal M}^{\mathrm{HE}}:= \coprod_{c\in \mathrm{NS}(X)}{\mathcal M}^{\mathrm{HE}}(L_c,h_c)\to \mathrm {Pic}(X). \end{aligned}$$

The moduli space ${\mathcal M}^{\mathrm {HE}}$ has a natural group structure defined by tensor product of Hermite-Einstein connections and, with respect to this structure, KH _g is an isomorphism of real Lie groups.

3.1.3 Moduli Spaces of Flat S¹-Connections

Recall that a Hermitian line bundle (L, h) on a compact differentiable manifold X admits a unitary flat connection if and only if c ₁(L) ∈Tors. This follows easily using the cohomology exact sequence associated with the short exact sequence of constant sheaves on X

Therefore the moduli space ${\mathcal M}_{\mathrm {fl}}$ of flat S¹-connections on X decomposes as

$$\displaystyle \begin{aligned}{\mathcal M}_{\mathrm{fl}}=\coprod_{c\in \mathrm{Tors}} {\mathcal M}_{\mathrm{fl}}(L_c,h_c), \end{aligned}$$

where (L _c, h _c) is a Hermitian line bundle of Chern class c, and ${\mathcal M}_{\mathrm {fl}}(L_c,h_c)$ denotes the moduli space of flat unitary connections on (L _c, h _c). The classical classification theorem for flat connections gives an identification

given by the map hol which assigns to any flat connection its holonomy representation. Note that ${\mathcal M}_{\mathrm {fl}}$ has a natural Lie group structure, and fits in the short exact sequence

where ${\mathcal M}_{\mathrm {fl}}^0$ is the moduli space of flat unitary connections on the trivial Hermitian line bundle.

Remark 9

Let X be a compact differentiable manifold. The moduli space ${\mathcal M}_{\mathrm {fl}}^0$ is canonically isomorphic to the quotient $H^1(X,i{\mathbb R})/H^1(X,2\pi i{\mathbb Z})$-torsor, so it is a real torus of dimension b ₁(X). In particular ${\mathcal M}_{\mathrm {fl}}$ is compact, and the connected component of its unit element is the torus ${\mathcal M}_{\mathrm {fl}}^0$.

Let now X be a compact complex manifold, and g be a Gauduchon metric on X. Any flat connection on a Hermitian line bundle on X is obviously Hermite-Einstein, so we get an obvious inclusion ${\mathcal M}_{\mathrm {fl}}\hookrightarrow {\mathcal M}^{\mathrm {HE}}$ which identifies ${\mathcal M}_{\mathrm {fl}}$ with a subgroup of ${\mathcal M}^{\mathrm {HE}}$.

Remark 10

The images

$$\displaystyle \begin{aligned}\mathrm {Pic}_{\mathrm{ufl}}(X):= KH_g({\mathcal M}_{\mathrm{fl}}),\ \mathrm {Pic}_{\mathrm{ufl}}^0(X):= KH_g({\mathcal M}_{\mathrm{fl}}^0)\end{aligned}$$

of ${\mathcal M}_{\mathrm {fl}}$ (${\mathcal M}_{\mathrm {fl}}^0$) in Pic(X) (respectively Pic⁰(X)) are independent of g; the first (respectively second) image coincides with the subgroup of isomorphism classes of (topologically trivial) holomorphic line bundles ${\mathcal L}$ on X admitting a Hermitian metric h with A _h flat.

Corollary 11

Let X be a complex surface, and g be a Gauduchon metric on X. One has

In particular, the kernel is independent of the Gauduchon metric g, and is a compact Lie group of real dimension b ₁(X).

Proof

The inclusion is obvious and holds for manifolds of arbitrary dimension. Conversely, let $[{\mathcal L}]\in \mathrm {Pic}^T(X)$ with $\mathrm {deg}_g({\mathcal L})=0$. Remark 8 shows that ${\mathcal L}\simeq {\mathcal L}_A$ for a Hermite-Einstein connection $A\in {\mathcal A}^{\mathrm {HE}}(L_c)$, where $c:= c_1({\mathcal L})\in \mathrm {Tors}$. Since $\mathrm {deg}_g({\mathcal L})=0$, formula (3.12) gives i Λ_g F _A = 0. Taking into account that iF _A is a (1,1)-form, it follows that $\frac {i}{2\pi }F_A$ is an anti-selfdual 2-form on the compact, oriented Riemannian 4-manifold (X, g). Since this form is also closed, it follows that it is harmonic, so it coincides with the harmonic representative of the Chern class $c_1^{\mathrm {DR}}(L)$ in de Rham cohomology. But this de Rham class vanishes, because c ₁(L) ∈Tors. Therefore $\frac {i}{2\pi }F_A=0$, which shows that A is flat, so $[A]\in {\mathcal M}_{\mathrm {fl}}$, and $[{\mathcal L}]\in KH_g({\mathcal M}_{\mathrm {fl}})=\mathrm {Pic}_{\mathrm {ufl}}(X)$ as claimed. The other claims follow from Remarks 9 and 10. $\blacksquare$

The real dimension of Pic⁰(X) is 2q(X), where $q(X):= \dim (H^1(X,{\mathcal O}_X))$ is the irregularity of X. By Remark 9 the real dimension of $\mathrm {Pic}_{\mathrm {ufl}}^0(X)$ is b ₁(X). Taking into account Corollary 11 we obtain:

Corollary 12

Let X be a complex surface, and let q(X) be its irregularity.

• (1) One has 2q(X) − 1⩽b ₁(X)⩽2q(X).

• (2) If b ₁(X) is even, then b ₁(X) = 2q(X), Pic_ufl(X) = Pic^T(X) and the degree map associated with any Gauduchon metric on X is a topological invariant.

• (3) If b ₁(X) is odd, then b ₁(X) = 2q(X) − 1, Pic_ufl(X) has real codimension 1 in Pic^T(X) and the degree map associated with any Gauduchon metric on X induces an isomorphism

  

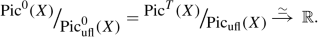
The identity

$$\displaystyle \begin{aligned}b_1(X)=\left\{ \begin{array}{ccc} 2q(X) &\mathrm{if} & b_1(X) \mbox{ is even},\\ 2q(X)-1 &\mathrm{if} & b_1(X) \mbox{ is odd}, \end{array} \right. \end{aligned}$$

is well known [BHPV]. Our proof uses gauge theoretical methods, and gives a geometric interpretation of this identity.