Abstract
Infinite-state systems such as distributed protocols are challenging to verify using interactive theorem provers or automatic verification tools. Of these techniques, deductive verification is highly expressive but requires the user to annotate the system with inductive invariants. To relieve the user from this labor-intensive and challenging task, invariant inference aims to find inductive invariants automatically. Unfortunately, when applied to infinite-state systems such as distributed protocols, existing inference techniques often diverge, which limits their applicability.
This paper proposes user-guided invariant inference based on phase invariants, which capture the different logical phases of the protocol. Users conveys their intuition by specifying a phase structure, an automaton with edges labeled by program transitions; the tool automatically infers assertions that hold in the automaton’s states, resulting in a full safety proof. The additional structure from phases guides the inference procedure towards finding an invariant.
Our results show that user guidance by phase structures facilitates successful inference beyond the state of the art. We find that phase structures are pleasantly well matched to the intuitive reasoning routinely used by domain experts to understand why distributed protocols are correct, so that providing a phase structure reuses this existing intuition.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others

1 Introduction
Infinite-state systems such as distributed protocols remain challenging to verify despite decades of work developing interactive and automated proof techniques. Such proofs rely on the fundamental notion of an inductive invariant. Unfortunately, specifying inductive invariants is difficult for users, who must often repeatedly iterate through candidate invariants before achieving an inductive invariant. For example, the Verdi project’s proof of the Raft consensus protocol used an inductive invariant with 90 conjuncts and relied on significant manual proof effort [61, 62].
The dream of invariant inference is that users would instead be assisted by automatic procedures that could infer the required invariants. While other domains have seen successful applications of invariant inference, using techniques such as abstract interpretation [18] and property-directed reachability [10, 21], existing inference techniques fall short for interesting distributed protocols, and often diverge while searching for an invariant. These limitations have hindered adoption of invariant inference.
Our Approach. The idea of this paper is that invariant inference can be made drastically more effective by utilizing user-guidance in the form of phase structures. We propose user-guided invariant inference, in which the user provides some additional information to guide the tool towards an invariant. An effective guidance method must (1) match users’ high-level intuition of the proof, and (2) convey information in a way that an automatic inference tool can readily utilize to direct the search. In this setting invariant inference turns a partial, high-level argument accessible to the user into a full, formal correctness proof, overcoming scenarios where procuring the proof completely automatically is unsuccessful.
Our approach places phase invariants at the heart of both user interaction and algorithmic inference. Phase invariants have an automaton-based form that is well-suited to the domain of distributed protocols. They allow the user to convey a high-level temporal intuition of why the protocol is correct in the form of a phase structure. The phase structure provides hints that direct the search and allow a more targeted generalization of states to invariants, which can facilitate inference where it is otherwise impossible.
This paper makes the following contributions:
-
(1)
We present phase invariants, an automaton-based form of safety proofs, based on the distinct logical phases of a certain view of the system. Phase invariants closely match the way domain experts already think about the correctness of distributed protocols by state-machine refinement à la Lamport [e.g. 43].
-
(2)
We describe an algorithm for inferring inductive phase invariants from phase structures. The decomposition to phases through the phase structure guides inference towards finding an invariant. The algorithm finds a proof over the phase structure or explains why no such proof exists. In this way, phase invariants facilitate user interaction with the algorithm.
-
(3)
Our algorithm reduces the problem of inferring inductive phase invariants from phase structures to the problem of solving a linear system of Constrained Horn Clauses (CHC), irrespective of the inference technique and the logic used. In the case of universally quantified phase inductive invariants for protocols modeled in EPR (motivated by previous deductive approaches [50, 51, 60]), we show how to solve the resulting CHC using a variant of \(\text {PDR}^\forall \) [40].
-
(4)
We apply this approach to the inference of invariants for several interesting distributed protocols. (This is the first time invariant inference is applied to distributed protocols modeled in EPR.) In the examples considered by our evaluation, transforming our high-level intuition about the protocol into a phase structure was relatively straightforward. The phase structures allowed our algorithm to outperform in most cases an implementation of \(\text {PDR}^\forall \) that does not exploit such structure, facilitating invariant inference on examples beyond the state of the art and attaining faster convergence.
Overall, our approach demonstrates that the seemingly inherent intractability of sifting through a vast space of candidate invariants can be mitigated by leveraging users’ high-level intuition.
2 Preliminaries
In this section we provide background on first-order transition systems. Sorts are omitted for simplicity. Our results extend also to logics with a background theory.
Notation. \(\textit{FV}({\varphi })\) denotes the set of free variables of \(\varphi \). \(\mathcal {F}_{\varSigma }(V)\) denotes the set of first-order formulas over vocabulary \(\varSigma \) with \(\textit{FV}({\varphi }) \subseteq V\). We write \(\forall \mathcal {V}.\ \varphi \Longrightarrow \psi \) to denote that the formula \(\forall \mathcal {V}.\ \varphi \rightarrow \psi \) is valid. We sometimes use \(f_a\) as a shorthand for f(a).
Transition Systems. We represent transition systems symbolically, via formulas in first-order logic. The definitions are standard. A vocabulary \(\varSigma \) consisting of constant, function, and relation symbols is used to represent states. Post-states of transitions are represented by a copy of \(\varSigma \) denoted \(\varSigma ' = \{ a' \mid a \in \varSigma \}\). A first-order transition system over \(\varSigma \) is a tuple \({\textit{TS}}= (\textit{Init}, {\textit{TR}})\), where \(\textit{Init}\in \mathcal {F}_{\varSigma }(\emptyset )\) describes the initial states, and \({\textit{TR}}\in \mathcal {F}_{\hat{\varSigma }}(\emptyset )\) with \(\hat{\varSigma }= \varSigma \uplus \varSigma '\) describes the transition relation. The states of \({\textit{TS}}\) are first-order structures over \(\varSigma \). A state \({s}\) is initial if \({s}\,\models \,\textit{Init}\). A transition of \({\textit{TS}}\) is a pair of states \({s}_1,{s}_2\) over a shared domain such that \(({s}_1,{s}_2)\,\models \,{\textit{TR}}\), \((s_1,s_2)\) being the structure over that domain in which \(\varSigma \) in interpreted as in \({s}_1\) and \(\varSigma '\) as in \({s}_2\). \({s}_1\) is also called the pre-state and \({s}_2\) the post-state. Traces are finite sequences of states \(\sigma _1, \sigma _2, \ldots \) starting from an initial state such that there is a transition between each pair of consecutive states. The reachable states are those that reside on traces starting from an initial state.
Safety. A safety property \(P\) is a formula in \(\mathcal {F}_{\varSigma }(\emptyset )\). We say that \({\textit{TS}}\) is safe, and that \(P\) is an invariant, if all the reachable states satisfy \(P\). \(\textit{Inv}\in \mathcal {F}_{\varSigma }(\emptyset )\) is an inductive invariant if (i) \(\textit{Init}\Longrightarrow \textit{Inv}\) (initiation), and (ii) \(\textit{Init}\wedge {\textit{TR}}\Longrightarrow \textit{Inv}'\) (consecution), where \(\textit{Inv}'\) is obtained from \(\textit{Inv}\) by replacing each symbol from \(\varSigma \) with its primed counterpart. If also (iii) \(\textit{Inv}\Longrightarrow P\) (safety), then it follows that \({\textit{TS}}\) is safe.
3 Running Example: Distributed Key-Value Store
We begin with a description of the running example we refer to throughout the paper.
The sharded key-value store with retransmissions (KV-R), adapted from IronFleet [33, §5.2.1], is a distributed hash table where each node owns a subset of the keys, and keys can be dynamically transferred among nodes to balance load. The safety property ensures that each key is globally associated with one value, even in the presence of key transfers. Messages might be dropped by the network, and the protocol uses retransmissions and sequence numbers to maintain availability and safety.
Figure 1 shows code modeling the protocol in a relational first-order language akin to Ivy [45], which compiles to EPR transition systems. The state of nodes and the network is modeled by global relations. Lines 1 to 4 declare uninterpreted sorts for keys, values, clients, and sequence numbers. Lines 6 to 14 describe the state, consisting of: (i) local state of clients pertaining to the table (which nodes are \(\mathtt {owner}\)s of which keys, and the local shard of the \(\mathtt {table}\) mapping keys to values); (ii) local state of clients pertaining to sent and received messages (\(\mathtt {seqnum\_sent}\), \(\mathtt {unacked}\), \(\mathtt {seqnum\_recvd}\)); and (iii) the state of the network, comprised of two kinds of messages (\(\mathtt {transfer\_msg}\), \(\mathtt {ack\_msg}\)). Each message kind is modeled as a relation whose first two arguments indicate the source and destination of the message, and the rest carry the message’s payload. For example, \(\mathtt {ack\_msg}\) is a relation over two nodes and a sequence number, with the intended meaning that a tuple \((c_1, c_2, s)\) is in \(\mathtt {ack\_msg}\) exactly when there is a message in the network from \(c_1\) to \(c_2\) acknowledging a message with sequence number s.
The initial states are specified in Lines 17 to 18. Transitions are specified by the actions declared in Lines 20 to 66. Actions can fire nondeterministically at any time when their precondition (\(\mathtt {require}\) statements) holds. Hence, the transition relation comprises of the disjunction of the transition relations induced by the actions. The state is mutated by modifying the relations. For example, message sends are modeled by inserting a tuple into the corresponding relation (e.g. line 27), while message receives are modeled by requiring a tuple to be in the relation (e.g. line 32), and then removing it (e.g. line 33). The updates in lines 61 and 65 remove a set of tuples matching the pattern.
Transferring keys between nodes begins by sending a \(\mathtt {transfer\_msg}\) from the owner to a new node (line 20), which stores the key-value pair when it receives the message (line 39). Upon sending a transfer message the original node cedes ownership (line 26) and does not send new transfer messages. Transfer messages may be dropped (line 30). To ensure that the key-value pair is not lost, retransmissions are performed (line 35) with the same sequence number until the target node acknowledges (which occurs in line 47). Acknowledge messages themselves may be dropped (line 53). Sequence numbers protect from delayed transfer messages, which might contain old values (line 42).
Lines 68 to 71 specify the key safety property: at most one value is associated with any key, anywhere in the network. Intuitively, the protocol satisfies this because each key k is either currently (1) owned by a node, in which case this node is unique, or (2) it is in the process of transferring between nodes, in which case the careful use of sequence numbers ensures that the destination of the key is unique. As is typical, it is not straightforward to translate this intuition into a full correctness proof. In particular, it is necessary to relate all the different components of the state, including clients’ local state and pending messages.
Invariant inference strives to automatically find an inductive invariant establishing safety. This example is challenging for existing inference techniques (Sect. 6). This paper proposes user-guided invariant inference based on phase-invariants to overcome this challenge. The rest of the paper describes our approach, in which inference is provided with the phase structure in Fig. 2, matching the high level intuitive explanation above. The algorithm then automatically infers facts about each phase to obtain an inductive invariant. Sect. 4 describes phase structures and inductive phase invariants, and Sect. 5 explains how these are used in user-guided invariant inference.
4 Phase Structures and Invariants
In this section we introduce phase structures and inductive phase invariants. These are used for guiding automatic invariant inference in Sect. 5. Proofs appear in [24].
4.1 Phase Invariants
Definition 1
(Quantified Phase Automaton). A quantified phase automaton (phase automaton for short) over \(\varSigma \) is a tuple \(\mathcal {A}= (\mathcal {Q}, \iota , \mathcal {V}, \delta _{}, \varphi _{})\) where: \(\mathcal {Q}\) is a finite set of phases. \(\iota \in \mathcal {Q}\) is the initial phase. \(\mathcal {V}\) is a set of variables, called the automaton’s quantifiers. \(\delta _{}: \mathcal {Q}\times \mathcal {Q}\rightarrow \mathcal {F}_{\hat{\varSigma }}(\mathcal {V})\) is a function labeling every pair of phases by a transition relation formula, such that \(\textit{FV}({\delta _{(q,p)}}) \subseteq \mathcal {V}\) for every \((q,p) \in \mathcal {Q}\times \mathcal {Q}\). \(\varphi _{}: \mathcal {Q}\rightarrow \mathcal {F}_{\varSigma }(\mathcal {V})\) is a function labeling every phase by a phase characterization formula, s.t. \(\textit{FV}({\varphi _{q}}) \subseteq \mathcal {V}\) for every \(q\in \mathcal {Q}\).
Intuitively, \(\mathcal {V}\) should be understood as free variables that are implicitly universally quantified outside of the automaton’s scope. For each assignment to these variables, the automaton represents the progress along the phases from the point of view of this assignment, and thus \(\mathcal {V}\) is also called the view (or view quantifiers).
We refer to \((\mathcal {Q}, \iota , \mathcal {V}, \delta _{})\), where \(\varphi _{}\) is omitted, as the phase structure (or the automaton structure) of \(\mathcal {A}\). We refer by the edges of \(\mathcal {A}\) to \( \mathcal {R}= \{(q,p) \in \mathcal {Q}\times \mathcal {Q}\mid \delta _{(q,p)} \not \equiv {\textit{false}}\}. \) A trace of \(\mathcal {A}\) is a sequence of phases \(q_0,\ldots ,q_n\) such that \(q_0 = \iota \) and \((q_i,q_{i+1}) \in \mathcal {R}\) for every \(0 \le i < n\). We say that \(\mathcal {A}\) is deterministic if for every \((q,p_1), (q,p_2) \in \mathcal {R}\) s.t. \(p_1 \ne p_2\), the formula \(\delta _{(q,p_1)} \wedge \delta _{(q,p_2)}\) is unsatisfiable.
Example 1
Figure 2 shows a phase automaton for the running example, with the view of a single key k. It describes the protocol as transitioning between two distinct (logical) phases of k: owned ( ) and transferring (\(\texttt {T}[k]\)). The edges are labeled by actions of the system. A wildcard * means that the action is executed with an arbitrary argument. The two central actions are (i) reshard, which transitions from
) and transferring (\(\texttt {T}[k]\)). The edges are labeled by actions of the system. A wildcard * means that the action is executed with an arbitrary argument. The two central actions are (i) reshard, which transitions from  to \(\texttt {T}[k]\), but cannot execute in \(\texttt {T}[k]\), and (ii) recv_transfer_message, which does the opposite. The rest of the actions do not cause a phase change and appear on a self loop in each phase. Actions related to keys other than k are considered as self-loops, and omitted here for brevity. Some actions are disallowed in certain phases, namely, do not label any outgoing edge from a phase, such as
to \(\texttt {T}[k]\), but cannot execute in \(\texttt {T}[k]\), and (ii) recv_transfer_message, which does the opposite. The rest of the actions do not cause a phase change and appear on a self loop in each phase. Actions related to keys other than k are considered as self-loops, and omitted here for brevity. Some actions are disallowed in certain phases, namely, do not label any outgoing edge from a phase, such as
 in
in  . Characterizations for each phase are depicted in Fig. 2 (bottom). Without them, Fig. 2 represents a phase structure, which serves as the input to our inference algorithm. We remark that the choice of automaton aims to reflect the safety property of interest. In our example, one might instead imagine taking the view of a single node as it interacts with multiple keys, which might seem intuitive from the standpoint of implementing the system. However, it is not appropriate for the proof of value uniqueness, since keys pass in and out of the view of a single client.
. Characterizations for each phase are depicted in Fig. 2 (bottom). Without them, Fig. 2 represents a phase structure, which serves as the input to our inference algorithm. We remark that the choice of automaton aims to reflect the safety property of interest. In our example, one might instead imagine taking the view of a single node as it interacts with multiple keys, which might seem intuitive from the standpoint of implementing the system. However, it is not appropriate for the proof of value uniqueness, since keys pass in and out of the view of a single client.
We now formally define phase invariants as phase automata that overapproximate the behaviors of the original system.
Definition 2
(Language of Phase Automaton). Let \(\mathcal {A}\) be a quantified phase automaton over \(\varSigma \), and \(\overline{\sigma } = \sigma _0,\ldots ,\sigma _n\) a finite sequence of states over \(\varSigma \), all with domain \({D}\). Let \(v: \mathcal {V}\rightarrow {D}\) be a valuation of the automaton quantifiers. We say that:
-
\(\overline{\sigma }, v\,\models \,\mathcal {A}\) if there exists a trace of phases \(q_0,\ldots ,q_n\) such that \((\sigma _i, \sigma _{i+1}), v\,\models \,\delta _{(q_i, q_{i+1})}\) for every \(0 \le i < n\) and \(\sigma _i, v\,\models \,\varphi _{q_i}\) for every \(0 \le i \le n\).
-
\(\overline{\sigma }\,\models \,\mathcal {A}\) if \(\overline{\sigma }, v\,\models \,\mathcal {A}\) for every valuation v.
The language of \(\mathcal {A}\) is \(\mathcal {L}(\mathcal {A}) = \{ \overline{\sigma } \mid \overline{\sigma }\,\models \,\mathcal {A}\}\).
Definition 3
(Phase Invariant). A phase automaton \(\mathcal {A}\) is a phase invariant for a transition system \({\textit{TS}}\) if \(\mathcal {L}({\textit{TS}}) \subseteq \mathcal {L}(\mathcal {A})\), where \(\mathcal {L}({\textit{TS}})\) denotes the set of finite traces of \({\textit{TS}}\).
Example 2
The phase automaton of Fig. 2 is a phase invariant for the protocol: intuitively, whenever an execution of the protocol reaches a phase, its characterizations hold. This fact may not be straightforward to establish. To this end we develop the notion of inductive phase invariants.
4.2 Establishing Safety and Phase Invariants with Inductive Phase Invariants
To establish phase invariants, we use inductiveness:
Definition 4
(Inductive Phase Invariant). \(\mathcal {A}\) is inductive w.r.t. \({\textit{TS}}= (\textit{Init}, {\textit{TR}})\) if:
-
Initiation: \(\textit{Init}\Longrightarrow \left( \forall \mathcal {V}. \ \varphi _{\iota }\right) \) .
-
Inductiveness: for all \((q,p) \in \mathcal {R}\), \(\forall \mathcal {V}. \ \left( \varphi _{q} \wedge \delta _{(q,p)} \Longrightarrow \varphi _{p}'\right) \).
-
Edge Covering: for every \(q\in \mathcal {Q}\), \(\forall \mathcal {V}. \ \left( \varphi _{q} \wedge {\textit{TR}}\Longrightarrow \bigvee _{(q,p) \in \mathcal {R}}{\delta _{(q,p)}}\right) \).
Example 3
The phase automaton in Fig. 2 is an inductive phase invariant. For example, the only disallowed transition in
 is recv_transfer_message, which indeed cannot execute in
is recv_transfer_message, which indeed cannot execute in
 according to the characterization in line 75. Further, if, for example, a protocol’s transition from
according to the characterization in line 75. Further, if, for example, a protocol’s transition from
 matches the labeling of the edge to
matches the labeling of the edge to
 (i.e. a reshard action on k), the post-state necessarily satisfies the characterizations of
(i.e. a reshard action on k), the post-state necessarily satisfies the characterizations of
 : for instance, the post-state satisfies the uniqueness of unreceived transfer messages (line 82) because in the pre-state there are none (line 75).
: for instance, the post-state satisfies the uniqueness of unreceived transfer messages (line 82) because in the pre-state there are none (line 75).
Lemma 1
If \(\mathcal {A}\) is inductive w.r.t. \({\textit{TS}}\) then it is a phase invariant for \({\textit{TS}}\).
Remark 1
The careful reader may notice that the inductiveness requirement is stronger than needed to ensure that the characterizations form a phase invariant. It could be weakened to require for every \(q\in \mathcal {Q}\): \( \forall \mathcal {V}. \ \varphi _{q} \wedge {\textit{TR}}\Longrightarrow \bigvee _{(q,p) \in \mathcal {R}}{\delta _{(q,p)} \wedge \varphi _{p}'}. \) However, as we explain in Sect. 5, our notion of inductiveness is crucial for inferring inductive phase automata, which is the goal of this paper. Furthermore, for deterministic phase automata, the two requirements coincide.
Inductive Invariants vs. Inductive Phase Invariants. Inductive invariants and inductive phase invariants are closely related:
Lemma 2
If \(\mathcal {A}\) is inductive w.r.t. \({\textit{TS}}\) then \( \forall \mathcal {V}. \ \bigvee _{q\in \mathcal {Q}}{\varphi _{q}} \) is an inductive invariant for \({\textit{TS}}\). If \(\textit{Inv}\) is an inductive invariant for \({\textit{TS}}\), then the phase automaton \(\mathcal {A}_{\textit{Inv}} = (\{q\}, \{q\}, \emptyset , \delta _{}, \varphi _{})\), where \(\delta _{(q,q)} = {\textit{TR}}\) and \(\varphi _{q} = \textit{Inv}\) is an inductive phase automaton w.r.t. \({\textit{TS}}\).
In this sense, phase inductive invariants are as expressive as inductive invariants. However, as we show in this paper, their structure can be used by a user as an intuitive way to guide an automatic invariant inference algorithm.
Safe Inductive Phase Invariants. Next we show that an inductive phase invariant can be used to establish safety.
Definition 5
(Safe Phase Automaton). Let \(\mathcal {A}\) be a phase automaton over \(\varSigma \) with quantifiers \(\mathcal {V}\). Then \(\mathcal {A}\) is safe w.r.t. \(\forall \mathcal {V}. \ \mathcal {P}\) if \(\forall \mathcal {V}. \ \left( \varphi _{q} \Longrightarrow \mathcal {P}\right) \) holds for every \(q\in \mathcal {Q}\).
Lemma 3
If \(\mathcal {A}\) is inductive w.r.t. \({\textit{TS}}\) and safe w.r.t. \(\forall \mathcal {V}. \ \mathcal {P}\) then \(\forall \mathcal {V}. \, \mathcal {P}\) is an invariant of \({\textit{TS}}\).
5 Inference of Inductive Phase Invariants
In this section we turn to the inference of safe inductive phase invariants over a given phase structure, which guides the search. Formally, the problem we target is:
Definition 6
(Inductive Phase Invariant Inference). Given a transition system \({\textit{TS}}= (\textit{Init}, {\textit{TR}})\), a phase structure \(\mathcal {S}= (\mathcal {Q}, \iota , \mathcal {V}, \delta _{})\) and a safety property \(\forall \mathcal {V}. \ \mathcal {P}\), all over \(\varSigma \), find a safe inductive phase invariant \(\mathcal {A}\) for \({\textit{TS}}\) over the phase structure S, if one exists.
Example 4
Inference of an inductive phase invariant is provided with the phase structure in Fig. 2, which embodies an intuitive understanding of the different phases the protocol undergoes (see Example 1). The algorithm automatically finds phase characterizations forming a safe inductive phase invariant over the user-provided structure. We note that inference is valuable even after a phase structure is provided: in the running example, finding an inductive phase invariant is not easy; in particular, the characterizations in Fig. 2 relate different parts of the state and involve multiple quantifiers.
5.1 Reduction to Constrained Horn Clauses
We view each unknown phase characterization, \(\varphi _{q}\), which we aim to infer for every \(q\in \mathcal {Q}\), as a predicate \(I_q\). The definition of a safe inductive phase invariant induces a set of second-order Constrained Horn Clauses (CHC) over \(I_q\):
where \(\mathcal {V}\) denotes the quantifiers of \(\mathcal {A}\). All the constraints are linear, namely at most one unknown predicate appears at the lefthand side of each implication.
Constraint (4) captures the original safety requirement, whereas (3) can be understood as additional safety properties that are specified by the phase automaton (since no unknown predicates appear in the righthand side of the implications).
A solution \(\mathbf {I}\) to the CHC system associates each predicate \(I_q\) with a formula \(\psi _q\) over \(\varSigma \) (with \(\textit{FV}({\psi _q}) \subseteq \mathcal {V}\)) such that when \(\psi _q\) is substituted for \(I_q\), all the constraints are satisfied (i.e., the corresponding first-order formulas are valid). A solution to the system induces a safe inductive phase automaton through characterizing each phase \(q\) by the interpretation of \(I_q\), and vice versa. Formally:
Lemma 4
Let \(\mathcal {A}= (\mathcal {Q}, \mathcal {R}, \iota , \mathcal {V}, \delta _{}, \varphi _{})\) with \(\varphi _{q} = {\mathbf {I}}_q\). Then \(\mathcal {A}\) is a safe inductive phase invariant wrt. \({\textit{TS}}\) and \(\forall \mathcal {V}.\ \mathcal {P}\) if and only if \(\mathbf {I}\) is a solution to the CHC system.
Therefore, to infer a safe inductive phase invariant over a given phase structure, we need to solve the corresponding CHC system. In Sect. 6.1 we explain our approach for doing so for the class of universally quantified phase characterizations. Note that the weaker definition of inductiveness discussed in Remark 1 would prevent the reduction to CHC as it would result in clauses that are not Horn clauses.
Completeness of Inductive Phase Invariants. There are cases where a given phase structure induces a safe phase invariant \(\mathcal{A}\), but not an inductive one, making the CHC system unsatisfiable. However, a strengthening into an inductive phase invariant can always be used to prove that \(\mathcal {A}\) is an invariant if (i) the language of invariants is unrestricted, and (ii) the phase structure is deterministic, namely, does not cover the same transition in two outgoing edges. Determinism of the automaton does not lose generality in the context of safety verification since every inductive phase automaton can be converted to a deterministic one; non-determinism is in fact unbeneficial as it mandates the same state to be characterized by multiple phases (see also Remark 1). These topics are discussed in detail in the extended version [24].
Remark 2
Each phase is associated with a set of states that can reach it, where a state \(\sigma \) can reach phase \(q\) if there is a sequence of program transitions that results in \(\sigma \) and can lead to \(q\) according to the automaton’s transitions. This makes a phase structure different from a simple syntactical disjunctive template for inference, in which such semantic meaning is unavailable.
5.2 Phase Structures as a Means to Guide Inference
The search space of invariants over a phase structure is in fact larger than that of standard inductive invariants, because each phase can be associated with different characterizations. Sometimes the disjunctive structure of the phases (Lemma 2) uncovers a significantly simpler invariant than exists in the syntactical class of standard inductive invariants explored by the algorithm, but this is not always the case.Footnote 1 Nonetheless, the search for an invariant over the structure is guided, through the following aspects:
-
(1)
Phase decomposition. Inference of an inductive phase invariant aims to find characterizations that overapproximate the set of states reachable in each phase (Remark 2). The distinction between phases is most beneficial when there is a considerable difference between the sets associated with different phases and their characterizations. For instance, in the running example, all states without unreceived transfer messages are associated with
 , whereas all states in which such messages exist are associated with
, whereas all states in which such messages exist are associated with 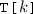 —a distinction captured by the characterizations in lines 75 and 82 in Fig. 2.
—a distinction captured by the characterizations in lines 75 and 82 in Fig. 2.Differences between phases would have two consequences. First, since each phase corresponds to fewer states than all reachable states, generalization—the key ingredient in inference procedures—is more focused. The second consequence stems from the fact that inductive characterizations of different phases are correlated. It is expected that a certain property is more readily learnable in one phase, while related facts in other phases are more complex. For instance, the characterization in line 75 in Fig. 2 is more straightforward than the one in line 82. Simpler facts in one phase can help characterize an adjacent phase when the algorithm analyzes how that property evolves along the edge. Thus utilizing the phase structure can improve the gradual construction of overapproximations of the sets of states reachable in each phase.
-
(2)
Disabled transitions. A phase automaton explicitly states which transitions of the system are enabled in each phase, while the rest are disabled. Such impossible transitions induce additional safety properties to be established by the inferred phase characterizations. For example, the phase invariant in Fig. 2 forbids a
 in
in  , a fact that can trigger the inference of the characterization in line 75. These additional safety properties direct the search for characterizations that are likely to be important for the proof.
, a fact that can trigger the inference of the characterization in line 75. These additional safety properties direct the search for characterizations that are likely to be important for the proof. -
(3)
Phase-awareness. Finally, while a phase structure can be encoded in several ways (such as ghost code), a key aspect of our approach is that the phase decomposition and disabled transitions are explicitly encoded in the CHC system in Sect. 5.1, ensuring that they guide the otherwise heuristic search.
In Sect. 6.2 we demonstrate the effects of aspects (1)–(3) on guidance.
6 Implementation and Evaluation
In this section we apply invariant inference guided by phase structures to distributed protocols modeled in EPR, motivated by previous deductive approaches [50, 51, 60].
6.1 Phase-\(\text {PDR}^\forall \) for Inferring Universally Quantified Characterizations
We now describe our procedure for solving the CHCs system of Sect. 5.1. It either (i) returns universally quantified phase characterizations that induce a safe inductive phase invariant, (ii) returns an abstract counterexample trace demonstrating that this is not possible, or (iii) diverges.
EPR. Our procedure handles transition systems expressed using the extended Effectively PRopositional fragment (EPR) of first order logic [51, 52], and infers universally quantified phase characterizations. Satisfiability of (extended) EPR formulas is decidable, enjoys the finite-model property, and supported by solvers such as Z3 [46] and iProver [41].
Phase-\({{\varvec{PDR}}}^\forall \) . Our procedure is based on \(\text {PDR}^\forall \) [40], a variant of PDR [10, 21] that infers universally quantified inductive invariants. PDR computes a sequence of frames \(\mathcal {F}_0, \ldots , \mathcal {F}_n\) such that \(\mathcal {F}_i\) overapproximates the set of states reachable in i steps. In our case, each frame \(\mathcal {F}_i\) is a mapping from a phase \(q\) to characterizations. The details of the algorithm are standard for PDR; we describe the gist of the procedure in the extended version [24]. We only stress the following: Counterexamples to safety take into account the safety property as well as disabled transitions. Search for predecessors is performed by going backwards on automaton edges, blocking counterexamples from preceding phases to prove an obligation in the current phase. Generalization is performed w.r.t. all incoming edges. As in \(\text {PDR}^\forall \), proof obligations are constructed via diagrams [12]; in our setting these include the interpretation for the view quantifiers (see [24] for details).
Edge Covering Check in EPR. In our setting, Eqs. (1), (2) and (4) fall in EPR, but not Eq. (3). Thus, we restrict edge labeling so that each edge is labeled with a \({\textit{TR}}\) of an action, together with an alternation-free precondition. It then suffices to check implications between the preconditions and the entire \({\textit{TR}}\) (see the extended version [24]). Such edge labeling is sufficiently expressive for all our examples. Alternatively, sound but incomplete bounded quantifier instantiation [23] could be used, potentially allowing more complex decompositions of \({\textit{TR}}\).
Absence of Inductive Phase Characterizations. What happens when the user gets the automaton wrong? One case is when there does not exist an inductive phase invariant with universal phase characterizations over the given structure. When this occurs, our tool can return an abstract counterexample trace—a sequence of program transitions and transitions of the automaton (inspired by [40, 49])—which constitutes a proof of that fact (see the extended version [24]). The counterexample trace can assist the user in debugging the automaton or the program and modifying them. For instance, missing edges occurred frequently when we wrote the automata of Sect. 6, and we used the generated counterexample traces to correct them.
Another type of failure is when an inductive phase invariant exists but the automaton does not direct the search well towards it. In this case the user may decide to terminate the analysis and articulate a different intuition via a different phase structure. In standard inference procedures, the only way to affect the search is by modifying the transition system; instead, phase structures equip the user with an ability to guide the search.
6.2 Evaluation
We evaluate our approach for user-guided invariant inference by comparing Phase-\(\text {PDR}^\forall \) to standard \(\text {PDR}^\forall \). We implemented \(\text {PDR}^\forall \) and Phase-\(\text {PDR}^\forall \) in mypyvy [2], a new system for invariant inference inspired by Ivy [45], over Z3 [46]. We study:
-
1.
Can Phase-\(\text {PDR}^\forall \) converge to a proof when \(\text {PDR}^\forall \) does not (in reasonable time)?
-
2.
Is Phase-\(\text {PDR}^\forall \) faster than \(\text {PDR}^\forall \)?
-
3.
Which aspects of Phase-\(\text {PDR}^\forall \) contribute to its performance benefits?
Protocols. We applied \(\text {PDR}^\forall \) and Phase-\(\text {PDR}^\forall \) to the most challenging examples admitting universally-quantified invariants, which previous works verified using deductive techniques. The protocols we analyzed are listed below and in Table 1. The full models appear in [1]. The KV-R protocol analyzed is taken from one of the two realistic systems studied by the IronFleet paper [33] using deductive verification.
Phase Structures. The phase structures we used appear in [1]. In all our examples, it was straightforward to translate the existing high-level intuition of important and relevant distinctions between phases in the protocol into the phase structures we report. For example, it took us less than an hour to finalize an automaton for KV-R. We emphasize that phase structures do not include phase characterizations; the user need not supply them, nor has to understand the inference procedure. Our exposition of the phase structures below refers to an intuitive meaning of each phase, but this is not part of the phase structure provided to the tool.
(1) Achieving Convergence Through Phases. In this section we consider the effect of phases on inference for examples on which standard \(\text {PDR}^\forall \) does not converge in 1 hr.
Examples. Sharded key-value store with retransmissions (KV-R): see Sect. 3 and Example 1. This protocol has not been modeled in decidable logic before.
Cache Coherence. This example implements the classic MESI protocol for maintaining cache coherence in a shared-memory multiprocessor [36], modeled in decidable logic for the first time. Cores perform reads and writes to memory, and caches snoop on each other’s requests using a shared bus and maintain the invariant that there is at most one writer of a particular cache line. For simplicity, we consider only a single cache line, and yet the example is still challenging for \(\text {PDR}^\forall \). Standard explanations of this protocol in the literature already use automata to describe this invariant, and we directly exploit this structure in our phase automaton. Phase Structure: There are 10 phases in total, grouped into three parts corresponding to the modified, exclusive, and shared states in the classical description. Within each group, there are additional phases for when a request is being processed by the bus. For example, in the shared group, there are phases for handling reads by cores without a copy of the cache line, writes by such cores, and also writes by cores that do have a copy. Overall, the phase structure is directly derived from textbook descriptions, taking into account that use of the shared bus is not atomic. Results and Discussion. Measurements for these examples appear in Table 1. Standard \(\text {PDR}^\forall \) fails to converge in less than an hour on 13 out of 16 seeds for KV-R and all 16 seeds for the cache. In contrast, Phase-\(\text {PDR}^\forall \) converges to a proof in a few minutes in all cases. These results demonstrate that phase structures can effectively guide the search and obtain an invariant quickly where standard inductive invariant inference does not.
(2) Enhancing Performance Through Phases. In this section we consider the use of phase structures to improve the speed of convergence to a proof.
Examples. Distributed lock service, adapted from [61], allows clients to acquire and release locks by sending requests to a central server, which guarantees that only one client holds each lock at a time. Phase structure: for each lock, the phases follow the 4 steps by which a client completes a cycle of acquire and release. We also consider a simpler variant with only a single lock, reducing the arity of all relations and removing the need for an automaton view. Its phase structure is the same, only for a single lock.
Simple quorum-based consensus, based on the example in [60]. In this protocol, nodes propose themselves and then receive votes from other nodes. When a quorum of votes for a node is obtained, it becomes the leader and decides on a value. Safety requires that decided values are unique. The phase structure distinguishes between the phases before any node is elected leader, once a node is elected, and when values are decided. Note that the automaton structure is unquantified.
Leader election in a ring [13, 51], in which nodes are organized in a directional ring topology with unique IDs, and the safety property is that an elected leader is a node with the highest ID. Phase structure: for a view of two nodes \(n_1,n_2\), in the first phase, messages with the ID of \(n_1\) are yet to advance in the ring past \(n_2\), while in the second phase, a message advertising \(n_1\) has advanced past \(n_2\). The inferred characterizations include another quantifier on nodes, constraining interference (see Sect. 7).
Sharded key-value store (KV) is a simplified version of KV-R above, without message drops and the retransmission mechanism. The phase structure is exactly as in KV-R, omitting transitions related to sequence numbers and acknowledgment. This protocol has not been modeled in decidable logic before.
Results and Discussion. We compare the performance of standard \(\text {PDR}^\forall \) and Phase-\(\text {PDR}^\forall \) on the above examples, with results shown in Table 1. For each example, we ran the two algorithms on 16 different Z3 random seeds. Measurements were performed on a 3.4GHz AMD Ryzen Threadripper 1950X with 16 physical cores, running Linux 4.15.0, using Z3 version 4.7.1. By disabling hyperthreading and frequency scaling and pinning tasks to dedicated cores, variability across runs of a single seed was negligible.
In all but one example, Phase-\(\text {PDR}^\forall \) improves performance, sometimes drastically; for example, performance for leader election in a ring is improved by a factor of 60. Phase-\(\text {PDR}^\forall \) also improves the robustness of inference [27] on this example, as the standard deviation falls from 39 in \(\text {PDR}^\forall \) to 0.04 in Phase-\(\text {PDR}^\forall \).
The only example in which a phase structure actually diminishes inference effectiveness is simple consensus. We attribute this to an automaton structure that does not capture the essence of the correctness argument very well, overlooking votes and quorums. This demonstrates that a phase structure might guide the search towards counterproductive directions if the user guidance is “misleading”. This suggests that better resiliency of interactive inference framework could be achieved by combining phase-based inference with standard inductive invariant-based reasoning. We are not aware of a single “good” automaton for this example. The correctness argument of this example is better captured by the conjunction of two automata (one for votes and one for accumulating a quorum) with different views, but the problem of inferring phase invariants for mutually-dependent automata is a subject for future work.
(3) Anatomy of the Benefit of Phases. We now demonstrate that each of the beneficial aspects of phases discussed in Sect. 5.2 is important for the benefits reported above.
Phase Decomposition. Is there a benefit from a phase structure even without disabled transitions? An example to a positive answer to this question is leader election in a ring, which demonstrates a huge performance benefit even without disabled transitions.
Disabled Transitions. Is there a substantial gain from exploiting disabled transitions? We compare Phase-\(\text {PDR}^\forall \) on the structure with disabled transitions and a structure obtained by (artificially) adding self loops labeled with the originally impossible transitions, on the example of lock service with multiple locks (Sect. 6.2), seeing that it demonstrates a performance benefit using Phase-\(\text {PDR}^\forall \) and showcases several disabled transitions in each phase. The result is that without disabled transitions, the mean running time of Phase-\(\text {PDR}^\forall \) on this example jumps from 2.73 s to 6.24 s. This demonstrates the utility of the additional safety properties encompassed in disabled transitions.
Phase-Awareness. Is it important to treat phases explicitly in the inference algorithm, as we do in Phase-\(\text {PDR}^\forall \) (Sect. 6.1)? We compare our result on convergence of KV-R with an alternative in which standard \(\text {PDR}^\forall \) is applied to an encoding of the phase decomposition and disabled transition by ghost state: each phase is modeled by a relation over possible view assignments, and the model is augmented with update code mimicking phase changes; the additional safety properties derived from disabled transitions are provided; and the view and the appropriate modification of the safety property are introduced. This translation expresses all information present in the phase structure, but does not explicitly guide the inference algorithm to use this information. The result is that with this ghost-based modeling the phase-oblivious \(\text {PDR}^\forall \) does not converge in 1 h on KV-R in any of the 16 runs, whereas it converges when Phase-\(\text {PDR}^\forall \) explicitly directs the search using the phase structure.
7 Related Work
Phases in Distributed Protocols. Distributed protocols are frequently described in informal descriptions as transitioning between different phases. Recently, PSync [19] used the Heard-Of model [14], which describes protocols as operating in rounds, as a basis for the implementation and verification of fault-tolerant distributed protocols. Typestates [e.g.] [25, 59] also bear some similarity to the temporal aspect of phases. State machine refinement [3, 28] is used extensively in the design and verification of distributed systems (see e.g. [33, 47]). The automaton structure of a phase invariant is also a form of state machine; our focus is on inference of characterizations establishing this.
Interaction in Verification. Interactive proof assistants such as Coq [8] and Isabelle/HOL [48] interact with users to aid them as they attempt to prove candidate inductive invariants. This differs from interaction through phase structures and counterexample traces. Ivy uses interaction for invariant inference by interactive generalization from counterexamples [51]. This approach is less automatic as it requires interaction for every clause of the inductive invariant. In terminology from synthesis [30], the use of counterexamples is synthesizer-driven interaction with the tool, while interaction via phase structures is mainly user-driven. Abstract counterexample traces returned by the tool augment this kind of interaction. As [38] has shown, interactive invariant inference, when considered as a synthesis problem (see also [27, 55]) is related to inductive learning.
Template-Based Invariant Inference. Many works employ syntactical templates for invariants, used to constrain the search [e.g.] [7, 16, 54, 57, 58]. The different phases in a phase structure induce a disjunctive form, but crucially each disjunct also has a distinct semantic meaning, which inference overapproximates, as explained in Sect. 5.2.
Automata in Safety Verification. Safety verification through an automaton-like refinement of the program’s control has been studied in a number of works. We focus on related techniques for proof automation. The Automizer approach to the verification of sequential programs [34, 35] is founded on the notion of a Floyd-Hoare automaton, which is an unquantified inductive phase automaton; an extension to parallel programs [22] uses thread identifiers closed under the symmetry rule, which are related to view quantifiers. Their focus is on the automatic, incremental construction of such automata as a union of simpler automata, where each automaton is obtained from generalizing the proof/infeasibility of a single trace. In our approach the structure of the automaton is provided by the user as a means of conveying their intuition of the proof, while the annotations are computed automatically. A notable difference is that in Automizer, the generation of characterizations in an automaton constructed from a single trace does not utilize the phase structure (beyond that of the trace), whereas in our approach the phase structure is central in generalization from states to characterizations. In trace partitioning [44, 53], abstract domains based on transition systems partitioning the program’s control are introduced. The observation is that recording historical information forms a basis for case-splitting, as an alternative to fully-disjunctive abstractions. This differs from our motivation of distinguishing between different protocol phases. The phase structure of the domain is determined by the analyser, and can also be dynamic. In our work the phase structure is provided by the user as guidance. We use a variant of \(\text {PDR}^\forall \), rather than abstract interpretation [17], to compute universally quantified phase characterizations. Techniques such as predicate abstraction [26, 29] and existential abstraction [15], as well as the safety part of predicate diagrams [11], use finite languages for the set of possible characterizations and lack the notion of views, both essential for handling unbounded numbers of processes and resources. Finally, phase splitter predicates [56] share our motivation of simplifying invariant inference by exposing the different phases the loop undergoes. Splitter predicates correspond to inductive phase characterizations [56, Theorem 1], and are automatically constructed according to program conditionals. In our approach, decomposition is performed by the user using potentially non-inductive conditions, and the inductive phase characterizations are computed by invariant inference. Successive loop splitting results in a sequence of phases, whereas our approach utilizes arbitrary automaton structures. Borralleras et al. [9] also refine the control-flow graph throughout the analysis by splitting on conditions, which are discovered as preconditions for termination (the motivation is to expose termination proof goals to be established): in a sense, the phase structure is grown from candidate characterizations implying termination. This differs from our approach in which the phase structure is used to guide the inference of characterizations.
Quantified Invariant Inference. We focus here on the works on quantifiers in automatic verification most closely related to our work. In predicate abstraction, quantifiers can be used internally as part of the definitions of predicates, and also externally through predicates with free variables [26, 42]. Our work uses quantifiers both internally in phases characterizations and externally in view quantifiers. The view is also related to the bounded number of quantifiers used in view abstraction [5, 6]. In this work we observe that it is useful to consider views of entities beyond processes or threads, such as a single key in the store. Quantifiers are often used to their full extent in verification conditions, namely checking implication between two quantified formulas, but they are sometimes employed in weaker checks as part of thread-modular proofs [4, 39]. This amounts to searching for invariants provable using specific instantiations of the quantifiers in the verification conditions [31, 37]. In our verification conditions, the view quantifiers are localized, in effect performing a single instantiation. This is essential for exploiting the disjunctive structure under the quantifiers, allowing inference to consider a single automaton edge in each step, and reflecting an intuition of correctness. When necessary to constrain interference, quantifiers in phase characterizations can be used to establish necessary facts about interfering views. Finally, there exist algorithms other than \(\text {PDR}^\forall \) for solving CHC by predicates with universal invariants [e.g. 20, 32].
8 Conclusion
Invariant inference techniques aiming to verify intricate distributed protocols must adjust to the diverse correctness arguments on which protocols are based. In this paper we have proposed to use phase structures as means of conveying users’ intuition of the proof, to be used by an automatic inference tool as a basis for a full formal proof. We found that inference guided by a phase structure can infer proofs for distributed protocols that are beyond reach for state of the art inductive invariant inference methods, and can also improve the speed of convergence. The phase decomposition induced by the automaton, the use of disabled transitions, and the explicit treatment of phases in inference, all combine to direct the search for the invariant. We are encouraged by our experience of specifying phase structures for different protocols. It would be interesting to integrate the interaction via phase structures with other verification methods and proof logics, as well as interaction schemes based on different, complementary, concepts. Another important direction for future work is inference beyond universal invariants, required for example for the proof of Paxos [50].
References
Examples code. https://github.com/wilcoxjay/mypyvy/tree/master/examples/cav19
mypyvy repository. https://github.com/wilcoxjay/mypyvy
Abadi, M., Lamport, L.: The existence of refinement mappings. Theor. Comput. Sci. 82(2), 253–284 (1991). https://doi.org/10.1016/0304-3975(91)90224-P
Abadi, M., Lamport, L.: Conjoining specifications. ACM Trans. Program. Lang. Syst. 17(3), 507–534 (1995)
Abdulla, P.A., Haziza, F., Holík, L.: All for the price of few. In: Giacobazzi, R., Berdine, J., Mastroeni, I. (eds.) VMCAI 2013. LNCS, vol. 7737, pp. 476–495. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-35873-9_28
Abdulla, P.A., Haziza, F., Holík, L.: Parameterized verification through view abstraction. STTT 18(5), 495–516 (2016). https://doi.org/10.1007/s10009-015-0406-x
Alur, R., et al.: Syntax-guided synthesis. In: Dependable Software Systems Engineering, pp. 1–25 (2015)
Bertot, Y., Castéran, P.: Interactive Theorem Proving and Program Development - Coq’Art: The Calculus of Inductive Constructions. TTCS. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-662-07964-5
Borralleras, C., Brockschmidt, M., Larraz, D., Oliveras, A., Rodríguez-Carbonell, E., Rubio, A.: Proving termination through conditional termination. In: Legay, A., Margaria, T. (eds.) TACAS 2017. LNCS, vol. 10205, pp. 99–117. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54577-5_6
Bradley, A.R.: SAT-based model checking without unrolling. In: Jhala, R., Schmidt, D. (eds.) VMCAI 2011. LNCS, vol. 6538, pp. 70–87. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-18275-4_7
Cansell, D., Méry, D., Merz, S.: Predicate diagrams for the verification of reactive systems. In: Grieskamp, W., Santen, T., Stoddart, B. (eds.) IFM 2000. LNCS, vol. 1945, pp. 380–397. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-40911-4_22
Chang, C., Keisler, H.: Model Theory. Studies in Logic and the Foundations of Mathematics. Elsevier Science, Amsterdam (1990)
Chang, E., Roberts, R.: An improved algorithm for decentralized extrema-finding in circular configurations of processes. Commun. ACM 22(5), 281–283 (1979)
Charron-Bost, B., Schiper, A.: The heard-of model: computing in distributed systems with benign faults. Distrib. Comput. 22(1), 49–71 (2009). https://doi.org/10.1007/s00446-009-0084-6
Clarke, E.M., Grumberg, O., Peled, D.A.: Model Checking. MIT Press, Cambridge (2001). http://books.google.de/books?id=Nmc4wEaLXFEC
Colón, M.A., Sankaranarayanan, S., Sipma, H.B.: Linear invariant generation using non-linear constraint solving. In: Hunt, W.A., Somenzi, F. (eds.) CAV 2003. LNCS, vol. 2725, pp. 420–432. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45069-6_39
Cousot, P., Cousot, R.: Systematic design of program analysis frameworks. In: Symposium on Principles of Programming Languages, pp. 269–282. ACM Press, New York (1979)
Cousot, P., Cousot, R.: Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: Conference Record of the Fourth ACM Symposium on Principles of Programming Languages, Los Angeles, California, USA, January 1977, pp. 238–252 (1977). https://doi.org/10.1145/512950.512973. http://doi.acm.org/10.1145/512950.512973
Dragoi, C., Henzinger, T.A., Zufferey, D.: Psync: a partially synchronous language for fault-tolerant distributed algorithms. In: Proceedings of the 43rd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2016, St. Petersburg, FL, USA, 20–22 January 2016, pp. 400–415 (2016). https://doi.org/10.1145/2837614.2837650. http://doi.acm.org/10.1145/2837614.2837650
Drews, S., Albarghouthi, A.: Effectively propositional interpolants. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9780, pp. 210–229. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41540-6_12
Eén, N., Mishchenko, A., Brayton, R.K.: Efficient implementation of property directed reachability. In: International Conference on Formal Methods in Computer-Aided Design, FMCAD 2011, Austin, TX, USA, October 30–02 November 2011, pp. 125–134 (2011)
Farzan, A., Kincaid, Z., Podelski, A.: Proof spaces for unbounded parallelism. In: Proceedings of the 42nd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2015, Mumbai, India, 15–17 January 2015, pp. 407–420 (2015). https://doi.org/10.1145/2676726.2677012. http://doi.acm.org/10.1145/2676726.2677012
Feldman, Y.M.Y., Padon, O., Immerman, N., Sagiv, M., Shoham, S.: Bounded quantifier instantiation for checking inductive invariants. In: Legay, A., Margaria, T. (eds.) TACAS 2017. LNCS, vol. 10205, pp. 76–95. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54577-5_5
Feldman, Y.M.Y., Wilcox, J.R., Shoham, S., Sagiv, M.: Inferring inductive invariants from phase structures. Technical report (2019). https://arxiv.org/abs/1905.07739
Field, J., Goyal, D., Ramalingam, G., Yahav, E.: Typestate verification: abstraction techniques and complexity results. Sci. Comput. Program. 58(1–2), 57–82 (2005)
Flanagan, C., Qadeer, S.: Predicate abstraction for software verification. In: Conference Record of POPL 2002: The 29th SIGPLAN-SIGACT Symposium on Principles of Programming Languages, Portland, OR, USA, 16–18 January 2002, pp. 191–202 (2002). https://doi.org/10.1145/503272.503291. http://doi.acm.org/10.1145/503272.503291
Garg, P., Löding, C., Madhusudan, P., Neider, D.: ICE: a robust framework for learning invariants. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 69–87. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_5
Garland, S.J., Lynch, N.: Using I/O automata for developing distributed systems. In: Foundations of Component-Based Systems, pp. 285–312. Cambridge University Press, New York (2000). http://dl.acm.org/citation.cfm?id=336431.336455
Graf, S., Saidi, H.: Construction of abstract state graphs with PVS. In: Grumberg, O. (ed.) CAV 1997. LNCS, vol. 1254, pp. 72–83. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-63166-6_10
Gulwani, S.: Synthesis from examples: interaction models and algorithms. In: 14th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing, SYNASC 2012, Timisoara, Romania, 26–29 September 2012, pp. 8–14 (2012). https://doi.org/10.1109/SYNASC.2012.69
Gurfinkel, A., Shoham, S., Meshman, Y.: SMT-based verification of parameterized systems. In: Proceedings of the 24th ACM SIGSOFT International Symposium on Foundations of Software Engineering, FSE 2016, Seattle, WA, USA, 13–18 November 2016, pp. 338–348 (2016). https://doi.org/10.1145/2950290.2950330. http://doi.acm.org/10.1145/2950290.2950330
Gurfinkel, A., Shoham, S., Vizel, Y.: Quantifiers on demand. In: Lahiri, S.K., Wang, C. (eds.) ATVA 2018. LNCS, vol. 11138, pp. 248–266. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-01090-4_15
Hawblitzel, C., et al.: Ironfleet: proving practical distributed systems correct. In: Proceedings of the 25th Symposium on Operating Systems Principles, SOSP 2015, Monterey, CA, USA, 4–7 October 2015, pp. 1–17 (2015). https://doi.org/10.1145/2815400.2815428. http://doi.acm.org/10.1145/2815400.2815428
Heizmann, M., Hoenicke, J., Podelski, A.: Refinement of trace abstraction. In: Palsberg, J., Su, Z. (eds.) SAS 2009. LNCS, vol. 5673, pp. 69–85. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03237-0_7
Heizmann, M., Hoenicke, J., Podelski, A.: Software model checking for people who love automata. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 36–52. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_2
Hennessy, J.L., Patterson, D.A.: Computer Architecture: A Quantitative Approach, 6th edn. Morgan Kaufmann, San Francisco (2017)
Hoenicke, J., Majumdar, R., Podelski, A.: Thread modularity at many levels: a pearl in compositional verification. In: Proceedings of the 44th ACM SIGPLAN Symposium on Principles of Programming Languages, POPL 2017, Paris, France, 18–20 January 2017, pp. 473–485 (2017). http://dl.acm.org/citation.cfm?id=3009893
Jha, S., Seshia, S.A.: A theory of formal synthesis via inductive learning. Acta Inf. 54(7), 693–726 (2017). https://doi.org/10.1007/s00236-017-0294-5
Jones, C.B.: Tentative steps toward a development method for interfering programs. ACM Trans. Program. Lang. Syst. 5(4), 596–619 (1983). https://doi.org/10.1145/69575.69577. http://doi.acm.org/10.1145/69575.69577
Karbyshev, A., Bjørner, N., Itzhaky, S., Rinetzky, N., Shoham, S.: Property-directed inference of universal invariants or proving their absence. J. ACM 64(1), 7:1–7:33 (2017). https://doi.org/10.1145/3022187. http://doi.acm.org/10.1145/3022187
Korovin, K.: iProver – an instantiation-based theorem prover for first-order logic (system description). In: Armando, A., Baumgartner, P., Dowek, G. (eds.) IJCAR 2008. LNCS (LNAI), vol. 5195, pp. 292–298. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-71070-7_24
Lahiri, S.K., Bryant, R.E.: Predicate abstraction with indexed predicates. ACM Trans. Comput. Log. 9(1), 4 (2007). https://doi.org/10.1145/1297658.1297662. http://doi.acm.org/10.1145/1297658.1297662
Lamport, L.: Specifying Systems. The TLA+ Language and Tools for Hardware and Software Engineers. Addison-Wesley (2002)
Mauborgne, L., Rival, X.: Trace partitioning in abstract interpretation based static analyzers. In: Sagiv, M. (ed.) ESOP 2005. LNCS, vol. 3444, pp. 5–20. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-31987-0_2
McMillan, K.L., Padon, O.: Deductive verification in decidable fragments with ivy. In: Podelski, A. (ed.) SAS 2018. LNCS, vol. 11002, pp. 43–55. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-99725-4_4
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Newcombe, C., Rath, T., Zhang, F., Munteanu, B., Brooker, M., Deardeuff, M.: How amazon web services uses formal methods. Commun. ACM 58(4), 66–73 (2015). https://doi.org/10.1145/2699417. http://doi.acm.org/10.1145/2699417
Nipkow, T., Wenzel, M., Paulson, L.C. (eds.): Isabelle/HOL. LNCS, vol. 2283. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45949-9
Padon, O., Immerman, N., Shoham, S., Karbyshev, A., Sagiv, M.: Decidability of inferring inductive invariants. In: Proceedings of the 43rd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2016, St. Petersburg, FL, USA, 20–22 January 2016, pp. 217–231 (2016). https://doi.org/10.1145/2837614.2837640. http://doi.acm.org/10.1145/2837614.2837640
Padon, O., Losa, G., Sagiv, M., Shoham, S.: Paxos made EPR: decidable reasoning about distributed protocols. PACMPL 1(OOPSLA), 108:1–108:31 (2017). https://doi.org/10.1145/3140568. http://doi.acm.org/10.1145/3140568
Padon, O., McMillan, K.L., Panda, A., Sagiv, M., Shoham, S.: Ivy: safety verification by interactive generalization. In: Proceedings of the 37th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2016, Santa Barbara, CA, USA, 13–17 June 2016, pp. 614–630 (2016)
Ramsey, F.P.: On a problem in formal logic. In: Proceedings on London Mathematical Society (1930)
Rival, X., Mauborgne, L.: The trace partitioning abstract domain. ACM Trans. Program. Lang. Syst. 29(5), 26 (2007). https://doi.org/10.1145/1275497.1275501. http://doi.acm.org/10.1145/1275497.1275501
Sankaranarayanan, S., Sipma, H.B., Manna, Z.: Constraint-based linear-relations analysis. In: Giacobazzi, R. (ed.) SAS 2004. LNCS, vol. 3148, pp. 53–68. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-27864-1_7
Sharma, R., Aiken, A.: From invariant checking to invariant inference using randomized search. Formal Methods Syst. Des. 48(3), 235–256 (2016). https://doi.org/10.1007/s10703-016-0248-5
Sharma, R., Dillig, I., Dillig, T., Aiken, A.: Simplifying loop invariant generation using splitter predicates. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 703–719. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_57
Srivastava, S., Gulwani, S.: Program verification using templates over predicate abstraction. In: Proceedings of the 2009 ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2009, Dublin, Ireland, 15–21 June 2009, pp. 223–234 (2009)
Srivastava, S., Gulwani, S., Foster, J.S.: Template-based program verification and program synthesis. STTT 15(5–6), 497–518 (2013)
Strom, R.E., Yemini, S.: Typestate: a programming language concept for enhancing software reliability. IEEE Trans. Softw. Eng. 12(1), 157–171 (1986)
Taube, M., et al.: Modularity for decidability of deductive verification with applications to distributed systems. In: Proceedings of the 39th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2018, Philadelphia, PA, USA, 18–22 June 2018, pp. 662–677 (2018). https://doi.org/10.1145/3192366.3192414. http://doi.acm.org/10.1145/3192366.3192414
Wilcox, J.R., et al.: Verdi: a framework for implementing and formally verifying distributed systems. In: Proceedings of the 36th ACM SIGPLAN Conference on Programming Language Design and Implementation, Portland, OR, USA, 15–17 June 2015, pp. 357–368 (2015). https://doi.org/10.1145/2737924.2737958. http://doi.acm.org/10.1145/2737924.2737958
Woos, D., Wilcox, J.R., Anton, S., Tatlock, Z., Ernst, M.D., Anderson, T.E.: Planning for change in a formal verification of the raft consensus protocol. In: Proceedings of the 5th ACM SIGPLAN Conference on Certified Programs and Proofs, Saint Petersburg, FL, USA, 20–22 January 2016, pp. 154–165 (2016). https://doi.org/10.1145/2854065.2854081. http://doi.acm.org/10.1145/2854065.2854081
Acknowledgements
We thank Kalev Alpernas, Javier Esparza, Neil Immerman, Shachar Itzhaky, Oded Padon, Andreas Podelski, Tom Reps, and the anonymous referees for insightful comments which improved this paper. This publication is part of a project that has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. [759102-SVIS]). The research was partially supported by Len Blavatnik and the Blavatnik Family foundation, the Blavatnik Interdisciplinary Cyber Research Center, Tel Aviv University, the Israel Science Foundation (ISF) under grant No. 1810/18, the United States-Israel Binational Science Foundation (BSF) grant No. 2016260, and the National Science Foundation under Grant No. 1749570. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Feldman, Y.M.Y., Wilcox, J.R., Shoham, S., Sagiv, M. (2019). Inferring Inductive Invariants from Phase Structures. In: Dillig, I., Tasiran, S. (eds) Computer Aided Verification. CAV 2019. Lecture Notes in Computer Science(), vol 11562. Springer, Cham. https://doi.org/10.1007/978-3-030-25543-5_23
Download citation
DOI: https://doi.org/10.1007/978-3-030-25543-5_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25542-8
Online ISBN: 978-3-030-25543-5
eBook Packages: Computer ScienceComputer Science (R0)







 , whereas all states in which such messages exist are associated with
, whereas all states in which such messages exist are associated with 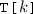 —a distinction captured by the characterizations in lines 75 and 82 in Fig.
—a distinction captured by the characterizations in lines 75 and 82 in Fig.  in
in  , a fact that can trigger the inference of the characterization in line 75. These additional safety properties direct the search for characterizations that are likely to be important for the proof.
, a fact that can trigger the inference of the characterization in line 75. These additional safety properties direct the search for characterizations that are likely to be important for the proof.