Abstract
This work contains two major parts: comprehensively studying the security notions of cryptographic hash functions against quantum attacks and the relationships between them; and revisiting whether Merkle-Damgård and related iterated hash constructions preserve the security properties of the compression function in the quantum setting. Specifically, we adapt the seven notions in Rogaway and Shrimpton (FSE’04) to the quantum setting and prove that the seemingly stronger attack model where an adversary accesses a challenger in quantum superposition does not make a difference. We confirm the implications and separations between the seven properties in the quantum setting, and in addition we construct explicit examples separating an inherently quantum notion called collapsing from several proposed properties. Finally, we pin down the properties that are preserved under several iterated hash schemes. In particular, we prove that the ROX construction in Andreeva et al. (Asiacrypt’07) preserves the seven properties in the quantum random oracle model.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The compression function is not given as a random oracle. Rather apart from the compression function, the construction has access to a public random function that is given as a black-box.
- 2.
Some standard notions have appeared in the literature before [HRS16].
References
Alagic, G., Majenz, C., Russell, A., Song, F.: Quantum-secure message authentication via blind-unforgeability. arXiv preprint arXiv:1803.03761 (2018)
Andreeva, E., Neven, G., Preneel, B., Shrimpton, T.: Seven-property-preserving iterated hashing: ROX. In: Kurosawa, K. (ed.) ASIACRYPT 2007. LNCS, vol. 4833, pp. 130–146. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-76900-2_8
Alagic, G., Russell, A.: Quantum-secure symmetric-key cryptography based on hidden shifts. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10212, pp. 65–93. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_3
Ambainis, A., Rosmanis, A., Unruh, D.: Quantum attacks on classical proof systems: the hardness of quantum rewinding. In: 2014 IEEE 55th Annual Symposium on Foundations of Computer Science (FOCS), pp. 474–483. IEEE (2014)
Boneh, D., Dagdelen, Ö., Fischlin, M., Lehmann, A., Schaffner, C., Zhandry, M.: Random oracles in a quantum world. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 41–69. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_3
Bertoni, G., Daemen, J., Peeters, M., Van Assche, G.: Sponge functions. In: Ecrypt Hash Workshop (2007). http://sponge.noekeon.org/
Bellare, M., Rogaway, P.: Collision-resistant hashing: towards making UOWHFs practical. In: Kaliski, B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 470–484. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0052256
Boneh, D., Zhandry, M.: Secure signatures and chosen ciphertext security in a quantum computing world. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 361–379. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_21
Czajkowski, J., Groot Bruinderink, L., Hülsing, A., Schaffner, C., Unruh, D.: Post-quantum security of the sponge construction. In: Lange, T., Steinwandt, R. (eds.) PQCrypto 2018. LNCS, vol. 10786, pp. 185–204. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-79063-3_9
Damgård, I.B.: A design principle for hash functions. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 416–427. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_39
Eaton, E., Song, F.: Making existential-unforgeable signatures strongly unforgeable in the quantum random-oracle model. In: 10th Conference on the Theory of Quantum Computation, Communication and Cryptography, TQC 2015. LIPIcs, vol. 44, pp. 147–162. Schloss Dagstuhl (2015). https://eprint.iacr.org/2015/878
Hülsing, A., Rijneveld, J., Song, F.: Mitigating multi-target attacks in hash-based signatures. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9614, pp. 387–416. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49384-7_15
Kaplan, M., Leurent, G., Leverrier, A., Naya-Plasencia, M.: Breaking symmetric cryptosystems using quantum period finding. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 207–237. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_8
Merkle, R.C.: One way hash functions and DES. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 428–446. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_40
Secure hash standard (SHS) & SHA-3 standard. FIPS PUB 180–4 & 202 (2015). http://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.180-4.pdf. http://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.202.pdf
Rogaway, P., Shrimpton, T.: Cryptographic hash-function basics: definitions, implications, and separations for preimage resistance, second-preimage resistance, and collision resistance. In: Roy, B., Meier, W. (eds.) FSE 2004. LNCS, vol. 3017, pp. 371–388. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-25937-4_24
Shoup, V.: A composition theorem for universal one-way hash functions. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 445–452. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_32
Song, F.: A note on quantum security for post-quantum cryptography. In: Mosca, M. (ed.) PQCrypto 2014. LNCS, vol. 8772, pp. 246–265. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11659-4_15
Santoli, T.: Schaffner, Christian: using Simon’s algorithm to attack symmetric-key cryptographic primitives. Quantum Inf. Comput. 17(1&2), 65–78 (2017)
Unruh, D.: Quantum proofs of knowledge. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 135–152. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_10
Unruh, D.: Quantum position verification in the random oracle model. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 1–18. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_1
Unruh, D.: Collapse-binding quantum commitments without random oracles. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 166–195. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_6
Unruh, D.: Computationally binding quantum commitments. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 497–527. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_18
Watrous, J.: Zero-knowledge against quantum attacks. SIAM J. Comput. 39(1), 25–58 (2009)
Zhandry, M.: How to construct quantum random functions. In: FOCS 2012, pp. 679–687. IEEE (2012)
Zhandry, M.: Secure identity-based encryption in the quantum random oracle model. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 758–775. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_44
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Appendices
A \(\text {CLAPS}\) Separation Proofs
Here we show that \(\text {CLAPS}\) does not imply \(\text {aPreQ}\), \(\text {aSecQ}\), or \(\text {ePreQ}\), completing the diagram in Fig. 2.
1.1 A.1

Theorem 5
If a collapsing function family exists, then there is a function family H that is \((t,\varepsilon )\)-\(\text {CLAPS}\) with negligible \(\varepsilon \), but with
 .
.
Proof Summary. Since the key k in the collapsing game is chosen uniformly at random, a collapsing function can have a constant number of “bad” keys that, for example, result in a constant function \(H_k\). Finding a preimage for such a function is obviously trivial. Given a collapsing function F, we exhibit a function H that is collapsing, but for which
 .
.
Proof
Suppose
 is \((t,\varepsilon )\)-\(\text {CLAPS}\), and define H as follows:
is \((t,\varepsilon )\)-\(\text {CLAPS}\), and define H as follows:

Lemma 5
H is \((t,\varepsilon ')\)-\(\text {CLAPS}\), where
 .
.
The obvious adversary suffices to break \(\text {aPreQ}\) on H: A picks
 , and B outputs any x. Since we assume \(\varepsilon \) to be negligible, \(\varepsilon '\) is negligible as well, and the theorem is immediate from Lemma 5.
, and B outputs any x. Since we assume \(\varepsilon \) to be negligible, \(\varepsilon '\) is negligible as well, and the theorem is immediate from Lemma 5.
Proof
(Proof of Lemma 5). Let (A, B) be a correct qpt adversary with
 . We construct a correct qpt adversary \((A',B')\) for F as follows:
. We construct a correct qpt adversary \((A',B')\) for F as follows:

We claim that \((A',B')\) is correct: If \(A'\) does not fail, then
 , and by the premise that (A, B) is correct,
, and by the premise that (A, B) is correct,
 .
.
Suppose \(A'\) doesn’t fail, and the challenger for \((A',B')\) is running \(\text {Game}_1\). Then B receives \(S,\mathcal {M}(X)\), and (A, B) sees \(\text {Game}_1\). On the other hand, if the challenger for \((A',B')\) is running \(\text {Game}_2\), X is unmeasured, and (A, B) sees \(\text {Game}_2\).
Since the probability that \(A'\) fails is
 ,
,
 . Therefore
. Therefore
 .
.
1.2 A.2

Theorem 6
If a collapsing function family exists, then there is a function family H that is \((t,\varepsilon )\)-\(\text {CLAPS}\) with negligible \(\varepsilon \), but with
 .
.
Proof Summary. This proof uses the same H as the proof of Theorem 5. Given a collapsing function F, this H is also collapsing, but has a single “bad” key \(\hat{k}\) s.t.
 ,
,
 . If an adversary can control the key and chooses \(\hat{k}\), then whichever x the challenger picks, any other element of \(\textit{dom}(H_k)\) is a second preimage. Since the proof is identical to Theorem 5, we omit it for brevity.
. If an adversary can control the key and chooses \(\hat{k}\), then whichever x the challenger picks, any other element of \(\textit{dom}(H_k)\) is a second preimage. Since the proof is identical to Theorem 5, we omit it for brevity.
1.3 A.3
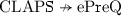
Theorem 7
If a collapsing function family exists, then there is a function family H that is \((t,\varepsilon )\)-\(\text {CLAPS}\) with negligible \(\varepsilon \), but
 .
.
Proof Summary. If the image \(\hat{y}\) of some element x in the domain of H is fixed, regardless of the key k, then an adversary can find a preimage of an element y of his choice easily: All he must do is choose
 , and whatever k the adversary picks, x is a preimage. But if x is the only preimage of y, this property does not help in creating superpositions of preimages to use in the collapsing game. So H may still be collapsing.
, and whatever k the adversary picks, x is a preimage. But if x is the only preimage of y, this property does not help in creating superpositions of preimages to use in the collapsing game. So H may still be collapsing.
Proof
Suppose
 is \((t,\varepsilon )\)-\(\text {CLAPS}\). We define a new function
is \((t,\varepsilon )\)-\(\text {CLAPS}\). We define a new function
 as follows:
as follows:

Lemma 6
H is \((t,\varepsilon )\)-\(\text {CLAPS}\).
The obvious adversary suffices to break \(\text {ePreQ}\) on H: A picks
 and B outputs \(0^m\). Thus, the theorem is immediate from Lemma 6.
and B outputs \(0^m\). Thus, the theorem is immediate from Lemma 6.
Proof
(Proof of Lemma 6). Let (A, B) be a correct qpt adversary with
 . We construct a qpt adversary \((A',B')\) for F as follows:
. We construct a qpt adversary \((A',B')\) for F as follows:

\((A',B')\) is correct by construction. We claim that
 . Consider the following cases:
. Consider the following cases:
-
1.
Suppose
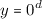 . Then by the premise that (A, B) is correct,
. Then by the premise that (A, B) is correct,
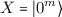 , since \(0^m\) is the only preimage of \(0^d\). In this case
, since \(0^m\) is the only preimage of \(0^d\). In this case
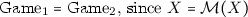 , so
, so
 for both (A, B) and \((A',B')\).
for both (A, B) and \((A',B')\). -
2.
Suppose
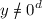 , and the challenger for (A, B) is running \(\text {Game}_1\). Then B receives \(\mathcal {M}(X)\), so B sees \(\text {Game}_2\).
, and the challenger for (A, B) is running \(\text {Game}_1\). Then B receives \(\mathcal {M}(X)\), so B sees \(\text {Game}_2\). -
3.
Suppose
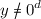 , and the challenger for (A, B) is running \(\text {Game}_2\). By the premise that (A, B) is correct, when A produces X,
, and the challenger for (A, B) is running \(\text {Game}_2\). By the premise that (A, B) is correct, when A produces X, 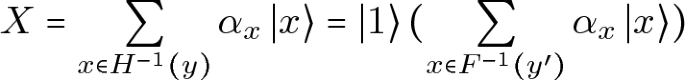
So the measurement at step 2 of \(A'\) does not collapse X. Hence, B sees \(\text {Game}_2\).
Therefore
 .
.
B
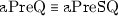
Theorem 8
Equations 4 and 11 are equivalent. I.e.,

Three equivalent games showing that measuring the K wire before the end does not change the \(\text {aPreSQ}\) game—hence \(\text {aPreSQ}\) and \(\text {aPreQ}\) are equivalent. Figure a is the same as \(\text {aPreSQ}\); Fig. c is functionally equivalent to \(\text {aPreQ}\); and Fig. b is intermediate between the two. The state register S from Eqs. 4 and 11 is omitted for clarity.
Proof
(Proof of Theorem 8).
Let each part A, B of the adversary be a unitary operator and let
 be the size of a key,
be the size of a key,
 be the size of a message, and
be the size of a message, and
 be the size of a digest. We illustrate the circuits for three games in Fig. 3.
be the size of a digest. We illustrate the circuits for three games in Fig. 3.
Lemma 7
Game 1 is equivalent to Game 2.
Lemma 8
Game 2 is equivalent to Game 3.
We claim that the theorem follows from Lemmas 7 and 8. Note that Game 1 is exactly the \(\text {aPreSQ}\) game, as defined in Eq. 11. In Game 3, the output of A and B, with the exception of the state register S, are measured immediately, so without loss of generality, we may assume that their output is classical. Thus Game 3 is equivalent to the \(\text {aPreQ}\) game (Eq. 4).
In the following two proofs, let \(\mathcal {M}_n\) denote measuring the first n qubits in the standard basis and leaving the rest untouched. In other words,

Proof
(Proof of Lemma 7).
It suffices to show that for any unitary B and all
 ,
,
 commutes with
commutes with
 . This is immediate, since
. This is immediate, since
 .
.
Proof
(Proof of Lemma 8).
We must show that \(U_{H(x')}\) commutes with \(\mathcal {M}_n\). Since

is a unitary operator that leaves the K register untouched, it can be viewed as using the K register solely as control bits for \(\text {CNOT}\) gates, interspersed with unitaries on the Y register. Let \(\text {CNOT}_{i,j}\) denote a \(\text {CNOT}\) gate with control i and target j, and V denote an arbitrary unitary that acts on the Y register. Then for
 and
and
 for all
for all
 ,
,

Given the definition of \(\mathcal {M}_n\) in Eq. 15, we must show all the factors in Eq. 16 commute with
 . Clearly this is the case for
. Clearly this is the case for
 , by the same reasoning as in the proof of Lemma 7. Similarly, it is well known that measurement of the control qubit commutes with \(\text {CNOT}\).
, by the same reasoning as in the proof of Lemma 7. Similarly, it is well known that measurement of the control qubit commutes with \(\text {CNOT}\).
C ROX Constructions
1.1 C.1 Extracting Compression-Function Collisions (Lemma 2)
Proof
(Proof of Lemma 2). We claim that the following procedure extracts a compression-function with overwhelming probability:

Let \(\bar{x},\bar{x}'\) and be the first n bits of \(\hat{x},\hat{x}'\), and \(\lambda ,\lambda '\) be their respective lengths. We must show that there always exists a colliding pair \((x,x')\). We consider two cases:
-
Case i. Suppose
 or
or
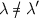 . Then since \(x_\ell \) and \(x_{\ell '}'\) each contains at least one full output from \(\text {RO}_2\),
. Then since \(x_\ell \) and \(x_{\ell '}'\) each contains at least one full output from \(\text {RO}_2\),
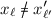 except with probability
except with probability
 . In this case the inputs to the last application of \(H_k\) form a collision for \(H_k\).
. In this case the inputs to the last application of \(H_k\) form a collision for \(H_k\). -
Case ii. Otherwise,
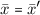 and
and
 . In this case, the padding applied to \(\hat{x}\) and \(\hat{x}'\) will be identical. But the mask schedule taken from \(\text {RO}_1\) will be identical as well. So since
. In this case, the padding applied to \(\hat{x}\) and \(\hat{x}'\) will be identical. But the mask schedule taken from \(\text {RO}_1\) will be identical as well. So since
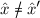 , there must be block pair, \((b_{i^*},b'_{i'^*})\) on which they differ. Since the masks and padding match, these form a collision for \(H_k\).
, there must be block pair, \((b_{i^*},b'_{i'^*})\) on which they differ. Since the masks and padding match, these form a collision for \(H_k\).
1.2 C.2 Embedding Messages (Lemma 3)
Proof
(Proof of Lemma 3). Let
 , where
, where
 and
and
 , and define the following procedure:
, and define the following procedure:

In steps 5 and 6, the above procedure requires us to program a random oracle. To do so, we invoke witness search from [ES15], where a witness is some image of \(\text {RO}_{1,2}\) corresponding to an input that starts with \(\bar{x}\). Since \(\bar{x}\) is chosen at random, and since the codomains of \(\text {RO}_{1,2}\) are much larger than their domains, the random search problem in [HRS16] can be reduced to this, with \(2^n\) marked items in a set of
 , so the success probability is \(O(q^2/2^n)\).
, so the success probability is \(O(q^2/2^n)\).
1.3 C.3 Extracting Compression-Function Preimages (Lemma 4)
Proof
(Proof of Lemma 4). We claim that the following procedure extracts a collision-function preimage with overwhelming probability:

By construction,
 as desired. The only calls to H and \(\text {RO}_1,\text {RO}_2\) are in the partial computation of \(\textsf {ROX}^{(H)}(x)\). Since we omit one call to H, the procedure calls it \(\ell (x)-1\) times.
as desired. The only calls to H and \(\text {RO}_1,\text {RO}_2\) are in the partial computation of \(\textsf {ROX}^{(H)}(x)\). Since we omit one call to H, the procedure calls it \(\ell (x)-1\) times.
D ROX Property-Preservation Proofs
1.1 D.1 ROX Preserves \(\text {aPreQ}\)
Proof
(Proof of Theorem 1). Let (A, B) be a \((t,\varepsilon )\) quantum adversary for \(\text {aPreQ}\) on \(\textsf {ROX}^{(H)}\), making
 oracle queries. We construct an adversary \((A',B')\) for H using an additional \(\textit{poly}(n)\) oracle queries:
oracle queries. We construct an adversary \((A',B')\) for H using an additional \(\textit{poly}(n)\) oracle queries:

By Lemma 4, if
 , then
, then
 , and \(A'\) wins the aPreQ-game. Note that
, and \(A'\) wins the aPreQ-game. Note that
 for \(g'\Vert h'\) chosen at random, while A would expect a \(\hat{y}\) to be \(H_k(g\Vert h)\), where g contains at least 2b bits of \(\text {RO}_2(\bar{x},\cdot )\), and
for \(g'\Vert h'\) chosen at random, while A would expect a \(\hat{y}\) to be \(H_k(g\Vert h)\), where g contains at least 2b bits of \(\text {RO}_2(\bar{x},\cdot )\), and
 for some d. The view of (A, B) in the simulated run in \((A',B')\) is thus identical to the real aPreQ-game, unless (A, B) can distinguish y and \(\hat{y}\) using at most q queries. We show that A can distinguish them with probability at most \(q^2/{2^n}\). Hence
for some d. The view of (A, B) in the simulated run in \((A',B')\) is thus identical to the real aPreQ-game, unless (A, B) can distinguish y and \(\hat{y}\) using at most q queries. We show that A can distinguish them with probability at most \(q^2/{2^n}\). Hence
 .
.
We argue that if some challenger that knew x were to reprogram \(\text {RO}_{1,2}\) on inputs corresponding to x, no algorithm would be able to discover this except with negligible probability. In the Witness-Search game from [ES15], let P(w) output 1 if and only if
 and
and
 for some
for some
 . Next, let
. Next, let
 and
and
 . This amounts to finding a preimage with a suffix from a set in a random function. Hence
. This amounts to finding a preimage with a suffix from a set in a random function. Hence  by reducing a random search problem developed in [HRS16] to it. Thus we can safely reprogram \(\text {RO}_{1,2}\) at points corresponding to P being true, and h, g are indistinguishable from the random values supplied by \(B'\).
by reducing a random search problem developed in [HRS16] to it. Thus we can safely reprogram \(\text {RO}_{1,2}\) at points corresponding to P being true, and h, g are indistinguishable from the random values supplied by \(B'\).
1.2 D.2 ROX Preserves \(\text {aSecQ}\)
Proof
(Proof of Theorem 3). Let (A, B) be a \((t,\varepsilon )\) adversary for \(\text {aSecQ}\) on \(\textsf {ROX}^{(H)}\) making
 oracle queries. We construct an adversary \((A',B')\) for H, using an additional
oracle queries. We construct an adversary \((A',B')\) for H, using an additional
 oracle queries:
oracle queries:

By Lemma 3, Embed-Message adds an additional
 applications of H and an additional
applications of H and an additional
 oracle queries and alters the success probability of A by at most
oracle queries and alters the success probability of A by at most
 , where
, where
 is the number of queries A makes. By Lemma 2, Extract-Collision adds
is the number of queries A makes. By Lemma 2, Extract-Collision adds
 applications of H and
applications of H and
 oracle queries and fails w.p. \(\frac{1}{2^n}\). Assuming both succeed,
oracle queries and fails w.p. \(\frac{1}{2^n}\). Assuming both succeed,
 w.p. \(\frac{1}{\textit{poly}(n)}\). Hence
w.p. \(\frac{1}{\textit{poly}(n)}\). Hence
 .
.
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Hamlin, B., Song, F. (2019). Quantum Security of Hash Functions and Property-Preservation of Iterated Hashing. In: Ding, J., Steinwandt, R. (eds) Post-Quantum Cryptography. PQCrypto 2019. Lecture Notes in Computer Science(), vol 11505. Springer, Cham. https://doi.org/10.1007/978-3-030-25510-7_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-25510-7_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25509-1
Online ISBN: 978-3-030-25510-7
eBook Packages: Computer ScienceComputer Science (R0)




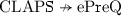
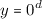 . Then by the premise that (A, B) is correct,
. Then by the premise that (A, B) is correct,
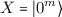 , since
, since 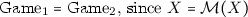 , so
, so
 for both (A, B) and
for both (A, B) and 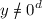 , and the challenger for (A, B) is running
, and the challenger for (A, B) is running 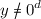 , and the challenger for (A, B) is running
, and the challenger for (A, B) is running 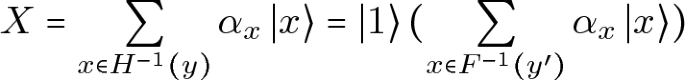
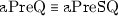

 or
or
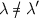 . Then since
. Then since 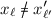 except with probability
except with probability
 . In this case the inputs to the last application of
. In this case the inputs to the last application of 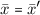 and
and
 . In this case, the padding applied to
. In this case, the padding applied to 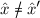 , there must be block pair,
, there must be block pair,