Melting and Solidification

Abstract

Solid–liquid phase changes, including melting and solidification, are treated in this chapter, starting with the classification of solid–liquid phase changes and generalized boundary conditions at the interface. Different approaches to the solution of melting and solidification problems are introduced, including exact, integral, and numerical solutions. Finally, solidification in contact melting is presented.

Problems

• 5.1. A horizontal cylinder is embedded in infinite solid paraffin. The initial temperature of the paraffin is equal to its melting temperature and the surface temperature of the cylinder is greater than the melting point of paraffin. The melting occurs around the cylinder. The three possible shapes of solid–liquid interfaces are given in Fig. P5.1. Discuss which one should form and for what reason. If the PCM becomes ice (the surface temperature of the cylinder is less than 4 °C), what is your answer?

  

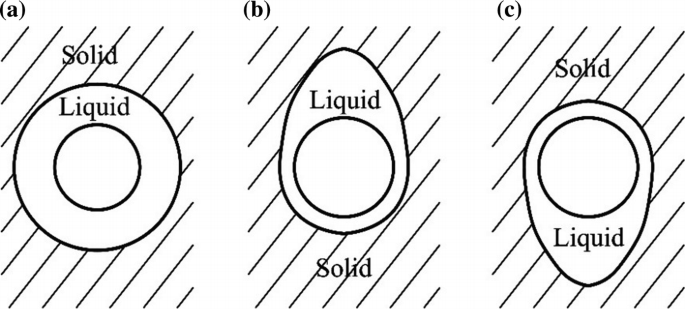
  Fig. P5.1

• 5.2. A horizontal cylinder is embedded in liquid paraffin with a temperature above its melting point. From time $t = 0$, the surface temperature of the cylinder is suddenly decreased to a temperature below the melting point, and then the solidification process occurs around the cylinder. Discuss the effect of natural convection on the solid–liquid interface shape.

• 5.3. In the thermal energy storage system that is shown in Fig. P5.3, the PCM is n-Octadecane (the thermal conductivity of solid is 0.358 W/m-K) and the transfer fluid is water. The liquid with a temperature below the melting point flows through the tube. The solidification process occurs in the annulus. To enhance the heat transfer in the system, one engineer suggests installing longitudinal fins on the PCM side. Others suggest installing longitudinal fins on the fluid side. In your opinion, who is right?

  

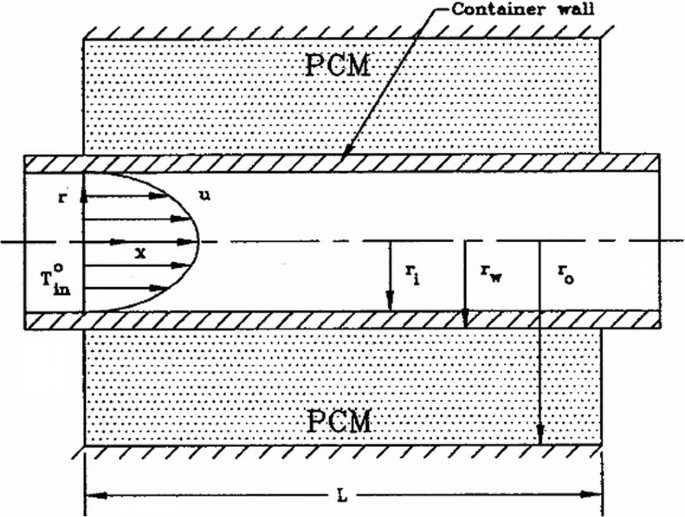
  Fig. P5.3

• 5.4. The energy balance at the solid–liquid interface for a melting problem given by Eq. (5.8) is obtained by assuming that Fourier’s conduction model is valid. When the temperature gradient is very high or the duration of heating is extremely short, Fourier’s conduction model is no longer valid. Instead, the heat flux and temperature gradient are related by

  $$q^{{\prime \prime }} (x,t) + \tau \frac{{\partial q^{{\prime \prime }} (x,t)}}{\partial t} = - k\frac{\partial T(x,t)}{\partial x}$$

  where $\tau$ is the thermal relaxation time. Apply the above equation for heat flux in both solid and liquid phases and derive the energy balance at the interface. The thermal relaxation times for both phases can be assumed to be the same.

• 5.5. When heat flux and temperature gradient are related by the equation of the previous problem, there may be a discontinuity of temperature at the solid–liquid interface (see Fig. P5.5). Modify the energy balance that you obtained in Problem 5.4 to account for the contribution of sensible heat to the interfacial energy balance.

• 5.6. For a two-dimensional melting/solidification problem, the energy balance equation at the interface is

  $$k_{\rm s} \frac{{\partial T_{\rm s} (x,y,t)}}{\partial n} - k_{\ell } \frac{{\partial T_{\ell } (x,y,t)}}{\partial n} = \rho h_{{{\rm s}\ell }} v_{n} \quad \quad x = s(y,t)$$

  The above equation is not convenient for the analytical solution or numerical solution because it contains derivatives of the temperature along the ${\mathbf{n}}$-direction. Prove that the above equation can be rewritten as

  $$\left[ {1 + \mathop {\left( {\frac{\partial s}{\partial y}} \right)}\nolimits^{2} } \right]\left[ {k_{\rm s} \frac{{\partial T_{\rm s} }}{\partial x} - k_{\ell } \frac{{\partial T_{\ell } }}{\partial x}} \right] = \rho h_{{{\rm s}\ell }} \frac{\partial s}{\partial t}\quad \quad x = s(y,t)$$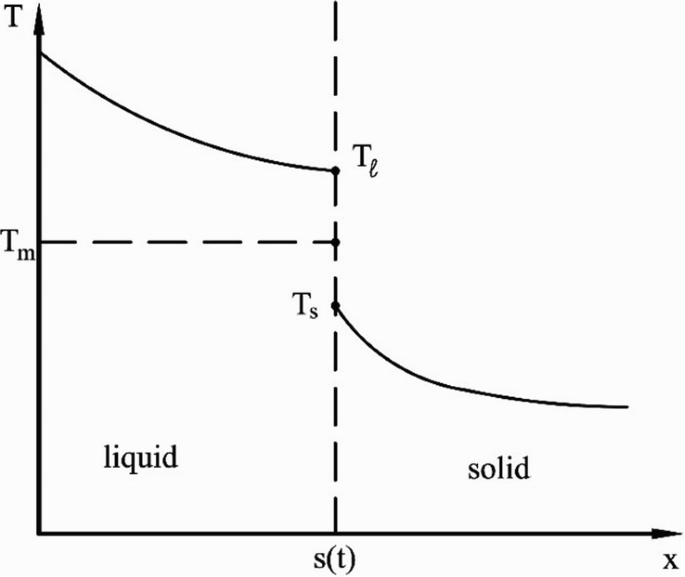

  

  Fig. P5.5

• 5.7. A solid PCM with a uniform initial temperature $T_{\rm i}$ below the melting point $T_{\rm m}$ is in a half-space $x > 0.$ At time $t = 0,$ the temperature at the boundary $x = 0$ is suddenly increased to a temperature $T_{0}$ above the melting point of the PCM. The melting process occurs from the time $t = 0.$ The densities of the PCM for both phases are assumed to be the same and the natural convection in the liquid phase can be neglected. Show that Eqs. (5.35)–(5.41), which are nondimensional governing equations for solidification in a semi-infinite region, are also valid for this problem provided that subscripts 1 and 2 represent liquid and solid, respectively.

• 5.8. The governing equation of the one-region phase-change problem discussed in Sect. 5.3.3, Eq. (5.42) can also be reduced to an ordinary differential equation by introducing a similarity variable: $\eta = X/(2\sqrt \tau )$, which is referred to as the similarity solution. Obtain the exact solution of the one-region problem using the similarity solution.

• 5.9. A solid PCM with a uniform initial temperature equal to the melting point $T_{\rm m}$ is in a half-space $x > 0.$ At time $t = 0,$ the surface of the semi-infinite body is exposed to a fluid at temperature $T_{\infty }$. The convective heat transfer coefficient between the PCM and the fluid is h. Assume that the densities of the PCM for both phases are the same and that natural convection in the liquid phase is negligible. The temperature distribution in the liquid phase can be constructed based on the solution of heat conduction in a semi-infinite region subject to the boundary condition of the third kind. Find the transient location of the solid–liquid interface.

• 5.10. To solve heat conduction in a semi-infinite body with a convective boundary condition by using the integral solution, the temperature distribution in the thermal penetration depth must be determined. If it can be assumed to be a second-order polynomial function, determine the unknown constants in the polynomial function.

• 5.11. Find thermal penetration depth for heat conduction in a semi-infinite body with convective boundary condition. The temperature distribution in the thermal penetration depth can be assumed to be a second-order polynomial function.

• 5.12. Solve for melting in a semi-infinite body with convective heating. The temperature distribution in the liquid phase can be assumed to be a second-order polynomial function.

• 5.13. Solve for melting in a subcooled semi-infinite solid with constant wall temperature by using the integral approximate method. The temperature distribution in the liquid phase can be assumed to be a linear distribution. The temperature distribution in the solid phase can be assumed to be a second-order polynomial function.

• 5.14. The dimensionless governing equations of melting in a subcooled semi-infinite solid with constant heat flux heating were given in Eqs. (5.145)–(5.151). Solve the problem using a semi-exact solution: exact solution in the liquid (see Example 5.1) and integral solution in the solid (see Sect. 5.4.3).

• 5.15. You are given a one-dimensional heat sink to analyze. It works by melting a block of encased wax. The block of wax (PCM) is one centimeter thick. The heat sink operates by keeping one wall at 10 °C above the wax melt temperature. Assume that the solid PCM is uniformly at the melting point at time t = 0. The heat sink is used up when all of the PCM is liquid. The wax has the following properties: T_m = 0^o C, c_p = 1 J/kg-K, $h_{{{\rm s}\ell }}$ = 100 J/kg, In calculating thermal capacity, what error would result if only the latent heat—and not also the sensible heat rise—is accounted for?

• 5.16. Since the surface temperature of an ablation material is very high, the surface is subjected to convective and radiation cooling. Modify the energy balance at the surface of the ablating material—Eq. (5.175)—and obtain the ablation velocity with the convective and radiation cooling effects considered.

• 5.17. The surface heat flux in the ablation problem discussed in Sect. 5.4.4 was assumed as constant, and only steady-state solution was discussed. The heat flux during ablation is usually a function of time. A finite slab with thickness L and an initial temperature of T_i ($T_{\rm i} < T_{\rm m}$) is subject to a variable heat flux $q_{0}^{{\prime \prime }} (t) = Ae^{\rm t}$ at the surface x = 0. The surface x = L can be assumed to be adiabatic. Since the initial temperature of the slab is below the melting point, it must be preheated before ablation begins. Analyze the preheating and ablation problem using integral approximate method. It is assumed that the thermal penetration depth in the ablating material never reaches to x = L so the ablating material can be treated as a semi-infinite solid. The temperature distribution in the solid can be assumed as the second-degree polynomial function.

  

  Fig. P5.18

• 5.18. Derive the quasi-steady formulation for the temperature of the ablative material and substrate when a constant heat flux $q_{\rm w}^{{\prime \prime }}$ is applied to the surface of the ablative material, as shown in Fig. P5.18. Develop the governing equations, including the boundary conditions and initial conditions needed. The two materials in this problem are assumed to be homogenous, isotropic, and in good contact with each other. The inner surface is assumed to be adiabatic. The temperature distribution is initially uniform and then exposed to a constant external heat flux on the outer surface of the ablative material. A phase change occurs at the outer surface, and the new material is immediately removed upon formation. Find the ablation rate for the limiting case of infinite thickness of the ablation material at steady state.

• 5.19. A horizontal cylinder is embedded in solid paraffin with a temperature equal to the melting point of paraffin. From time $t = 0$, a constant heat flux is applied to the inner surface of the tube so that melting occurs around the tube. Assume that the thickness of the tube is negligible. Solve the melting problem using the integral approximate method.

• 5.20. The physical model of melting in an eccentric annulus is shown in Fig. P5.20. The PCM fills the eccentric annulus with outer radius r_o, inner radius r_i, and eccentricity e. The initial temperature of the PCM is assumed to be at its freezing temperature, T_m. At the beginning, t = 0, the temperatures of the outer and inner walls of the eccentric annulus are suddenly reduced to a temperature T_c, below the freezing temperature. The freezing process will occur simultaneously at the outer and inner walls of the eccentric annulus. It is assumed that the freezing at the inside of the outer wall and at the outside of the inner wall can be solved independently. Before the freezing fronts meet, the freezing volume is the sum of the volumes at the inside of the outer wall and the outside of the inner wall. After the freezing fronts meet, the freezing rate will decrease since the freezing process stopped at the locations where the freezing fronts met. Therefore, the freezing rate needs to be calculated for two different stages: before and after the freezing fronts meet. The radius of the inner and outer freezing fronts can be determined by an integral solution. Obtain the rate of freezing as a function of time.

  

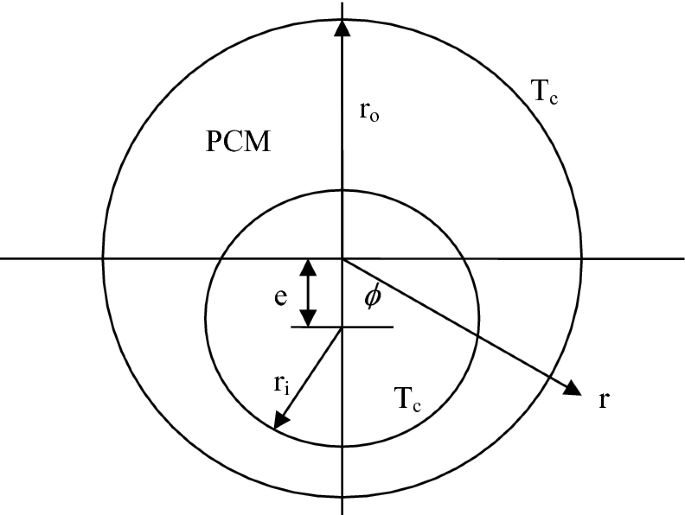
  Fig. P5.20

• 5.21. In a shell-and-tube latent heat thermal energy storage system, as shown in Fig. P5.3, the solid PCM at melting point fills in the shell side, while the transfer fluid flows inside the tube. It is assumed that (1) the inlet velocity of the transfer fluid is fully developed, but the heat transfer on the tube side is in the thermal entry region, (2) the quasi-steady assumption is applicable to convective heat transfer inside the tube, (3) the axial conductions in both the tube side and shell side are assumed to be negligible, and (4) the tube wall is assumed to be very thin so that its heat capacity and axial conduction can be neglected. Find the transient location of the melting front before it reaches the adiabatic wall of the thermal energy storage device by analyzing forced convective heat transfer inside the tube and melting on the shell side.

• 5.22. A line heat source with intensity of $q^{{\prime }} \, ( {\text{W/m)}}$ is located at r = 0 in an infinite solid as shown in Fig. P5.22. The initial temperature of the solid, T_i, is below the melting point, T_m, so that this is a two-region melting problem. Develop the governing equations of the problem and obtain the transient location of the melting front. The temperature distributions in the liquid and solid phases can be constructed using an exponential integral function in the form of ${\text{Ei[}} - r^{2} /(4\alpha t)]$, where $Ei(z) = \int_{\rm z}^{\infty } {\frac{{\text{e}^{ - z} }}{z}\text{d}z}$.

  

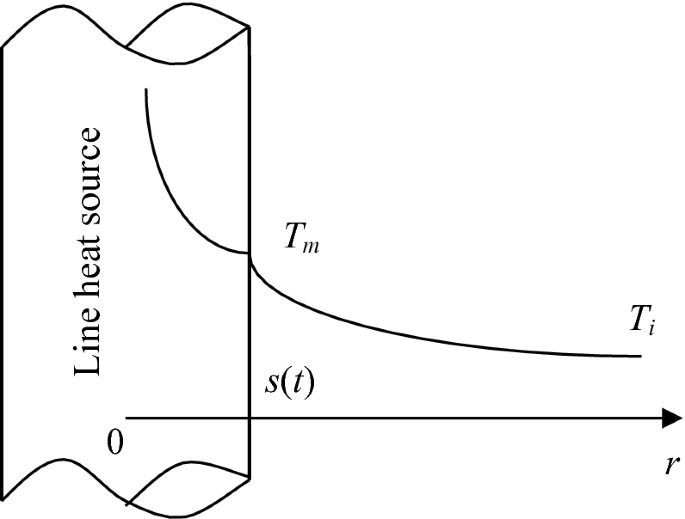
  Fig. P5.22

• 5.23. One-region melting in a semi-infinite body with constant surface temperature can be described by Eqs. (5.42)–(5.45). In a quasi-stationary approximate solution, the derivative of the temperature in the liquid phase with respect to time is assumed to be zero ($\partial \theta /\partial \tau = 0$). Consequently, the energy Eq. (5.42) is simplified as

  $$\frac{{\text{d}^{2} \theta }}{{\text{d}X^{2} }} = 0\quad \quad 0 < X < S(\tau ),\quad \tau > 0$$

  Solve the melting problem using quasi-stationary approximate solution and compare your results with integral solution for Ste = 0.1, 0.2, and 0.4.

• 5.24. A very long cylindrical biological material with a radius of r₀ is placed in a freezer at temperature $T_{0}$, which is assumed to be the surface temperature of the cylinder during freezing. Assume that the biological material can be treated as single-component PCM with a well-defined melting point, T_m, and that its initial temperature is at T_m. The freezing process is so slow that heat transfer in a frozen layer can be regarded as a quasi-steady-state process. Estimate the time it takes to freeze the entire cylinder.

• 5.25. Solve melting around a hollow sphere with boundary condition of the first kind by using the quasi-stationary method. The initial temperature of the PCM is assumed to be equal to the melting point.

• 5.26. A liquid PCM with initial temperature T_i ($T_{\rm i} > T_{\rm m}$) enters a circular tube with diameter D and wall temperature T_w ($T_{\rm w} < T_{\rm m}$, see Fig. P5.26). The liquid PCM is cooled in the tube and solidification begins at $x = L_{\rm s}$. While the diameter of the liquid channel shrinks as a result of solidification, the Nusselt number is assumed to be a constant before and after solidification begins. Assuming that axial conduction in the liquid and solid PCM are negligible and that the solidification inside the tube is steady-state, obtain the length at which solidification begins and the thickness of the solid layer. The properties of the liquid and solid PCM can be assumed to be the same.

  

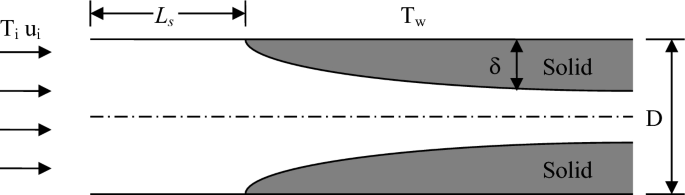
  Fig. P5.26

• 5.27. The liquidus 1 in the phase diagram, Fig. 5.16, can be approximated by a $\omega (T) = 1.678 \times 10^{ - 3} - 1.602 \times 10^{ - 2} T - 2.857 \times 10^{ - 4} T^{2}$$- 4.491 \times 10^{ - 6} T^{3}$, where the unit of temperature is °C. The local temperature and concentration of NH₄Cl at a point in the mushy zone formed by solidification are T_m = −10 °C and $\omega$ m = 10%, respectively. What is the local solid fraction,$f$, (i.e., mass fraction of the solid) in the mushy zone?

• 5.28. An NH₄Cl–H₂O solution is used as a phase-change material (PCM) in a cold storage system designed to be operated at –10 °C. In order to maintain the mobility of the mushy PCM, the maximum allowable solid fraction is 0.5. What is the appropriate concentration of NH₄Cl?

• 5.29. Show that the energy equation for the enthalpy model, Eq. (5.282), satisfies the energy equations for both the liquid and solid phases, Eqs. (5.20) and (5.22), as well as, energy balance, Eq. (5.26).

• 5.30. In the enthalpy method, we obtained an enthalpy equation for the numerical solution:

  $$h_{j}^{n + 1} = \frac{\Delta t}{{\rho \mathop {\left( {\Delta x} \right)}\nolimits^{2} }}\left( {k_{{j + \tfrac{1}{2}}} T_{j + 1}^{n} + k_{{j - \tfrac{1}{2}}} T_{j - 1}^{n} } \right) + \left( {h_{j}^{n} - \frac{{\Delta t\left( {k_{{j + \tfrac{1}{2}}} + k_{{j - \tfrac{1}{2}}} } \right)}}{{\rho \mathop {\left( {\Delta x} \right)}\nolimits^{2} }}T_{j}^{n} } \right),\quad j = 2,,N - 1$$

  Prove that the above equation is stable only if the following equation is satisfied:

  $$\frac{{max(\alpha_{\rm s} ,\alpha_{\ell } )\Delta t}}{{\mathop {\left( {\Delta x} \right)}\nolimits^{2} }} \le \frac{1}{2}$$

• 5.31. Phase change of a PCM occurs over a range of temperatures ($T_{\rm m} - \Delta T,$ $T_{\rm m} + \Delta T$). A finite slab of this PCM with thickness L has an initial temperature $T_{\rm i}$, which is below $T_{\rm m} - \Delta T$. At time t = 0, the temperature of the left surface suddenly increases to $T_{0} > T_{\rm m} + \Delta T,$ while the right surface remains insulated. Give the governing equations using enthalpy method and design the solution procedure.

• 5.32. You are given a one-dimensional melting problem that you need to solve with an explicit numerical scheme. The phase-change material is n-Octadecane.

  • (a) Given a time step of 0.1 s, find the minimum Δx necessary for stable numerical solution.

  • (b) Given a Δx of 1 mm, find the minimum time step necessary for stable numerical solution.

  • (c) What is the requirement for numerical simulation using the implicit method?

• 5.33. Show that the enthalpy–temperature relation in Fig. 5.25 can be represented analytically by Eq. (5.306).

• 5.34. Most materials that are used as solid-to-liquid PCMs have poor thermal conductivity. Describe at least three ways of increasing thermal conductivity to melt the material located “far” from the heat source.

• 5.35. In a convection-controlled melting or solidification process, the heat transfer coefficient is a function of the thermal properties of the PCMs, a characteristic length L, the temperature difference $\Delta T$, the buoyancy force ${\text{g}}\beta \Delta T$, and the latent heat of fusion $h_{{{\rm s}\ell }}$:

  $$h = h(k,\mu ,c_{\rm p} ,\rho ,L,\Delta T,g\beta \Delta T,h_{{{\rm s}\ell }} ,t)$$

  where t is time. Using Buckingham’s Π theorem shows that the number of nondimensional variables is 5, as opposed to the 10 dimensional variables in the above equation. Furthermore, use dimensional analysis to show that

  $${Nu} = f\left( {{Gr} ,\Pr ,{Ste} , {Fo} } \right)$$

  where Gr and Fo are Grashof and Fourier numbers.