Energy Methods

Abstract

When an archer draws a bow and shoots an arrow, it demonstrates that energy can be stored in an object when work is done to deform it relative to a reference state. Many advanced techniques used in mechanics of materials, including finite elements, are based on energy methods. This chapter discusses some of the fundamental concepts underlying these methods. The work done by a force or couple is first defined. By equating the work done by stress components in deforming a cubic element, the strain energy per unit volume of an isotropic linear elastic material subjected to a general state of stress is shown to be $u=\frac{1}{2}\left({\sigma}_x{\varepsilon}_x+{\sigma}_y{\varepsilon}_y+{\sigma}_z{\varepsilon}_z+{\tau}_{xy}{\gamma}_{xy}+{\tau}_{yz}{\gamma}_{yz}+{\tau}_{xz}{\gamma}_{xz}\right).$ With this result the strain energy of simple structural elements subjected to loads can be derived. For example, the strain energy of a prismatic bar of length L and cross-sectional area A that is subjected to axial loads P is U = P²L/2EA. By subjecting objects or structures to a force at a point and calculating the work done by the force, the displacement of the point in the direction of the force can be determined. Strain energy can be applied to a much broader class of problems using Castigliano’s second theorem. Consider an object of elastic material that is subjected to N external forces F₁, F₂,   … ,  F_N. Let u_i be the component of the deflection of the point of application of the ith force F_i in the direction of F_i. Then u_i = ∂U/∂F_i, where U is the strain energy resulting from the application of the N forces. If couples also act on an object, the angle of rotation of the point of application of the ith couple M_i in the direction of M_i is given by θ_i = ∂U/∂M_i. Examples of applications to trusses and beams are presented.

Appendices

Chapter Summary

11.1.1 Work

If the point to which the force F in Fig. (a) is applied moves along the x axis from x = 0 to x = x₀, the work done is

$$ W={\int}_0^{x_0}\;F\; dx. $$

If the force is a constant F = F₀, the work is W = F₀x₀. If F is proportional to x and its value is F₀ when x = x₀, the work is $W=\frac{1}{2}{F}_0{x}_0.$

When a couple of moment M rotates through an angle from θ = 0 to θ = θ₀ in the same direction as the couple, the work done is

$$ W={\int}_0^{\theta_0}\;M\; d\theta . $$

If the moment is a constant M = M₀, the work is W = M₀θ₀. If M is proportional to θ and its value is M₀ when θ = θ₀, the work is $W=\frac{1}{2}{M}_0{\theta}_0.$

11.1.2 Strain Energy

The strain energy per unit volume of an isotropic linearly elastic material subjected to a general state of stress is

$$ u=\frac{1}{2}\left({\sigma}_x{\varepsilon}_x+{\sigma}_y{\varepsilon}_y+{\sigma}_z{\varepsilon}_z+{\tau}_{xy}{\gamma}_{xy}+{\tau}_{yz}{\gamma}_{yz}+{\tau}_{xz}{\gamma}_{xz}\right). $$

(11.3)

11.1.3 Axially Loaded Bars

The strain energy of a prismatic bar of length L and cross-sectional area A that is subjected to an axial load P is

$$ U=\frac{P^2L}{2 EA}. $$

(11.11)

11.1.4 Beams

The strain energy of an element of a beam of width dx (Fig. (b)) is

$$ dU=\frac{M^2}{2 EI}\; dx. $$

(11.15)

11.1.5 Castigliano’s Second Theorem

Consider an object of elastic material that is subjected to N external forces F₁, F₂, …, F_N (Fig. (c)). Let u_i be the component of the deflection of the point of application of the ith force F_i in the direction of F_i. Then

$$ {u}_i=\frac{\partial U}{\partial {F}_i}, $$

(11.19)

where U is the strain energy resulting from the application of the N forces.

If couples also act on an object, the angle of rotation of the point of application of the ith couple M_i in the direction of M_i is given by

$$ {\theta}_i=\frac{\partial U}{\partial {M}_i}. $$

(11.20)

Review Problems

• 11.30 The two bars have cross-sectional area A = 1.4 in² and modulus of elasticity E = 12E6 psi. If an upward force F = 20, 000 lb is applied at B, what is the vertical component v of the deflection of point B?

  

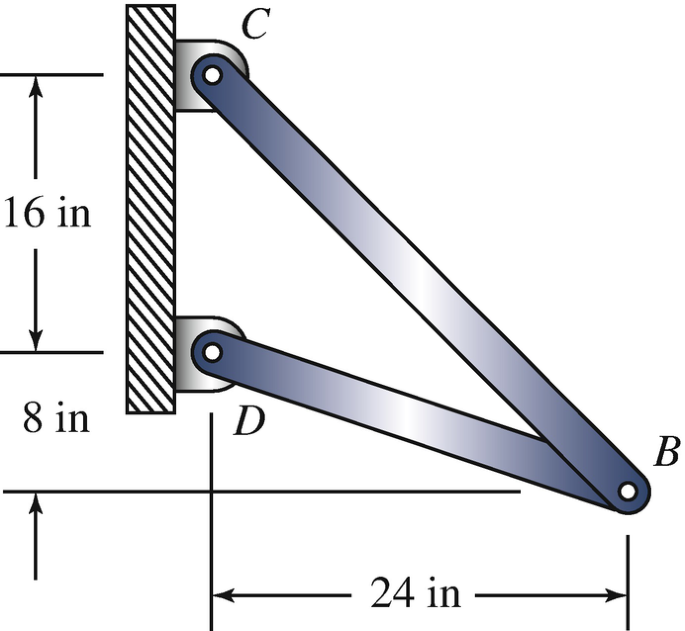
  Problems 11.30–11.31

• 11.31 The two bars have cross-sectional area A = 1.4 in² and modulus of elasticity E = 12E6 psi. If an upward force F = 20, 000 lb is applied at B, what is the horizontal component u of the deflection of point B?

• 11.32 The truss is made of steel bars with cross-sectional area A = 0.003 m² and modulus of elasticity E = 220 GPa. The suspended mass m = 5000 kg. Determine the vertical component v of the deflection of point B.

  

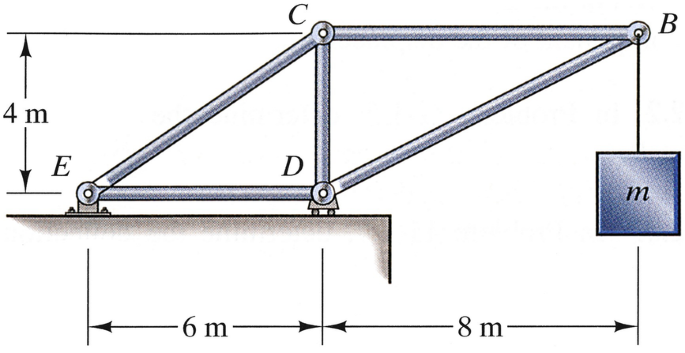
  Problems 11.32–11.33

• 11.33∗ The truss is made of steel bars with cross-sectional area A = 0.003 m² and modulus of elasticity E = 220 GPa. The suspended mass m = 5000 kg. Determine the horizontal component u of the deflection of point B.

• 11.34 Use strain energy to determine the angle through which the beam rotates at A, and confirm the value given in Appendix F.

  

  Problem 11.34

• 11.35∗ Use strain energy to determine the angle through which the beam rotates at A.

  

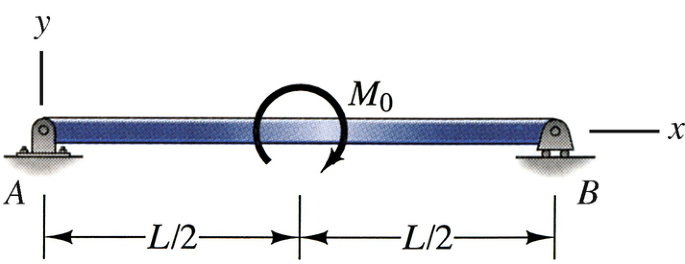
  Problem 11.35