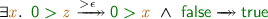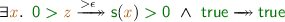Abstract
In term rewriting, reachability analysis is concerned with the problem of deciding whether or not one term is reachable from another by rewriting. Reachability analysis has several applications in termination and confluence analysis of rewrite systems. We give a unified view on reachability analysis for rewriting with and without conditions by means of what we call reachability constraints. Moreover, we provide several techniques that fit into this general framework and can be efficiently implemented. Our experiments show that these techniques increase the power of existing termination and confluence tools.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Reachability analysis for term rewriting [6] is concerned with the problem of, given a rewrite system  , a source term s and a target term t, deciding whether the source reduces to the target by rewriting, which is usually written
, a source term s and a target term t, deciding whether the source reduces to the target by rewriting, which is usually written  . A useful generalization of this problem is the (un)satisfiability of the following reachability problem: given terms s and t containing variables, decide whether there is a substitution \(\sigma \) such that
. A useful generalization of this problem is the (un)satisfiability of the following reachability problem: given terms s and t containing variables, decide whether there is a substitution \(\sigma \) such that  or not. This problem, also called (in)feasibility by Lucas and Guitiérrez [11], has various applications in termination and confluence analysis for plain and conditional rewriting.
or not. This problem, also called (in)feasibility by Lucas and Guitiérrez [11], has various applications in termination and confluence analysis for plain and conditional rewriting.
This can be understood as a form of safety analysis, as illustrated below.
Example 1
Let  be a term rewrite system consisting of the following rules for division (where
be a term rewrite system consisting of the following rules for division (where  stands for “successor”):
stands for “successor”):

The question “Can division yield an error?” is naturally formulated as the satisfiability of reachability from  . Unsurprisingly, the solution
. Unsurprisingly, the solution

shows that it is actually possible to obtain an error.
In termination analysis we are typically interested in unsatisfiability of reachability and can thereby rule out certain recursive calls as potential source of nontermination. For confluence analysis of conditional term rewriting, infeasibility is crucial: some other techniques do not apply before critical pairs are shown infeasible, and removal of infeasible rules simplifies proofs.
In this work we provide a formal framework that allows us to uniformly speak about (un)satisfiability of reachability for plain and conditional rewriting, and give several techniques that are useful in practice.
More specifically, our contributions are as follows:
-
We introduce the syntax and semantics of reachability constraints (Sect. 3) and formulate their satisfiability problem. We recast several concrete techniques for reachability analysis in the resulting framework.
-
We present a new, simple, and efficient technique for reachability analysis based on what we call the symbol transition graph of a rewrite system (Sect. 4.1) and extend it to conditional rewriting (Sect. 5.2).
-
Additionally, we generalize the prevalent existing technique for term rewriting to what we call look-ahead reachability (Sect. 4.2) and extend it to the conditional case (Sect. 5.3).
-
Then, we present a new result for conditional rewriting that is useful for proving conditional rules infeasible (Sect. 5.1).
-
Finally, we evaluate the impact of our work on existing automated tools NaTT [16] and ConCon [13] (Sect. 6).
2 Preliminaries
In the remainder, we assume some familiarity with term rewriting. Nevertheless, we recall required concepts and notations below. For further details on term rewriting, we refer to standard textbooks [3, 14].
Throughout the paper  denotes a set of function symbols with associated arities, and \(\mathcal {V}\) a countably infinite set of variables (so that fresh variables can always be picked) such that
denotes a set of function symbols with associated arities, and \(\mathcal {V}\) a countably infinite set of variables (so that fresh variables can always be picked) such that  . A term is either a variable
. A term is either a variable  or of the form \(f(t_1,\dots ,t_n)\), where n is the arity of
or of the form \(f(t_1,\dots ,t_n)\), where n is the arity of  and the arguments \(t_1,\dots ,t_n\) are terms. The set of all terms over
and the arguments \(t_1,\dots ,t_n\) are terms. The set of all terms over  and \(\mathcal {V}\) is denoted by
and \(\mathcal {V}\) is denoted by  . The set of variables occurring in a term t is denoted by \(\mathsf {Var}(t)\). The root symbol of a term \(t = f(t_1,\dots ,t_n)\) is f and denoted by \(\mathsf {root}(t)\). When we want to indicate that a term is not a variable, we sometimes write \(f(...)\), where “\(...\)” denotes an arbitrary list of terms.
. The set of variables occurring in a term t is denoted by \(\mathsf {Var}(t)\). The root symbol of a term \(t = f(t_1,\dots ,t_n)\) is f and denoted by \(\mathsf {root}(t)\). When we want to indicate that a term is not a variable, we sometimes write \(f(...)\), where “\(...\)” denotes an arbitrary list of terms.
A substitution is a mapping  . Given a term t, \(t\sigma \) denotes the term obtained by replacing every occurrence of variable x in t by \(\sigma (x)\). The domain of a substitution \(\sigma \) is
. Given a term t, \(t\sigma \) denotes the term obtained by replacing every occurrence of variable x in t by \(\sigma (x)\). The domain of a substitution \(\sigma \) is  , and \(\sigma \) is idempotent if
, and \(\sigma \) is idempotent if  for every
for every  . A renaming is a bijection
. A renaming is a bijection  . Two terms s and t are unifiable if \(s\sigma = t\sigma \) for some substitution \(\sigma \), which is called a unifier of s and t.
. Two terms s and t are unifiable if \(s\sigma = t\sigma \) for some substitution \(\sigma \), which is called a unifier of s and t.
A context is a term with exactly one occurrence of the special symbol  . We write C[t] for the term resulting from replacing
. We write C[t] for the term resulting from replacing  in context C by term t.
in context C by term t.
A rewrite rule is a pair of terms, written  , such that the variable conditions
, such that the variable conditions  and \(\mathsf {Var}(l) \supseteq \mathsf {Var}(r)\) hold. By a variant of a rewrite rule we mean a rule that is obtained by consistently renaming variables in the original rule to fresh ones. A term rewrite system (TRS) is a set
and \(\mathsf {Var}(l) \supseteq \mathsf {Var}(r)\) hold. By a variant of a rewrite rule we mean a rule that is obtained by consistently renaming variables in the original rule to fresh ones. A term rewrite system (TRS) is a set  of rewrite rules. A function symbol
of rewrite rules. A function symbol  is defined in
is defined in  if
if  , and the set of defined symbols in
, and the set of defined symbols in  is
is  . We call
. We call  a constructor.
a constructor.
There is an  -rewrite step from s to t, written
-rewrite step from s to t, written  , iff there exist a context C, a substitution \(\sigma \), and a rule
, iff there exist a context C, a substitution \(\sigma \), and a rule  such that \(s = C[l\sigma ]\) and \(t = C[r\sigma ]\). We write
such that \(s = C[l\sigma ]\) and \(t = C[r\sigma ]\). We write  if
if  (called a root step), and
(called a root step), and  (called a non-root step), otherwise. We say a term \(s_0\) is
(called a non-root step), otherwise. We say a term \(s_0\) is  -terminating if it starts no infinite rewrite sequence
-terminating if it starts no infinite rewrite sequence  , and say
, and say  is terminating if every term is
is terminating if every term is  -terminating.
-terminating.
For a relation \({\rightarrowtail } \subseteq A \times A\), we denote its transitive closure by \(\rightarrowtail ^+\) and reflexive transitive closure by \(\rightarrowtail ^*\). We say that  are joinable (meetable) at
are joinable (meetable) at  with respect to \(\rightarrowtail \) if \(a_i \rightarrowtail ^* b\) (\(b \rightarrowtail ^* a_i\)) for every
with respect to \(\rightarrowtail \) if \(a_i \rightarrowtail ^* b\) (\(b \rightarrowtail ^* a_i\)) for every  .
.
3 Reachability Constraint Satisfaction
In this section we introduce the syntax and semantics of reachability constraints, a framework that allows us to unify several concrete techniques for reachability analysis on an abstract level. Reachability constraints are first-order formulasFootnote 1 with a single binary predicate symbol whose intended interpretation is reachability by rewriting with respect to a given rewrite system.
Definition 1
(Reachability Constraints). Reachability constraints are given by the following grammar (where  and
and  )
)

To save some space, we use conventional notation like  and
and  .
.
As mentioned above, the semantics of reachability constraints is defined with respect to a given rewrite system. In the following we define satisfiability of constraints with respect to a TRS. (This definition will be extended to conditional rewrite systems in Sect. 5).
Definition 2
(Satisfiability). We defineFootnote 2 inductively when a substitution \(\sigma \) satisfies a reachability constraint \(\phi \) modulo a TRS  , written
, written  , as follows:
, as follows:
-
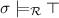 ;
; -
 if
if 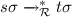 ;
; -
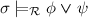 if
if  or
or  ;
; -
 if
if 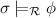 and
and  ;
; -
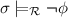 if
if  does not hold;
does not hold; -
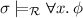 if
if 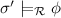 for every \(\sigma '\) that coincides with \(\sigma \) on
for every \(\sigma '\) that coincides with \(\sigma \) on 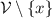 .
. -
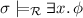 if
if 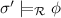 for some \(\sigma '\) that coincides with \(\sigma \) on
for some \(\sigma '\) that coincides with \(\sigma \) on  .
.
We say \(\phi \) and \(\psi \) are equivalent modulo  , written
, written  , when
, when  iff
iff  for all \(\sigma \). We say \(\phi \) and \(\psi \) are (logically) equivalent, written \(\phi \,\equiv _{}\,\psi \), if they are equivalent modulo any
for all \(\sigma \). We say \(\phi \) and \(\psi \) are (logically) equivalent, written \(\phi \,\equiv _{}\,\psi \), if they are equivalent modulo any  . We say \(\phi \) is satisfiable modulo
. We say \(\phi \) is satisfiable modulo  , written
, written  , if there is a substitution \(\sigma \) that satisfies \(\phi \) modulo
, if there is a substitution \(\sigma \) that satisfies \(\phi \) modulo  , and call \(\sigma \) a solution of \(\phi \) with respect to
, and call \(\sigma \) a solution of \(\phi \) with respect to  .
.
Checking for satisfiability of reachability constraints is for example useful for proving termination of term rewrite systems via the dependency pair method [2], or more specifically in dependency graph analysis. For the dependency pair method, we assume a fresh marked symbol \(f^\sharp \) for every  , and write \(s^\sharp \) to denote the term \(f^\sharp (s_1,\dots ,s_n)\) for \(s = f(s_1,\dots ,s_n)\). The set of dependency pairs of a TRS
, and write \(s^\sharp \) to denote the term \(f^\sharp (s_1,\dots ,s_n)\) for \(s = f(s_1,\dots ,s_n)\). The set of dependency pairs of a TRS  is
is  . The standard definition of the dependency graph of a TRS [2] can be recast using reachability constraints as follows:
. The standard definition of the dependency graph of a TRS [2] can be recast using reachability constraints as follows:
Definition 3
(Dependency Graph). Given a TRS  , its dependency graph
, its dependency graph  is the directed graph over
is the directed graph over  where there is an edge from
where there is an edge from  to
to  iff
iff  , where \(\alpha \) is a renaming of variables such that
, where \(\alpha \) is a renaming of variables such that  .
.
The nodes of the dependency graph correspond to the possible recursive calls in a program (represented by a TRS), while its edges encode the information which recursive calls can directly follow each other in arbitrary program executions. This is the reason why dependency graphs are useful for investigating the termination behavior of TRSs, as captured by the following result.
Theorem 1
([10]). A TRS  is terminating iff for every strongly connected component \(\mathcal {C}\) of an over approximation of
is terminating iff for every strongly connected component \(\mathcal {C}\) of an over approximation of  , there is no infinite chain
, there is no infinite chain  where every \(t_i\) is
where every \(t_i\) is  -terminating.
-terminating.
Example 2
Consider the TRS  of Toyama [15] consisting of the single rule
of Toyama [15] consisting of the single rule  . Its dependency graph
. Its dependency graph  consists of the single node:
consists of the single node:

To show  terminates it suffices to show that
terminates it suffices to show that  has no edge from (1) back to (1), that is, the unsatisfiability of the constraint (with a fresh variable
has no edge from (1) back to (1), that is, the unsatisfiability of the constraint (with a fresh variable  )
)

The most popular method today for checking reachability during dependency graph analysis is unifiability between the target and an approximation of the topmost part of the source (its “cap”) that does not change under rewriting, which is computed by the \(\mathsf {tcap}_{\mathcal {R}}\) function [9].
Definition 4
\(\mathbf{(}{\mathsf {tcap}_{}}\mathbf{).}\) Let  be a TRS. We recursively define \(\mathsf {tcap}_{\mathcal {R}}(t)\) for a given term t as follows: \(\mathsf {tcap}_{\mathcal {R}}(x)\) is a fresh variable if
be a TRS. We recursively define \(\mathsf {tcap}_{\mathcal {R}}(t)\) for a given term t as follows: \(\mathsf {tcap}_{\mathcal {R}}(x)\) is a fresh variable if  ; \(\mathsf {tcap}_{\mathcal {R}}(f(t_1,\dots ,t_n))\) is a fresh variable if \(u = f(\mathsf {tcap}_{\mathcal {R}}(t_1),\dots ,\mathsf {tcap}_{\mathcal {R}}(t_n))\) unifies with some left-hand side of the rules in
; \(\mathsf {tcap}_{\mathcal {R}}(f(t_1,\dots ,t_n))\) is a fresh variable if \(u = f(\mathsf {tcap}_{\mathcal {R}}(t_1),\dots ,\mathsf {tcap}_{\mathcal {R}}(t_n))\) unifies with some left-hand side of the rules in  ; otherwise, it is u.
; otherwise, it is u.
The standard way of checking for nonreachability that is implemented in most tools is captured by of the following proposition.
Proposition 1
If \(\mathsf {tcap}_{\mathcal {R}}(s)\) and t are not unifiable, then  .
.
Example 3
Proposition 1 cannot prove the unsatisfiability of (2) of Example 2, since the term cap of the source  , where
, where  ,
,  ,
,  are fresh variables, is unifiable with the target
are fresh variables, is unifiable with the target  .
.
4 Reachability in Term Rewriting
In this section we introduce some techniques for analyzing (un)satisfiability of reachability constraints. The first one described below formulates an obvious observation: no root rewrite step is applicable when starting from a term whose root is a constructor.
Definition 5
(Non-Root Reachability). For terms \(s = f(...)\) and \(t = g(...)\), we define the non-root reachability constraint  as follows:
as follows:
-
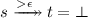 if \(f \ne g\), and
if \(f \ne g\), and -
 .
.
The intention of non-root reachability constraints is to encode zero or more steps of non-root rewriting, in the following sense.
Lemma 1
For  ,
,  iff
iff  .
.
Proof
The claim vacuously follows if \(\mathsf {root}(s) \ne \mathsf {root}(t)\). So let \(s = f(s_1,\dots ,s_n)\) and \(t = f(t_1,\dots ,t_n)\). We have  iff
iff  iff
iff  . \(\square \)
. \(\square \)
Combined with the observation that no root step is applicable to a term whose root symbol is a constructor, we obtain the following reformulation of a folklore result that reduces reachability to direct subterms.
Proposition 2
If \(s = f(...)\) with  and \(t \notin \mathcal {V}\), then
and \(t \notin \mathcal {V}\), then  .
.
Proposition 2 is directly applicable in the analysis of dependency graphs.
Example 4
Consider again the constraint  from Example 2. Since
from Example 2. Since  is not defined in
is not defined in  , Proposition 2 reduces this constraint to
, Proposition 2 reduces this constraint to  , that is,
, that is,

4.1 Symbol Transition Graphs
Here we introduce a new, simple and efficient way of overapproximating reachability by tracking the relation of root symbols of terms according to a given set of rewrite rules. We first illustrate the intuition by an example.
Example 5
Consider a TRS  consisting of rules of the following form:
consisting of rules of the following form:

Moreover, suppose  . Then we can make the following observations:
. Then we can make the following observations:
-
If
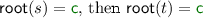 since non-root steps preserve the root symbol and no root steps are applicable to terms of the form
since non-root steps preserve the root symbol and no root steps are applicable to terms of the form  .
. -
If
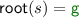 , then
, then 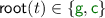 since non-root steps preserve the root symbol and the only possible root step is
since non-root steps preserve the root symbol and the only possible root step is 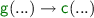 .
. -
If
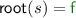 , then
, then 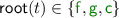 by the same reasoning.
by the same reasoning. -
If
 , then t can be any term and \(\mathsf {root}(t)\) can be arbitrary.
, then t can be any term and \(\mathsf {root}(t)\) can be arbitrary.
This informal argument is captured by the following definition.
Definition 6
(Symbol Transition Graphs). The symbol transition graph  of a TRS
of a TRS  over signature
over signature  is the graph
is the graph  , where \(f \rightarrowtail _{\mathcal {R}}g\) iff
, where \(f \rightarrowtail _{\mathcal {R}}g\) iff  contains a rule of form
contains a rule of form  or
or  with
with  .
.
The following result tells us that for non-variable terms the symbol transition graph captures the relation between the root symbols of root rewrite steps.
Lemma 2
If  then
then  .
.
Proof
By assumption there exist  and \(\sigma \) such that \(s = l\sigma \) and \(r\sigma = t\). If
and \(\sigma \) such that \(s = l\sigma \) and \(r\sigma = t\). If  then either
then either  or \(\mathsf {root}(s) = \mathsf {root}(l) \rightarrowtail _{\mathcal {R}}\mathsf {root}(t)\). Otherwise, \(\mathsf {root}(s) = \mathsf {root}(l) \rightarrowtail _{\mathcal {R}}\mathsf {root}(r) = \mathsf {root}(t)\). \(\square \)
or \(\mathsf {root}(s) = \mathsf {root}(l) \rightarrowtail _{\mathcal {R}}\mathsf {root}(t)\). Otherwise, \(\mathsf {root}(s) = \mathsf {root}(l) \rightarrowtail _{\mathcal {R}}\mathsf {root}(r) = \mathsf {root}(t)\). \(\square \)
Since every rewrite sequence is composed of subsequences that take place entirely below the root (and hence do not change the root symbol) separated by root steps, we can extend the previous result to rewrite sequences.
Lemma 3
If  then \(f \rightarrowtail _{\mathcal {R}}^* g\).
then \(f \rightarrowtail _{\mathcal {R}}^* g\).
Proof
We prove the claim for arbitrary s and f by induction on the derivation length of  . The base case is trivial, so consider
. The base case is trivial, so consider  . Since
. Since  , we have
, we have  with \(s' = f'(...)\). Thus the induction hypothesis yields \(f' \rightarrowtail _{\mathcal {R}}^* g\). If
with \(s' = f'(...)\). Thus the induction hypothesis yields \(f' \rightarrowtail _{\mathcal {R}}^* g\). If  then by Lemma 2 we conclude \(f \rightarrowtail _{\mathcal {R}}f' \rightarrowtail _{\mathcal {R}}^* g\), and otherwise \(f = f' \rightarrowtail _{\mathcal {R}}^* g\). \(\square \)
then by Lemma 2 we conclude \(f \rightarrowtail _{\mathcal {R}}f' \rightarrowtail _{\mathcal {R}}^* g\), and otherwise \(f = f' \rightarrowtail _{\mathcal {R}}^* g\). \(\square \)
It is now straightforward to derive the following from Lemma 3.
Corollary 1
If \(f \rightarrowtail _{\mathcal {R}}^* g\) does not hold, then  .
.
Example 6
The symbol transition graph for Example 5 is depicted in Fig. 1(a). By Corollary 1 we can conclude, for instance,  is unsatisfiable.
is unsatisfiable.
Corollary 1 is useful for checking (un)satisfiability of  , only if neither s nor t is a variable. However, the symbol transition graph is also useful for unsatisfiability in the case when s and t may be variables.
, only if neither s nor t is a variable. However, the symbol transition graph is also useful for unsatisfiability in the case when s and t may be variables.
Proposition 3
If  for \(t_1 = g_1(...), \,\ldots , t_n = g_n(...)\), then \(g_1, \ldots , g_n\) are meetable with respect to \(\rightarrowtail _{\mathcal {R}}\).
for \(t_1 = g_1(...), \,\ldots , t_n = g_n(...)\), then \(g_1, \ldots , g_n\) are meetable with respect to \(\rightarrowtail _{\mathcal {R}}\).
Proof
By assumption there is a substitution \(\sigma \) such that  . Clearly
. Clearly  is not possible. Thus, suppose \(x\sigma = f(...)\) for some f. Finally, from Lemma 3, we have \(f \rightarrowtail _{\mathcal {R}}^* g_1, \ldots , f \rightarrowtail _{\mathcal {R}}^* g_n\) and thereby conclude that \(g_1, \ldots , g_n\) are meetable at f. \(\square \)
is not possible. Thus, suppose \(x\sigma = f(...)\) for some f. Finally, from Lemma 3, we have \(f \rightarrowtail _{\mathcal {R}}^* g_1, \ldots , f \rightarrowtail _{\mathcal {R}}^* g_n\) and thereby conclude that \(g_1, \ldots , g_n\) are meetable at f. \(\square \)
The dual of Proposition 3 is proved in a similar way, but with some special care to ensure  .
.
Proposition 4
If  for \(s_1 = f_1(...), \ldots , s_n = f_n(...)\), then \(f_1, \ldots , f_n\) are joinable with respect to \(\rightarrowtail _{\mathcal {R}}\).
for \(s_1 = f_1(...), \ldots , s_n = f_n(...)\), then \(f_1, \ldots , f_n\) are joinable with respect to \(\rightarrowtail _{\mathcal {R}}\).
Example 7
(Continuation of Example 4). Due to Proposition 3, proving (3) unsatisfiable reduces to proving that  are not meetable with respect to \(\rightarrowtail _{\mathcal {R}}\). This is obvious from the symbol transition graph depicted in Fig. 1(b). Hence, we conclude the termination of
are not meetable with respect to \(\rightarrowtail _{\mathcal {R}}\). This is obvious from the symbol transition graph depicted in Fig. 1(b). Hence, we conclude the termination of  .
.
Example 8
Consider the following extension of  from Example 2.
from Example 2.

The resulting system is not terminating [15]. The corresponding symbol transition graph is depicted in Fig. 1(c), where  are meetable, as expected.
are meetable, as expected.
4.2 Look-Ahead Reachability
Here we propose another method for overapproximating reachability, which eventually subsumes the \(\mathsf {tcap}_{}\)-unifiability method when target terms are linear. Note that this condition is satisfied in the dependency graph approximation of left-linear TRSs. Our method is based on the observation that any rewrite sequence either contains at least one root step, or takes place entirely below the root. This observation can be captured using our reachability constraints.
Definition 7
(Root Narrowing Constraints). Let  be a rewrite rule with
be a rewrite rule with  . Then for terms s and t not containing \(x_1, \ldots , x_n\), the root narrowing constraint from s to t via
. Then for terms s and t not containing \(x_1, \ldots , x_n\), the root narrowing constraint from s to t via  is defined by
is defined by

We write  for
for  , where
, where  is a variant of
is a variant of  in which variables occurring in s or t are renamed to fresh ones.
in which variables occurring in s or t are renamed to fresh ones.
In the definition above, the intuition is that if there are any root steps inside a rewrite sequence then we can pick the first one, which is only preceded by non-root steps. The following theorem justifies this intuition.
Theorem 2
If  , then
, then  .
.
Proof
Let \(s = f(s_1,\dots ,s_n)\) and \(\sigma \) be a substitution. We show  iff
iff  . For the “if” direction suppose the latter. If
. For the “if” direction suppose the latter. If  , then t is of form \(f(t_1,\dots ,t_n)\) and
, then t is of form \(f(t_1,\dots ,t_n)\) and  for every
for every  , and thus
, and thus  . If
. If  , then we have a renamed variant
, then we have a renamed variant  of a rule in
of a rule in  such that
such that  . This indicates that there exists a substitution \(\sigma '\) that coincides with \(\sigma \) on
. This indicates that there exists a substitution \(\sigma '\) that coincides with \(\sigma \) on  , and satisfies
, and satisfies
-
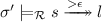 , that is, \(l = f(l_1,\dots ,l_n)\) and
, that is, \(l = f(l_1,\dots ,l_n)\) and 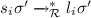 ;
; -
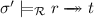 , that is,
, that is, 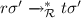 .
.
In combination, we have  .
.
Now consider the “only if” direction. Suppose that \(\sigma \) is an idempotent substitution such that  . We may assume idempotence, since from any solution \(\sigma '\) of
. We may assume idempotence, since from any solution \(\sigma '\) of  , we obtain idempotent solution \(\sigma \) by renaming variables in \(\mathsf {Var}(s) \cup \mathsf {Var}(t)\) to fresh ones. We proceed by the following case analysis:
, we obtain idempotent solution \(\sigma \) by renaming variables in \(\mathsf {Var}(s) \cup \mathsf {Var}(t)\) to fresh ones. We proceed by the following case analysis:
-
No root step is involved:
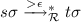 . Then Lemma 1 implies
. Then Lemma 1 implies  .
. -
At least one root step is involved: there is a rule
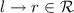 and a substitution \(\theta \) such that
and a substitution \(\theta \) such that 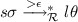 and
and 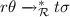 . Since variables in \(l\theta \) must occur in \(s\sigma \) (due to our assumptions on rewrite rules), we have \(l\theta = l\theta \sigma \) since \(\sigma \) is idempotent. Thus from Lemma 1 we have
. Since variables in \(l\theta \) must occur in \(s\sigma \) (due to our assumptions on rewrite rules), we have \(l\theta = l\theta \sigma \) since \(\sigma \) is idempotent. Thus from Lemma 1 we have 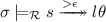 . Further, variables in \(r\theta \) must occur in \(l\theta \) and thus in \(s\theta \), we also have
. Further, variables in \(r\theta \) must occur in \(l\theta \) and thus in \(s\theta \), we also have 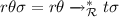 , and hence
, and hence  . This concludes
. This concludes 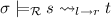 . \(\square \)
. \(\square \)
Proposition 2 is a corollary of Theorem 2 together with the following easy lemma, stating that if the root symbol of the source term is not a defined symbol, then no root step can occur.
Lemma 4
If  then
then  .
.
Example 9
Consider the TRS  consisting of the following rules:
consisting of the following rules:

Applying Theorem 2 once reduces the reachability constraint  to the disjunction of
to the disjunction of
-
1.
 ,
, -
2.
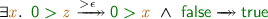
-
3.
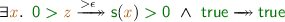
-
4.

Disjuncts 1, 3, and 4 expand to  by definition of
by definition of  . For disjunct 2, applying Theorem 2 or Proposition 2 to
. For disjunct 2, applying Theorem 2 or Proposition 2 to  yields
yields  .
.
Note that Theorem 2 can be applied arbitrarily often. Thus, to avoid nontermination in an implementation, we need to control how often it is applied. For this purpose we introduce the following definition.
Definition 8
\(\mathbf{(}k\mathbf{\text {-}Fold~Look\text {-}Ahead).}\) We define the k-fold look-ahead transformation with respect to a TRS  as follows:
as follows:

which is homomorphically extended to reachability constraints. Here,  is defined as in Definition 7, but k controls the number of root steps to be expanded:
is defined as in Definition 7, but k controls the number of root steps to be expanded:

It easily follows from Theorem 2 and induction on k that the k-fold look-ahead preserves the semantics of reachability constraints.
Corollary 2
 .
.
The following results indicate that, whenever \(\mathsf {tcap}_{\mathcal {R}}\)-unifiability (Proposition 1) proves  unsatisfiable for linear t, \(\mathsf {L}_{\mathcal {R}}^{1}\) can also conclude it.
unsatisfiable for linear t, \(\mathsf {L}_{\mathcal {R}}^{1}\) can also conclude it.
Lemma 5
Let \(s = f(s_1,\dots ,s_n)\) and  be a linear term, and suppose that \(f(\mathsf {tcap}_{\mathcal {R}}(s_1),\dots ,\mathsf {tcap}_{\mathcal {R}}(s_n))\) does not unify with t or any left-hand side in
be a linear term, and suppose that \(f(\mathsf {tcap}_{\mathcal {R}}(s_1),\dots ,\mathsf {tcap}_{\mathcal {R}}(s_n))\) does not unify with t or any left-hand side in  . Then
. Then  .
.
Proof
By structural induction on s. First, we show  . This is trivial if \(\mathsf {root}(t) \ne f\). So let \(t = f(t_1,\dots ,t_n)\). By assumption there is an
. This is trivial if \(\mathsf {root}(t) \ne f\). So let \(t = f(t_1,\dots ,t_n)\). By assumption there is an  such that \(\mathsf {tcap}_{\mathcal {R}}(s_i)\) does not unify with \(t_i\). Hence \(\mathsf {tcap}_{\mathcal {R}}(s_i)\) cannot be a fresh variable, and thus \(s_i\) is of the form \(g(u_1,\dots ,u_m)\) and \(\mathsf {tcap}_{\mathcal {R}}(s_i) = g(\mathsf {tcap}_{\mathcal {R}}(u_1),\dots ,\mathsf {tcap}_{\mathcal {R}}(u_m))\) is not unifiable with any left-hand side in
such that \(\mathsf {tcap}_{\mathcal {R}}(s_i)\) does not unify with \(t_i\). Hence \(\mathsf {tcap}_{\mathcal {R}}(s_i)\) cannot be a fresh variable, and thus \(s_i\) is of the form \(g(u_1,\dots ,u_m)\) and \(\mathsf {tcap}_{\mathcal {R}}(s_i) = g(\mathsf {tcap}_{\mathcal {R}}(u_1),\dots ,\mathsf {tcap}_{\mathcal {R}}(u_m))\) is not unifiable with any left-hand side in  . Therefore, the induction hypothesis applies to \(s_i\), yielding
. Therefore, the induction hypothesis applies to \(s_i\), yielding  . This concludes
. This concludes  .
.
Second, we show  . To this end, we show for an arbitrary variant
. To this end, we show for an arbitrary variant  of a rule in
of a rule in  that
that  . This is clear if \(\mathsf {root}(l) \ne f\). So let \(l = f(l_1,\dots ,l_n)\). By assumption there is an
. This is clear if \(\mathsf {root}(l) \ne f\). So let \(l = f(l_1,\dots ,l_n)\). By assumption there is an  such that \(\mathsf {tcap}_{\mathcal {R}}(s_i)\) and \(l_i\) are not unifiable. By a similar reasoning as above the induction hypothesis applies to \(s_i\) and yields
such that \(\mathsf {tcap}_{\mathcal {R}}(s_i)\) and \(l_i\) are not unifiable. By a similar reasoning as above the induction hypothesis applies to \(s_i\) and yields  . This concludes
. This concludes  . \(\square \)
. \(\square \)
Corollary 3
If \(\mathsf {tcap}_{\mathcal {R}}(s)\) and t are not unifiable, then  .
.
5 Conditional Rewriting
Conditional rewriting is a flavor of rewriting where rules are guarded by conditions. On the one hand, this gives us a boost in expressiveness in the sense that it is often possible to directly express equations with preconditions and that it is easier to directly express programming constructs like the where-clauses of Haskell. On the other hand, the analysis of conditional rewrite systems is typically more involved than for plain rewriting.
In this section we first recall the basics of conditional term rewriting. Then, we motivate the importance of reachability analysis for the conditional case. Finally, we extend the techniques of Sect. 4 to conditional rewrite systems.
Preliminaries. A conditional rewrite rule  consists of two terms
consists of two terms  and r (the left-hand side and right-hand side, respectively) and a list \(\phi \) of pairs of terms (its conditions). A conditional term rewrite system (CTRS for short) is a set of conditional rewrite rules. Depending on the interpretation of conditions, conditional rewriting can be separated into several classes. For the purposes of this paper we are interested in oriented CTRSs, where conditions are interpreted as reachability constraints with respect to conditional rewriting. Hence, from now on we identify conditions
and r (the left-hand side and right-hand side, respectively) and a list \(\phi \) of pairs of terms (its conditions). A conditional term rewrite system (CTRS for short) is a set of conditional rewrite rules. Depending on the interpretation of conditions, conditional rewriting can be separated into several classes. For the purposes of this paper we are interested in oriented CTRSs, where conditions are interpreted as reachability constraints with respect to conditional rewriting. Hence, from now on we identify conditions  with the reachability constraint
with the reachability constraint  , and the empty list with
, and the empty list with  (omitting “
(omitting “ ” from rules).
” from rules).
The rewrite relation of a CTRS is layered into levels: given a CTRS  and level
and level  , the corresponding (unconditional) TRS
, the corresponding (unconditional) TRS  is defined recursively:
is defined recursively:

Then the (conditional) rewrite relation at level i, written  (or
(or  whenever
whenever  is clear from the context), is the plain rewrite relation
is clear from the context), is the plain rewrite relation  induced by the TRS
induced by the TRS  . Finally, the induced (conditional) rewrite relation of a CTRS
. Finally, the induced (conditional) rewrite relation of a CTRS  is defined by
is defined by  . At this point Definition 2 is extended to the conditional case in a straightforward manner.
. At this point Definition 2 is extended to the conditional case in a straightforward manner.
Definition 9
(Level Satisfiability). Let  be a CTRS and \(\phi \) a reachability constraint. We say that a substitution \(\sigma \) satisfies \(\phi \) modulo
be a CTRS and \(\phi \) a reachability constraint. We say that a substitution \(\sigma \) satisfies \(\phi \) modulo  at level i, whenever
at level i, whenever  . If we are not interested in a specific satisfying substitution we say that \(\phi \) is satisfiable modulo
. If we are not interested in a specific satisfying substitution we say that \(\phi \) is satisfiable modulo  at level i and write
at level i and write  (or just \(\mathsf {SAT}_{i}(\phi )\) whenever
(or just \(\mathsf {SAT}_{i}(\phi )\) whenever  is clear from the context).
is clear from the context).
5.1 Infeasibility
The main area of interest for reachability analysis in the conditional case is checking for infeasibility. While a formal definition of this concept follows below, for the moment, think of it as unsatisfiability of conditions. The two predominant applications of infeasibility are: (1) if the conditions of a rule are unsatisfiable, the rule can never be applied and thus safely be removed without changing the induced rewrite relation; (2) if the conditions of a conditional critical pair (which arises from confluence analysis of CTRSs) are unsatisfiable, then it poses no problem to confluence and can safely be ignored.
Definition 10
(Infeasibility). We say that a conditional rewrite rule  is applicable at level i with respect to a CTRS
is applicable at level i with respect to a CTRS  iff
iff  . A set \(\mathcal {S}\) of rules is infeasible with respect to
. A set \(\mathcal {S}\) of rules is infeasible with respect to  when no rule in \(\mathcal {S}\) is applicable at any level.
when no rule in \(\mathcal {S}\) is applicable at any level.
The next theorem allows us to remove some rules from a CTRS while checking for infeasibility of rules.
Theorem 3
A set \(\mathcal {S}\) of rules is infeasible with respect to a CTRS  iff it is infeasible with respect to
iff it is infeasible with respect to  .
.
Proof
The ‘only if’ direction is trivial. Thus we concentrate on the ‘if’ direction. To this end, assume that \(\mathcal {S}\) is infeasible with respect to  , but not infeasible with respect to
, but not infeasible with respect to  . That is, at least one rule in \(\mathcal {S}\) is applicable at some level with respect to
. That is, at least one rule in \(\mathcal {S}\) is applicable at some level with respect to  . Let m be the minimum level such that there is a rule
. Let m be the minimum level such that there is a rule  that is applicable at level m with respect to
that is applicable at level m with respect to  . Now if \(m = 0\) then
. Now if \(m = 0\) then  is applicable at level 0 and thus
is applicable at level 0 and thus  , which trivially implies
, which trivially implies  , contradicting the assumption that all rules in \(\mathcal {S}\) are infeasible with respect to
, contradicting the assumption that all rules in \(\mathcal {S}\) are infeasible with respect to  . Otherwise, \(m = k+1\) for some \(k \ge 0\) and since
. Otherwise, \(m = k+1\) for some \(k \ge 0\) and since  is applicable at level m we have
is applicable at level m we have  . Moreover, the rewrite relations
. Moreover, the rewrite relations  and
and  coincide (since all rules in \(\mathcal {S}\) are infeasible at levels smaller than m by our choice of m). Thus we also have
coincide (since all rules in \(\mathcal {S}\) are infeasible at levels smaller than m by our choice of m). Thus we also have  , again contradicting the assumption that all rules in \(\mathcal {S}\) are infeasible with respect to
, again contradicting the assumption that all rules in \(\mathcal {S}\) are infeasible with respect to  . \(\square \)
. \(\square \)
The following example from the confluence problems data base (Cops)Footnote 3 shows that Theorem 3 is beneficial for showing infeasibility of conditional rewrite rules.
Example 10
\({\textit{(}}\!\!\) Cops 794). Consider the CTRS  consisting of the two rules:
consisting of the two rules:

The \(\mathsf {tcap}_{}\)-method does not manage to conclude infeasibility of the first rule, since  for some fresh variable
for some fresh variable  and thus unifies with
and thus unifies with  . The reason for this result was that for computing \(\mathsf {tcap}_{\mathcal {R}}\) we had to recursively (in a bottom-up fashion) try to unify arguments of functions with left-hand sides of rules, which succeeded for the left-hand side of the first rule and the argument
. The reason for this result was that for computing \(\mathsf {tcap}_{\mathcal {R}}\) we had to recursively (in a bottom-up fashion) try to unify arguments of functions with left-hand sides of rules, which succeeded for the left-hand side of the first rule and the argument  , thereby obtaining
, thereby obtaining  which, in turn, unifies with the left-hand side of the second rule. But by Theorem 3 we do not need to consider the first rule for computing the term cap and thus obtain
which, in turn, unifies with the left-hand side of the second rule. But by Theorem 3 we do not need to consider the first rule for computing the term cap and thus obtain  which does not unify with
which does not unify with  and thereby shows that the first rule is infeasible.
and thereby shows that the first rule is infeasible.
5.2 Symbol Transition Graphs in the Presence of Conditions
In the presence of conditions in rules we replace Definition 6 by the following inductive definition:
Definition 11
(Inductive Symbol Transition Graphs). The symbol transition graph  of a CTRS
of a CTRS  over a signature
over a signature  is the graph
is the graph  where \(\rightarrowtail _{\mathcal {R}}\) is defined inductively by the following two inference rules:
where \(\rightarrowtail _{\mathcal {R}}\) is defined inductively by the following two inference rules:

Inductive and plain symbol transition graph of Example 11.
The example below shows the difference between the symbol transition graph for TRSs (which can be applied as a crude overapproximation also to CTRSs by dropping all conditions) and the inductive symbol transition graph for CTRSs.
Example 11
\({\textit{(}}\!\!\) Cops 293). Consider the CTRS consisting of the three rules:

The corresponding inductive symbol transition graph is depicted in Fig. 2(a) and implies unsatisfiability of  . Note that this conclusion cannot be drawn from the plain symbol transition graph of the TRS obtained by dropping the condition of the third rule, shown in Fig. 2(b).
. Note that this conclusion cannot be drawn from the plain symbol transition graph of the TRS obtained by dropping the condition of the third rule, shown in Fig. 2(b).
The inductive symbol transition graph gives us a sufficient criterion for concluding nonreachability with respect to a given CTRS, as shown in the following.
Lemma 6
If  then \(f \rightarrowtail _{\mathcal {R}}^* g\).
then \(f \rightarrowtail _{\mathcal {R}}^* g\).
Proof
Let \(s = f(...)\) and \(u = g(...)\) and assume that s rewrites to u at level i, that is,  . We prove the statement by induction on the level i. If \(i = 0\) then we are done, since
. We prove the statement by induction on the level i. If \(i = 0\) then we are done, since  is empty and therefore \(f(...) = s = u = g(...)\), which trivially implies \(f \rightarrowtail _{\mathcal {R}}^* g\). Otherwise, \(i = j + 1\) and we obtain the induction hypothesis (IH) that
is empty and therefore \(f(...) = s = u = g(...)\), which trivially implies \(f \rightarrowtail _{\mathcal {R}}^* g\). Otherwise, \(i = j + 1\) and we obtain the induction hypothesis (IH) that  implies \(\mathsf {root}(s) \rightarrowtail _{\mathcal {R}}^* \mathsf {root}(t)\) for arbitrary non-variable terms s and t. We proceed to show that
implies \(\mathsf {root}(s) \rightarrowtail _{\mathcal {R}}^* \mathsf {root}(t)\) for arbitrary non-variable terms s and t. We proceed to show that  implies \(f \rightarrowtail _{\mathcal {R}}^* g\) by an inner induction on the length of this derivation. If the derivation is empty, then \(f(...) = s = u = g(...)\) and therefore trivially \(f \rightarrowtail _{\mathcal {R}}^* g\). Otherwise, the derivation is of the shape
implies \(f \rightarrowtail _{\mathcal {R}}^* g\) by an inner induction on the length of this derivation. If the derivation is empty, then \(f(...) = s = u = g(...)\) and therefore trivially \(f \rightarrowtail _{\mathcal {R}}^* g\). Otherwise, the derivation is of the shape  for some non-variable term \(t = h(...)\) and we obtain the inner induction hypothesis that \(f \rightarrowtail _{\mathcal {R}}^* h\). It remains to show \(h \rightarrowtail _{\mathcal {R}}^* g\) in order to conclude the proof. To this end, consider the step
for some non-variable term \(t = h(...)\) and we obtain the inner induction hypothesis that \(f \rightarrowtail _{\mathcal {R}}^* h\). It remains to show \(h \rightarrowtail _{\mathcal {R}}^* g\) in order to conclude the proof. To this end, consider the step  for some context C, substitution \(\sigma \), and rule
for some context C, substitution \(\sigma \), and rule  such that
such that  . Now, by IH, we obtain that
. Now, by IH, we obtain that  or
or  or \(\mathsf {root}(s') \rightarrowtail _{\mathcal {R}}^* \mathsf {root}(t')\) for all
or \(\mathsf {root}(s') \rightarrowtail _{\mathcal {R}}^* \mathsf {root}(t')\) for all  . Thus, by Definition 11, we obtain that \(\mathsf {root}(l\sigma ) \rightarrowtail _{\mathcal {R}}\mathsf {root}(r\sigma )\). We conclude by a case analysis on the structure of the context C. If C is empty, that is
. Thus, by Definition 11, we obtain that \(\mathsf {root}(l\sigma ) \rightarrowtail _{\mathcal {R}}\mathsf {root}(r\sigma )\). We conclude by a case analysis on the structure of the context C. If C is empty, that is  , then \(h = \mathsf {root}(l\sigma ) \rightarrowtail _{\mathcal {R}}^* \mathsf {root}(r\sigma ) = g\) and we are done. Otherwise, \(h = \mathsf {root}(t) = \mathsf {root}(u) = g\) and therefore trivially \(h \rightarrowtail _{\mathcal {R}}^* g\). \(\square \)
, then \(h = \mathsf {root}(l\sigma ) \rightarrowtail _{\mathcal {R}}^* \mathsf {root}(r\sigma ) = g\) and we are done. Otherwise, \(h = \mathsf {root}(t) = \mathsf {root}(u) = g\) and therefore trivially \(h \rightarrowtail _{\mathcal {R}}^* g\). \(\square \)
Corollary 4
If \(f \rightarrowtail _{\mathcal {R}}^* g\) does not hold, then  .
.
5.3 Look-Ahead Reachability in the Presence of Conditions
In the following definition we extend our look-ahead technique from plain rewriting to conditional rewriting.
Definition 12
(Conditional Root Narrowing Constraints). Let  be a conditional rewrite rule with
be a conditional rewrite rule with  . Then for terms s and t not containing \(x_1, \ldots , x_n\), the conditional root narrowing constraint from s to t via
. Then for terms s and t not containing \(x_1, \ldots , x_n\), the conditional root narrowing constraint from s to t via  is defined by
is defined by

We write  for
for  , where
, where  is a variant of
is a variant of  in which variables occurring in s or t are renamed to fresh ones.
in which variables occurring in s or t are renamed to fresh ones.
And we obtain a result similar to Theorem 2.
Lemma 7
If  , then
, then  .
.
Example 12
\({\textit{(}}\!\!\) Cops 793). Consider the CTRS  consisting of the two rules:
consisting of the two rules:

To show infeasibility of the first rule we can safely remove it from  by Theorem 3, resulting in the modified CTRS
by Theorem 3, resulting in the modified CTRS  . Then we have to check
. Then we have to check  which is made easier by the following chain of equivalences:
which is made easier by the following chain of equivalences:

Since satisfiability of the final constraint above implies  and we also have
and we also have  , we can conclude unsatisfiability of the original constraint by Corollary 4 and hence that the first rule of
, we can conclude unsatisfiability of the original constraint by Corollary 4 and hence that the first rule of  is infeasible.
is infeasible.
6 Assessment
We implemented our techniques in the TRS termination prover NaTT [16]Footnote 4 version 1.8 for dependency graph analysis, and the CTRS confluence prover ConCon [13]Footnote 5 version 1.7 for infeasibility analysis. In both cases we only need a complete satisfiability checker, or equivalently, a sound unsatisfiability checker. Hence, to conclude unsatisfiability of given reachability constraints, we apply Corollary 2 with appropriate k together with a complete approximation of constraints. One such approximation is the symbol transition graph (Corollary 1). In the following we describe the experimental results on TRS termination and CTRS confluence. Further details of our experiments can be found at http://cl-informatik.uibk.ac.at/experiments/reachability/.
TRS Termination. For plain rewriting, we take all the 1498 TRSs from the TRS standard category of the termination problem data base version 10.6,Footnote 6 the benchmark used in the annual Termination Competition [8], and over-approximate their dependency graphs. This results in 1 133 963 reachability constraints, which we call “edges” here. Many of these edges are actually satisfiable, but we do not know the exact number (the problem is undecidable in general).
For checking unsatisfiability of edges, we combine Corollary 2 for various values of k (0, 1, 2, 3, and 8), and either Corollary 1 or ‘None’. Here ‘None’ concludes unsatisfiability only for constraints that are logically equivalent to  . In Table 1 we give the number of edges that could be shown unsatisfiable. Here, the ‘UNSAT’ row indicates the number of detected unsatisfiable edges and the ‘time’ row indicates the total runtime in seconds. (We ran our experiments on an Amazon EC2 instance model c5.xlarge: 4 virtual 3.0 GHz Intel Xeon Platinum CPUs on 8 GB of memory).
. In Table 1 we give the number of edges that could be shown unsatisfiable. Here, the ‘UNSAT’ row indicates the number of detected unsatisfiable edges and the ‘time’ row indicates the total runtime in seconds. (We ran our experiments on an Amazon EC2 instance model c5.xlarge: 4 virtual 3.0 GHz Intel Xeon Platinum CPUs on 8 GB of memory).
The starting point is \(\mathsf {L}_{\mathcal {R}}^{1}\) + None, which corresponds to the \(\mathsf {tcap}_{}\) technique, the method that was already implemented in NaTT before. The benefit of symbol transition graphs turns out to be quite significant, while the overhead in runtime seems acceptable. Moreover, increasing k of the look-ahead reasonably improves the power of unsatisfiability checks, both with and without the symbol transition graph technique. In terms of the overall termination proving power, NaTT using only \(\mathsf {tcap}_{}\) solves 1039 out of the 1498 termination problems, while using \(\mathsf {L}_{\mathcal {R}}^{8}\) and Corollary 1, it proves termination of 18 additional problems.
CTRS Confluence. For conditional rewriting, we take the 148 oriented CTRSs of Cops,Footnote 7 a benchmark of confluence problems used in the annual Confluence Competition [1]. Compared to version 1.5 of ConCon (the winner of the CTRS category in the last competition in 2018) our new version (1.7) can solve five more systems (that is a gain of roughly 3%) by incorporating a combination of Theorem 3, inductive symbol transition graphs (Corollary 4), and k-fold look-ahead (Lemma 7), where for the latter we fixed \(k = 1\) since we additionally have to control the level of conditional rewriting.
7 Related Work
Reachability is a classical topic in term rewriting; cf. Genet [7] for a survey. Some modern techniques include the tree-automata-completion approach [5, 6] and a Knuth-Bendix completion-like approach [4]. Compared to these lines of work, first of all our interest is not directly in reachability problems but their (un)satisfiability. Middeldorp [12] proposed tree-automata techniques to approximate dependency graphs and made a theoretical comparison to an early term-cap-unifiability method [2], a predecessor of the \(\mathsf {tcap}_{}\)-based method. It is indeed possible (after some approximations of input TRSs) to encode our satisfiability problems into reachability problems between regular tree languages. However, our main motivation is to efficiently test reachability when analyzing other properties like termination and confluence. In that setting, constructing tree automata often leads to excessive overhead.
Our work is inspired by the work of Lucas and Gutiérrez [11]. Their feasibility sequences serve the same purpose as our reachability constraints, but are limited to atoms and conjunctions. Our formulation, allowing other constructions of logic formulas, is essential for introducing look-ahead reachability.
8 Conclusion
We introduced reachability constraints and their satisfiability problem. Such problems appear in termination and confluence analysis of plain and conditional rewriting. Moreover, we proposed two efficient techniques to prove (un)satisfiability of reachability constraints, first for plain and then for conditional rewriting. Finally, we implemented these techniques in the termination prover NaTT and the confluence prover ConCon, and experimentally verified their significance.
Notes
- 1.
While in general we allow an arbitrary first-order logical structure for formulas, for the purpose of this paper, negation and universal quantification are not required.
- 2.
It is also possible to give a model-theoretic account for these notions. However, the required preliminaries are outside the scope of this paper.
- 3.
- 4.
- 5.
- 6.
- 7.
References
Aoto, T., Hirokawa, N., Nagele, J., Nishida, N., Zankl, H.: Confluence competition 2015. In: Felty, A.P., Middeldorp, A. (eds.) CADE 2015. LNCS (LNAI), vol. 9195, pp. 101–104. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21401-6_5
Arts, T., Giesl, J.: Termination of term rewriting using dependency pairs. Theor. Compt. Sci. 236(1–2), 133–178 (2000). https://doi.org/10.1016/S0304-3975(99)00207-8
Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press, Cambridge (1998)
Burel, G., Dowek, G., Jiang, Y.: A completion method to decide reachability in rewrite systems. In: Lutz, C., Ranise, S. (eds.) FroCoS 2015. LNCS (LNAI), vol. 9322, pp. 205–219. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24246-0_13
Felgenhauer, B., Thiemann, R.: Reachability, confluence, and termination analysis with state-compatible automata. Inf. Comput. 253, 467–483 (2017). https://doi.org/10.1016/j.ic.2016.06.011
Feuillade, G., Genet, T., Viet Triem Tong, V.: Reachability analysis over term rewriting systems. J. Autom. Reason. 33(341), 341–383 (2004). https://doi.org/10.1007/s10817-004-6246-0
Genet, T.: Reachability analysis of rewriting for software verification. Habilitation à diriger des recherches, Université de Rennes 1 (2009)
Giesl, J., Mesnard, F., Rubio, A., Thiemann, R., Waldmann, J.: Termination competition (termCOMP 2015). In: Felty, A.P., Middeldorp, A. (eds.) CADE 2015. LNCS (LNAI), vol. 9195, pp. 105–108. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21401-6_6
Giesl, J., Thiemann, R., Schneider-Kamp, P.: Proving and disproving termination of higher-order functions. In: Gramlich, B. (ed.) FroCoS 2005. LNCS (LNAI), vol. 3717, pp. 216–231. Springer, Heidelberg (2005). https://doi.org/10.1007/11559306_12
Hirokawa, N., Middeldorp, A.: Dependency pairs revisited. In: van Oostrom, V. (ed.) RTA 2004. LNCS, vol. 3091, pp. 249–268. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-25979-4_18
Lucas, S., Gutiérrez, R.: Use of logical models for proving infeasibility in term rewriting. Inf. Process. Lett. 136, 90–95 (2018). https://doi.org/10.1016/j.ipl.2018.04.002
Middeldorp, A.: Approximating dependency graphs using tree automata techniques. In: Goré, R., Leitsch, A., Nipkow, T. (eds.) IJCAR 2001. LNCS, vol. 2083, pp. 593–610. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45744-5_49
Sternagel, T., Middeldorp, A.: Conditional confluence (system description). In: Dowek, G. (ed.) RTA 2014. LNCS, vol. 8560, pp. 456–465. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08918-8_31
TeReSe: Term Rewriting Systems. Cambridge Tracts in Theoretical Computer Science, vol. 55. Cambridge University Press, Cambridge (2003)
Toyama, Y.: Counterexamples to termination for the direct sum of term rewriting systems. Inf. Process. Lett. 25(3), 141–143 (1987). https://doi.org/10.1016/0020-0190(87)90122-0
Yamada, A., Kusakari, K., Sakabe, T.: Nagoya termination tool. In: Dowek, G. (ed.) RTA 2014. LNCS, vol. 8560, pp. 466–475. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08918-8_32
Acknowledgments
We thank Aart Middeldorp and the anonymous reviewers for their insightful comments. This work is supported by the Austrian Science Fund (FWF) project P27502 and ERATO HASUO Metamathematics for Systems Design Project (No. JPMJER1603), JST.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Sternagel, C., Yamada, A. (2019). Reachability Analysis for Termination and Confluence of Rewriting. In: Vojnar, T., Zhang, L. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2019. Lecture Notes in Computer Science(), vol 11427. Springer, Cham. https://doi.org/10.1007/978-3-030-17462-0_15
Download citation
DOI: https://doi.org/10.1007/978-3-030-17462-0_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17461-3
Online ISBN: 978-3-030-17462-0
eBook Packages: Computer ScienceComputer Science (R0)


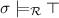 ;
; if
if 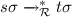 ;
;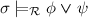 if
if  or
or  ;
; if
if 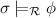 and
and  ;
;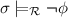 if
if  does not hold;
does not hold;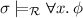 if
if 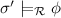 for every
for every 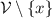 .
.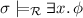 if
if 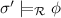 for some
for some  .
.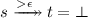 if
if  .
.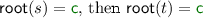 since non-root steps preserve the root symbol and no root steps are applicable to terms of the form
since non-root steps preserve the root symbol and no root steps are applicable to terms of the form  .
.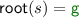 , then
, then 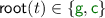 since non-root steps preserve the root symbol and the only possible root step is
since non-root steps preserve the root symbol and the only possible root step is 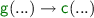 .
.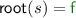 , then
, then 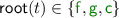 by the same reasoning.
by the same reasoning. , then t can be any term and
, then t can be any term and 
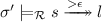 , that is,
, that is, 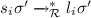 ;
;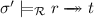 , that is,
, that is, 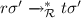 .
.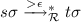 . Then Lemma
. Then Lemma  .
.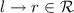 and a substitution
and a substitution 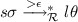 and
and 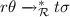 . Since variables in
. Since variables in 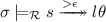 . Further, variables in
. Further, variables in 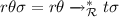 , and hence
, and hence  . This concludes
. This concludes 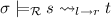 .
.  ,
,