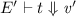Incremental $\lambda$-Calculus in Cache-Transfer Style

Abstract

Incremental computation requires propagating changes and reusing intermediate results of base computations. Derivatives, as produced by static differentiation [7], propagate changes but do not reuse intermediate results, leading to wasteful recomputation. As a solution, we introduce conversion to Cache-Transfer-Style, an additional program transformations producing purely incremental functional programs that create and maintain nested tuples of intermediate results. To prove CTS conversion correct, we extend the correctness proof of static differentiation from STLC to untyped $\lambda$-calculus via step-indexed logical relations, and prove sound the additional transformation via simulation theorems.

To show ILC-based languages can improve performance relative to from-scratch recomputation, and that CTS conversion can extend its applicability, we perform an initial performance case study. We provide derivatives of primitives for operations on collections and incrementalize selected example programs using those primitives, confirming expected asymptotic speedups.

1 Introduction

After computing a base output from some base input, we often need to produce updated outputs corresponding to updated inputs. Instead of rerunning the same base program on the updated input, incremental computation transforms the input change to an output change, potentially reducing asymptotic time complexity and significantly improving efficiency, especially for computations running on large data sets.

Incremental $\lambda$-Calculus (ILC) [7] is a recent framework for higher-order incremental computation. ILC represents changes from a base value $v _{1}$ to an updated value $v _{2}$ as a first-class change value $dv$. Since functions are first-class values, change values include function changes.

ILC also statically transforms base programs to incremental programs or derivatives, that are functions mapping input changes to output changes. Incremental language designers can then provide their language with (higher-order) primitives (with their derivatives) that efficiently encapsulate incrementalizable computation skeletons (such as tree-shaped folds), and ILC will incrementalize higher-order programs written in terms of these primitives.

Alas, ILC only incrementalizes efficiently self-maintainable computations [7, Sect. 4.3], that is, computations whose output changes can be computed using only input changes, but not the inputs themselves [11]. Few computations are self-maintainable: for instance, mapping self-maintainable functions on a sequence is self-maintainable, but dividing numbers is not! We elaborate on this problem in Sect. 2.1. In this paper, we extend ILC to non-self-maintainable computations. To this end, we must enable derivatives to reuse intermediate results created by the base computation.

Many incrementalization approaches remember intermediate results through dynamic memoization: they typically use hashtables to memoize function results, or dynamic dependence graphs [1] to remember a computation trace. However, looking up intermediate results in such dynamic data structure has a runtime cost that is hard to optimize; and reasoning on dynamic dependence graphs and computation traces is often complex. Instead, ILC produces purely functional programs, suitable for further optimizations and equational reasoning.

To that end, we replace dynamic memoization with static memoization: following Liu and Teitelbaum [20], we transform programs to cache-transfer style (CTS). A CTS function outputs their primary result along with caches of intermediate results. These caches are just nested tuples whose structure is derived from code, and accessing them does not involve looking up keys depending on inputs. Instead, intermediate results can be fetched from these tuples using statically known locations. To integrate CTS with ILC, we extend differentiation to produce CTS derivatives: these can extract from caches any intermediate results they need, and produce updated caches for the next computation step.

The correctness proof of static differentiation in CTS is challenging. First, we must show a forward simulation relation between two triples of reduction traces (the first triple being made of the source base evaluation, the source updated evaluation and the source derivative evaluation; the second triple being made of the corresponding CTS-translated evaluations). Dealing with six distinct evaluation environments at the same time was error prone on paper and for this reason, we conducted the proof using Coq [26]. Second, the simulation relation must not only track values but also caches, which are only partially updated while in the middle of the evaluation of derivatives. Finally, we study the translation for an untyped $\lambda$-calculus, while previous ILC correctness proofs were restricted to simply-typed $\lambda$-calculus. Hence, we define which changes are valid via a logical relation and show its fundamental property. Being in an untyped setting, our logical relation is not indexed by types, but step-indexed. We study an untyped language, but our work also applies to the erasure of typed languages. Formalizing a type-preserving translation is left for future work because giving a type to CTS programs is challenging, as we shall explain.

In addition to the correctness proof, we present preliminary experimental results from three case studies. We obtain efficient incremental programs even on non self-maintainable functions.

We present our contributions as follows. First, we summarize ILC and illustrate the need to extend it to remember intermediate results via CTS (Sect. 2). Second, in our mechanized formalization (Sect. 3), we give a novel proof of correctness for ILC differentiation for untyped $\lambda$-calculus, based on step-indexed logical relations (Sect. 3.4). Third, building on top of ILC differentiation, we show how to transform untyped higher-order programs to CTS (Sect. 3.5) and we show that CTS functions and derivatives simulate correctly their non-CTS counterparts (Sect. 3.7). Finally, in our case studies (Sect. 4), we compare the performance of the generated code to the base programs. Section 4.4 discusses limitations and future work. Section 5 discusses related work and Sect. 6 concludes. Our mechanized proof in Coq, the case study material, and the extended version of this paper with appendixes are available online at https://github.com/yurug/cts.

2 ILC and CTS Primer

In this section we exemplify ILC by applying it on an average function, show why the resulting incremental program is asymptotically inefficient, and use CTS conversion and differentiation to incrementalize our example efficiently and speed it up asymptotically (as confirmed by benchmarks in Sect. 4.1). Further examples in Sect. 4 apply CTS to higher-order programs and suggest that CTS enables incrementalizing efficiently some core database primitives such as joins.

2.1 Incrementalizing $average$ via ILC

Our example computes the average of a bag of numbers. After computing the base output $y _{1}$ of the average function on the base input bag $xs _{1}$, we want to update the output in response to a stream of updates to the input bag. Here and throughout the paper, we contrast base vs updated inputs, outputs, values, computations, and so on. For simplicity, we assume we have two updated inputs $xs _{2}$ and $xs _{3}$ and want to compute two updated outputs $y _{2}$ and $y _{3}$. We express this program in Haskell as follows:

To compute the updated outputs $y _{2}$ and $y _{3}$ in $average _{3}$ faster, we try using ILC. For that, we assume that we receive not only updated inputs $xs _{2}$ and $xs _{3}$ but also input change $dxs _{1}$ from $xs _{1}$ to $xs _{2}$ and input change $dxs _{2}$ from $xs _{2}$ to $xs _{3}$. A change $dx$ from $x _{1}$ to $x _{2}$ describes the changes from base value $x _{1}$ to updated value $x _{2}$, so that $x _{2}$ can be computed via the update operator $\oplus$ as $x _{1}\oplus dx$. A nil change is a change from base value $x$ to updated value $x$ itself.

ILC differentiation automatically transforms the $average$ function to its derivative $daverage \mathrel {::} Bag \;\mathbb {Z}\rightarrow \varDelta ( Bag \;\mathbb {Z})\rightarrow \varDelta \mathbb {Z}$. A derivative maps input changes to output changes: here, $dy _{1}\mathrel {=} daverage \; xs _{1}\; dxs _{1}$ is a change from base output $y _{1}\mathrel {=} average \; xs _{1}$ to updated output $y _{2}\mathrel {=} average \; xs _{2}$, hence $y _{2}\mathrel {=} y _{1}\oplus dy _{1}$.

Thanks to $daverage$’s correctness, we can rewrite $average _{3}$ to avoid expensive calls to $average$ on updated inputs and use $daverage$ instead:

In general, also the value of a function $f \mathrel {::} A \rightarrow B$ can change from a base value $f _{1}$ to an updated value $f _{2}$, mainly when $f$ is a closure over changing data. In that case, the change from base output $f _{1}\; x _{1}$ to updated output $f _{2}\; x _{2}$ is given by $df \; x _{1}\; dx$, where $df \mathrel {::} A \rightarrow \varDelta A \rightarrow \varDelta B$ is now a function change from $f _{1}$ to $f _{2}$. Above, $average$ exemplifies the special case where $f _{1}\mathrel {=} f _{2}\mathrel {=} f$: then the function change $df$ is a nil change, and $df \; x _{1}\; dx$ is a change from $f _{1}\; x _{1}\mathrel {=} f \; x _{1}$ and $f _{2}\; x _{2}\mathrel {=} f \; x _{2}$. That is, a nil function change for $f$ is a derivative of $f$.

2.2 Self-maintainability and Efficiency of Derivatives

Alas, derivatives are efficient only if they are self-maintainable, and $daverage$ is not, so $incrementalAverage _{3}$ is no faster than $average _{3}$! Consider the result of differentiating $average$:

Just like $average$ combines $sum$, $length$, and $div$, its derivative $daverage$ combines those functions and their derivatives. $daverage$ recomputes base intermediate results $s$, $n$ and $r$ exactly as done in $average$, because they might be needed as base inputs of derivatives. Since $r$ is unused, its recomputation can be dropped during later optimizations, but expensive intermediate results $s$ and $n$ are used by $ddiv$:

Function $ddiv$ computes the difference between the updated and the original result, so it needs its base inputs $a$ and $b$. Hence, $daverage$ must recompute $s$ and $n$ and will be slower than $average$!

Typically, ILC derivatives are only efficient if they are self-maintainable: a self-maintainable derivative does not inspect its base inputs, but only its change inputs, so recomputation of its base inputs can be elided. Cai et al. [7] leave efficient support for non-self-maintainable derivatives for future work.

But this problem is fixable: executing $daverage \; xs \; dxs$ will compute exactly the same $s$ and $n$ as executing $average \; xs$, so to avoid recomputation we must simply save $s$ and $n$ and reuse them. Hence, we CTS-convert each function $f$ to a CTS function $fC$ and a CTS derivative $dfC$: CTS function $fC$ produces, together with its final result, a cache containing intermediate results, that the caller must pass to CTS derivative $dfC$.

CTS-converting our example produces the following code, which requires no wasteful recomputation.

For each function $f$, we introduce a type $FC$ for its cache, such that a CTS function $fC$ has type $A \rightarrow ( B , FC )$ and CTS derivative $dfC$ has type $A \rightarrow \varDelta A \rightarrow FC \rightarrow (\varDelta B , FC )$. Crucially, CTS derivatives like $daverageC$ must return an updated cache to ensure correct incrementalization, so that application of further changes works correctly. In general, if $( y _{1}, c _{1})\mathrel {=} fC \; x _{1}$ and $( dy , c _{2})\mathrel {=} dfC \; x _{1}\; dx \; c _{1}$, then $( y _{1}\oplus dy , c _{2})$ must equal the result of the base function $fC$ applied to the updated input $x _{1}\oplus dx$, that is $( y _{1}\oplus dy , c _{2})\mathrel {=} fC \;( x _{1}\oplus dx )$.

For CTS-converted functions, the cache type $FC$ is a tuple of intermediate results and caches of subcalls. For primitive functions like $div$, the cache type $DivC$ could contain information needed for efficient computation of output changes. In the case of $div$, no additional information is needed. The definition of $divC$ uses $div$ and produces an empty cache, and the definition of $ddivC$ follows the earlier definition for $ddiv$, except that we now pass along an empty cache.

Finally, we can rewrite $average _{3}$ to incrementally compute $y _{2}$ and $y _{3}$:

Since functions of the same type translate to CTS functions of different types, in a higher-order language CTS translation is not always type-preserving; however, this is not a problem for our case studies (Sect. 4); Sect. 4.1 shows how to map such functions, and we return to this problem in Sect. 4.4.

3 Formalization

We now formalize CTS-differentiation for an untyped Turing-complete $\lambda$-calculus, and formally prove it sound with respect to differentiation. We also give a novel proof of correctness for differentiation itself, since we cannot simply adapt Cai et al. [7]’s proof to the new syntax: Our language is untyped and Turing-complete, while Cai et al. [7]’s proof assumed a strongly normalizing simply-typed $\lambda$-calculus and relied on its naive set-theoretic denotational semantics. Our entire formalization is mechanized using Coq [26]. For reasons of space, some details are deferred to the appendix.

Fig. 1.

Our language of lambda-lifted programs. Tuples can be nullary.

Transformations. We introduce and prove sound three term transformations, namely differentiation, CTS translation and CTS differentiation, that take a function to its corresponding (non-CTS) derivative, CTS function and CTS derivative. Each CTS function produces a base output and a cache from a base input, while each CTS derivative produces an output change and an updated cache from an input, an input change and a base cache.

Proof technique. To show soundness, we prove that CTS functions and derivatives simulate respectively non-CTS functions and derivatives. In turn, we formalize (non-CTS) differentiation as well, and we prove differentiation sound with respect to non-incremental evaluation. Overall, this shows that CTS functions and derivatives are sound relatively to non-incremental evaluation. Our presentation proceeds in the converse order: first, we present differentiation, formulated as a variant of Cai et al. [7]’s definition; then, we study CTS differentiation.

By using logical relations, we simplify significantly the setup of Cai et al. [7]. To handle an untyped language, we employ step-indexed logical relations. Besides, we conduct our development with big-step operational semantics because that choice simplifies the correctness proof for CTS conversion. Using big-step semantics for a Turing complete language restricts us to terminating computations. But that is not a problem: to show incrementalization is correct, we need only consider computations that terminate on both old and new inputs, following Acar et al. [3] (compared with in Sect. 5).

Structure of the formalization. Section 3.1 introduces the syntax of the language we consider in this development, and introduces its four sublanguages , , and . Section 3.2 presents the syntax and the semantics of , the source language for our transformations. Section 3.3 defines differentiation and its target language , and Sect. 3.4 proves differentiation correct. Section 3.5 defines CTS conversion, comprising CTS translation and CTS differentiation, and their target languages and . Section 3.6 presents the semantics of . Finally, Sect. 3.7 proves CTS conversion correct.

Notations. We write  for a sequence of X of some unspecified length $X_1, \ldots , X_m$.

3.1 Syntax for

A superlanguage. To simplify our transformations, we require input programs to have been lambda-lifted [15] and converted to A’-normal form (A’NF). Lambda-lifted programs are convenient because they allow us to avoid a specific treatment for free variables in transformations. A’NF is a minor variant of ANF [24], where every result is bound to a variable before use; unlike ANF, we also bind the result of the tail call. Thus, every result can thus be stored in a cache by CTS conversion and reused later (as described in Sect. 2). This requirement is not onerous: A’NF is a minimal variant of ANF, and lambda-lifting and ANF conversion are routine in compilers for functional languages. Most examples we show are in this form.

In contrast, our transformation’s outputs are lambda-lifted but not in A’NF. For instance, we restrict base functions to take exactly one argument—a base input. As shown in Sect. 2.1, CTS functions take instead two arguments—a base input and a cache—and CTS derivatives take three arguments—an input, an input change, and a cache. We could normalize transformation outputs to inhabit the source language and follow the same invariants, but this would complicate our proofs for little benefit. Hence, we do not prescribe transformation outputs to satisfy the same invariants, and we rather describe transformation outputs through separate grammars.

As a result of this design choice, we consider languages for base programs, derivatives, CTS programs and CTS derivatives. In our Coq mechanization, we formalize those as four separate languages, saving us many proof steps to check the validity of required structural invariants. For simplicity, in this paper we define a single language called  (for $\lambda$-Lifted). This language satisfies invariants common to all these languages (including some of the A’NF invariants). Then, we define sublanguages of . We describe the semantics of informally, and we only formalize the semantics of its sublanguages.

Syntax for terms. The  language is a relatively conventional lambda-lifted $\lambda$-calculus with a limited form of pattern matching on tuples. The syntax for terms and values is presented in Fig. 1. We separate terms and values in two distinct syntactic classes because we use big-step operational semantics. Our -bindings are non-recursive as usual, and support shadowing. Terms cannot contain $\lambda$-expressions directly, but only refer to closures through the environment, and similarly for literals and primitives; we elaborate on this in Sect. 3.2. We do not introduce case expressions, but only bindings that destructure tuples, both in -bindings and $\lambda$-expressions of closures. Our semantics does not assign meaning to match failures, but pattern-matchings are only used in generated programs and our correctness proofs ensure that the matches always succeed. We allow tuples to contain terms of form , which update base values with changes in , because A’NF-converting these updates is not necessary to the transformations. We often inspect the result of a function call “”, which is not a valid term in our syntax. Hence, we write “” as a syntactic sugar for “” with chosen fresh.

Syntax for closed values. A closed value is either a closure, a tuple of values, a literal, a primitive, a nil change for a primitive or a replacement change. A closure is a pair of an evaluation environment  and a $\lambda$-abstraction closed with respect to . The set of available literals is left abstract. It may contain usual first-order literals like integers. We also leave abstract the primitives like if-then-else or projections of tuple components. Each primitive  comes with a nil change, which is its derivative as explained in Sect. 2. A change value can also represent a replacement by some closed value . Replacement changes are not produced by static differentiation but are useful for clients of derivatives: we include them in the formalization to make sure that they are not incompatible with our system. As usual, environments  map variables to closed values.

Sublanguages of . The source language for all our transformations is a sublanguage of  named , where A stands for A’NF. To each transformation we associate a target language, which matches the transformation image. The target language for CTS conversion is named , where “C” stands for CTS. The target languages of differentiation and CTS differentiation are called, respectively, and , where the “I” stands for incremental.

3.2 The Source Language

We show the syntax of in Fig. 2. As said above, is a sublanguage of denoting lambda-lifted base terms in A’NF. With no loss of generality, we assume that all bound variables in programs and closures are distinct. The step-indexed big-step semantics (Fig. 3) for base terms is defined by the judgment written  (where n can be omitted) and pronounced “Under environment , base term  evaluates to closed value  in n steps.” Intuitively, our step-indexes count the number of “nodes” of a big-step derivation.¹ As they are relatively standard, we defer the explanations of these rules to Appendix B.

Fig. 2.

Static differentiation ; syntax of its target language , tailored to the output of differentiation; syntax of its source language . We assume that in the same binds both and and that $\alpha$-renaming preserves this invariant. We also define the base environment  and the updated environment  of a change environment .

Fig. 3.

Step-indexed big-step semantics for base terms of source language .

Expressiveness. A closure in the base environment can be used to represent a top-level definition. Since environment entries can point to primitives, we need no syntax to directly represent calls of primitives in the syntax of base terms. To encode in our syntax a program with top-level definitions and a term to be evaluated representing the entry point, one can produce a term  representing the entry point together with an environment  containing as values any top-level definitions, primitives and literals used in the program. Semi-formally, given an environment mentioning needed primitives and literals, and a list of top-level function definitions defined in terms of , we can produce a base environment , with $\mathcal {L}$ defined by:

Correspondingly, we extend all our term transformations to values and environments to transform such encoded top-level definitions.

Our mechanization can encode n-ary functions “” through unary functions that accept tuples; we encode partial application using a primitive such that, essentially, ; suspended partial applications are represented as closures. This encoding does not support currying efficiently, we further discuss this limitation in Sect. 4.4.

Control operators, like recursion combinators or branching, can be introduced as primitive operations as well. If the branching condition changes, expressing the output change in general requires replacement changes. Similarly to branching we can add tagged unions.

To check the assertions of the last two paragraphs, the Coq development contains the definition of a primitive as well as a primitive for a fixpoint combinator, allowing general recursion and recursive data structures as well.

3.3 Static Differentiation from to

Previous work [7] defines static differentiation for simply-typed $\lambda$-calculus terms. Figure 2 transposes differentiation as a transformation from to and defines ’s syntax.

Fig. 4.

Step-indexed big-step semantics for the change terms of .

Differentiating a base term  produces a change term , its derivative. Differentiating final result variable  produces its change variable . Differentiation copies each binding of an intermediate result to the output and adds a new binding for its change . If is bound to tuple , then will be bound to the change tuple . If is bound to function application “”, then will be bound to the application of function change to input and its change . We explain differentiation of environments later in this section.

Evaluating recomputes all intermediate results computed by . This recomputation will be avoided through cache-transfer style in Sect. 3.5. A comparison with the original static differentiation [7] can be found in Appendix A.

Semantics for . We move on to define how change terms evaluate to change values. We start by defining necessary definitions and operations on changes, such as define change values , change environments , and the update operator $\oplus$.

Closed change values are particular values . They are either a closure change, a tuple change, a literal change, a replacement change or a primitive nil change. A closure change is a closure containing a change environment  and a $\lambda$-abstraction expecting a value and a change value as arguments to evaluate a change term into an output change value. An evaluation environment  follows the same structure as -bindings of change terms: it binds variables to closed values and each variable  is immediately followed by a binding for its associated change variable . As with -bindings of change terms, $\alpha$-renamings in an environment  must rename  into  if  is renamed into . We define the update operator $\oplus$ to update a value with a change. This operator is a partial function written “”, defined as follows:

where .

Replacement changes can be used to update all values (literals, tuples, primitives and closures), while tuple changes can only update tuples, literal changes can only update literals, primitive nil can only update primitives and closure changes can only update closures. A replacement change overrides the current value  with a new one . On literals, $\oplus$ is defined via some interpretation function $\delta _{\oplus }$, which takes a literal and a literal change to produce an updated literal. Change update for a closure ignores  instead of computing something like . This may seem surprising, but we only need $\oplus$ to behave well for valid changes (as shown by Theorem 3.1): for valid closure changes, must behave anyway similarly to , which Cai et al. [7] show to be a nil change. Hence, and both behave like , so $\oplus$ can ignore and only consider environment updates. This definition also avoids having to modify terms at runtime, which would be difficult to implement safely. We could also implement as a function that invokes both and on its argument, as done by Cai et al. [7], but we believe that would be less efficient when $\oplus$ is used at runtime. As we discuss in Sect. 3.4, we restrict validity to avoid this runtime overhead.

Having given these definitions, we show in Fig. 4 a step-indexed big-step semantics for change terms, defined through judgment  (where n can be omitted). This judgment is pronounced “Under the environment , the change term evaluates into the closed change value in n steps.” Rules and are unsurprising. To evaluate function calls in -bindings “” we have three rules, depending on the shape of . These rules all recompute the value  of  in the original environment, but compute differently the change  to . If replaces the value of , recomputes  from scratch in the new environment, and bind  to  when evaluating the body. If is the nil change for primitive , computes by running ’s derivative through function . If is a closure change, invokes it normally to compute its change . As we show, if the closure change is valid, its body behaves like ’s derivative, hence incrementalizes correctly.

Closure changes with non-nil environment changes represent partial application of derivatives to non-nil changes; for instance, if takes a pair and is a non-nil change, constructs a closure change containing , using the derivative of mentioned in Sect. 3.2. In general, such closure changes do not arise from the rules we show, only from derivatives of primitives.

3.4 A New Soundness Proof for Static Differentiation

In this section, we show that static differentiation is sound (Theorem 3.3) and that Eq. (1) holds:

(1)

whenever $da$ is a valid change from $a_1$ to $a_2$ (as defined later). One might want to prove this equation assuming only that $a_1 \oplus da = a_2$, but this is false in general. A direct proof by induction on terms fails in the case for application (ultimately because $f_1\,\oplus \, df = f_2$ and $a_1\,\oplus \, da = a_2$ do not imply that $f_1\; a_1\,\oplus \, df \;a_1\; da = f_2\;a_2$). As usual, this can be fixed by introducing a logical relation. We call ours validity: a function change is valid if it turns valid input changes into valid output changes.

Fig. 5.

Step-indexed validity, through judgments for values and for terms.

Static differentiation is only sound on input changes that are valid. Cai et al. [7] show soundness for a strongly normalizing simply-typed $\lambda$-calculus using denotational semantics. Using an operational semantics, we generalize this result to an untyped and Turing-complete language, so we must turn to a step-indexed logical relation [3, 4].

Validity as a step-indexed logical relation. We say that “ is a valid change from to , up to k steps” and write

to mean that is a change from to and that is a valid description of the differences between  and , with validity tested with up to k steps. This relation approximates validity; if a change is valid at all approximations, it is simply valid (between and ); we write then (omitting the step-index k) to mean that validity holds at all step-indexes. We similarly omit step-indexes k from other step-indexed relations when they hold for all k.

To justify this intuition of validity, we show that a valid change from  to  goes indeed from  to  (Theorem 3.1), and that if a change is valid up to k steps, it is also valid up to fewer steps (Lemma 3.2).

Theorem 3.1

( $\oplus$ agrees with validity )

If holds for all $k > 0$, then .

Lemma 3.2

(Downward-closure)

If $N \ge n$, then implies .

Crucially, Theorem 3.1 enables (a) computing from a valid change and its source, and (b) showing Eq. (1) through validity. As discussed, $\oplus$ ignores changes to closure bodies to be faster, which is only sound if those changes are nil; to ensure Theorem 3.1 still holds, validity on closure changes must be adapted accordingly and forbid non-nil changes to closure bodies. This choice, while unusual, does not affect our results: if input changes do not modify closure bodies, intermediate changes will not modify closure bodies either. Logical relation experts might regard this as a domain-specific invariant we add to our relation. Alternatives are discussed by Giarrusso [10, Appendix C].

As usual with step-indexing, validity is defined by well-founded induction over naturals ordered by <; to show well-foundedness we observe that evaluation always takes at least one step.

Validity for values, terms and environments is formally defined by cases in Fig. 5. First, a literal change is a valid change from to . Since the function $\delta _\oplus$ is partial, the relation only holds for the literal changes which are valid changes for . Second, a replacement change  is always a valid change from any value  to . Third, a primitive nil change is a valid change between any primitive and itself. Fourth, a tuple change is valid up to step n, if each of its components is valid up to any step strictly less than n. Fifth, we define validity for closure changes. Roughly speaking, this statement means that a closure change is valid if (i) its environment change  is valid for the original closure environment  and for the new closure environment ; and (ii) when applied to related values, the closure bodies  are related by , as defined by the auxiliary judgment for validity between terms under related environments (defined in Appendix C). As usual with step-indexed logical relations, in the definition for this judgment about terms, the number k of steps required to evaluate the term  is subtracted from the number of steps n that can be used to relate the outcomes of the term evaluations.

Soundness of differentiation. We can state a soundness theorem for differentiation without mentioning step-indexes; thanks to this theorem, we can compute the updated result not by rerunning a computation, but by updating the base result with the result change that we compute through a derivative on the input change. A corollary shows Eq. (1).

Theorem 3.3

(Soundness of differentiation in ). If is a valid change environment from base environment to updated environment , that is , and if converges both in the base and updated environment, that is and , then evaluates under the change environment  to a valid change between base result and updated result , that is , and .

We must first show that derivatives map input changes valid up to k steps to output changes valid up to k steps, that is, the fundamental property of our step-indexed logical relation:

Lemma 3.4

(Fundamental Property)

For each n, if then .

Fig. 6.

Cache-Transfer Style translation and syntax of its target language .

3.5 CTS Conversion

Figures 6 and 7 define both the syntax of and and CTS conversion. The latter comprises CTS differentiation , from to , and CTS translation , from to .

Syntax definitions for the target languages and . Terms of follow again $\lambda$-lifted A’NF, like , except that a -binding for a function application “” now binds an extra cache identifier besides output . Cache identifiers have non-standard syntax: it can be seen as a triple that refers to the value identifiers and . Hence, an $\alpha$-renaming of one of these three identifiers must refresh the cache identifier accordingly. Result terms explicitly return cache  through syntax . Caches are encoded through nested tuples, but they are in fact a tree-like data structure that is isomorphic to an execution trace. This trace contains both immediate values and the execution traces of nested function calls.

The syntax for  matches the image of the CTS derivative and witnesses the CTS discipline followed by the derivatives: to determine , the derivative of  evaluated at point with change  expects the cache produced by evaluating  in the base term. The derivative returns the updated cache which contains the intermediate results that would be gathered by the evaluation of . The result term of every change term returns the computed change and a cache update , where each value identifier  of the input cache is updated with its corresponding change .

Fig. 7.

CTS differentiation and syntax of its target language . Beware applies a left-inverse of during pattern matching.

CTS conversion and differentiation. These translations use two auxiliary functions: which computes the cache term of a term , and , which computes the cache update of ’s derivative.

CTS translation on terms, , accepts as inputs a global term and a subterm of . In tail position (), the translation generates code to return both the result and the cache  of the global term . When the transformation visits -bindings, it outputs extra bindings for caches  on function calls and visits the -body.

Similarly to , CTS derivation  accepts a global term  and a subterm  of . In tail position, the translation returns both the result change and the cache update . On -bindings, it does not output bindings for  but for , it outputs extra bindings for as in the previous case and visits the -body.

To handle function definitions, we transform the base environment through and (translations of environments are done pointwise, see Appendix D). Since includes , we describe to also cover . Overall, CTS-converts each source closure to a CTS-translated function, with body , and to the CTS derivative  of . This CTS derivative pattern matches on its input cache using cache pattern . That way, we make sure that the shape of the cache expected by  is consistent with the shape of the cache produced by . The body of derivative  is computed by CTS-deriving ’s body via .

3.6 Semantics of and

An evaluation environment of contains both values and cache values. Values  resemble values , cache values  match cache terms  and change values  match change values . Evaluation environments  for change terms must also bind change values, so functions in change closures take not just a base input  and an input change , like in , but also an input cache . By abuse of notation, we reuse the same syntax  to both deconstruct and construct caches.

Base terms of the language are evaluated using a conventional big-step semantics, consisting of two judgments. Judgment “” is read “Under evaluation environment , base term evaluates to value and cache ”. The semantics follows the one of ; since terms include extra code to produce and carry caches along the computation, the semantics evaluates that code as well. For space reasons, we defer semantic rules to Appendix E. Auxiliary judgment “” evaluates cache terms into cache values: It traverses a cache term and looks up the environment for the values to be cached.

Change terms of are also evaluated using a big-step semantics, which resembles the semantics of and . Unlike those semantics, evaluating cache updates is evaluated using the $\oplus$ operator (overloaded on values and changes). By lack of space, its rules are deferred to Appendix E. This semantics relies on three judgments. Judgment “” is read “Under evaluation environment , change term evaluates to change value and updated cache ”. The first auxiliary judgment “” defines evaluation of cache update terms. The final auxiliary judgment “” describes a limited form of pattern matching used by CTS derivatives: namely, how a cache pattern matches a cache value  to produce a change environment .

3.7 Soundness of CTS Conversion

The proof is based on a simulation in lock-step, but two subtle points emerge. First, we must relate environments that do not contain caches, with environments that do. Second, while evaluating CTS derivatives, the evaluation environment mixes caches from the base computation and updated caches computed by the derivatives.

Theorem 3.7 follows because differentiation is sound (Theorem 3.3) and evaluation commutes with CTS conversion; this last point requires two lemmas. First, CTS translation of base terms commutes with our semantics:

Lemma 3.5

(Commutation for base evaluations)

For all and , if , there exists , .

Second, we need a corresponding lemma for CTS translation of differentiation results: intuitively, evaluating a derivative and CTS translating the resulting change value must give the same result as evaluating the CTS derivative. But to formalize this, we must specify which environments are used for evaluation, and this requires two technicalities.

Assume derivative  evaluates correctly in some environment . Evaluating CTS derivative  requires cache values from the base computation, but they are not in ! Therefore, we must introduce a judgment to complete a CTS-translated environment with the appropriate caches (see Appendix F).

Next, consider evaluating a change term of the form , where  is a standard single-hole change-term context—that is, for , a sequence of -bindings. When evaluating , we eventually evaluate in a change environment updated by : the change environment  contains both the updated caches coming from the evaluation of  and the caches coming from the base computation (which will be updated by the evaluation of ). Again, a new judgment, given in Appendix F, is required to model this process.

With these two judgments, the second key Lemma stating the commutation between evaluation of derivatives and evaluation of CTS derivatives can be stated. We give here an informal version of this Lemma, the actual formal version can be found in Appendix F.

Lemma 3.6

(Commutation for derivatives evaluation)

If the evaluation of leads to an environment when it reaches the differentiated context where , and if the CTS conversion of under this environment completed with base (resp. changed) caches evaluates into a base value (resp. a changed value ) and a base cache value (resp. an updated cache value ), then under an environment containing the caches already updated by the evaluation of and the base caches to be updated, the CTS derivative of evaluates to such that and to the updated cache .

Finally, we can state soundness of CTS differentiation. This theorem says that CTS derivatives not only produce valid changes for incrementalization but that they also correctly consume and update caches.

Theorem 3.7

(Soundness of CTS differentiation)

If the following hypotheses hold:

• 1.
• 2.
• 3.

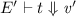
then there exists , , and such that:

• 1.
• 2.
• 3.
• 4.
• 5.

4 Incrementalization Case Studies

In this section, we investigate two questions: whether our transformations can target a typed language like Haskell and whether automatically transformed programs can perform well. We implement by hand primitives on sequences, bags and maps in Haskell. The input terms in all case studies are written in a deep embedding of  into Haskell. The transformations generate Haskell code that uses our primitives and their derivatives.

We run the transformations on three case studies: a computation of the average value of a bag of integers, a nested loop over two sequences and a more involved example inspired by Koch et al. [17]’s work on incrementalizing database queries. For each case study, we make sure that results are consistent between from scratch recomputation and incremental evaluation; we measure the execution time for from scratch recomputation and incremental computation as well as the space consumption of caches. We obtain efficient incremental programs, that is ones for which incremental computation is faster than from scratch recomputation. The measurements indicate that we do get the expected asymptotic improvement in time of incremental computation over from scratch recomputation by a linear factor while the caches grows in a similar linear factor.

Our benchmarks were compiled by GHC 8.2.2 and run on a 2.20 GHz hexa core Intel(R) Xeon(R) CPU E5-2420 v2 with 32 GB of RAM running Ubuntu 14.04. We use the $criterion$ [21] benchmarking library.

4.1 Averaging Bags of Integers

Section 2.1 motivates our transformation with a running example of computing the average over a bag of integers. We represent bags as maps from elements to (possibly negative) multiplicities. Earlier work [7, 17] represents bag changes as bags of removed and added elements. We use a different representation of bag changes that takes advantage of the changes to elements and provide primitives on bags and their derivatives. The CTS variant of $map$, that we call $mapC$, takes a function $fC$ in CTS and a bag $as$ and produces a bag and a cache. The cache stores for each invocation of $fC$, and therefore for each distinct element in $as$, the result of $fC$ of type $b$ and the cache of type $c$.

Inspired by Rossberg et al. [23], all higher-order functions (and typically, also their caches) are parametric over cache types of their function arguments. Here, functions $mapC$ and $dmapC$ and cache type $MapC$ are parametric over the cache type $c$ of $fC$ and $dfC$.

We wrote the $length$ and $sum$ functions used in our benchmarks in terms of primitives $map$ and $foldGroup$ and had their CTS function and CTS derivative generated automatically.

We evaluate whether we can produce an updated result with $daverageC$ shown in Sect. 2.1 faster than by from scratch recomputation with $average$. We expect the speedup of $daverageC$ to depend on the size of the input bag $n$. We fix an input bag of size $n$ as the bag containing the numbers from $\mathrm {1}$ to $n$. We define a change that inserts the integer $\mathrm {1}$ into the bag. To measure execution time of from scratch recomputation, we apply $average$ to the input bag updated with the change. To measure execution time of the CTS function $averageC$, we apply $averageC$ to the input bag updated with the change. To measure execution time of the CTS derivative $daverageC$, we apply $daverageC$ to the input bag, the change and the cache produced by $averageC$ when applied to the input bag. In all three cases we ensure that all results and caches are fully forced so as to not hide any computational cost behind laziness.

Fig. 8.

Benchmark results for $average$ and $totalPrice$

The plot in Fig. 8a shows execution time versus the size $n$ of the base input. To produce the base result and cache, the CTS transformed function $averageC$ takes longer than the original $average$ function takes to produce just the result. Producing the updated result incrementally is slower than from scratch recomputation for small input sizes, but because of the difference in time complexity becomes faster as the input size grows. The size of the cache grows linearly with the size of the input, which is not optimal for this example. We leave optimizing the space usage of examples like this to future work.

4.2 Nested Loops over Two Sequences

Next, we consider CTS differentiation on a higher-order example. To incrementalize this example efficiently, we have to enable detecting nil function changes at runtime by representing function changes as closures that can be inspected by incremental programs. Our example here is the Cartesian product of two sequences computed in terms of functions $map$ and $concat$.

We implemented incremental sequences and related primitives following Firsov and Jeltsch [9]: our change operations and first-order operations (such as $concat$) reuse their implementation. On the other hand, we must extend higher-order operations such as $map$ to handle non-nil function changes and caching. A correct and efficient CTS derivative $dmapC$ has to work differently depending on whether the given function change is nil or not: For a non-nil function change it has to go over the input sequence; for a nil function change it has to avoid that.

Cai et al. [7] use static analysis to conservatively approximate nil function changes as changes to terms that are closed in the original program. But in this example the function argument $(\lambda y \rightarrow ( x , y ))$ to $map$ in $cartesianProduct$ is not a closed term. It is, however, crucial for the asymptotic improvement that we avoid looping over the inner sequence when the change to the free variable $x$ in the change environment is .

To enable runtime nil change detection, we apply closure conversion to the original program and explicitly construct closures and changes to closures. While the only valid change for closed functions is their nil change, for closures we can have non-nil function changes. A function change $df$, represented as a closure change, is nil exactly when all changes it closes over are nil.

We represent closed functions and closures as variants of the same type. Correspondingly we represent changes to a closed function and changes to a closure as variants of the same type of function changes. We inspect this representation at runtime to find out if a function change is a nil change.

We use the same benchmark setup as in the benchmark for the average computation on bags. The input of size $n$ is a pair of sequences $( xs , ys )$. Each sequence initially contains the integers from $\mathrm {1}$ to $n$. Updating the result in reaction to a change $dxs$ to the outer sequence $xs$ takes less time than updating the result in reaction to a change $dys$ to the inner sequence $ys$. While a change to the outer sequence $xs$ results in an easily located change in the output sequence, a change for the inner sequence $ys$ results in a change that needs a lot more calculation to find the elements it affects. We benchmark changes to the outer sequence $xs$ and the inner sequence $ys$ separately where the change to one sequence is the insertion of a single integer $\mathrm {1}$ at position $\mathrm {1}$ and the change for the other one is the nil change.

Fig. 9.

Benchmark results for $cartesianProduct$

Figure 9 shows execution time versus input size. In this example again preparing the cache takes longer than from scratch recomputation alone. The speedup of incremental computation over from scratch recomputation increases with the size of the base input sequences because of the difference in time complexity. Eventually we do get speedups for both kinds of changes (to the inner and to the outer sequence), but for changes to the outer sequence we get a speedup earlier, at a smaller input size. The size of the cache grows super linearly in this example.

4.3 Indexed Joins of Two Bags

Our goal is to show that we can compose primitive functions into larger and more complex programs and apply CTS differentiation to get a fast incremental program. We use an example inspired from the DBToaster literature [17]. In this example we have a bag of orders and a bag of line items. An order is a pair of an order key and an exchange rate. A line item is a pair of an order key and a price. We build an index mapping each order key to the sum of all exchange rates of the orders with this key and an index from order key to the sum of the prices of all line items with this key. We then merge the two maps by key, multiplying corresponding sums of exchange rates and sums of prices. We compute the total price of the orders and line items as the sum of those products.

Unlike DBToaster, we assume our program is already transformed to explicitly use indexes, as above. Because our indexes are maps, we implemented a change structure, CTS primitives and their CTS derivatives for maps.

To build the indexes, we use a $groupBy$ function built from primitive functions $foldMapGroup$ on bags and $singleton$ for bags and maps respectively. The CTS function $groupByC$ and the CTS derivative $dgroupByC$ are automatically generated. While computing the indexes with $groupBy$ is self-maintainable, merging them is not. We need to cache and incrementally update the intermediately created indexes to avoid recomputing them.

We evaluate the performance in the same way we did in the other case studies. The input of size $n$ is a pair of bags where both contain the pairs $( i , i )$ for $i$ between $\mathrm {1}$ and $n$. The change is an insertion of the order $(\mathrm {1},\mathrm {1})$ into the orders bag. For sufficiently large inputs, our CTS derivative of the original program produces updated results much faster than from scratch recomputation, again because of a difference in time complexity as indicated by Fig. 8b. The size of the cache grows linearly with the size of the input in this example. This is unavoidable, because we need to keep the indexes.

4.4 Limitations and Future Work

Typing of CTS programs. Functions of the same type $f _{1}, f _{2}\mathrel {::} A \rightarrow B$ can be transformed to CTS functions $f _{1}\mathrel {::} A \rightarrow ( B , C _{1}), f _{2}\mathrel {::} A \rightarrow ( B , C _{2})$ with different cache types $C _{1}, C _{2}$, since cache types depend on the implementation. This heterogeneous typing of translated functions poses difficult typing issues, e.g. what is the translated type of a $list \;( A \rightarrow B )$? We cannot hide cache types behind existential quantifiers because they would be too abstract for derivatives, which only work on very specific cache types. We can fix this problem with some runtime overhead by using a single type $Cache$, defined as a tagged union of all cache types or, maybe with more sophisticated type systems—like first-class translucent sums, open existentials or Typed Adapton’s refinement types [12]—that could be able to correctly track down cache types properly.

In any case, we believe that these machineries would add a lot of complexity without helping much with the proof of correctness. Indeed, the simulation relation is more handy here because it maintains a global invariant about the whole evaluations (typically the consistency of cache types between base computations and derivatives), not many local invariants about values as types would.

One might wonder why caches could not be totally hidden from the programmer by embedding them in the derivatives themselves; or in other words, why we did not simply translate functions of type $A \rightarrow B$ into functions of type $A \rightarrow B \times (\varDelta A \rightarrow \varDelta B)$. We tried this as well; but unlike automatic differentiation, we must remember and update caches according to input changes (especially when receiving a sequence of such changes as in Sect. 2.1). Returning the updated cache to the caller works; we tried closing over the caches in the derivative, but this ultimately fails (because we could receive function changes to the original function, but those would need access to such caches).

Comprehensive performance evaluation. This paper focuses on theory and we leave benchmarking in comparison to other implementations of incremental computation to future work. The examples in our case study were rather simple (except perhaps for the indexed join). Nevertheless, the results were encouraging and we expect them to carry over to more complex examples, but not to all programs. A comparison to other work would also include a comparison of space usage for auxiliary data structure, in our case the caches.

Cache pruning via absence analysis. To reduce memory usage and runtime overhead, it should be possible to automatically remove from transformed programs any caches or cache fragments that are not used (directly or indirectly) to compute outputs. Liu [19] performs this transformation on CTS programs by using absence analysis, which was later extended to higher-order languages by Sergey et al. [25]. In lazy languages, absence analysis removes thunks that are not needed to compute the output. We conjecture that the analysis could remove unused caches or inputs, if it is extended to not treat caches as part of the output.

Unary vs n-ary abstraction. We only show our transformation correct for unary functions and tuples. But many languages provide efficient support for applying curried functions such as $div \mathrel {::}\mathbb {Z}\rightarrow \mathbb {Z}\rightarrow \mathbb {Z}$. Naively transforming such a curried function to CTS would produce a function $divC$ of type $\mathbb {Z}\rightarrow (\mathbb {Z}\rightarrow (\mathbb {Z}, DivC _{2})), DivC _{1}$ with $DivC _{1}\mathrel {=}()$, which adds excessive overhead. In Sect. 2 and our evaluation we use curried functions and never need to use this naive encoding, but only because we always invoke functions of known arity.

5 Related Work

Cache-transfer-style. Liu [19]’s work has been the fundamental inspiration to this work, but her approach has no correctness proof and is restricted to a first-order untyped language. Moreover, while the idea of cache-transfer-style is similar, it’s unclear if her approach to incrementalization would extend to higher-order programs. Firsov and Jeltsch [9] also approach incrementalization by code transformation, but their approach does not deal with changes to functions. Instead of transforming functions written in terms of primitives, they provide combinators to write CTS functions and derivatives together. On the other hand, they extend their approach to support mutable caches, while restricting to immutable ones as we do might lead to a logarithmic slowdown.

Finite differencing. Incremental computation on collections or databases by finite differencing has a long tradition [6, 22]. The most recent and impressive line of work is the one on DBToaster [16, 17], which is a highly efficient approach to incrementalize queries over bags by combining iterated finite differencing with other program transformations. They show asymptotic speedups both in theory and through experimental evaluations. Changes are only allowed for datatypes that form groups (such as bags or certain maps), but not for instance for lists or sets. Similar ideas were recently extended to higher-order and nested computation [18], though only for datatypes that can be turned into groups. Koch et al. [18] emphasize that iterated differentiation is necessary to obtain efficient derivatives; however, ANF conversion and remembering intermediate results appear to address the same problem, similarly to the field of automatic differentiation [27].

Logical relations. To study correctness of incremental programs we use a logical relation among base values $v _{1}$, updated values $v _{2}$ and changes $dv$. To define a logical relation for an untyped $\lambda$-calculus we use a step-indexed logical relation, following Ahmed [4], Appel and McAllester [5]; in particular, our definitions are closest to the ones by Acar et al. [3], who also work with an untyped language, big-step semantics and (a different form of) incremental computation. However, they do not consider first-class changes. Technically, we use environments rather than substitution, and index our big-step semantics differently.

Dynamic incrementalization. The approaches to incremental computation with the widest applicability are in the family of self-adjusting computation [1, 2], including its descendant Adapton [14]. These approaches incrementalize programs by combining memoization and change propagation: after creating a trace of base computations, updated inputs are compared with old ones in O(1) to find corresponding outputs, which are updated to account for input modifications. Compared to self-adjusting computation, Adapton only updates results that are demanded. As usual, incrementalization is not efficient on arbitrary programs, but only on programs designed so that input changes produce small changes to the computation trace; refinement type systems have been designed to assist in this task [8, 12]. To identify matching inputs, Nominal Adapton [13] replaces input comparisons by pointer equality with first-class labels, enabling more reuse.

6 Conclusion

We have presented a program transformation which turns a functional program into its derivative and efficiently shares redundant computations between them thanks to a statically computed cache.

Although our first practical case studies show promising results, this paper focused on putting CTS differentiation on solid theoretical ground. For the moment, we only have scratched the surface of the incrementalization opportunities opened by CTS primitives and their CTS derivatives: in our opinion, exploring the design space for cache data structures will lead to interesting new results in purely functional incremental programming.