Abstract
We present a sound and complete bisimilarity for an untyped \(\lambda \)-calculus with higher-order local references. Our relation compares values by applying them to a fresh variable, like normal-form bisimilarity, and it uses environments to account for the evolving store. We achieve completeness by a careful treatment of evaluation contexts comprising open stuck terms. This work improves over Støvring and Lassen’s incomplete environment-based normal-form bisimilarity for the \(\lambda \rho \)-calculus, and confirms, in relatively elementary terms, Jaber and Tabareau’s result, that the state construct is discriminative enough to be characterized with a bisimilarity without any quantification over testing arguments.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Two terms are contextually equivalent if replacing one by the other in a bigger program does not change the behavior of the program. The quantification over program contexts makes contextual equivalence hard to use in practice and it is therefore common to look for more effective characterizations of this relation. In a calculus with local state, such a characterization has been achieved either through logical relations [1, 5, 15], which rely on types, denotational models [6, 10, 13], or coinductively defined bisimilarities [9, 12, 17,18,19].
Koutavas et al. [8] argue that to be sound w.r.t. contextual equivalence, a bisimilarity for state should accumulate the tested terms in an environment to be able to try them again as the store evolves. Such environmental bisimilarities usually compare terms by applying them to arguments built from the environment [12, 17, 19], and therefore still rely on some universal quantification over testing arguments. An exception is Støvring and Lassen’s bisimilarity [18], which compares terms by applying them to a fresh variable, like one would do with a normal-form (or open) bisimilarity [11, 16]. Their bisimilarity characterizes contextual equivalence in a calculus with control and state, but is not complete in a calculus with state only: there exist equivalent terms that are not related by the bisimilarity. Jaber and Tabareau [6] go further and propose a sound and complete Kripke Open Bisimilarity for a calculus with local state, which also compares terms by applying them to a fresh variable, but uses notions from Kripke logical relations, namely transition systems of invariants, to reason about heaps.
In this paper, we propose a sound and complete normal-form bisimilarity for a call-by-value \(\lambda \)-calculus with local references which relies on environments to handle heaps. We therefore improve over Støvring and Lassen’s work, since our relation is complete, by following a different, potentially simpler, path than Jaber and Tabareau, since we use environments to represent possible worlds and do not rely on any external structures such as transition systems of invariants. Moreover, we do not need types and define our relation in an untyped calculus.
We obtain completeness by treating carefully normal forms that are not values, i.e., open stuck terms of the form \(E[x\,v]\). First, we distinguish in the environment the terms which should be tested multiple times from the ones that should be run only once, namely the evaluation contexts like \(E\) in the above term. The latter are kept in a separate environment that takes the form of a stack, according to the idea presented by Laird [10] and by Jagadeesan et al. [7]. Second, we relate the so-called deferred diverging terms [5, 6], i.e., open stuck terms which hide a diverging behavior in the evaluation context \(E\), with the regular diverging terms.
It may be worth stressing that our congruence proof is based on the machinery we have developed before [3] and is simpler than Støvring and Lassen’s one, in particular in how it accounts for the extensionality of functions.
We believe that this work makes a contribution to the understanding of how one should adjust the normal-form bisimulation proof principle when the calculus under consideration becomes less discriminative, assuming that one wishes to preserve completeness of the theory. In particular, it is quite straightforward to define a complete normal-form bisimilarity for the \(\lambda \)-calculus with first-class continuations and global store, with no need to refer to other notions than the ones already present in the reduction semantics. Similarly, in the \(\lambda \mu \rho \)-calculus (continuations and local references), one only needs to introduce environments to ensure soundness of the theory, but essentially nothing more is required to obtain completeness [18]. In this article we show which new ingredients are needed when moving from these two highly expressive calculi to the corresponding, less discriminative ones—with global or local references only—that do not offer access to the current continuation.
The rest of this paper is as follows. In Sect. 2, we study a simple calculus with global store to see how to reach completeness in that case. In particular, we show in Sect. 2.2 how we deal with deferred diverging terms. We remind in Sect. 2.3 the notion of diacritical progress [3] and the framework our bisimilarity and its proof of soundness are based upon. We sketch the completeness proof in Sect. 2.4. Section 2 paves the way for the main result of the paper, described in Sect. 3, where we turn to the calculus with local store. We define the bisimilarity in Sect. 3.2, prove its soundness and completeness in Sect. 3.3, and use it in Sect. 3.4 on examples taken from the literature. We conclude in Sect. 4, where we discuss related work and in particular compare our work to Jaber and Tabareau’s. A companion report expands on the proofs [4].
2 Global Store
We first consider a calculus where terms share a global store and present how we deal with deferred diverging terms to get a complete bisimilarity.
2.1 Syntax, Semantics, and Contextual Equivalence
We extend the call-by-value \(\lambda \)-calculus with the ability to read and write a global memory. We let \(x\), \(y\), ... range over term variables and \(l\) range over references. A store, denoted by \(h\), \(g\), is a finite map from references to values; we write \(\mathsf {dom}(h)\) for the domain of \(h\), i.e., the set of references on which \(h\) is defined. We write \(\emptyset \) for the empty store, \(h\mathop \uplus g\) for the union of two stores, assuming \(\mathsf {dom}(h)\cap \mathsf {dom}(g)= \emptyset \). The syntax of terms and contexts is defined as follows.

The term \(l:=t;s\) evaluates \(t\) (if possible) and stores the resulting value in \(l\) before continuing as \(s\), while \(!l\) reads the value kept in \(l\). When writing examples and in the completeness proofs, we use natural numbers, booleans, the conditional \(\textsf {if }\ldots \textsf { then }\ldots \textsf { else }\ldots \), local definitions \(\textsf {let} \ldots \textsf {in} \ldots \), sequence \(\textsf {;}\), and unit \(()\) assuming the usual call-by-value encodings for these constructs.
A \(\lambda \)-abstraction \(\lambda x.t\) binds \(x\) in \(t\); we write \(\mathsf {fv}(t)\) (respectively \(\mathsf {fv}(E)\)) for the set of free variables of \(t\) (respectively \(E\)). We identify terms up to \(\alpha \)-conversion of their bound variables. A variable or reference is fresh if it does not occur in any other entities under consideration, and a store is fresh if it maps references to pairwise distinct fresh variables. A term or context is closed if it has no free variables. We write \(\mathsf {fr}(t)\) for the set of references that occur in t.
The call-by-value semantics of the calculus is defined on configurations \(\langle h \;|\; t \rangle \) such that \(\mathsf {fr}(t) \subseteq \mathsf {dom}(h)\) and for all \(l\in \mathsf {dom}(h)\), \(\mathsf {fr}(h{(l)}) \subseteq \mathsf {dom}(h)\). We let \(c\) and \(d\) range over configurations. We write \(t\{v/x\}\) for the usual capture-avoiding substitution of \(x\) by \(v\) in \(t\), and we let  range over simultaneous substitutions \(.\{v_1/x_1\} \ldots \{v_n/x_n\}\). We write \(h[l := v]\) for the operation updating the value of \(l\) to \(v\). The reduction semantics \(\mathrel \rightarrow \) is defined by the following rules.
range over simultaneous substitutions \(.\{v_1/x_1\} \ldots \{v_n/x_n\}\). We write \(h[l := v]\) for the operation updating the value of \(l\) to \(v\). The reduction semantics \(\mathrel \rightarrow \) is defined by the following rules.
The well-formedness condition on configurations ensures that a read operation \(!l\) cannot fail. We write \(\mathrel {\mathrel \rightarrow ^*}\) for the reflexive and transitive closure of \(\mathrel \rightarrow \).
A term \(t\) of a configuration \(\langle h \;|\; t \rangle \) which cannot reduce further is called a normal form. Normal forms are either values or open-stuck terms of the form \(E[x\,v]\); closed normal forms can only be \(\lambda \)-abstractions. A configuration terminates, written \(c\Downarrow \) if it reduces to a normal-form configuration; otherwise it diverges, written \(c\Uparrow \), like configurations running \(\varOmega \mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}(\lambda x.x\,x)\,(\lambda x.x\,x)\).
Contextual equivalence equates terms behaving the same in all contexts. A substitution  closes a term \(t\) if
closes a term \(t\) if  is closed; it closes a configuration \(\langle h \;|\; t \rangle \) if it closes \(t\) and the values in \(h\).
is closed; it closes a configuration \(\langle h \;|\; t \rangle \) if it closes \(t\) and the values in \(h\).
Definition 1
\(t\) and \(s\) are contextually equivalent, written \(t\mathrel \equiv s\), if for all contexts \(E\), fresh stores \(h\), and closing substitutions  ,
,  iff
iff  .
.
Testing only evaluation contexts is not a restriction, as it implies the equivalence w.r.t. all contexts \(\mathrel \equiv _C\): one can show that \(t\mathrel \equiv _C s\) iff \(\lambda x.t\mathrel \equiv _C \lambda x.s\) iff \(\lambda x.t\mathrel \equiv \lambda x.s\).
2.2 Normal-Form Bisimulation
Informal Presentation. Two open terms are normal-form bisimilar if their normal forms can be decomposed into bisimilar subterms. For example in the plain \(\lambda \)-calculus, a stuck term \(E[x\,v]\) is bisimilar to \(t\) if \(t\) reduces to a stuck term \(F[x\,w]\) so that respectively \(E\), \(F\) and \(v\), \(w\) are bisimilar when they are respectively plugged with and applied to a fresh variable.
Such a requirement is too discriminating for many languages, as it distinguishes terms that should be equivalent. For instance in plain \(\lambda \)-calculus, given a closed value \(v\), \(t\mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}x\,v\) is not normal form bisimilar to \(s\mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}(\lambda y.x\,v) \,(x\,v)\). Indeed, \(\square \) is not bisimilar to \((\lambda y.x\,v) \,\square \) when plugged with a fresh z: the former produces a value z while the latter reduces to a stuck term \(x\,v\). However, \(t\) and \(s\) are contextually equivalent, as for all closed value \(w\), \(t\{w/x\}\) and \(s\{w/x\}\) behave like \(w\,v\): if \(w\,v\) diverges, then they both diverges, and if \(w\,v\) evaluates to some value \(w'\), then they also evaluates to \(w'\). Similarly, \(x\,v\,\varOmega \) and \(\varOmega \) are not normal-form bisimilar (one is a stuck term while the other is diverging), but they are contextually equivalent by the same reasoning.
The terms \(t\) and \(s\) are no longer contextually equivalent in a \(\lambda \)-calculus with store, since a function can count how many times it is applied and change its behavior accordingly. More precisely, \(t\) and \(s\) are distinguished by the context  . But this counting trick is not enough to discriminate \(x\,v\,\varOmega \) and \(\varOmega \), as they are still equivalent in a \(\lambda \)-calculus with store. Although \(x\,v\,\varOmega \) is a normal form, it is in fact always diverging when we replace \(x\) by an arbitrary closed value \(w\), either because \(w\,v\) itself diverges, or it evaluates to some \(w'\) and then \(w' \,\varOmega \) diverges. A stuck term which hides a diverging behavior has been called deferred diverging in the literature [5, 6].
. But this counting trick is not enough to discriminate \(x\,v\,\varOmega \) and \(\varOmega \), as they are still equivalent in a \(\lambda \)-calculus with store. Although \(x\,v\,\varOmega \) is a normal form, it is in fact always diverging when we replace \(x\) by an arbitrary closed value \(w\), either because \(w\,v\) itself diverges, or it evaluates to some \(w'\) and then \(w' \,\varOmega \) diverges. A stuck term which hides a diverging behavior has been called deferred diverging in the literature [5, 6].
It turns out that being able to relate a diverging term to a deferred diverging term is all we need to change from the plain \(\lambda \)-calculus normal-form bisimilarity to get a complete equivalence when we add global store. We do so by distinguishing two cases in the clause for open-stuck terms: a configuration \(\langle h \;|\; E[x\,v] \rangle \) is related to \(c\) either if \(c\) can reduce to a stuck configuration with related subterms, or if \(E\) is a diverging context, and we do not require anything of \(c\). The resulting simulation is not symmetric as it relates a deferred diverging configuration with any configuration \(c\) (even converging one), but the corresponding notion of bisimulation equates such configuration only to either a configuration of the same kind or a diverging configuration such as \(\langle h \;|\; \varOmega \rangle \).
Progress. We define simulation using the notion of diacritical progress we developed in a previous work [2, 3], which distinguishes between active and passive clauses. Roughly, passive clauses are between simulation states which should be considered equal, while active clauses are between states where actual progress is taking place. This distinction does not change the notions of bisimulation or bisimilarity, but it simplifies the soundness proof of the bisimilarity. It also allows for the definition of powerful up-to techniques, relations that are easier to use than bisimulations but still imply bisimilarity. For normal-form bisimilarity, our framework enables up-to techniques which respects \(\eta \)-expansion [3].
Progress is defined between objects called candidate relations, denoted by \(\mathrel {\mathcal R}\), \(\mathrel {\mathcal S}\), \(\mathrel {\mathcal T}\). A candidate relation \(\mathrel {\mathcal R}\) contains pairs of configurations, and a set of configurations written \({\mathrel {\mathcal R} \uparrow }\), which we expect to be composed of diverging or deferred diverging configurations (for such relations we take \({\mathrel {\mathcal R}^{-1} \uparrow }\) to be \({\mathrel {\mathcal R} \uparrow }\)). We extend \(\mathrel {\mathcal R}\) to stores, terms, values, and contexts with the following definitions.

We use these extensions to define progress as follows.
Definition 2
A candidate relation \(\mathrel {\mathcal R}\) progresses to \(\mathrel {\mathcal S}\), \(\mathrel {\mathcal T}\) written \(\mathrel {\mathcal R}\mathop \rightarrowtail \mathrel {\mathcal S}, \mathrel {\mathcal T}\), if \(\mathrel {\mathcal R}\mathop \subseteq \mathrel {\mathcal S}\), \(\mathrel {\mathcal S}\mathop \subseteq \mathrel {\mathcal T}\), and
-
1.
\(c\mathrel {\mathcal R}d\) implies
-
if \(c\mathrel \rightarrow c'\), then \(d\mathrel {\mathrel \rightarrow ^*}d'\) and \(c' \mathrel {\mathcal T}d'\);
-
if \(c= \langle h \;|\; v \rangle \), then \(d\mathrel {\mathrel \rightarrow ^*}\langle g \;|\; w \rangle \),
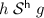 , and
, and 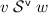 ;
; -
if \(c= \langle h \;|\; E[x\,v] \rangle \), then either
-
\(d\mathrel {\mathrel \rightarrow ^*}\langle g \;|\; F[x\,w] \rangle \),
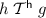 ,
, 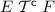 , and
, and 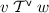 , or
, or -
\(E\mathop {\in }{\mathrel {\mathcal T} \uparrow ^{\mathsf c}}\).
-
-
-
2.
\(c\mathop {\in }{\mathrel {\mathcal R} \uparrow }\) implies \(c\ne \langle h \;|\; v \rangle \) for all \(h\) and \(v\) and
-
if \(c\mathrel \rightarrow c'\), then \(c' \mathop {\in }{\mathrel {\mathcal T} \uparrow }\);
-
if \(c= \langle h \;|\; E[x\,v] \rangle \), then \(E\mathop {\in }{\mathrel {\mathcal T} \uparrow ^{\mathsf c}}\).
-
A normal-form simulation is a candidate relation \(\mathrel {\mathcal R}\) such that \(\mathrel {\mathcal R}\mathop \rightarrowtail \mathrel {\mathcal R}, \mathrel {\mathcal R}\), and a bisimulation is a candidate relation \(\mathrel {\mathcal R}\) such that \(\mathrel {\mathcal R}\) and \(\mathrel {\mathcal R}^{-1}\) are simulations. Normal-form bisimilarity \(\mathrel \approx \) is the union of all normal-form bisimulations.
We test values and contexts by applying or plugging them with a fresh variable \(x\), and running them in a fresh store; with a global memory, the value represented by \(x\) may access any reference and assign it an arbitrary value, hence the need for a fresh store. The stores of two bisimilar value configurations must have the same domain, as it would be easy to distinguish them otherwise by testing the content of the references that would be in one store but not in the other.
The main novelty compared to usual definitions of normal-form bisimilarity [3, 11] is the set of (deferred) diverging configurations used in the stuck terms clause. We detect that \(E\) in a configuration \(\langle h \;|\; E[x\,v] \rangle \) is (deferred) diverging by running \(\langle h' \;|\; E[y] \rangle \) where \(y\) and \(h'\) are fresh; this configuration may then diverge or evaluate to an other deferred diverging configuration \(\langle h \;|\; E'[x\,v] \rangle \).
Like in the plain \(\lambda \)-calculus [3], \(\mathrel {\mathcal R}\) progresses towards \(\mathrel {\mathcal S}\) in the value clause and \(\mathrel {\mathcal T}\) in the others; the former is passive while the others are active. Our framework prevents some up-to techniques from being applied after a passive transition. In particular, we want to forbid the application of bisimulation up to context as it would be unsound: we could deduce that \(v\,x\) and \(w\,x\) are equivalent for all \(v\) and \(w\) just by building a candidate relation containing \(v\) and \(w\).
Example 1
To prove that \(\langle h \;|\; x\,v\,\varOmega \rangle \mathrel \approx \langle h \;|\; \varOmega \rangle \) holds for all \(v\) and \(h\), we prove that  is a bisimulation. Indeed, \(\langle h \;|\; x\,v\,\varOmega \rangle \) is stuck with \(\langle g \;|\; y\,\varOmega \rangle \mathop {\in }{\mathrel {\mathcal R} \uparrow }\) for fresh \(y\) and \(g\), and we have \(\langle g \;|\; y\,\varOmega \rangle \mathrel \rightarrow \langle g \;|\; y\,\varOmega \rangle \). Conversely, the transition \(\langle h \;|\; \varOmega \rangle \mathrel \rightarrow \langle h \;|\; \varOmega \rangle \) is matched by \(\langle h \;|\; x\,v\,\varOmega \rangle \mathrel {\mathrel \rightarrow ^*}\langle h \;|\; x\,v\,\varOmega \rangle \) and the resulting terms are in \(\mathrel {\mathcal R}\).
is a bisimulation. Indeed, \(\langle h \;|\; x\,v\,\varOmega \rangle \) is stuck with \(\langle g \;|\; y\,\varOmega \rangle \mathop {\in }{\mathrel {\mathcal R} \uparrow }\) for fresh \(y\) and \(g\), and we have \(\langle g \;|\; y\,\varOmega \rangle \mathrel \rightarrow \langle g \;|\; y\,\varOmega \rangle \). Conversely, the transition \(\langle h \;|\; \varOmega \rangle \mathrel \rightarrow \langle h \;|\; \varOmega \rangle \) is matched by \(\langle h \;|\; x\,v\,\varOmega \rangle \mathrel {\mathrel \rightarrow ^*}\langle h \;|\; x\,v\,\varOmega \rangle \) and the resulting terms are in \(\mathrel {\mathcal R}\).
2.3 Soundness
In this framework, proving that \(\mathrel \approx \) is sound is a consequence that a form of bisimulation up to context is valid, a result which itself may require to prove that other up-to techniques are valid. We distinguish the techniques which can be used in passive clauses (called strong up-to techniques), from the ones which cannot. An up-to technique (resp. strong up-to technique) is a function f such that \(\mathrel {\mathcal R}\mathop \rightarrowtail \mathrel {\mathcal R}, f(\mathrel {\mathcal R})\) (resp. \(\mathrel {\mathcal R}\mathop \rightarrowtail f(\mathrel {\mathcal R}), f(\mathrel {\mathcal R})\)) implies \(\mathrel {\mathcal R}\mathop \subseteq \mathrel \approx \). To show that a given f is an up-to technique, we rely on a notion of respectfulness, which is simpler to prove and gives sufficient conditions for f to be an up-to technique.
We briefly recall the notions we need from our previous work [2]. We extend \(\subseteq \) and \(\cup \) to functions argument-wise (e.g., \((f \cup g)(\mathrel {\mathcal R})=f(\mathrel {\mathcal R}) \cup g(\mathrel {\mathcal R})\)), and given a set \(\mathfrak {F}\) of functions, we also write \(\mathfrak {F}\) for the function defined as \(\bigcup _{f \in \mathfrak {F}} f\). We define \(f^\omega \) as \(\bigcup _{n \in \mathbb N} f^n\). We write \(\mathsf {id}\) for the identity function on relations, and \(\widehat{f}\) for \(f \mathop \cup \mathsf {id}\). A function f is monotone if \(\mathrel {\mathcal R}\mathop \subseteq \mathrel {\mathcal S}\) implies \(f(\mathrel {\mathcal R}) \mathop \subseteq f(\mathrel {\mathcal S})\). We write \(\mathcal {P}_{ fin }(\mathrel {\mathcal R})\) for the set of finite subsets of \(\mathrel {\mathcal R}\), and we say f is continuous if it can be defined by its image on these finite subsets, i.e., if \(f(\mathrel {\mathcal R}) \mathop \subseteq \bigcup _{\mathrel {\mathcal S}\in \mathcal {P}_{ fin }(\mathrel {\mathcal R})}f(\mathrel {\mathcal S})\). The up-to techniques we use are defined by inference rules with a finite number of premises, so they are trivially continuous.
Definition 3
A function f evolves to g, h, written  , if for all \(\mathrel {\mathcal R}\) and \(\mathrel {\mathcal T}\), \(\mathrel {\mathcal R}\mathop \rightarrowtail \mathrel {\mathcal R}, \mathrel {\mathcal T}\) implies \(f(\mathrel {\mathcal R}) \mathop \rightarrowtail g(\mathrel {\mathcal R}), h(\mathrel {\mathcal T})\). A function f strongly evolves to g, h, written
, if for all \(\mathrel {\mathcal R}\) and \(\mathrel {\mathcal T}\), \(\mathrel {\mathcal R}\mathop \rightarrowtail \mathrel {\mathcal R}, \mathrel {\mathcal T}\) implies \(f(\mathrel {\mathcal R}) \mathop \rightarrowtail g(\mathrel {\mathcal R}), h(\mathrel {\mathcal T})\). A function f strongly evolves to g, h, written  , if for all \(\mathrel {\mathcal R}\), \(\mathrel {\mathcal S}\), and \(\mathrel {\mathcal T}\), \(\mathrel {\mathcal R}\mathop \rightarrowtail \mathrel {\mathcal S}, \mathrel {\mathcal T}\) implies \(f(\mathrel {\mathcal R}) \mathop \rightarrowtail g(\mathrel {\mathcal S}), h(\mathrel {\mathcal T})\).
, if for all \(\mathrel {\mathcal R}\), \(\mathrel {\mathcal S}\), and \(\mathrel {\mathcal T}\), \(\mathrel {\mathcal R}\mathop \rightarrowtail \mathrel {\mathcal S}, \mathrel {\mathcal T}\) implies \(f(\mathrel {\mathcal R}) \mathop \rightarrowtail g(\mathrel {\mathcal S}), h(\mathrel {\mathcal T})\).
Evolution can be seen as progress for functions on relations. Evolution is more restrictive than strong evolution, as it requires \(\mathrel {\mathcal R}\) such that \(\mathrel {\mathcal R}\mathop \rightarrowtail \mathrel {\mathcal R}, \mathrel {\mathcal T}\).
Definition 4
A set \(\mathfrak {F}\) of continuous functions is respectful if there exists \(\mathfrak {S}\) such that \(\mathfrak {S}\subseteq \mathfrak {F}\) and
-
for all \(f \in \mathfrak {S}\), we have
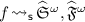 ;
; -
for all \(f \in \mathfrak {F}\), we have
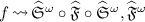 .
.
In words, a function is in a respectful set \(\mathfrak {F}\) if it evolves towards a combination of functions in \(\mathfrak {F}\) after active clauses, and in \(\mathfrak {S}\) after passive ones. When checking that f is regular (second case), we can use a regular function at most once after a passive clause. The (possibly empty) subset \(\mathfrak {S}\) intuitively represents the strong up-to techniques of \(\mathfrak {F}\). If \(\mathfrak {S}_1\) and \(\mathfrak {S}_2\) are subsets of \(\mathfrak {F}\) which verify the conditions of the definition, then \(\mathfrak {S}_1 \cup \mathfrak {S}_2\) also does, so there exists the largest subset of \(\mathfrak {F}\) which satisfies the conditions, written \({\mathsf {strong}(\mathfrak {F})}\).
Lemma 1
Let \(\mathfrak {F}\) be a respectful set.
-
If \(f \in \mathfrak {F}\), then f is an up-to technique. If \(f \in {\mathsf {strong}(\mathfrak {F})}\), then f is a strong up-to technique.
-
For all \(f \in \mathfrak {F}\), we have \(f(\mathrel \approx ) \mathop \subseteq \mathrel \approx \).
Showing that f is in a respectful set \(\mathfrak {F}\) is easier than proving it is an up-to technique. Besides, proving that a bisimulation up to context is respectful implies that \(\mathrel \approx \) is preserved by contexts thanks to the last property of Lemma 1.
The up-to techniques for the calculus with global store are given in Fig. 1. The techniques \(\mathsf {subst}_{}\) and \(\mathsf {plug}_{}\) allow to prove that \(\mathrel \approx \) is preserved by substitution and by evaluation contexts. The remaining ones are auxiliary techniques which are used in the respectfulness proof: \(\mathsf {red}\) relies on the fact that the calculus is deterministic to relate terms up to reduction steps. The technique \(\mathsf {div}\) allows to relate a diverging configuration to any other configuration, while \(\mathsf {plugdiv}\) states that if \(E\) is a diverging context, then \(\langle h \;|\; E[t] \rangle \) is a diverging configuration for all \(h\) and \(t\). We distinguish the technique \(\mathsf {plug}_{\mathsf {c}}\) from \(\mathsf {plug}_{\uparrow }\) to get a more fine-grained classification, as \(\mathsf {plug}_{\mathsf {c}}\) is the only one which is not strong.
Lemma 2
The set \(\mathfrak {F}\mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}\{ \mathsf {subst}_{}, \mathsf {plug}_{m}, \mathsf {red}, \mathsf {div}, \mathsf {plugdiv}\ |\ m \in \{ \mathsf {c}, \uparrow \} \}\) is respectful, with \({\mathsf {strong}(\mathfrak {F})}= \mathfrak {F}\setminus \{ \mathsf {plug}_{\mathsf {c}}\}\).
We omit the proof, as it is similar but much simpler than for the calculus with local store of Sect. 3. We deduce that \(\mathrel \approx \) is sound using Lemma 1.
Theorem 1
For all \(t\), \(s\), and fresh store \(h\), if \(\langle h \;|\; t \rangle \mathrel \approx \langle h \;|\; s \rangle \), then \(t\mathrel \equiv s\).
2.4 Completeness
We prove the reverse implication by building a bisimulation which contains \(\mathrel \equiv \).
Theorem 2
For all \(t\), \(s\), if \(t\mathrel \equiv s\), then for all fresh stores \(h\), \(\langle h \;|\; t \rangle \mathrel \approx \langle h \;|\; s \rangle \).
Proof
(Sketch). It suffices to show that the candidate \(\mathrel {\mathcal R}\) defined as

is a simulation. We proceed by case analysis on the behavior of \(\langle h \;|\; t \rangle \). The details are in the report [4]; we sketch the proof in the case when \(\langle h \;|\; t \rangle \mathrel {\mathcal R}\langle g \;|\; s \rangle \), \(t= E[x\,v]\), and \(E\) is not deferred diverging.
A first step is to show that \(\langle g \;|\; s \rangle \) also evaluates to an open-stuck configuration with \(x\) in function position. To do so, we consider a fresh \(l\) and we define  such that
such that  sets \(l\) at 1 when it is first applied if \(y= x\), and at 2 if \(y\ne x\). Then
sets \(l\) at 1 when it is first applied if \(y= x\), and at 2 if \(y\ne x\). Then  sets \(l\) at 1, which should also be the case of
sets \(l\) at 1, which should also be the case of  , and it is possible only if \(\langle g \;|\; s \rangle \mathrel {\mathrel \rightarrow ^*}\langle g' \;|\; F[x\,w] \rangle \) for some \(g'\), \(F\), and \(w\).
, and it is possible only if \(\langle g \;|\; s \rangle \mathrel {\mathrel \rightarrow ^*}\langle g' \;|\; F[x\,w] \rangle \) for some \(g'\), \(F\), and \(w\).
We then have to show that  ,
,  , and
, and  . We sketch the proof for the contexts, as the proofs for the values and the stores are similar. Given \(h_f\) a fresh store, \(y\) a fresh variable, \(E'\) a context, \(h_{E'}\) a store,
. We sketch the proof for the contexts, as the proofs for the values and the stores are similar. Given \(h_f\) a fresh store, \(y\) a fresh variable, \(E'\) a context, \(h_{E'}\) a store,  a closing substitution, we want
a closing substitution, we want  iff
iff  .
.
Let \(l\) be a fresh reference. Assuming \(\mathsf {dom}(h)= \{ l_1 \ldots l_n \}\), given a term \(t\), we write \(\bigcup _{i} l_i:=h;t\) for \(l_1:=h(l_1);\ldots l_n:=h(l_n);t\). We define

The substitution  behaves like
behaves like  except that when
except that when  is applied for the first time, it replaces its argument by
is applied for the first time, it replaces its argument by  and sets the store to \(h_f \mathop \uplus h_{E'}\). Therefore
and sets the store to \(h_f \mathop \uplus h_{E'}\). Therefore  , but this configuration then behaves like
, but this configuration then behaves like  . Similarly,
. Similarly,  evaluates to a configuration equivalent to
evaluates to a configuration equivalent to  , and since
, and since  implies
implies  , we can conclude from there.
, we can conclude from there.
3 Local Store
We adapt the ideas of the previous section to a calculus where terms create their own local store. To be able to deal with local resources, the relation we define mixes principles from normal-form and environmental bisimilarities.
3.1 Syntax, Semantics, and Contextual Equivalence
In this section, the terms no longer share a global store, but instead must create local references before storing values. We extend the syntax of Sect. 2 with a construct to create a new reference.

Reference creation \(\mathsf {new~} l := v \mathsf {~in~} t\) binds \(l\) in \(t\); we identify terms up to \(\alpha \)-conversion of their references. We write \(\mathsf {fr}(t)\) and \(\mathsf {fr}(E)\) for the set of free references of \(t\) or \(E\), and a term or context is reference-closed if its set of free references is empty. Following [18] and in contrast with [5, 6], references are not values, but we can still give access to a reference \(l\) by passing \(\lambda x.!l\) and \(\lambda x.l:=x;\lambda y.y\).
As before, the semantics is defined on configurations \(\langle h \;|\; t \rangle \) verifying \(\mathsf {fr}(t)\subseteq \mathsf {dom}(h)\) and for all \(l\in \mathsf {dom}(h)\), \(\mathsf {fr}(h{(l)}) \subseteq \mathsf {dom}(h)\). We add to the rules of Sect. 2 the following one for reference creation.
We remind that \(\mathop \uplus \) is defined for disjoint stores only, so the above rule assumes that \(l\notin \mathsf {dom}(h)\), which is always possible using \(\alpha \)-conversion.
We define contextual equivalence on reference-closed terms as we expect programs to allocate their own store.
Definition 5
Two reference-closed terms \(t\) and \(s\) are contextually equivalent, written \(t\mathrel \equiv s\), if for all reference-closed evaluation contexts \(E\) and closing substitutions  ,
,  iff
iff  .
.
3.2 Bisimilarity
With local stores, an external observer no longer has direct access to the stored values. In presence of such information hiding, a sound bisimilarity relies on an environment to accumulate terms which should be tested in different stores [8].
Example 2
Let  and \(f_2 \mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}\lambda x.\textsf {true}\). If we compare \(\mathsf {new~} l := \textsf {true} \mathsf {~in~} f_1\) and \(f_2\) only once in the empty store, they would be seen as equivalent as they both return \(\textsf {true}\), however \(f_1\) modify its store, so running \(f_1\) and \(f_2\) a second time distinguishes them.
and \(f_2 \mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}\lambda x.\textsf {true}\). If we compare \(\mathsf {new~} l := \textsf {true} \mathsf {~in~} f_1\) and \(f_2\) only once in the empty store, they would be seen as equivalent as they both return \(\textsf {true}\), however \(f_1\) modify its store, so running \(f_1\) and \(f_2\) a second time distinguishes them.
Environments generally contain only values [17], except in \(\lambda \mu \rho \) [18], where plugged evaluation contexts are kept in the environment when comparing open-stuck configurations. In contrast with \(\lambda \mu \rho \), our environment collects values, and we use a stack for registering contexts [7, 10]. Unlike values, contexts are therefore tested only once, following a last-in first-out ordering. The next example shows that considering contexts repeatedly would lead to an overly-discriminating bisimilarity. For the stack discipline of testing contexts in action see Example 8 in Sect. 3.4.
Example 3
With the same \(f_1\) and \(f_2\) as in Example 2, the terms \(t\mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}\mathsf {new~} l := \textsf {true} \mathsf {~in~} f_1 \,(x\,\lambda y.y)\) and \(s\mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}f_2 \,(x\,\lambda y.y)\) are contextually equivalent. Roughly, for all closing substitution  , \(t\) and \(s\) either both diverge (if
, \(t\) and \(s\) either both diverge (if  diverges), or evaluate to \(\textsf {true}\), since
diverges), or evaluate to \(\textsf {true}\), since  cannot modify the value in \(l\). Testing \(f_1 \,\square \) and \(f_2 \,\square \) twice would discriminate them and wrongfully distinguish \(t\) and \(s\).
cannot modify the value in \(l\). Testing \(f_1 \,\square \) and \(f_2 \,\square \) twice would discriminate them and wrongfully distinguish \(t\) and \(s\).
Remark 1
The bisimilarity for \(\lambda \mu \rho \) runs evaluation contexts several times and is still complete because of the \(\mu \) operator, which, like call/cc, captures evaluation contexts, and may then execute them several times.
We let \(\mathcal E\) range over sets of pairs of values, and \(\epsilon \) over sets of values. Similarly, we write \(\varSigma \) for a stack of pairs of evaluation contexts and \(\sigma \) for a stack of evaluation contexts. We write \(\odot \) for the empty stack, \(\mathop {{:}{:}}\) for the operator putting an element on top of a stack, and \(\mathop {\mathbin {++}}\) for the concatenation of two stacks. The projection operator \(\pi _{1}\) transforms a set or stack of pairs into respectively a set or stack of single elements by taking the first element of each pair. A candidate relation \(\mathrel {\mathcal R}\) can be composed of:
-
quadruples \((\mathcal E, \varSigma , c, d)\), written \(\mathcal E, \varSigma \vdash c \mathrel {\mathcal R} d\), meaning that \(c\) and \(d\) are related under \(\mathcal E\) and \(\varSigma \);
-
quadruples \((\mathcal E, \varSigma , h, g)\), written \(\mathcal E, \varSigma \vdash h \mathrel {\mathcal R} g\), meaning that the elements of \(\mathcal E\) and the top of \(\varSigma \) should be related when run with the stores \(h\) and \(g\);
-
triples \((\epsilon , \sigma , c)\), written \(\epsilon , \sigma \vdash c \mathop {\in }{\mathrel {\mathcal R} \uparrow }\), meaning that either \(c\) is (deferred) diverging, or \(\sigma \) is non-empty and contains a (deferred) diverging context;
-
triples \((\epsilon , \sigma , h)\), written \(\epsilon , \sigma \vdash h \mathop {\in }{\mathrel {\mathcal R} \uparrow }\), meaning that \(\sigma \) is non-empty and contains a (deferred) diverging context.
Definition 6
A candidate relation \(\mathrel {\mathcal R}\) progresses to \(\mathrel {\mathcal S}\), \(\mathrel {\mathcal T}\) written \(\mathrel {\mathcal R}\mathop \rightarrowtail \mathrel {\mathcal S}, \mathrel {\mathcal T}\), if \(\mathrel {\mathcal R}\mathop \subseteq \mathrel {\mathcal S}\), \(\mathrel {\mathcal S}\mathop \subseteq \mathrel {\mathcal T}\), and
-
1.
\(\mathcal E, \varSigma \vdash c \mathrel {\mathcal R} d\) implies
-
if \(c\mathrel \rightarrow c'\), then \(d\mathrel {\mathrel \rightarrow ^*}d'\) and \(\mathcal E, \varSigma \vdash c' \mathrel {\mathcal T} d'\);
-
if \(c= \langle h \;|\; v \rangle \), then either
-
\(d\mathrel {\mathrel \rightarrow ^*}\langle g \;|\; w \rangle \), and \(\mathcal E\cup \{ (v, w) \}, \varSigma \vdash h \mathrel {\mathcal S} g\), or
-
\(\varSigma \ne \odot \) and \(\pi _{1}(\mathcal E)\cup \{ v\}, \pi _{1}(\varSigma ) \vdash h \mathop {\in }{\mathrel {\mathcal S} \uparrow }\);
-
-
if \(c= \langle h \;|\; E[x\,v] \rangle \), then either
-
\(d\mathrel {\mathrel \rightarrow ^*}\langle g \;|\; F[x\,w] \rangle \), and \(\mathcal E\cup \{ (v, w)\}, (E, F) \mathop {{:}{:}}\varSigma \vdash h \mathrel {\mathcal S} g\), or
-
\(\pi _{1}(\mathcal E)\cup \{v\}, E\mathop {{:}{:}}\pi _{1}(\varSigma ) \vdash h \mathop {\in }{\mathrel {\mathcal S} \uparrow }\).
-
-
-
2.
\(\mathcal E, \varSigma \vdash h \mathrel {\mathcal R} g\) implies
-
if
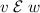 , then \(\mathcal E, \varSigma \vdash \langle h \;|\; v\,x \rangle \mathrel {\mathcal S} \langle g \;|\; w\,x \rangle \) for a fresh \(x\);
, then \(\mathcal E, \varSigma \vdash \langle h \;|\; v\,x \rangle \mathrel {\mathcal S} \langle g \;|\; w\,x \rangle \) for a fresh \(x\); -
if \(\varSigma = (E, F) \mathop {{:}{:}}\varSigma '\), then \(\mathcal E, \varSigma ' \vdash \langle h \;|\; E[x] \rangle \mathrel {\mathcal S} \langle g \;|\; F[x] \rangle \) for a fresh \(x\).
-
-
3.
\(\epsilon , \sigma \vdash c \mathop {\in }{\mathrel {\mathcal R} \uparrow }\) implies
-
if \(c\mathrel \rightarrow c'\), then \(\epsilon , \sigma \vdash c' \mathop {\in }{\mathrel {\mathcal T} \uparrow }\);
-
if \(c= \langle h \;|\; v \rangle \), then \(\sigma \ne \odot \) and \(\epsilon \cup \{ v\}, \sigma \vdash h \mathop {\in }{\mathrel {\mathcal S} \uparrow }\);
-
if \(c= \langle h \;|\; E[x\,v] \rangle \), then \(\epsilon \cup \{ v\}, E\mathop {{:}{:}}\sigma \vdash h \mathop {\in }{\mathrel {\mathcal S} \uparrow }\).
-
-
4.
\(\epsilon , \sigma \vdash h \mathop {\in }{\mathrel {\mathcal R} \uparrow }\) implies that \(\sigma \ne \odot \) and
-
if \(v\in \epsilon \), then \(\epsilon , \sigma \vdash \langle h \;|\; v\,x \rangle \mathop {\in }{\mathrel {\mathcal S} \uparrow }\) for a fresh \(x\);
-
if \(\sigma = E\mathop {{:}{:}}\sigma '\), then \(\epsilon , \sigma ' \vdash \langle h \;|\; E[x] \rangle \mathop {\in }{\mathrel {\mathcal S} \uparrow }\) for a fresh \(x\).
-
A normal-form simulation is a candidate relation \(\mathrel {\mathcal R}\) such that \(\mathrel {\mathcal R}\mathop \rightarrowtail \mathrel {\mathcal R}, \mathrel {\mathcal R}\), and a bisimulation is a candidate relation \(\mathrel {\mathcal R}\) such that \(\mathrel {\mathcal R}\) and \(\mathrel {\mathcal R}^{-1}\) are simulations. Normal-form bisimilarity \(\mathrel \approx \) is the union of all normal-form bisimulations.
When \(\mathcal E, \varSigma \vdash c \mathrel {\mathcal R} d\), we reduce \(c\) until we get a value \(v\) or a stuck term \(E[x\,v]\). At that point, either \(d\) also reduces to a normal form of the same kind, or we test (the first projection of) the stack \(\varSigma \) for divergence, assuming it is not empty. In the former case, we add the values to \(\mathcal E\) and the evaluation contexts at the top of \(\varSigma \), getting a judgment of the form \(\mathcal E', \varSigma ' \vdash h \mathrel {\mathcal R} g\), which then tests the environment and the stack by running either terms in \(\mathcal E'\) or at the top of \(\varSigma '\).
Example 4
We sketch the bisimulation proof for the terms \(t\) and \(s\) of Example 3. Because \(\langle \emptyset \;|\; t \rangle \mathrel {\mathrel \rightarrow ^*}\langle l:=\textsf {true} \;|\; f_1 \,{(x\,\lambda y.y)} \rangle \) and \(\langle \emptyset \;|\; s \rangle = \langle \emptyset \;|\; f_2 \,{(x\,\lambda y.y)} \rangle \), we need to define \(\mathrel {\mathcal R}\) such that \(\{ (\lambda y.y, \lambda y.y) \}, (f_1 \,\square , f_2 \,\square ) \mathop {{:}{:}}\odot \vdash l:=\textsf {true} \mathrel {\mathcal R} \emptyset \). Testing the equal values in the environment is easy with up-to techniques. For the contexts on the stack, we need \(\{ (\lambda y.y, \lambda y.y) \}, \odot \vdash \langle l:=\textsf {true} \;|\; f_1\,z \rangle \mathrel {\mathcal R} \langle \emptyset \;|\; f_2\,z \rangle \) for a fresh z. Since \(\langle l:=\textsf {true} \;|\; f_1\,z \rangle \mathrel {\mathrel \rightarrow ^*}\langle l:=\textsf {false} \;|\; \textsf {true} \rangle \) and \(\langle \emptyset \;|\; f_2\,z \rangle \mathrel {\mathrel \rightarrow ^*}\langle \emptyset \;|\; \textsf {true} \rangle \), we need \(\{ (\lambda y.y, \lambda y.y), (\textsf {true}, \textsf {true}) \}, \odot \vdash l:=\textsf {false} \mathrel {\mathcal R} \emptyset \), which is simple to check.
Example 5
In contrast, we show that \(t' \mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}\mathsf {new~} l := \textsf {true} \mathsf {~in~} f_1 \,(x\,\lambda y.l:=y;y)\) and \(s' \mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}f_2 \,(x\,\lambda y.y)\) are not bisimilar. We would need to build \(\mathrel {\mathcal R}\) such that \(\{ (\lambda y.l:=y;y, \lambda y.y) \}, (f_1 \,\square , f_2 \,\square ) \mathop {{:}{:}}\odot \vdash l:=\textsf {true} \mathrel {\mathcal R} \emptyset \). Testing the values in the environment, we want \(\{ (\lambda y.l:=y;y, \lambda y.y), (z, z) \}, (f_1 \,\square , f_2 \,\square ) \mathop {{:}{:}}\odot \vdash l:=z \mathrel {\mathcal R} \emptyset \) for a fresh z. Executing the contexts on the stack, we get a stuck term of the form  and a value \(\textsf {true}\), which cannot be related, because the former is not deferred diverging.
and a value \(\textsf {true}\), which cannot be related, because the former is not deferred diverging.
The terms \(t'\) and \(s'\) are therefore not bisimilar, and they are indeed not contextually equivalent, since \(t'\) gives access to its private reference by passing \(\lambda y.l:=y;y\) to \(x\). The function represented by \(x\) can then change the value of \(l\) to \(\textsf {false}\) and break the equivalence.
The last two cases of the bisimulation definition aim at detecting a deferred diverging context. The judgment \(\epsilon , \sigma \vdash h \mathop {\in }{\mathrel {\mathcal R} \uparrow }\) roughly means that if \(\sigma = E_n \mathop {{:}{:}}\ldots E_1 \mathop {{:}{:}}\odot \), then the configuration \(\langle h' \;|\; E_1[\ldots E_n[x]] \rangle \) diverges for all fresh \(x\) and all \(h'\) obtained by running a term from \(\mathcal E\) with the store \(h\). As a result, when \(\epsilon , \sigma \vdash h \mathop {\in }{\mathrel {\mathcal R} \uparrow }\), we have two possibilities: either we run a term from \(\mathcal E\) in \(h\) to potentially change \(h\), or we run the context at the top of \(\sigma \) (which cannot be empty in that case) to check if it is diverging. In both cases, we get a judgment of the form \(\epsilon , \sigma ' \vdash c \mathop {\in }{\mathrel {\mathcal R} \uparrow }\). In that case, either \(c\) diverges and we are done, or it terminates, meaning that we have to look for divergence in \(\sigma '\).
Example 6
We prove that \(\langle \emptyset \;|\; x\,v\,\varOmega \rangle \) and \(\langle \emptyset \;|\; \varOmega \rangle \) are bisimilar. We define \(\mathrel {\mathcal R}\) such that \(\emptyset , \odot \vdash \langle \emptyset \;|\; x\,v\,\varOmega \rangle \mathrel {\mathcal R} \langle \emptyset \;|\; \varOmega \rangle \), for which we need \(\{v\}, \square \,\varOmega \mathop {{:}{:}}\odot \vdash \emptyset \mathop {\in }{\mathrel {\mathcal R} \uparrow }\), which itself holds if \(\{v\}, \odot \vdash \langle \emptyset \;|\; y\,\varOmega \rangle \mathop {\in }{\mathrel {\mathcal R} \uparrow }\).
Finally, only the two clauses where a reduction step takes place are active; all the others are passive, because they are simply switching from one judgment to the other without any real progress taking place. For example, when comparing value configurations, we go from a configuration judgment \(\mathcal E, \varSigma \vdash c \mathrel {\mathcal R} d\) to a store judgment \(\mathcal E, \varSigma \vdash h \mathrel {\mathcal R} g\) or a diverging store judgment \(\mathcal E, \varSigma \vdash h \mathop {\in }{\mathrel {\mathcal R} \uparrow }\). In a (diverging) store judgment, we simply decide whether we reduce a term from the store of from the stack, going back to a (diverging) configuration judgment. Actual progress is made only when we start reducing the chosen configuration.
3.3 Soundness and Completeness
We briefly discuss the up-to techniques we need to prove soundness. We write \(\mathcal E\{(v, w)/x\}\) for the environment  , and we also define \(\varSigma \{(x, w)/x\}\), \(\epsilon \{v/x\}\), and \(\sigma \{v/x\}\) as expected. To save space, Fig. 2 presents the up-to techniques for the configuration judgment only; see the report [4] for the other judgments.
, and we also define \(\varSigma \{(x, w)/x\}\), \(\epsilon \{v/x\}\), and \(\sigma \{v/x\}\) as expected. To save space, Fig. 2 presents the up-to techniques for the configuration judgment only; see the report [4] for the other judgments.
As in Sect. 2.3, the techniques \(\mathsf {subst}_{}\) and \(\mathsf {plug}_{}\) allow to reason up to substitution and plugging into an evaluation context, except that the substituted values and plugged contexts must be taken from respectively the environment and the top of the stack. The technique \(\mathsf {div}\) relates a diverging configuration to any configuration, like in the calculus with global store. The technique \(\mathsf {ccomp}\) allows to merge successive contexts in the stack into one. The weakening technique \(\mathsf {weak}\), originally known as bisimulation up to environment [17], is an usual technique for environmental bisimulations. Making the environment smaller creates a weaker judgment, as having less testing terms means a less discriminating candidate relation. Bisimulation up to reduction \(\mathsf {red}\) is also standard and allows for a big-step reasoning by ignoring reduction steps. Finally, the technique \(\mathsf {refl}\) allows to introduce identical contexts in the stack, but also values in the environment or terms in configurations (see the report [4]).
We denote by \(\mathsf {subst}_{\mathsf {c}}\) the up to substitution technique restricted to the configuration and diverging configuration judgments, and by \(\mathsf {subst}_{\mathsf {s}}\) the restriction to the store and diverging store judgments.
Lemma 3
The set \(\mathfrak {F}\mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}\{ \mathsf {subst}_{m}, \mathsf {plug}_{}, \mathsf {ccomp}, \mathsf {div}, \mathsf {weak}, \mathsf {red}, \mathsf {refl}\ |\ m \in \{ \mathsf {c}, \mathsf {s}\} \}\) is respectful, with \({\mathsf {strong}(\mathfrak {F})}= \{ \mathsf {subst}_{\mathsf {s}}, \mathsf {ccomp}, \mathsf {div}, \mathsf {weak}, \mathsf {red}, \mathsf {refl}\}\).
In contrast with Sect. 2.3 and our previous work [3], \(\mathsf {subst}_{\mathsf {c}}\) is not strong, because values are taken from the environment. Indeed, with \(\mathsf {subst}_{\mathsf {c}}\) strong, from \(\{ (v, w) \}, \odot \vdash \emptyset \mathrel {\mathcal R} \emptyset \), we could derive \(\{ (v, w) \}, \odot \vdash \langle \emptyset \;|\; x\,y \rangle \mathrel {\mathsf {refl}(\mathrel {\mathcal R})} \langle \emptyset \;|\; x\,y \rangle \) and then \(\{ (v, w) \}, \odot \vdash \langle \emptyset \;|\; v\,x \rangle \mathrel {\mathsf {subst}_{\mathsf {c}}(\mathrel {\mathsf {refl}(\mathrel {\mathcal R})})} \langle \emptyset \;|\; w\,x \rangle \) for any \(v\) and \(w\), which would be unsound.
The respectfulness proofs are in the report [4]. Using \(\mathsf {refl}\), \(\mathsf {plug}_{}\), \(\mathsf {subst}_{\mathsf {c}}\), and Lemma 1 we prove that \(\mathrel \approx \) is preserved by evaluation contexts and substitution, from which we deduce it is sound w.r.t. contextual equivalence.
Theorem 3
For all \(t\) and \(s\), if \(\emptyset , \odot \vdash \langle \emptyset \;|\; t \rangle \mathrel \approx \langle \emptyset \;|\; s \rangle \), then \(t\mathrel \equiv s\).
To establish completeness, we follow the proof of Theorem 2, i.e., we construct a candidate relation \(\mathrel {\mathcal R}\) that contains \(\mathrel \equiv \) and prove it is a simulation by case analysis on the behavior of the related terms.
Theorem 4
For all \(t\) and \(s\), if \(t\mathrel \equiv s\), then \(\emptyset , \odot \vdash \langle \emptyset \;|\; t \rangle \mathrel \approx \langle \emptyset \;|\; s \rangle \).
The main difference is that the contexts and closing substitutions are built from the environment using compatible closures [17], to take into account the private resources of the related terms. We discuss the proof in the report [4].
3.4 Examples
Example 7
We start by the so-called awkward example [5, 6, 15]. Let
We equate \(\mathsf {new~} l := 0 \mathsf {~in~} v\) and \(w\), building the candidate \(\mathrel {\mathcal R}\) incrementally, starting from \(\{ (v, w) \}, \odot \vdash l:=0 \mathrel {\mathcal R} \emptyset \).
Running \(v\) and \(w\) with a fresh variable f, we obtain \(\langle l:=0 \;|\; E_1[f\,()] \rangle \) and \(\langle \emptyset \;|\; E_2[f\,()] \rangle \) with \(E_1 \mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}\square ;l:=1;f\,();!l\) and \(F_1 \mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}\square ;f\,();1\). Ignoring the identical unit arguments (using \(\mathsf {refl}\)), we need \(\{ (v, w) \}, (E_1, F_1) \mathop {{:}{:}}\odot \vdash l:=0 \mathrel {\mathcal R} \emptyset \); from that point, we can either test \(v\) and \(w\) again, resulting into an extra pair \((E_1, F_1)\) on the stack, or run \(\langle l:=0 \;|\; E_1[g] \rangle \) and \(\langle \emptyset \;|\; F_1[g] \rangle \) for a fresh g instead.
In the latter case, we get \(\langle l:=1 \;|\; E_2[g\,()] \rangle \) and \(\langle \emptyset \;|\; F_2[g\,()] \rangle \), with \(E_2 \mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}\square ;!l\) and \(F_2 \mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}\square ;1\), so we want \(\{ (v, w) \}, (E_2, F_2) \mathop {{:}{:}}\odot \vdash l:=1 \mathrel {\mathcal R} \emptyset \) (ignoring again the units). From there, testing \(v\) and \(w\) produces \(\{ (v, w) \}, (E_1, F_1)\,\mathop {{:}{:}}\,(E_2, F_2) \mathop {{:}{:}}\odot \vdash l:=0 \mathrel {\mathcal R} \emptyset \), while executing \(\langle l:=1 \;|\; E_2[x] \rangle \) and \(\langle \emptyset \;|\; F_2[x] \rangle \) for a fresh \(x\) gives us \(\langle l:=1 \;|\; 1 \rangle \) and \(\langle \emptyset \;|\; 1 \rangle \). This analysis suggests that \(\mathrel {\mathcal R}\) should be composed only of judgments of the form \( \{(v, w) \}, \varSigma \vdash l:=n \mathrel {\mathcal R} \emptyset \) such that \(n \in \{ 0, 1\}\) and
-
\(\varSigma \) is an arbitrary stack composed only of pairs \((E_1, F_1)\) or \((E_2, F_2)\);
-
if \(\varSigma = (E_2, F_2) \mathop {{:}{:}}\varSigma '\), then \(n=1\).
We can check that such a candidate is a bisimulation, and it ensures that when \(l\) is read (when \(E_2\) is executed), it contains the value 1.
Example 8
As a variation on the awkward example, let
We show that \(\langle \emptyset \;|\; \mathsf {new~} l := 1 \mathsf {~in~} v \rangle \) and \(\langle \emptyset \;|\; w \rangle \) are bisimilar. Let \(E\mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}\square ;l:=!l-1;!l> 0\) and \(F\mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}\square ;\textsf {true}\). We write \((E, F)^n\) for the stack \(\odot \) if \(n=0\) and \((E, F)\,\mathop {{:}{:}}\,(E, F)^{n-1}\) otherwise. Then the candidate \(\mathrel {\mathcal R}\) verifying \( \{(v, w)\}, (E, F)^n \vdash l:=n+1 \mathrel {\mathcal R} \emptyset \) for any n is a bisimulation. Indeed, running \(v\) and \(w\) increases the value stored in \(l\) and adds a pair \((E, F)\) on the stack. If \(n > 0\), we can run a copy of \(E\) and \(F\), thus decreasing the value in \(l\) by 1, and then returning \(\textsf {true}\) in both cases.
Example 9
This deferred divergence example comes from Dreyer et al. [5]. Let

We prove that \(\mathsf {new~} l := \textsf {false} \mathsf {~in~} \mathsf {new~} k := \textsf {false} \mathsf {~in~} v_2\) is equivalent to \(w_2\). Informally, if f in \(w_2\) applies its argument \(w_1\), the term diverges. Divergence also happens in \(v_2\) but in a delayed fashion, as \(v_1\) first sets \(k\) to \(\textsf {true}\), and the continuation  then diverges. Similarly, if f stores \(w_1\) or \(v_1\) to later apply it, then divergence also occurs in both cases: in that case \(t\) sets \(l\) to \(\textsf {true}\), and when \(v_1\) is later applied, it diverges.
then diverges. Similarly, if f stores \(w_1\) or \(v_1\) to later apply it, then divergence also occurs in both cases: in that case \(t\) sets \(l\) to \(\textsf {true}\), and when \(v_1\) is later applied, it diverges.
To build a candidate \(\mathrel {\mathcal R}\), we execute \(\langle l:=\textsf {false}; k:=\textsf {false} \;|\; v_2 \,f \rangle \) and \(\langle \emptyset \;|\; w_2 \,f \rangle \) for a fresh f, which gives us \(\langle l:=\textsf {false}; k:=\textsf {false} \;|\; E[f \,v_1] \rangle \) and \(\langle \emptyset \;|\; F[f \,w_1] \rangle \) with \(E\mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}\square ;t\) and \(F\mathrel {{\mathop {=}\limits ^{\mathsf {def}}}}\square ;\lambda y.y\). We consider \(\{ (v_2, w_2), (v_1, w_1) \}, (E, F) \mathop {{:}{:}}\emptyset \vdash l:=\textsf {false}; k:=\textsf {false} \mathrel {\mathcal R} \emptyset \), for which we have several checks to do. The interesting one is running \(\langle l:=\textsf {false}; k:=\textsf {false} \;|\; v_1\,x \rangle \) and \(\langle \emptyset \;|\; w_1\,x \rangle \), as we get \(\langle l:=\textsf {false}; k:=\textsf {true} \;|\; \lambda y.y \rangle \) and \(\langle \emptyset \;|\; \varOmega \rangle \). In that case, we are showing that the stack contains divergence, by establishing that \(\{v_2, v_1, \lambda y.y\}, E\mathop {{:}{:}}\emptyset \vdash l:=\textsf {false}; k:=\textsf {true} \mathop {\in }{\mathrel {\mathcal R} \uparrow }\), and indeed, we have \(\langle l:=\textsf {false}; k:=\textsf {true} \;|\; E[x] \rangle \mathrel {\mathrel \rightarrow ^*}\langle l:=\textsf {false}; k:=\textsf {true} \;|\; \varOmega \rangle \) for a fresh \(x\). In the end, the relation \(\mathrel {\mathcal R}\) verifying
for all n is a bisimulation up to \(\mathsf {refl}\) and \(\mathsf {red}\).
4 Related Work and Conclusion
Related Work. As pointed out in Sect. 1, the other bisimilarities defined for state either feature universal quantification over testing arguments [9, 12, 17, 19], or are complete only for a more expressive language [18]. Kripke logical relations [1, 5] also involve quantification over arguments when testing terms of a functional type. Finally, denotational models [10, 13] can also be used to prove program equivalence, by showing that the denotations of two terms are equal. However, computing such denotations is difficult in general, and the automation of this task is so far restricted to a language with first-order references [14].
The work most closely related to ours is Jaber and Tabareau’s Kripke Open Bisimulation (KOB) [6]. A KOB tests functional terms with fresh variables and not with related values like a regular logical relation would do. To relate two given configurations, one has to provide a World Transition System (WTS) which states the invariants the heaps of the configurations should satisfy and how to go from one invariant to the other during the evaluation. Similarly, the bisimulations for the examples of Sect. 3.4 state properties which could be seen as invariants about the stores at different points of the evaluation.
The difficulty for KOB as well as with our bisimilarity is to come up with the right invariants about the heaps, expressed either as a WTS or as a bisimulation. We believe that choosing a technique over the other is just a matter of preference, depending on whether one is more comfortable with game semantics or with coinduction. It would be interesting to see if there is a formal correspondence between KOB and our bisimilarity; we leave this question as a future work.
Conclusion. We define a sound and complete normal-form bisimilarity for higher-order local state, with an environment to be able to run terms in different stores. We distinguish in the environment values which should be tested several times from the contexts which should be executed only once. The other difficulty is to relate deferred and regular diverging terms, which is taken care of by the specific judgments about divergence. The lack of quantification over arguments make the bisimulation proofs quite simple.
A future work would be to make these proofs even simpler by defining appropriate up-to techniques. The techniques we use in Sect. 3.3 to prove soundness turn out to be not that useful when establishing the equivalences of Sect. 3.4, except for trivial ones such as up to reduction or reflexivity. The difficulty in defining the candidate relations for the examples of Sect. 3.4 is in finding the right property relating the stack \(\varSigma \) to the store, so maybe an up-to technique could make this task easier.
As pointed out in Sect. 1, our results can be seen as an indication of what kind of additional infrastructure in a complete normal-form bisimilarity is required when the considered syntactic theory becomes less discriminative—in our case, when control operators vanish from the picture, and mutable state is the only extension of the \(\lambda \)-calculus. A question one could then ask is whether we can find a less expressive calculus—maybe the plain \(\lambda \)-calculus itself—for which a suitably enhanced normal-form bisimilarity is still complete.
References
Ahmed, A., Dreyer, D., Rossberg, A.: State-dependent representation independence. In: Pierce, B.C. (ed.) Proceedings of the Thirty-Fifth Annual ACM Symposium on Principles of Programming Languages, pp. 340–353. ACM Press, January 2009
Aristizábal, A., Biernacki, D., Lenglet, S., Polesiuk, P.: Environmental bisimulations for delimited-control operators with dynamic prompt generation. Logical Methods Comput. Sci. 13(3) 2017
Biernacki, D., Lenglet, S., Polesiuk, P.: Proving soundness of extensional normal-form bisimilarities. In: Silva, A. (ed.) Proceedings of the 33rd Annual Conference on Mathematical Foundations of Programming Semantics (MFPS XXXIII), Ljubljana, Slovenia. Electronic Notes in Theoretical Computer Science, vol. 336, pp. 41–56, June 2017
Biernacki, D., Lenglet, S., Polesiuk, P.: A complete normal-form bisimilarity for state. Research report RR-9251, Inria, Nancy, France, January 2019
Dreyer, D., Neis, G., Birkedal, L.: The impact of higher-order state and control effects on local relational reasoning. J. Funct. Program. 22(4–5), 477–528 (2012)
Jaber, G., Tabareau, N.: Kripke open bisimulation – a marriage of game semantics and operational techniques. In: Feng, X., Park, S. (eds.) APLAS 2015. LNCS, vol. 9458, pp. 271–291. Springer, Cham (2015)
Jagadeesan, R., Pitcher, C., Riely, J.: Open bisimulation for aspects. Trans. Aspect-Oriented Softw. Dev. 5, 72–132 (2009)
Koutavas, V., Levy, P.B., Sumii, E.: From applicative to environmental bisimulation. In: Mislove, M., Ouaknine, J. (eds.) Proceedings of the 27th Annual Conference on Mathematical Foundations of Programming Semantics (MFPS XXVII), Pittsburgh, PA, USA. ENTCS, vol. 276, pp. 215–235, May 2011
Koutavas, V., Wand, M.: Small bisimulations for reasoning about higher-order imperative programs. In: Morrisett, J.G., Jones, S.L.P. (eds.) POPL 2006, Charleston, SC, USA, pp. 141–152. ACM Press (2006)
Laird, J.: A fully abstract trace semantics for general references. In: Arge, L., Cachin, C., Jurdziński, T., Tarlecki, A. (eds.) ICALP 2007. LNCS, vol. 4596, pp. 667–679. Springer, Heidelberg (2007)
Lassen, S.B.: Eager normal form bisimulation. In: Panangaden, P. (ed.) LICS 2005, Chicago, IL, pp. 345–354. IEEE Computer Society Press (2005)
Madiot, J.-M., Pous, D., Sangiorgi, D.: Bisimulations up-to: beyond first-order transition systems. In: Baldan, P., Gorla, D. (eds.) CONCUR 2014. LNCS, vol. 8704, pp. 93–108. Springer, Heidelberg (2014)
Murawski, A.S., Tzevelekos, N.: Game semantics for good general references. In: Proceedings of the 26th Annual IEEE Symposium on Logic in Computer Science, LICS 2011, pp. 75–84. IEEE Computer Society, June 2011
Murawski, A.S., Tzevelekos, N.: Algorithmic games for full ground references. Formal Methods Syst. Des. 52(3), 277–314 (2018)
Pitts, A., Stark, I.: Operational reasoning for functions with local state. In: Gordon, A., Pitts, A. (eds.) Higher Order Operational Techniques in Semantics, pp. 227–273. Publications of the Newton Institute, Cambridge University Press (1998)
Sangiorgi, D.: The lazy lambda calculus in a concurrency scenario. In: Scedrov, A. (ed.) LICS 1992, Santa Cruz, California, pp. 102–109. IEEE Computer Society (1992)
Sangiorgi, D., Kobayashi, N., Sumii, E.: Environmental bisimulations for higher-order languages. ACM Trans. Program. Lang. Syst. 33(1), 1–69 (2011)
Støvring, K., Lassen, S.B.: A complete, co-inductive syntactic theory of sequential control and state. In: Felleisen, M. (ed.) SIGPLAN Notices, POPL 2007, Nice, France, vol. 42, no. 1, pp. 161–172. ACM Press (2007)
Sumii, E.: A complete characterization of observational equivalence in polymorphic \(\lambda \)-calculus with general references. In: Grädel, E., Kahle, R. (eds.) CSL 2009. LNCS, vol. 5771, pp. 455–469. Springer, Heidelberg (2009)
Acknowledgements
We thank Guilhem Jaber and the anonymous reviewers for their comments. This work was supported by the National Science Centre, Poland, grant no. 2014/15/B/ST6/00619 and by COST Action EUTypes CA15123.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Biernacki, D., Lenglet, S., Polesiuk, P. (2019). A Complete Normal-Form Bisimilarity for State. In: Bojańczyk, M., Simpson, A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2019. Lecture Notes in Computer Science(), vol 11425. Springer, Cham. https://doi.org/10.1007/978-3-030-17127-8_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-17127-8_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17126-1
Online ISBN: 978-3-030-17127-8
eBook Packages: Computer ScienceComputer Science (R0)





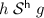 , and
, and 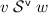 ;
;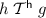 ,
, 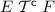 , and
, and 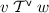 , or
, or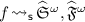 ;
;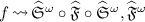 .
.
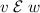 , then
, then 
