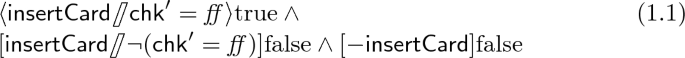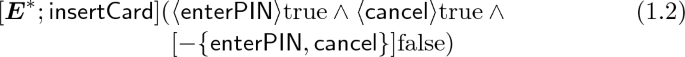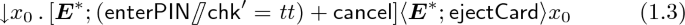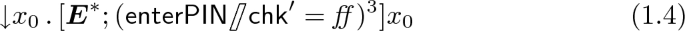Abstract
We propose \(\mathcal {E}^{\downarrow } \)-logic as a formal foundation for the specification and development of event-based systems with local data states. The logic is intended to cover a broad range of abstraction levels from abstract requirements specifications up to constructive specifications. Our logic uses diamond and box modalities over structured actions adopted from dynamic logic. Atomic actions are pairs  where e is an event and \(\psi \) a state transition predicate capturing the allowed reactions to the event. To write concrete specifications of recursive process structures we integrate (control) state variables and binders of hybrid logic. The semantic interpretation relies on event/data transition systems; specification refinement is defined by model class inclusion. For the presentation of constructive specifications we propose operational event/data specifications allowing for familiar, diagrammatic representations by state transition graphs. We show that \(\mathcal {E}^{\downarrow } \)-logic is powerful enough to characterise the semantics of an operational specification by a single \(\mathcal {E}^{\downarrow } \)-sentence. Thus the whole development process can rely on \(\mathcal {E}^{\downarrow } \)-logic and its semantics as a common basis. This includes also a variety of implementation constructors to support, among others, event refinement and parallel composition.
where e is an event and \(\psi \) a state transition predicate capturing the allowed reactions to the event. To write concrete specifications of recursive process structures we integrate (control) state variables and binders of hybrid logic. The semantic interpretation relies on event/data transition systems; specification refinement is defined by model class inclusion. For the presentation of constructive specifications we propose operational event/data specifications allowing for familiar, diagrammatic representations by state transition graphs. We show that \(\mathcal {E}^{\downarrow } \)-logic is powerful enough to characterise the semantics of an operational specification by a single \(\mathcal {E}^{\downarrow } \)-sentence. Thus the whole development process can rely on \(\mathcal {E}^{\downarrow } \)-logic and its semantics as a common basis. This includes also a variety of implementation constructors to support, among others, event refinement and parallel composition.
A. Madeira—Supported by ERDF through COMPETE 2020 and by National Funds through FCT with POCI-01-0145-FEDER-016692 and UID/MAT/04106/2019, in a contract foreseen in nos. 4–6 of art. 23 of the DL 57/2016, changed by DL 57/2017.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Event-based systems are an important kind of software systems which are open to the environment to react to certain events. A crucial characteristics of such systems is that not any event can (or should) be expected at any time. Hence the control flow of the system is significant and should be modelled by appropriate means. On the other hand components administrate data which may change upon the occurrence of an event. Thus also the specification of admissible data changes caused by events plays a major role.
There is quite a lot of literature on modelling and specification of event-based systems. Many approaches, often underpinned by graphical notations, provide formalisms aiming at being constructive enough to suggest particular designs or implementations, like e.g., Event-B [1, 7], symbolic transition systems [17], and UML behavioural and protocol state machines [12, 16]. On the other hand, there are logical formalisms to express desired properties of event-based systems. Among them are temporal logics integrating state and event-based styles [4], and various kinds of modal logics involving data, like first-order dynamic logic [10] or the modal \(\mu \)-calculus with data and time [9]. The gap between logics and constructive specification is usually filled by checking whether the model of a constructive specification satisfies certain logical formulae.
In this paper we are interested in investigating a logic which is capable to express properties of event/data-based systems on various abstraction levels in a common formalism. For this purpose we follow ideas of [15], but there data states, effects of events on them and constructive operational specifications (see below) were not considered. The advantage of an expressive logic is that we can split the transition from system requirements to system implementation into a series of gradual refinement steps which are more easy to understand, to verify, and to adjust when certain aspects of the system are to be changed or when a product line of similar products has to be developed.
To that end we propose \(\mathcal {E}^{\downarrow } \)-logic, a dynamic logic enriched with features of hybrid logic. The dynamic part uses diamond and box modalities over structured actions. Atomic actions are of the form  with e an event and \(\psi \) a state transition predicate specifying the admissible effects of e on the data. Using sequential composition, union, and iteration we obtain complex actions that, in connection with the modalities, can be used to specify required and forbidden behaviour. In particular, if E is a finite set of events, though data is infinite we are able to capture all reachable states of the system and to express safety and liveness properties. But \(\mathcal {E}^{\downarrow } \)-logic is also powerful enough to specify concrete, recursive process structures by integrating state variables and binders from hybrid logic [6] with the subtle difference that our state variables are used to denote control states only. We show that the dynamic part of the logic is bisimulation invariant while the hybrid part, due to the ability to bind names to states, is not.
with e an event and \(\psi \) a state transition predicate specifying the admissible effects of e on the data. Using sequential composition, union, and iteration we obtain complex actions that, in connection with the modalities, can be used to specify required and forbidden behaviour. In particular, if E is a finite set of events, though data is infinite we are able to capture all reachable states of the system and to express safety and liveness properties. But \(\mathcal {E}^{\downarrow } \)-logic is also powerful enough to specify concrete, recursive process structures by integrating state variables and binders from hybrid logic [6] with the subtle difference that our state variables are used to denote control states only. We show that the dynamic part of the logic is bisimulation invariant while the hybrid part, due to the ability to bind names to states, is not.
An axiomatic specification \( Sp = (\varSigma , Ax )\) in \(\mathcal {E}^{\downarrow } \) is given by an event/data signature \(\varSigma = (E, A)\), with a set E of events and a set A of attributes to model local data states, and a set of \(\mathcal {E}^{\downarrow } \)-sentences \( Ax \), called axioms, expressing requirements. For the semantic interpretation we use event/data transition systems (edts). Their states are reachable configurations \(\gamma = (c, \omega )\) where c is a control state, recording the current state of execution, and \(\omega \) is a local data state, i.e., a valuation of the attributes. Transitions between configurations are labelled by events. The semantics of a specification \( Sp \) is “loose” in the sense that it consists of all edts satisfying the axioms of the specification. Such structures are called models of \( Sp \). Loose semantics allows us to define a simple refinement notion: \( Sp _1\) refines to \( Sp _2\) if the model class of \( Sp _2\) is included in the model class of \( Sp _1\). We may also say that \( Sp _2\) is an implementation of \( Sp _1\).
Our refinement process starts typically with axiomatic specifications whose axioms involve only the dynamic part of the logic. Hybrid features will successively be added in refinements when specifying more concrete behaviours, like loops. Aiming at a concrete design, the use of an axiomatic specification style may, however, become cumbersome since we have to state explicitly also all negative cases, what the system should not do. For a convenient presentation of constructive specifications we propose operational event/data specifications, which are a kind of symbolic transition systems equipped again with a model class semantics in terms of edts. We will show that \(\mathcal {E}^{\downarrow } \)-logic, by use of the hybrid binder, is powerful enough to characterise the semantics of an operational specification. Therefore we have not really left \(\mathcal {E}^{\downarrow } \)-logic when refining axiomatic by operational specifications. Moreover, since several constructive notations in the literature, including (essential parts of) Event-B, symbolic transition systems, and UML protocol state machines, can be expressed as operational specifications, \(\mathcal {E}^{\downarrow } \)-logic provides a logical umbrella under which event/data-based systems can be developed.
In order to consider more complex refinements we take up an idea of Sannella and Tarlecki [18, 19] who have proposed the notion of constructor implementation. This is a generic notion applicable to specification formalisms based on signatures and semantic structures for signatures. As both are available in the context of \(\mathcal {E}^{\downarrow } \)-logic, we complement our approach by introducing a couple of constructors, among them event refinement and parallel composition. For the latter we provide a useful refinement criterion relying on a relationship between syntactic and semantic parallel composition. The logic and the use of the implementation constructors will be illustrated by a running example.
Hereafter, in Sect. 2, we introduce syntax and semantics of \(\mathcal {E}^{\downarrow } \)-logic. In Sect. 3, we consider axiomatic as well as operational specifications and demonstrate the expressiveness of \(\mathcal {E}^{\downarrow } \)-logic. Refinement of both types of specifications using several implementation constructors is considered in Sect. 4. Section 5 provides some concluding remarks. Proofs of theorems and facts can be found in [11].
2 A Hybrid Dynamic Logic for Event/Data Systems
We propose the logic \(\mathcal {E}^{\downarrow } \) to specify and reason about event/data-based systems. \(\mathcal {E}^{\downarrow } \)-logic is an extension of the hybrid dynamic logic considered in [15] by taking into account changing data. Therefore, we first summarise our underlying notions used for the treatment of data. We then introduce the syntax and semantics of \(\mathcal {E}^{\downarrow } \) with its hybrid and dynamic logic features applied to events and data.
2.1 Data States
We assume given a universe \(\mathcal {D}\) of data values. A data signature is given by a set A of attributes. An A-data state \(\omega \) is a function \(\omega : A \rightarrow \mathcal {D}\). We denote by \(\varOmega (A)\) the set of all A-data states. For any data signature A, we assume given a set \(\varPhi (A)\) of state predicates to be interpreted over single A-data states, and a set \(\varPsi (A)\) of transition predicates to be interpreted over pairs of pre- and post-A-data states. The concrete syntax of state and transition predicates is of no particular importance for the following. For an attribute \(a \in A\), a state predicate may be \(a > 0\); and a transition predicate e.g. \(a' = a + 1\), where a refers to the value of attribute a in the pre-data state and \(a'\) to its value in the post-data state. Still, both types of predicates are assumed to contain \(\mathrm {true}\) and to be closed under negation (written \(\lnot \)) and disjunction (written \(\vee \)); as usual, we will then also use \(\mathrm {false}\), \(\wedge \), etc. Furthermore, we assume for each \(A_0 \subseteq A\) a transition predicate \(\mathrm {id}_{A_0} \in \varPsi (A)\) expressing that the values of attributes in \(A_0\) are the same in pre- and post-A-data states.
We write \(\omega \models ^{\mathcal {D}}_{A} \varphi \) if \(\varphi \in \varPhi (A)\) is satisfied in data state \(\omega \); and \((\omega _1, \omega _2) \models ^{\mathcal {D}}_{A} \psi \) if \(\psi \in \varPsi (A)\) is satisfied in the pre-data state \(\omega _1\) and post-data state \(\omega _2\). In particular, \((\omega _1, \omega _2) \models ^{\mathcal {D}}_{A} \mathrm {id}_{A_0}\) if, and only if, \(\omega _1(a_0) = \omega _2(a_0)\) for all \(a_0 \in A_0\).
2.2 \(\mathcal {E}^{\downarrow } \)-Logic
Definition 1
An event/data signature (ed signature, for short) \(\varSigma = (E, A)\) consists of a finite set of events E and a data signature A. We write \(E(\varSigma )\) for E and \(A(\varSigma )\) for A. We also write \(\varOmega (\varSigma )\) for \(\varOmega (A(\varSigma ))\), \(\varPhi (\varSigma )\) for \(\varPhi (A(\varSigma ))\), and \(\varPsi (\varSigma )\) for \(\varPsi (A(\varSigma ))\). The class of ed signatures is denoted by \( Sig ^{\mathcal {E}^{\downarrow }}\).
Any ed signature \(\varSigma \) determines a class of semantic structures, the event/data transition systems which are reachable transition systems with sets of initial states and events as labels on transitions. The states are pairs \(\gamma = (c, \omega )\), called configurations, where c is a control state recording the current execution state and \(\omega \) is an \(A(\varSigma )\)-data state; we write \(c(\gamma )\) for c and \(\omega (\gamma )\) for \(\omega \).
Definition 2
A \(\varSigma \)-event/data transition system (\(\varSigma \)-edts, for short) \(M = (\varGamma , R, \varGamma _0)\) over an ed signature \(\varSigma \) consists of a set of configurations \(\varGamma \subseteq C \times \varOmega (\varSigma )\) for a set of control states C; a family of transition relations \(R = (R_e \subseteq \varGamma \times \varGamma )_{e \in E(\varSigma )}\); and a non-empty set of initial configurations \(\varGamma _0 \subseteq \{ c_0 \} \times \varOmega _0\) for an initial control state \(c_0 \in C\) and a set of initial data states \(\varOmega _0 \subseteq \varOmega (\varSigma )\) such that \(\varGamma \) is reachable via R, i.e., for all \(\gamma \in \varGamma \) there are \(\gamma _0 \in \varGamma _0\), \(n \ge 0\), \(e_1, \ldots , e_n \in E(\varSigma )\), and \((\gamma _i, \gamma _{i+1}) \in R_{e_{i+1}}\) for all \(0 \le i < n\) with \(\gamma _n = \gamma \). We write \(\varGamma (M)\) for \(\varGamma \), C(M) for C, \(R(M)\) for R, \(c_0(M)\) for \(c_0\), \(\varOmega _0(M)\) for \(\varOmega _0\), and \(\varGamma _0(M)\) for \(\varGamma _0\). The class of \(\varSigma \)-edts is denoted by \( Edts ^{\mathcal {E}^{\downarrow }}(\varSigma )\).
Atomic actions are given by expressions of the form  with e an event and \(\psi \) a state transition predicate. The intuition is that the occurrence of the event e causes a state transition in accordance with \(\psi \), i.e., the pre- and post-data states satisfy \(\psi \), and \(\psi \) specifies the possible effects of e. Following the ideas of dynamic logic we also use complex, structured actions formed over atomic actions by union, sequential composition and iteration. All kinds of actions over an ed signature \(\varSigma \) are called \(\varSigma \)-event/data actions (\(\varSigma \)-ed actions, for short). The set \(\varLambda (\varSigma )\) of \(\varSigma \)-ed actions is defined by the grammar
with e an event and \(\psi \) a state transition predicate. The intuition is that the occurrence of the event e causes a state transition in accordance with \(\psi \), i.e., the pre- and post-data states satisfy \(\psi \), and \(\psi \) specifies the possible effects of e. Following the ideas of dynamic logic we also use complex, structured actions formed over atomic actions by union, sequential composition and iteration. All kinds of actions over an ed signature \(\varSigma \) are called \(\varSigma \)-event/data actions (\(\varSigma \)-ed actions, for short). The set \(\varLambda (\varSigma )\) of \(\varSigma \)-ed actions is defined by the grammar

where \(e \in E(\varSigma )\) and \(\psi \in \varPsi (\varSigma )\). We use the following shorthand notations for actions: For a subset \(F = \{ e_1, \ldots , e_k \} \subseteq E(\varSigma )\), we use the notation F to denote the complex action  and \(-F\) to denote the action \(E(\varSigma ) \setminus F\). For the action \(E(\varSigma )\) we will write \(\varvec{E}\). For \(e \in E(\varSigma )\), we use the notation e to denote the action
and \(-F\) to denote the action \(E(\varSigma ) \setminus F\). For the action \(E(\varSigma )\) we will write \(\varvec{E}\). For \(e \in E(\varSigma )\), we use the notation e to denote the action  and \(-e\) to denote the action \(\varvec{E} \setminus \{ e \}\). Hence, if \(E(\varSigma ) = \{ e_1, \ldots , e_n\}\) and \(e_i \in E(\varSigma )\), the action \(-e_i\) stands for
and \(-e\) to denote the action \(\varvec{E} \setminus \{ e \}\). Hence, if \(E(\varSigma ) = \{ e_1, \ldots , e_n\}\) and \(e_i \in E(\varSigma )\), the action \(-e_i\) stands for  .
.
The actions \(\varLambda (\varSigma )\) are interpreted over a \(\varSigma \)-edts M as the family of relations \((R(M)_{\lambda } \subseteq \varGamma (M) \times \varGamma (M))_{\lambda \in \varLambda (\varSigma )}\) defined by
-
 ,
, -
\(R(M)_{\lambda _1 + \lambda _2} = R(M)_{\lambda _1} \cup R(M)_{\lambda _2}\), i.e., union of relations,
-
\(R(M)_{\lambda _1 ; \lambda _2} = R(M)_{\lambda _1} ; R(M)_{\lambda _2}\), i.e., sequential composition of relations,
-
\(R(M)_{\lambda ^*} = (R(M)_{\lambda })^*\), i.e., reflexive-transitive closure of relations.
To define the event/data formulae of \(\mathcal {E}^{\downarrow } \) we assume given a countably infinite set X of control state variables which are used in formulae to denote the control part of a configuration. They can be bound by the binder operator \( \downarrow x\) and accessed by the jump operator \( @ x\) of hybrid logic. The dynamic part of our logic is due to the modalities which can be formed over any ed action over a given ed signature. \(\mathcal {E}^{\downarrow } \) thus retains from hybrid logic the use of binders, but omits free nominals. Thus sentences of the logic become restricted to express properties of configurations reachable from the initial ones.
Definition 3
The set \(\mathrm {Frm}^{\mathcal {E}^{\downarrow }}(\varSigma )\) of \(\varSigma \)-ed formulae over an ed signature \(\varSigma \) is given by
where \(\varphi \in \varPhi (\varSigma )\), \(x \in X\), and \(\lambda \in \varLambda (\varSigma )\). We write \([\lambda ] \varrho \) for \(\lnot \langle \lambda \rangle \lnot \varrho \) and we use the usual boolean connectives as well as the constant \(\mathrm {false}\) to denote \(\lnot \mathrm {true}\).Footnote 1 The set \(\mathrm {Sen}^{\mathcal {E}^{\downarrow }}(\varSigma )\) of \(\varSigma \)-ed sentences consists of all \(\varSigma \)-ed formulae without free variables, where the free variables are defined as usual with \( \downarrow x\) being the unique operator binding variables.
Given an ed signature \(\varSigma \) and a \(\varSigma \)-edts M, the satisfaction of a \(\varSigma \)-ed formula \(\varrho \) is inductively defined w.r.t. valuations \(v : X \rightarrow C(M)\), mapping variables to control states, and configurations \(\gamma \in \varGamma (M)\):
-
\(M, v, \gamma \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \varphi \) iff \(\omega (\gamma ) \models ^{\mathcal {D}}_{A(\varSigma )} \varphi \);
-
\(M, v, \gamma \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } x\) iff \(c(\gamma ) = v(x)\);
-
\(M, v, \gamma \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \downarrow x \,.\, \varrho \) iff \(M, v\{ x \mapsto c(\gamma ) \}, \gamma \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \varrho \);
-
\(M, v, \gamma \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } @ x \,.\, \varrho \) iff \(M, v, \gamma ' \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \varrho \) for all \(\gamma ' \in \varGamma (M)\) with \(c(\gamma ') = v(x)\);
-
\(M, v, \gamma \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \langle \lambda \rangle \varrho \) iff \(M, v, \gamma ' \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \varrho \) for some \(\gamma ' \in \varGamma (M)\) with \((\gamma , \gamma ') \in R(M)_{\lambda }\);
-
\(M, v, \gamma \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \mathrm {true}\) always holds;
-
\(M, v, \gamma \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \lnot \varrho \) iff \(M, v, \gamma \not \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \varrho \);
-
\(M, v, \gamma \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \varrho _1 \vee \varrho _2\) iff \(M, v, \gamma \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \varrho _1\) or \(M, v, \gamma \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \varrho _2\).
If \(\varrho \) is a sentence then the valuation is irrelevant. M satisfies a sentence \(\varrho \in \mathrm {Sen}^{\mathcal {E}^{\downarrow }}(\varSigma )\), denoted by \(M \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \varrho \), if \(M, \gamma _0 \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \varrho \) for all \(\gamma _0 \in \varGamma _0(M)\).
By borrowing the modalities from dynamic logic [9, 10], \(\mathcal {E}^{\downarrow } \) is able to express liveness and safety requirements as illustrated in our running ATM example below. There we use the fact that we can state properties over all reachable states by sentences of the form \([\varvec{E}^*]\varphi \). In particular, deadlock-freedom can be expressed by \([\varvec{E}^*]\langle \varvec{E}\rangle \mathrm {true}\). The logic \(\mathcal {E}^{\downarrow } \), however, is also suited to directly express process structures and, thus, the implementation of abstract requirements. The binder operator is essential for this. For example, we can specify a process which switches a boolean value, denoted by the attribute \(\mathsf {val}\), from \( tt \) to \( ff \) and back by the following sentence:

2.3 Bisimulation and Invariance
Bisimulation is a crucial notion in both behavioural systems specification and in modal logics. On the specification side, it provides a standard way to identify systems with the same behaviour by abstracting the internal specifics of the systems; this is also reflected at the logic side, where bisimulation frequently relates states that satisfy the same formulae. We explore some properties of \(\mathcal {E}^{\downarrow } \) w.r.t. bisimilarity. Let us first introduce the notion of bisimilarity in the context of \(\mathcal {E}^{\downarrow } \):
Definition 4
Let \(M_1, M_2\) be \(\varSigma \)-edts. A relation \(B \subseteq \varGamma (M_1) \times \varGamma (M_2)\) is a bisimulation relation between \(M_1\) and \(M_2\) if for all \((\gamma _1, \gamma _2) \in B\) the following conditions hold:
- (atom):
-
for all \(\varphi \in \varPhi (\varSigma )\), \(\omega (\gamma _1) \models ^{\mathcal {D}}_{A(\varSigma )} \varphi \) iff \(\omega (\gamma _2) \models ^{\mathcal {D}}_{A(\varSigma )} \varphi \);
- (zig):
-
for all
 and for all \(\gamma _1' \in \varGamma (M_1)\) with
and for all \(\gamma _1' \in \varGamma (M_1)\) with  , there is a \(\gamma _2' \in \varGamma (M_2)\) such that
, there is a \(\gamma _2' \in \varGamma (M_2)\) such that  and \((\gamma _1', \gamma _2') \in B\);
and \((\gamma _1', \gamma _2') \in B\); - (zag):
-
for all
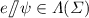 and for all \(\gamma _2' \in \varGamma (M_2)\) with
and for all \(\gamma _2' \in \varGamma (M_2)\) with  , there is a \(\gamma _1' \in \varGamma (M_1)\) such that
, there is a \(\gamma _1' \in \varGamma (M_1)\) such that  and \((\gamma _1', \gamma _2') \in B\).
and \((\gamma _1', \gamma _2') \in B\).
\(M_1\) and \(M_2\) are bisimilar, in symbols \(M_1 \sim M_2\), if there exists a bisimulation relation \(B \subseteq \varGamma (M_1) \times \varGamma (M_2)\) between \(M_1\) and \(M_2\) such that
-
(init)
for any \(\gamma _1 \in \varGamma _0(M_1)\), there is a \(\gamma _2 \in \varGamma _0(M_2)\) such that \((\gamma _1,\gamma _2)\in B\) and for any \(\gamma _2 \in \varGamma _0(M_2)\), there is a \(\gamma _1 \in \varGamma _0(M_1)\) such that \((\gamma _1,\gamma _2)\in B\).
Now we are able to establish a Hennessy-Milner like correspondence for a fragment of \(\mathcal {E}^{\downarrow } \). Let us call hybrid-free sentences of \(\mathcal {E}^{\downarrow } \) the formulae obtained by the grammar
Theorem 1
Let \(M_1, M_2\) be bisimilar \(\varSigma \)-edts. Then \(M_1 \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \varrho \) iff \(M_2 \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \varrho \) for all hybrid-free sentences \(\varrho \).
The converse of Theorem 1 does not hold, in general, and the usual image-finiteness assumption has to be imposed: A \(\varSigma \)-edts M is image-finite if, for all \(\gamma \in \varGamma (M)\) and all \(e \in E(\varSigma )\), the set \(\{ \gamma ' \mid (\gamma , \gamma ') \in R(M)_e \}\) is finite. Then:
Theorem 2
Let \(M_1, M_2\) be image-finite \(\varSigma \)-edts and \(\gamma _1 \in \varGamma (M_1)\), \(\gamma _2 \in \varGamma (M_2)\) such that \(M_1,\gamma _1\models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \varrho \) iff \(M_2,\gamma _2 \models ^{\mathcal {E}^{\downarrow }}_{\varSigma } \varrho \) for all hybrid-free sentences \(\varrho \). Then there exists a bisimulation B between \(M_1\) and \(M_2\) such that \((\gamma _1,\gamma _2)\in B\).
3 Specifications of Event/Data Systems
3.1 Axiomatic Specifications
Sentences of \(\mathcal {E}^{\downarrow } \)-logic can be used to specify properties of event/data systems and thus to write system specifications in an axiomatic way.
Definition 5
An axiomatic ed specification \( Sp = (\varSigma ( Sp ), Ax ( Sp ))\) in \(\mathcal {E}^{\downarrow } \) consists of an ed signature \(\varSigma ( Sp ) \in Sig ^{\mathcal {E}^{\downarrow }}\) and a set of axioms \( Ax ( Sp ) \subseteq \mathrm {Sen}^{\mathcal {E}^{\downarrow }}(\varSigma ( Sp ))\).
The semantics of \( Sp \) is given by the pair \((\varSigma ( Sp ), \mathrm {Mod}( Sp ))\) where \(\mathrm {Mod}( Sp ) = \{ M \in Edts ^{\mathcal {E}^{\downarrow }}(\varSigma ( Sp )) \mid M \models ^{\mathcal {E}^{\downarrow }}_{\varSigma ( Sp )} Ax ( Sp ) \}\). The edts in \(\mathrm {Mod}( Sp )\) are called models of \( Sp \) and \(\mathrm {Mod}( Sp )\) is the model class of \( Sp \).
As a direct consequence of Theorem 1 we have:
Corollary 1
The model class of an axiomatic ed specification exclusively expressed by hybrid-free sentences is closed under bisimulation.
This result does not hold for sentences with hybrid features. For instance, consider the specification  : An edts with a single control state \(c_0\) and a loop transition \(R_e= \{ (\gamma _0, \gamma _0) \}\) for \(c(\gamma _0) = c_0\) is a model of \( Sp \). However, this is obviously not the case for its bisimilar edts with two control states \(c_0\) and c and the relation \(R'_e=\{ (\gamma _0, \gamma ), (\gamma , \gamma _0) \}\) with \(c(\gamma _0) = c_0\), \(c(\gamma ) = c\) and \(\omega (\gamma _0) = \omega (\gamma )\).
: An edts with a single control state \(c_0\) and a loop transition \(R_e= \{ (\gamma _0, \gamma _0) \}\) for \(c(\gamma _0) = c_0\) is a model of \( Sp \). However, this is obviously not the case for its bisimilar edts with two control states \(c_0\) and c and the relation \(R'_e=\{ (\gamma _0, \gamma ), (\gamma , \gamma _0) \}\) with \(c(\gamma _0) = c_0\), \(c(\gamma ) = c\) and \(\omega (\gamma _0) = \omega (\gamma )\).
Example 1
As a running example we consider an ATM. We start with an abstract specification \( Sp _0\) of fundamental requirements for its interaction behaviour based on the set of events \(E_0 = \{ \mathsf {insertCard}, \mathsf {enterPIN}, \mathsf {ejectCard}, \mathsf {cancel} \}\)Footnote 2 and on the singleton set of attributes \(A_0 = \{ \mathsf {chk} \}\) where \(\mathsf {chk}\) is boolean valued and records the correctness of an entered PIN. Hence our first ed signature is \(\varSigma _0 = (E_0, A_0)\) and \( Sp _0 = (\varSigma _0, Ax _0)\) where \( Ax _0\) requires the following properties expressed by corresponding axioms (0.1–0.3):
-
“Whenever a card has been inserted, a correct PIN can eventually be entered and also the transaction can eventually be cancelled.”
 (0.1)
(0.1) -
“Whenever either a correct PIN has been entered or the transaction has been cancelled, the card can eventually be ejected.”
 (0.2)
(0.2) -
“Whenever an incorrect PIN has been entered three times in a row, the current card is not returned.” This means that the card is kept by the ATM which is not modelled by an extra event. It may, however, still be possible that another card is inserted afterwards. So an \(\mathsf {ejectCard}\) can only be forbidden as long as no next card is inserted.
 (0.3)
(0.3)where \(\lambda ^n\) abbreviates the n-fold sequential composition \(\lambda ; \ldots ; \lambda \).
The semantics of an axiomatic ed specification is loose allowing usually for many different realisations. A refinement step is therefore understood as a restriction of the model class of an abstract specification. Following the terminology of Sannella and Tarlecki [18, 19], we call a specification refining another one an implementation. Formally, a specification \( Sp '\) is a simple implementation of a specification \( Sp \) over the same signature, in symbols \( Sp \mathrel {\rightsquigarrow } Sp '\), whenever \(\mathrm {Mod}( Sp ) \supseteq \mathrm {Mod}( Sp ')\). Transitivity of the inclusion relation ensures gradual step-by-step development by a series of refinements.
Example 2
We provide a refinement \( Sp _0 \mathrel {\rightsquigarrow } Sp _1\) where \( Sp _1 = (\varSigma _0, Ax _1)\) has the same signature as \( Sp _0\) and \( Ax _1\) are the sentences (1.1–1.4) below; the last two use binders to specify a loop. As is easily seen, all models of \( Sp _1\) must satisfy the axioms of \( Sp _0\).
-
“At the beginning a card can be inserted with the effect that \(\mathsf {chk}\) is set to \( ff \); nothing else is possible at the beginning.”
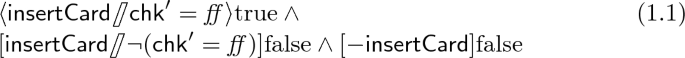
-
“Whenever a card has been inserted, a PIN can be entered (directly afterwards) and also the transaction can be cancelled; but nothing else.”
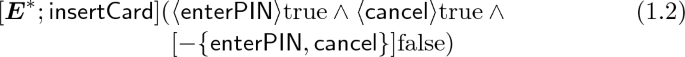
-
“Whenever either a correct PIN has been entered or the transaction has been cancelled, the card can eventually be ejected and the ATM starts from the beginning.”
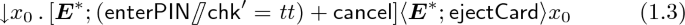
-
“Whenever an incorrect PIN has been entered three times in a row the ATM starts from the beginning.” Hence the current card is kept.
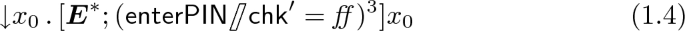
3.2 Operational Specifications
Operational event/data specifications are introduced as a means to specify in a more constructive style the properties of event/data systems. They are not appropriate for writing abstract requirements for which axiomatic specifications are recommended. Though \(\mathcal {E}^{\downarrow } \)-logic is able to specify concrete models, as discussed in Sect. 2, the use of operational specifications allows a graphic representation close to familiar formalisms in the literature, like UML protocol state machines, cf. [12, 16]. As will be shown in Sect. 3.3, finite operational specifications can be characterised by a sentence in \(\mathcal {E}^{\downarrow } \)-logic. Therefore, \(\mathcal {E}^{\downarrow } \)-logic is still the common basis of our development approach. Transitions in an operational specification are tuples \((c, \varphi , e, \psi , c')\) with c a source control state, \(\varphi \) a precondition, e an event, \(\psi \) a state transition predicate specifying the possible effects of the event e, and \(c'\) a target control state. In the semantic models an event must be enabled whenever the respective source data state satisfies the precondition. Thus isolating preconditions has a semantic consequence that is not expressible by transition predicates only. The effect of the event must respect \(\psi \); no other transitions are allowed.
Definition 6
An operational ed specification \(O = (\varSigma , C,T,(c_0, \varphi _0))\) is given by an ed signature \(\varSigma \), a set of control states C, a transition relation specification \(T \subseteq C \times \varPhi (\varSigma ) \times E(\varSigma ) \times \varPsi (\varSigma ) \times C\), an initial control state \(c_0 \in C\), and an initial state predicate \(\varphi _0 \in \varPhi (\varSigma )\), such that C is syntactically reachable, i.e., for every \(c \in C \setminus \{ c_0 \}\) there are \((c_0, \varphi _1, e_1, \psi _1, c_1), \ldots , (c_{n-1}, \varphi _n, e_n,\psi _n,c_n) \in T\) with \(n > 0\) such that \(c_n = c\). We write \(\varSigma (O)\) for \(\varSigma \), etc.
A \(\varSigma \)-edts M is a model of O if \(C(M) = C\) up to a bijective renaming, \(c_0(M) = c_0\), \(\varOmega _0(M) \subseteq \{ \omega \mid \omega \models ^{\mathcal {D}}_{A(\varSigma )} \varphi _0 \}\), and if the following conditions hold:
-
for all \((c, \varphi , e, \psi , c') \in T\) and \(\omega \in \varOmega (A(\varSigma ))\) with \(\omega \models ^{\mathcal {D}}_{A(\varSigma )} \varphi \), there is a \(((c, \omega ),(c', \omega ')) \in R(M)_e\) with \((\omega ,\omega ') \models ^{\mathcal {D}}_{A(\varSigma )} \psi \);
-
for all \(((c, \omega ), (c', \omega ')) \in R(M)_e\) there is a \((c, \varphi , e, \psi , c') \in T\) with \(\omega \models ^{\mathcal {D}}_{A(\varSigma )} \varphi \) and \((\omega ,\omega ') \models ^{\mathcal {D}}_{A(\varSigma )} \psi \).
The class of all models of O is denoted by \(\mathrm {Mod}(O)\). The semantics of O is given by the pair \((\varSigma (O), \mathrm {Mod}(O))\) where \(\varSigma (O) = \varSigma \).
Example 3
We construct an operational ed specification, called \( ATM \), for the ATM example. The signature of \( ATM \) extends the one of \( Sp _1\) (and \( Sp _0\)) by an additional integer-valued attribute \(\mathsf {trls}\) which counts the number of attempts to enter a correct PIN (with the same card). \( ATM \) is graphically presented in Fig. 1. The initial control state is \( Card \), and the initial state predicate is \(\mathrm {true}\). Preconditions are written before the symbol \(\mathbin {\rightarrow }\). If no precondition is explicitly indicated it is assumed to be \(\mathrm {true}\). Due to the extended signature, \( ATM \) is not a simple implementation of \( Sp _1\), and we will only formally justify the implementation relationship in Example 5.
Operational specifications can be composed by a syntactic parallel composition operator which synchronises shared events. Two ed signatures \(\varSigma _1\) and \(\varSigma _2\) are composable if \(A(\varSigma _1) \cap A(\varSigma _2) = \emptyset \). Their parallel composition is given by \(\varSigma _1 \otimes \varSigma _2 = (E(\varSigma _1) \cup E(\varSigma _2), A(\varSigma _1) \cup A(\varSigma _2))\).
Definition 7
Let \(\varSigma _1\) and \(\varSigma _2\) be composable ed signatures and let \(O_1\) and \(O_2\) be operational ed specifications with \(\varSigma (O_1) = \varSigma _1\) and \(\varSigma (O_2) = \varSigma _2\). The parallel composition of \(O_1\) and \(O_2\) is given by the operational ed specification \(O_1 \parallel O_2 = (\varSigma _1 \otimes \varSigma _2,C,T,(c_0, \varphi _0))\) with \(c_0 = (c_0(O_1), c_0(O_2))\), \(\varphi _0 = \varphi _0(O_1) \wedge \varphi _0(O_2)\), and C and T are inductively defined by \(c_0 \in C\) and
-
for \(e_1 \in E(\varSigma _1) \setminus E(\varSigma _2)\), \(c_1, c_1' \in C(O_1)\), and \(c_2 \in C(O_2)\), if \((c_1, c_2) \in C\) and \((c_1, \varphi _1, e_1,\psi _1,c_1') \in T(O_1)\), then \((c_1', c_2) \in C\) and \(((c_1, c_2), \varphi _1, e_1, \psi _1 \wedge \mathrm {id}_{A(\varSigma _2)},(c_1', c_2)) \in T\);
-
for \(e_2 \in E(\varSigma _2) \setminus E(\varSigma _1)\), \(c_2, c_2' \in C(O_2)\), and \(c_1 \in C(O_1)\), if \((c_1, c_2) \in C\) and \((c_2, \varphi _2, e_2,\psi _2,c_2') \in T(O_2)\), then \((c_1, c_2') \in C\) and \(((c_1, c_2), \varphi _2, e_2, \psi _2 \wedge \mathrm {id}_{A(\varSigma _1)},(c_1, c_2')) \in T\);
-
for \(e \in E(\varSigma _1) \cap E(\varSigma _2)\), \(c_1, c_1' \in C(O_1)\), and \(c_2, c_2' \in C(O_2)\), if \((c_1, c_2) \in C\), \((c_1, \varphi _1, e, \psi _1, c_1') \in T(O_1)\), and \((c_2, \varphi _2, e,\psi _2,c_2') \in T(O_2)\), then \((c_1', c_2') \in C\) and \(((c_1, c_2), \varphi _1 \wedge \varphi _2, e, \psi _1 \wedge \psi _2, (c_1', c_2')) \in T\).Footnote 3
3.3 Expressiveness of \(\mathcal {E}^{\downarrow } \)-Logic
We show that the semantics of an operational ed specification O with finitely many control states can be characterised by a single \(\mathcal {E}^{\downarrow }\)-sentence \(\varrho _O\), i.e., an edts M is a model of O iff \(M \models ^{\mathcal {E}^{\downarrow }}_{\varSigma (O)} \varrho _O\). Using Algorithm 1, such a characterising sentence is
where \(c_0 = c_0(O)\) and \(\varphi _0 = \varphi _0(O)\). Algorithm 1 closely follows the procedure in [15] for characterising a finite structure by a sentence of \(\mathcal {D}^{\downarrow } \)-logic. A call \(\mathrm {sen}(c,I, V, B)\) performs a recursive breadth-first traversal through O starting from c, where I holds the unprocessed quadruples \((\varphi , e, \psi , c')\) of transitions outgoing from c, V the remaining states to visit, and B the set of already bound states. The function first requires the existence of each outgoing transition of I, provided its precondition holds, in the resulting formula, binding any newly reached state. Then it requires that no other transitions with source state c exist using calls to \(\mathrm {fin}\). Having visited all states in V, it finally requires all states in \(C(O)\) to be pairwise different.

It is \(\mathrm {fin}(c)\) where this algorithm mainly deviates from [15]: To ensure that no other transitions from c exist than those specified in O, \(\mathrm {fin}(c)\) produces the requirement that at state c, for every event e and for every subset P of the transitions outgoing from c, whenever an e-transition can be done with the combined effect of P but not adhering to any of the effects of the currently not selected transitions, the e-transition must have one of the states as its target that are target states of P. The rather complicated formulation is due to possibly overlapping preconditions where for a single event e the preconditions of two different transitions may be satisfied simultaneously. For a state c, where all outgoing transitions for the same event have disjoint preconditions, the \(\mathcal {E}^{\downarrow } \)-formula returned by \(\mathrm {fin}(c)\) is equivalent to

Example 4
We show the first few steps of representing the operational ed specification \( ATM \) of Fig. 1 as an \(\mathcal {E}^{\downarrow } \)-sentence \(\varrho _{ ATM }\). This top-level sentence is

The first call of \(\mathrm {sen}( Card , \ldots )\) explores the single outgoing transition from \( Card \) to \( PIN \), adds \( PIN \) to the bound states, and hence expands to

Now all outgoing transitions from \( Card \) have been explored and the next call of \(\mathrm {sen}( Card ,\emptyset , \ldots )\) removes \( Card \) from the set of states to be visited, resulting in
As there is only a single outgoing transition from \( Card \), the special case of disjoint preconditions applies for the finalisation call, and \(\mathrm {fin}( Card )\) results in

4 Constructor Implementations
The implementation notion defined in Sect. 3.1 is too simple for many practical applications. It requires the same signature for specification and implementation and does not support the process of constructing an implementation. Therefore, Sannella and Tarlecki [18, 19] have proposed the notion of constructor implementation which is a generic notion applicable to specification formalisms which are based on signatures and semantic structures for signatures. We will reuse the ideas in the context of \(\mathcal {E}^{\downarrow } \)-logic.
The notion of constructor is the basis: for signatures \(\varSigma _1, \ldots ,\varSigma _n, \varSigma \in Sig ^{\mathcal {E}^{\downarrow }}\), a constructor \(\kappa \) from \((\varSigma _1, \ldots , \varSigma _n)\) to \(\varSigma \) is a (total) function \(\kappa : Edts ^{\mathcal {E}^{\downarrow }}(\varSigma _1) \times \ldots \times Edts ^{\mathcal {E}^{\downarrow }}(\varSigma _n) \rightarrow Edts ^{\mathcal {E}^{\downarrow }}(\varSigma )\). Given a constructor \(\kappa \) from \((\varSigma _1, \ldots , \varSigma _n)\) to \(\varSigma \) and a set of constructors \(\kappa _i\) from \((\varSigma _i^1, \ldots , \varSigma _i^{k_i})\) to \(\varSigma _i\), \(1\le i \le n\), the constructor \((\kappa _1, \ldots , \kappa _n);\kappa \) from \((\varSigma _1^1, \ldots , \varSigma _1^{k_1}, \ldots , \varSigma _n^1, \ldots , \varSigma _n^{k_n})\) to \(\varSigma \) is obtained by the usual composition of functions. The following definitions apply to both axiomatic and operational ed specifications since the semantics of both is given in terms of ed signatures and model classes of edts. In particular, the implementation notion allows to implement axiomatic specifications by operational specifications.
Definition 8
Given specifications \( Sp , Sp _1, \ldots , Sp _n\) and a constructor \(\kappa \) from \((\varSigma ( Sp _1),\ldots ,\varSigma ( Sp _n))\) to \(\varSigma ( Sp )\), the tuple \(\langle Sp _1, \ldots , Sp _n\rangle \) is a constructor implementation via \(\kappa \) of \( Sp \), in symbols \( Sp \mathrel {\rightsquigarrow }_\kappa \langle Sp _1, \dots , Sp _n\rangle \), if for all \(M_i \in \mathrm {Mod}( Sp _i)\) we have \(\kappa (M_1, \ldots ,M_n) \in \mathrm {Mod}( Sp ).\) The implementation involves a decomposition if \(n > 1\).
The notion of simple implementation in Sect. 3.1 is captured by choosing the identity. We now introduce a set of more advanced constructors in the context of ed signatures and edts. Let us first consider two central notions for constructors: signature morphisms and reducts. For data signatures \(A, A'\) a data signature morphism \(\sigma : A \rightarrow A'\) is a function from A to \(A'\). The \(\sigma \)-reduct of an \(A'\)-data state \(\omega ' : A' \rightarrow \mathcal {D}\) is given by the A-data state \(\omega ' | \sigma : A \rightarrow \mathcal {D}\) defined by \((\omega ' | \sigma )(a) = \omega '(\sigma (a))\) for every \(a \in A\). If \(A \subseteq A'\), the injection of A into \(A'\) is a particular data signature morphism and we denote the reduct of an \(A'\)-data state \(\omega '\) to A by \(\omega ' \upharpoonright A\). If \(A = A_1 \cup A_2\) is the disjoint union of \(A_1\) and \(A_2\) and \(\omega _i\) are \(A_i\)-data states for \(i \in \{ 1, 2 \}\) then \(\omega _1+\omega _2\) denotes the unique A-data state \(\omega \) with \(\omega \upharpoonright A_i = \omega _i\) for \(i \in \{ 1, 2 \}\). The \(\sigma \)-reduct \(\gamma | \sigma \) of a configuration \(\gamma = (c, \omega ')\) is given by \((c, \omega ' | \sigma )\), and is lifted to a set of configurations \(\varGamma '\) by \(\varGamma ' | \sigma = \{ \gamma ' | \sigma \mid \gamma ' \in \varGamma ' \}\).
Definition 9
An ed signature morphism \(\sigma = (\sigma _{E}, \sigma _{A}) : \varSigma \rightarrow \varSigma '\) is given by a function \(\sigma _{E} : E(\varSigma ) \rightarrow E(\varSigma ')\) and a data signature morphism \(\sigma _{A} : A(\varSigma ) \rightarrow A(\varSigma ')\). We abbreviate both \(\sigma _{E}\) and \(\sigma _{A}\) by \(\sigma \).
Definition 10
Let \(\sigma : \varSigma \rightarrow \varSigma '\) be an ed signature morphism and \(M'\) a \(\varSigma '\)-edts. The \(\sigma \)-reduct of \(M'\) is the \(\varSigma \)-edts \(M' | \sigma = (\varGamma , R, \varGamma _0)\) such that \(\varGamma _0 = \varGamma _0(M') | \sigma \), and \(\varGamma \) and \(R = (R_e)_{e \in E(\varSigma )}\) are inductively defined by \(\varGamma _0 \subseteq \varGamma \) and for all \(e \in E(\varSigma )\), \(\gamma ', \gamma '' \in \varGamma (M')\): if \(\gamma ' | \sigma \in \varGamma \) and \((\gamma ', \gamma '') \in R(M')_{\sigma (e)}\), then \(\gamma '' | \sigma \in \varGamma \) and \((\gamma ' | \sigma , \gamma '' | \sigma ) \in R_e\).
Definition 11
Let \(\sigma : \varSigma \rightarrow \varSigma '\) be an ed signature morphism. The reduct constructor \(\kappa _{\sigma }\) from \(\varSigma '\) to \(\varSigma \) maps any \(M' \in Edts ^{\mathcal {E}^{\downarrow }}(\varSigma ')\) to its reduct \(\kappa _{\sigma }(M') = M' | \sigma \). Whenever \(\sigma _{A}\) and \(\sigma _{E}\) are bijective functions, \(\kappa _\sigma \) is a relabelling constructor. If \(\sigma _{E}\) and \(\sigma _{A}\) are injective, \(\kappa _\sigma \) is a restriction constructor.
Example 5
The operational specification \( ATM \) is a constructor implementation of \( Sp _1\) via the restriction constructor \(\kappa _{\iota }\) determined by the inclusion signature morphism \(\iota : \varSigma ( Sp _1) \rightarrow \varSigma ( ATM )\), i.e., \( Sp _1 \mathrel {\rightsquigarrow }_{\kappa _\iota } ATM \).
A further refinement technique for reactive systems (see, e.g., [8]), is the implementation of simple events by complex events, like their sequential composition. To formalise this as a constructor we use composite events \(\varTheta (E)\) over a given set of events E, given by the grammar \(\theta \, {:}{:=}\, e \mid \theta + \theta \mid \theta ;\theta \mid \theta ^*\) with \(e \in E\). They are interpreted over an (E, A)-edts M by \(R(M)_{\theta _1 + \theta _2} = R(M)_{\theta _1} \cup R(M)_{\theta _2}\), \(R(M)_{\theta _1; \theta _2} = R(M)_{\theta _1}; R(M)_{\theta _2}\), and \(R(M)_{\theta ^*} = (R(M)_{\theta })^*\). Then we can introduce the intended constructor by means of reducts over signature morphisms mapping atomic to composite events:
Definition 12
Let \(\varSigma , \varSigma '\) be ed signatures, \(D'\) a finite subset of \(\varTheta (E(\varSigma '))\), \(\varDelta ' = (D',A(\varSigma '))\), and \(\alpha : \varSigma \rightarrow \varDelta '\) an ed signature morphism. The event refinement constructor \(\kappa _\alpha \) from \(\varDelta '\) to \(\varSigma \) maps any \(M' \in Edts ^{\mathcal {E}^{\downarrow }}(\varDelta ')\) to its reduct \(M' | \alpha \in Edts ^{\mathcal {E}^{\downarrow }}(\varSigma )\).
Finally, we consider a semantic, synchronous parallel composition constructor that allows for decomposition of implementations into components which synchronise on shared events. Given two composable signatures \(\varSigma _1\) and \(\varSigma _2\), the parallel composition \(\gamma _1 \otimes \gamma _2\) of two configurations \(\gamma _1 = (c_1, \omega _1)\), \(\gamma _2 = (c_2, \omega _2)\) with \(\omega _1 \in \varOmega (A(\varSigma _1))\), \(\omega _2 \in \varOmega (A(\varSigma _2))\) is given by \(((c_1, c_2), \omega _1 + \omega _2)\), and lifted to two sets of configurations \(\varGamma _1\) and \(\varGamma _2\) by \(\varGamma _1 \otimes \varGamma _2 = \{ \gamma _1 \otimes \gamma _2 \mid \gamma _1 \in \varGamma _1,\ \gamma _2 \in \varGamma _2 \}\).
Definition 13
Let \(\varSigma _1, \varSigma _2\) be composable ed signatures. The parallel composition constructor \(\kappa _\otimes \) from \((\varSigma _1, \varSigma _2)\) to \(\varSigma _1 \otimes \varSigma _2\) maps any \(M_1 \in Edts ^{\mathcal {E}^{\downarrow }}(\varSigma _1)\), \(M_2 \in Edts ^{\mathcal {E}^{\downarrow }}(\varSigma _2)\) to \(M_1 \otimes M_2 = (\varGamma , R, \varGamma _0) \in Edts ^{\mathcal {E}^{\downarrow }}(\varSigma _1 \otimes \varSigma _2)\), where \(\varGamma _0 = \varGamma _0(M_1) \otimes \varGamma _0(M_2)\), and \(\varGamma \) and \(R = (R_e)_{E(\varSigma _1) \cup E(\varSigma _2)}\) are inductively defined by \(\varGamma _0 \subseteq \varGamma \) and
-
for all \(e_1 \in E(\varSigma _1) \setminus E(\varSigma _2)\), \(\gamma _1, \gamma _1' \in \varGamma (M_1)\), and \(\gamma _2 \in \varGamma (M_2)\), if \(\gamma _1 \otimes \gamma _2 \in \varGamma \) and \((\gamma _1, \gamma _1') \in R(M_1)_{e_1}\), then \(\gamma _1' \otimes \gamma _2 \in \varGamma \) and \((\gamma _1 \otimes \gamma _2, \gamma _1' \otimes \gamma _2) \in R_{e_1}\);
-
for all \(e_2 \in E(\varSigma _2) \setminus E(\varSigma _1)\), \(\gamma _2, \gamma _2' \in \varGamma (M_2)\), and \(\gamma _1 \in \varGamma (M_1)\), if \(\gamma _1 \otimes \gamma _2 \in \varGamma \) and \((\gamma _2, \gamma _2') \in R(M_2)_{e_2}\), then \(\gamma _1 \otimes \gamma _2' \in \varGamma \) and \((\gamma _1 \otimes \gamma _2, \gamma _1 \otimes \gamma _2') \in R_{e_2}\);
-
for all \(e \in E(\varSigma _1) \cap E(\varSigma _2)\), \(\gamma _1, \gamma _1' \in \varGamma (M_1)\), and \(\gamma _2, \gamma _2' \in \varGamma (M_2)\), if \(\gamma _1 \otimes \gamma _2 \in \varGamma \), \((\gamma _1, \gamma _1') \in R(M_1)_{e_1}\), and \((\gamma _2, \gamma _2') \in R(M_2)_{e_2}\), then \(\gamma _1' \otimes \gamma _2' \in \varGamma \) and \((\gamma _1 \otimes \gamma _2, \gamma _1' \otimes \gamma _2') \in R_{e}\).
An obvious question is how the semantic parallel composition constructor is related to the syntactic parallel composition of operational ed specifications.
Proposition 1
Let \(O_1, O_2\) be operational ed specifications with composable signatures. Then \(\mathrm {Mod}(O_1) \otimes \mathrm {Mod}(O_2) \subseteq \mathrm {Mod}(O_1 \parallel O_2)\), where \(\mathrm {Mod}(O_1) \otimes \mathrm {Mod}(O_2)\) denotes \(\kappa _\otimes (\mathrm {Mod}(O_1),\mathrm {Mod}(O_2))\).
The converse \(\mathrm {Mod}(O_1 \parallel O_2) \subseteq \mathrm {Mod}(O_1) \otimes \mathrm {Mod}(O_2)\) does not hold: Consider the ed signature \(\varSigma = (E, A)\) with \(E = \{ e \}\), \(A = \emptyset \), and the operational ed specifications \(O_i = (\varSigma ,C_i,T_i,(c_{i, 0},\varphi _{i, 0}))\) for \(i \in \{ 1, 2 \}\) with \(C_1 = \{ c_{1, 0} \}\), \(T_1 = \{ (c_{1, 0},\mathrm {true},e, \mathrm {false},c_{1, 0}) \}\), \(\varphi _{1, 0} = \mathrm {true}\); and \(C_2 = \{ c_{2, 0} \}\), \(T_2 = \emptyset \), \(\varphi _{2, 0} = \mathrm {true}\). Then \(\mathrm {Mod}(O_1) = \emptyset \), but \(\mathrm {Mod}(O_1 \parallel O_2) = \{ M \}\) with M showing just the initial configuration.
The next theorem shows the usefulness of the syntactic parallel composition operator for proving implementation correctness when a (semantic) parallel composition constructor is involved. The theorem is a direct consequence of Proposition 1 and Definition 8.
Theorem 3
Let \( Sp \) be an (axiomatic or operational) ed specification, \(O_1, O_2\) operational ed specifications with composable signatures, and \(\kappa \) an implementation constructor from \(\varSigma (O_1) \otimes \varSigma (O_2)\) to \(\varSigma ( Sp )\): If \( Sp \mathrel {\rightsquigarrow }_\kappa O_1 \parallel O_2\), then \( Sp \mathrel {\rightsquigarrow }_{\kappa _\otimes ; \kappa } \langle O_1, O_2 \rangle \).
Example 6
We finish the refinement chain for the ATM specifications by applying a decomposition into two parallel components. The operational specification \( ATM \) of Example 3 (and Example 5) describes the interface behaviour of an ATM interacting with a user. For a concrete realisation, however, an ATM will also interact internally with other components, like, e.g., a clearing company which supports the ATM for verifying PINs. Our last refinement step hence realises the \( ATM \) specification by two parallel components, represented by the operational specification \( ATM '\) in Fig. 2a and the operational specification \( CC \) of a clearing company in Fig. 2b. Both communicate (via shared events) when an ATM sends a verification request, modelled by the event \(\mathsf {verifyPIN}\), to the clearing company. The clearing company may answer with \(\mathsf {correctPIN}\) or \(\mathsf {wrongPIN}\) and then the ATM continues following its specification. For the implementation construction we use the parallel composition constructor \(\kappa _\otimes \) from \((\varSigma ( ATM '),\varSigma ( CC ))\) to \(\varSigma ( ATM ') \otimes \varSigma ( CC )\). The signature of \( CC \) consists of the events shown on the transitions in Fig. 2b. Moreover, there is one integer-valued attribute \(\mathsf {cnt}\) counting the number of verification tasks performed. The signature of \( ATM '\) extends \(\varSigma ( ATM )\) by the events \(\mathsf {verifyPIN}\), \(\mathsf {correctPIN}\) and \(\mathsf {wrongPIN}\). To fit the signature and the behaviour of the parallel composition of \( ATM '\) and \( CC \) to the specification \( ATM \) we must therefore compose \(\kappa _\otimes \) with an event refinement constructor \(\kappa _\alpha \) such that \(\alpha (\mathsf {enterPIN}) = (\mathsf {enterPIN}; \mathsf {verifyPIN}; (\mathsf {correctPIN} + \mathsf {wrongPIN}))\); for the other events \(\alpha \) is the identity and for the attributes the inclusion. The idea is therefore that the refinement looks like \( ATM \mathrel {\rightsquigarrow }_{\kappa _\otimes ;\,\kappa _\alpha } \langle ATM ', CC \rangle \). To prove this refinement relation we rely on the syntactic parallel composition \( ATM ' \parallel CC \) shown in Fig. 2c, and on Theorem 3. It is easy to see that \( ATM \mathrel {\rightsquigarrow }_{\kappa _\alpha } ATM '\parallel CC \). In fact, all transitions for event \(\mathsf {enterPIN}\) in Fig. 1 are split into several transitions in Fig. 2c according to the event refinement defined by \(\alpha \). For instance, the loop transition from \( PIN \) to \( PIN \) with precondition \(\mathsf {trls < 2}\) in Fig. 1 is split into the cycle from \(( PIN , Idle )\) via \(( PINEntered , Idle )\) and \(( Verifying , Busy )\) back to \(( PIN , Idle )\) in Fig. 2c. Thus, we have \( ATM \mathrel {\rightsquigarrow }_{\kappa _\alpha } ATM '\parallel CC \) and can apply Theorem 3 such that we get \( ATM \mathrel {\rightsquigarrow }_{\kappa _\otimes ;\,\kappa _\alpha } \langle ATM ', CC \rangle \).
5 Conclusions
We have presented a novel logic, called \(\mathcal {E}^{\downarrow } \)-logic, for the rigorous formal development of event-based systems incorporating changing data states. To the best of our knowledge, no other logic supports the full development process for this kind of systems ranging from abstract requirements specifications, expressible by the dynamic logic features, to the concrete specification of implementations, expressible by the hybrid part of the logic.
The temporal logic of actions (TLA [13]) supports also stepwise refinement where state transition predicates are considered as actions. In contrast to TLA we model also the events which cause data state transitions. For writing concrete specifications we have proposed an operational specification format capturing (at least parts of) similar formalisms, like Event-B [1], symbolic transition systems [17], and UML protocol state machines [16]. A significant difference to Event-B machines is that we distinguish between control and data states, the former being encoded as data in Event-B. On the other hand, Event-B supports parameters of events which could be integrated in our logic as well. An institution-based semantics of Event-B has been proposed in [7] which coincides with our semantics of operational specifications for the special case of deterministic state transition predicates. Similarly, our semantics of operational specifications coincides with the unfolding of symbolic transition systems in [17] if we instantiate our generic data domain with algebraic specifications of data types (and consider again only deterministic state transition predicates). The syntax of UML protocol state machines is about the same as the one of operational event/data specifications. As a consequence, all of the aforementioned concrete specification formalisms (and several others) would be appropriate candidates for integration into a development process based on \(\mathcal {E}^{\downarrow } \)-logic.
There remain several interesting tasks for future research. First, our logic is not yet equipped with a proof system for deriving consequences of specifications. This would also support the proof of refinement steps which is currently achieved by purely semantic reasoning. A proof system for \(\mathcal {E}^{\downarrow } \)-logic must cover dynamic and hybrid logic parts at the same time, like the proof system in [15], which, however, does not consider data states, and the recent calculus of [5], which extends differential dynamic logic but does not deal with events and reactions to events. Both proof systems could be appropriate candidates for incorporating the features of \(\mathcal {E}^{\downarrow } \)-logic. Another issue concerns the separation of events into input and output as in I/O-automata [14]. Then also communication compatibility (see [2] for interface automata without data and [3] for interface theories with data) would become relevant when applying a parallel composition constructor.
Notes
- 1.
We use \(\mathrm {true}\) and \(\mathrm {false}\) for predicates and formulae; their meaning will always be clear from the context. For boolean values we will use instead the notations \( tt \) and \( ff \).
- 2.
For shortening the presentation we omit further events like withdrawing money, etc.
- 3.
Note that joint moves with e cannot become inconsistent due to composability of ed signatures.
References
Abrial, J.R.: Modeling in Event-B: System and Software Engineering. Cambridge University Press, Cambridge (2013)
de Alfaro, L., Henzinger, T.A.: Interface automata. In: Tjoa, A.M., Gruhn, V. (eds.) Proceedings 8th European Software Engineering Conference & 9th ACM SIGSOFT International Symposium Foundations of Software Engineering, pp. 109–120. ACM (2001)
Bauer, S.S., Hennicker, R., Wirsing, M.: Interface theories for concurrency and data. Theoret. Comput. Sci. 412(28), 3101–3121 (2011)
ter Beek, M.H., Fantechi, A., Gnesi, S., Mazzanti, F.: An action/state-based model-checking approach for the analysis of communication protocols for service-oriented applications. In: Leue, S., Merino, P. (eds.) FMICS 2007. LNCS, vol. 4916, pp. 133–148. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-79707-4_11
Bohrer, B., Platzer, A.: A hybrid, dynamic logic for hybrid-dynamic information flow. In: Dawar, A., Grädel, E. (eds.) Proceedings of 33rd Annual ACM/IEEE Symposium on Logic in Computer Science, pp. 115–124. ACM (2018)
Braüner, T.: Hybrid Logic and its Proof-Theory. Applied Logic Series. Springer, Heidelberg (2010). https://doi.org/10.1007/978-94-007-0002-4
Farrell, M., Monahan, R., Power, J.F.: An institution for Event-B. In: James, P., Roggenbach, M. (eds.) WADT 2016. LNCS, vol. 10644, pp. 104–119. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-72044-9_8
Gorrieri, R., Rensink, A.: Action refinement. In: Bergstra, J.A., Ponse, A., Smolka, S.A. (eds.) Handbook of Process Algebra, pp. 1047–1147. Elsevier, Amsterdam (2000)
Groote, J.F., Mousavi, M.R.: Modeling and Analysis of Communicating Systems. MIT Press, Cambridge (2014)
Harel, D., Kozen, D., Tiuryn, J.: Dynamic Logic. MIT Press, Cambridge (2000)
Hennicker, R., Madeira, A., Knapp, A.: A hybrid dynamic logic for event/data-based systems (2019). https://arxiv.org/abs/1902.03074
Knapp, A., Mossakowski, T., Roggenbach, M., Glauer, M.: An institution for simple UML state machines. In: Egyed, A., Schaefer, I. (eds.) FASE 2015. LNCS, vol. 9033, pp. 3–18. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46675-9_1
Lamport, L.: Specifying Systems: The TLA+ Language and Tools for Hardware and Software Engineers. Addison-Wesley, Boston (2003)
Lynch, N.A.: Input/output automata: basic, timed, hybrid, probabilistic, dynamic, \(\ldots \). In: Amadio, R.M., Lugiez, D. (eds.) CONCUR 2003. LNCS, vol. 2761, pp. 191–192. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45187-7_12
Madeira, A., Barbosa, L.S., Hennicker, R., Martins, M.A.: A logic for the stepwise development of reactive systems. Theoret. Comput. Sci. 744, 78–96 (2018)
Object Management Group: Unified Modeling Language 2.5. Standard formal/2015-03-01, OMG (2015)
Poizat, P., Royer, J.C.: A formal architectural description language based on symbolic transition systems and modal logic. J. Univ. Comp. Sci. 12(12), 1741–1782 (2006)
Sannella, D., Tarlecki, A.: Toward formal development of programs from algebraic specifications: implementations revisited. Acta Inf. 25(3), 233–281 (1988)
Sannella, D., Tarlecki, A.: Foundations of Algebraic Specification and Formal Software Development. EATCS Monographs in Theoretical Computer Science. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-17336-3
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Hennicker, R., Madeira, A., Knapp, A. (2019). A Hybrid Dynamic Logic for Event/Data-Based Systems. In: Hähnle, R., van der Aalst, W. (eds) Fundamental Approaches to Software Engineering. FASE 2019. Lecture Notes in Computer Science(), vol 11424. Springer, Cham. https://doi.org/10.1007/978-3-030-16722-6_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-16722-6_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-16721-9
Online ISBN: 978-3-030-16722-6
eBook Packages: Computer ScienceComputer Science (R0)




 ,
, and for all
and for all  , there is a
, there is a  and
and 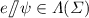 and for all
and for all  , there is a
, there is a  and
and