: Priority Aware Test Case Reduction

Abstract

Test cases play an important role in testing and debugging software. Smaller tests are easier to understand and use for these tasks. Given a test that demonstrates a bug, test case reduction finds a smaller variant of the test case that exhibits the same bug. Classically, one of the challenges for test case reduction is that the process is slow, often taking hours. For hierarchically structured inputs like source code, the state of the art is Perses, a recent grammar aware and queue driven approach for test case reduction. Perses traverses nodes in the abstract syntax tree (AST) of a program (test case) based on a priority order and tries to reduce them while preserving syntactic validity.

In this paper, we show that Perses’ reduction strategy suffers from priority inversion, where significant time may be spent trying to perform reduction operations on lower priority portions of the AST. We show that this adversely affects the reduction speed. We propose , a technique for priority aware test case reduction that avoids priority inversion. We implemented and evaluated it on the same set of benchmarks used in the Perses evaluation. Our results indicate that compared to Perses, is able to reduce test cases 1.3x to 7.8x faster and with 46% to 80% fewer queries.

1 Introduction

Test case reduction is a technique that aids in testing and debugging software. When an input for a program causes the program to exhibit a property of interest, like a bug, finding a smaller input that also exhibits the property can help to explain the behavior [1,2,3]. Given an input $I\in \mathbb {I}$ and an oracle $\psi :\mathbb {I}\rightarrow \mathbb {B}$ that performs a test and returns true iff a property holds, test case reduction aims to find a smaller input $I'$ such that $\psi (I')=\text{ true }$. Often, this problem is approached through Delta Debugging (DD), a longstanding and effective algorithm for test case reduction that essentially generalizes binary search [2]. However, for inputs with significant structure, generic DD can perform poorly, requiring significant time and not performing much reduction [3, 4]. For compilers in particular, where the inputs must be valid programs, this has led to specialized techniques like Hierarchical Delta Debugging [3, 4], language specific reducers like C-Reduce [5], and most recently to Syntax Guided Program Reduction as seen in Perses [6].

Syntax Guided Program Reduction (SGPR) is the present state of the art for compiler targeted test case reduction. The intuition behind SGPR is that the grammar defining the language of inputs eliminates many invalid sub-inputs from the search space. For example, when an input must adhere to the C programming language [7], removing the return type of a function declaration would not be valid because the C grammar specifies that the return type is required. Such syntactically invalid inputs are removed from the search space by SGPR.

Perses, a form of SGPR, takes as arguments not only a program p and oracle $\psi$, but also the context free grammar G of valid inputs [6]. It transforms the grammar so that removable parts of the input can be identified by the names of the grammar rules used to parse them. This also normalizes the grammar so that all removable components are expressed through quantifiers in an extended context free grammar [8], i.e. optionality (?) and lists (*, +). This transformation is illustrated in Fig. 1. Notice, for instance, that the recursive rule BAR denoting a list is transformed ($\Longrightarrow$) into a Kleene-+ quantified list. Individual elements of the list may be removed while preserving syntactic validity. Perses then parses the input of interest into an abstract syntax tree (AST) and traverses the AST while trying to (1) remove optional nodes and (2) perform DD to minimize the children of nodes representing lists. The grammar transformations have the benefit of making many syntactically correct removals easy and efficient to locate.

Fig. 1.

Overview of Perses grammar transformations for SGPR.

Perses has significantly improved the speed of program reduction. However, it still takes several hours to reduce some inputs. Consider the code in Listing 1.1 along with its AST in Fig. 3. This example is similar to a C program generated by the compiler testing tool CSmith [9]. In this example, Perses first considers the root node with ID of the AST. Since the rule for this node ends in _star, it is a list node, and its children are the elements of the list. Thus, Perses applies DD to the list of children for node to minimize the number of children. When such lists are long, significant time can be devoted to this task. We show in Sect. 4 that this can lead to substantial stalls in reduction, where no progress is made while a list is being processed. However, most of the children of this node have low token weight, the number of tokens beneath a given node that is denoted by w: in Fig. 3. Indeed, greater value would be found by focusing on just one of its children, node , which contains the majority of the input beneath it. By spending greater effort up front on portions of the AST of lesser value, Perses suffers from a form of priority inversion. Priority inversion occurs when a low priority task is scheduled instead of a high priority task. In this case, Perses focuses on removing low token weight nodes instead of high token weight nodes. Indeed, Perses may even fail to remove elements that would enable better reduction success overall. In this case, the declarations of foo, S, and d are used within the code beneath node . Thus, those uses need to be eliminated before any of the declarations can be removed successfully. In practice, we find that priority inversion has a significant impact on reduction time in SGPR.

To address priority inversion, we have developed priority aware reduction strategies for program reduction. By focusing the reduction effort on the nodes of the AST that cover the greatest number of tokens, we prioritize reduction of the most complex parts of the input first. This has multiple important benefits: (1) Dependencies between program elements are more likely to be broken by eliminating the complex uses first. (2) Stalls in reduction from unsuccessful rounds of DD can be mitigated. (3) By removing large portions of an input earlier on, each oracle query to $\psi$ can take less time because smaller inputs tend to be faster to check. We have designed and evaluated a tool, , that makes use of these techniques and found that it leads to consistent and significant performance improvements over Perses on the Perses benchmarks [6].

In summary, this paper makes the following contributions:

• 1. Priority awareness. We identify priority inversion as a key problem facing SGPR techniques and develop priority aware reduction strategies as a potential solution. Priority aware reduction strategies focus the reduction effort on the complex portions of an input first, enabling earlier and thus faster test case reduction (Sects. 3, 4.1).

• 2. Optimization. We identify redundancies in the reduction process when using Perses’ transformed grammars and develop a solution to prune them from the candidate search space (Sect. 3.2).

• 3. Significant performance improvement. We implemented our strategies in a tool, , and evaluated it on the same benchmarks used by Perses. Experimental results show that both removes more of the input earlier on and is faster overall. Compared to Perses, reduces test cases 1.3x to 7.8x faster and with 46% to 80% fewer oracle queries (Sect. 4.1).

2 Background and Motivation

Consider again the example in Fig. 3 and suppose that the oracle ($\psi$) checks that this program p should print "Hello World!" on line 24 (marked with ). Thus, the smallest subprogram for which $\psi$ returns true is the main function with the desired print statement.

Fig. 2.

One round of removal trials in Perses, and for the AST in Fig. 3. Numbers are node IDs.

Fig. 3.

AST of the program in Listing 1.1. w denotes the token weight of each node.

To search for this smaller input inside the original input, Perses traverses the AST using a priority queue ordered by the token weight. In each trial, the node with the maximum weight is removed from the work queue and traversed. In our example, the queue starts out containing only the root of the AST, node . Perses performs specific reduction operations on different types of nodes during traversal. For instance, on optional nodes, Perses tries to remove the optional child node. For list nodes, Perses minimizes the list of children using DD. Any remaining children of the traversed node are then added to the priority queue in order to be traversed in the future.

Observe that in this example, Perses will first examine node and remove it from the queue. Because is a list node, DD is applied to the children of . Different combinations of children are removed from and the result is checked by $\psi$ to find a smaller input. First, all children are removed and $\psi$ is checked. After this fails, the first half of the children ( and ) are removed, but $\psi$ returns false again because this removes required declarations. Since removing the second half of the children ( and ) also fails, the process continues recursively. First DD tries shrinking the list by removing each individual child, and next it tries only keeping each individual child. Ultimately none of the trials succeed, so all children are added to the queue, and reduction continues with node . The intervening node is not tested by SGPR because it is not syntactically removable. The next node removed from the work queue is node . This continues until the queue is empty. The precise trials exercised in this process are illustrated in Fig. 2(a). Note that 16 steps elapse until a successful trial occurs.

While the priorities used by Perses are controlled by the token weight, they determine how the children of the traversed nodes are removed. Thus, any node whose parent in the AST is a list is given the same priority as all other elements in the list. This is because DD recursively tries to minimize the entire list until no single element can be removed, regardless of the priorities of individual list elements. As a result, Perses must employ DD on the entirety of the children of even though it would be more beneficial to focus on just one child, node .

Instead, more directly models the priorities. We note that in an optional or list node, such as , each child may be removed in a syntactically valid fashion. We call such removable nodes nullable. When traversing a nullable node in the AST, we can simply try directly to remove it, adding its children if the removal fails. For instance, in the running example, we would visit first. Because cannot get removed, we would simply add its children to the priority queue. Note that all children of are nullable, but has the highest token weight. Thus, we next select to traverse but removing also fails. From the given token weights, we next traverse , which is syntactically not removable, and then , which we attempt to remove but is unsuccessful. Next is visited and successfully removed. Removing enables the removal of , and . Thus, they are removed in a single pass of the tree using , whereas Perses would require multiple traversals of the AST to remove them. This process continues until the desired output is achieved. As seen in Fig. 2(b), just 4 steps elapse until the first successful trial removes node .

Note that in this example, is able to reduce to the desired output in a single pass, while Perses requires multiple passes of the AST. In practice, all program reduction techniques continue until a fixed point is reached, including , however can achieve greater reduction in a single traversal of the AST, accelerating convergence on the fixed point.

This priority aware approach can still have drawbacks, however. After focusing on the highest priority nodes, there may be many lower priority nodes remaining. For example, there are multiple remaining nodes of weight 7 in the tree after performing the reduction by as described above. We also show experimentally that these lower priority nodes occur in practice in Sect. 5. The above approach of considers each node one at a time, which can have poor performance when reducing such long lists. In addition, we thus propose a hybrid approach that still prioritizes nodes by maximum token weight but also uses a list based reduction technique for spans of nodes that have the same token weight. This hybrid approach is able to achieve the benefits of being priority aware while still avoiding the cost of considering each node of the AST individually.

Section 3 presents the algorithms behind these techniques in detail.

3 Approach

Recall that the core of , similar to Perses, maintains a priority queue of the nodes in an AST and traverses the nodes in order to process them. It also makes use of Perses Normal Form, the result of the grammar transformations that Perses introduced [6]. The key difference is that instead of using the token weight of a parent node to determine when its nullable children may be removed, identifies all nullable nodes (see Sect. 3.2) and uses their token weights directly to prioritize the search. The core algorithm for this process is quite straightforward and presented in Algorithm 1.

Line 1 of the algorithm constructs the priority queue (a max-heap), initializing it with the root of the AST and using a parameterizable priority $\rho$. $\rho$ is simply a function that takes a node and returns its priority as a tuple. The priority queue selects the element with a lexicographically maximal priority, so ties on the first element of the priority tuple are broken by the second element and so on. As seen in Fig. 4, for , returns a pair of numbers, the token weight of the node and the position of the node in a decreasing, right-to-left, breadth first search. The specific breadth first order means that for an AST with n nodes, bfsOrder(p.root)=n, the last child c of p.root has bfsOrder(c)=n-1, and so on. Thus, if several nodes have the same token weight, the one highest in the AST and furthest to the right is selected next. This ordering decreases the chances of trying to remove a declaration before its uses [10].

Line 2 starts the core of the algorithm. While there are more nodes to explore in the queue, the node with the next highest priority is considered. If it is nullable and can be successfully removed, we remove it from the AST, otherwise we add its children to the queue so that they will also be traversed.

While the algorithm is surprisingly simple, we have found it to perform significantly better than the state of the art in practice. As we explore in Sect. 4.2, this results from prioritizing the search toward those portions of the input where reduction can have the greatest impact. To more closely compare with Perses, consider a version of Perses that upon visiting a list or optional node only tries removing each child of that node once¹. This “one node at a time” variant of Perses can also be implemented using Algorithm 1 by carefully choosing the priority formula $\rho$. Because Perses considers removing the children of the nodes it traverses, it actually prioritizes the work queue using the token weight of the parent rather than the token weight of nullable nodes being considered for removal. This leads to the alternative prioritizer $\rho _{\textit{perses}}$ presented in Fig. 4. Observe that all children of a list node receive the same token weight, that of the entire list. This can inflate the priority of some nodes in the work queue and leads to poor performance.

Fig. 4.

Prioritizers used for , node at a time Perses, and .

Like other program reduction algorithms [3, 5, 6, 11, 12], Algorithm 1 is used to compute a fixed point. That is, in practice the algorithm is repeated until no further reductions can be made. As in prior work, we omit this from our presentation for clarity. In theory, this means that the worst case complexity of the technique is $O(n^2)$ where n is the number of nodes in the AST. This arises when only one leaf of the AST is removed in each pass through the algorithm. In practice, most nodes are not syntactically nullable, and we show in Sect. 4.1 that performance of exceeds the state of the art.

In addition, while we focus on removing nodes of the AST, Perses also tries to replace non-list and -optional nodes with compatible nodes in their subtrees. We do not focus on this aspect of the algorithm. In practice, we found it to significantly hurt performance (see Sect. 4.1) and we consider efficient replacement strategies to be orthogonal to and outside the scope of this work.

3.1

The initial priority aware technique from Algorithm 1 can also encounter performance bottlenecks, however. The original motivation for using DD on lists of children in the AST was that its best case behavior is O(log(n)) where n is the number of children in the list. This is because it tries removing multiple children at the same time. Processing one node at a time, however, requires that every list element is considered individually, guaranteeing O(n) time for one round of Algorithm 1. Priority aware reduction that proceeds one node at a time faces a different set of inefficiencies that can still cause stalls in the reduction process.

Thus, we desire a means of removing multiple elements from lists at the same time while still preserving priority awareness. In order to achieve this, we developed , as presented in Algorithm 2. This approach uses a modified prioritizer as presented in Fig. 4 that first orders by token weight, then by parent traversal order, then by node traversal order. The effect this has is that all children of the same parent with the same weight are grouped together. As a result, we can remove them from the priority queue together and perform list based reduction (like DD) to more efficiently remove groups of elements in a list that have the same priority (for instance, nodes and get removed as a group in one trial using as shown in Fig. 2(c)). Because the search is still primarily directed by the token weights of the removed nodes, the technique still fully respects the priorities of the removed nodes.

Similar to the previous approach, line 1 of Algorithm 2 starts by creating the priority queue. Note that it specifically uses the prioritizer , which groups children having the same token weight in the priority queue. As long as there are more nodes to consider, line 3 takes all nodes from the queue with the same weight and parent. If the weight of a node is unique, this simply returns a list of length 1. Line 4 filters out non-nullable nodes from the trial, and line 5 just applies list based reduction to any nullable nodes. Lines 6 and 7 then remove the eliminated nodes from the tree and add the children of remaining nodes to the work queue. Again, this algorithm actually runs to a fixed point.

While the worst case behavior of DD is $O(n^2)$ [2], this can be improved to O(n) by giving up hard guarantees on minimality [13]. Since this reduction process is performed to a fixed point anyway, minimize on line 5 makes use of this O(n) approach to list based reduction (OPDD) without losing 1-minimality. As a result, the theoretical complexity of is the same as .

3.2 Nullability Pruning

Finally, we observed that many oracle queries were simply unnecessary. Specifically, recall that a node can be tagged nullable because it is an element of a list or a child of an optional node, as previously defined by Perses grammar transformations [6]. The complete algorithm for this tagging is in TagNullable of Algorithm 3. However, for example, a list of one element could contain another list of one element. In the AST, this appears as a chain of nodes, at least two of which are nullable. Removing any one of these nodes removes the same tokens from the AST. Thus, it is only necessary to select a single nullable node from any chain of nodes, and the others can be disregarded.

We exploit this through an optimization called nullability pruning. We traverse every chain of nodes in the AST, preserving the nullability of the highest node in the chain and removing nullability from those below it. The complete algorithm is presented in PruneNullable of Algorithm 3. In effect, it is just a depth first search that removes redundant nullability from nodes along the way instantaneously.

In practice, we find that this can statically (ahead of time) prune most of the AST from the search space. Specifically, in the benchmarks we examine in Sect. 4, we find that of 1,593,875 total nullable nodes, 17% are redundant optional nodes and 44% are redundant list element nodes. We observe the impact of this pruning on the actual reduction process in Sect. 4.1.

4 Evaluation

We evaluate ’s performance and examine the impact of priority inversion on reduction by answering the following research questions:

• RQ1. How does perform compared to Perses in terms of reduction time and speed, number of oracle queries, and size of the reduced test case?

• RQ2. Does priority inversion adversely affect the reduction efficiency? In particular, does reduction require more work with a traversal order suffering from priority inversion?

4.1 RQ1. Performance: vs. Perses

Experimental Set-Up. We evaluate on the set of C test cases used in the evaluation of Perses, including the oracle scripts provided by authors of Perses. While using these, we observed that they still allowed for some undefined behavior [5, 14], so we updated all oracles to reject test case variants with undefined behavior. As a result, we were able to reproduce bugs for 14 out of 20 original test cases. The remaining benchmarks that could not reproduce their original failures were elided for this study. Since the implementation of Perses’ components is not publicly available, we implemented the Perses grammar transformations and reduction based on the algorithms available in the paper [6] using the C++ bindings of ANTLR [15]. All of our implementations have been made available². Our experiments were conducted on an Intel Xeon E5-2630 CPU and 64 GB memory running Ubuntu.

Variants of Reduction Techniques. To better explain performance differences, we benchmark several algorithms that each add one difference. All approaches compute fixed points as previously described.

• Perses DD- The removal-based algorithm of Perses that applies DD on children of list nodes [6].

• Perses OPDD- The same as Perses DD but using the O(n) reduction algorithm of OPDD [13]. It is faster than Perses DD in practice.

• Perses N- The one node at a time Perses that does not apply DD on list elements but removes them one by one using Perses’ parent oriented priorities.

• - This uses the algorithm but does not apply nullability pruning optimization proposed in Sect. 3.2.

• - Our proposed removal algorithm that also applies nullability pruning.

• - The hybrid version of with nullability pruning and OPDD as its version of DD.

Table 1. Original and reduced test case size and number of oracle queries.

Table 2. Reduction time and speed for different variants of reduction techniques.

Reduction Performance. We compare these techniques in terms of the number of oracle queries (Q), reduction quality or size of the final reduced test case (R), reduction time (T), and reduction speed or the average number of tokens removed per second (E). Results are presented in Tables 1 and 2. The best values of queries, time, and speed are highlighted for each test case. As can be seen, in all cases, either or outperform all variants of Perses. Compared to the full removal-based Perses algorithm (Perses DD), our proposed algorithms reduce 1.3x to 7.8x faster and with 46% to 80% fewer queries. The results across variants suggest that these benefits arise from priority awareness and nullability pruning. Due to fixed point computation, all approaches produce test cases from which no one token can be removed while satisfying $\psi$ (1-minimal) [2], but they can produce different final reduced test cases [2]. On average, yields reduced test cases with 574 tokens compared to Perses DD with 609 tokens.

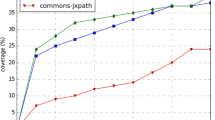
In addition, we graphed the reduction progress of each test case for the different variants. Fig. 5 shows the percentage of remaining tokens over time during reduction. For sake of space, we only include graphs for six of the test cases. Note that the y-axis is log scaled. and show much faster convergence to a reduced test case compared to Perses variants. Recall that the only factor differentiating Perses N from is the order in which the queue of nodes is traversed. Unlike Perses N, does not suffer from priority inversion and guides the reduction process based on token weights of the nodes to remove. As can be seen, this advantage leads to faster convergence to a reduced test case. We examine the impact of priority inversion on reduction speed more rigorously in Sect. 4.2.

Fig. 5.

Converging to a reduced test case in six variants of reduction techniques.

Fig. 6.

Distributions of token removal attempts for and Perses N.

Replacement. As mentioned in Sect. 3, Perses also considers a replacement strategy for non-list or -optional nodes in addition to removal for other nodes. For instance, in Fig. 3, Perses will attempt to replace node with node because they both match the same grammar rule (compound_stmt). This replacement fails since required declarations will get removed and $\psi$ will return false.

Including replacement significantly increases the work done by reduction. For completeness, we implemented Perses DD with replacement as described in their paper [6] and defined a four-hour timeout for the reduction process. In 11 out of 14 cases, Perses DD with replacement could not finish the reduction process before reaching the timeout. In the remaining three, it generated reduced test cases with the same size or slightly smaller while performing a significantly larger number of oracle queries (more than $3\times$ over Perses DD without replacement).

4.2 RQ2. The Impact of Priority Inversion

As shown in Fig. 5, avoiding priority inversion leads to faster convergence. One explanation for this is that priority awareness may decrease the amount of work required to remove a token (as seen in the motivating example). We explore this in a case study on gcc-64990 with 148,931 tokens. The number of removal attempts for a token is number of times a single token is considered for removal. Removing any ancestor of a token in the AST will remove that token, so if a first attempt fails, a deeper ancestor may be attempted. We compute this for every token of the test case to get a sense of the work required for each token. A better traversal order of the AST should cause fewer overall token removal attempts. To measure only the impact of different traversal orders, we compare with Perses N. As described in Sect. 4.1, they follow the exact same reduction rules and differ only in their traversal orders.

Figure 6 depicts histograms of the distributions of token removal attempts for and Perses N. For clearer visualization, we show only the distributions for the number of attempts less than or equal to 20. We can see how Perses N distribution is inclined toward a larger number of removal attempts, an indicator of more work required in order to remove individual tokens. In addition, we statically measure that the difference between the removal attempt distributions is significant. We use a one sided Wilcoxon rank-sum test [16] to determine whether the distribution of Perses N is indeed greater than that of . The p-value computed for our data was less than $2.2e^{-16}$ which strongly supports this observation.

5 Discussion

as a sweet spot in reducing test cases: As discussed earlier, unlike Perses, does not suffer from priority inversion because it prioritizes the search primarily on the token weight of nodes being considered for removal. Moreover, unlike , it does not strictly remove one node at a time and allows the removal of nodes with the same weight and the same parent as a group. Hence, it can be considered a sweet spot in reducing test cases. We conduct two studies that can further explore this idea.

(1) Oracle Verification Time. The number of oracle queries is a common metric used in similar studies to reason about reduction efficiency since it directly impacts the total reduction time [2, 3, 6, 13, 17]. For instance, both and perform fewer oracle queries and take less time than Perses. However, the number of oracle queries is not the only factor involved. The time required to run each of these queries, or oracle verification time, also affects the total running time. For instance, as presented in Sect. 4.1, has the smallest number of oracle queries in 12 out of 14 test cases. However, in terms of total reduction time and speed, is the fastest in 8 out of 14 cases, even while performing more queries compared to in 6 of them. Oracle verification time can depend on multiple elements such as the size and complexity of the test case. Since takes advantage of the possibility to remove more than one node at a time, it may try variants of the test case that are smaller and may be faster to verify compared to . To check this hypothesis, we conducted a case study on gcc-64990 and recorded the running time of each oracle query during reduction. As shown in Tables 1 and 2, reduces this test case in 932 s with 2,632 queries, and has a total reduction time of 916 s (16 s shorter) while performing 3,148 oracle queries (516 more queries). Both techniques yield the same final test case.

Figure 7 depicts the distribution of oracle verification times in and , showing that has more queries that take longer compared to . The shorter queries in directly decrease its overall reduction time making it reduce test cases with fewer queries compared to Perses and shorter queries compared to .

Fig. 7.

Distribution of oracle verification time for and .

Fig. 8.

Distribution of token weights of nodes visited during reduction.

(2) Distribution of Token Weights. The motivation behind proposing as discussed in Sect. 3.1 was that if lists in a test case shrink after removing nodes with large unique token weights, applying DD on list elements with the same weight can be beneficial. In fact, the more of the remaining nodes that share token weights, the more beneficial using DD becomes since it provides the opportunity to remove those nodes in just one trial. This can avoid the possibly time-consuming process of visiting nodes one by one. To understand the distribution of token weights in practice, we perform (the one node at a time removal) on gcc-64990 and record token weights of nodes visited during the removal process. Figure 8 shows the distribution with 5 as the median of token weights of nodes visited during the reduction. The small median motivates the use of in practice since it indicates that half of the nodes have one of only five different token weights and can benefit from the grouped removals.

Syntactic vs Semantic Validity: Perses and discard syntactically invalid variants of the test case during reduction. However, there are also semantically invalid queries such as removing the declaration of a variable before removing its use. SGPR techniques cannot entirely avoid these queries since they guide the reduction process based on the syntax of the grammar. However, the priority order of can mitigate this problem. By prioritizing by token weight, it is more likely to visit and remove uses before spending effort on declarations. One reason for this is that a higher token weight tends to mean that there are more uses beneath that node. For instance, in Fig. 3, uses of variables a, b and c are descendants of node with nodes , and as their declarations. removes the uses by first removing while Perses tries to remove the declarations first due to priority inversion. Hence, prunes nodes in one pass of the AST that Perses may require a fixed point mode to remove.

Threats to Validity: We evaluated on the same set of C test cases used in the evaluation of Perses. The implementation of Perses’ grammar transformations and reduction is not publicly available, so we reimplemented Perses as described in its paper. Our implementation has been made available to provide a consistent platform for future work. However, the exact implementations, environmental settings and the scripts to check the property of interest can all impact the final results. For instance, the final sizes of the reduced test cases reported for the original Perses’ implementation [6] are smaller than those using our reimplemented version of Perses. As discussed in Sect. 4.1, this may be because Perses’ oracles allowed for undefined behavior, which can lead through smaller but invalid reduced test cases. To mitigate this problem, we made the oracles strictly prevent undefined behavior for both and Perses. Note that significantly outperforms both Perses’ original implementation [6] and our reimplementation in terms of number of oracle queries.

While the techniques presented in are general in ability, our evaluation focuses on C in order to compare with Perses. Further investigation is required to claim that the performance benefits extend to other languages.

6 Related Work

The closest work to this paper is Perses [6]. Unlike , it suffers from priority inversion that adversely affects the reduction speed. Other generic test case reduction techniques are Delta Debugging (DD) [2], its O(n) variant [13], and Berkeley Delta [18]. These face challenges when reducing hierarchical inputs. Several techniques focus on reducing hierarchically structured test cases [3, 4, 6, 11, 12, 19, 20]. Among these, only Perses is priority aware, in spite of its priority inversion. Indeed, most techniques process the input level by level. Like , Perses and Simp [20] are notable exceptions in that they can search across levels when deciding how to reduce. However, Simp is specific to SQL Queries. GTR [12] is notable in that it is trained when to apply different reduction operations. Finally, C-Reduce [5] is a tool for reducing C/C++ test cases that requires extensive domain-specific knowledge.

7 Conclusions

We have shown that the prior state of the art for test case reduction suffers from priority inversion and that this causes a significant increase in reduction time. We proposed priority aware reduction techniques, and , that focus reduction effort where they can have the most impact. These techniques can speed reduction by 1.3$\times$ to 7.8$\times$ over the prior state of the art.